НАЗВАНИЯ КОМПОНЕНТОВ
ДЕЙСТВИЯ СЛОЖЕНИЯ
СЛАГАЕМОЕ СЛАГАЕМОЕ СУММА
5 + 3 = 8
СУММА
ЧТОБЫ НАЙТИ НЕИЗВЕСТНОЕ СЛАГАЕМОЕ. НУЖНО ИЗ СУММЫ ВЫЧЕСТЬ ИЗВЕСТНОЕ СЛАГАЕМОЕ.
СЛОЖЕНИЕ ПРОВЕРЯЕТСЯ ВЫЧИТАНИЕМ. ЧТОБЫ ПРОВЕРИТЬ СЛОЖЕНИЕ, НУЖНО ИЗ СУММЫ ВЫЧЕСТЬ ОДНО ИЗ СЛАГАЕМЫХ. ТОГДА МЫ ПОЛУЧИМ ВТОРОЕ.
НАЗВАНИЯ КОМПОНЕНТОВ
ДЕЙСТВИЯ ВЫЧИТАНИЯ
УМЕНЬШАЕМОЕ ВЫЧИТАЕМОЕ РАЗНОСТЬ
6 – 2 = 4
РАЗНОСТЬ
- ЧТОБЫ НАЙТИ НЕИЗВЕСТНОЕ УМЕНЬШАЕМОЕ, НУЖНО К РАЗНОСТИ ПРИБАВИТЬ ВЫЧИТАЕМОЕ.
- ЧТОБЫ НАЙТИ НЕИЗВЕСТНОЕ ВЫЧИТАЕМОЕ НУЖНО ИЗ УМЕНЬШАЕМОГО ВЫЧЕСТЬ РАЗНОСТЬ.
ВЫЧИТАНИЕ ПРОВЕРЯЕТСЯ СЛОЖЕНИЕМ.
ЧТОБЫ ПРОВЕРИТЬ ВЫЧИТАНИЕ, НУЖНО К РАЗНОСТИ ПРИБАВИТЬ ВЫЧИТАЕМОЕ. ТОГДА МЫ ПОЛУЧИМ ВЫЧИТАЕМОЕ.
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
|
. |
ТОЧКА |
|
|
ПРЯМАЯ НЕ ИМЕЕТ НАЧАЛА И КОНЦА |
|
|
ЛУЧ ИМЕЕТ НАЧАЛО И КОНЕЦ. |
|
|
ОТРЕЗОК ИМЕЕТ НАЧАЛО И КОНЕЦ. |
|
|
КРУГ |
|
|
ОВАЛ |
|
|
ТРЕУГОЛЬНИК |
|
|
ПРЯМОУГОЛЬНИК – это четырехугольник, у которого все углы прямые и противоположные стороны равны. Квадрат является прямоугольником. Только у него все четыре сторон равны. |
|
|
МНОГОУГОЛЬНИКИ (шестиугольник, четырехугольник) |
ПЕРИМЕТР – ЭТО СУММА ДЛИН ВСЕХ СТОРОН ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ.
РАЗРЯДЫ ЕДИНИЦ, ДЕСЯТКОВ, СОТЕН
СУММА РАЗРЯДНЫХ СЛАГАЕМЫХ
ДЕСЯТКИ ЕДИНИЦЫ
СОТНИ ДЕСЯТКИ ЕДИНИЦЫ
АЛГОРИТМ ПИСЬМЕННОГО СЛОЖЕНИЯ
1.Пишу десятки под десятками, единицы под единицами.
2. Складываю единицы.
3. Складываю десятки.
4. Читаю ответ.
Пример:
1. Сумма чисел 45 и 23.
2. Пишу десятки под десятками, единицы под единицами.
3. Складываю единицы. 5 + 3 = 8. Пишу 8 под единицами.
4. Складываю десятки. 4 + 2 = 6. Пишу 6 под десятками.
5. Сумма равна 68.
|
|
4 |
5 |
|
|
|
2 |
3 |
|
|
|
6 |
8 |
АЛГОРИТМ ПИСЬМЕННОГО СЛОЖЕНИЯ
- Пишу десятки под десятками, а единицы под единицами.
- Вычитаю единицы.
- Вычитаю десятки.
- Читаю ответ.
Пример:
- Разность чисел 57 и 26.
- Пишу десятки под десятками, единицы под единицами.
- Вычитаю единицы: 7 – 6 = 1. Пишу 1 под единицами.
- Вычитаю десятки: 5 – 2 + 3. Пишу 3 под десятками.
- Разность равна 31.
|
|
5 |
7 |
|
|
|
2 |
6 |
|
|
|
3 |
1 |
|
УВЕЛИЧИТЬ НА…ЕДИНИЦ |
+ |
|
УМЕНЬШИТЬ НА…ЕДИНИЦ |
– |
|
НА СКОЛЬКО БОЛЬШЕ |
+ |
|
НА СКОЛЬКО МЕНЬШЕ |
СВОЙСТВА СЛОЖЕНИЯ
ОТ ПЕРЕСТАНОВКИ МЕСТ СЛАГАЕМЫХ, СУММА НЕ МЕНЯЕТСЯ.
3 + 2 = 2 + 3
СУММА РАВНА ОДНОМУ ИЗ СЛАГАЕМЫХ, ЕСЛИ ДРУГОЕ СЛАГАЕОМОЕ РАВНО 0.
3 + 0 = 3
СВОЙСТВА ВЫЧИТАНИЯ
УМЕНЬШАЕМОЕ РАВНО РАЗНОСТИ, ЕСЛИ ВЫЧИТАЕМООЕ РАВНО 0.
3 – 0 = 3
РАЗНОСТЬ РАВНА О, ЕСЛИ УМЕНЬШАЕМОЕ РАВНО ВЫЧИТАЕМОМУ.
3 – 3 = 0
ПРАВИЛА ОФОРМЛЕНИЯ
1. РЕШЕНИЕ БУКВЕННЫХ ВЫРАЖЕНИЙ.
Найди значение выражений 15 + а – 13, при а = 5, а = 10.
15 + а – 13, если а = 5, то
15 + 5 – 13 = 7
15 + а – 13, если а = 10, то
15 + 10 – 13 = 12
2.РЕШЕНИЕ УРАВНЕНИЙ (РАССУЖДЕНИЕ)
15 – х = 8
В этом уравнении неизвестное – вычитаемое. Чтобы найти неизвестное вычитаемое, нужно и уменьшаемого вычесть разность.
|
1 |
5 |
– |
х |
= |
8 |
|
|
х |
= |
1 |
5 |
– |
8 |
|
|
х |
= |
7 |
||||
|
1 |
5 |
– |
7 |
= |
8 |
|
|
8 |
= |
8 |
||||
13 + х = 20
В этом уравнение неизвестное – слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое)
|
1 |
3 |
+ |
х |
= |
2 |
0 |
|
х |
= |
2 |
0 |
– |
1 |
3 |
|
х |
= |
7 |
||||
|
1 |
3 |
+ |
7 |
= |
2 |
0 |
|
2 |
0 |
= |
2 |
0 |
||
НАЗВАНИЯ КОМПОНЕНТОВ
ДЕЙСТВИЯ УМНОЖЕНИЯ
МНОЖИТЕЛЬ МНОЖИТЕЛЬ ПРОИЗВЕДЕНИЕ
3 · 4 = 12
ПРОИЗВЕДЕНИЕ
СЛООЖЕНИЕ ОДИНАКОВЫХ СЛАГАЕМЫХ МОЖНО ЗАМЕНИТЬ УМНОЖЕНИЕМ.
Знак умножения – точка(·).
3 + 3 + 3 + 3 = 12
(по 3 взяли 4 раза)
3 · 4 = 12
От перестановки мест множителей, произведение не меняется.
2 · 3 = 6
3 · 2 = 6
2 · 3 = 3 · 2
НАЗВАНИЯ КОМПОНЕНТОВ
ДЕЙСТВИЯ УМНОЖЕНИЯ
ДЕЛИМОЕ ДЕЛИТЕЛЬ ЧАСТНОЕ
6 : 3 = 2
ЧАСТНОЕ
Чтобы найти неизвестно делимое, нужно частное умножить
на делитель.
2 · 3 = 6
Чтобы найти неизвестный
делитель, нужно делимое разделить на частное.
6 : 2 = 3
- Деление по содержанию
12 яблок разложили на тарелки, по 3 яблока на каждую тарелку. Сколько тарелок понадобилось?
Для того, чтобы решить задачу, нужно ответить на вопрос – СКОЛЬКО РАЗ В 12 СОДЕРЖИТСЯ ПО 3.
12 : 3 = 4
- Деление на равные части
12 яблок разложили на 4 тарелки поровну. Сколько яблок на каждой тарелке?
Рассуждаем:
Берем 4 яблока, раскладываем по одному яблоку на каждую тарелку. Затем берем еще 4 яблока, раскладываем еще по одному яблоку в тарелку. И берем еще 4 яблока, раскладываем опять по одному яблоку в тарелку. Таким образом, для того, чтобы решить задачу, нужно ответить на вопрос – СКОЛЬКО РАЗ В 12 СОДЕРЖИТСЯ ПО 4.
СВЯЗЬ
МЕЖДУ РЕЗУЛЬТАТОМ И
КОМПОНЕНТАМИ УМНОЖЕНИЯ
4 · 2 = 8
8 : 4 = 2
8 : 2 = 4
Если произведение двух множителей разделить на один из них, то получится другой множитель.
З А Д А Ч И И И Х В И Д Ы
2 КЛАСС
- Разбор задачи происходит по плану:
Настя собрала букет из ромашек и васильков. В букете 6 ромашек, а васильков на 3 больше. Сколько в букете васильков?
- О ком говорится в задаче? О чем говорится в задаче?
- Повтори условие задачи.
- Вопрос задачи.
- Из каких цветов делала букет Настя?
- Сколько было ромашек?
- Знаем ли мы сколько было васильков?/ Сколько было васильков. Что нам известно про васильки?
- Что нужно узнать?
По окончании разбора записывается краткая запись, делается схема или рисунок.
- В задаче всегда пишется пояснение во всех действия, кроме последнего.
- В задаче с более, чем в 1 действие, пишется выражение.
- Ответ пишется строго по вопросу задачи.
- ЗАДАЧИ НА НАХОЖДЕНИЕ СУММЫ
На полке стояло 7 синих машинок и 10 красных машинок. Сколько машинок всего стояло на полке?
I – 7 м.
? м.
II – 10 м.
1)7 + 10 = 17 (м.)
Ответ: 17 машинок всего стояло на полке.
На полке стояло 7 синих машинок, а красных на 3 больше. Сколько машинок всего стояло на полке?
I – 7 м.
? м.
II – ? м., на 3 м. >, чем
1) 7 + 3 = 10(м.) – красных
2) 7 + 10 = 17 (м.)
Ответ: 17 машинок всего стояло на полке.
7 + (7 + 10)= 17
- ЗАДАЧИ НА НАХОЖДЕНИЕ
ОСТАТКА(РАЗНОСТИ), НЕИЗВЕСТНОГО
УМЕНЬШАЕМОГО И ВЫЧИТАЕМОГО
а) нахождение остатка (разности)
На ёлке висело 28 игрушек, 7 игрушек разбилось. Сколько игрушек осталось на ёлке?
Было – 28 игр.
Разбилось – 7 игр.
Осталось – ? игр.
1)28 – 7 = 21 (игр.)
Ответ: 21 игрушка осталась на ёлке.
б) нахождение уменьшаемого
На ёлке висели игрушки, когда разбилось 7 игрушек, осталась 21. Сколько игрушек было на ёлке?
Чтобы ответить на вопрос этой задачи, нужно определить, как найти уменьшаемое.
Было – ? игр.
Разбилось – 7 игр.
Осталось – 21 игр.
1)7 + 21 = 28 (игр.)
Ответ: 28 игрушек было на ёлке.
в) нахождение вычитаемого
На ёлке висело 28 игрушек, когда несколько игрушек разбилось, осталось висеть 21 игрушка. Сколько игрушек разбилось?
Чтобы ответить на вопрос этой задачи, нужно определить, как найти неизвестное вычитаемое.
Было – 28 игр.
Разбилось – ? игр.
Осталось – 21 игр.
1) 28 – 21 = 7 (игр.)
Ответ: 7 игрушек разбилось.
ЗАДАЧИ НА НАХОЖДЕНИЕ
НЕИЗВЕСТНОГО СЛАГАЕМОГО
На стоянке стояло 7 машин. Когда несколько машин приехало, их стало 9. Сколько машин приехало?
Чтобы решить эту задачу, нужно вспомнить, как найти неизвестное слагаемое.
Было – 7 м.
Приехало – ? м.
Стало – 9 м.
1)9 – 7 = 2 (м.)
Ответ: 2 машины приехало.
ЗАДАЧИ НА НАХОЖДЕНИЕ
НЕИЗВЕСТНОГО ТРЕТЬЕГО СЛАГАЕМОГО
На складе было 8 мешков зерна: 3 мешка пшеницы, 2 мешок проса и несколько мешков овса. Сколько мешков овса было на складе?
Пшеница – 3 м.
Просо – 2 м. 8 м.
Овёс – ? м.
I способ
1) 3 + 2 = 5 (м.) – пшена и просо вместе
2) 8 – 5 = 3 (м.)
Ответ: 3 мешка овса было на складе.
II способ
1) 8 – 3 = 5 (м.) – просо и овса вместе
2) 5 – 2 = 3 (м.)
Ответ: 3 мешка овса было на складе.
ЗАДАЧИ
НА РАЗНОСТНОЕ СРАВНЕНИЕ
В саду было 8 кустов малины и 5 кусков крыжовника. На сколько больше кустов малины, чем кустов крыжовника?
Чтобы решить эту задачу надо вспомнить, с помощью какого действия можно узнать, на сколько одно число больше другого.
Малина – 8 к., на ? к. >, чем
Крыжовник – 5 к.
1) 8 – 5 = 3 (к.)
Ответ: на 3 куста малины больше, чем кустов крыжовника.
Летом засушили 4 кг грибов, а засолили 10 кг грибов. На сколько меньше грибов засушили, чем засолили?
Засушили – 4 кг, на ? кг <, чем
Засолили – 10 кг
1) 10 – 4 = 6 (кг)
Ответ: на 6 килограмм грибов меньше засолили, чем засушили.
ЗАДАЧИ
НА УВЕЛИЧЕНИЕ ИЛИ УМЕНЬШЕНИЯ ЧИСЛО НА НЕСКОЛЬКО ЕДИНИЦ
В Тихом океане 9 морей, а в Атлантическом на 3 моря меньше. Сколько морей в Атлантическом океане?
Рассуждаем так – В Атлантическом океане морей столько же, сколько и в Тихом, но без 3.
Тихий – 9 м.
Атлантический – ? м., на 3 м. <, чем
1) 9 – 3 = 6 (м.)
Ответ: 6 морей в Атлантическом океане.
Антон нашел 5 боровиков, а сыроежек на 4 больше. Сколько сыроежек нашел Антон?
Рассуждаем так – Антон нашел сыроежек столько же, сколько боровиков и еще 4.
Боровики – 5 шт.
Сыроежки – ? шт., на 4 шт. >, чем
1) 5 + 4 = 9 (шт.)
Ответ: 9 сыроежек нашел Антон.
ЗАДАЧИ С ВЕЛИЧИНАМИ
ЦЕНА, КОЛИЧЕСТВО, СТОИМОСТЬ
Толя купил 3 тетради по 10 рублей каждая. Сколько стоили все тетради.
|
Цена |
Количество |
Стоимость |
|
10 р. |
3 т. |
? р. |
Чтобы найти стоимость, нужно цену умножить на количество.
1) 10 · 3 = 30 (р.)
Ответ: 30 рублей стоили все тетради.
Толя купил 3 тетради. За всю покупку заплатил 30 рублей. Сколько рублей стоила каждая тетрадь?
|
Цена |
Количество |
Стоимость |
|
? р. |
3 т. |
30 р. |
Чтобы найти цену, нужно стоимость разделить на количество.
1) 30 : 3 = 10 (р.)
Ответ: 10 рублей стоила каждая тетрадь.
Толя на тридцать рублей купил тетрадей. Сколько тетрадей купил Толя, если одна тетрадь стоит 10 рублей.
|
Цена |
Количество |
Стоимость |
|
10 р. |
? т. |
30 р. |
Чтобы найти количество, нужно стоимость разделить на цену.
1) 30 : 10 = 3 (т.)
Ответ: 3 тетради купил Толя.
ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА
В НЕСКОЛЬКО РАЗ
У Васи 3 Машинки, а у Коли в 3 раза больше, чем у Васи. Сколько машинок у Коли?
(по 2 берем 3 раза)
? м.
2 м.
? м.
- 2 · 3 = 6 (м.)
Ответ: 6 машинок у Коли.
Если в задаче говорится,
что число больше в несколько раз,
то задача решается умножением.
ЗАДАЧИ НА УМЕНЬШЕНИЕ ЧИСЛА
В НЕСКОЛЬКО РАЗ
В пруду плавало 9 уток, а гусей в 3 раза меньше. Сколько уток плавало в пруду?
(делим на три равные части;
узнаем сколько предметов в одной части)
- 9 : 3 = 3 (пт.)
Ответ: 3 утки плавало в пруду.
Если в задаче говорится,
что число меньше в несколько раз,
то задача решается делением.
|
УВЕЛИЧИТЬ В…ЕДИНИЦ |
· |
|
УМЕНЬШИТЬ В…ЕДИНИЦ |
: |
|
УВЕЛИЧИТЬ НА…ЕДИНИЦ |
+ |
|
УМЕНЬШИТЬ НА…ЕДИНИЦ |
– |
з класс
ПЛОЩАДЬ. ЕДИНИЦЫ ПЛОЩАДИ.
Квадрат, сторона которого 1 см, – это единица площади – квадратный сантиметр.
1 см2
1 дм2 = 100 см2
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
а а
b
S = a · b
ЗАДАЧИ
НА ПРИВЕДЕНИЕ К ЕДИНИЦЕ
На 2 окнах 8 комнатных растений. Сколько комнатных растений на 3 окнах?
?р.
8р.
?р.
- 8 : 2 = 4 (р.) – на одном окне
- 4 · 3 = 9 (р.)
Ответ: 9 комнатных растений на 3 окнах.
Привести к единице нам помогает деление.
ПРИМЕРЫ
СХЕМАТИЧЕСКИХ ЧЕРТЕЖЕЙ
ДЛЯ РАЗНЫХ ТИПОВ ЗАДАЧ
- Задачи на нахождение уменьшаемого, вычитаемого, остатка.
Пример (простая задача на нахождение остатка).
В вазе было 10 яблок. 8 яблок съели. Сколько яблок осталость?
8 яб.
? яб.
10 яб.
Пример (составная задача на нахождение остатка).
В книге 48 страниц. Даша читала книгу в течение трёх дней, по 9 страниц ежедневно. Сколько страниц ей осталось прочитать?
? стр.
?стр.
9 стр.
48 стр.
Аналогично составляются
схемы для обратных задач.
- Задачи на разностное сравнение.
Прмиер.
Высота дома 16 м, а сарая 4 м. На сколько дом выше, чем сарай?
?м.
16 м
4 м
Памятки по математике для учащихся 1-4 классов
|
2 +3 = 5 2 – первое слагаемое 3 – второе слагаемое 5 – значение суммы (2 + 3) – сумма |
6 – 2 = 4 6 – уменьшаемое 2 – вычитаемое 4 – значение разности (6 – 2) – разность |
ПОДСКАЗКИ (в условии задачи) на … больше + на … меньше – в … раз больше × в … раз меньше : |
|
8 × 2 =16 8 – первый множитель 2 – второй множитель 16 – значение произведения (8 × 2) – произведение |
18: 2 = 9 18 – делимое 2 – делитель 9 – значение частного (18: 2) – частное |
ВОПРОСЫ Во ? раз больше : Во ? раз меньше : На ? больше – На ? меньше – |
|
ЕДИНИЦЫ МАССЫ 1т = 1000кг 1т = 10ц 1ц = 100 кг 1кг = 1000г |
ЕДИНИЦЫ ДЛИНЫ 1км = 1000м 1дм = 10см 1м = 10дм 1дм = 100мм 1м = 100см 1 см = 10мм 1м = 1000мм |
|
|
ЕДИНИЦЫ ВРЕМЕНИ 1век = 100 лет 1неделя = 7 суток 1год = 12 месяцев 1сутки = 24 часа 1год = 52 недели 1час = 60 минут 1 год = 365 или 366 суток 1минута = 60 секунд 1 месяц = 30 или 31 сутки (февраль 28 или 29 дней) |
||
|
ЕДИНИЦЫ ПЛОЩАДИ 1см2 = 100мм2 1м2 = 100дм2 1км2 = 1.000.000м 2 1дм2 = 100см2 1м2 = 10.000см 2 |
||
|
ПЕРИМЕТР (сумма длин сторон) Р▀ = а + в + а + в Р■ = а + а + а + а Р▲ = а + в + с Р▀ = (а + в) × 2 Р■ = а × 4 а – сторона треугольника Р▀ = (а × 2) + (в × 2) а – сторона квадрата в – сторона треугольника а – длина прямоугольника с – сторона треугольника в – ширина прямоугольника Р измеряется в км, м, дм, см, мм |
||
|
ПЛОЩАДЬ S▀ = а × в S■ = а × а а – длина прямоугольника а – сторона квадрата в – ширина прямоугольника S измеряется в км2, м2, дм2, см2, мм2 |
||
|
S – расстояние (км) S = V × t V – скорость (км/ч) V = S : t t – время (ч) t = S : V |
||
|
Ст – стоимость Ст = Ц × К Ц – цена Ц = Ст : К К – количество К = Ст : К 1 рубль = 100копеек |
Математика
Компоненты арифметических действий и их взаимосвязь.
-
Компоненты при сложении:
1слагаемое, 2слагаемое, сумма.
-
Компоненты при вычитании:
уменьшаемое, вычитаемое, разность.
-
Компоненты при умножении:
1 множитель, 2множитель, произведение.
-
Компоненты при делении:
делимое, делитель , частное.
-
Назвать результаты всех действий:
при сложении – сумма
при вычитании – разность
при умножении – произведение
при делении – частное
-
Как найти неизвестное слагаемое?
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Х+4=12 или 4+х=12
Х=12-4 х=12-4
Х=8 х=8____
8+4=12 4+8=12
12=12 12=12
-
Как найти неизвестное уменьшаемое?
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Х-7=3
Х=3+7
Х=10
10-7=3
3=3
-
Как найти неизвестное вычитаемое?
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
8-х =5
х=8-5
х=3
8-3=5
5=5
9 Как найти неизвестный множитель?
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х·3=6 4·х=8
х=6:3 х=8:4
х=2 х=2
2·3=6 4·2=8
6=6 8=8
10 Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
х:5=3
х=3·5
х=15
15:5=3
3=3
-
Как найти неизвестный делитель?
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
6:х=2
х =6:2
х=3
6:3=2
2=2
Геометрический материал.
-
Что такое квадрат?
Квадрат – это прямоугольник, у которого все стороны равны.
-
Что такое прямоугольник?
Прямоугольник – это четырёхугольник, у которого все углы прямые. Противоположные стороны прямоугольника равны.
-
Что такое треугольник?
Треугольник – многоугольник, у которого три угла и три стороны.
15 Что такое четырёхугольник?
Четырёхугольник – геометрическая фигура, у которой четыре угла и четыре стороны.
-
Что такое периметр?
Периметр ( Ρ) – это сумма длин сторон какой-нибудь геометрической фигуры.
-
Что такое площадь?
Площадь (S) – это внутренняя часть какой-нибудь геометрической фигуры
(прямоугольника, квадрата и т.д)
-
Как найти периметр квадрата?
У квадрата 4 стороны, равные между собой. Чтобы найти периметр (Р) квадрата, нужно длину одной стороны (а) умножить на 4.
Р□ = a · 4
-
Как найти периметр прямоугольника?
Чтобы найти периметр прямоугольника, нужно сложить все 4 стороны прямоугольника
Или
сложить длину и ширину прямоугольника и умножить на 2.
Ρ=a+b+a+b
или
Ρ=(a+b)·2
-
Как найти периметр треугольника?
Чтобы найти периметр треугольника, нужно сложить все 3 стороны.
-
Как найти сторону квадрата, если известен периметр?
У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.
a=Ρ:4
-
Как найти сторону прямоугольника, если известен периметр и другая сторона?
Чтобы найти сторону прямоугольника, нужно
Ρ разделить на 2 и вычесть другую сторону.
a=Ρ:2 – b
b=Ρ:2 – a
22 В каких единицах измеряется периметр?
Периметр измеряется в мм, см, дм, метрах.
23 Как найти площадь квадрата?
Площадь квадрата равна произведению двух его сторон.
S□ = a · a
24 Как найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, надо длину прямоугольника умножить на его ширину.
S = a · b
25 Как найти сторону прямоугольника, если известна площадь и другая его сторона?
Чтобы найти одну из сторон прямоугольника, нужно площадь прямоугольника разделить на известную сторону.
a=S : b
b= S : a
26 В каких единицах измеряется площадь?
Площадь измеряется в квадратных единицах: мм², см², дм², м².
27 Назвать единицы длины.
Единицы длины – мм, см, дм, м, км.
28 Рассказать таблицу мер длины.
1см = 10мм
1дм = 10см
1дм = 100мм
1м = 10 дм
1м = 100 см
1км = 1000м
29 Сколько квадратных сантиметров
в 1квадратном метре?
1м² = 10 000см²
30 Сколько квадратных дециметров
в 1 квадратном метре?
1м² = 100дм²
31 Рассказать таблицу мер площади.
1м² = 100дм² = 10 000см²
1дм² = 100см² = 10 000мм²
1см² = 100мм²
Масса.
32 Назвать единицы массы.
Масса измеряется в граммах, килограммах, центнерах, тоннах.
33 Рассказать таблицу мер массы.
1кг = 1000г
1ц = 100кг
1т = 10ц
1т = 1000кг
Время.
34 Назвать единицы измерения времени.
Время измеряется секундами, минутами, часами, сутками, неделями, месяцами, годами, веками.
35 Рассказать таблицу мер времени.
1мин = 60сек.
1час = 60мин
1час = 3600сек.
1сут. = 24часа
1год = 12мес. = 365сут. или 366сут.
1век = 100лет
Взаимосвязь скорости, времени и расстояния.
36 Как найти скорость?
Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.
v = S : t
37 Как найти время?
Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость ( v ).
t = S : v
38 Как найти расстояние?
Чтобы найти расстояние ( S ), нужно скорость ( v ) умножить на время ( t ).
S = v · t
Взаимосвязь цены, количества, стоимости.
39 Что такое цена?
Цена – стоимость одного предмета, единицы товара.
40 Как найти стоимость?
Чтобы найти стоимость, нужно цену умножить на количество.
Ст = Ц · К
41 Как найти цену?
Чтобы найти цену, нужно стоимость разделить на количество.
Ц = Ст : К
42 Как найти количество?
Чтобы найти количество, нужно стоимость разделить на цену.
К = Ст : Ц
43 Задачи на дроби.
Дробь – ⅔
2 – числитель
3 – знаменатель
44 Как найти дробь числа?
Чтобы найти дробь числа, нужно число разделить на знаменатель, а потом умножить на числитель.
45 Как найти число по дроби?
Чтобы найти число по дроби, нужно число разделить на числитель и умножить на знаменатель.
Взаимосвязь работы, времени и производительности.
46 Что такое производительность?
Как найти производительность?
Производительностью ( v ) называют работу, выполненную за единицу времени.
Чтобы найти производительность ( v ), надо всю выполненную работу разделить на время.
v = A : t
47 Как найти выполненную работу?
Выполненная работа равна производительности, умноженной на время работы.
A = v · t
48 Как найти время работы?
Чтобы узнать время работы, надо работу разделить на производительность.
t = A : v
49 Как найти среднее арифметическое?
Чтобы найти среднее арифметическое надо сумму разделить на число слагаемых.
ПАМЯТКА «КАК РЕШАТЬ ЗАДАЧИ»
1. Прочитай задачу и представь себе то, о чем в ней говорится.
2. Выдели условие и вопрос.
3. Запиши условие кратко или выполни чертёж.
4. Подумай можно ли сразу ответить на вопрос задачи. Если нет, то почему. Что надо узнать сначала, что потом?
5. Составь план решения.
6. Выполни решение.
7. Проверь решение и запиши ответ задачи.
Примерный план ответа-рассуждения ученика при решении задачи:
Анализ задачи.
1. Известно, что … (расскажи условие задачи)
2. Надо узнать… (повтори вопрос)
3. Чтобы ответить на вопрос задачи, надо …
4. Сразу мы не можем ответить на вопрос задачи, так как не знаем…
5. Поэтому в первом действии мы узнаем …
6. Во втором действии мы ответим на вопрос задачи. Для этого … ( какое действие выполняем)
7. Ответ …















КАК УЧИТЬ ТЕОРЕМУ.
-
ПРОЧИТАЙ ТЕОРЕМУ – ПОЛОЖЕНИЕ, ТРЕБУЮЩЕЕ ДОКАЗАТЕЛЬСТВА.
-
ВЫДЕЛИ УСЛОВИЕ ( что дано) И ЗАКЛЮЧЕНИЕ (что надо доказывать).
-
ВЫУЧИ ФОРМУЛИРОВКУ ТЕОРЕМЫ.
-
ЗАПИШИ УСЛОВИЕ И ЗАКЛЮЧЕНИЕ ТЕОРЕМЫ УСЛОВНЫМИ ЗНАКАМИ.
-
РАССМОТРИ ЧЕРТЕЖИ В КНИГЕ.
-
ЧИТАЙ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПО КНИГЕ, ОБОСНОВЫВАЯ КАЖДЫЙ ПУНКТ ТЕОРЕМАМИ, АКСИОМАМИ, С ОПРЕДЕЛЕНИЯМИ, ИЗУЧЕННЫМИ РАННЕЕ, СЛЕДИ ПО ЧЕРТЕЖУ В КНИГЕ.
-
ПОВТОРИ ДОКАЗАТЕЛЬСТВО ЕЩЁ РАЗ.
-
ЗАКРОЙ КНИГУ, СДЕЛАЙ СВОЙ ЧЕРТЁЖ, А ЕСЛИ ТЕОРЕМА НА СТЕРЕОМЕТРИЧЕСКИЙ МАТЕРИАЛ, СДЕЛАЙ ПРОСТЕЙШУЮ МОДЕЛЬ.
-
ДОКАЖИ ТЕОРЕМУ САМОСТОЯТЕЛЬНО.
-
ПРОВЕРЬ СЕБЯ, ПРОЧИТАВ ЕЩЁ РАЗ ПО КНИГЕ.
-
ПОПРОБУЙ НАЙТИ ДРУГИЕ СПОСОБЫ ДОКАЗАТЕЛЬСТВ.
КАК РЕШИТЬ ЗАДАЧУ ПО МАТЕМАТИКЕ.
-
ПРОЧИТАЙ ВНИМАТЕЛЬНО УСЛОВИЕ ЗАДАЧИ.
-
ЕЩЁ РАЗ ПРОЧИТАЙ УСЛОВИЕ ЗАДАЧИ И ОБРАТИ ВНИМАНИЕ НА ГЛАВНЫЙ ВОПРОС.
-
ЕСЛИ НУЖНО-СДЕЛАЙ ЧЕРТЕЖ.
-
ПОДУМАЙ, ЧТО НУЖНО ЗНАТЬ, ЧТОБЫ ОТВЕТИТЬ НА ВОПРОС ЗАДАЧИ.
-
ОБРАТИ ВНИМАНИЕ НА ТО,ЧТО ИЗВЕСТНО В ЗАДАЧЕ.
-
РАЗБЕЙ ЗАДАЧУ НА ЧАСТИ,ПОСТАВЬ К КАЖДОЙ ЧАСТИ ВОПРОС, ОПРЕДЕЛИ ПОСЛЕДОВАТЕЛЬНОСТЬ ИХ РЕШЕНИЯ.
-
РЕШИ КАЖДУЮ ПРОСТУЮ ЗАДАЧУ.
-
НАЙДИ РАЦИОНАЛЬНОЕ РЕШЕНИЕ ВСЕЙ ЗАДАЧИ.
-
ЗАПИШИ ПОЛНЫЙ ОТВЕТ.
КАК РЕШИТЬ ЗАДАЧУ ПО АЛГЕБРЕ.
-
ПРОЧИТАЙ ВНИМАТЕЛЬНО УСЛОВИЕ ЗАДАЧИ.
-
ЕЩЁ РАЗ ПРОЧИТАЙ УСЛОВИЕ ЗАДАЧИ И ОБРАТИ ВНИМАНИЕ НА ГЛАВНЫЙ ВОПРОС ЗАДАЧИ.
-
СДЕЛАЙ ЧЕРТЕЖ.
-
ВЫБЕРИ НЕИЗВЕСТНОЕ И ОБОЗНАЧЬ ЕГО БУКВОЙ.
-
УВЯЖИ ДАННЫЕ ЗАДАЧИ С ВЫБРАННЫМ НЕИЗВЕСТНЫМ,Т.Е. ДАЙ ОБЪЯСНЕНИЕ РЕШЕНИЯ ЗАДАЧИ.
-
ОБРАТИ ВНИМАНИЕ НА ОБОСНОВАНИЕ ЗАПИСИ УРАВНЕНИЯ.
-
ВНИМАТЕЛЬНО РЕШИ УРАВНЕНИЕ И ОТБРОСЬ КОРНИ, КОТОРЫЕ НЕ УДОВЛЕТВОРЯЮТ УСЛОВИЮ ЗАДАЧИ.
-
СДЕЛАЙ ПРОВЕРКУ ПО УСЛОВИЮ ЗАДАЧИ, А НЕ УРАВНЕНИЯ.
-
ЗАПИШИ ПОЛНЫЙ ОТВЕТ.
-
ОБРАТИ ВНИМАНИЕ , НЕЛЬЗЯ ЛИ ЗАДАЧУ РЕШИТЬ БОЛЕЕ РАЦИОНАЛЬНО.
УЧИСЬ ВСЕГДА КОНТРОЛИРОВАТЬ СВОЮ РАБОТУ.
-
СТАРАЙСЯ ВСЕГДА САМ ИСПРАВИТЬ СВОИ ОШИБКИ.
-
ЛУЧШАЯ ПРОВЕРКА УСОВЕНИЯ МАТЕРИАЛА – ПЕРЕСКАЗ ЕГО СВОЕМУ ТОВАРИЩУ.
-
КАК МОЖНО БОЛЬШЕ И ЧАЩЕ ПЕРЕДАВАЙ СВОИ ЗНАНИЯ ДРУГИМ:
А) ЭТО БЛАГОРОДНО;
Б) ЭТО СДЕЛАЕТ ТВОИ ЗНАНИЯ БОЛЕЕ СОЗНАТЕЛЬНЫМИ И ПРОЧНЫМИ.
КАК ВЫПОЛНИТЬ И ОФОРМИТЬ ЛАБОРАТОРНУЮ РАБОТУ.
-
ЗАПИШИ НАИМЕНОВАНИЕ РАБОТЫ.
-
СФОРМУЛИРУЙ ЦЕЛЬ РАБОТЫ.
-
СОСТАВЬ ПЕРЕЧЕНЬ ОБОРУДОВАНИЯ,НЕОБХОДИМОГО ДЛЯ ЕЁ ПРОВЕДЕНИЯ.
-
КРАТКО ИЗЛОЖИ ТЕОРИЮ ДАННОЙ РАБОТЫ.
-
СДЕЛАЙ ЧЕРТЕЖИ (схему) В РАБОТЕ.
-
НАЧЕРТИ ТАБЛИЦУ И ВНЕСИ В НЕЁ НЕОБХОДИМЫЕ ПОКАЗАНИЯ ПРИБОРОВ.
-
ВЫЧЕСЛИ ИСКОМУЮ ВЕЛИЧИНУ ПО РЕЗУЛЬТАТАМ ИЗМЕРЕНИЙ.
-
СДЕЛАЙ ВЫВОД.
КАК НАУЧИТЬСЯ МЫСЛИТЬ.
МЫШЛЕНИЕ – ПРОЦЕСС ПОЗНАНИЯ ОБЩИХ И СУЩСТВЕННЫХ СВОЙСТВ ПРЕДМЕТОВ И ЯВЛЕНИЙ, ПОЗНАНИЯ СВЯЗЕЙ И ОТНОШЕНИЙ, СУЩЕСТВУЮЩИХ МЕЖДУ НИМИ.
-
НЕОБХОДИМО ВСЕГДА УСТАНАВЛИВАТЬ ПРЧИННО-СЛЕДСТВЕННЫЕ СВЯЗИ МЕЖДУ СОБЫТИЯМИ И ЯВЛЕНИЯМИ.
-
ВЫ ВСЕГДА ДОЛЖНЫ УМЕТЬ ОТВЕТИТЬ НА ВОПОС «ПОЧЕМУ?».
-
НИКОГДА НЕ РАССТАВАЙТЕСЬ С ВОПРОСОМ « ПОЧЕМУ?». БУДЬТЕ ВСЕГДА « ПОЧЕМУЧКАМИ». ИЩИТЕ, СПРАШИВАЙТЕ, ДОХОДИТЕ ДО СУТИ ЯВЛЕНИЯ.
-
ВСЕГДА СРАВНИВАЙТЕ, СОПОСТОВЛЯЙТЕ. ЭТО ПОЗВОЛЯЕТ УГЛУБИТЬ ЗНАНИЯ, УВИДЕТЬ СУЩЕСТВЕННОЕ В ЯВЛЕНИЯХ, ВЕЩАХ.
-
НЕОБХОДИМО РАССМАТРИВАТЬ ВСЕ ВЕЩИ И ЯВЛЕНИЯ В РАЗВИТИИ, Т.Е. СЛЕДИТЬ , КАК ОНИ ЗАРОДИЛИСЬ, ЧЕМ СТАЛИ И КУДА СТРЕМЯТСЯ.
-
ОЧЕНЬ ПЛОХО, ЕСЛИ УЧЕНИК ЗАУЧИТ ЧУЖИЕ СЛОВА И МЫСЛИ И СТАНЕТ ИХ ВОСПРОИЗВОДИТЬ, ПОДОБНО ПОПУГАЮ.
УЧИСЬ РАЦИОНАЛЬНО ОРГАНИЗОВЫВАТЬ СВОЮ РАБОТУ.
-
НАЧИНАЙ РАБОТУ ОТДОХНУВШИМ. ЛУЧШЕ ВСЕГО ОБЕСПЕЧИВАЕТ ОТДЫХ СОН ИЛИ 1,5 -2 – ЧАСОВОЕ ПРЕБЫВАНИЕ НА СВЕЖЕМ ВОЗДУХЕ ( игры, прогулки, спорт). НО НЕ БОЛЬШЕ , ИНАЧЕ ОПЯТЬ УСТАНЕШЬ.
-
ПРЕЖДЕ ЧЕМ НАЧИНАТЬ РАБОТУ, ДАЙ СЕБЕ ОТЧЁТ, ЧТО ТЫ ДОЛЖЕН СДЕЛАТЬ, СКОЛЬКО ЭТО ДОЛЖНО ЗАНЯТЬ ВРЕМЕНИ, НАМЕТИТЬ ПОРЯДОК РАБОТЫ.
-
НАМЕЧАЯ ГРАФИ К РАБОТЫ , ПОМНИ, ЧТО НАИБОЛЕЕ ВЫСОКАЯ ПРОИЗВОДИТЕЛЬНОСТЬ ТРУДА НАСТУПАЕТ ЧЕРЕЗ 20-30 МИНУТ ПОСЛЕ НАЧАЛА РАБОТЫ. БОЛЕЕ СЛОЖНУЮ РАБОТУ ЦЕЛЕСООБРАЗНО ВЫПОЛНЯТЬ ИМЕННО В ЭТО ВРЕМЯ.
-
ПРИГОТОВЬ, ЧТО ПОНАДОБИТЬСЯ ДЛЯ РАБОТЫ.
-
СТАРАЙСЯ В ПОЦЕССЕ РАБОТЫ ПРИДЕРЖИВАТЬСЯ НАМЕЧЕННОГО ГРАФИКА.
-
1-й час МОЖНО РАБОТАТЬ БЕЗ ПЕРЕРЫВА. В ПОЛСЕДУЮЩЕЕ ВРЕМЯ ДОЛЖНЫ БЫТЬ ПЕРЕРЫВЫ ( 5-10 мин.) ЧЕРЕЗ 40-50 МИНУТ НАПРЯЖЕННОЙ РАБОТЫ. НЕ ДЕЛАЙ ОТДЫХ ПРОДОЛЖИТЕЛЬНЫМ, ЭТО МОЖЕТ СНИЗИТЬ РАБОТОСПОСОБНОСТЬ.
-
ВЫПОЛНЕННОЕ ЗАДАНИЕ УБЕРИ СО СТОЛА, ЧТОБЫ ОНО НЕ МЕШАЛО.
-
ЕСЛИ КАКОЕ-ЛИБО ИЗ ЗАДАНИЙ НЕ МОЖЕШЬ ВЫПОЛНИТЬ СРАЗУ, НЕ РАССТРАИВАЙСЯ, ОТЛОЖИ ЕГО, ПОПЫТАЙСЯ СДЕЛАТЬ ЕГО ЧЕРЕЗ НЕКОТОРОЕ ВРЕМЯ.
КАК СТАТЬ ВНИМАТЕЛЬНЫМ.
-
НАЧИНАЯ ЛЮБУЮ РАБОТУ, ЯСНО ПРЕДСТАВЬ СЕБЕ ЦЕЛЬ РАБОТЫ, А ТАКЖЕ ПУТИ И СРЕДСТВА. ПРИ ПОМОЩИ КОТОРЫХ БУДЕТЕ ДОБИВАТЬСЯ НАМЕЧЕННОЙ ЦЕЛИ.
-
ВНИМАНИЕ БЫВАЕТ ПРОИЗВОЛЬНОЕ (когда вы заставляете себя быть внимательным) И НЕПРОИЗВОЛЬНОЕ ( поддерживается без всяких усилий с вашей стороны).ВАМ НЕОБХОДИМО ПРИЛОЖИТЬ ВОЛЕВОЕ УСИЛИЕ, ЧТОБЫ РАЗВИВАТЬ ПРОИЗВОЛЬНОЕ ВНИМАНИЕ.
-
ЧТОБЫ НАУЧИТЬСЯ СОСРЕДОТОЧИТЬСЯ, НУЖНО ВСЕ ПОЛУЧАЕМЫЕ ЗНАНИЯ СВЯЗЫВАТЬ В ЦЕПОЧКИ.
-
УСТОЙЧИВОСТИ ВНИМАНИЯ ПОМОГУТ РАЗЛИЧНОГО РОДА ЗАПИСИ В ТЕТРАДИ, ПЛАНЫ, КОНСПЕКТЫ, СХЕМЫ и т.д.. УЖЕ САМО ВЕДЕНИЕ ЗАПИСЕЙ ЗАСТАВЛЯЕТ БЫТЬ ВНИМАТЕЛЬНЫМ ,т. к. ОБЯЗЫВАЕТ СЛЕДИТЬ ЗА МЫСЛЬЮ, РАЗВИВАЕМОЙ УЧИТЕЛЕМ.
-
НАУЧИТЕСЬ СОЗДАВАТЬ ВОКРУГ СЕБЯ НАИЛУЧШИЕ УСЛОВИЯ ДЛЯ ОБОСТРЕНИЯ ВНИМАНИЯ. ДЛЯ ЭТОГО УБЕРИТЕ ВСЕ, ЧТО МОЖЕТ ОТВЛЕЧЬ ОТ РАБОТЫ.
-
УСТОЙЧИВОСТЬ ВНИМАНИЯ ВО МНОГОМ ЗАВИСИТ ОТ ВАШЕГО НАСТРОЕНИЯ И ИНТЕРЕСА К УЧЕНИЮ. БЕЗ ИНТЕРЕСА УЧИТЬСЯ ТРУДНО.
-
НАУЧИТЕСЬ ПЕРЕКЛЮЧАТЬ ВНИМАНИЕ С ОДНОГО ОБЪЕКТА НА ДРУГОЙ И РАСПРЕДЕЛЯТЬ ЕГО МЕЖДУ НЕСКОЛЬКИМИ ОБЪЕКТАМИ ( это требование жизни) ДЛЯ ЭТОГО ПОПРОБУЙТЕ ПИСАТЬ ЧИСЛА ОТ 1 ДО 20 И ОДНОВРЕМЕННО НАЗЫВАТЬ ИХ В ОБРАТНОМ ПОРЯДКЕ. ТМП РАБОТЫ ЗАМЕДЛЯЕТСЯ, НО ПОДОБНЫЕ УПРАЖНЕНИЯ ПОМОГУТ НАУЧИТЬСЯ ПЕРЕКЛЮЧАТЬ ВНИМАНИЕ.
КАК ГОТОВИТЬ ДОМАШНЕЕ ЗАДАНИЕ.
-
ПЕРВОЕ УСЛОВИЕ ХОРОШЕЙ ПОДГОТОВКИ ДОМАШНЕГО ЗАДАНИЯ – ЭТО ВНИМАТЕЛЬНОСТЬ, АКТИВНАЯ И СОЗНАТЕЛЬНАЯ РАБОТА НА УРОКЕ. ПОЛУЧАЯ ДОМАШНЕЕ ЗАДАНИЕ, ТВЁРДО УЯСНИТЕ НЕ ТОЛЬКО ТО, ЧТО НАДО СДЕЛАТЬ ПО СОДЕРЖАНИЮ УРОКА, НО И КАК ВЫПОЛНИТЬ ЗАДАНИЕ , КАКИМИ ПРИЁМАМИ.
-
ПРИУЧИТЕ СЕБЯ ВЫПОЛНЯТЬ УРОКИ В ТОЧНО УСТАНОВЛЕННОЕ ВРЕМЯ В УДОБНОМ ДЛЯ СЕБЯ РАСПОРЯДКЕ. ЧЕРЕДУЙТЕ ТРУДНЫЕ ПРЕДМЕТЫ С БОЛЕЕ ЛЁГКИМИ. УСТНЫЙ МАТЕРИАЛ ПОВТОРЯЙТЕ ПЕРЕД ВЫПОЛНЕНИЕМ ПИСЬМЕННЫХ ПРЕДЛОЖЕНИЙ.
-
ЕСЛИ НА УРОКЕ НЕ ИЗУЧАЛСЯ ТРУДНЫЙ МАТЕРИАЛ, ТО В ЭТОТ ДЕНЬ ЕГО ДОМА НУЖНО ЗАКРЕПИТЬ , ВЫПОЛНИТЬ УПРАЖНЕНИЕ К ЭТОЙ ТЕМЕ.
-
ЕСЛИ ВАМ НАДО ИЗУЧИТЬ БОЛЬШОЙ ПО ОБЪЁМУ МАТЕРИАЛ, РАСПРЕДЕЛИТЕ ЕГО НА ЧАСТИ И ГЛАВНОЕ, СНАЧАЛА ПОЙМИТЕ МАТЕРИАЛ, А ПОТОМ УЖЕ СТАРАЙТЕСЬ ЕГО ЗАПОМНИТЬ.
-
ПОСЛЕ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ ПРОВЕРЬ СВОИ ЗНАНИЯ И СВОЕВРЕМЕННО ИСПРАВЬ СВОИ ОШИБКИ. НЕ ДУМАЙТЕ, ЧТО ИСПРАВИВ ОШИБКУ ВЫ ОТ НЕЁ ИЗБАВИЛИСЬ НАВСЕГДА. ГЛАВНОЕ НЕ В ИСПРАВЛЕНИИ ОШИБКИ , А В УСТРАНЕНИИ ПРИЧИН, ЕЁ ПОРОДИВШИХ.
КАК РЕШИТЬ ЗАДАЧУ ПО ГЕОМЕТРИИ.
-
ПРОЧИТАЙ ВНИМАТЕЛЬНО УСЛОВИЕ ЗАДАЧИ.
-
ЧИТАЯ УСЛОВИЕ ЗАДАЧИ ВТОРОЙ РАЗ, УСТАНОВИ ЗАВИСИМОСТЬ МЕЖДУ ЧИСЛОВЫМИ ДАННЫМИ.
-
СДЕЛАЙ ЧЕРТЁЖ СООТВЕТСТВЕННО ЧИСЛОВЫМ ДАННЫМ ЗАДАЧИ.
-
ЗАПИШИ СПРАВА ОТ ЧЕРТЕЖА УСЛОВИЕ ЗАДАЧИ.
-
НАЙДИ НА ЧЕРТЕЖЕ ФИГУРУ (если надо, выполни дополнительное построение).
-
ПОДУМАЙ, ЧТО НАДО УЗНАТЬ ДЛЯ ЕГО НАХОЖДЕНИЯ.
-
ПОЛЬЗУЯСЬ УСЛОВИЕМ ЗАДАЧИ, ЧЕРТЕЖОМ И РАННЕЕ ИЗУЧЕННЫМ МАТЕРИАЛОМ, НАЙДИ НЕОБХОДИМЫЕ ЭЛЕМЕНТЫ.
-
КОГДА У ТЕБЯ ЕСТЬ ОБЩИЙ ПЛАН РЕШЕНИЯ ЗАДАЧИ, ЗАПИШИ ЕГО.
-
КАЖДОЕ ДЕЙСТВИЕ СОПРОВОЖДАЙ КРАТКИМИ ОБЪЯСНЕНИЯМИ.
-
ПРОМЕЖУТОЧНЫХ НАИМЕНОВАНИЙ НЕ ПИШИ.
-
ПОСМОТРИ, УДОВЛЕТВОРЯЕТ ЛИ НАЙДЕННОЕ РЕШЕНИЕ УСЛОВИЮ ЗАДАЧИ И ЧЕРТЕЖУ.
-
ВЫПИШИ ОТВЕТ ЗАДАЧИ.
-
ПОДУМАЙ, МОЖНО ЛИ РЕШИТЬ ЗАДАЧУ ДРУГИМ СПОСОБОМ.
-
РЕШАЙ ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НАЧИНАЯ С ГЛАВНОГО ВОПРОСА ( методом синтеза).
КАК РАБОТАТЬ С КНИГОЙ.
-
СНАЧАЛО БЕГЛО ПРОСМОТРИ СОДЕРЖАНИЕ ВСЕЙ КНИГИ ( статьи, монографии).ДАЙ СЕБЕ ОТЧЕТ, НАСКОЛЬКО ЭТОТ МАТЕРИАЛ ТЕБЕ НУЖЕН. НА КАКИЕ ВОПРОСЫ ОН МОЖЕТ ТЕБЕ ОТВЕТИТЬ.
-
ПРИСТУПАЙ К ВДУМЧИВОМУ СПЛОШНОМУ ЧТЕНИЮ.
-
ПРИ ЧТЕНИИ :
а) ОТМЕЧАЙ ОСНОВНЫЕ ИДЕИ (мысленно или карандашом);
б) СЛЕДИ, КАК ОНИ РАЗВИВАЮТСЯ (НЕТ ЛИ СВОЕГО МАТЕРИАЛА ДЛЯ ПОДТВЕРЖДЕНИЯ ИЛИ, НАОБОРОТ, ОПРОВЕРЖЕНИЯ ИХ, ПОПЫТАЙТЕСЬ ИХ СОПОСТАВИТЬ С ТЕМИ ЗНАНИЯМИ, КОТОРЫЕ У ТЕБЯ ЕСТЬ).
в) ЭТИ «СМЫСЛОВЫЕ ЕДИНИЦЫ», «ОПОРНЫЕ ПУНКТЫ» МОЖЕШЬ ПРОНУМЕРОВАТЬ (потом вписать);
г) ДАЙ СЕБЕ ОТЧЁТ О СВЯЗИ МЕЖДУ ЭТИМИ «ЕДИНИЦАМИ», ВЫДЕЛИ ГЛАВНЫЕ ИЗ НИХ, ВТОРОСТЕПЕННЫЕ, УЯСНИ ИХ ПОЛСЕДОВАТЕЛЬНОСТЬ, РЕШИ НАСКОЛЬКО ОНА УДАЧНА;
д) ДАЙ ОТЧЁТ В ОСНОВНОЙ, ВЕДУЩЕЙ ИДЕЕ РАБОТЫ.ВЫРАЗИ СВОЕ ОТНОШЕНИЕ К НЕЙ.
4. ПРИ СЛОЖНОМ МАТРИАЛЕ НУЖНО ЕЩЁ РАЗ ВЕРНУТЬСЯ К ВТОРИЧНОМУ ПРОСМОТРУ НАИБОЛЕЕ ТРУДНЫХ МЕСТ, ВЫКЛАДОК, ДОКАЗАТЕЛЬСТВ. ЦЕЛЕСООБРАЗНО ПРОДЕЛАТЬ ИХ САМОМУ НА БУМАГЕ.
5. ДЛЯ САМОКОНТРОЛЯ ПРАВИЛЬНОСТИ ПОНИМАНИЯ УСВОЕННЫХ ИДЕЙ РЕКОМЕНДУЕМ ПРОДЕЛАТЬ УПРАЖНЕНИЯ, РЕШИТЬ ЗАДАЧУ.
6. В КОНЦЕ РАБОТЫ, ЕСЛИ НЕТ СМЫСЛА КОНСПЕКТИРОВАТЬ ЕЁ СОДЕРЖАНИЕ, ХОРОШО СДЕЛАТЬ ЗАПИСИ ОСНОВНЫХ ИДЕЙ.
7. ПРИ САМОСТОЯТЕЛЬНОЙ РАБОТЕ НАД МАТЕРИАЛОМ НЕ УВЛЕКАЙСЯ ФАКТАМИ, НЕ СТРЕМИСЬ ВСЕ ИХ ЗАПОМНИТЬ, ЗНАЙ, ЧТО ОСНОВНОЙ СМЫСЛ ТВОЕЙ РАБОТЫ ЗАКЛЮЧАЕТСЯ В ОВЛАДЕНИИ НОВЫМИ ИДЕЯМИ, КОТОРЫЕ ТЫ ВСЕГДА СМОЖЕШЬ ИЛЛЮСТРИРОВАТЬ СВОИМИ ПРИМЕРАМИ.
КАК НАУЧИТЬСЯ ЗАПОМИНАТЬ.
ПАМЯТЬ –ЭТО ПРОЦЕСС ЗАПОМИНАНИЯ, СОХРАНЕНИЯ И ПОЛСЕДУЮЩЕГО ВОСПРОИЗВЕДЕНИЯ ТОГО, ЧТО ЧЕЛОВЕК РАНЬШЕ ВОСПРИНИМАЛ, ПЕРЕЖИВАЛ И ДЕЛАЛ.
1. ОТБИРАТЬ ДЛЯ ЗАПОМИНАНИЯ НУЖНО САМОЕ ГЛАВНОЕ, ВАЖНОЕ, НЕОБХОДИМОЕ.
2. НИЧЕГО НЕ ЗАПОМИНАЙТЕ , ПРЕДВАРИТЕЛЬНО НЕ ОСМЫСЛИВ. ОСМЫСЛИТЬ – ЗНАЧИТ УСТАНОВИТЬ ПРИЧИНУ ЯВЛЕНИЯ ИЛИ ФАКТА, НАЙТИ ОЦЕНКУ ИЛИ ОПРЕДЕЛЕНИЕ, УСТАНОВИТЬ СОБСТВЕННОЕ ОТНОШЕНИЕ У ИЗУЧЕННОМУ МАТЕРИАЛУ.
3. ВИДЫ ПАМЯТИ –ЗРИТЕЛЬНАЯ, СЛУХОВАЯ, МОТОРНАЯ. СТАРАЙТЕСЬ ПОЛЬЗОВАТЬСЯ ВСЕМИ ТРЕМЯ ОДНОВРЕМЕННО. НО ПОМНИТЕ – ЛУЧШЕ ОДИН РАЗ УВИДЕТЬ , ЧЕМ СТО РАЗ УСЛЫШАТЬ. ГЛАЗ СПОСОБЕН ВОСПРИНИМАТЬ ВО МНОГО РАЗ БЫСТРЕЕ, ЧЕМ УХО.
4. НЕ ТОРОПИТЕСЬ : ВЫЯСНИТЕ СКОЛЬКО ВРЕМЕНИ ВАМ НАДО НА ОСВОЕНИЕ ТОГО ИЛИ ИНОГО МАТЕРИАЛА. У КАЖДОГО УЧЕНИКА СВОИ ВРЕМЕННЫЕ НОРМЫ ЗАПОМИНАНИЯ.
5. ВАЖНО ТОЧНО ЗНАТЬ , ЧТО НУЖНО ЗАПОМНИТЬ И ДЛЯ КАКОЙ ЦЕЛИ.
6. НЕБОЛЬШОЙ ПО ОБЪЕМУ МАТЕРИАЛ , ЛУЧШЕ УЧИТЬ СРАЗУ, А ТРУДНЫЙ И БОЛЬШОЙ ПО ЧАСТЯМ, НО ПРЕДВАРИТЕЛЬНО ПОЗНАКОМИВШИСЬ СО ВСЕМ ЗАДАНИЕМ.
7. ЛУЧШЕ ЗАПОМИНАЕТСЯ ТОТ УЧЕБНЫЙ МАТЕРИАЛ, КОТОРЫЙ ВЫ ДОБЫЛИ САМИ. ПОЭТОМУ ПРОЯВЛЯЙТЕ САМОСТОЯТЕЛЬНОСТЬ В УЧЁБЕ.
8. ТРУДНО ИЗУЧАТЬ ТО, ЧТО ВАМ НЕ НРАВИТЬСЯ,ПОЭТОМУ ЗАСТАВЬТЕ СЕБЯ ПОЛЮБИТЬ УЧЕБНЫЙ ПРЕДМЕТ, ПОВЕРЬТЕ В ЕГО ЖИЗНЕННУЮ ЦЕННОСТЬ И НЕОБХОДИМОСТЬ,ПОИЩИТЕ В ЛЮБОМ УЧЕБНОМ ПРЕДМЕТЕ ИНТЕРЕСНОЕ, УДИВИТЕЛЬНОЕ – И УСПЕХ ОБЕСПЕЧЕН.
9. ПОМНИТЕ. ЧТО ВЫ ДОЛЖНЫ БЫТЬ НЕ ХОДЯЧЕЙ ЭНЦИКЛОПЕДИЕЙ, А ЧЕЛОВЕКОМ ИДЕЙ И БОЛЬШОГО СЕРДЦА!
УЧИСЬ РАЦИОНАЛЬНО РАБОТАТЬ НАД ДОМАШНИМ ЗАДАНИЕМ.
-
ПРЕЖДЕ, ЧЕМ ПРИМЕШЬСЯ ЗА ВЫПОЛНЕНИЯ ЗАДАНИЯ, ЧЕТКО СФОРМУЛИРУЙ ДЛЯ СЕБЯ ЦЕЛЬ, КОТОРУЮ БУДЕТ ПРЕСЛЕДОВАТЬ ТВОЯ РАБОТА.
-
ФОРМУЛИРУЯ ЦЕЛЬ, ДАЙ СЕБЕ ОТЧЕТ , ЧТО ТЕБЕ ДОЛЖНО ДАТЬ ВЫПОЛНЕНИЕ ЗАДАНИЯ, К КОТОРОМУ ТЫ ПРИСТУПАЕШЬ.
-
ПОСЛЕ ФОРМУЛИРОВАНИЯ ЦЕЛИ РАБОТЫ НЕ ТОРОПИСЬ ЛБРАЩАТЬСЯ К УЧЕБНИКУ. ВСПОМНИ , ЧТО ТЫ ЗНАЕШЬ ПО ЭТОМУ ВОПРОСУ , ЧТО ЧИТАЛ , ЧТО СЛЫШАЛ. ПОСМОТРИ ЗАПИСИ В ТЕТРАДИ, ОНИ ПОМОГУТ ТЕБЕ ВОССТАНОВИТЬ ОБЪЯСНЕНИЕ УЧИТЕЛЯ.
-
ОБРАЩАЙСЯ К УЧЕБНИКУ ЛИШЬ С ОПРЕДЕЛЕННОЙ ЦЕЛЬЮ. РАБОТАЙ С НИМ ЭКОНОМНО.ЕСЛИ СОДЕРЖАНИЕ МАТЕРИАЛА ГРОМОЗДКО , НО ТЫ ЕГО ПОНЯЛ НА УРОКЕ, УЧЕБНИК ДОЛЖЕН ТЕБЕ ПОМОЧЬ ЗАКРЕПИТЬ ЕГО.
-
ЕСЛИ ТЕБЕ НУЖНО ВЫПОЛНИТЬ УПРАЖНЕНИЕ, РЕШИТЬ ЗАДАЧУ, ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ПОВТОРЯЙ НЕ ДО ВЫПОЛНЕНИЯ ЗАДАНИЯ И НЕ ПОСЛЕ НЕГО, А В ПРОЦЕССЕ РАБОТЫ НАД НИМ.
-
ПРИ ВЫПОЛНЕНИИ УЧЕБНЫХ ЗАДАНИЙ ПРИБЕГАЙ К ЧТЕНИЮ ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ, ЛУЧШЕ ВСЕГО ПРИ ЭТОМ ВЫДЕЛИТЬ ОДНО ОСНОВНОЕ ПОСОБИЕ, НАД КОТОРЫМ БУДЕШЬ РАБОТАТЬ СИСТЕМАТИЧЕСКИ, К ДРУГИМ ЖЕ ПРИБЕГАЙ ПО МЕРЕ НАДОБНОСТИ.
Памятка
(в помощь ученику)
Математика
(1 – 4
классы)
1
класс
Числовой ряд от 1 до 20
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19, 20.
Сравнение чисел
Сравнить два числа – значит узнать,
какое из них больше, а какое – меньше.
Знаки сравнения:
2 = 2 (= равно, столько же)
2 ˂ 3 (˂ меньше)
3 ˃ 2 (˃ больше)
Равенство – это два одинаковых
числа или два выражения с одинаковым значением, соединённые знаком =:
5 = 5
17 + 3 = 3 + 17
Неравенство – это два разных
числа или два выражения с разным значением, соединённые знаком ˃ (больше)
или ˂ (меньше):
9 ˂ 10
10 +1 ˃ 5 – 4
Сложение – это математическое
действие с ис-пользованием знака +.
Слагаемые – это числа, которые
складываются при сложении.
Сумма – это результат сложения.
первое слагаемое
второе слагаемое сумма
2
+ 3 = 5
Помни, если одно слагаемое равно
0, то сумма равна второму слагаемому:
5 + 0 =
5 0 + 3 = 3
Если оба слагаемых равны 0, то и сумма
равна 0:
0 + 0 = 0
Переместительный
закон сложения
От перемены мест слагаемых сумма не
меняется:
4 + 3 = 7
3 + 4 = 7
Однозначное число – это число,
которое состоит из одного знака (цифры):
1, 2, 3, 4, 5, 6,
7, 8, 9, 0
Двузначное число – это число,
которое состоит из двух знаков (цифр):
10, 11, 12, 13,
14, 15, 16, 17, 18, 19, 20
Десяток – это 10 единиц.
Разряды чисел: единицы и десятки
2 – две единицы;
7 – семь единиц;
15 – один десяток и пять единиц;
13 – один десяток и три единицы;
19 – один десяток и девять единиц;
20 – два десятка.
Состав числа
(первый десяток)
|
10 |
|||||||||||||||||
|
9 |
9 |
1 |
|||||||||||||||
|
8 |
8 |
1 |
8 |
2 |
|||||||||||||
|
7 |
7 |
1 |
7 |
2 |
7 |
3 |
|||||||||||
|
6 |
6 |
1 |
6 |
2 |
6 |
3 |
6 |
4 |
|||||||||
|
5 |
5 |
1 |
5 |
2 |
5 |
3 |
5 |
4 |
5 |
5 |
|||||||
|
4 |
4 |
1 |
4 |
2 |
4 |
3 |
4 |
4 |
4 |
5 |
4 |
6 |
|||||
|
3 |
3 |
1 |
3 |
2 |
3 |
3 |
3 |
4 |
3 |
5 |
3 |
6 |
3 |
7 |
|||
|
2 |
2 |
1 |
2 |
2 |
2 |
3 |
2 |
4 |
2 |
5 |
2 |
6 |
2 |
7 |
2 |
8 |
|
|
1 |
1 |
1 |
2 |
1 |
3 |
1 |
4 |
1 |
5 |
1 |
6 |
1 |
7 |
1 |
8 |
1 |
9 |
Вычитание – это математическое
действие, обратное сложению, с использованием знака —.
Уменьшаемое – это число, из
которого вычитают.
Вычитаемое – это число, которое
вычитают.
Разность – это результат
вычитания.
уменьшаемое
вычитаемое разность
5
– 3 = 2
Таблица сложения
|
+ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Таблица вычитания
|
– |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Именованные числа – это числа,
полученные при измерении величин и сопровождающиеся названием единицы
измерения:
2 кг, 4 см, 8 л
Простые именованные числа –
только одна еди-ница измерения:
7 кг, 9 см, 15 л
Составные именованные числа –
несколько еди-ниц измерения:
1 дм 3 см, 3 ч 20
мин
Литр – это единица измерения
ёмкости.
Килограмм – это единица
измерения массы.
Сантиметр, дециметр – это
единицы измерения длины.
Учимся
решать задачи
Задачи на
нахождение суммы двух чисел
Задачи этого вида решаются сложением,
потому что находим сумму.
Белка
припасла для друзей 4 грибочка и 5 орешков. Сколько всего гостинцев приготовила
белка?
Грибов – 4 шт.
Орехов – 5 шт.
Решение:
4 + 5 = 9
(гост.)
Ответ: 9
гостинцев.
Задачи на
нахождение остатка
Задачи этого
вида решаются вычитанием, потому что находим остаток.
На ветке
было 7 ягод рябины. Снегирь склевал 3 ягоды. Сколько ягод осталось?
Было – 7 яг.
Склевал – 3 яг.
Осталось – ?
Решение:
7 – 3 = 4 (яг.)
Ответ: 4 ягоды.
Задачи на
увеличение числа
на несколько
единиц
Во дворе
гуляло 6 утят. А гусят на 2 больше. Сколько гуляло гусят?
Утята – 6 шт.
Гусята – ?, на
2 шт. больше
Решение:
6 + 2 = 8
(гус.)
Ответ: 8 гусят.
Задачи на
уменьшение числа
на несколько
единиц
На столе лежало
9 столовых ложек, а чайних на 3 меньше. Сколько чайних ложек лежало на столе?
Столовые ложки – 9 шт.
Чайные ложки –
?, на 3 шт. меньше
Решение:
9 – 3 = 6
(лож.)
Ответ: 6 чайных
ложек.
Задачи на
разностное сравнение двух чисел
Чтобы узнать,
на сколько одно число больше (меньше) другого, нужно из большего вычесть
меньшее.
В одной корзине
7 яблок, а в другой – 10 груш. На сколько груш больше, чем яблок?
Яблоки – 7
шт. на ?
Груши – 10
шт. больше
Решение:
10 – 7 = 3
(гр.)
Ответ: на 3
груши.
В одной корзине
7 яблок, а в другой – 10 груш. На сколько яблок меньше, чем груш?
Яблоки – 7
шт. на ?
Груши – 10
шт. меньше
Решение:
10 – 7 = 3
(гр.)
Ответ: на 3
груши.
Задачи на
нахождение неизвестного слагаемого
В таких задачах
неизвестно слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть
известное слагаемое.
Два петушка
нашли 8 червячков. Первый нашёл 5. Сколько червячков нашёл второй петушок?
Первый
петушок – 5 черв. 8 черв.
Второй петушок
– ?
5 + □ = 8
Решение:
8 – 5 = 3
(черв.)
Ответ: 3
червячка.
Задачи на
нахождение неизвестного уменьшаемого
В таких задачах
неизвестно уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к разности
прибавить вычитаемое.
На тарелке
лежали пряники. Когда дети взяли 4 пряника, на тарелке осталось 8. Сколько
пряников было на тарелке?
Было – ?
Взяли – 4 пр.
Осталось – 8
пр.
□ – 4 = 8
Решение:
8 + 4 = 12
(пр.)
Ответ: 12
пряников.
Задачи на
нахождение неизвестного вычитаемого
В таких задачах
неизвестно вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из
уменьша-емого вычесть разность.
В вазе стояло 7
гвоздик. Когда несколько гвоздик отдали, в вазе осталось 5 гвоздик. Сколько
гвоздик отдали?
Было – 7 гв.
Отдали – ?
Осталось – 5
гв.
7 – □ = 5
Решение:
7 – 5 = 2 (гв.)
Ответ: 2
гвоздики.
Задачи в косвенной
форме
При решении
таких задач нужно помнить: если одна величина на несколько единиц больше
(меньше), то другая на столько же единиц меньше (больше).
Брату 5 лет, он
на 2 года старше сестры. Сколько лет сестре?
Брат –
5 лет, на 2 года старше
Сестра
– ?
Решение:
5 – 2 = 3
(года)
Ответ: 3 года.
Составные задачи
Составные
задачи состоят из нескольких простих и решаются в два и больше действия.
Решение таких
задач можно записывать по действиям или выражениям.
Если решение
задачи записывается по действиям, то в каждом действии, кроме последнего, нужно
записывать пояснение.
Рыбак поймал 2
щуки, а лещей на 8 больше. Сколько всего рыб поймал рыбак?
Щуки –
2 шт. ?
Лещи – ?, на 8
шт. больше
Решение:
1). 2 + 8 = 10
(л.) – лещи
2). 2 + 10 = 12
(р.)
Ответ: всего 12
рыб.
К кормушке
прилетели птицы: 10 воробьёв, снегирей на 7 меньше, а синиц на 2 больше, чем
снегирей. Сколько всего птиц прилетело к кормушке?
Воробьи
– 10 шт.
Снегири – ?, на 7
меньше ?
Синицы – ?, на
больше
Решение:
1). 10 – 7 = 3
(сн.) – снегири
2). 3 + 2 = 5
(син.) – синицы
3). 10 + 3 + 5
= 18 (пт.)
Ответ: 18 птиц.
Задачи на нахождение
слагаемого и вычитаемого
Папа съел 5
груш, мама – 3, а сын на 6 груш меньше, чем папа и мама вместе. Сколько груш
съел сын?
Папа –
5 гр. ?
Мама – 3 гр.
Сын – ?, на 6
груш меньше
Решение:
1). 5 + 3 = 8
(гр.) – папа и мама вместе
2). 8 – 6 = 2
(гр.)
Ответ: 2 груши.
Основы геометрии
Точка (.)
– обозначается загалавной буквой латинского алфавита: А, В, Е, О, С и т. д.
Буква пишется рядом с точкой.
В .
М
. С .
К .
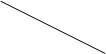
Прямая линия
( ) – не имеет ни начала, ни конца – она бесконечна.
Кривая линия ( ) –
так же не имеет ни нача-ла, ни конца – она безконечна.
Отрезок
– это часть прямой линии, ограниченная двумя точками – началом и концом.
Луч –
это прямая линия, которая имеет начало, но не имеет конца.
Ломаная
линия – состоит из отрезков, последо-вательно соединённых друг с другом.
 |
|||

Треугольник – это геометрическая
фигура, у которой три угла и три стороны.
Четырёхугольник – это
геометрическая фигура, у которой четыре угла и четыре стороны.

2
класс
Счёт десятками
10, 20, 30, 40,
50, 60, 70, 80, 90, 100
100 (сто) – 10
десятков (десять десятков)
Разряды чисел:
единицы десятки
сотни
78 – 7 десятков и
8 единиц;
100 – 1 сотня;
124 – 1 сотня 2
десятка и 4 единицы.
Метр, миллиметр – единицы
измерения длины.
|
1 см = 10 мм |
|
1 м = 100 см = |
Рубль, копейка – денежные
единицы измерения.
Копейки-монеты:
Рубли:
Обратные
задачи
К любой задаче можно составить
несколько обратных задач.
Чтобы составить обратную задачу, нужно
то, что было неизвестным в задаче, сделать известным, а известное –
неизвестным.
Дана задача:
Вера купила блокнот за 6 р. и
карандаш за 4 р. Сколько всего рублей стоили блокнот и карандаш вместе?
Блокнот – 6 р. ?
Карандаш – 4 р.
Решение:
6 + 4 = 10 (р.)
Ответ: 10 рублей.
Теперь составим обратные задачи:
На 10 р. Вера купила блокнот и
карандаш. Блокнот стоил 6 р. Сколько стоил карандаш?
Блокнот – 6 р.
10 р.
Карандаш – ?
Решение:
10 – 6 = 4 (р.)
Ответ: 4 рубля.
На 10 р. Вера купила блокнот и
карандаш. Карандаш стоил 4 р. Сколько стоил блокнот?
Блокнот –
? 10 р.
Карандаш – 4 р.
Решение:
10 – 4 = 6 (р.)
Ответ: 6 рублей.
Секунда, минута, час, сутки, неделя, месяц,
год, век – измерительные единицы времени.
|
1 минута = 60 |
|
1 час = 60 минут |
|
1 сутки = 24 |
|
1 неделя = 7 |
|
1 месяц = 30 или (в феврале 28 |
|
1 год = 12 52 недели = 365 |
|
1 век (столетие) |
Длина ломаной
Чтобы узнать длину ломаной, необходимо
сложить длину каждого звена (то есть найти сумму этих длин):
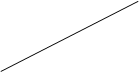
4 см 3 см
2 см
2 см + 4 см + 3 см = 10 см
Дина ломаной равна 10 см.
Порядок выполнения
действий (скобки)
Действия, записанные в скобках,
выполняют первыми:
2 д 1 д 2 д 1 д
10 – (6 + 3) = 1 9 + (8 – 5) =
12
Периметр многоугольника – это сумма длин
всех его сторон. Обозначается периметр заглавной буквой Р (пэ) латинского
алфавита.
А В Р
= АВ + ВD + СD + АС
 |
С D
Свойства сложения
Результат сложения не изменится, если
соседние слагаемые заменить их суммой:
6 + 9 + 4 + 1 = (6 +4) + (9 + 1) = 10
+ 10 = 20
17 + 8 + 3 + 2 = ( 17 + 3) + (8 + 2) =
20 + 10 = 30
Устные
вычисления
Единицы складываются с единицами,
десятки складываются с десятками:
27 + 2 = 20 + (7 + 2) = 20 + 9 =
29
20 и 7
56 + 30 = (50 + 30) + 6 = 80 + 6
= 86
50
и 6
Единицы вычитают из единиц, десятки
вычитают из десятков:
36 – 2 = 30 + (6 – 2) = 30 +4 =
34
30 и 6
36 – 20 = (30 – 20) + 6 = 10 + 6
= 16
30 и 6
26 + 4 = 20 + (6 + 4) = 20 + 10
= 30
20 и 6
30 – 7 = 20 + (10 – 7) = 20 + 3
= 23
20 и 10
60 – 24 = (60 – 20) – 4 = 40 – 4
= 36
20 и 4
100 – 2 = 90 + (10 – 2) = 90 + 8
+ 98
90 и 10
26 + 7 = (26 + 4) + 3 = 30 + 3 =
33
4 и 3
35 – 7 = (35 – 5) – 2 = 30 – 2 =
28
5 и 2
Буквенные выражения – это
выражения, содер-жащие не только числа, но и буквы.
Помни, что в математике в буквенных
выраже-ниях используются буквы латинского алфавита:
8 + d (восемь плюс дэ);
c – 5 (цэ минус
пять);
x + 7 (икс плюс
семь).
Латинский алфавит
Aa (а) Kk (ка) Tt (тэ)
Bb (бэ) Ll (эль) Uu (у)
Cc (цэ) Mm (эм) Vv (вэ)
Dd (дэ) Nn (эн) Ww (дубль вэ)
Ee (е)
Oo (о) Xx (икс)
Ff (эф) Pp (пэ) Yy (игрек)
Gg (гэ) Qq (ку) Zz (зэт)
Hh (ха) Rr (эр)
Ii (и)
Ss (эс)
Уравнение – это равенство,
содержащее неизве-стное число, которое надо найти:
х + 4 = 12 Проверка:
х = 12 – 4 8 + 4 = 12
х = 8 12 = 12
7 – х = 2 Проверка:
х = 7 – 2 7 – 5 = 2
х = 5 2 = 2
Проверка сложения
Если из суммы двух слагаемых вычесть
одно из них, то получится другое слагаемое:
42 + 7 =
49 27 + 3 = 30
Проверка: 49 – 7 = 42
Проверка: 30 – 3 = 27
Проверка вычитания
Если к разности прибавить вычитаемое,
то получится уменьшаемое:
69 – 50 = 19
100 – 20 = 80
Проверка: 19 + 50 = 69 Проверка:
80 + 20 = 100
Письменные вычисления (в столбик)
десятки единицы десятки единицы
4 5 5 7
+ —
2 3 2 6
6 8
3 1
Угол – это два луча, выходящие
из одной точки.
Точка, из которой выходят лучи,
называется вершиной угла, а сами лучи – сторонами угла.
Виды угла:
острый прямой
тупой
(меньше прямого) (равен 900) (больше
прямого)
Письменные вычисления (в столбик)
десятки единицы
десятки единицы
3
7 3 7
+
15 + 10
4 8 5
3
7 (и ещё 1) 5 8
(и
ещё 1)
0

(1
запоминаем) (1 запоминаем)
85
90
Прямоугольник – это
четырёхугольник, у кото-рого все углы прямые и противоположные стороны равны
между собой:

В С АВ = СD
ВС = АD
А D
Письменные вычисления (в
столбик)
десятки единицы
десятки единицы
8
7 (занимаем
1 десяток)
(не
0, а 10)
+
10 4 0
1 3 —
8
9 (и ещё 1)
0 3 2

(1
запоминаем)
100
десятки единицы
(занимаем 1 десяток) (не 0, а 10)
5
0
— 2
4
2 6
Квадрат – это прямоугольник, у
которого все стороны равны:

С АВ = ВС = СD = АD
А D
Умножение – это сложение
одинаковых слагае-мых. Знак умножения – точка (•):
3 • 4 = 12
Читают так: по 3 взять 4 раза,
получится 12 или 3 умножить на 4, получится 12.
первый множитель второй
множитель произведение
2 • 8 = 16
Деление – это действие, обратное
умножению. Знак деления две точки (:):
6 : 2 = 3
Читают так: 6 разделить на 2, получится
3.
делимое делитель частное
12 : 4 = 3
Связь каждого
множителя с произведением
Если произведение двух множителей
разделить на один из них, то получится другой множитель:
7 • 2 = 14
8 • 4 = 32 9 • 2 = 18
14 : 7 = 2 32 : 8 = 4 18 : 9
= 2
14 : 2 = 7 32 : 4 = 8 18 : 2
= 9
Умножение и
деление с числом 10
При умножении числа на 10, нужно справа
дописать к этому числу нуль:
5 • 10 = 5 • 1 десяток = 5 десятков
= 50
При делении числа на 10, нужно
отбросить от числа справа нуль:
30 : 10 = 3 (3 десятка разделить на
1 десяток, получится 3)
Задачи на
нахождение произведения двух чисел
Толя купил 3 тетради, по 10
рублей каждая. Сколько стоили все тетради?
Рисунок к задаче:
1 тетрадь
□□□□□□□□□□
2 тетрадь
□□□□□□□□□□ ?
3 тетрадь
□□□□□□□□□□
1 т. – 10 р.
3 т. – ? р.
Решение:
10 • 3 = 30 (р.)
Ответ: 30 рублей.
Задачи на
нахождение частного двух чисел
15 шариков раздали 5 ученикам
поровну. Сколько шариков получил каждый ученик?
Рисунок к задаче:
оооǀоооǀоооǀоооǀооо
15 ш. – 5 уч.
? ш. – 1 уч.
Решение:
15 : 5 = 3 (ш.)
Ответ: 3 шарика.
Табличное
умножение и деление на 2, 3
|
• |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
|
: |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
Памятки – помощники в выполнении домашнего задания по математике
Наука математика, как и любая другая наука, имеет два раздела: теорию и практику. Невозможно решать задачи, уравнения, неравенства не зная алгоритмов их решения. Можно заучить один алгоритм, например, алгоритм решения линейного уравнения, но применить этот алгоритм для уравнения которое имеет скобки, будет невозможно. И многие ученики могут в 5 классе «потеряться» в такой ситуации: зная как находить неизвестное слагаемое, уменьшаемое, вычитаемое или неизвестный множитель, они могут не распространить эти правила на скобку.
Внедряя ФГОС второго поколения в образовательный процесс, мы в школе внедряем в образовательную практику системно-деятельностный подход. Процесс самообразования и самосовершенствования продолжается для человека всю жизнь, но начинается именно в стенах школы. Поэтому в школе истинное усвоение знаний не должно сводиться к простому заучиванию информации. Усвоенные знания предполагают эффективное использование этой информации, для чего необходимо их органическое усвоение. А это возможно только при условии самостоятельной работы по переработке информации. И лучше чтобы такая работа начиналась уже в процессе накопления этой информации, ее анализа и присвоения. Так для наших учеников пассивный способ получения информации превращается в активный, при котором работает не только память, но и мысль познающего. Учащийся, получивший информацию активным способом, может стать творческой личностью. Поэтому, используя современные образовательные технологии, учителя превращают ученика в субъект образовательного процесса, способного к самостоятельной работе и самооценке.
Но с другой стороны, для успешного изучения математики, ее необходимо учить! Учить теоретические моменты, начиная от определений математических понятий и заканчивая доказательством теорем, логическими выкладками решения задач.
Именно в них иногда скрываются методы решения заданий, пусть даже и не стандартные и не рациональные. А учитель на уроке становится лишь «путеводителем» по этим ветвистым дорожкам математических знаний. Учитель должен в голове у ученика «складывать» воедино те знания, которые разрознено даются в каждом классе. Так как программа по математике предполагает изучение темы уравнения, но в каждом классе, изучаются посильные уравнения возрасту и развитию учеников данного возраста.
Большинство школ – это школы полного дня. В них ученики находятся целый день и получают весь спектр образовательных услуг. Во второй половине дня для учащихся организовывается самоподготовка. Это важный этап режима дня школьников. Самостоятельное выполнение домашнего задания позволяют ученикам отрабатывать умения и навыки, приобретенные на уроках, устранять пробелы в знаниях по предметам учебного плана, а так же позволяют развивать учеников (формировать интерес к предмету, умение применять имеющиеся знания в нестандартной ситуации, воспитывать осознанное отношение к полученному заданию и его выполнению). Таким образом, самоподготовка это процесс, который организует сам ученик (это то, к чему мы стремимся). Задача классного руководителя на самоподготовке сначала научить, а затем помогать школьнику развивать в себе умение самоорганизации: самостоятельно готовить свое рабочее место, содержать его в порядке в течение второй половины дня; планировать свою деятельность на данную работу, на весь день; самостоятельно выполнять полученные задания; самостоятельно работать с учебником и справочной литературой; позитивно относиться к временным неудачам, делать соответствующие выводы; осуществлять самоконтроль; объективно оценивать результаты своего труда.
Учитывая вышесказанное, предлагаем памятку для учеников по выполнению домашнего задания по математике. Следуя указаниям этой памятки, знания ученика будут системными, прочными и результат обучения будет только «5».
Памятка по выполнению домашнего задания по математике:
- Прочитай учебник, параграф, в котором описывается изучаемая тема, даже если тема не новая.
- Выучи правила, определения, выделенные в этом параграфе жирным шрифтом или находящиеся в рамке.
- Просмотри в рабочей тетради классную работу: какая тема изучалась, какие задания выполнялись, просмотри алгоритмы выполнения заданий.
- Повтори правила и определения по тетради (так как учитель может уже упростить правила и алгоритмы, данные в учебнике, показать их наиболее рациональное использование и т.п.).
- Выполни устные домашние задания.
- Выполни письменные домашние здания.
- Повтори определения понятий, алгоритмы и правила без учебника или тетради.
Как видим из памятки, ученик должен хорошо уметь работать с учебным пособием: учебником, справочником, словарем или электронными носителями, содержащими информацию по теме. В современном обществе все больше пользуется спросом дистанционное обучение. И здесь ученик остается наедине с учебником, учебным пособием. Самостоятельное изучение математического материла по учебнику дело сложное. Это зависит, прежде всего, от изложения материала в учебнике. К особенностям учебников математики можно отнести: своеобразный язык математики, абстрактность теории, сжатость и краткость изложения (одна из основных проблем современного учебника), широкое применение символики, преобладание дедуктивного метода изложения информации, тесная связь текста с иллюстрациями и чертежами. Следует отметить, что в текстах учебников математики имеются так называемые «пробелы в тексте» – это ссылки на уже известный материал, формулы или теоремы. Ученики не всегда самостоятельно могут восстановить эти «пробелы текста». В силу изложенных особенностей математического текста самостоятельное чтение приводит к недопониманию прочитанного, тем более неумению применять полученные знания в нестандартных ситуациях.
Для эффективного самостоятельного изучения математики предлагаем памятки по работе с параграфами ученика математики, алгебры и геометрии.
Памятка работы с параграфом учебника математики для учеников 5-6 классов.
- Прочитай заголовок и попытайся ответить на вопрос: «О чем будет говориться в этом параграфе?».
- Просмотри текст параграфа, обращая внимание на иллюстрации, правила, примеры.
- Почитай текст. Установи связь текста и иллюстраций, правил, примеров рассмотренных ранее.
- Как выделено главное в тексте (правила, алгоритмы выполнения действий и т.п.).
- Приведи свои примеры к тексту.
- Раздели текст на смысловые части. Сколько их получилось?
- Озаглавь части текста и составь план.
- Выполни письменное задание.
- Повтори прочитанное по плану, затем без него.
- Проговори несколько раз правила. Выучи наизусть.
Памятка работы с параграфом учебника математики для учащихся 7-9 классов.
- Прочитайте заголовок параграфа. Что вы уже знаете об этом? Что вы говорили в классе об этом?
- Прочитайте текст параграфа.
- Выучите формулировки теорем, определения, правила, алгоритмы решения заданий.
- Установите связь между иллюстрациями, рисунками, чертежами и текстом.
- Разделите текст на части, озаглавьте их, запишите план в тетрадь.
- Выполните письменное домашнее задание.
- Перескажите теоретические сведения, прочитанные из параграфа, согласно вашему плану.
- Приведите собственные примеры в доказательство прочитанного.
Памятка работы с учебником математики для учащихся 10-11 классов.
- Прочитайте заголовок параграфа. Что вы записали в классе по этому вопросу?
- Просмотрите текст параграфа. Рассмотрите иллюстрации, попробуйте их объяснить.
- Прочитайте текст параграфа. Заучите определения, формулировки, правила. Восстановите «пробелы текста».
- Рассмотрите алгоритмы решения заданий.
- Выполните письменное домашнее задание.
- Перескажите прочитанный материал.
- Составьте схему прочитанного материала или табличный вариант.
Слушая внимательно учителя на уроке, умея работать с учебником, выполняя самостоятельно домашнее задание, школьники смогут сами учиться, смогут сами добывать знания и будут уметь их правильно применять в той или иной ситуации.
Всего комментариев: 1
Порядок вывода комментариев:

В помощь учителю
Уважаемые коллеги! Опубликуйте свою педагогическую статью или сценарий мероприятия на Учительском портале и получите свидетельство о публикации методического материала в международном СМИ.
Для добавления статьи на портал необходимо зарегистрироваться.
Конкурсы
Диплом и справка о публикации каждому участнику!
© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены