Простые параллельные схемы
Добавлено 3 января 2020 в 22:12
В данной статье мы изложим три принципа, которые вы должны понимать в отношении параллельных цепей:
- напряжение: напряжение одинаково на всех компонентах в параллельной цепи;
- ток: общий ток цепи равен сумме токов отдельных ветвей;
- сопротивление: отдельные сопротивления уменьшают общее сопротивление, а не увеличивают его.
Давайте взглянем на несколько примеров параллельных схем, демонстрирующих эти принципы.
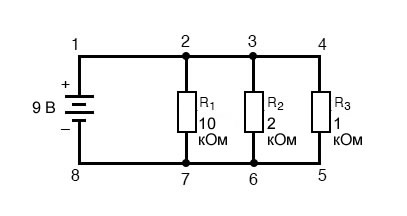
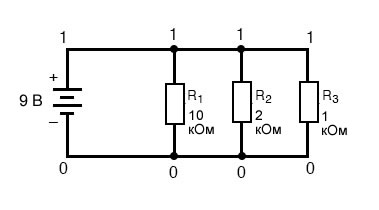
Начнем с параллельной схемы, состоящей из трех резисторов и одной батареи:
Напряжение в параллельных цепях
Первый принцип, который следует понимать в отношении параллельных цепей, заключается в том, что напряжение на всех компонентах в цепи одинаково. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между этими наборами общих точек, всегда должно быть одинаковым.
Следовательно, в приведенной выше схеме напряжение на R1 равно напряжению на R2, которое равно напряжению на R3, которое равно напряжению на батарее.
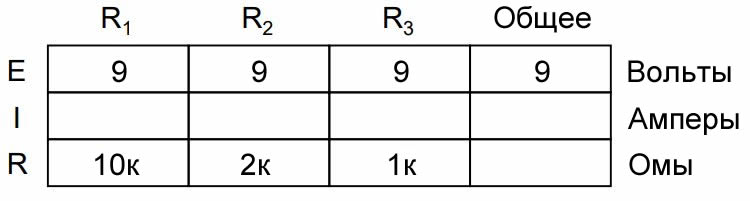
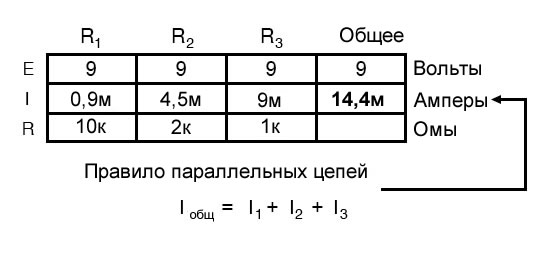
Это равенство напряжений можно представить в таблице для наших начальных значений:
Применение закона Ома к простым параллельным цепям
Как и в случае с последовательными цепями, применимо то же предостережение для закона Ома: чтобы вычисления работали правильно, значения напряжения, тока и сопротивления должны быть в одном контексте.
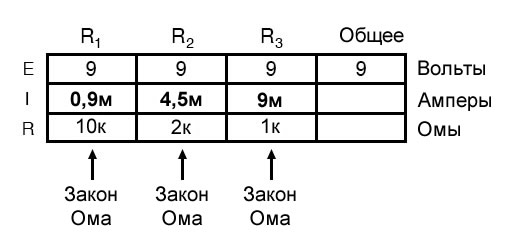
Однако в приведенной выше схеме мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что нам известно напряжение на каждом резисторе (9 вольт) и сопротивление каждого резистора:
[I_{R1}=frac{E_{R1}}{R_1} qquad I_{R2}=frac{E_{R2}}{R_2} qquad I_{R3}=frac{E_{R3}}{R_3}]
[I_{R1}=frac{9 В}{10 кОм} = 0,9 мА]
[I_{R2}=frac{9 В}{2 кОм} = 4,5 мА]
[I_{R3}=frac{9 В}{1 кОм} = 9 мА]
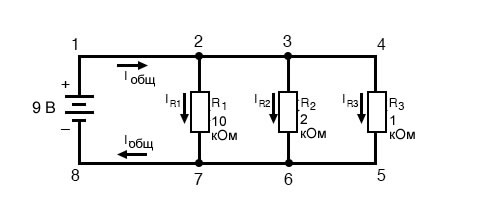
На данный момент мы еще не знаем, каков общий ток или полное сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому столбцу («Общее»). Однако если мы внимательно подумаем о том, что происходит, то должно стать очевидным, что полный ток должен равняться сумме всех отдельных токов резисторов («ветвей»):
По мере того, как полный ток выходит из положительной (+) клеммы батареи в точке 1 и проходит по цепи, часть тока отделяется в точке 2 и проходит через R1, еще часть отделяется в точке 3, чтобы пройти через R2, а оставшаяся часть проходит через R3. Подобно реке, разветвляющейся на несколько меньших потоков, общая скорость всех потоков должна быть равна скорости потока всей реки.
То же самое происходит, когда токи через R1, R2 и R3 объединяются, чтобы течь обратно к отрицательному выводу батареи (-) в направлении точки 8: поток тока из точки 7 в точку 8 должен равняться сумме токов (ветвей) через R1, R2 и R3.
Это второй принцип параллельных цепей: полный ток цепи равен сумме токов отдельных ветвей.
Используя этот принцип, мы можем заполнить ячейку для общего тока в нашей таблице суммой IR1, IR2 и IR3:
Как рассчитывать полное сопротивление в параллельных цепях
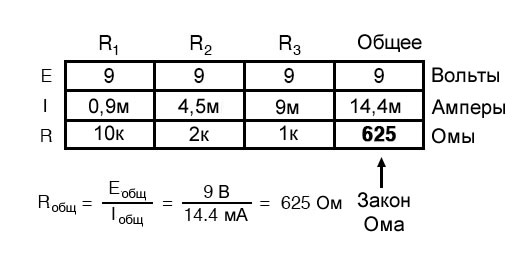
Наконец, применив закон Ома к крайнему правому столбцу («Общее»), мы можем вычислить полное сопротивление цепи:
Формула сопротивления в параллельных цепях
Обратите внимание на кое-что очень важное. Общее сопротивление цепи составляет всего 625 Ом: меньше, чем у любого из отдельных резисторов. В последовательной цепи, где полное сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть больше, чем сопротивление любого из резисторов по отдельности.
Однако здесь, в параллельной цепи, верно обратное: мы говорим, что отдельные сопротивления уменьшают общее сопротивление, а не увеличивают его.
Этот принцип завершает нашу триаду «правил» для параллельных цепей, для которых, как и для последовательных цепей, есть три правила: для напряжения, тока и сопротивления.
Математически зависимость между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом:
[R_{общ} = frac{1}{frac{1}{R_1}+frac{1}{R_2}+frac{1}{R_3}}]
Эта же базовая форма уравнения работает для любого количества резисторов, соединенных вместе параллельно, просто добавьте столько членов 1/R к знаменателю дроби, сколько необходимо для размещения всех параллельных резисторов в цепи.
Как изменить схему нумерации параллельной цепи для SPICE
Как и в случае с последовательной схемой, мы можем использовать компьютерный анализ, чтобы перепроверить наши расчеты. Во-первых, конечно, мы должны описать нашу схему для SPICE в понятных ему терминах. Я начну с повторного рисования схемы:
И снова мы обнаруживаем, что исходная схема нумерации, используемая для идентификации точек в цепи, должна быть изменена для работы со SPICE.
В SPICE все электрически общие точки должны иметь одинаковые номера узлов. Так SPICE узнает, что с чем и как связано.
В простой параллельной схеме все точки являются электрически общими в одном из двух наборов точек. Для нашей схемы провод, соединяющий верхние части всех компонентов, будет иметь один номер узла, а провод, соединяющий нижние части компонентов, будет иметь другой номер.
Оставаясь верным соглашению о включении нуля в качестве номера узла, я выбираю числа 0 и 1:
Пример, подобный этому, делает обоснование выбора номеров узлов в SPICE довольно понятным. Поскольку все компоненты имеют общие наборы чисел, компьютер «знает», что все они подключены параллельно друг другу.
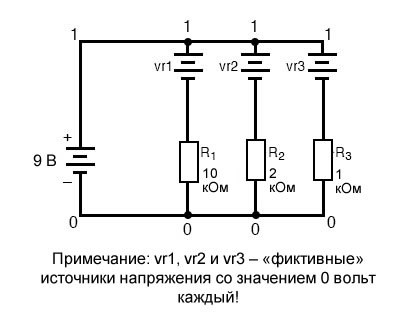
Чтобы отобразить в SPICE токи ветвей, нам нужно последовательно с каждым резистором вставить источник нулевого напряжения, а затем связать наши измерения тока с этими источниками.
По какой-то причине создатели программы SPICE сделали так, чтобы ток можно было рассчитывать только через источник напряжения. Это несколько раздражающее требование программы моделирования SPICE. После добавления каждого из этих «фиктивных» источников напряжения необходимо создать несколько новых номеров узлов, чтобы подключить их к соответствующим резисторам:
Все фиктивные источники напряжения настроены на 0 вольт, чтобы не влиять на работу схемы.
Как проверить результаты компьютерного анализа
Файл описания схемы, или список соединений, выглядит так:
Parallel circuit
v1 1 0
r1 2 0 10k
r2 3 0 2k
r3 4 0 1k
vr1 1 2 dc 0
vr2 1 3 dc 0
vr3 1 4 dc 0
.dc v1 9 9 1
.print dc v(2,0) v(3,0) v(4,0)
.print dc i(vr1) i(vr2) i(vr3)
.endЗапустив компьютерный анализ, мы получаем следующие результаты:
| v1 | v(2) | v(3) | v(4) |
|---|---|---|---|
| 9.000E+00 | 9.000E+00 | 9.000E+00 | 9.000E+00 |
| напряжение батареи | напряжение R1 | напряжение R2 | напряжение R3 |
| v1 | i(vr1) | i(vr2) | i(vr3) |
|---|---|---|---|
| 9.000E+00 | 9.000E-04 | 4.500E-03 | 9.000E-03 |
| напряжение батареи | ток R1 | ток R2 | ток R3 |
Эти значения действительно совпадают со значениями, рассчитанными ранее по закону Ома: 0,9 мА для IR1, 4,5 мА для IR2 и 9 мА для IR3. При параллельном подключении, естественно, все резисторы имеют одинаковое падение напряжения (9 вольт, как на батарее).
Три правила параллельных цепей
Таким образом, параллельная цепь определяется как такая цепь, в которой все компоненты подключены между одними и теми же наборами электрически общих точек. Другими словами, все компоненты соединены клеммами друг с другом. Из этого определения следуют три правила параллельных цепей:
- все компоненты имеют одинаковое напряжение;
- сопротивления уменьшают меньшее общее сопротивление;
- токи ветвей в сумме равны большему общему току.
Как и в случае с последовательными цепями, все эти правила находят корень в определении параллельной цепи. Если вы полностью понимаете это определение, то правила – не более чем сноски к определению.
Резюме
- Компоненты в параллельной цепи имеют одинаковое напряжение: Eобщ = E1 = E2 = . . . = En
- Общее сопротивление в параллельной цепи меньше любого из отдельных сопротивлений: Rобщ = 1 / (1/R1 + 1/R2 + . . . + 1/Rn)
- Общий ток в параллельной цепи равен сумме токов отдельных ветвей: Iобщ = I1 + I2 + . . . +In.
Теги
LTspiceSPICEЗакон ОмаМоделированиеОбучениеПараллельная цепь
Загрузить PDF
Загрузить PDF
При подсоединении электрических устройств к питанию можно использовать либо линейное, либо параллельное подключение. При параллельном подключении ток идет по нескольким направлениям, и каждое устройство имеет собственную цепь питания. Преимуществом параллельного подключения является то, что при поломке одного устройства, ток не перестанет поступать к остальным. [1]
Кроме того, несколько устройств могут подключаться к сети одновременно без снижения мощности в ваттах. Создание параллельной электрической цепи не является сложной задачей, а потому служит отличным проектом, позволяющим понять принцип работы электричества.
-
1
Учитывайте возраст и навыки человека, который будет выполнять проект. Создание параллельной цепи является отличным и простым экспериментом для учеников школы, изучающих электричество. Данным метод прекрасно подходит для младших учеников, которые могут быль не очень ловкими, и которым вы не можете доверить использовать острые инструменты.
- Если эксперимент с параллельной электрической цепью является частью плана урока, то можно попросить детей составить свой список вопросов и предположений о том, что произойдет во время эксперимента и почему.
-
2
Выберите источник питания. Самым дешевым и наиболее удобным источником питания будет батарейка. При этом отличным выбором является девятивольтовая батарея.
-
3
Выберите электрические устройства. Именно их вы и будете подключать к источнику питания. Мы опишем создание параллельной электрической цепи на примере лампочек (их понадобится две штуки); также можно использовать диоды.
-
4
Подготовьте провода. Вы будете использовать алюминиевую фольгу в качестве проводов при создании электроцепи. Именно фольга будет соединять источник питания с устройствами.
- Вырежьте из фольги четыре узких полосы: две по 20 см и две по 10 см. По ширине они должны быть примерно с диаметр соломинки для питья.
-
5
Длинные полосы фольги присоедините к батарее. Теперь вы готовы начать создавать параллельную электрическую цепь.
- Возьмите одну из 20-сантиметровых полос и присоедините к плюсу на батарее. [2]
- Возьмите другую 20-сантиметровую полосу и присоедините к минусу на батарее. [3]
- Возьмите одну из 20-сантиметровых полос и присоедините к плюсу на батарее. [2]
-
6
Подсоедините лампочки. Теперь вы можете присоединить устройства к импровизированным проводам из фольги.
- Возьмите две 10-сантиметровых полосы и одним концом намотайте на длинную полосу, выходящую из плюса на батарее. Одну 10-сантиметровую полосу присоедините неподалеку от конца 20-сантиметровой полосы, а вторую – примерно на 8 см ближе к батарее. [4]
- Оберните свободные концы коротких полосок вокруг лампочек. Вам может понадобиться прикрепить их с помощью изоленты.
- Возьмите две 10-сантиметровых полосы и одним концом намотайте на длинную полосу, выходящую из плюса на батарее. Одну 10-сантиметровую полосу присоедините неподалеку от конца 20-сантиметровой полосы, а вторую – примерно на 8 см ближе к батарее. [4]
-
7
Замкните параллельную электрическую цепь. Когда вы закончите соединять все элементы параллельной цепи, ваши лампочки начнут светиться.
- Приложите лампочки ко второй длинной полосе фольги, идущей от минуса батареи.
- Лампочки должны ярко засветиться!
Реклама
-
1
Выберите данный метод в качестве усложненного проекта. Несмотря на то, что создание параллельной цепи является несложной задачей, в данном случае вам потребуется иметь при себе провода и выключатель. Этот метод подойдет для учеников постарше.
- Данный метод подразумевает зачистку концов проводов, но если у вас нет для этого специального инструмента (стриппера), или если вы не хотите доверять эту работу детям, то можете обратиться к вышеуказанному упрощенному методу.
-
2
Соберите все необходимое для создания параллельной электрической цепи. Потребуется немногое: источник питания, провода, как минимум, два устройства (потребляющих электричество) и выключатель.
- Мы рекомендуем использовать в качестве источника питания батарею. Вам отлично подойдет девятивольтовая батарея.
- Вы будете использовать изолированные провода для передачи электричества. Подойдут любые провода такого вида, но обычно нетрудно найти медные.
- Вам придется нарезать провод на несколько кусков, поэтому убедитесь в том, что у вас достаточно его длины (0,7-1,0 м).
- Мы планируем использовать в качестве электрических устройств лампочки, но также могут быть использованы диоды.
- Выключатель и все остальное вы сможете найти в любом магазине электротоваров или в хозяйственном магазине.
-
3
Подготовьте провода. По проводам будет передаваться питание от батареи к устройствам.
- Разрежьте имеющийся провод на пять кусков (длиной по 15-20 см).
- Осторожно удалите примерно по 1,5 см изоляции с каждого конца всех кусков проводов.
- Лучше всего использовать стриппер для зачистки проводов, но если у вас его нет, то можно применить ножницы или кусачки (только не повредите сам провод).
-
4
Присоедините первую лампочку к батарее. Подключите один из проводов к плюсу на батарее и примотайте второй его конец к левой стороне одной из лампочек. [5]
-
5
Начните присоединять выключатель к батарее. Возьмите другой кусок провода и присоедините его одним концом к минусу батареи. Второй его конец подключите к выключателю. [6]
-
6
Присоедините выключатель к первой лампочке. Взяв другой кусок провода, присоедините его сначала к выключателю, а затем к правой стороне первой лампочки. [7]
-
7
Подсоедините вторую лампочку. Возьмите четвертый кусок провода и прикрепите его одним концом к левой стороне первой лампочки, а затем присоедините другой конец к левой стороне второй лампочки.[8]
-
8
Завершите создание параллельной электроцепи. Взяв последний кусок провода, присоедините его одним концом к правой стороне первой лампочки, а второй конец прикрепите к правой стороне второй лампочки.
-
9
Включите выключатель. Включите выключатель, и вы увидите, что обе лампочки начнут светиться. Поздравляем, вы успешно создали параллельную электрическую цепь!
Реклама
Советы
- Вам может показаться удобным фиксировать все места соединений с помощью изоленты.
Реклама
Предупреждения
- Не используйте высокий вольтаж и большую силу тока в амперах без надлежащей защиты.
- При зачистке концов проводов не повредите сам провод. Лучше всего пользоваться специально предназначенным для этого стриппером.
- Будьте осторожны с лампочками, они достаточно хрупкие.
Реклама
Об этой статье
Эту страницу просматривали 8682 раза.
Была ли эта статья полезной?

Расчет электрической цепи, рассмотренный в предыдущей статье, можно распространить на цепи, содержащие произвольное число приемников, соединенных параллельно.
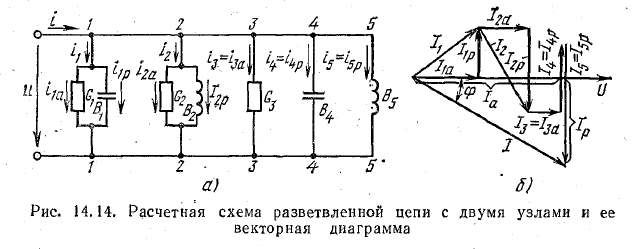
На рис. 14.14, а параллельно соединены те же элементы цепи, которые были рассмотрены при последовательном соединении (см. рис. 14.7, а). Предположим, что для этой цепи известны напряжение u = Umsinωt. и параметры элементов цепи R, L, С. Требуется найти токи в цепи и мощность.
Векторная диаграмма для цепи с параллельным соединением ветвей. Метод векторных диаграмм
Для мгновенных величин в соответствии с первым законом Кирхгофа уравнение токов
Представляя ток в каждой ветви суммой активной и реактивной составляющих, получим
Для действующих токов нужно написать векторное уравнение
Численные значения векторов токов определяются произведением напряжения и проводимости соответствующей ветви.
На рис. 14.14, б построена векторная диаграмма, соответствующая этому уравнению. За исходный вектор принят, как обычно при расчете цепей с параллельным соединением ветвей, вектор напряжения U, а затем нанесены векторы тока в каждой ветви, причем направления их относительно вектора напряжения выбраны в соответствии с характером проводимости ветвей. Начальной точкой при построении диаграммы токов выбрана точка, совпадающая с началом вектора напряжения. Из этой точки проведен вектор l1a активного тока ветви I (по фазе совпадает c напряжением), а из конца его проведен вектор I1p реактивного тока той же ветви (опережает напряжение на 90°). Эти два вектора являются составляющими вектора I1 тока первой ветви. Далее в том же порядке отложены векторы токов других ветвей. Следует обратить внимание на то, что проводимость ветви 3-3 активная, поэтому реактивная составляющая тока в этой ветви равна нулю. В ветвях 4-4 и 5-5 проводимости реактивные, поэтому в составе этих токов нет активных составляющих.
Расчетные формулы для цепи с параллельным соединением ветвей. Метод векторных диаграмм
Из векторной диаграммы видно, что все активные составляющие векторов тока направлены одинаково — параллельно вектору напряжения, поэтому векторное сложение их можно заменить арифметическими найти активную составляющую общего тока: Iа = I1a + I2a + I3a.
Реактивные составляющие векторов токов перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая общего тока в цепи определяется их алгебраической суммой, в которой индуктивные токи считаются положительными, а емкостные — отрицательными: Ip = — I1p + I2p — I4p + I5p.
Векторы активного, реактивного и полного тока всей цепи образуют прямоугольный треугольник, из которого следует
Подставив величины токов в ветвях, выраженные через напряжение и соответствующие проводимости, получим
где ∑Gn — общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей; ∑Bn — общая реактивная
проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;
Таким образом получена знакомая уже формула (14.12), связывающая напряжение, ток и проводимость цепи [ср. (14.12) и (14.8)].
Следует обратить внимание на возможные ошибки при определении полной проводимости цепи по известным проводимостям отдельных ветвей: нельзя складывать арифметически проводимости ветвей, если токи в них не совпадают по фазе.
Полную проводимость цепи в общем случае определяют как гипотенузу прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активная и реактивная проводимости всей цепи:

Активную мощность цепи можно представить как арифметическую сумму активных мощностей ветвей.
Реактивная мощность цепи равна алгебраической сумме мощностей ветвей. В этом случае индуктивная мощность берется положительной, а емкостная — отрицательной:
Расчет цепи без определения проводимостей ветвей
Расчет электрической цепи при параллельном соединении ветвей можно выполнить без предварительного определения активных и реактивных проводимостей, т. е. представляя элементы цепи в схеме замещения их активными и реактивными сопротивлениями (рис. 14.15, а).
Определяют токи в ветвях по формуле (14.4);
где Z1, Z2 и т. д. — полные сопротивления ветвей.
Полное сопротивление ветви, в которую входят несколько элементов, соединенных последовательно, определяют по формуле (14.5).

и т. д. для всех ветвей.
В этом случае отпадает необходимость определения углов ф1 ф2 и построения их на чертеже.
Ток в неразветвленной части цепи
Общий ток и мощность цепи определяются далее в том же порядке, какой был показан ранее (см. формулы (14.10), (14.15), (14.16)].
Задача




Теория / 5.5. Параллельное соединение RLC элементов
Рассмотрим схему, в которой резистор, индуктивность
и емкость подключены к источнику
синусоидального напряжения
Состояние параллельной цепи описывается первым законом
Кирхгофа:
Выразим токи в ветвях через напряжение:
Подставим эти выражения в первый закон Кирхгофа:
Для упрощения расчетов перейдем к символической форме
записи:
Здесь Y – полная комплексная проводимость цепи:
Построим векторную диаграмму (рис. 5.15).
Поскольку ко всем элементам цепи приложено одно и то
же напряжение, то сначала строим вектор напряжения U, затем последовательно суммируем вектора токов, учитывая,
что ток в резистивном элементе совпадает по фазе с напряжением, ток в
индуктивности отстает от напряжения на 90о, ток в емкости опережает
напряжение на 90о.
Из векторной диаграммы можно получить треугольник токов
(рис. 5.16).
Этот треугольник векторный, сторонами его являются
активная составляющая тока Ir, реактивная Ib = Il+Ic, модуль которой равен Ib = Il-Ic и общий ток цепи I.
Из треугольника токов можно найти: модуль общего тока
угол сдвига фаз между напряжением и током
Поделив все стороны треугольника токов на напряжение,
получим подобный ему треугольник проводимостей, катетами которого являются
активная проводимость g, реактивная проводимость, равная разности индуктивной
и емкостной проводимостей b = bL – bC , а гипотенузой – модуль полной проводимости цепи у (рис. 5.17).
Из треугольника проводимостей можно определить: полную проводимость цепи
сдвиг фаз между напряжением и током
активную проводимость
реактивную проводимость
В электронике мы часто можем столкнуться как с последовательными, так и параллельными цепями.
Последовательное соединение – это схема, в которой компоненты соединены в последовательную цепь. Это дает току только один путь, через который он будет течь.
Параллельная цепь – это схема, в которой компоненты соединены параллельно друг другу. Таким образом, ток будет течь несколькими путями.
Часто схема представляет собой смесь последовательных и параллельных соединений.
Последовательные цепи
Ток в последовательных цепях
Ток в последовательной цепи на всем пути одинаков. Одинаковое количество тока протекает через все компоненты. Чтобы найти текущий ток, нужно использовать закон Ома:
I = U/R
Сопротивление в последовательных цепях
Если у вас есть несколько резисторов, соединенных последовательно, очень легко найти общее сопротивление. Все, что вам нужно сделать, это найти сумму всех значений сопротивлений:
Rобщ. = R1+R2+R3
Емкость в последовательных цепях
Конденсаторы, соединенные последовательно, немного сложнее для расчета.
Это формула для расчета значений емкости:
Параллельные цепи
Вычисление сопротивления и емкости в параллельной цепи довольно забавно.
Для параллельного расчета сопротивлений используется тот же метод, который используется для последовательного расчета конденсаторов. И наоборот.
Ток в параллельных цепях
Ток в параллельных цепях может отличаться от пути к пути. Чтобы найти ток в необходимом вам пути, вы используете закон Ома:
I = U/R
Расчет сопротивления в параллельных цепях
Чтобы рассчитать сопротивление в параллельной цепи, используйте следующую формулу:
Расчет емкости в параллельных цепях
Вы рассчитываете емкость в параллельном контуре, просто взяв сумму всех значений емкости.
Сtotal = C1+C2+C3
Все очень просто! 😉
Напишите свои комментарии и вопросы в поле для комментариев ниже. Я буду рад ответить на них.