Как составить параллельный график функции - Сайт, где вы сможете решить свои вопросы

имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.

перпендикулярны при любых значениях свободных членов.

равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).

Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .

При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

где c – произвольное число, и изображены на рис. 13, 14, 15.

Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;

где p, q, r – произвольные числа.

В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

что и требовалось.

откуда вытекает, что уравнение (4) задает прямую линию вида (3).

В случае, когда уравнение (5) решений вообще не имеет.

Замечание 2 . При любом значении r₁ , не совпадающем с r прямая линия, заданная уравнением

параллельна прямой, заданной уравнением (4) .

Замечание 3 . При любом значении r₂ прямая линия, заданная уравнением

перпендикулярна прямой, заданной уравнением (4) .

Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и

В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде

где r₁ – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство

В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде

где r₂ – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b₁ и y = kx + b₂ ,

имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны .

имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.

y = kx + b₁ и

перпендикулярны при любых значениях свободных членов.

Угловой коэффициент прямой линии

Рис.10

Рис.11

Рис.12

Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .

При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

Прямые, параллельные оси ординат

Прямые, параллельные оси Oy , задаются формулой

где c – произвольное число, и изображены на рис. 13, 14, 15.

Рис.13

Рис.14

Рис.15

Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

где p, q, r – произвольные числа.

В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

что и требовалось.

В случае, когда получаем:

откуда вытекает, что уравнение (4) задает прямую линию вида (3).

В случае, когда q = 0, p = 0, уравнение (4) имеет вид

и при r = 0 его решением являются точки всей плоскости:

В случае, когда уравнение (5) решений вообще не имеет.

Замечание 2 . При любом значении r₁ , не совпадающем с r прямая линия, заданная уравнением

параллельна прямой, заданной уравнением (4) .

Замечание 3 . При любом значении r₂ прямая линия, заданная уравнением

перпендикулярна прямой, заданной уравнением (4) .

Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и

параллельной к прямой
перпендикулярной к прямой (8).

В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде

Итак, уравнение прямой, параллельной к прямой

В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде

График линейной функции, его свойства и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0;
и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».

Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!

Свойства линейной функции

Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит y = b — четная;
b = 0, k ≠ 0, значит y = kx — нечетная;
b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (-b/k, 0);
ось ординат OY — в точке (0; b).
x=-b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, — b /_k) и положительные значения на промежутке (- b /_k, +∞)
При k b /_k, +∞) и положительные значения на промежутке (-∞, — b /_k).
Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
Если k > 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1 /₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 1 /₂x + 3, y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Теперь рассмотрим графики функций y = -2x + 3, y = — 1 /₂x + 3, y = -x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
график функции y = 2x — 2 (b = -2) пересекает ось OY в точке (0; -2).

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = — b /_k.
Координаты точки пересечения с осью OX: (- b /_k; 0)

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
2 = -4(-3) + b
b = -10
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.

Уравнение параллельной прямой

Альтернативная формула:
Прямая, проходящая через точку M₁(x₁; y₁) и параллельная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).

Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника 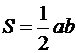, где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
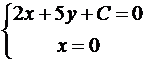
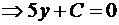
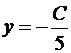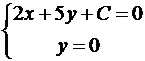
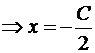Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 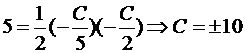. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /₇x – 4 /₇ (здесь a = 5 /₇). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .

Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.

Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).

[spoiler title=”источники:”]

http://www.resolventa.ru/spr/algebra/degree1.htm

http://b4.cooksy.ru/articles/kak-zapisat-uravnenie-pryamoy-parallelnoy-grafiku-funktsii

[/spoiler]

Источник

1) Найти точку пересечения прямых:

y=2,5−0,5x

y=−5x−2

Для построения графика каждой линейной функции составим таблицу значений.

Для функции

y=2,5−0,5x

имеем:

(x)	(0)	(5)
(y)	(2,5)	(0)

Через полученные точки проведём прямую

Для функции

y=−5x−2

имеем:

(x)	(0)	(-0,4)
(y)	(-2)	(0)

Через полученные точки проведём прямую

Прямые

пересекаются в точке (А(-1;3)).

2) Определить, в какой точке пересекаются прямые:

y=2x−3

y=2x+1

Угловые коэффициенты линейных функций одинаковые (k=2), то есть прямые

y=2x−3

y=2x+1

параллельные, они не пересекаются.

3) Определить, в какой точке пересекаются прямые:

y=3x+11

y=−x+11

Угловые коэффициенты данных линейных функций различны:

k1=3

k2=−1

— прямые пересекаются в одной точке.

Можно заметить, что обе прямые проходят через точку ((0; 11)).

Значит, точка ((0;11)) и есть точка пересечения данных

прямых.

Источник

В этой статье мы рассмотрим линейную функцию, график линейной функции и его свойства. И, как обычно, решим несколько задач на эту тему.

Линейной функцией называется функция вида y=kx+b

В уравнении функции число , которое мы умножаем на называется коэффициентом наклона.

Например, в уравнении функции y=-2x+3 ;

в уравнении функции y=-2+3x ;

в уравнении функции y=-x ;

в уравнении функции y=5 .

Графиком линейной функции является прямая линия.

1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции , удобно взять x=0 и x=3 , тогда ординаты эти точек будут равны y=2 и y=3 .

Получим точки А(0;2) и В(3;3). Соединим их и получим график функции :

2. В уравнении функции y=kx+b коэффициент отвечает за наклон графика функции:

Коэффициент отвечает за сдвиг графика вдоль оси :

На рисунке ниже изображены графики функций y=2x+3 ; ; y=x+3

Заметим, что во всех этих функциях коэффициент больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение , тем круче идет прямая.

Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций y=-2x+3 ; ; y=-x+3

На этот раз во всех функциях коэффициент меньше нуля, и все графики функций наклонены влево.

Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций y=2x+3 ; y=2x ; y=2x-2

Теперь во всех уравнениях функций коэффициенты равны. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)

График функции y=2x (b=0) пересекает ось OY в точке (0;0) – начале координат.

График функции y=2x-2 (b=-2) пересекает ось OY в точке (0;-2)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b .

Если k<0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b<0, то график функции y=kx+b имеет вид:

Если k<0 и b<0, то график функции y=kx+b имеет вид:

Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:

Ординаты всех точек графика функции y=b равны

Если b=0, то график функции y=kx проходит через начало координат:

Это график прямой пропорциональности.

3. Отдельно отмечу график уравнения x=a . График этого уравнения представляет собой прямую линию, параллельую оси все точки которой имеют абсциссу x=a .

Например, график уравнения x=3 выглядит так:

Внимание! Уравнение x=a не является функцией, так как различным значениям функции соответствует одно и то же значение аргумента, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции $y=k_1{x}+b_1$ параллелен графику функции $y=k_2{x}+b_2$ , если k_1=k_2

5. Условие перпендикулярности двух прямых:

График функции $y=k_1{x}+b_1$ перпендикулярен графику функции $y=k_2{x}+b_2$ , если или $k_1=-1/{k_2}$

6. Точки пересечения графика функции с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k . То есть точка пересечения с осью OX имеет координаты ( -b/k ;0):

Рассмотрим решение задач.

1. Постройте график функции , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.

В уравнении функции y=kx+b два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.

а) Из того, что график функции y=kx+b параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид y=-4x+b

б) Нам осталось найти b. Известно, что график функции y=-4x+b проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:

отсюда b=-10

Таким образом, нам надо построить график функции

Точка А(-3;2) нам известна, возьмем точку B(0;-10)

Поставим эти точки в координатной плоскости и соединим их прямой:

2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).

Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой y=kx+b . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y=kx+b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k=3 . Подставим значение k в первое уравнение системы, и получим b=-2.

Итак, уравнение прямой y=3x-2 .

3. Постройте график уравнения

Чтобы найти, при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учесть ОДЗ каждого множителя.

Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений:

Построим графики всех уравнений совокупности в одной коорднатной плоскости. Это и есть график уравнения :

4. Постройте график функции , если он перпендикулярен прямой и проходит через точку М(-1;2)

Мы не будем строить график, только найдем уравнение прямой.

а) Так как график функции y=kx+b , если он перпендикулярен прямой , следовательно , отсюда k=2 . То есть уравнение функции имеет вид y=2x+b

б) Мы знаем, что график функции y=2x+b проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:

, отсюда b=4 .

Следовательно, наша функция имеет вид: y=2x+4 .

5. Постройте график функции $y=(x^2-1)(1/{x-1}-1/{x+1})+x$

Упростим выражение, стоящее в правой части уравнения функции.

Важно! Прежде чем упрощать выражение, найдем его ОДЗ.

Знаменатель дроби не может быть равен нулю, поэтому x<>1 , x<>-1 .

$(x^2-1)(1/{x-1}-1/{x+1})+x =$

Тогда наша функция принимает вид:

То есть нам надо построить график функции y=x+2 и выколоть на нем две точки: с абсциссами x=1 и x=-1:

И.В. Фельдман, репетитор по математике.

Источник

§ 1 Взаимное расположение графиков линейных функций

Из курса геометрии мы знаем, что 2 прямые на плоскости могут совпадать, т.е. иметь бесконечно много общих точек; пересекаться, т.е. иметь одну общую точку или не пересекаться, т. е. не иметь ни одной общей точки. Такие прямые называются параллельными.

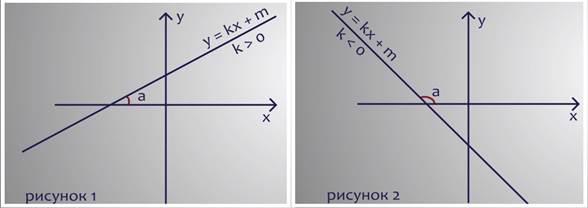
Линейная функция задаётся равенством вида у = kх + m. Коэффициент k называют угловым коэффициентом. Он «отвечает» за угол наклона прямой относительно положительного направления оси х. Если k > 0, то угол наклона острый (как на рисунке 1), если k < 0, то угол наклона тупой (как на рисунке 2).

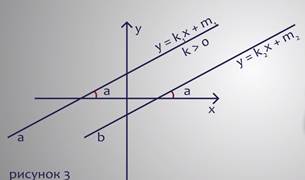
А теперь посмотрим на рисунок 3. На нём изображены 2 прямые, заданные уравнениями у = k1 + m1 и у = k2 + m2. Предположим, что k1 = k2. Это означает, что углы наклона прямой одинаковы. Это соответственные углы, а значит данные нам прямые параллельны по признаку параллельных прямых.

Таким образом, если 2 линейные функции имеют одинаковый угловой коэффициент, то их графики будут параллельны. Если же угловые коэффициенты не равны, то графики будут пересекаться.

Например, даны линейные функции, заданные формулами у = 2х – 1 и у = 2х + 3. Как будут располагаться на плоскости их графики по отношению друг к другу? Так как угловой коэффициент первой функции k1 = 2 и угловой коэффициент второй функции k2 = 2, то графики будут параллельны.

Или другая пара: у = х – 3 и у = 2х + 3. У первой функции коэффициент k1 = 1, а у второй функции коэффициент k2 = 2. Это неравные коэффициенты, поэтому графики этих функций будут пересекаться. А в каком же случае прямые будут совпадать?

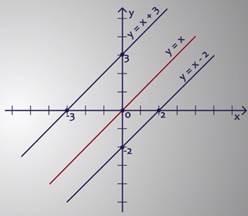
Для ответа надо сначала ответить на другой вопрос: а за что «отвечает» коэффициент m? Давайте посмотрим на рисунок, на котором изображены графики трёх функций:

у = х, у = х + 3 и у = х – 2.

У всех трёх функций угловой коэффициент k= 1, т. е. графики параллельны. Но обратите внимание: график функции у = х проходит через начало координат, здесь m = 0. График функции у = х + 3 получен сдвигом графика у = х на 3 единицы вверх, как показывает коэффициент m = 3.

График функции у = х – 2 получен сдвигом графика у = х на 2 единицы вниз, как показывает коэффициент m = –2. Иначе говоря, коэффициент m отвечает за параллельный перенос графика у = kх относительно начала координат на m единиц вдоль оси у.

Теперь можно ответить на поставленный вопрос. 2 прямые будут совпадать, если у них одинаковые угловые коэффициенты и коэффициент m1равен коэффициенту m2.

§ 2 Краткие итоги по теме урока

Графики линейных функций по отношению друг к другу на плоскости могут быть параллельны, если угловые коэффициенты k1 и k2 равны, а коэффициенты m1 и m2 различны. Могут пересекаться в случае, когда угловые коэффициенты k1 и k2 не равны. А также могут совпадать, если угловые коэффициенты k1 и k2 равны и коэффициенты m1 и m2 так же равны. График функции у = kх проходит через начало координат, т. к. коэффициент m = 0, а график функции у = kх + m проходит через точку (0; m).

Источник

Параллельный перенос, сжатие и растяжение графиков. Построение графиков с модулями.

Графики многих функций можно получить из ранее рассмотренных с помощью элементарных геометрических преобразований: параллельного переноса, сжатия, растяжения, симметричного отображения. Рассмотрим некоторые из этих преобразований. Для каждого из элементарных преобразований предлагается два способа построения графика: с помощью преобразования графика и с помощью преобразования системы координат. Обучающийся должен выбрать тот, который кажется ему проще и овладеть им. В каждом случае считается известным график функции у = f(х).

Параллельный перенос графиков

График функции у = /(x) + Ь получается из графика функции у = f(х) с помощью его переноса на вектор b = (0; b). Действительно, в этом случае ко всем ординатам графика у = f(х) прибавляется величина b, что означает сдвиг графика вдоль оси Оу. Если b > 0, то график функции у = f(х) переносится вверх параллельно оси Oy на b, если b < 0, то график функции у = f(x) переносится вниз параллельно оси Oy на |b| (рис. 49). Заметим, что вместо переноса графика, можно перенести в противоположном направлении ось Ox (если b > 0 — вниз, если b < 0 — вверх), прибавив ко всем значениям по оси Oy величину b.

Рис. 49. Построение графика функции у = f(x) + b

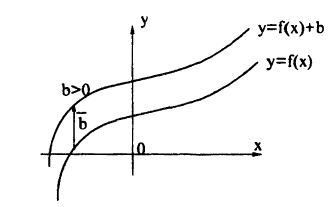
Пример:

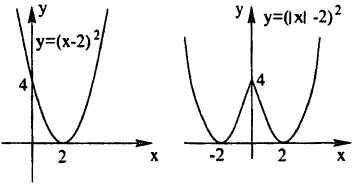
График функции у = x² — 1 (рис. 50) смещен на 1 вниз параллельно оси Oy относительно графика функции у = х².

Рис. 50. Построение графика функции у = x² — 1

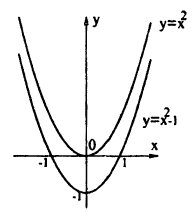
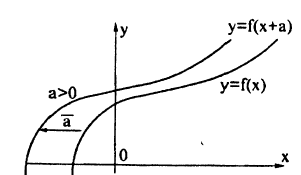
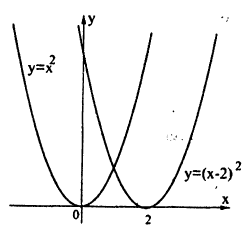
График функции у = f(x+a) получается с помощью переноса графика функции у = f(x) на вектор а = (—а;0). Действительно, перейдя к новым координатам X = х + α, Y = у параллельным переносом вдоль оси Ox на —а, заметим, что относительно новых координат получится исходный график функции Y = f(X). Если а > 0, то старые координаты получаются из новых сдвигом направо вдоль оси Ox на α, т.к. х = X — а. Если же сдвигать график, а не систему координат, то его нужно двигать в противоположном направлении — налево. Итак, если а > 0, то график функции у = f(x) переносится налево параллельно оси Ox на а, если а < 0, то график функции у = f(x) переносится направо вдоль оси Ox на ∣α∣ (рис. 51). Вместо переноса графика можно перенести в противоположном направлении ось Oy (если α > 0 — вправо, если α < 0 — влево), отняв от всех значений по оси Ox величину а.

Пример:

График функции у = (x- 2)² смещен на 2 ед. вправо параллельно оси Ox относительно графика функции у = х². (рис. 52).

Рис. 51. Построение графика функции у = f(x + а)

Рис. 52. Построение графика функции у = (х — 2)²

Сжатие и растяжение графиков

График функции у = kf(x), где к ∈ R, получается с помощью ’’растяжения” графика функции у = f(x) в к раз в направлении от оси Ох. ’’Растяжение” здесь понимается как умножение на к ординат всех точек графика у = f(x)∙ При k > 1 это будет действительно растяжение в к раз от оси Ox вдоль оси Оу. При 0 < k < 1 это будет сжатие в 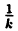раз к оси Ox вдоль оси Оу. При k ≤ -1 это будет растяжение в ∣k∣ раз с последующим симметричным отображением относительно оси Ox (перевернуть сверху вниз); при -1 ≤ k < 0 это будет сжатие в 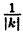раз и симметрия относительно оси Ox ( рис. 53). В частности, график функции у = —f(x) получается симметричным отображением относительно оси Ox графика функции у = f(x).

Вместо преобразования графика при k > 0 можно исправить значения по оси Оу, умножив их на k. При k < 0 в этом случае пришлось бы менять направление оси, что неудобно; лучше перевернуть график сверху вниз.

График функции у = f(kx), где k ∈ R, получается с помощью ’’сжатия” графика у = f(x) в к раз в направлении к оси Оу. ’’Сжатие” здесь понимается как деление на к абсцисс всех точек графика у = f(x). Действительно, если, например, f(1) =0, то, сделав замену X = kх, Y = у, получим, что функция у = f(kx) обращается в нуль при kх = 1, т.е. при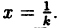

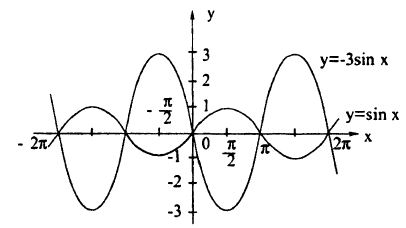
Рис. 53. Построение графика функции у = — 3 sin х

При k > 1 график функции у = f(x) сжимается в k раз к оси Oy вдоль оси Ох; при 0 < k < 1 график функции у = f(x) растягивается в 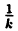раз от оси Oy вдоль оси Ох; при k ≤ — 1 исходньй график сжимается в |k| раз и симметрично отражается относительно оси Oy (слева направо); при -1 ≤ k < 0 исходный график растягивается в 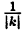раз с последующей симметрией относительно оси Оу.

В частности, график функции у = f(-x) получается из графика функции у = f(-x) симметрией относительно оси Оу.

Вместо преобразования графика при k > 0 можно исправить значения по оси Ох, поделив их на k. При k < 0 в этом случае следует предварительно перевернуть график слева направо.

Пример:

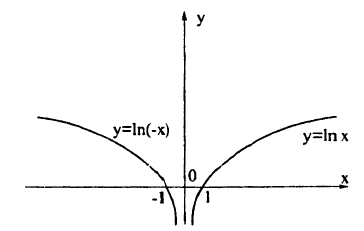
График функции у = cos 2х получается из графика у = cos х сжатием в 2 раза к оси Оу; график функции у = ln(—х) получается из графика у = ln х симметрией относительно оси Oy ( рис. 54).

Рис. 54. Построение трафика функции у = ln(-х)

Пользуясь изложенными методами, приведем последовательность преобразований при построении графика функции у = f(kx + b), если дан график функции у = f(x):

нарисовать график функции у = f(x);
получить график функции у = f(x + b), сдвинув исходный на вектор b = (-b; 0), как описано в п. 5.1;
получить график функции у = f(kx + b), “сжав” предыдущий в к раз к оси Оу, как описано выше.

Пример:

Написать последовательность преобразований и построить график функции у = .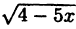

Решение:

Построение графика показано на рис. 55

Замечание:

Теперь понятно, что если функция у = f(x) периодическая с периодом Т, то функция у = К ∙ f(kx + b) + а тоже периодическая с периодом T₁ = 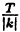. (п. 3.5 лекции 3). Действительно, график последней функции получается из исходного сдвигом вдоль оси Ох, что не меняет период, последующим “сжатием“ вдоль оси Ох, что “уменьшает» период в |k| раз (период T делится на |k|), и окончательным умножением всех ординат на К с последующим прибавлением а, что также не изменяет получившийся период T₁ =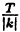

Построение графиков с модулями

График функции у = ∣f(x)∣ получается из графика функции у = f(x) следующим образом (рис. 56)

все части графика функции у = f(x), лежащие ниже оси Ох, следует отобразить вверх симметрично относительно этой оси;
оставшиеся внизу части исходного графика следует стереть.

Действительно, по определению модуля действительного числа имеем:
(5.1)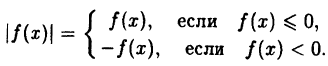

Таким образом, те участки исходного графика, которые лежат не ниже оси Ox (f(x) ≥ 0), менять не нужно, а для тех участков, которые лежат ниже оси Ох, нужно построить функцию у = —f(x). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Ох. Заметим, что полученный график лежит не ниже оси Ох, что естественно, т.к. |f(x)| ≥ 0 для ∀x ∈ D(f).

Рис. 55. Построение графика функции у =

Рис. 56. Построение графика функции у = |f(x)|

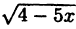
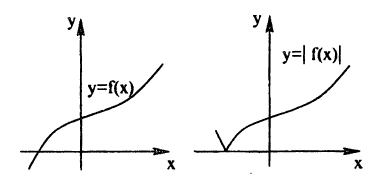
Пример:

Построение графика функции у = |х² — 1| показано на рис. 57.

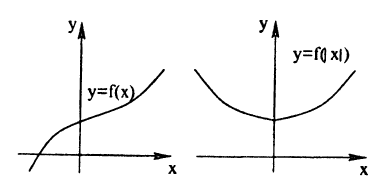
График функции у = f (|x|) получается из графика функции у = f(х) следующим образом (рис. 58):

все части графика функции у = f(x), лежащие слева от оси Оу, следует стереть;
о оставшуюся часть графика следует отобразить налево симметрично относительно оси Оу.

Действительно, по определению модуля действительного числа имеем:
(5.2)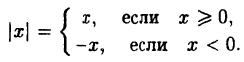

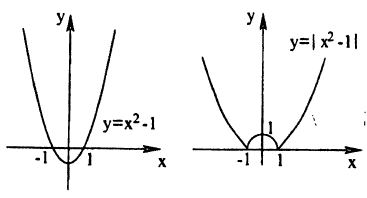
Рис. 57. Построение графика функции у = |x² — 1|

Таким образом, не нужно изменять те участки исходного графика, для которых х ≥ 0, а для х<0 (слева от оси Оу) следует построить график функции у = f(—х). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Оу. Заметим, что полученный график симметричен относительно оси Оу, что естественно, т.к. функция у = f(|x|) четная (докажите самостоятельно).

Рис. 58. Построение графика функции у = f(|x|)

Пример:

Построение графика функции у = (|x| — 2)² показано на рис. 59

Элементарными методами можно строить эскизы графиков более сложных функций.

Пример:

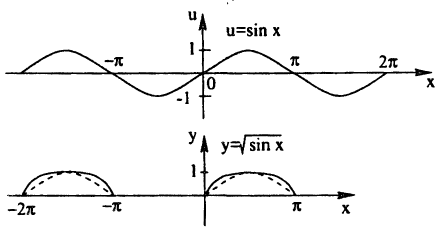
Построить эскиз графика у =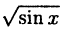

Решение:

Построение графика показано на рис. 60. Заметим, что график отсутствует там, где sin х < О, так как D(x) = {x| sin х ≥ 0}

Рис. 59. Построение графика функции у = (∣x∣ — 2)²

Кроме того, так как √u > и при 0 < u < 1, то график у = 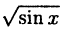(сплошная линия) будет лежать не ниже графика у = sin x (пунктирная линия), если их нарисовать в одних осях.

Рис. 60. Построение графика функции у = √sinx

Построение графиков функций с примерами

Пример:

C помощью элементарных преобразований постройте график функции: у = x² — х — 2.

Решение:

Выделим полный квадрат из правой части уравнения функции: у = x² — х — 2 ⇔ y = x²-x+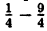 ⇔ у = 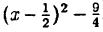. График этой функции получается следующей последовательностью элементарных преобразований (рис. 61):
1) y =x²
2) у =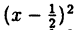. Сдвиг вправо вдоль Ox на .
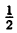3) у = 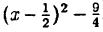. Сдвиг вниз вдоль Oy на .

Рис. 61. Построение графика функции у = x² — х — 2

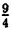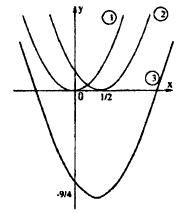
Пример:

Используя сложение, деление функций, постройте график функции: у = х + .

Решение:

В одних осях координат нарисуем графики следующих функций (рис. 62):
1) у = х,
2) y=,
3) y = x + .

Рис. 62. Построение графика функции у = х +

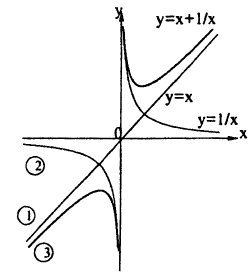
Пример:

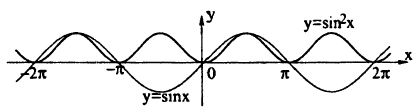
Постройте график сложной функции у = sin² х.

Решение:

В одних осях координат нарисуем графики функций:

1) y = sin x,
2) y = sin² х.

Учитывая, что квадрат числа меньшего единицы, меньше исходного числа, получим график (рис. 63)

Рис. 63. Построение графика функции у = sin² х

Пример:

Постройте график функции в полярной системе координат: r = 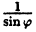(прямая линия).

Решение:

Вычислим значения г для некоторых значений ∈ (0; π) — см. таблицу.

	0
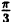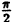r	∞	2			∞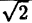

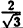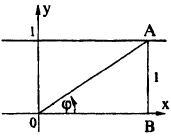
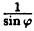
Рис. 64. График функции r =

Соединив плавной линией найденные точки, получим линию вдоль оси Ох, проходящую через точку (0;1). Докажем что эта линия — прямая (рис. 64). Действительно: из Δ ОAВ ⇒ cos = = 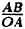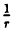⇒ r = .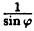

Пример:

Постройте линию, описываемую уравнением, у =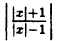

Решение:

Сначала построим график функции у =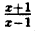 (рис. 65). Затем, пользуясь определением |x| (2.1), строим график (рис. 66) функции у =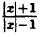

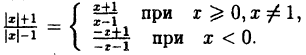
Наконец, строим линию описываемую уравнением у = 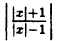(рис. 67):

Рис. 65. График функции у =

Рис. 66. График функции у =

Рис. 67. График функции у =

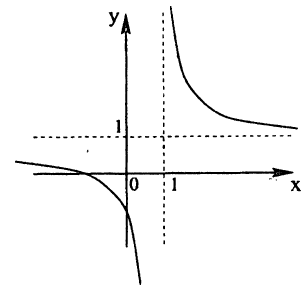
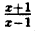
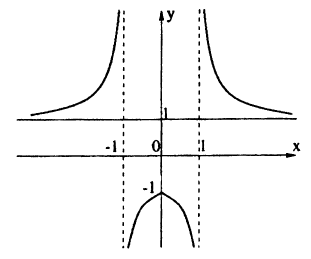
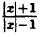
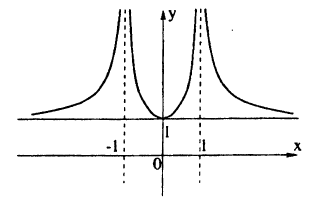
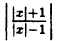
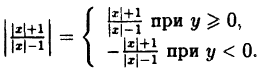
Пример:

Постройте линию, описываемую уравнением у =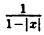

Решение:

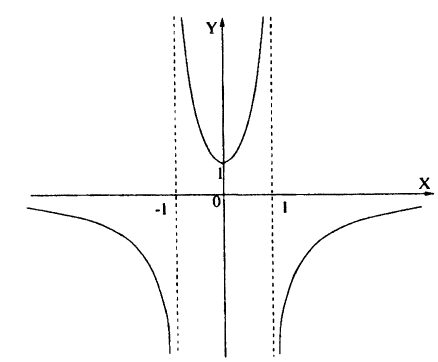
Для построения графика данного примера сначала постройте график функции у =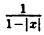. Затем, в соответствии с определением |х|, сотрите ту часть графика, которая расположена слева от оси Оу, а оставшуюся справа часть, отразите симметрично оси Оу.

Ответ: рис. 68.

Рис. 68. График функции у =

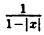
Пример:

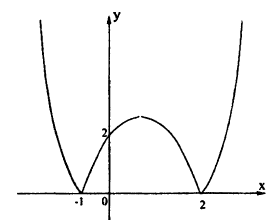
Постройте линию, описываемую уравнением у = |х² — х -2|.

Решение:

Для построения графика данного примера сначала постройте график функции у = х² — х — 2. Затем отразите симметрично оси Ox ту часть графика, которая осталась снизу от оси Ох. Затем сотрите ту часть графика, которая расположена в нижней полуплоскости.

Ответ: рис. 69.

Рис. 69. График функции у = |х² — х — 2|

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

Прямые, параллельные оси ординат

Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

График линейной функции, его свойства и формулы

Понятие функции

Понятие линейной функции

Свойства линейной функции

Построение линейной функции

Решение задач на линейную функцию

Уравнение параллельной прямой

Параллельный перенос графиков

Сжатие и растяжение графиков

Построение графиков с модулями

Построение графиков функций с примерами

Вам также может понравиться

Как найти пароль от wifi iphone

Как найти интернет героя

Как составить задачу на движение вдогонку 4 класс

Добавить комментарий Отменить ответ