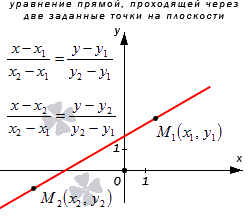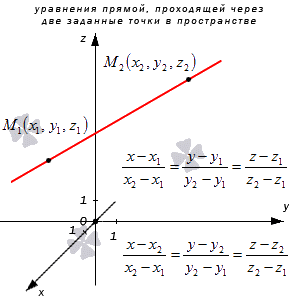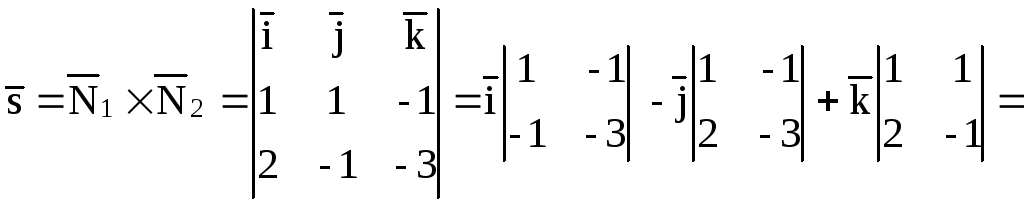Как составить параметрическое уравнение прямой проходящей через две точки

Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.

Уравнение прямой, проходящей через две заданные точки на плоскости

Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.

Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.

Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a, проходящей через две несовпадающие точки M1(x1, y1) и M2(x2, y2), находящиеся в декартовой системе координат.

В каноническом уравнении прямой на плоскости, имеющего вид x-x1ax=y-y1ay, задается прямоугольная система координат Оху с прямой, которая пересекается с ней в точке с координатами M1(x1, y1) с направляющим вектором  a→=(ax, ay).

Необходимо составить каноническое уравнение прямой a, которая пройдет через две точки с координатами M1(x1, y1) и M2(x2, y2).

Прямая а имеет направляющий вектор M1M2→ с координатами(x2-x1, y2-y1), так как пересекает точки М1 и М2. Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение  с координатами направляющего вектора M1M2→=(x2-x1, y2-y1) и координатами лежащих на них точках M1(x1, y1) и M2(x2, y2). Получим уравнение вида x-x1x2-x1=y-y1y2-y1 или x-x2x2-x1=y-y2y2-y1.

Рассмотрим рисунок, приведенный ниже.

Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M1(x1, y1) и M2(x2, y2). Получим уравнение вида x=x1+(x2-x1)·λy=y1+(y2-y1)·λ или x=x2+(x2-x1)·λy=y2+(y2-y1)·λ.

Рассмотрим подробней на решении нескольких примеров.

При необходимости  решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.

Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y=kx+b. Если необходимо найти значение углового коэффициента k и числа b, при которых уравнение y=kx+b определяет линию в системе Оху, которая проходит через  точки M1(x1, y1) и M2(x2, y2), где x1≠x2. Когда x1=x2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М1М2 определена общим неполным уравнением вида x-x1=0.

Потому как точки М1 и М2 находятся на прямой, тогда их координаты удовлетворяют уравнению y1=kx1+bи y2=kx2+b. Следует решить систему уравнений y1=kx1+by2=kx2+b относительно k и b.

Для этого найдем k=y2-y1x2-x1b=y1-y2-y1x2-x1·x1 или k=y2-y1x2-x1b=y2-y2-y1x2-x1·x2.

С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y=y2-y1x2-x1·x+y2-y2-y1x2-x1·x1 или y=y2-y1x2-x1·x+y2-y2-y1x2-x1·x2.

Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве

Если в трехмерном пространстве имеется прямоугольная система координат Охуz с двумя заданными несовпадающими точками с координатами M1(x1, y1, z1) и M2(x2, y2, z2), проходящая через них прямая M1M2, необходимо получить уравнение этой прямой.

Имеем, что канонические уравнения вида x-x1ax=y-y1ay=z-z1az и параметрические вида x=x1+ax·λy=y1+ay·λz=z1+az·λспособны задать линию в системе координат Охуz, проходящую через точки, имеющие координаты (x1, y1, z1) с направляющим вектором a→=(ax, ay, az).

Прямая M1M2 имеет направляющий вектор вида M1M2→=(x2-x1, y2-y1, z2-z1), где прямая проходит через точку M1(x1, y1, z1) и M2(x2, y2, z2), отсюда каноническое уравнение может быть вида x-x1x2-x1=y-y1y2-y1=z-z1z2-z1 или x-x2x2-x1=y-y2y2-y1=z-z2z2-z1, в свою очередь параметрические x=x1+(x2-x1)·λy=y1+(y2-y1)·λz=z1+(z2-z1)·λ или x=x2+(x2-x1)·λy=y2+(y2-y1)·λz=z2+(z2-z1)·λ.

Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве  и уравнение прямой.

Суть уравнения прямой, проходящей через две заданные точки

Можно представить, что на плоскости с координатами Oxy расположена пара точек: (M_{0}(x_{0},y_{0})), (M_{1}(x_{1},y_{1}))

Необходимо сделать вывод формулы для прямой, которая пересекает эти заданные точки.

Точка (М (х, у)) соответствует прямой (M_{0} M_{1}) только в том случае, когда ее радиус-вектор (vec{OM}) соответствует следующему условию:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(vec{OM}=left(1-t right)times vec{OM_{0}}+ttimes vec{OM_{1}})

Где t является некоторым действительным числом (параметром). Координатная форма уравнения имеет следующий вид:

Данное равенство в алгебре называют аффинным уравнением прямой с пересечением двух точек в пространстве: (M_{0}(x_{0},y_{0})) и (M_{1}(x_{1},y_{1})).

Определив параметр t с помощью первого и второго уравнений системы, можно получить доказательство следующего соотношения:

(frac{x-x_{0}}{x_{1}-x_{0}}=t=frac{y-y_{0}}{y_{1}-y_{0}})

Если исключить коэффициент t, то можно вывести уравнение прямой, проходящей через две точки: (M_{0}(x_{0},y_{0})) и (M_{1}(x_{1},y_{1})).

Формула будет иметь следующий вид:

(frac{x-x_{0}}{x_{1}-x_{0}}=frac{y-y_{0}}{y_{1}-y_{0}})

Данное равенство вытекает из канонического уравнения, если выбрать направляющим вектором:

(vec{p}=avec{i}+bvec{j})

Вектор (vec{M_{0}M_{1}}) будет равен:

(vec{M_{0}M_{1}}=left(x_{1}-x_{0} right)vec{i}+left(y_{1}-y_{0} right)vec{j})

То есть, замещая следующие параметры:

(a=x_{1}-x_{0})

(b=y_{1}-y_{0})

Уравнение прямой в отрезках

Пусть координатные оси включают две точки: (X_{1}left(x_{1},0 right)) и (Y_{1}left(0, y_{1} right))

Следует отметить следующее условие:

(x_{1}neq 0)

(y_{1}neq 0)

Необходимо записать уравнение прямой, которая проходит через заданные точки, подставив в формулу:

(x_{0}=x_{1})

(y_{0}=0)

(x_{1}=0)

(y_{1}=y_{1})

В результате уравнение принимает следующий вид:

(frac{x-x_{1}}{0-x_{1}}=frac{y-0}{y_{1}-0}Leftrightarrow -frac{x}{x_{1}}+1=frac{y}{y_{1}}Leftrightarrow 1=frac{x}{x_{1}}+frac{y}{y_{1}})

Если поменять местами правую и левую части уравнения, то равенство примет такой вид:

(frac{x}{x_{1}}+frac{y}{y_{1}}=1)

(x_{1}neq 0)

(y_{1}neq 0)

Данную формулу называют уравнением прямой в отрезках. С помощью прямой, которая пересекает точки: (X_{1}left(x_{1},0 right)) и (Y_{1}left(0, y_{1} right))

координатные оси делят на отрезки х₁ на оси абсцисс и у₁ на оси ординат. Длины отрезков будут рассчитаны следующим образом:

(OX_{1}=left|x_{1} right|)

(OY_{1}=left|y_{1} right|)

Как записать формулу, канонический вид

Какой-либо вектор, отличный от нуля, проходит по данной прямой или параллельно ей, называют направляющим вектором этой прямой. Для обозначения направляющего вектора произвольной прямой используют букву (bar{a})

Координаты данного вектора обозначают с помощью букв l, m, n. Таким образом, можно прийти к следующему уравнению:

(bar{a}=left{l; m; n right})

При известном значении одной точки (M_{0}left(x_{0};y_{0};z_{0} right)) и направляющего вектора (bar{a}=left{l; m; n right}) прямой, то для нее будут записаны следующие уравнения:

(frac{x-x_{0}}{l}=frac{y-y_{0}}{m}=frac{z-z_{0}}{n})

Уравнение в таком виде называют каноническим.

Параметрическое уравнение прямой, проходящей через две точки

Канонические уравнения для прямой, которая пересекает следующие точки:

(M_{1}left(x_{1};y_{1};z_{1} right))

(M_{2}left(x_{2};y_{2};z_{2} right))

будет записано в следующем виде:

(frac{x-x_{1}}{x_{2}-x_{1}}=frac{y-y_{1}}{y_{2}-y_{1}}=frac{z-z_{1}}{z_{2}-z_{1}})

Равные отношения можно обозначить буквой t в канонических уравнениях. В итоге они приобретают такой вид:

(frac{x-x_{0}}{l}=frac{y-y_{0}}{m}=frac{z-z_{0}}{n}=t)

Исход из этого, получается равенство:

(x=x_{0}+lt)

(y=y_{0}+mt)

(z=z_{0}+nt)

Данные равенства являются параметрическими уравнениями прямой, которая пересекает точку (M_{0}left(x_{0};y_{0}; z right)) в направлении вектора (bar{a}=left{l; m; n right})

В данном случае t является произвольно изменяющимся параметром, x, y, z представляют собой функции от t. Если изменяется t, то значения x, y, z также меняются. Таким образом, точка M (x; y; z) перемещается вдоль прямой. Если параметр t использовать в качестве переменного времени, а уравнения представить в виде формул, описывающих движение точки М, то с помощью данных уравнений можно определить прямолинейное и равномерное движение точки М. При t равным 0 точка М будет совпадать с точкой M₀.

Скорость V точки М обладает постоянным значением и рассчитывается по формуле:

(V=sqrt{l^{2}+m^{2}+n^{2}})

Примеры задач с решением

Задача 1

Необходимо построить прямую, которая проходит через следующие точки: А (2, 1, 1), В (3, 1, -2).

Решение

Уравнение прямой, которая проходит через точки:

(Aleft(x_{1},y_{1},z_{1} right))

(Bleft(x_{2},y_{2},z_{2} right))

будет иметь следующий вид:

(frac{x-x_{1}}{x_{2}-x_{1}}=frac{y-y_{1}}{y_{2}-y_{1}}=frac{z-z_{1}}{z_{2}-z_{1}})

После того, как координаты точек А и В будут применены к первому уравнению, оно будет записано в такой форме:

(frac{x-2}{3-2}=frac{y-1}{1-1}=frac{z-1}{-2-1})

После некоторых преобразований получается:

(frac{x-2}{1}=frac{y-1}{0}=frac{z-1}{-3})

В данном случае наличие ноля в знаменателе не обозначает деление на ноль. Параметрическое уравнение прямой будет записано таким образом:

(t=frac{x-2}{1})

(t=frac{ y-1}{0})

(t=frac{z-1}{-3})

Если выразить переменные x, y, z с помощью параметра t, в итоге получится:

(x = t + 2)

(y = 1)

(z = -3 * t + 1)

Ответ: каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2), будет записано в следующем виде:

(frac{x-2}{1}=frac{y-1}{0}=frac{z-1}{-3})

Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2), будет записано в следующем виде:

(x = t + 2)

(y = 1)

(z = -3 * t + 1)

Задача 2

Требуется построить прямую, которая проходит через точки А (1, 1/5, 1) и В (-2, 1/2, -2).

Решение

Уравнение для прямой, которая пересекает заданные точки:

(Aleft(x_{1},y_{1},z_{1} right))

(Bleft(x_{2},y_{2},z_{2} right))

будет записано таким образом:

(frac{x-x_{1}}{x_{2}-x_{1}}=frac{y-y_{1}}{y_{2}-y_{1}}=frac{z-z_{1}}{z_{2}-z_{1}})

После подстановки координат точек А и В в исходную формулу, она приобретет такой вид:

(frac{x-1}{-2-1}=frac{y-frac{1}{5}}{frac{1}{2}-frac{1}{5}}=frac{z-1}{-2-1})

или

(frac{x-1}{-3}=frac{y-frac{1}{5}}{frac{3}{10}}=frac{z-1}{-3})

Далее можно записать параметрическое уравнение прямой:

(t=frac{x-1}{-3})

(t=frac{y-frac{1}{5}}{frac{3}{10}})

(t=frac{z-1}{-3})

Выразив переменные x, y, z с помощью параметра t, можно получить следующее уравнение:

(x=-3times t+1)

(y=frac{3}{10}t+frac{1}{5})

(z=-3times t+1)

Ответ: каноническое уравнение прямой, пересекающей заданные точки A(1, 1/5, 1) и B(−2, 1/2, −2) записано в следующем виде:

(frac{x-1}{-3}=frac{y-frac{1}{5}}{frac{3}{10}}=frac{z-1}{-3})

параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

(x=-3times t+1)

(y=frac{3}{10}t+frac{1}{5})

(z=-3times t+1)

3.1. Канонические
уравнения прямой.

Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

(см. рис.18).Обозначим через
вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторыколлинеарны, следовательно, их
соответствующие координаты пропорциональны:

(3.3.1)

Эти уравнения
называются каноническими
уравнениями прямой.

Пример: Написать
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору

Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:

Это канонические
уравнения прямой.

Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.

3.2.
Параметрические
уравнения прямой.

Пусть прямая
задана каноническими уравнениями

Обозначим тогдаВеличина t
называется параметром и может принимать
любые значения:
.

Выразим x,
y
и z
через t
:

(3.2.1)

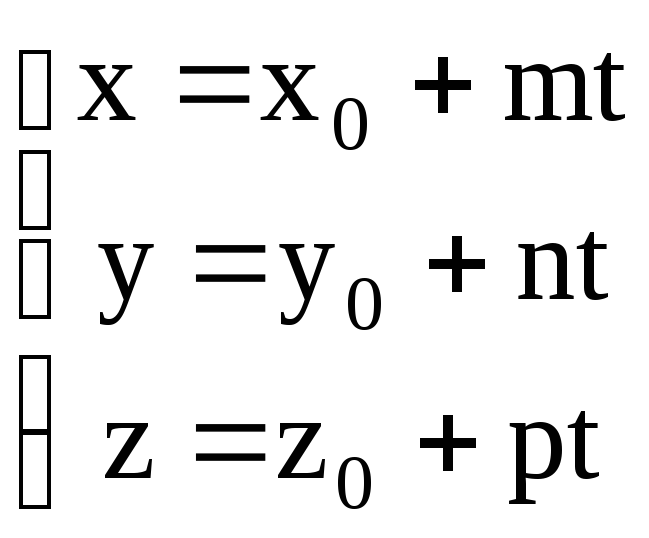
Полученные уравнения
называются параметрическими
уравнениями прямой.

Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору

Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:

Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):

Итак,
– параметрические уравнения данной
прямой.

Ответ:

Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).

Решение:
Вектор является направляющим
вектором искомой прямой.

Найдем вектор .

= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

– это искомые
параметрические уравнения прямой.

3.3. Уравнения
прямой, проходящей через две заданные
точки.

Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Векторможно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
находим
по формулам (3.1.1):).

(3.3.1)

Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки

Решение:

Применяем
формулу (3.3.1)

Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

– это параметрические
уравнения прямой.

Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки

Решение:

По формулам
(3.3.1) получим:

Это канонические
уравнения.

Переходим к
параметрическим уравнениям:

– параметрические
уравнения.

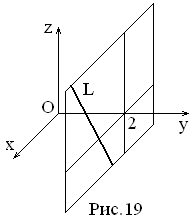
Полученная прямая
параллельна оси oz
(см. рис.21).

3.4. Прямая как
линия пересечения двух плоскостей.

Пусть в
пространстве даны две плоскости

и

Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:

Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий векторКоординаты точкиполучим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть

Пример 1.
Составить
канонические уравнения прямой

Решение: Пусть
z
= 0. Решим систему

Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.

Итак, точка
лежит на искомой прямой.

Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:

Уравнения прямой
находим по формулам (3.1.1):

Ответ: .

Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).

Пример 2.
Составить канонические и параметрические
уравнения прямой

Решение:
Пусть y
= 0. Тогда система примет вид:

Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку

Для нахождения
второй точки положим x
= 0. Будем иметь:

То есть

Далее применяем
формулы (3.3.1):

Получили канонические
уравнения прямой.

Составим
параметрические уравнения прямой:

Ответ:

; .

3.5. Взаимное
расположение двух прямых в пространстве.

Пусть прямые
заданы уравнениями:

:

;: .

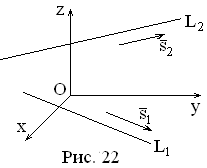
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот уголнаходим по формуле из векторной алгебры:

или

(3.5.1)

Если прямые перпендикулярны
(),то
Следовательно,

(3.5.2)

Это условие
перпендикулярности двух прямых в
пространстве.

Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть

(3.5.3)

Это условие
параллельности двух прямых в пространстве.

Пример 1. Найти
угол между прямыми:

а).
и

б). и

Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий векторвторой прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему

Затем найдем их векторное произведение:

(см. пример 1
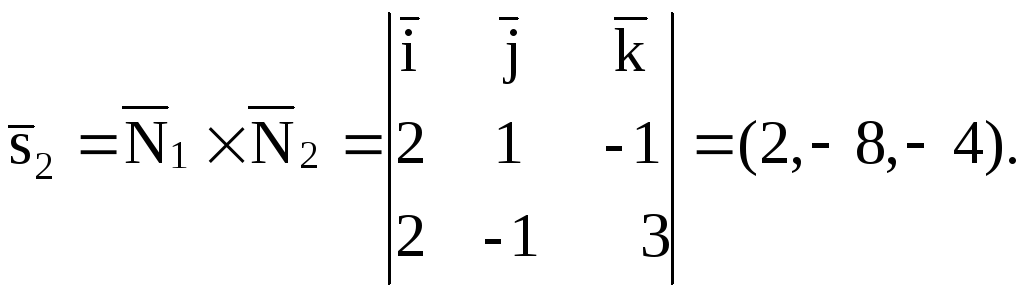
пункта 3.4).

По формуле (3.5.1)
получим:

Следовательно,

б). Запишем
направляющие векторы данных прямых:
Векторыколлинеарны, так как их соответствующие
координаты пропорциональны:

Значит прямые
параллельны (),
то есть

Ответ: а).
б).

Пример 2. Доказать
перпендикулярность прямых:

и

Решение:
Запишем направляющий вектор первой
прямой

Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:

Вычислим их векторное произведение:

(См. пример 1пункта 3.4).

Применим условие
перпендикулярности прямых (3.5.2):

Условие выполнено;
следовательно, прямые перпендикулярны
().

Соседние файлы в предмете Математика

• #
• #
• #
• #
• #
• #
• #
• #
• #

  03.03.20154.96 Кб8Содержание OneNote.onetoc2

• #