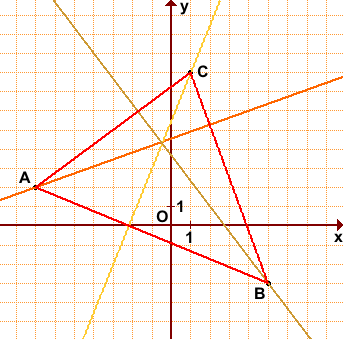
Уравнение высоты треугольника
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Как найти параметрическое уравнение высоты треугольника
И в итоге: x+2y+z-9=0
это вы написали уравнение плоскости, проходящей через точку С перпендикулярно АВ.
Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости
I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»
Нужно найти не длину, а уравнение CH.
II. «Можно воспользоваться двойным векторным произведением. и найти направляющий вектор высоты. »
То есть:
AC<2,2,2>
AB
Нужно найти не длину, а уравнение CH. – Если найдёте `H`, то сможете написать уравнение по двум точкам.
Так? – Да. только вычисления не проверял. а в том, что получили, можно сократить на 36.
Уравнение высоты треугольника по координатам формула
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Даны координаты вершин треугольника 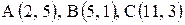
1) Вычислить длину стороны 
2) Составить уравнение линии 
3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.
4) Найти точку пересечения медиан.
5) Найти косинус внутреннего угла при вершине В.
6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

1. Длина стороны ВС равна модулю вектора 
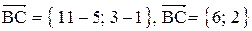

2. Уравнение прямой ВС: 
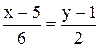
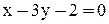
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку 

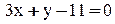
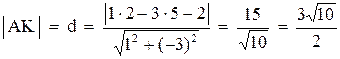
4. Найдем координаты точки N – середины стороны ВС:

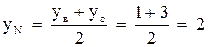
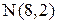
Точка пересечения медиан О делит каждую медиану на отрезки в отношении 
Используем формулы деления отрезка в данном отношении 

5. Косинус угла при вершине В найдем как косинус угла между векторами 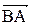
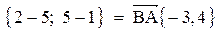
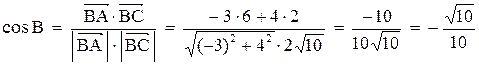
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы 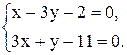
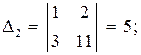

Точка К является серединой отрезка АМ.
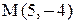
Контрольные варианты к задаче 2
Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение линии ВС;
3) составить уравнение высоты, проведенной из вершины А;
4) вычислить длину высоты, проведенной из вершины А;
5) найти точку пересечения медиан;
6) вычислить внутренний угол при вершине В;
7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.
| 1. | 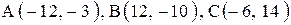 . . |
2. |  . . |
| 3. |  . . |
4. |  . . |
| 5. |  . . |
6. |  . . |
| 7. |  . . |
8. |  . . |
| 9. | 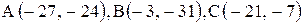 . . |
10. | 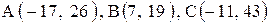 . . |
| 11. | 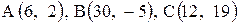 . . |
12. |  . . |
| 13. |  . . |
14. | 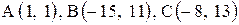 . . |
| 15. | 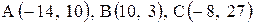 . . |
16. |  . . |
| 17. | 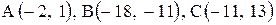 . . |
18. | 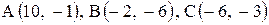 . . |
| 19. | 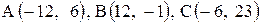 . . |
20. |  . . |
| 21. | 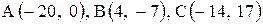 . . |
22. | 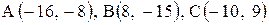 . . |
| 23. | 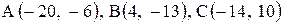 . . |
24. | 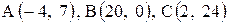 . . |
| 25. |  . . |
26. | 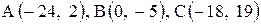 . . |
| 27. | 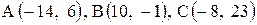 . . |
28. | 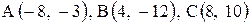 . . |
| 29. | 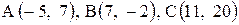 . . |
30. | 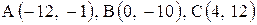 . . |
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10637 – 

Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @
Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)
Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:
Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0
Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9
Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:
y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.
10 = (32/3) + d,
d = -2/3
Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0
Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: XE = 6, YE = -1
Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.
(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0
Это уравнение медианы AE.
Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:
S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв. ед.)
[spoiler title=”источники:”]
http://diary.ru/~eek/p183898406_uravnenie-vysoty-treugolnika-v-prostranstve.htm
http://4apple.org/uravnenie-vysoty-treugolnika-po-koordinatam/
[/spoiler]
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Параметрическое уравнение высоты в треугольнике
|
|||
|
Написать параметрическое уравнение высоты, проведенной из вершины А на сторону ВС в треугольнике АВС. А(2,1,-1), В(1,3,0), С(4,1,7). Что нужно почитать, что бы понять как решить эту задачу?
|
||
| Вернуться к началу |
|
||
|
dr Watson |
Заголовок сообщения: Re: Параметрическое уравнение высоты в треугольнике
|
|
Знать надо почти ничего. Вариант А. ВАРИАНТ В. PS. Чтобы в данном контексте пишется слитно. Раздельно пишется во фразах типа “что бы мне ещё поесть”, “что бы я ни делал, ничего не получается”
|
|
| Вернуться к началу |
|
| За это сообщение пользователю dr Watson “Спасибо” сказали: vas999 |
|
|
vas999 |
Заголовок сообщения: Re: Параметрическое уравнение высоты в треугольнике
|
|
dr Watson писал(а): Вариант А. А(2,1,-1), В(1,3,0), С(4,1,7). [math]overrightarrow{BC} = left( 4-1,1-3,7-0 right)=left( 3,-2,7 right)[/math] Параметрические уравнения прямой: [math]left{!begin{aligned} Так?
|
|
| Вернуться к началу |
|
|
vas999 |
Заголовок сообщения: Re: Параметрическое уравнение высоты в треугольнике
|
|
dr Watson писал(а): 1. Пишем уравнение плоскости через точку [math]A[/math] перпендикулярно вектору [math]BC[/math]. А(2,1,-1), В(1,3,0), С(4,1,7). 1. [math]3left( x-2 right) -2left( y-1 right)+7left( z+1 right) =0[/math] 2. [math]3left( 1+3 lambdaright)-2left( 3-2 lambda right)+7left( 0+7lambda right) +3 = 0[/math] Так?
|
|
| Вернуться к началу |
|
|
vas999 |
Заголовок сообщения: Re: Параметрическое уравнение высоты в треугольнике
|
|
dr Watson писал(а): 3. Из условия перпендикулярности находим параметр, то есть получаем конкретно точку [math]D.[/math] Остаётся написать параметрическое уравнение прямой, проходящей через точки [math]A[/math] и [math]D,[/math] а это Вы уже умеете, если прошли п.1. 3. [math]overrightarrow{AB}=left( 1-2,3-1,0+1 right) =left( -1,2,1 right)[/math] Это и есть ответ?
|
|
| Вернуться к началу |
|
Ника
Высший разум
(181432)
13 лет назад
Решение:
1) Найдем уравнение медианы АМ, для этого найдем координаты точки М (4;3;5)
(х-1)/(4-1)=(у-2)/(3-2)=(z-3)/(5-3)
(x-1)/3=(y-2)/1=(z-3)/2 – искомое уравнение медианы.
2) Найдем каноническое уравнение высоты АН, для этого найдем уравнение стороны ВС:
(x-3)/2=(y-4)/(-2)=(z-4)/2
Направляющий вектор этой прямой n(2;-2;2) является нормальным вектором для плоскости проходящей через точку А и перпендикулярно прямой ВС
2(x-1)-2(y-2)+2(z-3)=0
x-y+z-2=0 – уравнение плоскости, найдем основание перпендикуляра, точку Н:
(x-3)/2=t
(y-4)/(-2)=t
(z-4)/2=t
Получили:
x=2t+3
y=2t+4
z=2t+4
2t+3-2t-4+2t+4-2=0
2t=-1
t=-0.5
Тогда H(2;3;3)
Уравнение высоты:
(x-1)/1=(y-2)/1=(z-3)/0
Елена Гужвенко
Гений
(53581)
13 лет назад
Помогу про высоту.
1) Найти вектор ВС=(2,-2,3), он будет перпендикулярен высоте АН.
2) Найдем координаты любого вектора (х, у, z), параллельного АН, то есть перпендикулярного ВС.
Возьмем х=0, у=1, найдем z с помощью скалярного произведения ВС на (0,1,z):
2*0+(-2)*1+3*z=0
-2=-3z
z=2/3
Нашли вектор, параллельный АН, тогда уравнение высоты АН:
(x-1)/0=(y-2)/1=(z-3)/(2/3) каноническое уравнение высоты АН
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Параметрическое уравнение высоты тр-ка
|
|
16/02/07 |
Здравствуйте!
|
|
|
|
|
ewert |
|
||
11/05/08 |
Для начала полезно вспомнить (или узнать), что такое параметрические уравнения прямой и в чём геометрический смысл их коэффициентов.
|
||
|
|
|||
|
Мироника |
|
|
16/02/07 |
Параметрические уравнения прямой в пространстве имеют вид Добавлено спустя 2 минуты 49 секунд:
Но как их найти?
|
|
|
|
|
ewert |
|
||
11/05/08 |
Мироника писал(а): Параметрические уравнения прямой в пространстве имеют вид Добавлено спустя 2 минуты 49 секунд: Но как их найти? Правильно. Мироника писал(а): Получается, что Да нет конечно! с чего вдруг?
|
||
|
|
|||
|
Someone |
|
||
23/07/05 |
|||
|
|
|||
|
ewert |
|
||
11/05/08 |
(я так понял, что Мироника таким своеобразным способом записала равенство нулю скалярного произведения)
|
||
|
|
|||
|
Мироника |
|
|
16/02/07 |
Мироника писал(а): Да нет конечно! с чего вдруг?
Мне ведь нужно найти параметрические уравнения высоты из вершины В на сторону АС. Следовательно? искомая прямая перпендикулярна АС. Вот я и пользуюсь условием перпендикулярности прямых в пространстве Добавлено спустя 1 минуту 51 секунду:
ой, поняла. я хотела написать
|
|
|
|
|
Someone |
|
||
23/07/05 |
В чем здесь ошибка? В том, что это вовсе не условие перпендикулярности.
|
||
|
|
|||
|
Алексей К. |
|
|
29/09/06 |
Мироника писал(а): Получается, что Так это или не так, но это, по-моему, совсем не интересно.
|
|
|
|
|
Мироника |
|
|
16/02/07 |
|
|
|
|
|
Someone |
|
||
23/07/05 |
ой, поняла. я хотела написать Да, это другое дело. Только этого для решения задачи не хватит: уравнение одно, а неизвестных три или две, если учесть, что они нужны с точностью до пропорциональности.
|
||
|
|
|||
|
Мироника |
|
|
16/02/07 |
|
|
|
|
|
ewert |
|
||
11/05/08 |
Вообще-то эту задачу можно решать кучей способов. Вот, на мой взгляд, логически наиболее прямолинейный (хотя и не самый очевидный). 1). Находим (с помощью векторного произведения) вектор, перпендикулярный к треугольнику.
2). Находим (аналогично) вектор, перпендикулярный к только что найденному и к вектору Это и будет искомый направляющий вектор высоты.
|
||
|
|
|||
|
Алексей К. |
|
|
29/09/06 |
Скалярное произведение
|
|
|
|
|
Someone |
|
||
23/07/05 |
Ну, вот у Вас есть точка Добавлено спустя 2 минуты 26 секунд: Во как активно Вам помогают…
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Пример.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
Решение:
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:













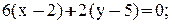
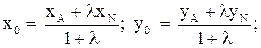
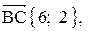
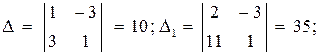
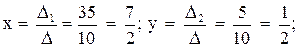






 – координаты направляющего вектора
– координаты направляющего вектора




 как уравнение некой подвижной точки
как уравнение некой подвижной точки  , и спросим себя: “при каком
, и спросим себя: “при каком  вектор
вектор  ?” Это и будет вожделенная высота.
?” Это и будет вожделенная высота. .
.
 на
на  равно нулю.
равно нулю. и точка
и точка  . При каком условии будет
. При каком условии будет  ?
?