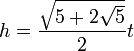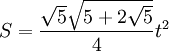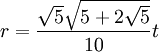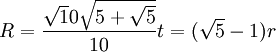Как составить пентагон

Знаете, почему Пентагон так называется? Конечно, знаете – из-за формы здания, которое имеет 5 углов. Ну точнее, пентагоном называют правильный пятиугольник, у которого все стороны и все углы равны. Но почему здание штаб-квартиры Министерства обороны США получило именно такую форму? А ведь это довольно казусная история, хотя и, наверное, разочарует поклонников различных теорий заговоров.

У Пентагона, кстати, есть забавный рекорд – это самое крупное в мире офисное здание с одним владельцем (в данном случае – американскому Минобороны). Ну сотрудников в этой организации много, работы тоже – так что это понятно. Тем более, что строительство довольно экстренно началось во время Второй мировой войны – точнее, 11 сентября 1941 года.

Эту дату многие помнят как день 9/11, хотя в этом случае чаще говорят о двух башнях Всемирного торгового центра – но Пентагон тогда тоже был атакован, сильно пострадало здание и погибли люди, в память о которых теперь на месте тех событий установлен мемориал. Так что всё это была привязано именно к круглой дате – 60 лет начала строительства Пентагона.

Работы шли максимально ускоренными темпами – днём открытия нового здания Минобороны в США считают 15 января 1943 года.

На фоне этой торопливости интересно то, что здание должно было быть построено вообще в другом месте. Речь о территории так называемой Арлингтонской экспериментальной фермы (на фото выше), которая была расположена на правом берегу реки Потомак и принадлежала Министерству сельского хозяйства. Если спросите про то, что за эксперименты там проводили, то сообщаем, что выращивали и выводили новые сорта конопли.

А теперь чуть-чуть геометрии. У правильного пятиугольника внутренний угол равен 108 градусам. Это ровно столько, сколько составлял угол между двумя дорогами, идущими вдоль отданной под строительство территории.

Поскольку архитекторам была поставлена задача освоить этот участок, то они и решили вписать здание в угол между дорогами. Ну а дальше уже чистое творчество – если нужно сделать угол 108 градусов, то, как говорится, правильный пятиугольник сам напрашивается. Тем более места хватало.

Кстати, длина каждой из пяти сторон Пентагона – 281 метр (площадь, периметр и пр. теперь можно спокойно подсчитать тем, кому интересно), здание является пятиэтажкой общей высотой 23,5 метра, но есть ещё два подземных этажа.

Ещё интересных циферок: общая длина всех коридоров в Пентагоне составляет 28 километров, при этом планировка такова, что между двумя самыми удалёнными точками – идти максимум 7 минут. А ещё в здании насчитывается 7754 окна.

Виновником того, что Пентагон в итоге построили в другом месте, считается лично Франклин Рузвельт, президент США, который, как теперь рассказывают, заявил, что в этом месте здание закрывает хороший вид на Вашингтон, Капитолийский холм и всё вот это (ну то есть на другой берег Potomac River) и потребовал перенести его. Немного поломав голову, военные нашли ещё одно место – ниже по течению реки.

Понятно, что сам проект никто переделывать не стал, так что пятиугольник уже не надо было впихивать в угол между дорогами. Хотя потом с этим вопросом тоже решили довольно неплохо, сделав парковку в виде “прислонённого” к пентагону треугольника.

И уже вдоль его сторон были проложены дороги – в итоге они пересекаются под острым углом, а сверху это всё похоже на какой-нибудь фантастический космический корабль из Star Wars.

Собственно, это и есть главный секрет Пентагона – никаких масонских заговоров, дьявольской символики и т.д.

Притянуть к секретам можно разве что не очень афишируемый (но всем известный) факт о том, что в здании в 2 раза больше туалетов, чем положено по норме на тех примерно 27 тысяч служащих, что туда помещается. Почему так вышло?

Причина простая – расовую сегрегацию в армии США отменили только в 1948 году, так что туалеты в Пентагоне делали раздельными. Но, видимо, их было одинаковое количество – никакой дискриминации.

Есть, правда, ещё одна забавная деталь: поскольку пятиугольник Пентагона правильный, у него есть геометрический центр. Он находится во внутреннем дворе и на фото видно, что это какое-то небольшое строение точно такой же формы – такой мини-пентагончик.

Так вот, это кафе, которое в своё время получило название Cafe Ground Zero, что можно перевести как “Эпицентр”.

Но не столько из-за того, что находится в самом центре, хотя и выглядит как “яблочко” мишени, сколько из-за приколов на тему ядерного удара со стороны СССР. В Пентагоне шутили, что наверняка советское военное руководство уверено, что это вход в подземный бункер, поэтому ракеты уже наведены на эту точку. Возможно, так и было.

***

Все изображения можно увеличить, кликнув по ним. Все иллюстрации в статье – insideheadline.com, pxhere.com и wikimedia.org. Если вам понравилось, ставьте лайк и подписывайтесь на канал!

Пентагон (фигура)

Полезное

Как сделать из четырехугольника один пятиугольник, три четырехугольника и пять треугольников?

Математика | 1 – 4 классы

Как сделать из четырехугольника один пятиугольник, три четырехугольника и пять треугольников.

Начертить четырехугольник, в нем два отрезка начертить так, чтобы получился пятиугольник, три четырехугольника и пять треугольников?

Начертить четырехугольник, в нем два отрезка начертить так, чтобы получился пятиугольник, три четырехугольника и пять треугольников.

Как поделить четырехугольник двумя отрезками на пятиугольник, 3 четырехугольника, 5 треугольников?

Как поделить четырехугольник двумя отрезками на пятиугольник, 3 четырехугольника, 5 треугольников.

Начерти пятиугольник АВСDЕ и проведи прямую l так чтобы она разбила пятиугольник : а) на треугольник и шестиугольник б) на треугольник и пятиугольник : в) на четырехугольник и пятиугольник : г) на два?

Начерти пятиугольник АВСDЕ и проведи прямую l так чтобы она разбила пятиугольник : а) на треугольник и шестиугольник б) на треугольник и пятиугольник : в) на четырехугольник и пятиугольник : г) на два четырехугольника.

Как разделить четырехугольник отрезком так чтобы получился треугольник и пятиугольник?

Как разделить четырехугольник отрезком так чтобы получился треугольник и пятиугольник?

Сколько треугольников и четырехугольников в фигуре : “ЗВЕЗДА В ПЯТИУГОЛЬНИКЕ”?

Сколько треугольников и четырехугольников в фигуре : “ЗВЕЗДА В ПЯТИУГОЛЬНИКЕ”?

Как разрезать пятиугольник, чтобы получилось два треугольника и четырехугольник?

Как разрезать пятиугольник, чтобы получилось два треугольника и четырехугольник.

Начерти четырехугольник провести в нем отрезок так чтобы он разделил четырехугольник на треугольник и пятиугольник сфоткайте пожалуйста как вы сделали?

Начерти четырехугольник провести в нем отрезок так чтобы он разделил четырехугольник на треугольник и пятиугольник сфоткайте пожалуйста как вы сделали.

Четырехугольник в нем два отрезка так чтобы получился пятиугольник , три четырехугольника, и пять треугольников?

Четырехугольник в нем два отрезка так чтобы получился пятиугольник , три четырехугольника, и пять треугольников.

Как из прямоугольника сделать четырехугольник и пятиугольник одним разрезом?

Как из прямоугольника сделать четырехугольник и пятиугольник одним разрезом.

Что такое стороны треугольника, четырехугольника, пятиугольника?

Что такое стороны треугольника, четырехугольника, пятиугольника.

Вы открыли страницу вопроса Как сделать из четырехугольника один пятиугольник, три четырехугольника и пять треугольников?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 1 – 4 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Смешной вопрос. 1. Больше учиться. Слушать преподавателя. 2. Нанять репетитора. 3. Усердно зубрить уроки дома. 4. Пытаться выделяться.

V1 = a ^ 3 при увеличении ребра в 3 раза V2 = (3a) ^ 3 = 27a ^ 3 Значит масса увеличиться в 27 раз.

(650 – 120) + (240 + 20) = 790 1000 – (650 – 120) = 470 (168 + 120) + 240 = 1128.

Только если 0, ибо |х|> = 0.

20 * 12 + 15 * 15 = 465 деталей.

3 суток = 3 * 24 = 72 часа 72 + 13 = 85 часов 85 часов = 85 * 60 = 5100 минут.

60 – 45 = 15 15 + 13 = 28 Ответ : 28 мин он затратил на дорогу.

60 – 45 = 15 15 + 13 = 28 ответ : 28.

5 ч 49 мин 40 с + 3 мин 30 с = 5 ч 53 мин 10 с.

14. а) |x| = 5 – 2 = 3, ОТВЕТ х = – 3, х = 3. Б) |x| = 7 + 3 = 10, ОТВЕТ х = – 10, х = 10. В) |x| = 10 – 4 = 6, ОТВЕТ х = – 6, х = 6. Г) |x| = 9 – 9 = 0, ОТВЕТ х = 0. Д) |x| = 0, 92 – 0, 8 = 0, 12 ОТВЕТ х = – 0, 12, х = 0, 12. Е) |x| = 1 + 0, 6 ..

Геометрия многоугольника: пятиугольники, шестиугольники и додекагоны

Немногие геометрические фигуры столь же разнообразны, как многоугольники. Они включают в себя знакомый треугольник, квадрат и пятиугольник, но это только начало.

В геометрии многоугольник — это любая двумерная форма, которая удовлетворяет следующим условиям:

• Состоит из трех или более прямых
• Закрыто без отверстий или разрывов в форме
• Имеет пары линий, которые соединяются в углах или вершинах, где они образуют углы
• Имеет равное количество сторон и внутренних углов

Двумерный означает плоский, как лист бумаги. Кубы не являются полигонами, потому что они трехмерны. Круги не являются полигонами, потому что они не содержат прямых линий.

Специальный вид многоугольника может иметь углы, которые не все равны. В этом случае это называется неправильным многоугольником.

О полигонах

” data-tracking-container=”true” exists=”yes” data-lazy-src=”https://gadgetshelp.com/wp-content/uploads/images/lfw/a5b33ec3369c8daa115f36ceaabcf4c0.jpg”/>

Де Агостини / А. Дагли Орти / Getty Images

Название многоугольника происходит от двух греческих слов:

• Поли, что означает много
• Гон, что означает угол

Формы, которые являются полигонами

• Треугольник (треугольник): 3 стороны
• Тетрагон (квадрат): 4 стороны
• Пентагоны: 5 сторон
• Шестиугольник: 6 сторон
• Семиугольник: 7 сторон
• Восьмиугольники: 8 сторон
• Нонагон: 9 сторон
• Декагон: 10 граней
• Undecagon: 11 сторон
• Додекагоны: 12 сторон

Как называются полигоны

Названия отдельных многоугольников получаются из числа сторон или углов, которыми обладает форма. Полигоны имеют одинаковое количество сторон и углов.

Общим названием большинства полигонов является греческий префикс «сторон», прикрепленный к греческому слову «угол» (gon).

Примеры этого для пяти- и шестигранных правильных многоугольников:

• Пента (по- гречески означает пять) + гон = пентагон
• Гекса (по-гречески означает шесть) + гон = шестиугольник

Есть исключения из этой схемы именования. В частности, со словами, которые чаще всего используются для некоторых полигонов:

• Треугольник: Использует греческий префикс Tri , но вместо греческого угольник , латинский угол используется. Trigon — правильное геометрическое имя, но оно используется редко.
• Четырехсторонний : Производный от латинского префикса quadri, означающего четыре, прикрепленного к слову боковой, что является еще одним латинским словом, означающим сторону.
• Квадрат : Иногда четырехсторонний многоугольник (квадрат) называют четырехугольником или четырехугольником .

N-угольники

Полигоны с более чем 10 сторонами встречаются нечасто, но следуют тому же греческому соглашению об именовании. Итак, 100-сторонний многоугольник называется гектогоном .

Однако в математике пятиугольники иногда более удобно называть n-гонами :

• 11-гонник: гендекагон
• 12-Гон: Додекагон
• 20-летний гонщик: Икосагон
• 50-гонник: пятиконечный
• 1000-гон: чилиагон
• 1000000-гон: мегагон

В математике н-гоны и их греческие аналоги взаимозаменяемы.

Предел полигона

Теоретически, нет ограничения на количество сторон, которые может иметь многоугольник.

По мере того, как размер внутренних углов многоугольника увеличивается, а длина его сторон становится короче, многоугольник приближается к кругу, но никогда не достигает его.

Классификация полигонов

Регулярные и неправильные полигоны

Полигоны классифицируются на основании того, равны ли все углы или стороны.

• Правильныймногоугольник : все углы имеют одинаковый размер, и все стороны равны по длине.
• Нерегулярныймногоугольник : Не имеет равных углов или сторон одинаковой длины.

Выпуклые против вогнутых полигонов

Второй способ классификации полигонов — по размеру их внутренних углов.

• Выпуклые многоугольники: не имеют внутренних углов больше 180 °.
• Вогнутые многоугольники : имеют как минимум один внутренний угол, превышающий 180 °.

Простые и сложные полигоны

Еще один способ классификации полигонов — это то, как линии, образующие многоугольник, пересекаются.

• Простые многоугольники : линии соединяются или пересекаются только один раз — в вершинах.
• Сложные полигоны : линии пересекаются более одного раза.

Названия сложных многоугольников иногда отличаются от названий простых многоугольников с одинаковым числом сторон.

• Регулярный образный шестигранник представляет собой шестигранный, простой многоугольник.
• Звездообразная гексаграмма представляет собой шестигранный сложный многоугольник, созданный путем наложения двух равносторонних треугольников.

Правило суммы внутренних углов

Ян Лишман / Getty Images

Как правило, каждый раз, когда сторона добавляется в многоугольник, например:

• От треугольника до четырехугольника (три-четыре стороны)
• От пятиугольника до шестиугольника (пять-шесть сторон)

еще 180 ° добавляется к сумме внутренних углов.

Это правило можно записать в виде формулы:

(n — 2) × 180 °

где n равно числу сторон многоугольника.

Таким образом, сумма внутренних углов для шестиугольника может быть найдена с помощью формулы:

(6 — 2) × 180 ° = 720 °

Сколько треугольников в этом многоугольнике?

Приведенная выше формула внутреннего угла получается путем деления многоугольника на треугольники, и это число можно найти с помощью вычисления:

п — 2

В этой формуле n равно числу сторон многоугольника.

Шестиугольник (шесть сторон) можно разделить на четыре треугольника (6-2) и додекагон на 10 треугольников (12-2).

Размер угла для правильных многоугольников

Для правильных многоугольников, в которых все углы одинакового размера, а стороны одинаковой длины, размер каждого угла в многоугольнике можно рассчитать путем деления общего размера углов (в градусах) на общее количество сторон.

Для правильного шестигранного шестигранника каждый угол равен:

720 ° ÷ 6 = 120 °

Некоторые известные полигоны

Скотт Каннингем / Getty Images

Хорошо известные полигоны включают в себя:

Фермы

Фермы часто имеют треугольную форму. В зависимости от ширины и уклона крыши ферма может включать равносторонние или равнобедренные треугольники. Из-за их большой прочности, треугольники используются в строительстве мостов и велосипедных рам. Они видны в Эйфелевой башне.

Пентагон

Пентагон — штаб-квартира Министерства обороны США — берет свое название от его формы. Здание представляет собой пятисторонний, правильный пятиугольник.

Главная пластина

Другой известный пятисторонний правильный пятиугольник — домашняя тарелка на бейсбольном алмазе.

Поддельный Пентагон

Гигантский торговый центр недалеко от Шанхая, Китай, построен в форме правильного пятиугольника и иногда называется поддельным пятиугольником.

Снежинки

Каждая снежинка начинается с шестиугольника, но температура и влажность добавляют ветви и усики, так что каждая из них выглядит по-разному.

Пчелы и осы

Естественные шестиугольники также включают ульи, где каждая клетка в соте, которую пчелы строят для содержания меда, является шестиугольной. Гнезда бумажных ос также содержат гексагональные клетки, в которых они растут.

Тротуар гиганта

Шестиугольники также найдены на мощёной дорожке Гиганта, расположенной на северо-востоке Ирландии. Это естественная горная порода, состоящая из около 40000 взаимосвязанных базальтовых колонн, которые были созданы в виде лавы от медленно вулканического извержения вулкана.

Восьмиугольник

Восьмиугольник — имя, данное кольцу или клетке, используемому в боях Ultimate Fighting Championship (UFC), — берет свое название от своей формы. Это восьмигранный правильный восьмиугольник.

Стоп Знаки

Стоп-знак — один из самых знакомых дорожных знаков — еще один восьмигранный правильный восьмиугольник. Хотя цвет, формулировка или символы на знаке могут отличаться, восьмиугольная форма знака остановки используется во многих странах мира.

Как составить пятиугольник из треугольников и четырехугольника

И.М. СМИРНОВА, В.А. СМИРНОВ

Паркеты с древних времен привлекали к себе внимание людей. Ими мостили дороги, украшали полы в помещениях, стены домов, использовали в декоративно-прикладном искусстве. Знаменитый голландский ху­дожник Мариус Эшер (1898-1972) посвятил паркетам несколько своих картин. Среди них: “Всадники” (рис. 1), “Ящерицы” (рис. 2), “Летящие птицы” (рис. 3).

Проявление свойств паркетов сказывается на свойствах различных природных минералов и кристаллов. В то же время паркеты являются объектом исследования математиков. Глубокие результаты здесь получены отечественными учеными, академиками: А.Д. Александровым, Б.Н. Делоне, Е.С. Федоровым и др.

Здесь мы рассмотрим паркеты на евклидовой плоскости, на плоскости Лобачевского, на сфере и в пространстве.

1. Паркеты на плоскости

Паркетом на плоскости называется такое заполнение плоскости многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.

Паркет называется правильным, если он состоит из равных правильных многоугольников.

Примеры правильных паркетов дают заполнения плоскости:

а) правильными треугольниками (рис. 4);

б) квадратами (рис. 5);

в) правильными шестиугольниками (рис. 6).

Докажем, что другими равными правильными многоугольниками заполнить плоскость нельзя. Действительно, углы правильного n -уголь­ника равны . Заполним таблицу, состоящую из углов правильных n -угольников.

60

90

108

120

128 4 /₇

135

140

144

147 3 /₁₁

150

Если в одной вершине паркета сходится m пра­вильных n – угольников, то должно выполняться равенство откуда

Возможными допустимыми значениями n являются 3, 4 и 6. При остальных значениях n число m оказывается дробным. В част­ности, нельзя заполнить плоскость правильными пятиугольниками.

Можно подумать, что наличие только трех видов правильных паркетов обусловлено исключительно значениями углов правильных многоугольников, и если отказаться от требования правильности многоугольников, то число паркетов увеличится.

На самом деле, это не так. Даже, если отказаться от выпуклости многоугольников, или допускать в качестве сторон многоугольников кривые линии, т.е. рассматривать криволинейные многоугольники, то при некоторых естественных ограничениях на размеры многоугольников (о которых речь пойдет ниже) имеется только три вида таких паркетов:

1) из треугольников, в каждой вершине которого сходится шесть сторон;

2) из четырехугольников, в каждой вершине которого сходится четыре стороны;

3) из шестиугольников, в каждой вершине которого сходится три стороны.

Мы не будем доказывать это утверждение в общем виде, а рассмотрим несколько примеров, показывающих причину его справедливости.

Например, выясним, можно ли составить паркет из треугольников, в каждой вершине которого сходится три стороны.

Пусть в вершине A сходится три стороны AB , AC и AD (рис. 7, а). Так как паркет состоит из треугольников, то вершины B , C и D попарно должны соединяться линиями (рис. 7, б). Но в этом случае в вершинах B , C и D будет сходиться по три стороны и ни одной стороны нельзя будет добавить для продолжения паркета. Таким образом, фигуру на рисунке 7, б нельзя достроить до паркета на всей плоскости, т.е. искомого паркета не существует.

Самостоятельно покажите, что не существует паркета из треугольников, в каждой вершине которого сходится: а) четыре стороны; б) пять сторон.

Покажем, что не существует паркета, состоящего из четырехугольников, в каждой вершине которого сходится три стороны.

Рассмотрим четырехугольник ABCD (рис. 8, а). Из каждой его вершины должно выходить дополнительно по одной стороне AE , BF , CG , DH . Так как паркет состоит из четырехугольников, то концы этих сторон E , F , G , H должны попарно соединяться линиями (рис. 8, б). Но в этом случае в вершинах E , F , G и H будет сходиться по три стороны и ни одной стороны нельзя будет добавить для продолжения паркета. Таким образом, фигуру на рисунке 8, б нельзя достроить до паркета на всей плоскости, т.е. искомого паркета не существует.

Используя рисунок 9, самостоятельно покажите, что не существует паркета из пятиугольников, в каждой вершине которого сходится три стороны.

Выясним, существует ли паркет из треугольников, в каждой вершине которого сходится семь сторон.

Попробуем построить такой паркет. Начнем с вершины A , в которой сходится семь сторон. Расположим их концы B , C , D , E , F , G , H на окружности и соединим их хордами (рис. 10). В результате получим семь треугольников с общей вершиной A . Из вершин этих треугольников, отличных от A , должно дополнительно выходить по четыре стороны. Расположим концы этих сторон на окружности и соединим их хордами. В результате получим еще 28 треугольников. Этот процесс можно продолжать. Однако при этом придется или уменьшать стороны треугольников, являющиеся хордами окружностей, или увеличивать стороны треугольников, соединяющие вершины на соседних окружностях. Если же мы ограничим стороны треугольников снизу некоторым числом >0 и сверху некоторым числом >0, то, начиная с некоторого шага, построение паркета будет невозможным.

Оказывается, что не только это, но и никакое другое построение паркета из треугольников, в каждой вершине которого сходится семь сторон с указанными ограничениями, невозможно.

Аналогичным образом, не существует паркетов из треугольников, в каждой вершине которых сходится восемь или более сторон.

Из рассмотренных выше правильных паркетов из треугольников, квадратов и шестиугольников можно получать и другие паркеты. Например, на рисунках 11 – 13 показаны паркеты, полученные из квадратного паркета.

Самостоятельно получите новые паркеты из треугольного и шестиугольного паркетов.

Расширим способы составления паркетов из правильных многоугольни­ков, разрешив использовать в них правильные многоугольники с различным числом сторон. Это, так называемые, полуправильные паркеты.

Паркет называется полуправильным, если он состоит из правильных многоугольников (возможно с разным числом сторон), одинаково расположенных вокруг каждой вершины.

Обозначим через ₁, ₂, … углы правильных многоугольников, имеющих общую вершину. Расположим их в порядке возрастания _{1 2} … . Учитывая, что сумма всех таких углов должна быть равна 360 , составим таблицу, содержащую возможные наборы углов, и укажем соответствующие паркеты.

₁

₂

₃

₄

₅

₆

₁+ ₂+…=360

60

60

60

60

60

60

Правильный паркет из 3-ов (рис. 4)

60

60

60

60

120

Паркет из 3-ов и 6-ов (рис. 14)

60

60

60

90

90

Два паркета из 3-в и 4-в (рис. 15, 16)

60

60

90

150

60

60

120

120

Паркет из 3-в и 6-в (рис. 17)

60

90

90

120

Паркет из 3-в, 4-в и 6-в (рис. 18)

60

150

150

Паркет из 3-в и 12-в (рис. 19)

90

90

90

90

Правильный паркет из квадратов (рис. 5)

90

120

150

Паркет из 4-в, 6-в и 12-в

90

135

135

Паркет из 4-в и 8-в (рис. 21)

120

120

120

Правильный паркет из 6-ов (рис. 6)

Таким образом, всего имеется 8 типов полуправильных паркетов.

Для числа этих паркетов также существенным являются не величины углов и сторон, а число сторон в многоугольниках и вершинах.

Рассмотрим теперь вопрос о заполнении плоскости неправильными равными многоугольниками.

Теорема. Для любого четырехугольника существует паркет, состоящий из четырехугольников, равных исходному. Иначе говоря, четырехугольником произвольной формы можно заполнить всю плоскость.

Доказательство. Пусть дан четырехугольник АВС D (рис. 22). Рассмотрим центрально-симметричный ему четырехугольник относительно сере­дины стороны АВ. Исходный четырехугольник АВС D обозначим цифрой 1, а симметричный – цифрой 2. Теперь четырехугольник 2 отразим симметрично относительно середины его стороны ВС. Полученный четырехугольник обоз­начим цифрой 3 и отразим его симметрично относительно середины его стороны CD . Полученный четырехугольник обозначим цифрой 4. Четырехугольники 1, 2, 3 и 4 примыкают к общей вершине углами А, В, С и D . Поскольку сумма углов четырехугольника равна 360 , то эти четырехуголь­ники заполнят часть плоскости вокруг общей вершины. Такое же построе­ние можно провести вокруг каждой новой вершины, что и даст искомое за­полнение плоскости.

Заметим, что четырехугольники, закрашенные одним цветом (рис. 22), получаются друг из друга параллельным переносом.

Самостоятельно составьте паркет из равных невыпуклых четырехугольников.

Паркеты из неправильных многоугольников можно получить из полуправильных паркетов, используя двойственность.

Двойственным к паркету, состоящему из правильных многоугольников, называется паркет, вершины которого находятся в центрах многоугольников данного паркета.

Ясно, что двойственным к правильному паркету, состоящему из треугольников, является правильный паркет, состоящий из шестиугольников. Двойственным к правильному паркету, состоящему из шестиугольников, является правильный паркет, состоящий из треугольников. Правильный паркет, состоящий из квадратов, двойственен сам себе.

На рисунке 23 представлен паркет, состоящий из пятиугольников, двойственный паркету, изображенному на рисунке 14.

1. Можно ли составить паркет из правильных: а) пятиугольников; б) шестиугольников; в) семиугольников?

2. Можно ли составить паркет из правильных: а) восьмиугольников и четырехугольников; б) двенадцатиугольников и треугольников; в) десятиугольников и пятиугольников?

3. Можно ли составить паркет из равных треугольников произвольной формы?

4. Можно ли составить паркет из равных четырехугольников произвольной формы?

5. Нарисуйте паркет, составленный из четырехугольников, равных четырехугольнику, изображенному на рисунке 24.

6. Можно ли составить паркет из равных пятиугольников?

7. Можно ли составить паркет из равных шестиугольников произвольной формы?

8. Докажите, что с помощью центрально-симметричных шестиугольни­ков (даже невыпуклых) можно заполнить плоскость. Приведите пример соответствующего паркета.

9. Попробуйте построить паркет из семиугольников, в каждой вершине которого сходится три стороны. Возможно ли такое построение при ограничениях на стороны семиугольников?

10. Составьте паркет из греческих крестов (рис. 25).

11. Нарисуйте паркеты, двойственные к паркетам, изображенным на рисунках 15-21.

12. Докажите, что паркеты, двойственные к полуправильным паркетам, состоят из равных многоугольников. Найдите углы этих многоугольников.

13. Используя паркеты, изображенные на рисунках 14 – 21, нарисуйте паркеты, в каждой вершине которых сходится три стороны, и состоящие из равных: а) пятиугольников, шестиугольников и двенадцатиугольников; б) пятиугольников, шестиугольников и восьмиугольников; в) четырехугольников, шестиугольников, восьмиугольников и двенадцатиугольников; г) треугольников, восьмиугольников и шестнадцатиугольников.

14. Два равных выпуклых четырехугольника разрезали: первый – по одной диагонали, а второй – по другой диагонали. Докажите, что из по­лученных четырехугольников можно сложить параллелограмм.

15. Выпуклый четырехугольник разрезали на четыре части по отрез­кам, соединяющим середины его противоположных сторон. Докажите, что из этих частей можно сложить параллелограмм.

16. Придумайте паркеты, составленные из равных фигур, ограниченных кривыми линиями.

17. Найдите какие-нибудь условия на криволинейный четырехугольник, при которых из него можно составить паркет.

18. Выясните, как паркет на рисунке 3 может быть получен искривлением сторон паркета из четырехугольников.

19. Какое наименьшее число красок потребуется для раскраски правильных паркетов так, чтобы соседние многоугольники были окрашены в разные цвета?

20. Какое наименьшее число красок потребуется для раскраски полуправильных паркетов так, чтобы соседние многоугольники были окрашены в разные цвета?

2. Паркеты на плоскости Лобачевского

Несколько картин Мариуса Эшера посвящены паркетам на модели Пуанкаре плоскости Лобачевского (рис. 26). Будем для краткости называть ее плоскостью Лобачевского. Точками этой плоскости являются точки, расположенные внутри некоторого фиксированного круга, а прямыми – диаметры без концов и дуги окружностей (рис. 27), лежащих внутри этого круга и перпендикулярные его окружности. (Углом между двумя пересекающимися окружностями называется угол между касательными, проведенными в точке их пересечения.) Для того, чтобы определить равенство фигур на этой плоскости, напомним определение и свойства инверсии.

Инверсией относительно данной окружности с центром O и радиусом R называется преобразование, при котором точкам A плоскости, отличным от O сопоставляются точки A ’ на луче OA такие, что OA OA ’= R 2 . Точке O ничего не сопоставляется. (Иногда точке O сопоставляют бесконечно удаленную точку.)

Ясно, что если точка A принадлежит окружности, OA = R , то OA ’ = R и, следовательно, точка A переходит сама в себя.

Если точка A лежит внутри круга, OA R , то OA ’ > R и, следовательно, точка A переходит в точку вне круга.

Если точка A лежит вне круга, OA > R , то OA ’ R и, следовательно, точка A переходит в точку внутри круга.

Если точка A при инверсии переходит в точку A ’ , то точка A ’ при этой же инверсии переходит в точку A .

Пусть точка A лежит внутри данного круга с центром в точке O и радиусом R (рис. 28). Построим точку A ’ , в которую переходит точка A при инверсии. Для этого через точку A проведем хорду BC , перпендикулярную OA . Через точку B проведем касательную к окружности. Точка пересечения этой касательной с лучом OA будет искомой точкой A ’ . Действительно, треугольники OAB и OBA ’ подобны. Поэтому Следовательно, OA OA ’ = R 2 .

Инверсию относительно окружности можно рассматривать как аналог симметрии относительно прямой на плоскости. При симметрии относительно прямой полуплоскости меняются местами, а при инверсии относительно окружности меняются местами внутренняя и внешняя область окружности.

Установим несколько свойств инверсии.

Свойство 1. При инверсии относительно окружности с центром в точке O точки A , B переходят в точки A ’ , B ’ такие, что треугольники OAB и OB ’ A ’ подобны.

Действительно, в этом случае OA OA ’ = R 2 = OB OB ’ (рис. 29). Следовательно, Значит, треугольники OAB и OB ’ A ’ подобны.

Свойство 2. При инверсии относительно окружности с центром в точке O окружности, проходящие через точку O (без самой точки O ), переходят в прямые, не проходящие через точку O .

Действительно, пусть OA – диаметр окружности, проходящей через точку O , B – точка, принадлежащая этой окружности (рис. 30). Тогда угол OBA равен 90 и равен углу OA ’ B ’ . Следовательно, точка B ’ принадлежит прямой, проходящей через точку A ’ и перпендикулярной OA .

Свойство 3. При инверсии относительно окружности с центром в точке O окружности, не проходящие через точку O , переходят в окружности, не проходящие через точку O .

Действительно, пусть AB – диаметр окружности, не проходящей через точку O . Точка C принадлежит этой окружности (рис. 31). Тогда OCA = OA ’ C ’ , OCB = OB ’ C ’ . Следовательно, A ’ C ’ B ’ = OB ’ C ’ – OA ’ C ’ = OCB – OCA = ACB = 90 . Значит, точка C ’ будет принадлежать окружности с диаметром A ’ B ’ .

Свойство 4. При инверсии относительно окружности с центром в точке O окружности, перпендикулярные данной окружности, переходят сами в себя.

Действительно, пусть окружность пересекает данную окружность в точках A и B и образует с ней прямые углы (рис. 32). Тогда прямые OA и OB являются касательными к этой окружности. При инверсии окружность перейдет в окружность с теми же самыми касательными в точках A и B , т.е. в ту же самую окружность.

Заметим, что две окружности с центрами O , P и радиусами R , r перпендикулярны (рис. 32), если углы OAP и OBP – прямые. Значит, расстояние OP между центрами перпендикулярных окружностей равно .

Для плоскости Лобачевского будем называть симметрией инверсию относительно окружности, перпендикулярной данной. Кроме таких симметрий имеются еще и симметрии относительно прямых, проходящих через центр данной окружности.

Две фигуры на плоскости Лобачевского называются равными, если одну из них можно перевести в другую с помощью последовательного применения одной или нескольких симметрий.

Правильным многоугольником называется многоугольник, у которого равны все стороны и углы.

В отличие от обычной плоскости, на плоскости Лобачевского углы правильного n -угольника не равны , а могут принимать любые значения, большие нуля и меньшие .

Построим, например, правильный шестиугольник. Пусть дана окружность с центром O и радиусом R , ограничивающая плоскость Лобачевского. Будем называть ее окружностью Лобачевского. Проведем какую-нибудь окружность с центром P и радиусом r , пересекающую данную окружность и такую, что угол AOB больше 60 . Будем называть ее производящей окружностью. Поворачивая эту окружность вокруг центра O на углы, кратные 60 , получим шесть окружностей, дуги которых, расположенные внутри исходной окружности, ограничивают искомый правильный шестиугольник (рис. 33).

Выясним, какие углы имеет этот правильный шестиугольник. Напомним, что угол между двумя окружностями равен углу между касательными, проведенными в точке пересечения этих окружностей. Как не трудно видеть, угол между окружностями с центрами в точках P и P ₁ равен углу PQP ₁ (рис. 33). Имеем, OP = OP ₁ = , QP = QP ₁ = r . Так как угол POP ₁ равен 60 , то треугольник POP ₁ – равносторонний и, следовательно, PP ₁ = . С другой стороны, по теореме косинусов, PP ₁ 2 = QP 2 + QP ₁ 2 – 2 QP QP ₁ cos PQP ₁ = 2 r 2 – 2 r 2 cos PQP ₁ . Из равенства R 2 + r 2 = 2 r 2 – 2 r 2 cos PQP ₁ получаем

.

В частности, если R = r , то угол построенного правильного шестиугольника будет равен 90 .

Паркетом на плоскости Лобачевского называется такое ее заполнение многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.

Паркет называется правильным, если он состоит из равных правильных многоугольников.

Из сказанного выше следует, что в каждой вершине правильного паркета на плоскости Лобачевского может сходиться любое число правильных треугольников, большее шести; любое число правильных четырехугольников, большее четырех; любое число правильных пятиугольников, большее трех и т.д.

Таким образом, на плоскости Лобачевского имеется бесконечно много правильных паркетов из треугольников, четырехугольников, пятиугольников и т.д.

На рисунке 34 показан паркет из правильных шестиугольников. В каждой его вершине сходится четыре шестиугольника. Сначала был нарисован центральный правильный шестиугольник с углами при вершинах 90 . Другие правильные шестиугольники искомого паркета были получены из построенного правильного шестиугольника симметриями плоскости Лобачевского.Для плоскости Лобачевского будем называть симметрией инверсию относительно окружности, перпендикулярной данной. Кроме таких симметрий имеются еще и симметрии относительно прямых, проходящих через центр данной окружности.

На рисунке 35 показан паркет из правильных пятиугольников. В каждой его вершине сходится четыре пятиугольника. Сначала был нарисован центральный правильный пятиугольник с углами при вершинах 90 . Остальные пятиугольники были получены из него симметриями плоскости Лобачевского.

На рисунке 36 показан паркет из правильных треугольников. В каждой его вершине сходится восемь треугольников с углами при вершинах 45 .

1. Выясните, куда при инверсии относительно окружности с центром в точке O переходят прямые, проходящие через точку O .

2. При инверсии окружность перешла в окружность. Перешел ли: а) центр окружности в центр окружности; б) диаметр окружности в диаметр окружности?

3. На каком расстоянии от центра O окружности радиуса R должен находиться центр P окружности радиуса r , чтобы при инверсии относительно первой окружности вторая окружность переходила сама в себя?

4. Постройте прямую, проходящую через две данные точки A и B на плоскости Лобачевского (рис. 37).

5. Для данных прямых a и b на плоскости Лобачевского (рис. 38 а, б) постройте прямую b ’ , симметричную b относительно прямой a .

6. Для данных прямых a и b на плоскости Лобачевского (рис. 38 а, б) укажите симметрию, переводящую прямую a в прямую b .

7. Для данного отрезка OA на прямой a (рис. 39 а, б) постройте отрезки OB = 2 OA , OC = 3 OA .

8. Для данных точек O и A на прямой a (рис. 39 а, б) укажите симметрию, переводящую прямую a в себя и точку O – в точку A .

9. Определите понятие поворота на плоскости Лобачевского. Докажите, что поворот переводит фигуры на плоскости Лобачевского в равные им фигуры.

10. Докажите, что симметрия на плоскости Лобачевского сохраняет углы, т.е. если угол между прямыми a и b равен , то угол между прямыми a ’ и b ’ , симметричными a и b относительно некоторой прямой c , также равен .

11. Какие фигуры образуют окружности на плоскости Лобачевского?

12. Приведите пример треугольника на плоскости Лобачевского, около которого нельзя описать окружность.

13. Докажите, что около любого правильного многоугольника на плоскости Лобачевского можно описать окружность.

14. Объясните, как на плоскости Лобачевского можно построить правильный треугольник: а) с центром в центре плоскости Лобачевского; б) в вершиной в центре плоскости Лобачевского.

15. Объясните, как на плоскости Лобачевского можно построить правильный: а) четырехугольник; б) пятиугольник; в) восьмиугольник с центром в центре плоскости Лобачевского. Какого радиуса следует взять производящую окружность, и каким должно быть расстояние от ее центра до центра окружности Лобачевского, чтобы углы указанных правильных многоугольников были равны 90 ?

16. Из любого ли треугольника на плоскости Лобачевского можно составить паркет?

17. В каком случае из правильного треугольника на плоскости Лобачевского можно составить паркет?

18. Можно ли на плоскости Лобачевского составить паркет из правильных треугольников, в каждой вершине которого сходится: а) четыре стороны; б) пять сторон; в) шесть сторон; г) семь сторон?

19. Можно ли составить паркет из треугольников, равных данному треугольнику с углами 30 , 45 , 60 ?

20. Составьте паркет из какого-нибудь неправильного треугольника.

21. Выясните, каким условиям должны удовлетворять углы треугольника на плоскости Лобачевского, чтобы из него можно было составить паркет.

22. Можно ли на плоскости Лобачевского составить паркет из правильных четырехугольников, в каждой вершине которого сходится: а) четыре стороны; б) пять сторон; в) шесть сторон; г) семь сторон?

23. Составьте паркет из правильных четырехугольников, в каждой вершине которого сходится восемь сторон.

24. Выясните, каким условиям должны удовлетворять углы четырехугольника на плоскости Лобачевского, чтобы из него можно было составить паркет.

25. Составьте паркет из правильных восьмиугольников, в каждой вершине которого сходится четыре стороны.

26. Определите понятие полуправильного паркета на плоскости Лобачевского. Приведите пример.

27. Определите понятие двойственного паркета. Приведите пример.

28. Образуют ли дуги окружностей на рисунке 26 полуправильный паркет на плоскости Лобачевского?

29. Какое наименьшее число красок потребуется для раскраски паркетов на рисунках 34 – 36 так, чтобы соседние многоугольники были окрашены в разные цвета?

30. Для окружности на координатной плоскости, заданной уравнением x 2 + y 2 = R 2 , и точки A ( x ₀ , y ₀ ), найдите координаты точки A ’ , полученной из точки A инверсией относительно данной окружности.

31. Используя координатный метод, докажите, что при инверсии относительно окружности с центром в точке O (0, 0) окружности, не проходящие через точку O , переходят в окружности, не проходящие через точку O , а окружности, проходящие через точку O (без самой точки O ), переходят в прямые, не проходящие через точку O .

3. Паркеты на сфере

Напомним, что аналогом многоугольника на сфере является фигура, ограниченная дугами больших окружностей. Мы будем называть такие фигуры сферическими многоугольниками, а соответствующие дуги больших окружностей – сторонами. Легко видеть, что сферический многоугольник может быть получен как пересечение сферы и многогранного угла с вершиной в центре этой сферы. Сферический многоугольник называется правильным, если равны все его стороны и углы.

Паркетом на сфере называется такое заполнение сферы сферическими многоугольниками, при котором любые два сферических многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.

Паркет на сфере называется правильным, если он состоит из равных правильных сферических многоугольников.

Паркет на сфере называется полуправильным, если он состоит из правильных сферических многоугольников (возможно, с разным числом сторон) и для любых его вершин существует движение сферы, переводящее паркет сам в себя и одну из данных вершин в другую.

Отметим связь правильных и полуправильных паркетов на сфере с правильными и полуправильными многогранниками.

Напомним, что выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники и в каждой вершине сходится одинаковое число ребер.

Имеется пять типов правильных многогранников: тетраэдр, его гранями являются четыре правильных треугольника (рис. 40); гексаэдр ( куб) – многогранник, гранями которого являются шесть квадратов (рис. 41); октаэдр, его гранями являются восемь правильных треугольников (рис. 42); икосаэдр, его гранями являются двадцать правильных треугольников (рис. 43); додека­эдр, его гранями являются двенадцать правильных пятиугольников (рис. 44).

Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники, возможно, и с разным числом сторон, и для любых двух вершин существует движение, переводящее многогранник сам в себя и одну из данных вершин в другую.

К полуправильным многогранникам относятся правильные призмы, все ребра которых равны. Например, правильная шестиугольная призма на рисунке 45 имеет своими гранями два правильных шестиу­гольника – основания призмы, и шесть квадратов, образующих боковую по­верхность призмы. К полуправильным многогранникам относятся и, так на­зываемые, антипризмы с равными ребрами. На рисунке 46 мы видим пятиугольную антип­ризму, полученную из пятиугольной призмы поворотом одного из основа­ний относительно другого на угол 36 . Каждая вершина верхнего и нижне­го оснований соединена с двумя ближайшими вершинами другого основания.

Кроме этих двух бесконечных серий полуправильных многогранников, имеется еще 13 полуправильных многогранников, которые впервые открыл и описал Архимед – это тела Архимеда.

Самые простые из них получаются из правильных многогранников опе­рацией “усечения”, состоящей в отсечении плоскостями углов многогран­ника. Если срезать углы тетраэдра плоскостями, каждая из которых отсе­кает третью часть его ребер, выходящих из одной вершины, то получим усеченный тетраэдр, имеющий восемь граней (рис. 47). Из них четыре – правильные шестиугольники, и четыре – правильные треугольники. В каждой вершине этого многогранника сходятся три грани.

Если указанным образом срезать вершины октаэдра и икосаэдра, то получим соответственно усеченный октаэдр (рис. 48) и усеченный икосаэдр (рис. 49). Обратите внимание на то, что поверхность футбольно­го мяча изготавливают в форме поверхности усеченного икосаэдра. Из ку­ба и додекаэдра также можно получить усеченный куб (рис. 50) и усе­ченный додекаэдр (рис. 51).

Для того чтобы получить еще один полуправильный многогранник, проведем в кубе отсекающие плоскости через середины ребер, выходящих из одной вершины. В результате получим полуправильный многогранник, который называется кубооктаэдром (рис. 52). Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его название – кубооктаэдр.

Аналогично, если в додекаэдре отсекающие плоскости провести через середины ребер, выходящих из одной вершины, то получим многогранник, который называется икосододекаэдром (рис. 53). У него двадцать гра­ней – правильные треугольники, и двенадцать граней – правильные пятиу­гольники, т.е. все грани икосаэдра и додекаэдра.

Следующие два многогранника называются усеченный кубооктаэдр (рис. 54) и усеченный икосододекаэдр (рис. 55). Однако они не получаются операцией «усечения» из кубооктаэдра и икосододекаэдра, соответственно. Действительно, если в кубооктаэдре и икосододекаэдре провести отсекающие плоскости, то в сечениях получатся прямоугольники, а не квадраты, как требуется.

На рисунке 56 изображен ромбокубооктаэдр. Он состоит из гра­ней куба и октаэдра, к которым добавлены еще 12 квадратов.

На рисунке 57 изображен ромбоикосододекаэдр, состоящий из гра­ней икосаэдра, додекаэдра и еще 30 квадратов.

На рисунках 58 и 59 представлены соответственно, так называемые, плосконосый (иногда называют курносый) куб и плосконосый ( курносый) додекаэдр, которые состоят из граней куба или додекаэдра, окруженных правильными треу­гольниками.

Легко видеть, что каждому паркету на сфере, состоящему из правильных сферических многоугольников, можно сопоставить многогранник, вершинами которого будут вершины этого паркета. При этом правильному паркету на сфере соответствует правильный многогранник, а полуправильному паркету – полуправильный многогранник. Наоборот, каждому правильному и полуправильному многограннику можно сопоставить паркет на сфере, описанной около этого многогранника, вершинами которого будут вершины этого многогранника. При этом правильному многограннику соответствует правильный паркет на сфере, а полуправильному многограннику – полуправильный паркет.

Имеется взаимнооднозначное соответствие между правильными и полуправильными паркетами на сфере и правильными и полуправильными многогранниками. Таким образом, на сфере имеется пять правильных паркетов, соответствующих правильным многогранникам; две бесконечные серии полуправильных паркетов, соответствующих призмам и антипризмам, и 13 полуправильных паркетов, соответствующих телам Архимеда.

Также как и на плоскости, наличие только пяти типов правильных паркетов на сфере обусловлено не величинами углов правильных сферических многоугольников, а более общими топологическими свойствами сферы.

Топология – раздел геометрии, изучающий свойства фигур, не меняющиеся при непрерывных деформациях, включающих в себя растяжения, сжатия, изгибания и т.п. Две фигуры называются топологически эквивалентными, если одна из них получается из другой с помощью непрерывной деформации. Так, например, все n -угольники топологически эквивалентны, все простые замкнутые линии на плоскости топологически эквивалентны окружности.

Рассмотрим паркеты на сфере, образованные криволинейными многоугольниками. Паркет называется топологически правильным, если он состоит из одноименных многоугольников и в каждой вершине сходится одинаковое число сторон. Докажем, что существует только пять типов топологически правильных паркетов на сфере, которые соответствуют правильным многогранникам. Для этого воспользуемся теоремой Эйлера о числе вершин (В), ребер (Р) и граней (Г) выпуклого многогранника, переформулированной на язык паркетов.

Теорема. Для любого паркета на сфере выполняется следующее равенство:

где В – число вершин, Р – число сторон (ребер), Г – число многоугольников (граней) данного паркета.

Доказательство. Для данного паркета рассмотрим какую-нибудь его сторону (ребро), соединяющую две вершины. Стянем ее вместе с вершинами в одну точку. При этом число вершин уменьшится на единицу (вместо двух вершин стала одна), число ребер уменьшится на единицу, число граней не изменится. Следовательно, В – Р + Г при этом не изменится. Будем последовательно стягивать ребра, соединяющие различные вершины, пока не останется одна вершина, а стороны превратятся в петли с началом и концом в данной вершине. При этом В – Р + Г будет таким же, как и у исходного паркета. Уберем одно из ребер – петель. При этом число вершин не изменится, число ребер уменьшится на единицу, число граней уменьшится на единицу (две грани соединятся в одну). Следовательно, В – Р + Г при этом не изменится. Будем последовательно убирать ребра, пока не останется одно ребро. В результате В – Р + Г будет таким же, как у исходного паркета. При этом В = 1, Р = 1, Г = 2, т.е. В – Р + Г = 2. Значит, равенство В – Р + Г = 2 справедливо и для исходного паркета.

Теорема. На сфере существует только пять типов топологически правильных паркетов.

Доказательство. Пусть дан топологически правильный паркет на сфере, составленный из n -угольников, и в каждой вершине сходится m сторон. Ясно, что n и m больше или равны трем. Обозначим, как и раньше, В – число вершин, Р – число сторон (ребер) и Г – число многоугольников (граней) этого паркета. Тогда

Г n = 2P; Г = ; B m = 2P; В = .

По теореме Эйлера В – Р + Г = 2 и, следовательно,

Откуда Р = . Из полученного равенства, в частности, следует, что должно выполняться неравенство 2 n + 2 m – nm > 0, которое эквивалентно неравенству ( n – 2)( m – 2)

Найдем всевозможные значения n и m , удовлетворяющие найденному неравенству, и заполним следующую таблицу.

[spoiler title=”источники:”]

http://gadgetshelp.com/windows/geometriia-mnogougolnika-piatiugolniki-shestiugolniki-i-dodekagony/

http://vasmirnov.ru/Problems/parkety.htm

[/spoiler]

Игра «Пентагон» придумана Новосибирским клубом «Queen» и каждый этап её представляет собой вопрос и пять подсказок к нему (отсюда и такое интересное название).

Впрочем, давайте обо всём по порядку.

1. В игре «Пентагон» используется принцип подсказки и снижения очков.

2. Ответ может даваться после каждого сообщения-подсказки.

3. Если ответ дан правильно, засчитываются очки уровня (всего их пять – по числу подсказок).

4. Если ответ неверен, отнимается одно очко.

5. Игрок может повторять свои попытки ответить на вопрос после каждой подсказки, что соответствует переходу на более низкий уровень.

6. За правильный ответ очки присуждаются только единожды и соответствуют тому уровню, на котором игрок дал впервые правильный ответ.

7. Если после правильного ответа на вопрос игрок случайно даёт неправильный ответ, он лишается одного очка.

8. Игроки до конца тура не знают, какой ответ они дали – правильный или нет.

Вот примерные вопросы, которые можно использовать для игры в «Пентагон»:

Вопрос 1. Это средство передвижения.

1.1. В 1943 году в Германии каждый день выпускалось по 1,1 штуки.

1.2. Впервые это подробно было описано Жюлем Верном.

1.3. Про это была создана песня группы «Битлз».

1.4. Это средство передвижения, потерпевшее катастрофу, – постоянный источник угрозы для Норвегии.

1.5. Это средство К-21 атаковало линкор «Тирпиц».

Ответ: Подводная лодка.

Вопрос 2. Это телепередача.

2.1. Из шести слуг Киплинга в название её вошли имена трёх.

2.2. Это игровая телепередача.

2.3. Её символом долгое время была бабушка с книгой.

2.4. За время её существования её первый ведущий постарел более чем на 20 лет.

2.5. Сейчас её аналог проводится во многих странах (в том числе и в Беларуси).

Ответ: «Что? Где? Когда?»

Вопросы, приведённые здесь для детской викторины, посвящены одному и тому же изобретению, но первый и второй блоки подходят для учеников старших классов, а третий – для учеников среднего школьно возраста.  Выберите любые вопросы, наиболее подходящие для детской викторины, проводимой у Вас в школе, и включите их в интеллектуальную игру «Пентагон».

Для старшеклассников:

Блок 1.

5. Для арифмометра Однер придумал его специальную конструкцию.

4. Индейские цивилизации не пользовались им до того, как к ним пришли европейцы.

3. А. Хейли назвал свой роман об автомобилистах именно этим изобретением.

2.   Даже первые пароходы не обходились без него.

1. В часах и других механизмах они могут иметь зубцы.

Блок. 2.

5.  В 2000 году один австралиец его запатентовал.

4.   У боевых древнегреческих изделий их было два.

3.   Они используются в аттракционах, связанных своим названием с нечистой силой.

2   Иногда они бывают у кресел.

1.    У велосипеда их бывает 2, 3, изредка 4 штуки.

Для детей среднего школьного возраста:

Блок 1:

5.   На нем стоит древнеримская богиня судьбы.   .

4.   Их используют многие виды транспорта средств.

3. Они являются основой водяных, но не ветряных мельниц.

2.   Многие из них связаны со спицами.

1. Русское название его происходит от древнего слова «коло», означающего «круг».

Ответ на все три блока, как Вы уже, наверное, догадались сами – «колесо».

Эти вопросы «Пентагона» будут понятны даже маленьким детям –  для викторины 3 класс прекрасно подойдёт.  Содержит игра 3 вопроса:

Вопрос 1.

5. Они упоминаются в некоторых русских пословицах и поговорках.

4.  Маленьких детей иногда развлекают с помощью игры в неё.

3.   Одна из них стала персонажем очень известной задачки на перемещения.

2.  Их ни в коем случае нельзя пускать в огород.

1.   В сказке серый волк не справился с одной особью и семью ее детенышами.

Ответ: Козы.

Вопрос 2.

5.   Это животное дало название семейству, в ко­торое входят и манул, и каракал.

4.   По-китайски его название звучит как «мао».

3.  У Киплинга это весьма самостоятельная особа.

2.   В Древнем Египте ее первой спасали при по­жаре.

1.    Она помогает избавляться от мелких грызунов.

Ответ: Кошка.

Вопрос 3.

5.   Это пушистое домашнее животное бывает раз­ного цвета и окраски.

4.  Детеныш этого животного под головным убором однажды напугал двух мальчиков.

3.   Другой в сказке помог своему хозяину добыть богатство и титул.

2.   Сказочная представительница этого животного лишилась дома в результате большого несчас­тья.

1. А самого известного любит Дядя Федор.

Ответ: Кот.

Вообще такие вопросы (именно если проводится детская викторина (3 класс, 4 класс)) придумываются очень легко и игра (3 вопроса, приведённых выше – это всего лишь пример) в этом случае будет намного интереснее.

ВОПРОСЫ ДЛЯ УЧАЩИХСЯ : (6-11 классы)

Цель интеллектуальной игры – не только показать свои знания, но и получить новые, к тому же интеллектуальные игры прекрасно помогают детям научиться не только выигрывать, но и красиво проигрывать, а также работать в команде (например, если это такая интеллектуальная игра, как знаменитая «Что? Где? Когда?»). Именно поэтому игры такого плана особенно полезны для подростков – они приносят огромную пользу их пытливому, но не всегда настроенному на «правильную волну» уму. Вопросы, представлены ниже, подготовлены для викторины «Пентагон» и подойдут для подростков. Цель интеллектуальной игры и её правила уже описаны на нашем сайте. Содержит эта игра 15 вопросов.

Вопрос 1.

5. Коричневая, покрытая коричневой пылью, она помогла выявить шпиона.

4.   Раньше их делали из рога и слоновой кости, иногда из золота, а сейчас чаще всего  из пласт­массы, хотя встречаются экземпляры и из другого материала.

3. Существует поговорка, что если она отсутствует у муж­чины, то ему пора либо жениться, либо разво­диться.

2.   На парадном камзоле французского короля их было около 13 600.

1.  Маленькие дети до четырех лет часто не умеют их за­стегивать.

Ответ: Пуговица.

Вопрос 2.

5.   Не всем известно, что раньше он предназначался для изготовления сбитня.       –

4.   Мы все знаем случай, когда он стал главарём бунта против своей ленивой хозяйки.

3.Описан случай, когда его купили за полкопей­ки.

2. С ним не стоит ездить в Тулу.

1. У него мы с Машей чай пили вечерком.

Ответ: самовар.

Вопрос 3.

5. Считается, что они часто определяют не только внешний вид, но и черты характера мужчины.

4. Стрелки на них подчеркивают строгость и опрят­ность их владельца.

3. Они появились впервые в городе Брюгге.

2. Один из героев Маршака перепутал их с рубашкой.

1. Их совершенно невозможно одеть через голову.

Ответ: брюки.

Вопрос 4.

5. Это основной вид одежды древних египтян.

4. Не только цыганки, но и казачки могли носить сразу по пятнадцать и больше штук.

3. Мужчины в нашей стране их не носят.

2. Но есть страна, в которой они – часть национальной одежды.

1. В середине XX века изобрели самую короткую из них.

Ответ: юбка.

Вопрос 5.

5. На фабрике Уотмана это было гладким и плотным.

4.  Говорят, что она очень терпелива.

3.  В основном она состоит из целлюлозы.

2.  Раньше вместо нее использовали глину, воск или кожу.

1.  На ней учатся писать.

Ответ:  бумага.

Вопрос 6.

5. Большого размера у греков он назывался мафорий.

4. Белый в руках женщины когда-то означал пре­кращение битвы.

3. Клавдия Шульженко пела про него – в песне он был синего цвета.

2. Его порой используют только для части голо­вы.

1. Оренбургский пуховый можно пропустить через обручальное кольцо.

Ответ: платок.

Вопрос 7.

5. Из-за нее в 1648 году вспыхнуло восстание.

4. Это — суть шутки и мысли.

3. Она пятая в известном ряду.

2. Ее называют белой смертью.

1. Ее не рекомендуется сыпать на рану.

Ответ: соль.

Вопрос 8.

5. О существовании на Руси этого, всем сейчас известного бытового пред­мета впервые сообщается в письменном источ­нике 1636 года.

4. Еще в прошлом веке его нужно было «разво­дить».

3. Мужчины благодарны ему за «стрелы», а жен­щины за «гладкость».

2. Сейчас они в основном электриче­ские.

1. Для качественной работы этого устройства са­мое главное — нагрев до нужной температуры.

Ответ: утюг.

Вопрос 9.

5. Производство этого в России связано с именем Дмитрия Виноградова — друга Ломоносова по учению в Германии.

4. Тайну этого в Европе раскрыл ученик немецкого аптекаря, который учился из любого подходя­щего материала лепить пилюли.

3.  Елена Данько об этом написала книгу под названием «Китайский секрет».

2.  Сырье для этого китайцы выдерживали в земле десятки лет подряд.

1.  Материалом для этого служит каолин, но специ­алист всегда отличит саксонский от китайского или русского.

Ответ: фарфор.

Вопрос 10.

5. Его ближайшим родственникам посвящены названия нескольких созвездий.

4. Философ по имени Урсус назвал своего вос­питанника Гомо.

3. Установлена закономерность: в трудные времена (например, война) их численность в России всегда увеличивалась.                                 ,

2. Американский вид называется луговым, а в Индии пока еще водится красный вид.

1. В отличие от него работа никуда не убежит.

Ответ: волк.

Вопрос 11.

5. Так называют и режущий инструмент, и маленькую байдарку, и лист неких огородных растений.

4. Белковый состав этого очень близок к белко­вому составу рогов парнокопытных.

3. Прекращение их массового использования связано с изобретением спе­циального шарика.

2.  У А. С. Пушкина в стихотворении «Осень» к нему «тянутся пальцы».

1. Это служило украшением наряда и дам, и ка­валеров.

Ответ: перо.

Вопрос 12.

5. Это растение цветет в конце июня — начале июля.

4. Латыши поклоняются отдельным экземплярам, достигающим в высоту 30 м.

3. Из этого растения получается прекрасный мёд.

2. Его любят резчики по дереву.

1. Так как мошенники делали из него поддельные печати, оно стало символом фальшивки.

Ответ: липа.

Вопрос 13.

5. Одно из его старинных русских названий — убрусец.

4. Девушки на них показывали свое умение при подготовке приданного.

3. Платон Майборода написал о нем песню.

2.  На них ставят хлеб-соль.

1. Они бывают вафельные, салфеточные и махро­вые.

Ответ: полотенце.

Вопрос 14.

5. Впервые об этом животном на Руси можно узнать из летописи XII века.

4. У этого домашнего животного тоже есть молоч­ные зубы.

3. Всем знатокам давно известно, что на острове Мэн представители этого семейства лишены хвостов.

2. В русских монастырях их держали для борьбы с паразитами.

1. В Древнем Египте за их убийство полагалась смертная казнь.

Ответ: кошки.

Вопрос 15.

5. Из-за этих животных очень изменился ланд­шафт Греции.и других стран.

4. Это полорогие парнокопытные животные.

3. У одной из них был очень жестокий хозяин.

2. Один из них очень напугал Робинзона Крузо.

1. Их молоко очень полезно.

Ответ: козы.

В этом пакете в вопросах зашифрованы слова. Кстати, интеллектуальные игры такого плана можно проводить не только в школе, но и в лагере – вопросы интеллектуальной викторины  пишутся очень легко. Содержит наша игра 5 вопросов.

Вопрос 1.

5. Это — древнейший прибор.

4. Это — достоинство карты.

3. Это — заменители балла.

2. С этим не справилась Мартышка.

1. Это нарисовано на капюшоне королевской ко­бры.

Ответ: очки.

Вопрос 2.

5. С ним сравнивают либо совсем молодых, либо ста­рых, но бодрых.

4. Это – овощ.

3. Раньше брадобреи его подкладывали за щеку клиентам,

2. На юге растет тот, которого называют беше­ным.

1. Его срывают всегда зеленым и на еду, и на консервирование.

Ответ: огурец.

Вопрос 3.

5. Если его показывают в приключенческом фильме, то, скорее всего, он  попробует на вкус одного из отрицательных персонажей.

4. Он – самый лучший друг одного неизвестного науке существа.

3. Оказывается, он может проглотить звезду.

2. Как ни странно, в Ниле его представители встречаются не везде.

1. У нас он ассоциируется с зелёным цветом.

Ответ: крокодил.

Вопрос 4.

5. Его образует группа родственных учреждений.

4. Если добавить гласную к этому слову – получим фамилию изобретателя акваланга.

3. Это растительная форма.

2. В его гуще любят строить гнезда славки и другие пташки.

1. К нему можно отнести и жасмин, и сирень, розы.

Ответ: куст.

Вопрос 5.

5. Издавна они носят имена собственные (к примеру, Голодарь, Медведь, Лебедь, Козел).

4. Ими пользовались раньше железнодорожные кондукторы и водолазы.

3. В его названии дважды звучит старорусское слово, означающее круг.

2. У него есть язык.

1. Если работают сразу с тремя из них, раздается трезвон.

Ответ: колокол.

 Если интеллектуальные игры вроде «Пентагона» проводить в лагере, стоит подобрать несложные вопросы –  тогда викторина будет интересной для всех отдыхающих детей.

Источник: http://www.klubkontakt.net/publ/19-1-0-220

В нашей школе есть свои традиции. Одна
из них — интеллектуальные игры. Они проводятся
на уроках, если материалы игры соответствуют
изученной теме, в свободное время на турнирах или
на классных часах, во время дальних поездок, в
доброхотском или математическом школьном
лагере.

На уроке игра приоткрывает ребёнку
незнакомые грани изучаемой науки, помогает
по-новому взглянуть на привычный урок,
способствует возникновению у школьников
интереса к учебному предмету, значит, процесс
обучения становится более эффективным.

Игра “Пентагон” — это командное
соревнование. В командах может быть по 3-7 человек
(численность в команде зависит от общего
количества в классе или отряде). В одну игру в
командах должно быть поровну человек или + – 1) и 2
ведущих (один – ведёт игру, объявляя вопросы и
правильные ответы, а дугой – делает подсчёт
баллов).

“Пентагон” — самая популярная в
школе и интересная интеллектуальная игра. Такая
форма игры, как “Пентагон”, имеет наибольшую
информативность и развивает навыки анализа
информации. Ответы на вопросы в этой игре
обозначают один предмет, явление, лицо и т.п. (т.е.
являются существительными или именам собств.)
Вопросы здесь следующего вида: сначала говорится
о том, что это за предмет (музыкальный
инструмент/ученый/предмет быта/судно и т.п.), и тут
же объявляется первая подсказка. На обдумывание
каждой подсказки (их всего 5) дается определенное
одинаковое время (например, одна минута). В этот
период команды должны успеть подумать и сдать
ответ в письменном виде или принять подсказку во
внимание. По истечении отведенного времени
объявляется следующая подсказка. Если команда
ответила правильно после 1 подсказки, то ей
дается 5 баллов, после 2 – 4, после 3 – 3 и т.д. За
неправильный ответ вычитается 1 балл. Для
подсчёта баллов удобно использовать специальную
таблицу (см. Приложение).
Подсказка представляет из себя фразу, по которой
можно определить этот предмет. Первая подсказка
— самая сложная.

Вот пример вопроса. Тема вопроса:
“Слово”

1 подсказка. Одно из значений этого
многозначного слова – “узкая, плоская, слабо
выступающая из стены вертикальная полоса,
делящая стену по всей ее высоте”.
2 подсказка. Это часть ключицы в скелете человека.
3 подсказка. Это выдающаяся парная кость на спине.
4 подсказка. Это дворницкий инструмент небольших
размеров.
5 подсказка. Домохозяйки пользуются таким
предметом для переворачивания котлет, а во время
приема гостей – для раскладывания торта.

Ответ: лопатка.

Команды сдают ответ на листочке (карточке), на
котором указывают название команды, номер
вопроса и номер подсказки и, разумеется, ответ.
Ответные листы можно заготовить заранее по
образцу:

Предлагаю одну из игр “Пентагон” по русскому
языку, которую можно провести в 5, 6 или 7 классе.

Игра “Пентагон” по русскому языку по теме
“Лексическое значение слова”.

I. Тема вопроса: “Слово”. Ответ: огурец

1. Это слово означает овощ.
2. С ним сравнивают либо совсем юных, либо старых,
   но бодрых.
3. Раньше брадобреи подкладывали его за щеку
   клиентам.
4. На юге растёт тот, которого называют “бешеным”.
5. Его срывают всегда зелёным и на еду, и для
   консервирования.

II. Тема вопроса: “Предмет”.Ответ: колокол

1. Со старых времён они носят имена собственные,
   такие как Колодарь, Медведь, Лебедь, Козёл и даже
   Царь.
2. Ими пользовались раньше водолазы и
   железнодорожные кондукторы.
3. В названии этого предмета дважды звучит древнее
   русское слово, означающее круг.
4. У этого предмета есть язык, и он работает языком.
5. Если работают сразу с тремя из них, раздаётся
   трезвон.

III. Тема вопроса: “Многозначное слово”.Ответ:
очки

1. Этот древнейший прибор.
2. Это – достоинство карты.
3. Это – заменители баллов.
4. С ними не справилась Мартышка.
5. Это изображено на капюшоне королевской кобры.

IV. Тема вопроса: “Предмет”.Ответ: бумага

1. На фабрике Уотмана это было гладким и плотным.
2. Говорят, что “она очень терпелива”.
3. В основном, она состоит из целлюлозы.
4. Раньше вместо неё использовали глину, воск,
   кожу.
5. На ней учатся писать.

V. Тема вопроса: “Слово”.Ответ: барабан

1. Это слово называет венчающую часть здания,
   несущую купол, в форме цилиндра или
   многогранника.
2. Полый цилиндр в механизмах, а также вообще
   техническое устройство цилиндрической формы.
3. От этого слова возник хирургический термин,
   характеризующий часть слухового аппарата
   человека.
4. Это ударный мембранный музыкальный инструмент.
5. Если вам безразлично, значит, вам “всё по нему”

VI. Тема вопроса: “Многозначное слово”.Ответ:
тубус

1. Однокоренное слову, которое называет медный
   духовой музыкальный инструмент, самый большой по
   величине и самый низкий по звучанию.
2. Также оно однокоренное слову, называющему
   предмет для хранения полужидких веществ.
3. Это трубка, в которой заключены окуляры
   микроскопа.
4. По-итальянски корень звучит как tuba,
   по-французски как tube, а имя предмета
   произносится как латинский корень.
5. Цилиндрический футляр для хранения чертежей.

VII. Тема вопроса: “Многозначное слово”.Ответ:
глава

1. Наружная часть купольного перекрытия барабана
   в форме шлема, конуса, луковицы или зонтика.
2. Человек, исполняющий ведущую роль в руководстве
   административной единицы (района, города,
   государства).
3. Часть крупного литературного произведения.
4. Слово содержит характерное русское
   неполногласие.
5. Этим приходится всему хлеб…

VIII. Тема вопроса: “Предмет”.Ответ: самовар

1. Раньше он предназначался для изготовления
   сбитня.
2. Описан случай, когда он возглавил бунт против
   неряшливой и ленивой хозяйки.
3. Описан случай, когда его купили за полкопейки.
4. С ним не стоит ездить в Тулу.
5. У него “мы с Машей” чай пили вечерком.

IX. Тема вопроса: “Слово”.Ответ: инициатива

1. Термин, означающий право вносить проекты
   законов.
2. Слово пришло в русский язык из французского и
   позднелатинского (“начинать, начинаться”).
3. Имеет то же происхождение и те же
   орфограммы-гласные, что и слово инициалы.
4. Одно из значений – почин, побуждение к началу
   какого-либо дела, руководящая роль в каких-либо
   действиях.
5. Одно из значений – способность к
   самостоятельным активным действиям,
   предприимчивость.

X. Тема вопроса: “Многозначное слово”.Ответ:
программа

1. Слово пришло из французского языка со значением
   “объявление, афиша, распоряжение”.
2. Краткое изложение содержания и методических
   установок предмета, курса, преподаваемого в
   учебном заведении.
3. Изложение содержания и цели деятельности
   политической партии, организации или отдельного
   деятеля.
4. Порядок проведения чего-либо: праздника,
   концерта и т.д., а также листок с перечнем
   исполняемых номеров.
5. План предстоящей деятельности, работ,
   мероприятий.

XI. Тема вопроса: “Многозначное слово”.Ответ:
иммунитет

1. В немецкий язык это слово пришло из латинского
   языка со значением “освобождение от
   повинностей, податей, налогов”.
2. Право на неприкосновенность, предоставляемое
   лицам, занимающим особое место в государстве.
3. Первая безударная объясняется латинской
   приставкой im-.
4. В переносном значении это способность
   противостоять чему-либо, сохраняя спокойствие и
   невозмутимость.

Этот биологический термин означает
способность организма защищать собственную
целостность и биологическую индивидуальность.

Приложение