Как составить передаточную функцию объекта - Сайт, где вы сможете решить свои вопросы

2.6.1 Определение передаточной функции

Преобразование
ДУ по Лапласу дает возможность ввести
удобное понятие передаточной функции,
характеризующей динамические свойства
системы.

Например,
операторное уравнение

3s²Y(s)
+ 4sY(s)
+ Y(s)
= 2sX(s)
+ 4X(s)

можно
преобразовать, вынеся X(s)
и Y(s)
за скобки и поделив друг на друга:

Y(s)*(3s²
+ 4s
+ 1) = X(s)*(2s
+ 4)

Полученное
выражение называется передаточной
функцией.

Передаточной
функцией
называется отношение изображения
выходного воздействия Y(s)
к изображению входного X(s)
при нулевых начальных условиях.

(2.4)

Передаточная
функция является дробно-рациональной
функцией комплексной переменной:

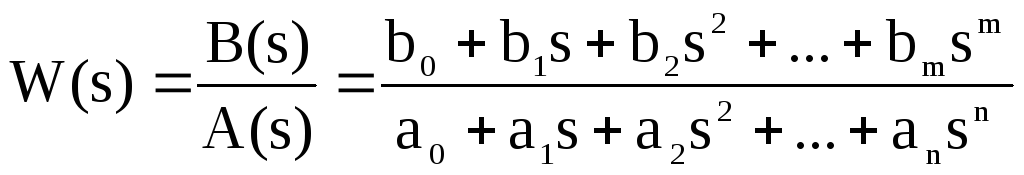где
B(s) = b₀
+ b₁s
+ b₂s²
+ … + b_m
s^m
– полином
числителя,

А(s)
= a₀
+ a₁s
+ a₂s²
+ … + a_n
sⁿ
– полином знаменателя.

Передаточная
функция имеет порядок, который определяется
порядком полинома знаменателя (n).

Из
(2.4) следует, что изображение выходного
сигнала можно найти как

Y(s)
= W(s)*X(s).

Так
как передаточная функция системы
полностью определяет ее динамические
свойства, то первоначальная задача
расчета АСР сводится к определению ее
передаточной функции.

2.6.2 Примеры типовых звеньев

Звеном
системы называется ее элемент, обладающий
определенными свойствами в динамическом
отношении. Звенья систем регулирования
могут иметь разную физическую природу
(электрические, пневматические,
механические и др. звенья), но описываться
одинаковыми ДУ, а соотношение входных
и выходных сигналов в звеньях описываться
одинаковыми передаточными функциями.

В
ТАУ выделяют группу простейших звеньев,
которые принято называть типовыми.
Статические и динамические характеристики
типовых звеньев изучены достаточно
полно. Типовые звенья широко используются
при определении динамических характеристик
объектов управления. Например, зная
переходную характеристику, построенную
с помощью самопишущего прибора, часто
можно определить, к какому типу звеньев
относится объект управления, а
следовательно, его передаточную функцию,
дифференциальное уравнение и т.д., т.е.
модель объекта. Типовые звенья Любое
сложное звено может быть представлено
как соединение простейших звеньев.

К
простейшим типовым звеньям относятся:

усилительное,

инерционное
(апериодическое 1-го порядка),
интегрирующие
(реальное и идеальное),
дифференцирующие
(реальное и идеальное),
апериодическое
2-го порядка,
колебательное,
запаздывающее.

1)
Усилительное звено.

Звено
усиливает входной сигнал в К раз.
Уравнение звена у = К*х, передаточная
функцияW(s)
= К. Параметр К называется коэффициентом
усиления.

Выходной сигнал
такого звена в точности повторяет
входной сигнал, усиленный в К раз (см.
рисунок 1.18).

у = K^.x.

При ступенчатом
воздействии h(t)
= K.

Примерами таких
звеньев являются: механические передачи,
датчики, безынерционные усилители и
др.

2)
Интегрирующее.

2.1)
Идеальное интегрирующее.

Выходная величина
идеального интегрирующего звена
пропорциональна интегралу входной
величины:

; W(s)
=

При подаче на вход
звена ступенчатого воздействия x(t) = 1
выходной сигнал постоянно возрастает
(см. рисунок 1.19):

h(t) = K^.t.

Это
звено астатическое, т.е. не имеет
установившегося режима.

Примером
такого звена может служить емкость,
наполняемая жидкостью. Входной параметр
– расход поступающей жидкости, выходной
– уровень. Изначально емкость пуста и
при отсутствии расхода уровень равен
нулю, но если включить подачу жидкости,
уровень начинает равномерно увеличиваться.

2.2)
Реальное интегрирующее.

Передаточная
функция этого звена имеет вид

W(s)
=
.

Переходная
характеристика в отличие от идеального
звена является кривой (см. рис. 1.20):

h(t)
= K^.(t
– T)
+ K^.T^.e
^–^t^/^T.

Примером
интегрирующего звена является двигатель
постоянного тока с независимым
возбуждением, если в качестве входного
воздействия принять напряжение питания
статора, а выходного – угол поворота
ротора. Если напряжение на двигатель
не подается, то ротор не двигается и
угол его поворота можно принять равным
нулю. При подаче напряжения ротор
начинает раскручиваться, а угол его
поворота сначала медленно вследствие
инерции, а затем быстрее увеличиваться
до достижения определенной скорости
вращения.

3)
Дифференцирующее.

3.1)
Идеальное дифференцирующее.

Выходная величина
пропорциональна производной по времени
от входной:

; W(s)
= K*s

При ступенчатом
входном сигнале выходной сигнал
представляет собой импульс (-функцию): h(t)
= K^.(t).

3.2)
Реальное дифференцирующее.

Идеальные
дифференцирующие звенья физически не
реализуемы. Большинство объектов,
которые представляют собой дифференцирующие
звенья, относятся к реальным дифференцирующим
звеньям, передаточные функции которых
имеют вид

W(s)
=
.

Переходная
характеристика: .

Пример
звена: электрогенератор. Входной параметр
– угол поворота ротора, выходной –
напряжение. Если ротор повернуть на
некоторый угол, то на клеммах появится
напряжение, но если ротор далее не
вращать, напряжение снизится до нуля.
Резко упасть оно не может вследствие
наличия индуктивности у обмотки.

4) Апериодическое
(инерционное).

Этому звену
соответствуют ДУ и ПФ вида

; W(s)
=
.

Определим характер
изменения выходной величины этого звена
при подаче на вход ступенчатого
воздействия величины х₀.

Изображение
ступенчатого воздействия: X(s)
=
.
Тогда изображение выходной величины:

Y(s)
= W(s)
X(s)
=

= K
x₀

Разложим дробь
на простые:

=

+

=

=

–

=

–

Оригинал первой
дроби по таблице: L^-1{}
= 1, второй:

L^-1{}
=
.

Тогда
окончательно получаем

y(t)
= K
x₀
(1 –
).

Постоянная Т
называется постоянной
времени.

Большинство
тепловых объектов являются апериодическими
звеньями. Например, при подаче на вход
электрической печи напряжения ее
температура будет изменяться по
аналогичному закону (см. рисунок 1.22).

5)
Звенья второго порядка

Звенья имеют ДУ и
ПФ вида

W(s)
=
.

При подаче на вход
ступенчатого воздействия амплитудой
х₀
переходная кривая будет иметь один из
двух видов: апериодический (при Т₁

2Т₂)
или колебательный (при Т₁ < 2Т₂).

В
связи с этим выделяют звенья второго
порядка:

апериодическое
2-го порядка (Т₁

2Т₂),
инерционное
(Т₁ < 2Т₂),
консервативное
(Т₁
= 0).

6)
Запаздывающее.

Если
при подаче на вход объекта некоторого
сигнала он реагирует на этот сигнал не
моментально, а спустя некоторое время,
то говорят, что объект обладает
запаздыванием.

Запаздывание
– это интервал времени от момента
изменения входного сигнала до начала
изменения выходного.

Запаздывающее
звено – это звено, у которого выходная
величина у в точности повторяет входную
величину х с некоторым запаздыванием
:

y(t)
= x(t
– ).

Передаточная
функция звена:

W(s)
= e^–^^s.

Примеры
запаздываний: движение жидкости по
трубопроводу (сколько жидкости было
закачано в начале трубопровода, столько
ее выйдет в конце, но через некоторое
время, пока жидкость движется по трубе),
движение груза по конвейеру (запаздывание
определяется длиной конвейера и скоростью
движения ленты) и т.д.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пeрeда́точная фу́нкция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи и цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.

В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета САР сводится к определению ее передаточной функции. При расчете настроек регуляторов широко используются достаточно простые динамические модели промышленных объектов управления. Передаточная функция является дробно-рациональной функцией комплексной переменной для разных систем.

Линейные стационарные системы[править | править код]

Пусть u(t) — входной сигнал линейной стационарной системы, а — её выходной сигнал. Тогда передаточная функция такой системы записывается в виде:

${displaystyle W(s)={frac {Y(s)}{U(s)}},}$

где

— оператор передаточной функции в преобразовании Лапласа,

— преобразования Лапласа для сигналов u(t)

соответственно:

${displaystyle U(s)={mathcal {L}}left{u(t)right}equiv int limits _{0}^{+infty }u(t)e^{-st},dt,}$

${displaystyle Y(s)={mathcal {L}}left{y(t)right}equiv int limits _{0}^{+infty }y(t)e^{-st},dt.}$

Дискретная передаточная функция[править | править код]

Для дискретных и дискретно-непрерывных систем вводится понятие дискретной передаточной функции. Пусть — входной дискретный сигнал такой системы, а — её дискретный выходной сигнал, . Тогда передаточная функция такой системы записывается в виде:

$W(z)={frac {Y(z)}{U(z)}}$

где и — z-преобразования для сигналов и соответственно:

$U(z)={mathcal {Z}}left{u(k)right}equiv sum _{{k=0}}^{infty }u(k)z^{{-k}}$

$Y(z)={mathcal {Z}}left{y(k)right}equiv sum _{{k=0}}^{{infty }}y(k)z^{{-k}}$

Связь с другими динамическими характеристиками[править | править код]

{displaystyle W(jomega )equiv W(s),s=jomega }

Импульсная переходная функция является оригиналом (в смысле преобразования Лапласа) для передаточной функции.

Свойства передаточной функции, полюсы и нули передаточной функции[править | править код]

1. Для стационарных систем (т. е. систем с неизменяемыми параметрами компонентов) и с сосредоточенными параметрами передаточная функция — это дробно-рациональная функция комплексной переменной :

$W(s)={frac {R(s)}{Q(s)}}={frac {b_{0}s^{m}+b_{1}s^{{m-1}}+dots +b_{m}}{a_{0}s^{n}+a_{1}s^{{n-1}}+dots +a_{n}}}$

2. Знаменатель и числитель передаточной функции — это характеристические полиномы дифференциального уравнения движения линейной системы. Полюсами передаточной функции называют корни характеристического полинома знаменателя, нули — корни характеристического полинома числителя.

3. В физически реализуемых системах порядок полинома числителя передаточной функции не может превышать порядка полинома её знаменателя , то есть

4. Импульсная переходная функция представляет собой оригинал (преобразования Лапласа) для передаточной функции.

5. При формальной замене в получается комплексная передаточная функция системы, описывающая одновременно амплитудно-частотную (в виде модуля этой функции) и фазо-частотную характеристики системы как её аргумент.

Матричная передаточная функция[править | править код]

Для MIMO-систем вводится понятие матричной передаточной функции. Матричная передаточная функция от вектора входа системы до вектора выхода — это матрица ${displaystyle W={w_{i,j}}}$ , элемент -й строки -го столбца представляет собой передаточную функцию системы от -й координаты вектора входа системы до -й координаты вектора выхода.

См. также[править | править код]

ЛАФЧХ
Частотный отклик
АФЧХ
Билинейное преобразование
Активационная функция

Ссылки[править | править код]

Передаточная функция
Программа преобразования передаточной функции в разностное уравнение

Источник

ГЛАВА 2

Передаточные функции и частотные характеристики

2.1. Передаточная функция

Помимо дифференциального уравнения, динамические свойства звена могут быть описаны также при помощи передаточной функции, которая представляет собой отношение операторного полинома воздействия к собственному операторному полиному, т.е. в общем виде передаточная функция звена определяется выражением

, (39)

а передаточная функция объекта, динамика которого описывается уравнением (13), выражением

. (40)

Рекомендуемые материалы

2.2. Частотная характеристика

В ряде случаев системы автоматического регулирования и входящие в состав их звенья работают под воздействием периодических и, в частности, гармонических возмущений. В связи с этим возникает необходимость исследовать работу систем также в режиме вынужденных колебаний с помощью, так называемого частотного метода. Отличительной особенностью частотного метода является также возможность применения его для экспериментального исследования динамических свойств реальных систем, аналитическое исследование которых невозможно.

Если на вход линейного звена подать гармоническое возмущение с амплитудой A₁ и частотой w, при этом , то по прошествии некоторого времени выходная координата также будет изменяться по гармоническому закону с той же частотой w, но с другой амплитудой А₂ и сдвигом колебаний по фазе j. Графически это показано на рис. 25.

Частотной характеристикой звена или амплитудно-фазовой частотной характеристикой называется зависимость амплитуды и фазы вынужденных гармонических колебаний от амплитуды и частоты входного возмущения.

Рис. 25. Вынужденные колебания САР

Для получения частотной функции, называемой также комплексной передаточной функцией, необходимо в выражение передаточной функции вместо р подставить iw, где , а w — круговая частота, т.е.

. (41)

Рис. 26. Амплитудно-фазовая характеристика

Последнее выражение в общем виде можно представить в прямоугольной системе координат:

, (42)

либо в полярной системе в виде показательной функции:

(43)

где — модуль, определяющий амплитуду колебаний;

— фаза.

Если изобразить частотную функцию (43) в виде вектора в комплексной плоскости , то при изменении частоты w от 0 до ∞ конец вектора опишет кривую, называемую амплитудно-фазовой характеристикой. Пример такой кривой приведен на рис. 26. Амплитудно-фазовые характеристики широко используются при исследовании динамических свойств систем.

2.3. Типовые динамические звенья

Несмотря на то, что звенья, входящие в состав различных САР, отличаются во многих случаях друг от друга как по конструктивному выполнению, так и по функциональному назначению, представляется возможным свести их к сравнительно небольшой группе звеньев, отличающихся одинаковыми динамическими свойствами. При такой классификации по динамическим свойствам звенья, переходные процессы в которых описываются одинаковыми уравнениями, относят к одному типу динамического эвена.

В теории автоматического регулирования принято различать следующие основные динамические звенья: пропорциональное или безынерционное, апериодическое или инерционное, колебательное, дифференцирующее, интегрирующее, с чистым запаздыванием.

Динамические свойства пропорционального или безынерционного звена описываются уравнением вида:

, (44)

а переходный процесс имеет вид, изображенный на рис. 27.

Рис. 27. Переходный процесс безынерционного звена

Передаточная и частотная функции этого звена описываются следующими выражениями:

; (45)

. (46)

Динамика апериодического звена описывается уравнением

. (47)

При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (см. рис. 22):

. (48)

Передаточная и частотная функции этого звена имеют следующие выражения:

;

(49)

Амплитудно-фазовая характеристика этого звена представлена на рис. 28.

Рис. 28. Амплитудно-фазовая характеристика

апериодического звена 1-го порядка

Динамика колебательного звена описывается уравнением

. (50)

При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (рис. 29):

, (51)

где — постоянная времени огибающей экспоненты;

Передаточная и частотная функции колебательного звена будут иметь выражения:

; (52)

. (53)

Рис. 29. График переходного процесса колебательного звена

Амплитудно-фазовая характеристика колебательного звена представлена на рис. 26.

В том случае, если в уравнении будет иметь место неравенство , то звено превращается в апериодическое 2-го порядка с переходной функцией

, (54)

где

;

Переходный процесс в этом случае будет иметь вид, представленный на рис. 30.

Рис. 30. График переходного процесса

апериодического звена 2-го порядка

Идеальным дифференцирующим называется звено, динамика которого описывается уравнением вида:

. (55)

График переходной функции этого звена показан на рис. 31 и представляет собой мгновенный импульс, который возникает только в момент подачи ступенчатого входного возмущения. Передаточная и частотная функции идеального дифференцирующего звена:

; . (56)

Рис. 31. Переходный процесс идеального

дифференцирующего звена

Большинство реальных систем обладают определенной инерционностью. Динамика инерционного дифференцирующего звена может быть описана уравнением вида:

. (57)

Рис. 32. Переходный процесс идеального интегрирующего звена

Динамика идеального интегрирующего звена описывается уравнением вида

(58)

или

, (59)

а в операторной форме

. (60)

Из уравнения (58) следует, что если на вход интегрирующего звена подать ступенчатое возмущение, то выходная величина будет со временем беспрерывно увеличиваться.

Графики переходного процесса такого звена показаны на рис. 32. Передаточная и частотная функции определяются по уравнениям:

(61)

Уравнение динамики реального интегрирующего звена будет:

. (62)

Дифференцируя обе части уравнения, можно получить другое выражение:

. (63)

В ряде случаев изменение выходной величины начинается не одновременно с изменением входной, а спустя некоторый промежуток времени, называемый запаздыванием.

Различают звенья с чистым или транспортным запаздыванием, примером которого может служить ленточный питатель (рис. 33). Если входной координатой считать положение шибера на питающем бункере 1 (х), а выходной координатой — количество материала, поступающего в бункер (Q), то переходная характеристика этого звена может быть описана уравнением

, (64)

где t — время;

— время чистого или транспортного запаздывания.

Рис. 33. Схема звена с чистым запаздыванием:

1, 3 – бункера; 2 – шибер

В общем случае любое звено с запаздыванием можно рассматривать состоящим из обыкновенного звена без запаздывания и идеального звена с чистым запаздыванием. Передаточная функция звена с запаздыванием в общем случае будет иметь выражение

, (65)

где W₀(p) — передаточная функция звена без запаздывания.

Рис. 34. Переходные процессы:

а – идеальное звено с чистым запаздыванием;

б – инерционное звено с чистым запаздыванием

Переходные процессы для идеального звена с запаздыванием и для инерционного звена при наличии чистого запаздывания приведены на рис. 34.

2.4. Соединение звеньев, алгебра передаточных функций

Выше была рассмотрена динамика отдельных звеньев, которые входят в состав САР и взаимодействуют между собой. В реальных САР встречаются разнообразные схемы соединения звеньев, которые можно свести к последовательному и параллельному соединению, а также их комбинации. В свою очередь при параллельном соединении может иметь место одинаковое направление входа и выхода либо противоположное. Рассмотрим выражения передаточных функций комплекса элементарных звеньев при различных способах их включения.

Рис. 35. Схема последовательного соединения звеньев

Последовательное соединение. Рассмотрим цепочку, состоящую из трех последовательно соединенных звеньев (рис. 35). На вход первого звена поступает величина х, а на выход последнего — у. Результирующая передаточная функция при последовательном соединении звеньев равна произведению передаточных функций отдельных звеньев:

. (66)

Параллельное соединение. Случай одинакового направления входа и выхода представлен на рис. 36.

Рис. 36. Схема параллельного соединения звеньев

Передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев:

. (67)

Случай противоположного направления сигналов (охват звена обратной связью) представлен на рис. 37. При включении обратной связи входной сигнал х алгебраически суммируется с сигналом, прошедшим через звено обратной связи, и при отрицательной обратной связи он равен:

В этом случае передаточная функция будет иметь вид:

. (68)

Рис. 37. Схема охвата звена обратной связью

При комбинированном соединении звеньев в САР необходимо контур разбить на отдельные цепи, в которых будут четко выражены последовательное и параллельное соединения, составить передаточные функции для этих цепей, а затем и для всего контура в целом. Таким образом, используя указанные зависимости, можно составить передаточную функцию сложной схемы, из которой при необходимости можно получить дифференциальное уравнение динамики системы.

Из выражения (68) для передаточной функции звена, охваченного обратной связью, принимая , можно легко получить выражение для передаточной функции замкнутой системы, схема которой показана на рис. 38.

Рис. 38. Схема замыкания звена

Передаточная функция замкнутой системы может быть представлена следующим образом:

, (69)

где — передаточная функция разомкнутой системы.

2.5. Уравнение динамики замкнутой системы

Система автоматического регулирования состоит из ряда звеньев, динамика которых в общем случае описывается дифференциальными уравнениями. Так как элементы САР находятся во взаимодействии друг с другом, а сама система является замкнутой, то математическим описанием САР будет являться система дифференциальных уравнений динамики звеньев, входящих в систему и их связей. Путем исключения промежуточных координат систему дифференциальных уравнений можно привести к одному дифференциальному уравнению, которое включает в себя только входные воздействия и выходную, регулируемую величину.

В качестве примера рассмотрим систему автоматического регулирования частоты вращения вала теплового двигателя, принципиальная схема которой приведена на рис. 39.

Структурная схема этой САР изображена на рис. 40. Динамику звеньев, входящих в состав системы, запишем в операторной форме:

объект — ;

чувствительный элемент — ; (70)

сервопривод — ,

где у — регулируемая величина;

x₂ — положение топливорегулирующего органа.

Рис. 39. Схемы САР частоты вращения вала дизель-генератора:

а — принципиальная; б — функциональная:

1 — золотник; 2 — поршень сервомотора; 3 — рычаг; 4 — грузы;

5 — муфта; 6 — вал регулятора;

СУ — корректирующее устройство; ЧЭ — чувствительный элемент;

ЗУ — задающее устройство; УС — устройство сравнения;

УУ — усилительное устройство; ИМ — исполнительный механизм;

f(t) — возмущающее воздействие; g(t) — управляющее воздействие

Решая систему (70), получим уравнение динамики замкнутой системы в операторной форме:

. (71)

Для этой же САР составим дифференциальное уравнение по передаточным функциям звеньев.

Рис. 40. Структурная схема САР частоты вращения

вала дизель-генератора

Для случая, когда возмущение приложено к объекту, передаточная функция замкнутой САР будет иметь выражение

где (для нашего случая) — передаточная функция объекта регулирования;

— передаточная функция регулятора.

Тогда

“Поиск творческой идеи” – тут тоже много полезного для Вас.

Отсюда уравнение динамики замкнутой системы

аналогично уравнению (71).

Вопросы для самоконтроля:

Дать понятие о передаточной функции и частотной характеристики.
Что представляет собой мгновенный импульс?
Уравнение динамики замкнутой системы.

Литература [2, 5, 6].

Источник

где xвых – выходная величина; xвх.i – i-я входная величина; a, b, c, … – коэффициенты, не зависящие от xвых и xвх.i, t – время.
Переменные x, описывающие систему, представляют собой функции времени и делятся на входные и выходные так, чтобы входные являлись причиной изменения выходных. Коэффициенты a, b, c, … описывают свойства системы.
Система называется стационарной, если коэффициенты a, b, c, … не зависят от времени, и нестационарной, если хотя бы один из них от времени зависит.
Система является нелинейной, если хотя бы один из коэффициентов a, b, c, … зависит от xвых или xвх..
Если система имеет одну выходную переменную, т.е. описывается одним уравнением вида (4.1), то она называется одномерной. Многомерные системы имеют более одной выходной величины и описываются системой уравнений вида (4.1).
Порядком рассматриваемой системы называется наивысший порядок производной в ее дифференциальном уравнении (или системе дифференциальных уравнений).
Левая часть уравнения (4.1) описывает собственное движение системы – изменение ее состояния в отсутствие внешних воздействий. Правая часть описывает влияние внешних воздействий на состояние системы.
Уравнение (4.1) относится только к системам без запаздывания. Для систем с запаздыванием хотя бы одна из величин xвых или xвх. должна быть представлена как функция с запаздывающим аргументом:

xвых(t – τ) или xвх(t – τ),

где τ – время запаздывания, характеризующее «отставание» той или иной функции.
Например, для объекта регулирования первого порядка без запаздывания с одной регулируемой величиной x уравнение (4.1) запишется как

Источник

2.6.1 Определение передаточной функции

2.6.2 Примеры типовых звеньев

Линейные стационарные системы[править | править код]

Дискретная передаточная функция[править | править код]

Связь с другими динамическими характеристиками[править | править код]

Свойства передаточной функции, полюсы и нули передаточной функции[править | править код]

Матричная передаточная функция[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Рекомендуемые материалы

Вам также может понравиться

Как найти гипотенузу четырехугольной пирамиды

Как найти все буквы в майнкрафт

Как найти фею террария

Добавить комментарий Отменить ответ