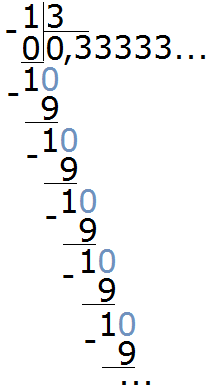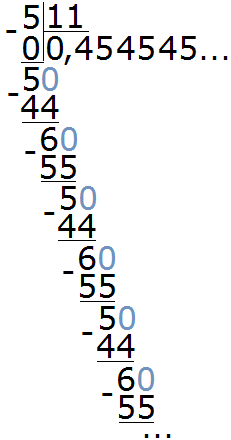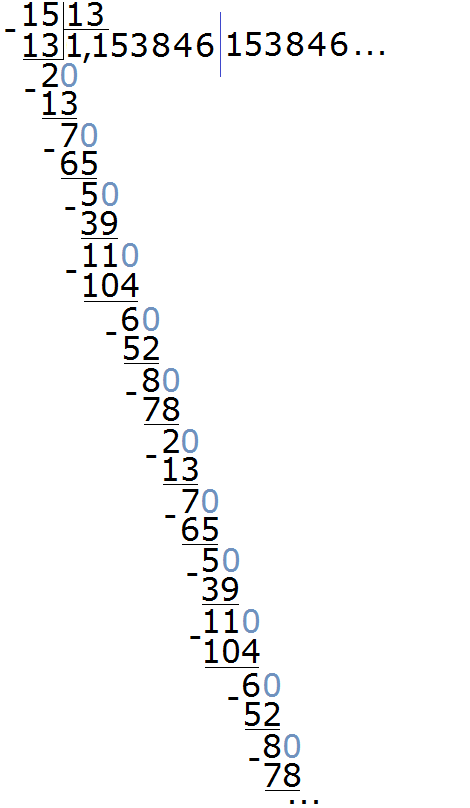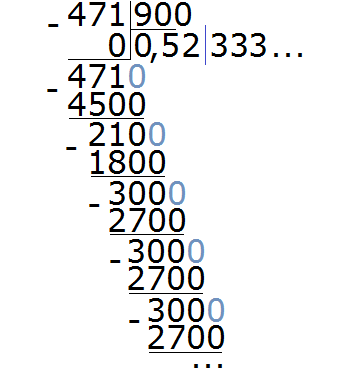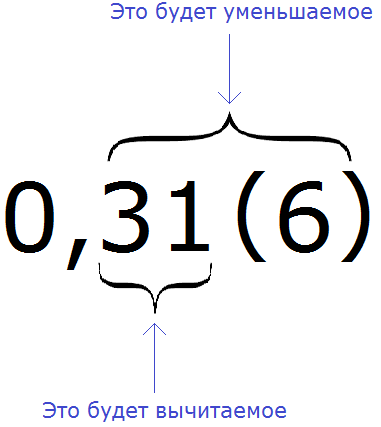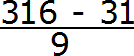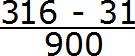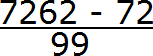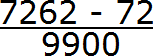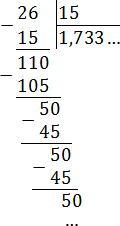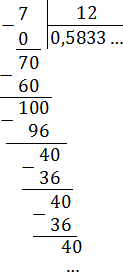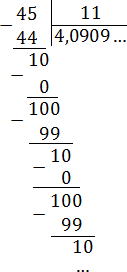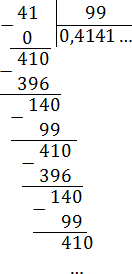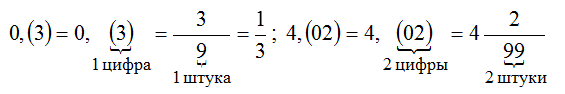Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:
0,66666666666666…
0,33333333333333…
0,68181818181818…
Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби и как с ними работать.
Получаем периодическую дробь
Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.
Итак, делим 1 на 3
Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.
Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.
В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:
0, (3)
Читается как «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11
Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:
0, (45)
Читается как «ноль целых и сорок пять в периоде»
Пример 3. Разделить 15 на 13
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:
1, (153846)
Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».
Пример 4. Разделить 471 на 900
В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:
0, 52 (3)
Читается как: «ноль целых пятьдесят две сотых и три в периоде».
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смéшанные.
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:
0, (3)
0, (6)
0, (5)
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смéшанной. Например, следующие периодические дроби являются смéшанными:
0,52 (3)
0,16 (5)
0,31 (6)
Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.
Избавляемся от хвоста
Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.
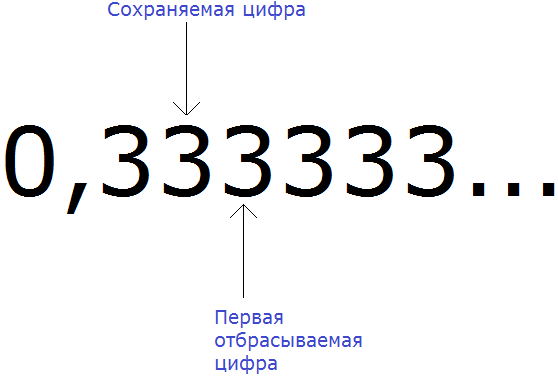
Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33
0, (3) ≈ 0,33
Округлим периодическую дробь 6,31 (6) до разряда тысячных.
Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317
6,31 (6) ≈ 6,317
Перевод чистой периодической дроби в обыкновенную дробь
Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для общего развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.
Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, то такую дробь называют чистой.
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.
Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби.
Итак, записываем в числителе период дроби 0, (3) то есть тройку:
А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).
В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:
Полученную дробь можно сократить на 3, тогда получим следующее:
Получили обыкновенную дробь .
Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается
Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.
Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:
А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).
В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:
Полученную дробь можно сократить эту дробь на 9, тогда получим следующее:
Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается
Перевод смешанной периодической дроби в обыкновенную дробь
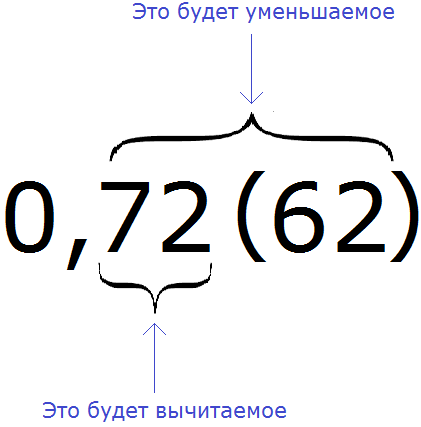
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)
В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)
В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Периодические десятичные дроби
10 февраля 2012
Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.
Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.
Периодическая десятичная дробь — это любая десятичная дробь, у которой:
- Значащая часть состоит из бесконечного количества цифр;
- Через определенные интервалы цифры в значащей части повторяются.
Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:
Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Возможны два варианта:
- В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным — см. урок «Десятичные дроби». Такие нас не интересуют;
- В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.
Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».
При этом будет происходить следующее:
- Сначала разделится целая часть, если она есть;
- Возможно, будет несколько чисел после десятичной точки;
- Через некоторое время цифры начнут повторяться.
Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.
Задача. Переведите обыкновенные дроби в периодические десятичные:

Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:
Как видим, остатки повторяются. Запишем дробь в «правильном» виде: 1,733 … = 1,7(3).
В итоге получается дробь: 0,5833 … = 0,58(3).
Записываем в нормальном виде: 4,0909 … = 4,(09).
Получаем дробь: 0,4141 … = 0,(41).
Переход от периодической десятичной дроби к обыкновенной
Рассмотрим периодическую десятичную дробь X = abc(a1b1c1). Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:
- Найдите период дроби, т.е. подсчитайте, сколько цифр находится в периодической части. Пусть это будет число k;
- Найдите значение выражения X · 10k. Это равносильно сдвигу десятичной точки на полный период вправо — см. урок «Умножение и деление десятичных дробей»;
- Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь;
- В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные.
Задача. Приведите к обыкновенной неправильной дроби числа:
- 9,(6);
- 32,(39);
- 0,30(5);
- 0,(2475).
Работаем с первой дробью: X = 9,(6) = 9,666 …
В скобках содержится лишь одна цифра, поэтому период k = 1. Далее умножаем эту дробь на 10k = 101 = 10. Имеем:
10X = 10 · 9,6666 … = 96,666 …
Вычитаем исходную дробь и решаем уравнение:
10X − X = 96,666 … − 9,666 … = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.
Теперь разберемся со второй дробью. Итак, X = 32,(39) = 32,393939 …
Период k = 2, поэтому умножаем все на 10k = 102 = 100:
100X = 100 · 32,393939 … = 3239,3939 …
Снова вычитаем исходную дробь и решаем уравнение:
100X − X = 3239,3939 … − 32,3939 … = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.
Приступаем к третьей дроби: X = 0,30(5) = 0,30555 … Схема та же самая, поэтому я просто приведу выкладки:
Период k = 1 ⇒ умножаем все на 10k = 101 = 10;
10X = 10 · 0,30555 … = 3,05555 …
10X − X = 3,0555 … − 0,305555 … = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.
Наконец, последняя дробь: X = 0,(2475) = 0,2475 2475 … Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:
k = 4 ⇒ 10k = 104 = 10 000;
10 000X = 10 000 · 0,2475 2475 = 2475,2475 …
10 000X − X = 2475,2475 … − 0,2475 2475 … = 2475;
9999X = 2475;
X = 2475 : 9999 = 25/101.
Смотрите также:
- Сравнение дробей
- Тест к уроку «Десятичные дроби» (2 вариант)
- Четырехугольная пирамида в задаче C2
- Как сдать ЕГЭ по математике
- Задача B5: площадь сектора
- Задача B4: тарифы на сотовую связь
Определение
Бесконечная десятичная дробь, у которой одна или несколько цифр повторяются в одной и той же
последовательности, называется периодической десятичной дробью.
Например. $0,1234444444 ldots ; 12,453737373737 ldots$
Повторяющиеся цифры – период – для сокращения записи пишут в круглых скобках.
Например. $0,12344444444 ldots=0,123(4)$ ;
$12,453737373737 ldots=12,45(37)$
Определение
Чистой периодической дробью называется периодическая дробь, у которой период начинается сразу после запятой.
Например. $2,4949 ldots=2,(49)$
Определение
Смешанной периодической дробью называется такая десятичная дробь, у которой между запятой и
периодом есть не менее одной неповторяющейся бесконечное число раз цифры.
Например. $0,11232323 ldots=0,11(23)$ ;
$1,54444 . .=1,5(4)$
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период,
а в знаменателе записать столько девяток, сколько цифр в периоде.
Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго
периода вычесть число, стоящее до первого периода, результат записать в
числителе; в
знаменатель записать
число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между
запятой и периодом.
Например. Запишем дробь $2,34(2)$ в виде обыкновенной
Читать первую тему – понятие дроби и виды дробей,
раздела дроби.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Периодические бесконечные десятичные дроби
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Винокурова Ю.-. 1
1МБОУ СОШ №9
Старкова Г.В. 1
1МБОУ СОШ №9 им М.И.Неделина
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение.
Сначала я бы хотела объяснить, почему я взяла эту тему. Я взяла эту тему для того чтобы объяснить и самой узнать:
1.откуда появились периодические бесконечные десятичные дроби.
2.какие виды существуют.
3.для чего служат периодические бесконечные десятичные дроби.
4.как составить периодическую бесконечную дробь.
Цель: узнать, что такое периодические бесконечные десятичные дроби.
Актуальность выдвинутой мной проблемы заключается в привлечении учащихся к решению нестандартных задач, которые часто можно встретить в современных учебниках по математике.
Помогла мне выбрать эту тему мой учитель по математике Старкова Галина Владимировна.
Глава 2
Периодическая десятичная дробь — это любая десятичная дробь, у которой:
Значащая часть состоит из бесконечного количества цифр;
Через определенные интервалы цифры в значащей части повторяются.
Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:
Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Глава 3
Существовало несколько высказываний как появились дроби и десятичные дроби.
1.Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби. Но единой записи дробей, как и целых чисел, не было.
2.В древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины: чи, цуни, доли, порядковые, шерстинки, тончайшие, паутинки, дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзю-Чун-Чжи принял за единицу не чи, а чжан=10 чи, тогда эта дробь выглядела так: 2чжана, 1 чи, 3 цуни, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Полную теорию десятичных дробей дал узбекский ученый Джемшид Гиясэддин алКаши в книги «ключ к арифметике», изданной в 1424 году, в которой он показал запись дроби в одну строку с числами в десятичной системе и дал правила действия с ними. Ученый пользовался несколькими способами написания дроби: то он применял вертикальную черту, то чернила черного и красного цветов.
Дроби в Греции.
Греки, как и египтяне, первоначально имели дроби только с числителем, равным единице, и записывали их словами, а позже символами, например, дробь записывали так: ٧ א ′ Герон Александрийский (1 век до н.э.) применял дроби общего вида и записывал их без дробной черты, числитель и знаменатель ставил рядом, причем числитель записывал с одним штрихом, а знаменатель записывал дважды и отмечал двумя штрихами, например, записывал так: ß′ ε′′ε′′ . У греков был знак, заменяющий слово «получается» , назывался этот знак «гигнестай». Диофант ( III в.н.э) дроби записывал почти так же, как и мы, только над чертой писал знаменатель, а под чертой – числитель, слово частица и затем знаменатель.
Десятичные дроби в древности.
Некоторые элементы десятичной дроби встречаются в трудах многих ученых Европы в XII, XIII, XIV веках. Полную теорию десятичных дробей дал узбекский ученый Джемшид Гиясэддин ал-Каши в книге «Ключ к арифметике», изданной в 1424 году. Но этот труд до европейских ученых своевременно не дошел. Только через 150 лет после выхода этой книги (1585) фламандский ученый Симон Стевин в своей книге «О десятичной» описал правила действия с десятичными дробями. Его и считают изобретателем десятичных дробей. Стевин десятичные дроби записывал так: 0,3752= 3 7 5 2 или 5,693= 5 6 9 3 . У других авторов встречалась запись 3,7= 3 7 или 3/7, или целую часть записывали чернилами одного цвета, дробную – чернилами другого цвета.
Современные десятичные дроби.
Современную запись, т.е. отделение целой части запятой, предложил Кеплер (1571-1630гг.). В странах, где говорят по английский (Англия, США, Канада и др.), и сейчас вместо запятой пишут точку, например, 2,3 пишут 2.3 и читают: два точка три.
Глава 4
Виды периодических десятичных дробей.
Периодические дроби бывают двух видов: чистые и смешанные.
Если в периодической дроби период начинается сразу же после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:
0, (3)
0, (6)
0, (5)
Видно, что в этих дробях период начинается сразу же после запятой.
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период, а в знаменателе записать столько девяток, сколько цифр в периоде.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смешанной. Например, следующие периодические дроби являются смешанными:
0,52 (3)
0,16 (5)
0,31 (6)
Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.
Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго периода вычесть число, стоящее до первого периода, результат записать в числителе; в знаменатель записать число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между запятой и периодом.
Например. Запишем дробь в виде обыкновенной.
Примеры:
1. 2,71136136136…..=2,7(136)-смешанная
2. 11,33333333…….=11,(3)чистая
Глава 5
Применяются периодические бесконечные десятичные дроби к примеру в профессиях:
1.Кулинария- Повара применяют десятичные дроби для составления меню.
2.Парикмахер- Парикмахер применяет десятичные дроби для приготовления раствора для покраски волос и для завивки.
3.Продавцам и покупателям-в магазине при взвешивании товара.
4. Экономисты и бухгалтеры- Экономисты и бухгалтеры используют десятичные дроби для составления отчетов, расчетов.
5.Строители- Строители используют десятичные дроби для составления сметы.
Глава 6
Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.
Бесконечно малая
Последовательность {displaystyle a_{n}} называется бесконечно малой, если {displaystyle lim limits _{nto infty }a_{n}=0}.
Например, последовательность чисел {displaystyle a_{n}={dfrac {1}{n}}} — бесконечно малая.
Функция называется бесконечно малой в окрестности точки {displaystyle x_{0}}, если {displaystyle lim limits _{xto x_{0}}f(x)=0}.
Функция называется бесконечно малой на бесконечности, если {displaystyle lim limits _{xto +infty }f(x)=0} либо {displaystyle lim limits _{xto -infty }f(x)=0}.
Также бесконечно малой является функция, представляющая собой разность
функции и её предела, то есть если {displaystyle lim limits _{xto +infty }f(x)=a}, то {displaystyle f(x)-a=alpha (x)}, {displaystyle lim limits _{xto +infty }(f(x)-a)=0}.
Подчеркнём, что бесконечно малую величину следует понимать как переменную величину (функцию), которая лишь в процессе своего изменения [при стремлении х{displaystyle x} к {displaystyle a}а (из {displaystyle lim limits _{xto a}f(x)=0})] делается меньше произвольного числа ( {displaystyle varepsilon }). Поэтому, например, утверждение типа «одна миллионная есть бесконечно малая величина» неверно: о числе [абсолютном значении] не имеет смысла говорить, что оно бесконечно малое.
Глава 7
Лейбниц и анализ бесконечно малых
Лейбниц и анализ бесконечно малых
«Почти все остальные крупные математики, — писал в XX веке Иозеф Хоффман, видный исследователь биографии Лейбница, — увлекались математикой уже в юные годы и разрабатывали радикально новые идеи. Однако этот период в жизни Лейбница не был ознаменован какими-либо заметными математическими открытиями». И в этом, и во многом другом Лейбниц очень отличается от Ньютона.
Когда Лейбниц прибыл в Париж, ему было уже 26 лет. К этому времени он был лишь поверхностно знаком с «Началами» Евклида и знал немногим больше элементарной арифметики, изученной в школе по книге Клавия. Как рассказывал много лет спустя один из его первых учеников Иоганн Бернулли, издание «Геометрии» Декарта с комментариями Ван Схотена, с которым Лейбниц бегло ознакомился в университете, показалось ему слишком сложным. В Нюрнберге, где он жил после получения степени доктора в Альдорфском университете (1666 год), он поверхностно изучил Geometria indivisibilibus Кавальери. Так что, когда он прибыл в Париж в марте 1672 года, его знания были весьма плачевными, хотя, по словам Хоффмана, математика была у Лейбница в крови.
Сохранилось множество рукописей и документов Лейбница, в частности почти все, написанное им в период обучения в Париже. Эти документы позволяют понять, как проходило его обучение и как он пришел к открытию анализа бесконечно малых.
В первый год в Париже Лейбниц был дилетантом в математике. Позднее он сам признавался, что мучился от недостатка знаний. В этом же году он впервые побывал в Лондоне, где при посредничестве Ольденбурга и Коллинза познакомился с английскими математиками. Его «святая простота», о которой он знал, его недооценка собственных возможностей вкупе с излишней открытостью и общительностью не раз приводили к недопониманию с британскими математиками и впоследствии стали одной из причин обвинений в плагиате.
Осенью 1672 года он познакомился с Христианом Гюйгенсом, самым известным ученым и математиком Европы, который в то время получал жалование во Французской академии наук. К тому времени Лейбниц уже совершил свое первое математическое открытие: он показал, как использовать разность для сложения чисел. Позднее он упоминал, что на мысль о взаимно обратной связи дифференцирования и интегрирования его навела взаимно обратная связь между сложением и вычитанием.
Рассуждения Лейбница были таковы. Допустим, что требуется найти сумму а1 +а2+ а3+ … + аn.Нам известно, что каждое из этих чисел является разностью двух других: ak= bk+1— bk.Следовательно, простое сокращение последовательных членов bkозначает, что а1 +а2+ а3+ … + аn= bn+1— b1.
Ввиду врожденного оптимизма и недостатка математических знаний Лейбниц посчитал, что открыл способ нахождения суммы произвольных рядов чисел. Его уверенность только усилилась, когда он поделился своим открытием с Гюйгенсом и тот предложил найти сумму чисел, обратных треугольным числам:
1/2 + 1/6 + 1/12 + 1/20 + …
По случайному совпадению, этот ряд — один из немногих, к которым применим способ, открытый Лейбницем, так как члены этого ряда имеют вид 1/n(n+1), то есть равны разности между 1/n и 1/(n+1). Таким образом,
1/2 + 1/6 + 1/12 + 1/20 + … = 1
Лейбниц вычислил суммы похожих рядов, образованных пирамидальными числами, и подготовил небольшую статью для публикации в Journal des Savants. Однако статья так и не увидела свет, поскольку весь 1673 год журнал не издавался. В этой статье Лейбниц цитирует Кавальери, Галилея, Валлиса, Грегори, Паскаля, Сен- Венсана и Архимеда, а также упоминает Гоббса как великого математика, что указывает на определенный прогресс в его образовании.
В январе 1673 года Лейбниц впервые посещает Лондон. Свой первый визит он нанес Генри Ольденбургу, секретарю Лондонского королевского общества и своему соотечественнику, который принял его с распростертыми объятиями.
Вывод:
1.периодическими бесконечными десятичными дробями занимались многие математики и говорили свою точку происхождения.
2.периодическая бесконечная десятичная дробь нужна в большинстве профессий.
3.периодическая бесконечная десятичная дробь:
1.Онисущественно обогащают наше представление о математике.
2.Ониоткрываютнамэстетическую сторону математики.
3.Они открывают математическую сторону окружающего мира.
4.Онимогутповысить интерес школьников к такой «сухой» и точной науке, как математика.
5.Они дают богатый материал для дополнительных исследовательских работ в школе.
4. Бесконечную периодическую десятичную дробь можно представить в виде обыкновенной дроби – это рациональное число.
Литература :
1. Серия «Мир Математики»- Истина в пределе «анализ бесконечно малых», Изд.:Де Агостини, 2014
2.Сайт «Яндекс. Картинки» https://yandex.ru/images/search?p=3&text
3. Сайт Формулы с примерами http://formula-xyz.ru/beskonechnye-desyatichnye-drobi.html
4. Учебно-методический портал http://sgt-portal.ks.ua/
5. Презентации по математике https://ppt4web.ru/matematika/desjatichnye-drobi-klass1.html
6. Сайт для подготовки к ОГЭ-ЕГЭ Раздел : Учебник https://youclever.org/book/desyatichnye-drobi-1
7. Сайт «Заочник.ру» https://www.zaochnik.com/spravochnik/matematika/dejstvitelnye-ratsionalnye-irratsionalnye-chisla/desjatichnye-drobi-opredelenija-zapis-primery-dejs/
8. Образовательный портал http://www.maam.ru/detskijsad/proekt-desjatichnye-drobi-vokrug-nas.html
9. Сайт для учителей http://uchitelya.com/matematika/21380-proekt-drobi-v-nashey-zhizni.html
10. Сайт по подготовке презентаций https://ppt4web.ru/matematika/periodicheskaja-drob-mne-ulybnulas.html
11.Портал «Википедия» https://ru.wikipedia.org/wiki/%D0%91%D0%B5%D1%81%D0%BA%D0%BE%D0%BD%D0%B5%D1%87%D0%BD%D0%BE_%D0%BC%D0%B0%D0%BB%D0%B0%D1%8F_%D0%B8_%D0%B1%D0%B5%D1%81%D0%BA%D0%BE%D0%BD%D0%B5%D1%87%D0%BD%D0%BE_%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%B0%D1%8F
12.https://yandex.ru/search/?text=%D0%A7%D0%B8%D1%81%D1%82%D0%BE%D0%B9%20%D0%BF%D0%B5%D1%80%D0%B8%D0%BE%D0%B4%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B9%20%D0%B4%D1%80%D0%BE%D0%B1%D1%8C%D1%8E%20%D0%BD%D0%B0%D0%B7%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%D1%81%D1%8F%20&lr=10743&rnd=40175
Просмотров работы: 1772
Математика
6 класс
Урок № 73
Бесконечные периодические десятичные дроби
Перечень рассматриваемых вопросов:
– понятие бесконечной периодической десятичной дроби;
– преобразование обыкновенных дробей в бесконечные периодические дроби;
– действия с периодическими дробями.
Тезаурус
Бесконечная периодическая десятичная дробь – это дробь, у которой одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодом и записывается в скобках.
Любое рациональное число p/q можно разложить в периодическую десятичную дробь.
Любая периодическая дробь есть десятичное разложение некоторого рационального числа.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Обыкновенную дробь можно разложить в конечную десятичную, если в знаменателе нет простых множителей, кроме 2 и 5.
Вы уже знаете, как это сделать.
1. Умножить числитель и знаменатель на одно и то же число, чтобы привести к знаменателю 10, 100, 1000 и т. д.;
2. Выполнить деление числителя на знаменатель.
Пример 1. Умножили числитель и знаменатель на 2.
Пример 2. Сначала сократили дробь.
Пример 3. Выполнили деление 3 на 125.
Рассмотрим примеры, когда привести к знаменателю 10, 100 и т. д. нельзя. Возможно только деление числителя на знаменатель.
Заметим, что при делении получаются повторяющиеся остатки и, соответственно, повторяющиеся цифры в частном. Из-за этого процесс деления бесконечен. Отсюда происходит бесконечная десятичная дробь.
Рассмотрим другие примеры.
Повторяющиеся цифры 3; 27; 6 называют периодом дроби. Бесконечные десятичные дроби 0,333…; 0,2727…; 0,1666… называют периодическими.
Записывают так:
0,(3)
0,(27)
0,1(6)
Читают так:
«Нуль целых и три в периоде»
«Нуль целых и 27 в периоде»
«Нуль целых одна десятая и шесть в периоде»
Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр (период дроби).
Отметим, что любое рациональное число p/q разлагается в периодическую десятичную дробь.
Любая периодическая дробь есть десятичное разложение некоторого рационального числа.
Замечание. При делении уголком десятичное разложение с периодом 9 не возникает.
Далее рассмотрим, как выполняются действия с периодическими дробями?
1. Сравните дроби
1/3 и 0,3
Запишем дробь 1/3 в виде бесконечной периодической дроби 0,333…
Запишем дробь 0,3 в следующем виде 0,300… Приписывая бесконечно много нулей, мы превращаем конечную дробь в равную ей бесконечную периодическую дробь с периодом 0.
Теперь можем сравнить: 0,333… > 0,300…
2. Разложите обыкновенную дробь в бесконечную периодическую десятичную дробь, округлите до десятых.
1/3 = 0,333… ≈ 0,3
5/9 = 0,555… ≈ 0,6
Разбор заданий тренировочного модуля
Задание 1
Представьте в виде периодической дроби. В ответе укажите её период.
период 6
период 4
период 18
период 6
Ответ: 6; 4; 18; 6.
Задание 2
Используя предыдущие задания, запишите периодическую дробь в виде обыкновенной дроби: 0,(3); 0,(5); 0,(6).
0,(3)
0,(5)
0,(6)
Ответ:
Задание 3 ⃰ (повышенного уровня сложности)
Задача: периодическую дробь 0,(1) записать в виде обыкновенной дроби.
Пусть х = 0,(1) = 0,111…
Умножим обе части на 10.
Получим
10 ∙ х = 1,111…
Найдём разность
10 ∙ х – х = 1,111… – 0,111…
Получим
9 ∙ х = 1
Значит,
Ответ:.