Множество – это одно из важнейших понятий математики. Грегор Кантор определял множество как «многое, мыслимое как единое». Множество рассматривается как родовое понятие, более широкое, нежели подмножества.
 Подмножество подразумевается как часть множества. Если предположить, что, скажем, класс, т.е. совокупность учеников, это множество X, то совокупность отсутствующих учеников – это подмножество P, которое принадлежит множеству Х (ведь отсутствующие ученики не перестали быть учениками конкретного класса).
Подмножество подразумевается как часть множества. Если предположить, что, скажем, класс, т.е. совокупность учеников, это множество X, то совокупность отсутствующих учеников – это подмножество P, которое принадлежит множеству Х (ведь отсутствующие ученики не перестали быть учениками конкретного класса).
В математикe понятие подмножество расширяется: подмножеством считается и само множество, и пустое множество. Например, если в нашем вымышленном классе из 23 учеников присутствую 23, это значит, что подмножество присутствующих совпадает с множеством всех учеников класса, в то время как подмножество болеющих учеников остается пустым.
Логику нашего примера можно перенести с класса, скажем, на геометрическую фигуру. Представим, что у нас есть круг (назовем его А), внутри которого находятся другие фигуры: квадрат B, овал C, треугольник D, ромб E и др. Получается, что B, C, D, E и др. являются подмножеством множества А.
Выделим из множества дробей 1/2, 2/3, 4/3, 2/5, 5/2, 7/7 подмножества правильных и неправильных дробей.
1. Вспомним, что правильная дробь – это дробь, у которой числитель меньше знаменателя; неправильная дробь – это дробь, у которой числитель больше знаменателя.
2. Следовательно, подмножество правильных дробей включает в себя дроби 1/2, 2/3, 2/5, подмножество неправильных дробей – дроби 4/3, 5/2. Дробь 7/7 является дробной записью целого числа (7/7 = 1). Мы выполнили наше задание.
У нескольких множеств может быть общая часть, которая называется пересечением множеств. Иными словами, пересечением двух множеств называется множество, состоящее из общих элементов.
Представим, что у нас есть два круга А и B, которые «надвинуты» один на другой. В этой общей части есть треугольники C, D и E. Значит, C, D, E являются пересечением множеств А и B.
Множества могут объединяться. Объединением двух множеств называется множество, состоящее из элементов, принадлежащих хотя бы одному из этих множеств. Предположим, что множество А – это совокупность уроков, которые мы посещаем в пятницу (русский язык, русская литература, физика, история, физкультура), а B – тех, которые мы посещаем в субботу (география, биология, история), тогда объединением этих множеств станет множество, включающее в себя русский язык, русскую литературу, физику, историю, физкультуру, географию и биологию.
Теория множеств ведет свое начало с XIX века – с трудов Б. Бальцано и Г. Кантора, причем последнему собственно и приписывают создание теории множеств, поскольку Кантор первым применил доказательства к бесчисленным множествам. Также Кантору принадлежит термин «элементы множества», который он мыслил как совокупность всех объектов, обладающих конкретным свойством. Следующим этапом развития теории множеств стали концепции Б. Рассела и Э. Цермело.
С тех пор теория множеств пополнилась многочисленными классификациями. Так, выделяется пустое множество, о котором мы уже знаем, это не содержащее ни одного элемента множество; универсальное множество – напротив, вбирает в себя все мыслимые объекты и др.
Теория множеств в данный момент активно изучается – особенно с точки зрения ее структуры (подмножества, надмножества, множества множеств) и др.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
-
Математика
Предыдущий вопрос
Следующий вопрос
deer16
3 года назад
Ответ
Ответ дан
egoryanich
Правильные:5/7;8/9;13/19;5/4;125/126.
Неправильные:4/5;384/383.
Ответы и объяснения
- deer16
Не тот ответ, который тебе нужен?
Найди нужный
-
Главная
-
ГДЗ
- 6 класс
- Математика
-
Виленкин учебник
- 60
Новая редакция 2018-2023 г.
Смотрите также:
-
Задание 60 в старой редакции (2011 – 2017 г.)
- Учебник старой редакции (2011 – 2017 г.)
Вернуться к содержанию учебника
Страница 17
55
56
57
58
59
60
61
62
63
64
65
Вопрос
Дано множество дробей 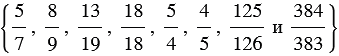 . Составьте подмножество:
. Составьте подмножество:
а) правильных дробей;
б) неправильных дробей.
Подсказка
Вспомните:
- Что называют множеством, подмножеством.
- Какие дроби называют правильными, какие неправильными.
Ответ
55
56
57
58
59
60
61
62
63
64
65



55
56
57
58
59
60
61
62
63
64
65
Вернуться к содержанию учебника
Смотрите также:
-
Задание 60 в старой редакции (2011 – 2017 г.)
- Учебник старой редакции (2011 – 2017 г.)
Выбери из множества
A = {
3
14
,
28
5
,
16
16
,
7
29
,
32
11
,
48
48
} подмножества B и C по следующим признакам:
B − правильные дроби
C − неправильные дроби
Какие из неправильных дробей равны 1?
Какие из них больше 1?

reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. 5 урок. Правильные и неправильные дроби. Номер №6
Решение
B − правильные дроби:
3
14
,
7
29
.
C − неправильные дроби:
28
5
,
16
16
,
32
11
,
48
48
.
Равны 1:
16
16
,
48
48
.
Больше 1 дроби:
28
5
,
32
11
.
Содержание
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом ПОЛИНОМ ОДНОЙ ПЕРЕМЕННОЙ.
Рациональные дроби
Будем обозначать через $ mathbb A_{} $ какое-либо из множеств $ mathbb Q, mathbb R_{} $ или
$ mathbb C_{} $.
Определения
Рациональной дробью или дробно-рациональной функцией над множеством $ mathbb A_{} $ называется выражение вида
$$frac{g(x)}{f(x)} npu {f(x),g(x) }subset mathbb A[x],
f(x)notequiv 0 .
$$
Для экономии места будем опускать слово «рациональный» и, по аналогии с числовыми дробями, записывать рациональную дробь в виде $ g_{}(x)/f(x) $.
Полином $ g_{}(x) $ называется числителем дроби, а $ f_{}(x) $ — знаменателем дроби.
Дроби $ g_1(x)/ f_1(x) $ и $ g_2(x)/f_2(x) $ называются равными если $ f_1(x)g_2(x)-f_2(x)g_1(x) equiv 0 $; будем этот факт записывать:
$$ frac{g_1(x)}{f_1(x)}equiv frac{g_2(x)}{f_2(x)} .$$
В противном случае дроби называются неравными.
П
Пример.
$$frac{x-1}{x^2-1} equiv frac{1}{x+1} ,$$
и, в общем случае,
$$frac{h(x)g(x)}{h(x)f(x)} equiv frac{g(x)}{f(x)} npu h(x)in mathbb A[x],,
h(x)notequiv 0 .
$$
♦
Фактически, предыдущее определение допускает «сокращение» дроби на общий множитель числителя и знаменателя. С точки зрения математического
анализа, такое сокращение корректно только в области определения дроби, т.е. для значений $ x_{} $, не обращающих знаменатель в нуль. Но мы будем пренебрегать
этим ограничением.
Дробь называется несократимой если ее числитель и знаменатель являются взаимно простыми полиномами.
Операции сложения и умножения дробей вводятся аксиоматически правилами
$$frac{g_1(x)}{f_1(x)}+frac{g_2(x)}{f_2(x)}=
frac{g_1(x)f_2(x)+g_2(x)f_1(x)}{f_1(x)f_2(x)} ;
frac{g_1(x)}{f_1(x)} cdot frac{g_2(x)}{f_2(x)}= frac{g_1(x)g_2(x)}{f_1(x)f_2(x)}
.
$$
Т
Теорема 1. Операции сложения и умножения дробей подчиняются аксиомам коммутативности, ассоциативности и дистрибутивности.
Еще одна аксиома связывает между собой два множества — множество полиномов над $ mathbb A_{} $ и множество дробей над $ mathbb A_{} $.
Условимся отождествлять дробь вида $ g(x)/1 $ с полиномом $ g_{}(x) $.
Тогда множество рациональных дробей будет включать в качестве подмножества
множество $ mathbb A[x] $.
=>
Обратной для дроби $ g_{}(x)/ f(x) $ относительно операции умножения будет дробь $ f_{}(x)/ g(x) $; предполагается, что $ f(x) notequiv 0, g(x) notequiv 0 $.
Дробь называется правильной если степень числителя меньше степени знаменателя.
Т
Теорема 2. Любую дробь можно представить в виде суммы полинома и правильной несократимой дроби.
Доказательство. Пусть $ operatorname{HOD}(f,g)=d(x) $ и $ f(x)equiv f_1(x)d(x),, g(x)equiv g_1(x)d(x) $.
Тогда
$$frac{g(x)}{f(x)}equiv frac{g_1(x)}{f_1(x)} npu operatorname{HOD}(f_1,g_1)=1 .
$$
Далее, если $ deg g_1 < deg f_1 $, то дробь уже правильная. В противном случае
разделим $ g_1 $ на $ f_1 $: $ g_1(x)equiv q(x)f_1(x)+r(x) $ при $ deg r< deg f_1 $. Тогда
$$
frac{g(x)}{f(x)}equiv q(x)+frac{r(x)}{f_1(x)} ,
$$
и мы получили представление указанное в теореме.
♦
Т
Теорема 3. Сумма и произведение правильных дробей являются
правильными дробями.
Разложение дроби на простейшие…
Т
Теорема 4. Если дробь $ g_{}(x)/f(x) $ над $ mathbb A_{} $
является правильной и ее знаменатель раскладывается в произведение взаимно простых множителей:
$$f(x)equiv f_1(x)f_2(x)quad npu quad {f_1(x),f_2(x) }subset mathbb A[x], operatorname{HOD}(f_1,f_2)=1 , deg f_1 < deg f, deg f_2 < deg f , $$
то
$$
frac{g(x)}{f(x)}equiv frac{g_1(x)}{f_1(x)}+frac{g_2(x)}{f_2(x)} ,
$$
где $ g_1(x)/ f_1(x) $ и $ g_2(x)/ f_2(x) $ — правильные дроби. Такое представление единственно.
Доказательство. На основании теоремы из
☞
ПУНКТА условие $ operatorname{HOD}(f_1(x),f_2(x))=1 $ эквивалентно
существованию в $ mathbb A_{} $ полиномов $ u_1(x) $ и $ u_2(x) $,
удовлетворяющих тождеству Безу $ u_1(x)f_1(x)+u_2(x)f_2(x)equiv 1 $. Тогда
$$
frac{g(x)}{f(x)}equivfrac{g(x)left(u_1(x)f_1(x)+u_2(x)f_2(x) right)}{f_1(x)f_2(x)}
equiv frac{g(x)u_1(x)}{f_2(x)}+frac{g(x)u_2(x)}{f_1(x)} .
$$
Возьмем в качестве $ g_1(x) $ остаток от деления $ g(x)u_2(x) $ на $ f_1(x) $:
$$
g(x)u_2(x) equiv q(x)f_1(x)+ g_1(x) , deg g_1 < deg f_1 .
$$
Тогда
$$
frac{g(x)}{f(x)}equiv frac{g(x)u_1(x)}{f_2(x)}+q(x)+
frac{g_1(x)}{f_1(x)} equiv
frac{g(x)u_1(x)+q(x)f_2(x)}{f_2(x)} + frac{g_1(x)}{f_1(x)} .
$$
Здесь $ {g(x)}/{f(x)} $ и $ {g_1(x)}/{f_1(x)} $ являются правильными
дробями. Но тогда, на основании теоремы 3, и их разность, т.е. дробь
$ {(g(x)u_1(x)+q(x)f_2(x))}/{f_2(x)} $ должна быть правильной.
Обозначив $ g_2(x)= g(x)u_1(x)+q(x)f_2(x) $, получим требуемое в теореме
представление.
Для доказательства единственности этого представления
предположим, что имеется еще одно представление
$$
frac{g(x)}{f(x)}equiv frac{widetilde{g}_1(x)}{f_1(x)}
+frac{widetilde{g}_2(x)}{f_2(x)}
$$
при обеих правильных дробях в правой части; пусть, для определенности,
$ g_1(x)notequiv widetilde{g}_1(x) $. Вычитая из одного представления
другое, приходим к тождеству
$$
left(g_1(x)- widetilde{g}_1(x) right) f_2(x) equiv
left(widetilde{g}_2(x) – g_2(x) right) f_1(x) .
$$
Поскольку $ operatorname{HOD}(f_1,f_2)=1 $, то, по теореме 2 из
☞
ПУНКТА, полином
$ g_1(x)- widetilde{g}_1(x) $ должен делиться на $ f_1(x) $. Последнее,
однако, невозможно, поскольку
$ deg left(g_1-widetilde{g}_1 right) < deg f_1 $.
♦
П
Пример. Разложить дробь
$$
frac{x^2+1}{x^5+x+1}
$$
в сумму правильных дробей.
Решение. Знаменатель может быть разложен на множители, например,
так:
$ x^5+x+1equiv (x^2+x+1)(x^3-x^2+1) $. Обозначив $ f_1(x)= x^2+x+1 $ ,
$ f_2(x) = x^3-x^2+1 $, ищем $ operatorname{HOD}(f_1,f_2) $ по алгоритму Евклида:
$$
begin{array}{lcl}
f_2(x) &equiv& (x-2)f_1(x) + (x+3) , \
f_1(x) &equiv& (x-2)(x+3) + 7 ;
end{array}
$$
очевидно $ operatorname{HOD}(f_1,f_2)=1 $. Полиномы, удовлетворяющие тождеству Безу,
можно получить с помощью континуант:
$$u_1(x)=1/7 (x^2 -4,x+5),,
u_2(x)=1/7 (-x+2) . $$
Далее, следуя схеме доказательства предыдущей теоремы,
делим $ g(x)u_2(x) $ на $ f_1(x) $:
$$g_1(x)=-1/7(3,x+1) ,
q(x)=1/7(-x+3) Rightarrow
$$
$$
Rightarrow
g_2(x)= g(x)u_1(x)+q(x)f_2(x)=1/7(3,x^2-5,x+8)
.
$$
Ответ.
$$frac{x^2+1}{x^5+x+1} equiv frac{-1/7(3,x+1)}{x^2+x+1}+
frac{1/7(3,x^2-5,x+8)}{x^3-x^2+1}
.
$$
=>
Если знаменатель правильной дроби $ g(x)/f(x) $ представляет собой
произведение
$$ f(x)equiv f_1(x)times dots times f_K(x) $$
попарно взаимно простых
полиномов из $ mathbb A_{}[x] $, то дробь может быть разложена на сумму правильных дробей
над $ mathbb A_{} $:
$$
frac{g(x)}{f(x)}equiv frac{g_1(x)}{f_1(x)} + dots + frac{g_K(x)}{f_K(x)}
.
$$
Такое разложение единственно.
=>
Пусть каноническое разложение полинома $ f_{}(x) $ над $ mathbb A_{} $
задается формулой
$$ f(x)equiv Phi_1^{{mathfrak m}_1}(x) Phi_2^{{mathfrak m}_2} (x)
times dots times Phi_K^{{mathfrak m}_K}(x) . $$
Тогда правильная дробь $ g_{}(x)/f(x) $ может быть разложена на сумму правильных дробей:
$$
frac{g(x)}{f(x)}equiv
frac{g_{1}(x)}{Phi_1^{{mathfrak m}_1}(x)}+dots+
frac{g_{K}(x)}{Phi_K^{{mathfrak m}_K}(x)} ;
$$
при этом полиномы $ g_{1}(x),dots,g_{K}(x) $ определяются однозначно.
Правильная дробь вида $ G(x)/Phi^{mathfrak m}(x) $, где $ Phi(x) $ является неприводимым полиномом над $ mathbb A_{} $ , называется
примарной дробью над $ mathbb A_{} $. Примарная дробь называется простейшей дробью над $ mathbb A_{} $, если $ deg G < deg Phi $.
Задача. Разложить данную правильную дробь на сумму простейших.
Т
Теорема 5. Любая примарная дробь над $ mathbb A_{} $ может быть представлена
в виде суммы простейших над $ mathbb A_{} $ и такое представление единственно.
Доказательство. Пусть $ G(x)/Phi^{{mathfrak m}}(x) $ — примарная. Если
$ deg G < deg Phi $, то теорема доказана. Пусть $ deg G ge deg Phi $,
тогда разделим $ G(x) $ на $ Phi(x) $: $ G(x)equiv Q(x)Phi(x)+G_1(x),,
deg G_1 < deg Phi $. Тогда
$$
frac{G(x)}{Phi^{{mathfrak m}}(x)}equiv frac{Q(x)}{Phi^{{mathfrak m}-1}(x)}
+frac{G_1(x)}{Phi^{{mathfrak m}}(x)} ,
$$
и вторая дробь справа, очевидно, простейшая. Если $ deg Q < deg Phi $, то теорема
доказана; в противном случае поделим $ Q(x) $ на $ Phi(x) $. Продолжаем процесс,
на каждом этапе степень числителя уменьшается по сравнению с предыдущим этапом.
За конечное число шагов мы добьемся того, чтобы эта степень стала меньшей
$ deg Phi $. Окончательное разложение на простейшие будет иметь вид:
$$
frac{G(x)}{Phi^{{mathfrak m}}(x)}equiv
frac{G_1(x)}{Phi^{{mathfrak m}}(x)}+frac{G_2(x)}{Phi^{{mathfrak m}-1}(x)} + dots +
frac{G_{mathfrak m}(x)}{Phi(x)} ;
$$
здесь, возможно, некоторые числители могут оказаться тождественно равными
нулю, а для остальных же будет выполняться условие $ deg G_j < deg Phi $.
♦
Т
Теорема 6. Любая правильная дробь над $ mathbb A_{} $ может быть
представлена в виде суммы простейших над $ mathbb A_{} $ и такое представление единственно.
Доказательство следует из следствия к теореме 4 и теоремы 5.
♦
П
Пример. Разложить дробь
$$
frac{x^5+2,x^4-x+1}{x^9+x^7+3,x^6-x^5+2,x^4+2,x^3-x^2+x+1}
$$
на простейшие над $ mathbb Q_{} $.
Решение. Сначала выписываем каноническое разложение
знаменателя1):
$$
x^9+x^7+3,x^6-x^5+2,x^4+2,x^3-x^2+x+1equiv (x^3-x+1)(x^3+x+1)^2 .
$$
Теперь следуем рассуждениям доказательства теоремы 5.
Обозначив $ f_1 = x^3-x+1,, f_2 = (x^3+x+1)^2 $, находим полиномы $ u_{1}(x) $
и $ u_{2}(x) $, удовлетворяющие тождеству Безу
$ u_1(x)f_1(x)+u_2(x)f_2(x)equiv 1 $. Алгоритм Евклида даст нам выражения
для частных
$$
begin{array}{lcl}
f_2(x) &equiv& (x^3+3,x+1)f_1(x) + 4,x^2 , \
f_1(x) &equiv& 1/4,x(4,x^2) + (1-x) , \
4x^2 &equiv & (-4,x-4)(1-x)+ 4 ,
end{array}
$$
которые мы используем для вычисления континуант
$$
begin{array}{|c|c|c|c|c|}
hline
j & 0 & 1 & 2 & 3 \
hline
q_j & – & x^3+3,x+1 & 1/4,x & -4,x-4 \
hline
K_j(q_1,q_2,dots,q_j) & 1 & x^3+3,x+1 &
1/4,x^4+3/4,x^2+
& -x^5-x^4-2,x^3- \
&&& +1/4,x+1 & -4,x^2-2,x-3 \
hline
K_{j-1}(q_2,dots,q_j) & – & 1 & 1/4,x & -x^2-x +1
\
hline
end{array}
$$
Учитывая знаки, получаем полиномы, удовлетворяющие тождеству
$$
f_1(x) left(x^5+x^4+2,x^3+4,x^2 +2,x+3right) +f_2(x) left(-x^2-x+1 right) equiv 4 ,
$$
откуда и получаются искомые полиномы:
$$u_1(x)=
1/4
left(x^5+x^4+2,x^3+4,x^2 +2,x+3right),
u_2(x)=
1/4 left(-x^2-x+1right) .
$$
Исходная дробь, следовательно, может быть представлена в виде
$$
(x^5+2,x^4-x+1)left(frac{u_2(x)}{x^3-x+1} +frac{u_1(x)}{(x^3+x+1)^2} right)
equiv
$$
$$
equiv
frac{1/2x^2-1/4}{x^3-x+1}
+frac{-1/2x^5-5/4x^3+1/2x^2+3/4x+5/4}{(x^3+x+1)^2}
,
$$
из которых первая является простейшей над $ mathbb Q_{} $, а вторая — не является.
Делим ее числитель на $ x^3+x+1 $.
Ответ.
$$
frac{frac{1}{2}x^2
-frac{1}{4}}{x^3-x+1}
+frac{-frac{1}{2}x^2-frac{3}{4}}{x^3+x+1}
+frac{x^2+frac{3}{2}x+2}{(x^3+x+1)^2}
.
$$
Еще один способ нахождения числителей простейших дробей при разложении на них правильной дроби состоит в подборе их коэффициентов; этот метод
мы проиллюстрируем в следующих пунктах.
…над множеством комплексных чисел
Согласно основной теоремы высшей алгебры, любой полином $ f_{}(x) $ с комплексными коэффициентами
может быть разложен на линейные множители:
$$
f(x)equiv a_0(x-lambda_1)^{{mathfrak m}_{1}}times
dots times
(x-lambda_{mathfrak r})^{{mathfrak m}_{{mathfrak r}}} , quad npu quad
{mathfrak m}_{1}+{mathfrak m}_{2}+dots+{mathfrak m}_{mathfrak r}=n= deg f
$$
и всех различных числах $ { lambda_1,dots,lambda_{mathfrak r } } subset mathbb C $. Следовательно,
простейшими над $ mathbb C_{} $ могут быть только дроби вида
$$
frac{A}{(x-lambda)^k} quad npu kin mathbb N .
$$
Из теоремы $ 6 $ тогда следует, что разложение дроби $ g_{}(x)/f(x) $ на простейшие над $ mathbb C_{} $ имеет вид
$$
begin{array}{lcll}
displaystyle
frac{g(x)}{f(x)} &=& displaystyle frac{A_{1,1}}{(x-lambda_1)}+frac{A_{1,2}}{(x-lambda_1)^2}+
dots+ frac{A_{1,{mathfrak m}_1}}{(x-lambda_1)^{{mathfrak m}_1}}+ & \
&+& displaystyle frac{A_{2,1}}{(x-lambda_2)}+frac{A_{2,2}}{(x-lambda_2)^2}+
dots+ frac{A_{2,{mathfrak m}_2}}{(x-lambda_2)^{{mathfrak m}_2}}+ & \
&+&dots + & \
&+& displaystyle frac{A_{{mathfrak r},1}}{(x-lambda_{mathfrak r})}+frac{A_{{mathfrak r},2}}{(x-lambda_{mathfrak r})^2}+
dots+ frac{A_{{mathfrak r},{mathfrak m}_{mathfrak r}}}{(x-lambda_{mathfrak r})^{{mathfrak m}_{mathfrak r}}} &= \
&& & displaystyle = sum_{j=1}^{mathfrak r} sum_{ell=1}^{{mathfrak m}_j} frac{A_{j,ell}}{ (x-lambda_j)^{ell}}
.
end{array}
$$
П
Пример. Разложить дробь
$$
frac{-(2+3, mathbf i )x+(1-10, mathbf i)}{x^3+3 mathbf i, x^2-3(1+2 mathbf i )x+10-5 mathbf i}
$$
на простейшие над $ mathbb C_{} $.
Решение. Разложение знаменателя на линейные множители:
$$
x^3+3 mathbf i , x^2-3(1+2 mathbf i )x+10-5 mathbf i equiv (x+1+2 mathbf i )^2(x -2 – mathbf i)
.
$$
Следовательно, разложение на простейшие:
$$
frac{A_1}{x+1+2 mathbf i }+frac{A_2}{(x+1+2 mathbf i )^2 }+frac{A_3}{x-2- mathbf i }
.
$$
Величины $ A_1,A_2,A_3 $ находим методом неопределенных коэффициентов.
После приведения к общему знаменателю, в числителе получаем полином
$$A_1(x+1+2 mathbf i)(x-2- mathbf i)+A_2(x-2- mathbf i )+A_3(x+1+2 mathbf i )^2 = $$
$$=(A_1+A_3)x^2+left((-1+ mathbf i), A_1+A_2+(2+4 mathbf i)A_3 right)x-5 mathbf i,A_1
-(2+ mathbf i ) ,A_2 +(-3+4 mathbf i )A_3 ,
$$
который должен быть тождественно равен числителю исходной дроби, т.е.
$ -(2+3, mathbf i )x+(1-10, mathbf i) $.
Отсюда получаем систему линейных уравнений
$$
left{ begin{array}{rrrl}
A_1+& &A_3= & 0, \
(-1+ mathbf i), A_1+&A_2+& (2+4 mathbf i)A_3= & -(2+3, mathbf i ), \
-5 mathbf i, A_1 – & (2 + mathbf i) A_2 +& (-3+4 mathbf i)A_3= & 1-10, mathbf i
end{array}
right.
$$
имеющую единственное решение: $ A_1=1,, A_2=1,, A_3=-1 $.
Ответ.
$$
frac{1}{x+1+2 mathbf i }+frac{1}{(x+1+2 mathbf i)^2 }+frac{-1}{x-2- mathbf i } .
$$
В частном случае, когда корень полинома $ f_{}(x) $ оказываются простым, структура соответствующей ему
простейшей дроби вычисляется особенно просто.
Т
Теорема 7. Если $ lambda_1 $ — простой корень полинома $ f_{}(x) $, то
в разложении дроби $ g_{}(x)/f(x) $ на простейшие входит не более одной дроби, содержащей в знаменателе $ (x- lambda_1) $; эта дробь имеет вид
$$ frac{g(lambda_1)}{f^{prime}(lambda_1)(x-lambda_1)} . $$
Доказательство. Пусть $ lambda_1 $ — корень полинома $ f_{}(x) $, тогда $ f(x)equiv (x-lambda_1)f_2(x) $, где $ f_2(x) in mathbb C[x], deg f_2 = deg f -1 $; если при этом корень $ lambda_1 $ — простой, то $ f_2(lambda_1) ne 0 $. На основании теоремы 4 имеет место разложение
$$
frac{g(x)}{f(x)} equiv frac{A_1}{x-lambda_1}+ frac{g_2(x)}{f_2(x)} .
$$
Это равенство имеет место тогда и только тогда, когда
$$ g(x)equiv A_1f_2(x)+g_2(x)(x-lambda_1) . $$
Если подставить в него $ lambda_1 $, то получим $ g(lambda_1)=A_1f_2(lambda_1) $. Продифференцируем тождество $ f(x)equiv (x-lambda_1)f_2(x) $ по $ x_{} $ и подставим $ x=lambda_1 $, получим: $ f^{prime}(lambda_1)=f_2(lambda_1) $.
♦
=>
Если все корни $ lambda_{1},dots,lambda_n $ полинома
$ f_{}(x) $ являются простыми, то имеет место следующая формула Лагранжа:
$$
frac{g(x)}{f(x)}=sum_{j=1}^n frac{g(lambda_j)}{f^{prime}(lambda_j)(x-lambda_j)} .
$$
=>
Если все корни $ lambda_{1},dots,lambda_n $ полинома
$ f_{}(x) $ являются простыми, то
$$
frac{f^{prime}(x)}{f(x)}=sum_{j=1}^n frac{1}{x-lambda_j} .
$$
П
Пример. Разложить дробь
$$ frac{3,x^3-x+7}{4,x^4-8,x^3+4,x^2-9} $$
на простейшие над $ mathbb C_{} $.
Решение. Разложение знаменателя на линейные множители:
$$ 4,x^4-8,x^3+4,x^2-9 equiv 4, left(x- frac{1+ mathbf i sqrt{5}}{2}right)left(x- frac{1- mathbf i sqrt{5}}{2}right)left(x-frac{1+ sqrt{7}}{2}right)left(x-frac{1- sqrt{7}}{2}right) . $$
Поскольку все корни знаменателя простые, можно использовать формулу Лагранжа. Вычисляем значение дроби $ g(x)/f^{prime}(x) $ на корнях:
$$
frac{g(x)}{f^{prime}(x)}bigg|_{x=(1 pm mathbf i sqrt{5})/2}=frac{sqrt{5}}{48} (sqrt{5} pm mathbf i); quad
frac{g(x)}{f^{prime}(x)}bigg|_{x=(1 pm sqrt{7})/2}=frac{sqrt{7}}{336}(13,sqrt{7} pm 59 ) .
$$
Ответ.
$$
frac{frac{sqrt{5}}{48} (sqrt{5} + mathbf i)}{x- frac{1+ mathbf i sqrt{5}}{2}}
+frac{frac{sqrt{5}}{48} (sqrt{5} – mathbf i)}{x- frac{1- mathbf i sqrt{5}}{2}}
+frac{frac{sqrt{7}}{336}(13,sqrt{7} + 59 )}{x-frac{1+ sqrt{7}}{2}}
+frac{frac{sqrt{7}}{336}(13,sqrt{7} – 59 )}{x-frac{1- sqrt{7}}{2}} .
$$
Рассмотрим еще один частный случай знаменателя: $ f(x)equiv (x-lambda_1)^n $ при $ n>1 $. В этом случае для нахождения коэффициентов разложения правильной дроби $ g_{}(x)/f(x) $ на простейшие
$$
frac{g(x)}{f(x)} equiv frac{A_{1,1}}{x-lambda_1}+frac{A_{1,2}}{(x-lambda_1)^2}+dots+frac{A_{1,n}}{(x-lambda_1)^n}
$$
достаточно разложить полином $ g_{}(x) $ по степеням $ x-lambda_1 $, т.е. воспользоваться формулой Тейлора:
$$
begin{matrix}
g(x) &equiv & A_0+A_1(x-lambda_1)+A_2(x-lambda_1)^2+dots+A_n(x-lambda_1)^n \
&equiv & g(lambda_1) + g^{prime}(lambda_1) (x-lambda_1)+frac{g^{prime prime}(lambda_1)}{2!} (x-lambda_1)^2+dots +frac{g^{(n)}(lambda_1)}{n!} (x-lambda_1)^n .
end{matrix}
$$
Коэффициенты разложения можно вычислить по схеме Хорнера.
П
Пример. Разложить на простейшие дробь
$$
frac{x^4+(2-mathbf i),x^3+3(1-mathbf i),x^2+3(1-mathbf i),x-4,mathbf i}{(x-mathbf i)^5} .
$$
Решение. Раскладываем числитель по степеням $ x-mathbf i $ с использованием схемы Хорнера:
$$
begin{array}{c|rrrrrr}
& 1 & 2-mathbf i & 3(1-mathbf i) & 3(1-mathbf i) & -4,mathbf i \
hline
mathbf i & 1 & 2& 3-mathbf i & 4 & underline{0} \
mathbf i & 1 &2+ mathbf i& 2+ mathbf i& underline{3+2, mathbf i} \
mathbf i & 1 & 2+ 2,mathbf i & underline{3, mathbf i} \
mathbf i & 1 & underline{2+3, mathbf i} \
mathbf i & underline{1} \
end{array}
$$
$$
Rightarrow x^4+(2-mathbf i),x^3+3(1-mathbf i),x^2+3(1-mathbf i),x-4,mathbf i equiv
$$
$$
equiv (x-mathbf i)^4+(2+3,mathbf i)(x-mathbf i)^3+3mathbf i,(x-mathbf i)^2+(3+2,mathbf i)(x-mathbf i)
$$
и разложение дроби на простейшие имеет вид
$$
frac{1}{x-mathbf i}+ frac{2+3,mathbf i}{(x-mathbf i)^2} + frac{3mathbf i}{(x-mathbf i)^3}+ frac{3+2,mathbf i}{(x-mathbf i)^4} .
$$
♦
Как искать простейшие дроби в случае, когда знаменатель $ f_{}(x) $ имеет не менее двух корней, причем один из них — кратный? — Существует общий метод решения
этой задачи, основанный на представлении полинома $ g_{}(x) $ числителя дроби в виде так называемого интерполяционного полинома Эрмита (Лагранжа-Сильвестра). Для практических же расчетов можно предложить определить сначала с помощью теоремы 7 простейшие дроби, соответствующие простым корням полинома, а коэффициенты числителей оставшихся простейших дробей искать по методу неопределенных коэффициентов. В одном из следующих пунктов будет указано универсальное представление этих коэффициентов — с помощью теории определителей.
?
Пусть разложение полинома $ f_{}(x) $ на линейные множители имеет вид:
$$
f(x)equiv a_0(x-lambda_1)^{{mathfrak m}_{1}}times
dots times
(x-lambda_{mathfrak r})^{{mathfrak m}_{{mathfrak r}}} , quad npu quad
{mathfrak m}_{1}+{mathfrak m}_{2}+dots+{mathfrak m}_{mathfrak r}=n= deg f
$$
и всех различных числах $ { lambda_1,dots,lambda_{mathfrak r } } subset mathbb C $. Доказать, что
$$
frac{f^{prime}(x)}{f(x)} equiv frac{{mathfrak m}_{1}}{x-lambda_1}+frac{{mathfrak m}_{2}}{x-lambda_2}
+ dots + frac{{mathfrak m}_{{mathfrak r}}}{x-lambda_{mathfrak r}} .
$$
…над множеством вещественных чисел
Материал этого пункта существенно используется в задаче интегрирования рациональных дробей.
Согласно теореме, приведенной в
☞
ПУНКТЕ, любой полином $ f_{}(x) $ с вещественными коэффициентами
степени $ ge 1 $ может быть разложен над множеством $ mathbb R^{} $ на множители двух видов:
$$(x-lambda)^{mathfrak m} u (x^2+p,x+q)^{mathfrak M} quad npu
{lambda,p,q} subset mathbb R,, p^2-4,q<0 u {{mathfrak m},{mathfrak M}}subset mathbb N
. $$
Из этого следует, что простейшими над $ mathbb R_{} $ дробями могут быть только дроби вида
$$
frac{A}{(x-lambda)^{k}} quad u quad frac{Bx+C}{(x^2+p,x+q)^{ell}} quad
npu {k,ell } subset mathbb N .
$$
Практические способы разложения дроби $ g_{}(x)/f(x) $ на простейшие над $ mathbb R_{} $ могут быть получены развитием способов, разработанных для разложения на простейшие над $ mathbb C_{} $. Так, нетрудно проверить, что если в разложение дроби над $ mathbb C_{} $ входит слагаемое $ A/(x-lambda) $, то в это же разложение обязательно входит и $ overline{A}/(x-overline{lambda}) $, где ¯ означает комплексное сопряжение. Если при этом $ lambda_{} $ — мнимый корень полинома $ f_{}(x) $, то эти две простейшие дроби различны и их сумма
$$ frac{A}{x-lambda}+frac{overline{A}}{x-overline{lambda}}=frac{(A+overline{A})x-(Aoverline{lambda}+overline{A}lambda)}{x^2-(lambda+overline{lambda})x+ lambda overline{lambda}} = frac{ 2, mathfrak{Re}(A),x-2, mathfrak{Re}(Aoverline{lambda})}{x^2-2,mathfrak{Re}(lambda)x+ |lambda|^2}$$
будет вещественной дробью — простейшей над $ mathbb R_{} $.
П
Пример. Разложить дробь
$$ frac{3,x^3-x+7}{4,x^4-8,x^3+4,x^2-9} $$
на простейшие над $ mathbb R_{} $.
Решение. В предыдущем пункте было получено следующее разложение этой дроби над $ mathbb C_{} $:
$$
frac{frac{sqrt{5}}{48} (sqrt{5} + mathbf i)}{x- frac{1+ mathbf i sqrt{5}}{2}}
+frac{frac{sqrt{5}}{48} (sqrt{5} – mathbf i)}{x- frac{1- mathbf i sqrt{5}}{2}}
+frac{frac{sqrt{7}}{336}(13,sqrt{7} + 59 )}{x-frac{1+ sqrt{7}}{2}}
+frac{frac{sqrt{7}}{336}(13,sqrt{7} – 59 )}{x-frac{1- sqrt{7}}{2}} .
$$
Если объединить первые две дроби, то получим искомое разложение на простейшие над $ mathbb R_{} $:
$$frac{frac{5}{24}(x-1)}{x^2-x+frac{3}{2}}
+frac{frac{sqrt{7}}{336}(13,sqrt{7} + 59 )}{x-frac{1+ sqrt{7}}{2}}
+frac{frac{sqrt{7}}{336}(13,sqrt{7} – 59 )}{x-frac{1- sqrt{7}}{2}} .
$$
♦
П
Пример. Разложить дробь
$$
frac{x^2+1}{x^5-2,x^3-2,sqrt{2}, x^2+4,sqrt{2}}
$$
на простейшие над $ mathbb R_{} $.
Решение. Выписываем каноническое разложение знаменателя:
$$
x^5-2,x^3-2,sqrt{2}, x^2+4,sqrt{2}equiv
(x-sqrt{2})^2(x+sqrt{2})(x^2+sqrt{2},x+2) .
$$
Разложение на простейшие имеет вид
$$
frac{A_1}{x-sqrt{2}} + frac{A_2}{(x-sqrt{2})^2}+ frac{A_3}{x+sqrt{2}}
+frac{Bx+C}{x^2+sqrt{2},x+2} .
$$
Коэффициенты $ A_1,A_2,A_3,B $ и $ C_{} $ находим методом неопределенных коэффициентов.
После приведения к общему знаменателю, в числителе получаем полином
$$(A_1+A_3+B),x^4+(sqrt{2}A_1+A_2-sqrt{2}A_3 -sqrt{2}B+C),x^3 + $$
$$+(2,sqrt{2},A_2-2,B-sqrt{2}C),x^2
+(-2sqrt{2}, A_1+4,A_2-2 sqrt{2},A_3+2,sqrt{2}, B-2,C),x – $$
$$
-4,A_1+2 sqrt{2}A_2+4,A_3+2sqrt{2}C ,
$$
который должен быть тождественно равен $ x^{2}+1 $. Отсюда получаем систему
линейных уравнений
$$
left{ begin{array}{rrrrrl}
A_1+& &A_3+&B& = & 0, \
A_1+&A_2 – &sqrt{2}A_3 -&sqrt{2}B+ &C= & 0, \
&2,sqrt{2},A_2-&& 2,B-&sqrt{2}C =& 1, \
-2sqrt{2}, A_1+&4,A_2-&2 sqrt{2},A_3+&2,sqrt{2}, B-&2,C=&0, \
-4,A_1+&2 sqrt{2}A_2+&4,A_3+& &2sqrt{2}C=&1 ,
end{array}
right.
$$
имеющую единственное решение:
$$
A_1 = {scriptstyle 1}/{scriptstyle 48},
A_2={scriptstyle sqrt{2}}/{scriptstyle 8},
A_3={scriptstyle 3}/{scriptstyle 16},
B = -{scriptstyle 1}/{scriptstyle 6},
C = -{scriptstyle sqrt{2}}/{scriptstyle 12 }
.
$$
Ответ.
$$
-frac{{scriptstyle 1}/{scriptstyle 48}}{x-sqrt{2}}
+frac{{scriptstyle sqrt{2}}/{scriptstyle 8}}{(x-sqrt{2})^2}
+frac{{scriptstyle 3}/{scriptstyle 16}}{x+sqrt{2}}
-frac{{scriptstyle 1}/{scriptstyle 6},x
+{scriptstyle sqrt{2}}/{scriptstyle 12 }}{x^2+sqrt{2}x+2} .
$$
Интерполяция
Задача. Для таблицы значений
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_N \ hline
y & y_1 & y_2 &dots & y_N
end{array}
$$
при различных узлах $ {x_j} $ построить рациональную функцию в виде $ F(x)=g(x)/f(x) $ при $ g_{}(x) $ — полиноме степени $ le n $, $ f_{}(x) $ — полиноме степени $ le m $,
так, чтобы $ { F(x_j)=y_j }_{j=1}^N $. При этом $ N,n,m $ связаны соотношением:
$$ N=m+n+1 , . $$
В отличие от полиномиальной интерполяции, не всегда имеет решение.
§
Решение задачи см.
☞
ЗДЕСЬ.
Производные
В настоящем пункте существенно используются результаты из раздела ОПРЕДЕЛИТЕЛЬ.
Формулы для производных дробной функции становятся громоздкими с ростом порядков:
$$
left[ frac{g(x)}{f(x)} right]^{prime} = frac{g^{prime}(x)f(x)-g(x)f^{prime}(x)}{left[f(x)right]^2} ;
$$
$$
left[ frac{g(x)}{f(x)} right]^{prime prime} = frac{g^{prime prime}(x)[f(x)]^2-g(x)f(x)f^{prime prime}(x)-2,f(x)f^{prime}(x)g^{prime}(x)+2,g(x)[f^{prime}(x)]^2}{left[f(x)right]^3} .
$$
Однако эту громоздкость удается слегка упорядочить с использованием формализма определителей.
Т
Теорема 8. Имеет место равенство:
$$
left[ frac{g(x)}{f(x)} right]^{[k]} =
$$
$$
=frac{1}{left[f(x)right]^{k+1}}
left|begin{array}{cccccc}
f(x) & 0 & 0 & dots & 0 & g(x) \
f^{prime}(x) & f(x) & 0 & dots & 0 & g^{prime}(x) \
f^{prime prime}(x) & 2 f^{prime}(x) & f(x) & dots & 0 & g^{prime prime}(x) \
dots & & & & & dots \
f^{[k-1]}(x) & C_{k-1}^1 f^{[k-2]}(x) & C_{k-1}^2 f^{[k-3]}(x) & dots & f(x) & g^{[k-1]}(x) \
f^{[k]}(x) & C_{k}^1 f^{[k-1]}(x) & C_{k}^2 f^{[k-2]}(x) & dots & C_k^{k-1} f^{prime}(x) & g^{[k]}(x)
end{array}
right|_{(k+1)times (k+1)} ;
$$
здесь $ C_N^M $ — биномиальный коэффициент.
Доказательство. Если $ R(x)=g(x)/f(x) $, то $ R(x)f(x) equiv g(x) $. Последовательно дифференцируем произведение:
$$
begin{array}{ccccccc}
f(x) R(x) &=g(x) & & & & & \
f^{prime}(x) R(x) & +f(x)R^{prime}(x) &= g^{prime}(x) & & & & \
f^{prime prime}(x) R(x) &+ 2 f^{prime}(x) R^{prime}(x) & +f(x) R^{prime prime}(x) & = g^{prime prime}(x) & & & \
dots & & & & dots & & \
f^{[k]}(x) R(x) &+ C_{k}^1 f^{[k-1]}(x) R^{prime}(x) & + C_{k}^2 f^{[k-2]}(x) R^{prime prime}(x) & + dots + & \
& & +C_k^{k-1} f^{prime}(x) R^{[k-1]}(x) & +f(x)R^{[k]}(x) & = g^{[k]}(x) ; \
end{array}
$$
последняя формула — это формула Лейбница.
Эти равенства составляют систему линейных уравнений относительно величин $ R(x),R^{prime}(x),R^{prime prime}(x),dots, R^{[k]}(x) $. Эту систему можно решить по формулам Крамера; нас, собственно, интересует лишь одна компонента этого решения — последняя.
♦
Результат теоремы не предполагает рациональности дроби: числитель и знаменатель могут быть и неполиномиальны; лишь бы только требуемые производные от них были вычислимы.
Т
Теорема 9. Пусть $ lambda $ является корнем полинома $ f_{}(x) $ кратности $ mathfrak m $. Обозначим $ f_{lambda}(x)=f(x)/(x-lambda)^{mathfrak m} $ — частное от деления $ f_{}(x) $ на $ (x-lambda)^{mathfrak m} $. В разложение дроби $ g_{}(x)/f(x) $ на простейшие, слагаемые, содержащие в знаменателе $ (x-lambda) $, войдут в составе определителя:
$$
-frac{1}{left[f_{lambda}(lambda)right]^{mathfrak m}}
left|begin{array}{cccccc}
f_{lambda}(lambda) & 0 & 0 & dots & 0 & g(lambda) \
f_{lambda}^{prime}(lambda) & f_{lambda}(lambda) & 0 & dots & 0 & g^{prime}(lambda) \
f_{lambda}^{prime prime}(lambda) & 2 f_{lambda}^{prime}(lambda) & f_{lambda}(lambda) & dots & 0 & g^{prime prime}(lambda) \
dots & & & & & dots \
f_{lambda}^{[mathfrak m-1]}(lambda) & C_{mathfrak m-1}^1 f_{lambda}^{[mathfrak m-2]}(lambda) & C_{mathfrak m-1}^2 f_{lambda}^{[mathfrak m-3]}(lambda) & dots & f_{lambda}(lambda) & g^{[mathfrak m-1]}(lambda) \
displaystyle frac{1}{(x-lambda)^{mathfrak m}} & displaystyle frac{1}{(x-lambda)^{mathfrak m-1}} & displaystyle frac{1}{(x-lambda)^{mathfrak m-2}} & dots & displaystyle frac{1}{(x-lambda)} & 0
end{array}
right|_{(mathfrak m+1)times (mathfrak m+1)} .
$$
П
Пример. Разложить на простейшие дробь
$$
frac{3,x^6-11,x^5+19,x^4-22,x^3+15,x^2-6,x+1}{x^3(x-1)^4} .
$$
Решение. Если взять сначала $ lambda_{}=0 $, то для этого корня имеем: $ mathfrak m =3, f_{0}(x)=(x-1)^4 $ и все простейшие дроби, имеющие в знаменателе степени $ x_{} $, содержатся в выражении
$$
-frac{1}{[f_0(0)]^3}
left|begin{array}{cccc}
f_0(0) & 0 & 0 & g(0) \
f^{prime}_0(0) & f_0(0) & 0 & g^{prime}(0) \
f^{prime prime}_0(0) & 2,f^{prime}_0(0) & f_0(0) & g^{prime prime}(0) \
1/x^3 & 1/x^2 & 1/x & 0
end{array}
right|=
–
left|begin{array}{rrrr}
1 & 0 & 0 & 1 \
-4 & 1 & 0 & -6 \
12 & -8 & 1 & 30 \
1/x^3 & 1/x^2 & 1/x & 0
end{array}
right| =frac{1}{x^3}-frac{2}{x^2}+frac{1}{x} .
$$
Аналогично, для случая $ lambda_{}=1 $ имеем: $ mathfrak m =4, f_{1}(x)=x^3 $, и соответствующие простейшие дроби входят в состав выражения
$$
-frac{1}{[f_1(1)]^4}
left|begin{array}{ccccc}
f_1(1) & 0 & 0 & 0 & g(1) \
f^{prime}_1(1) & f_1(1) & 0 & 0 & g^{prime}(1) \
f^{prime prime}_1(1) & 2,f^{prime}_1(1) & f_1(1) & 0 & g^{prime prime}(1) \
f^{prime prime prime}_1(1) & 3,f^{prime prime}_1(1) & 3,f^{prime}_1(1) & f_1(1) & g^{prime prime prime}(1) \
displaystyle{frac{1}{(x-1)^4}} & displaystyle{frac{1}{(x-1)^3}} & displaystyle{frac{1}{(x-1)^2}} & displaystyle{frac{1}{(x-1)}} & 0
end{array}
right|=
$$
$$
=-
left|begin{array}{ccccc}
1 & 0 & 0 & 0 & -1 \
3 & 1 & 0 & 0 & -3 \
6 & 6 & 1 & 0 & -4 \
6 & 18 & 9 & 1 & 24 \
displaystyle{frac{1}{(x-1)^4}} & displaystyle{frac{1}{(x-1)^3}} & displaystyle{frac{1}{(x-1)^2}} & displaystyle{frac{1}{(x-1)}} & 0
end{array}
right| =
$$
$$
=frac{2}{x-1}+frac{1}{(x-1)^2}-frac{1}{(x-1)^4} .
$$
Ответ.
$$
frac{1}{x^3}-frac{2}{x^2}+frac{1}{x}+frac{2}{x-1}+frac{1}{(x-1)^2}-frac{1}{(x-1)^4} .
$$
Уничтожение иррациональности в знаменателе
Пусть $ f(x), g(x), g_1(x) $ — полиномы с рациональными коэффициентами, $ deg f=n $. Обозначим $ lambda_{1},dots,lambda_n $ корни $ f_{}(x) $.
Задача. Для рациональной дроби $ g_1(x)/g(x) $ найти полином $ G_{}(x) $
c рациональными коэффициентами и такой, чтобы
$$G(lambda_1)=g_1(lambda_1)/g(lambda_1), dots , G(lambda_n)=g_1(lambda_n)/g(lambda_n)
.
$$
Понятно, что эта постановка имеет смысл, если $ {g(lambda_j) ne 0}_{j=1}^n $, т.е. полиномы $ f_{}(x) $ и $ g_{}(x) $ взаимно просты.
П
Пример. Уничтожить иррациональность в знаменателе выражения
$$
frac{sqrt[3]{4}+5sqrt[3]{2}+7}{sqrt{2+sqrt[3]{2}}+sqrt[3]{2}+3} .
$$
Хотя эта задача и выглядит иначе, чем сформулированная в начале пункта, но она является именно частным случаем первой. В самом деле, обозначим
$$ lambda=sqrt{2+sqrt[3]{2}} quad Rightarrow quad lambda^2=2+sqrt[3]{2} quad Rightarrow quad (lambda^2-2)^3=2 , $$
т.е. $ lambda_{} $ является корнем полинома $ 6_{} $-й степени с целочисленными коэффициентами. С другой стороны, все иррациональности рассматриваемой дроби выражаются в полиномиальном виде от $ lambda_{} $:
$$
frac{sqrt[3]{4}+5sqrt[3]{2}+7}{sqrt{2+sqrt[3]{2}}+sqrt[3]{2}+3} = frac{(lambda^2-2)^2+5(lambda^2-2)+7}{lambda+lambda^2-2+3}=frac{lambda^4+lambda^2+1}{lambda^2+lambda+1} .
$$
§
Общая схема решения подобных задач
☞
ЗДЕСЬ.
Разложения в ряды…
Задача 1. Разложить дробь $ g_{}(x)/f(x) $ в ряд Тейлора по степеням переменной $ x_{} $.
Универсальная формула разложения произвольной функции $ G(x) $:
$$
G(0)+frac{G^{prime}(0)}{1!}x+frac{G^{prime prime}(0)}{2!}x^2+dots+ frac{G^{[j]}(0)}{j!}x^j+ dots ;
$$
лишь бы только можно было вычислить значения функции $ G(x) $ и ее производных в точке $ 0_{} $. Материалы предыдущего пункта позволяют вычислить значения производных дроби $ g_{}(x)/f(x) $; однако нас интересуют менее громоздкие способы — и их можно будет получить, воспользовавшись свойством полиномиальности $ g_{} (x) $ и $ f_{} (x) $.
Задача 2. Разложить дробь $ g_{}(x)/f(x) $ в ряд по отрицательным степеням переменной $ x_{} $; будем говорить о таком ряде, как о ряде Лорана.
… Тейлора
П
Разложить дробь
$$
frac{x^2+x+1}{x^4+3,x^3+2,x-1}
$$
в ряд Тейлора по степеням $ x_{} $.
Решение. Будем делить числитель на знаменатель «в столбик», но, в отличие от аналогичного алгоритма, использованного в пункте
☞
ДЕЛИМОСТЬ ПОЛИНОМОВ, располагать действия будем по возрастанию степеней $ x_{} $:
$$
begin{array}{rrrrrrrrrr|l}
1&+ x & +x^2 & & & && & & & -1+2,x+3,x^3+x^4 \
1&-2,x& &-3,x^3&-x^4& & & & && overline{ -1-3,x -7,x^2-17,x^3-44,x^4 -112,x^5+dots quad } \
hline
& 3,x&+x^2 &+3,x^3&+x^4& \
& 3,x&-6,x^2 & &-9,x^4 &-3,x^5 \
hline
&&7,x^{2}&+3,x^3&+10,x^4&+3,x^5 & \
&&7,x^{2}&-14,x^3&&-21,x^5 & -7,x^6 & \
hline
&&& 17,x^{3}&+10,x^4&+24,x^5 &+7,x^6 & \
&&& 17,x^{3}&-34,x^4& &-51,x^6 &-17, x^7 \
hline
&&&& 44,x^4 & +24,x^5 & +58,x^6 &+17,x^7 \
&&&& 44,x^4 & -88,x^5 & & -132,x^7 & -44, x^8 \
hline
&&&&& 112,x^5 & + dots
end{array}
$$
Процесс деления можно продолжать сколь угодно долго. Ответом задачи является ряд
$$ -1-3,x -7,x^2-17,x^3-44,x^4 -112,x^5+dots . $$
Если мы обрываем ряд на каком-то шаге, как оценить остаточный член? — Ответ на этот вопрос достаточно очевиден: имеем цепочку тождеств
$$
frac{x^2+x+1}{x^4+3,x^3+2,x-1} equiv -1 + x frac{3+x+3,x^2+x^3}{-1+2,x+3,x^3+x^4} equiv
$$
$$
equiv -1-3,x+x^2 frac{7+3,x+10,x^2+3,x^3}{-1+2,x+3,x^3+x^4}equiv
$$
$$
equiv -1-3,x -7,x^2 +x^3 frac{17+10,x+24,x^2+7,x^3 }{-1+2,x+3,x^3+x^4} equiv dots
$$
Выявим теперь закономерность в формировании последовательности коэффициентов ряда. Выпишем эту последовательность и умножим последовательные $ 5_{} $ членов этой последовательности на коэффициенты полинома знаменателя $ x^4+3,x^3+2,x-1 $, записанные по убыванию степеней $ x_{} $:
$$
begin{array}{crrrrrrr}
&-1 &-3 & -7 &-17 &-44 &-112 & dots \
times & 1 & 3 & 0 & 2 & -1 & \
hline
& -1 & -9 & 0 & – 34 & 44
end{array} qquad
begin{array}{crrrrrrr}
&-1 &-3 & -7 &-17 &-44 &-112 & dots \
times & & 1 & 3 & 0 & 2 & -1 & \
hline
& & -3 & -21 & 0 & -88 & 112
end{array}
$$
Сумма элементов получившихся строк оказывается равной $ 0_{} $. Подмеченная закономерность оказывается универсальной.
♦
Т
Теорема 10. Пусть
$$ f(x)=a_0x^n+dots+a_n, nge 1, a_0ne 0 $$
и2) $ a_nne 0 $. Пусть $ deg g(x) < deg f $. В разложении дроби $ g_{}(x)/f(x) $ в ряд Тейлора по степеням $ x_{} $:
$$
frac{g(x)}{f(x)} = t_0+t_1x+t_2x^2+dots = sum_{j=0}^{infty} t_jx^{j}
$$
коэффициенты разложения будут удовлетворять соотношению
$$ t_{K}a_0+t_{K+1}a_{1}+dots+t_{K+n}a_n = 0 quad npu quad forall K in {0,1,2,dots } . $$
Доказательство. Домножим разложение на $ f_{}(x) $ и приравняем коэффициенты при одинаковых степенях $ x_{} $ в тождестве
$$ g(x) equiv f(x) sum_{j=0}^{infty} t_jx^{j} = a_nt_0+(a_nt_1+a_{n-1}t_0)x+ (a_nt_2+a_{n-1}t_1+a_{n-2}t_0)x^2+dots+
$$
$$ +(a_nt_{n-1}+a_{n-1}t_{n-2}+dots+a_{1}t_0)x^{n-1}+ $$
$$+(a_nt_{n}+a_{n-1}t_{n-1}+dots+a_{0}t_0)x^{n}+(a_nt_{n+1}+a_{n-1}t_{n}+dots+a_{0}t_1)x^{n+1}+dots $$
По предположению, $ deg g < n $, поэтому все коэффициенты при $ x^{n},x^{n+1},dots $ должны быть равны нулю. Получаем бесконечную цепочку однотипных равенств, которые эквивалентны записанному в формулировке теоремы соотношению.
Это соотношение позволяет линейно выразить каждый коэффициент ряда, начиная с $ t_n $, через $ n_{} $ предшествующих; при этом закономерность вычисления не меняется с возрастанием номера коэффициента:
$$
t_{K+n}= – frac{1}{a_n} (t_{K}a_0+t_{K+1}a_{1}+dots+t_{K+n-1}a_{n-1}) .
$$
Для определения первых $ n_{} $ коэффициентов ряда имеем уравнения
$$
begin{array}{ll}
t_0a_n &=b_{n-1}, \
t_1a_n+t_0a_{n-1} & = b_{n-2}, \
t_2a_n+t_1a_{n-1}+t_0a_{n-2} & = b_{n-3}, \
dots & dots \
t_{n-1}a_n+t_{n-2}a_{n-1}+dots+t_0a_{1} & = b_{0},
end{array}
$$
в правых частях которых стоят коэффициенты полинома $ g(x)=b_0x^{n-1}+b_1x^{n-2}+dots+b_{n-1} $. Оказывается, что эти коэффициенты непосредственно влияют только на первые $ n_{} $ членов разложения в ряд Тейлора; как только они определены, оставшиеся будут задаваться соотношением, в котором коэффициенты $ b_0,b_1,dots,b_{n-1} $ не участвуют. Иными словами, у двух правильных дробей $ g_{}(x)/f(x) $ и $ tilde g_{}(x)/f(x) $ с одинаковыми знаменателями формирование коэффициентов разложения в ряд Тейлора происходит единообразно, начиная с коэффициента при степени $ x^{n} $; и различия между этими рядами формируется в коэффициентах при $ x^0,x^1,dots,x^{n-1} $.
♦
Последовательность $ {y_j}_{j=0}^{infty} $, формируемая по правилу: первые $ n_{} $ членов заданы произвольно, а каждый следующий определяется через $ n_{} $ предыдущих с помощью линейного соотношения
$$ y_{K+n} = A_1y_{K+n-1}+dots+A_{n}y_{K} quad npu quad forall K in {0,1,2,dots } $$
и при фиксированных числах $ A_1,dots,A_n $, $ A_nne 0 $, называется линейной рекуррентной последовательностью $ n_{} $-го порядка; само уравнение вида
$$ A_0y_{K+n}+A_1y_{K+n-1}+dots+A_{n}y_{K}=0 quad npu quad A_0ne 0, A_n ne 0 $$
относительно неизвестной последовательности $ {y_j}_{j=0}^{infty} $ называется линейным однородным разностным уравнением $ n_{} $-го порядка.
§
Подробное исследование этих объектов
☞
ЗДЕСЬ.
=>
Коэффициенты ряда Тейлора разложения правильной дроби, знаменатель которой является полиномом степени $ n_{} $ с отличным от нуля свободным членом, формируют линейную рекуррентную последовательность $ n_{} $-го порядка; при этом разностное уравнение, которое формирует эту последовательность, не зависит от коэффициентов числителя разлагаемой дроби.
П
Пример. Вычислить первые $ 7_{} $ членов разложения дроби
$$
frac{x^4-3,x^3+1}{3,x^5+x^3+2,x^2-x+4}
$$
в ряд Тейлора по степеням $ x_{} $.
Решение.
$$
begin{array}{lrcl}
4,t_0 &=1 & Rightarrow & t_0=1/4, \
4,t_1-t_0 & = 0 & Rightarrow & t_1=1/16, \
4,t_2-t_1+2,t_0 & = 0 & Rightarrow & t_2=-7/64, \
4,t_3-t_2+2,t_1+t_0 & =-3 & Rightarrow & c_3=-223/256, \
4,t_4-t_3+2,t_2+t_1 & = 1 & Rightarrow & c_4=73/1024,\
hline
4,t_5-t_4+2,t_3+t_2+3,t_0 & = 0 & Rightarrow & c_5=1201/4096, \
4,t_6-t_5+2,t_4+t_3+3,t_1 & = 0 & Rightarrow & c_6=3417/16384.
end{array}
$$
Ответ.
$$ frac{1}{4}+frac{1}{16}x-frac{7}{64}x^2-frac{223}{256}x^3+frac{73}{1024}x^4+frac{1201}{4096}x^5+frac{3417}{16384}x^6 . $$
Справедливо и обратное утверждение: любая последовательность $ {c_j}_{j=0}^{infty} $, элементы которой, начиная с какого-то номера $ K_0+n $, удовлетворяют разностному уравнению
$$ A_0t_{K+n}+A_1t_{K+n-1}+dots+A_{n}t_{K}=0 $$
при $ n in mathbb N, quad A_0ne 0, A_n ne 0, Kin {K_0,K_0+1,dots } $
представляет собой коэффициенты ряда Тейлора разложения рациональной дроби (не обязательно правильной!), в знаменателе которой стоит полином
$ A_0x^n+A_1x^{n-1}+dots+A_n $. Подробнее
☞
ЗДЕСЬ.
Во всех предыдущих рассуждениях настоящего пункта мы старательно обходили вопрос о сходимости ряда Тейлора, ограничиваясь лишь формальным построением этого ряда. Самое время заполнить этот пробел. Очевидно, достаточно будет решить этот вопрос для случая разложения функции $ 1/f(x) $. Воспользуемся возможностью разложения полинома $ f_{}(x) $ на линейные множители над множеством $ mathbb C_{} $:
$$
frac{1}{a_0x^n+a_1x^{n-1}+dots+a_n} equiv frac{1/a_0}{(x-lambda_1)timesdots times (x-lambda_n)}
$$
где $ {lambda_{1},dots,lambda_n } subset mathbb C $ — корни полинома $ f_{}(x) $ (с учетом их кратностей). Разложение дроби в ряд Тейлора может быть получено как с помощью алгоритмов, разобранных выше, так и как произведение разложений дробей вида
$$ frac{1}{x-lambda_j} . $$
Имеем:
$$
frac{1}{x-lambda_j}=-frac{1}{lambda_j}cdot frac{1}{1-x/lambda_j}=-frac{1}{lambda_j}left(1+frac{x}{lambda_j}+frac{x^2}{lambda_j^2}+dots+
frac{x^k}{lambda_j^k}+dots right)
$$
и ряд в правой части сходится абсолютно при $ |x/lambda_j|<1 $.
Т
Теорема 11. Пусть $ g_{}(x)/f(x) $ — правильная, несократимая дробь и $ f(0) ne 0 $. Тогда ряд Тейлора этой дроби по степеням переменной $ x_{} $ сходится абсолютно в круге комплексной плоскости, определяемом условием
$$ |x| < min_{j} |lambda_j| , $$
где $ lambda_{j} $ означает корень полинома $ f_{}(x) $.
Доказательство проводится средствами теории функции комплексной переменной и использует (привычную для курса математического анализа вещественной переменной) возможность перемножения абсолютно сходящихся рядов.
♦
П
Пример. Оценить радиус сходимости ряда из предыдущего примера.
Решение. Корни полинома $ 3,x^5+x^3+2,x^2-x+4 $:
$$ lambda_1 approx -1.159580, lambda_{2,3} approx underbrace{-0.158205 pm 1.033065 mathbf i}_{| |approx 1.045109}, lambda_{4,5} approx underbrace{0.737995pm 0.712803 mathbf i}_{| |approx 1.026023} . $$
Ответ. Ряд сходится при $ |x| < 1.026 $.
… Лорана
Задачу разложения дроби $ g_{}(x)/f(x) $ в ряд Лорана по степеням $ 1/x_{} $ можно свести к рассмотренной в предыдущем пункте задаче о разложении в ряд Тейлора. Если $ f(x)=a_0x^n+dots+a_n, nge 1, a_0ne 0, g(x)=b_0x^{n-1}+b_{1}x^{n-2}+dots+b_{n-1} $, то
$$ frac{g(x)}{f(x)}=frac{x^{n-1}left(b_0+b_1cdot 1/x + dots + b_{n-1} cdot 1/x^{n-1} right)}{x^nleft(a_0+a_1cdot 1/x+a_2 cdot 1/x^2+dots+ a_n cdot 1/x^nright)}= z frac{b_0+b_1z + dots + b_{n-1}z^{n-1}}{a_0+a_1z+a_2z^2+dots+ a_nz^n} $$
при $ z=1/x $. Дальше раскладываем дробь по положительным степеням $ z_{} $. Приведенные ниже результаты являются аналогами соответствующих результатов из предыдущего пункта.
Т
Теорема 12. Пусть $ f(x)=a_0x^n+dots+a_n, nge 1, a_0ne 0 $. Пусть $ deg g(x) < deg f $. В разложении дроби $ g_{}(x)/f(x) $ в ряд Лорана по степеням $ 1/x_{} $:
$$
frac{g(x)}{f(x)} = frac{c_0}{x}+frac{c_1}{x^2}+dots = sum_{j=0}^{infty} frac{c_j}{x^{j+1}}
$$
коэффициенты разложения будут удовлетворять соотношению
$$ c_{K+n}a_0+c_{K+n-1}a_{1}+dots+c_{K}a_n = 0 quad npu quad forall K in {0,1,2,dots } . $$
Обратим внимание на отличие этого соотношения от полученного при разложении $ g_{}(x)/f(x) $ в ряд Тейлора по положительным степеням $ x_{} $;
в теореме 10 оно имело вид
$$ t_{K}a_0+t_{K+1}a_{1}+dots+t_{K+n}a_n = 0 $$
Два соотношения отличаются порядком следования коэффициентов при соответствующих элементах рекуррентных последовательностей: $ (a_0,a_1,dots,a_n) $ и
$ (a_n,a_{n-1},dots,a_0) $.
Т
Теорема 13. Если все корни $ lambda_1,dots,lambda_{n} $ полинома $ f_{}(x) $ простые и $ deg g(x) < deg f $ то имеет место равенство
$$
c_k=sum_{j=1}^n frac{lambda_j^k g(lambda_j)}{f^{prime}(lambda_j)} quad npu quad forall k in {0,1,2,dots } .
$$
Доказательство. Воспользуемся формулой Лагранжа:
$$
frac{g(x)}{f(x)}=sum_{j=1}^{n}frac{g(lambda_j)}{f'(lambda_j)(x-lambda_j)} .
$$
Разложим теперь каждую дробь $ 1/(x-lambda_{j}) $ в ряд Лорана по степеням $ 1/x_{} $
$$
frac{1}{x-lambda_j}= frac{1}{x(1-lambda_j/x)}= frac{1}{x}left(1+ frac{lambda_j}{x}+frac{lambda_j^2}
{x^2}+dots right)
$$
и подставим в предыдущее равенство. Сравнивая коэффициенты
при одинаковых степенях $ x_{} $ в полученном ряду и в ряду $ sum_{j=0}^{infty} c_jx^{-j-1} $, получаем
требуемый результат.
♦
=>
Имеют место следующие формулы Ньютона, выражающие суммы степеней корней полинома ( суммы Ньютона) $ s_k=lambda_1^{k}+dots+lambda_n^k $ (при $ kin mathbb N $) через его коэффициенты:
$$
s_k=left{begin{array}{lr}
-(a_1s_{k-1}+a_2s_{k-2}+dots+a_{k-1}s_1+a_kk)/a_0,
&npu kle n ;\
-(a_1s_{k-1}+a_2s_{k-2}+dots+a_ns_{k-n})/a_0,
& npu k > n.
end{array}
right.
$$
Дополнительно полагают также $ s_{0}=n $ при любом наборе корней3).
Доказательство утверждения для случая простоты всех корней полинома следует из предыдущей теоремы — суммы Ньютона будут коэффициентами разложения
в ряд Лорана дроби $ f^{prime}(x)/f(x) $. Пусть теперь полином имеет кратные корни и его разложение на линейные множители имеет вид:
$$
f(x)equiv a_0(x-lambda_1)^{{mathfrak m}_{1}}times
dots times
(x-lambda_{mathfrak r})^{{mathfrak m}_{{mathfrak r}}} , quad npu quad
{mathfrak m}_{1}+{mathfrak m}_{2}+dots+{mathfrak m}_{mathfrak r}=n= deg f
$$
и всех различных числах $ { lambda_1,dots,lambda_{mathfrak r } } subset mathbb C $. Имеем (см. упражнение в конце
☞
ПУНКТА ):
$$
frac{f^{prime}(x)}{f(x)} equiv frac{{mathfrak m}_{1}}{x-lambda_1}+frac{{mathfrak m}_{2}}{x-lambda_2}
+ dots + frac{{mathfrak m}_{{mathfrak r}}}{x-lambda_{mathfrak r}} ,
$$
и дальнейшие рассуждения аналогичны предыдущему случаю.
♦
Т
Теорема 14. Пусть $ g_{}(x)/f(x) $ — правильная, несократимая дробь. Тогда ряд Лорана этой дроби по степеням $ 1/x_{} $ сходится абсолютно в области комплексной плоскости, определяемой условием
$$ |x| > max_{j} |lambda_j| , $$
где $ lambda_{j} $ означает корень полинома $ f_{}(x) $.
Задачи
Источники
[1]. Журавский А.М. Сборник задач по высшей алгебре. М.-Л. ГТТИ. 1933
