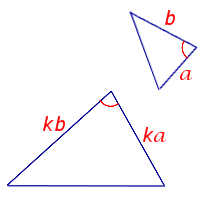
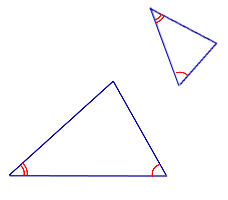
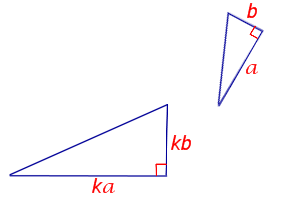
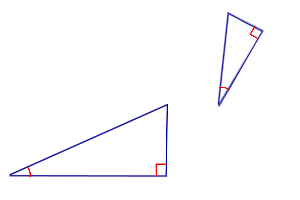
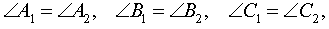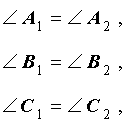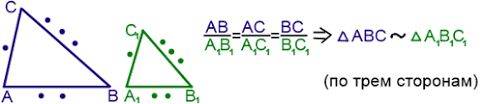Подобие прямоугольных треугольников обычно доказывают, используя не общие признаки, а специальные признаки подобия для прямоугольных треугольников.
Признаки подобия прямоугольных треугольников
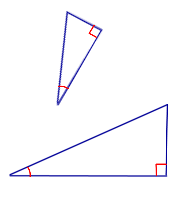
1- й признак подобия прямоугольных треугольников
( подобие прямоугольных треугольников по острому углу)
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
— прямоугольные (∠C=90º, ∠C=90º).
Если
то
(по острому углу).
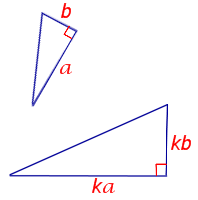
2- й признак подобия прямоугольных треугольников
( подобие прямоугольных треугольников по двум катетам)
Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
— прямоугольные (∠C=90º, ∠C=90º).
Если
то
(по двум катетам).
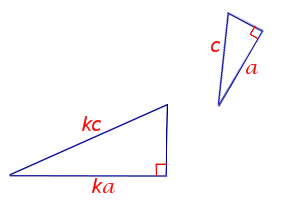
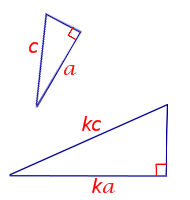
3- й признак подобия прямоугольных треугольников
( подобие прямоугольных треугольников по катету и гипотенузе)
Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
— прямоугольные (∠C=90º, ∠C=90º).
Если
то
(по катету и гипотенузе).
Из подобия прямоугольных треугольников следуют соотношения между высотой, проведённой к гипотенузе, гипотенузой, катетами и проекциями катетов на гипотенузу, а также свойство биссектрисы треугольника.
Как определить подобие прямоугольных треугольников
Подобные треугольники. Признаки подобия треугольников
Подобные треугольники
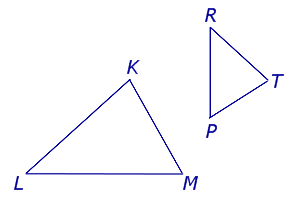
Рассмотрим два треугольника KLM и TRP (рис.1) и введём следующие обозначения.
длины сторон треугольника KLM , расположенные в порядке возрастания.
длины сторон треугольника TRP , расположенные в порядке возрастания.
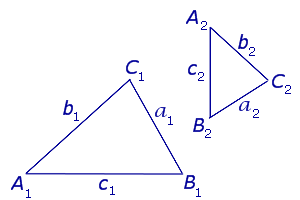
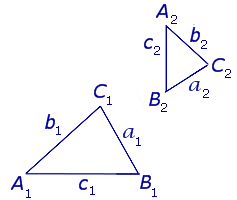
Переобозначим вершины треугольников KLM и TRP так, как показано на рисунке 2.
На рисунке 2 треугольник KLM обозначается как треугольник A1B1C1 , а треугольник TRP обозначается как треугольник A2B2C2 .
- вершины A1 и A2 , B1 и B2 , C1 и C2 называют сходственными вершинами ,
- стороны A1B1 и A2B2 , A1C1 и A2C2 , B1C1 и B2C2 называют сходственными сторонами ,
- углы A1 и A2 , B1 и B2 , C1 и C2 называют сходственными углами
Определение 2 . Треугольники A1B1C1 и A2B2C2 называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.
а, во-вторых, существует положительное число k , такое, что справедливы равенства:
| a1 = k a2 , b1 = k b2 , c1 = k c2 . | (1) |
Признаки подобия треугольников
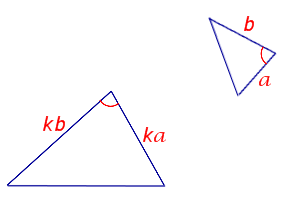
Признак подобия треугольников по двум сторонам и углу между ними
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны.
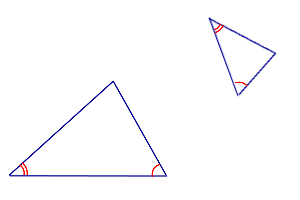
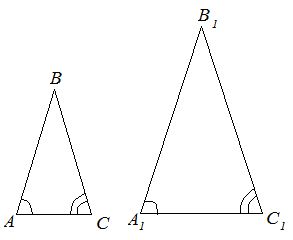
Признак подобия треугольников по двум углам
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
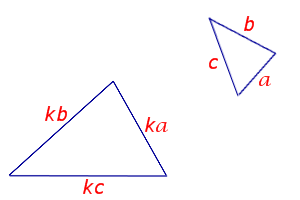
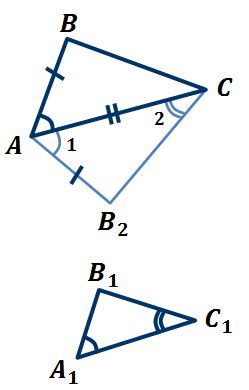
Признак подобия треугольников по трём сторонам
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны
| Название признака | Рисунок | Формулировка признака |
Формулировка признака подобия:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны.
| Признак подобия треугольников по двум сторонам и углу между ними | ||||||||
| Признак подобия треугольников по двум углам | ||||||||
|
Формулировка признака подобия: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. |
||||||||
| Признак подобия треугольников по трём сторонам | ||||||||
|
Формулировка признака подобия: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны Признаки подобия прямоугольных треугольниковПризнак подобия прямоугольных треугольников по двум катетам Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. Признак подобия прямоугольных треугольников по острому углу Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. Признак подобия прямоугольных треугольников по гипотенузе и катету Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
Формулировка признака подобия прямоугольных треугольников: Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
|
Признаки подобия прямоугольных треугольников

4
Средняя оценка: 4
Всего получено оценок: 127.
4
Средняя оценка: 4
Всего получено оценок: 127.
Подобие – это следующее понятие после равенства: как в математике после сложения идет умножение, так в геометрии после равенства треугольников изучают подобие. В реальной жизни подобие помогает, за счет вычислений по тени, определять реальные размеры зданий или высоких сооружений. В задачах на эту тему, благодаря подобию, можно найти значение сторон, воспользовавшись знакомым отношением.
Определения
Подобными называются треугольники, отношение сторон которых соответственно равны. Предположим треугольник АВС равен треугольнику DРН. Это значит, что:
$${АВover{DP}}={BCover{PH}}={ACover{DH}}=k$$
k это коэффициент подобия.
Для обычного треугольника существует три признака подобия. Именно через них доказываются признаки подобия прямоугольных треугольников.
Первый признак подобия: по двум углам. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Второй признак: по трем сторонам. Если три стороны одного треугольника пропорциональны соответственным сторонам другого треугольника, то такие треугольники подобны.
Третий признак: по двум сторонам и углу. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то такие треугольники подобны.
Эти определения необходимо знать, чтобы без проблем разобраться с подобием прямоугольных треугольников.
Признаки подобия прямоугольных треугольников
- Первый признак по острому углу: если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
Доказать этот признак очень просто. Достаточно вспомнить, что прямоугольным треугольником называется треугольник, который содержит в себе прямой угол. Значит, у двух прямоугольных треугольников, один из углов всегда равен другому. А один из острых углов так же равен соответственному углу в другом треугольнике. Значит, в таких треугольниках есть два равных между собой угла, и треугольники подобны по первому признаку подобия.
- Второй признак: по двум катетам. Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны. Между двумя катетами всегда заключен прямой угол. Значит, у нас имеется две пропорциональные стороны и равные углы между ними. Тогда треугольники подобны по третьему признаку подобия.
- Третий признак: по катету и гипотенузе. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны. Для доказательства признака нужно вспомнить понятие косинуса. Косинус угла это отношения прилежащего катета к гипотенузе.
$$cos(ACB)={BCover{AC}}$$
$$cos(DHP)={PHover{DH}}$$
При этом по условию: $${ACover{DH}}={BCover{PH}}$$. Из условия выразим ВС и подставим в значение косинуса.
$$ВС=РН*{АCover{DН}}$$
$$cos(ACB)={BCover{AC}}={PH*{ACover{DH}}over AC}={PHover{AC}}$$ – то есть косинусы углов равны, оба угла острые, значит и углы равны. Тогда треугольники подобны по двум сторонам и углу между ними.
Что мы узнали?
Мы разобрали понятие подобия, выделили все определения и теоремы, необходимые для доказательства трех признаков подобия прямоугольных треугольников. Мы показали, что эти признаки лишь следствие основных, т.е. эти свойства созданы чтобы упростить и сделать быстрее решение. А это значит, что если вдруг вы забыли признаки для прямоугольного треугольника, то всегда можно воспользоваться общими.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4
Средняя оценка: 4
Всего получено оценок: 127.
А какая ваша оценка?
Подобие прямоугольных треугольников и его применение
1 января 2016
Разумеется, подобными могут быть не только прямоугольные треугольники, но именно в них возникает несколько интересных свойств, которые могут значительно упростить решение сложных планиметрических задач.
Сегодня мы изучим механизм того, как возникают подобные прямоугольные треугольники, какие особенные свойства при этом возникают и как грамотно применять всё это в своей работе.
Всего в видео рассмотрено две ситуации:
- Подобие при проведении высоты к гипотенузе;
- Подобие после проведения линий, параллельных катетам.
В обоих случаях разбирать будем реальные задачи, чтобы сразу применять изученные свойства на практике.:)
Смотрите также:
- Основное свойство биссектрисы угла в треугольнике и его применение для решения задач
- Что такое теорема косинусов и как она помогает решать геометрические задачи
- Тест к уроку «Площади многоугольников на координатной сетке» (средний)
- Тригонометрические функции
- Задачи на проценты: считаем проценты с помощью пропорции
- Производительность совместного труда
Подобие – это понятие, характеризующее наличие одинаковой, не зависящей от размеров, формы у геометрических фигур.
Подобные фигуры – это фигуры, для которых существует взаимно-однозначное соответствие, при котором расстояние между любыми парами их соответствующих точек изменяется в одно и то же число раз.
Например, то, что фигуры F1 и F2 подобны, означает, что для любых двух точек M1 и N1 фигуры F1 и сопоставленных им точек M2 и N2 фигуры F2 выполняется соответствие (frac{M_1N_1}{M_2N_2}=k), где k – одно и то же число для всех точек (k > 0). Число k называется коэффициентом подобия.Преобразование фигуры F1 в фигуру F2, при котором расстояния между точками изменяются в одно и то же число раз, называется преобразованием подобия.
Гомотетия – это преобразование подобия. Это преобразование, в котором получаются подобные фигуры (фигуры, у которых соответствующие углы равны и стороны пропорциональны).
Гомотетия – это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу (OA_1=kcdot OA), где k – постоянное, отличное от нуля число, O – фиксированная точка. Точка O называется центром гомотетии, число k – коэффициентом гомотетии.
Свойства преобразования гомотетии:
1) При гомотетии прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, углы – в углы.
2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых). Стороны гомотетичных фигур пропорциональны, а углы равны.
Подобные треугольники – это треугольники, у которых углы равны, а стороны пропорциональны.
Свойства подобных треугольников
- Периметры подобных треугольников относятся как их соответствующие стороны: (frac{P_{A_1B_1C_1}}{P_{ABC}}=frac{A_1B_1}{AB}=frac{B_1C_1}{BC}=frac{A_1C_1}{AC}=k).
- Соответствующие линейные элементы подобных треугольников (медианы, высоты, биссектрисы и т. д.) относятся как их соответствующие стороны.
- Площади подобных фигур относятся как квадраты их соответствующих линейных размеров: (frac{S_{A_1B_1C_1}}{S_{ABC}}=frac{A_1B_1^2}{AB^2}=frac{B_1C_1^2}{BC^2}=frac{A_1C_1^2}{AC^2}=k^2).
1-й признак подобия треугольников
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
(left. begin{aligned} angle A=angle A_1\ angle B=angle B_1 end{aligned} right } Rightarrow Delta ABC sim Delta A_1B_1C_1)
2-й признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
3-й признак подобия треугольников
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Признаки подобия прямоугольных треугольников
- Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
- Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
- Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.