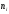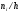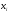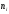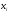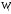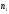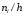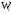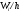Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 1
Построить полигон частот и
полигон относительных частот (частостей):
Решение
Вычислим относительные
частоты (частости):
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального
статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 2
Построить гистограмму
частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
Решение
Вычислим плотности
частоты:
Гистограмма частот
Кроме этой задачи на другой странице сайта есть
пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.
Пример 4
Построить кумулятивную
кривую:
Решение
Вычислим накопленные
частоты:
Кумулятивная кривая
Постройка полигона и гистограммы частот
Содержание:
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Определение
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),…, (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(W_i=frac{n_i}n)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Определение
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
(frac{n_ih}h=n_i)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Для
наглядности строят различные графики
статистического распределения, в
частности, полигон и гистограмму.
Определение.
Полигоном
частот называют ломаную, отрезки которой
соединяют точки (x1,
n1),
(x2,
n2),
…, (xk,
nk).
Для
построения полигона частот на оси
абсцисс откладывают варианты xi,
а на оси ординат – соответствующие им
частоты ni.
Точки (xi,
ni)
соединяют отрезками прямых и получают
полигон частот.
Определение.
Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки (x1,
w1),
(x2,
w2),
…, (xk,
wk).
Для
построения полигона частот на оси
абсцисс откладывают варианты xi,
а на оси ординат wi.
Точки (xi,
wi)
соединяют отрезками прямых и получают
полигон относительных частот.
На
рисунке изображен полигон относительных
частот следующего распределения:
|
x |
1,5 |
3,5 |
5,5 |
7,5 |
|
w |
0,1 |
0,2 |
0,4 |
0,3 |
Рис.
6. Полигон относительных частот.
В
случае непрерывного признака целесообразно
строить гистограмму, для чего интервал,
в котором заключены все наблюдаемые
значения признака, разбивают на несколько
частичных интервалов длинной h
и находят для каждого частичного
интервала ni
–
сумму частот вариант, попавших в i-ый
интервал.
Определение.
Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
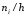(плотность частоты).
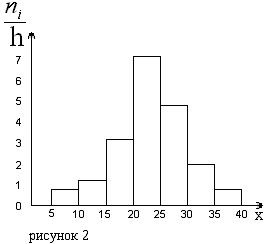
Рис.
7. Гистограмма частот.
Для
построения гистограммы частот на оси
абсцисс откладывают частичные интервалы,
а над ними проводят отрезки, параллельные
оси абсцисс, на расстоянии
.
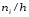Площадь
i-го
частичного прямоугольника равна
=
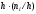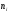─ сумме частот вариантi-го
интервала; следовательно, площадь
гистограммы частот равна сумме всех
частот, то есть объему выборки n.
На
рисунке 2 изображена гистограмма частот
распределения объема n=100,
приведенного в таблице 1.
|
Частичный
длиною |
Сумма |
Плотность |
|
5 |
4 |
0,8 |
|
10 |
6 |
1,2 |
|
15 |
16 |
3,2 |
|
20 |
36 |
7,2 |
|
25 |
24 |
4,8 |
|
30 |
10 |
2,0 |
|
34 |
4 |
0,8 |
Определение.
Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длинною h,
а высоты равны отношению
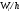(плотность относительной частоты).
Для
построения гистограммы относительных
частот на оси абсцисс откладывают
частичные интервалы, а над ними проводят
отрезки, параллельные оси абсцисс на
расстоянии
.
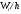Площадьi-го
частичного прямоугольника равна
=
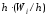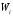─ относительной частоте вариант,
попавших вi-й
интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, то
есть единице.
Примеры.
-
В
результате выборки получена следующая
таблица распределения частот.
|
|
2 |
6 |
12 |
|
|
3 |
10 |
7 |
Построить
полигоны частот и относительных частот
распределения.
Для
начала построим полигон частот.
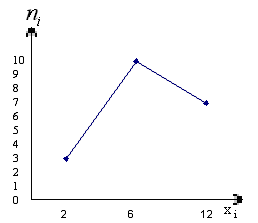
Рис.
8. Полигон частот.
Чтобы
построить полигон относительных частот
найдем относительные частоты, для чего
разделим частоты на объем выборки n.
n
=
3
+
10
+
7
=
20.
.
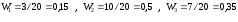Получаем
|
|
2 |
6 |
12 |
|
|
0,15 |
0,50 |
0,35 |
Построим
полигон относительных частот.
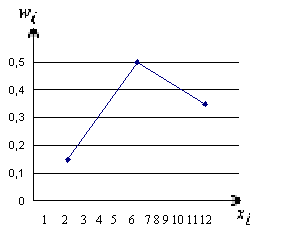
Рис.
9. Полигон относительных частот.
2.
Построить гистограммы частот и
относительных частот распределения.
Найдем
плотность частоты
:
|
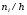Частичный
длиною |
Сумма |
Плотность |
|
2 |
9 |
3 |
|
5 |
10 |
3,3 |
|
8 |
25 |
8,3 |
|
11 |
6 |
2 |
Построим
гистограмму частот.
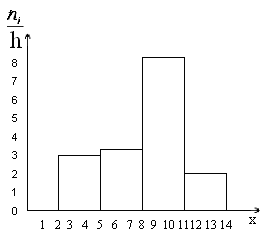
Рис.
10. Гистограмма частот.
Чтобы
построить гистограмму относительных
частот, нужно найти относительные
частоты. Для этого найдем объем выборки
n.
.
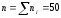Теперь
найдем относительные частоты
:
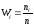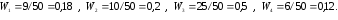
Получим:
|
Частичный |
Сумма
|
Плотность |
|
2 |
0,18 |
0,06 |
|
5 |
0,2 |
0,07 |
|
8 |
0,5 |
0,16 |
|
11 |
0,12 |
0,04 |
Плотности
частот
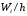нужно вычислить. При этомh
= 3.
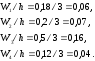
Построим
гистограмму относительных частот.
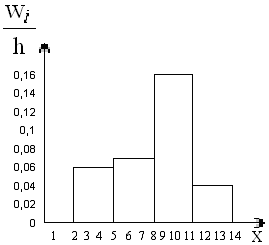
Рис.11.
Гистограмма относительных частот.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Полигон частот и гистограмма частот
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Полигон частот
Пусть нам дан ряд распределения, записанный с помощью таблицы:
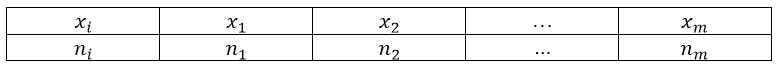
Рисунок 1.
Определение 1
Полигон частот — ломанная, которая соединяет точки $(x_m,n_m)$ ($m=1,2,dots ,m)$.
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие частоты. Полученные точки соединяют ломанной:
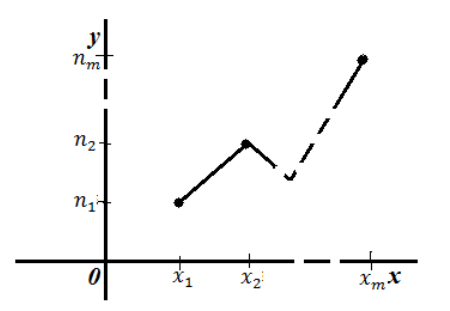
Рисунок 2. Полигон частот.
Помимо обычной частоты существует еще понятие относительной частоты.
Получаем следующую таблицу распределения относительных частот:
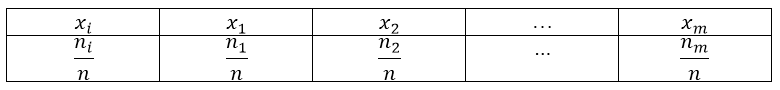
Рисунок 3.
Определение 2
Полигон относительных частот — ломанная, которая соединяет точки $(x_m,W_m)$ ($m=1,2,dots ,m)$.
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие относительные частоты. Полученные точки соединяют ломанной:
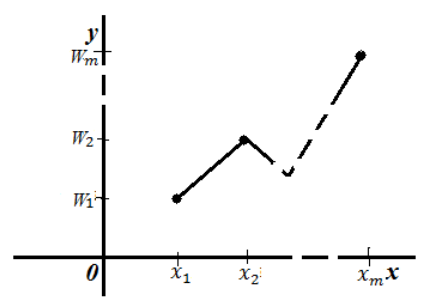
Рисунок 4. Полигон относительных частот.
Гистограмма частот
Помимо понятия полинома для непрерывных значений существует понятие гистограммы.
Определение 3
Гистограмма частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{n_i}{h}$:
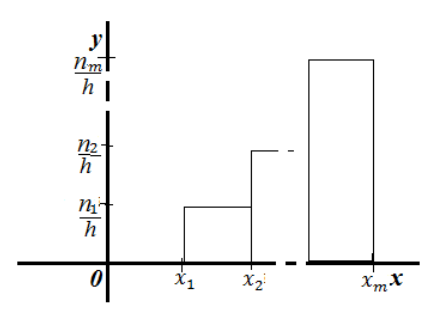
Рисунок 5. Гистограмма частот.
«Полигон частот и гистограмма частот» 👇
Заметим, что площадь одного такого прямоугольника $frac{n_ih}{h}=n_i$. Следовательно, площадь всей фигуры равна $sum{n_i}=n$, то есть равна объему выборки.
Определение 4
Гистограмма относительных частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{W_i}{h}$:
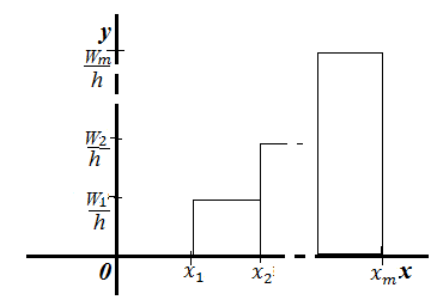
Рисунок 6. Гистограмма относительных частот.
Заметим, что площадь одного такого прямоугольника $frac{W_ih}{h}=W_i$. Следовательно, площадь всей фигуры равна $sum{W_i}=W=1$.
Примеры задачи на построение полигона и гистограммы
Пример 1
Пусть распределение частот имеет вид:
Рисунок 7.
Построить полигон относительных частот.
Решение.
Построим сначала ряд распределения относительных частот по формуле $W_i=frac{n_i}{n}$
Рисунок 8.
Получим следующий полигон относительных частот.
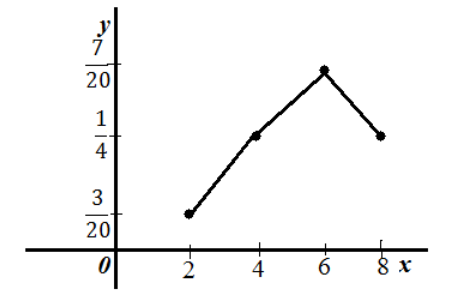
Рисунок 9.
Пример 2
Дан ряд непрерывного распределения частот:
Рисунок 10.
Решение.
Очевидно, что данном случае длина частичного интервала $h=2.$ Найдем высоты прямоугольников каждой точки разбиения.
При $x=1$: $frac{3}{2}=1,5$.
При $x=3$: $frac{5}{2}=2,5.$
При $x=6$: $frac{7}{2}=3,5.$
При $x=9$: $frac{9}{2}=4,5.$
Получаем следующую гистограмму частот:
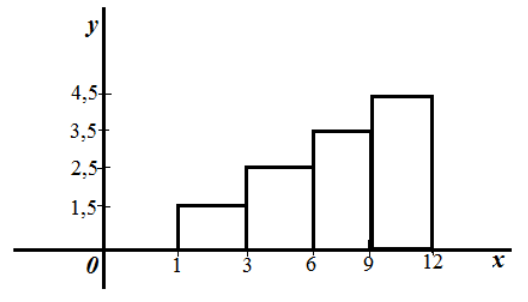
Рисунок 11.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 25.02.2023
Раздел 11 Элементы теории вероятностей и математической статистики
Лекция № 209 Представление данных (таблицы, диаграммы, графики).
Основная литература:
-
Уч. пособие “Алгебра. Элементы статистики и теории вероятностей” авторов Ю.Н. Макарычева и Н.Г. Миндюк
-
Математика: учебник / М.И. Башмаков. — Москва: КноРус, 2017.
-
Башмаков М.И. Математика. Задачник: учебное пособие для студ. Учреждений сред проф. образования. – 5-е изд., стер.- М.: Издательский центр «Академия», 2017 год.
-
Математика: учебник для учреждений нач. и сред. проф. образования /М.И. Башмаков.- 7-е изд., стер.- М.: Издательский центр «Академия», 2012 год.
-
http://www.drofa.ru/ (Методические пособия, статьи для обучения математике)
-
http://podgotovka-ege.ru/education/ (Сайт для подготовки к ЕГЭ)
-
https://multiurok.ru/seropol-irina
ВНИМАНИЕ!!! Материалы, представленные в лекции взяты из книги Уч. пособие “Алгебра. Элементы статистики и теории вероятностей” авторов Ю.Н. Макарычева и Н.Г. Миндюк. Книгу можно открыть:
1. В материалах, представленных в папке преподавателя файл Учебник. Алгебра элементы статистики и теории вероятностей. Миндюк, Макарычев.pdf (Для открытия файла на вашем компьютере или телефоне, должна быть установлена программа Adobe Acrobat –распространяется бесплатно).
2. Книгу можно открыть по ссылкам вашем браузере
https://uch-lit.ru/matematika-2/dlya-shkolnikov/makaryichev-yu-n-algebra-elementyi-stati
https://www.description-pdf.ru/2020/01/31/%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D1%8D%D0%BB%D0%B5%D0%BC%D0%B5%D0%BD%D1%82%D1%8B-%D1%81%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D0%BA%D0%B8-%D0%B8-%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D0%B8/
Конспект страницы учебника 22-27
Построение полигона, гистограммы
Полигоном частот называют ломаную, отрезки которой соединяют точки. Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты . Такие точки соединяют отрезками прямых и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки . Для построения полигона относительных частот на оси абсцисс откладывают варианты, а на оси ординат – соответствующие им относительные частоты (частости) . Такие точки соединяют отрезками прямых и получают полигон частот.
Задача 1: Построить полигон частот и полигон относительных частот (частостей):
|
хi |
2 |
7 |
8 |
15 |
16 |
17 |
|
ni |
15 |
35 |
64 |
55 |
21 |
10 |
Построим полигон частот.
По оси х – первая строка таблицы, по оси y – вторая строка, получим график
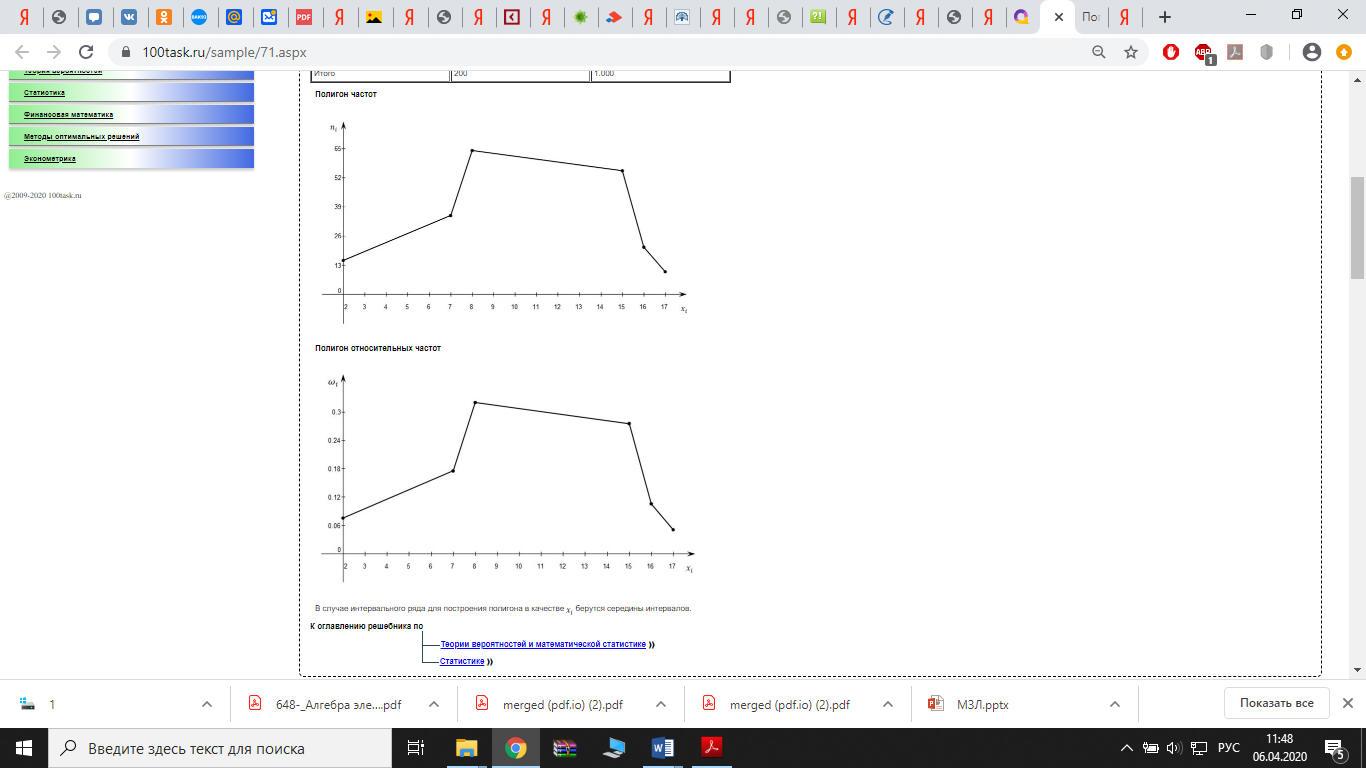
Вычислим относительные частоты (частости):
Сумма всех частот 15+35+64+55+21+10=200
Каждую частоту нужно разделить на сумму всех частот и записать в 3ий столбец, например 15/200=0,75; 35/200=0,175 …Получим таблицу
|
хi |
ni |
Относительные частоты, |
|
2 |
15 |
0,075 |
|
7 |
35 |
0,175 |
|
8 |
64 |
0,320 |
|
15 |
55 |
0,275 |
|
16 |
21 |
0,105 |
|
17 |
10 |
0,050 |
|
Итого |
200 |
1,000 |
Построим полигон относительных частот
В случае интервального ряда для построения полигона в качестве берутся середины интервалов.
Гистограмма
В случае интервального статистического распределения целесообразно построить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною, а высоты (в случае равных интервалов) должны быть пропорциональны частотам. При построении гистограммы с неравными интервалами по оси ординат наносят не частоты, а плотность частоты . Это необходимо сделать для устранения влияния величины интервала на распределение и иметь возможность сравнивать частоты.
В случае построения гистограммы относительных частот (гистограммы частостей) высоты в случае равных интегралов должны быть пропорциональны относительной частоте , а в случае неравных интервалов высота равна плотности относительной частоты .
Задача 2: Построить гистограмму частот и относительных частот (частостей)
|
2-5 |
5-8 |
8-11 |
11-14 |
14-17 |
17-20 |
|
|
15 |
35 |
64 |
55 |
21 |
10 |
Вычислим относительные частоты:
|
Интервалы, |
Относительные частоты, |
|
|
2 – 5 |
15 |
0,075 |
|
5 – 8 |
35 |
0,175 |
|
8 – 11 |
64 |
0,320 |
|
11 – 14 |
55 |
0,275 |
|
14 – 17 |
21 |
0,105 |
|
17 – 20 |
10 |
0,050 |
|
Итого |
200 |
1,000 |
Гистограмма частот
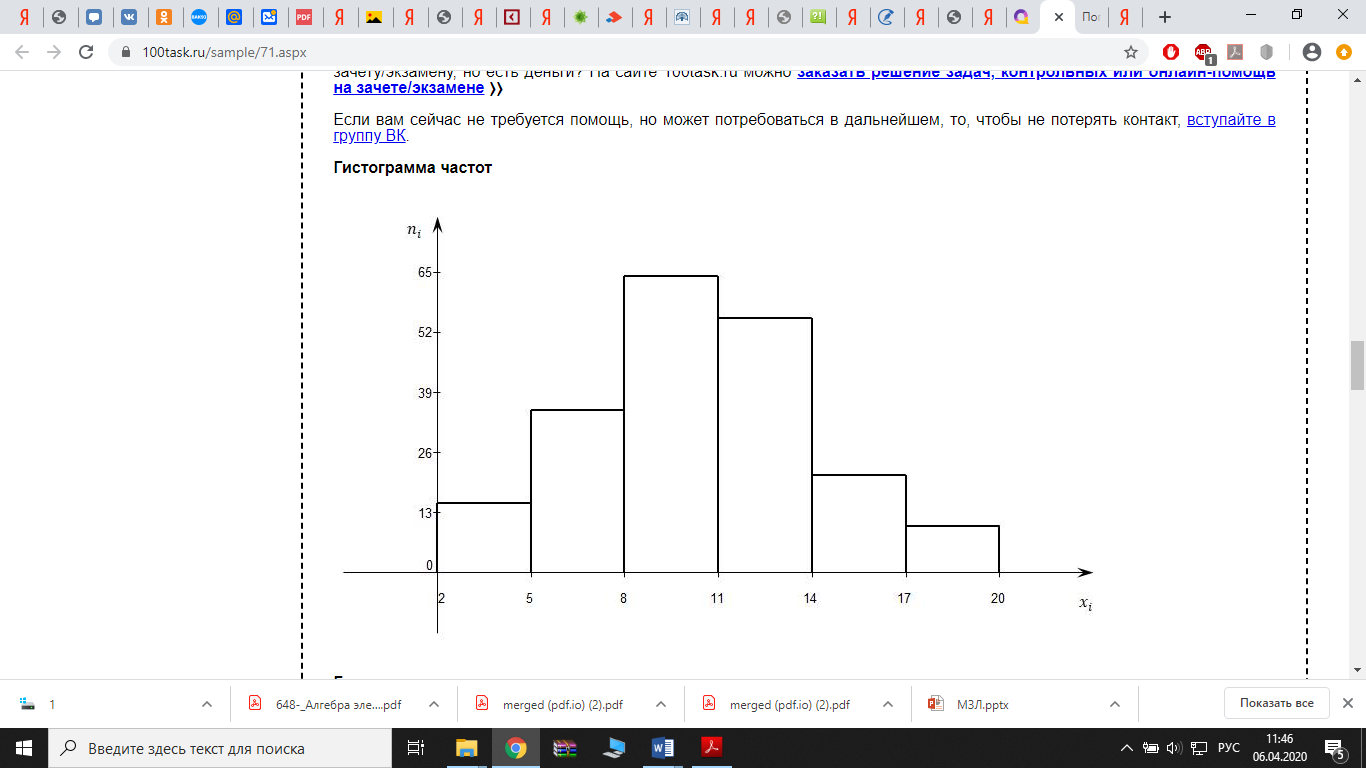
Гистограмма относительных частот
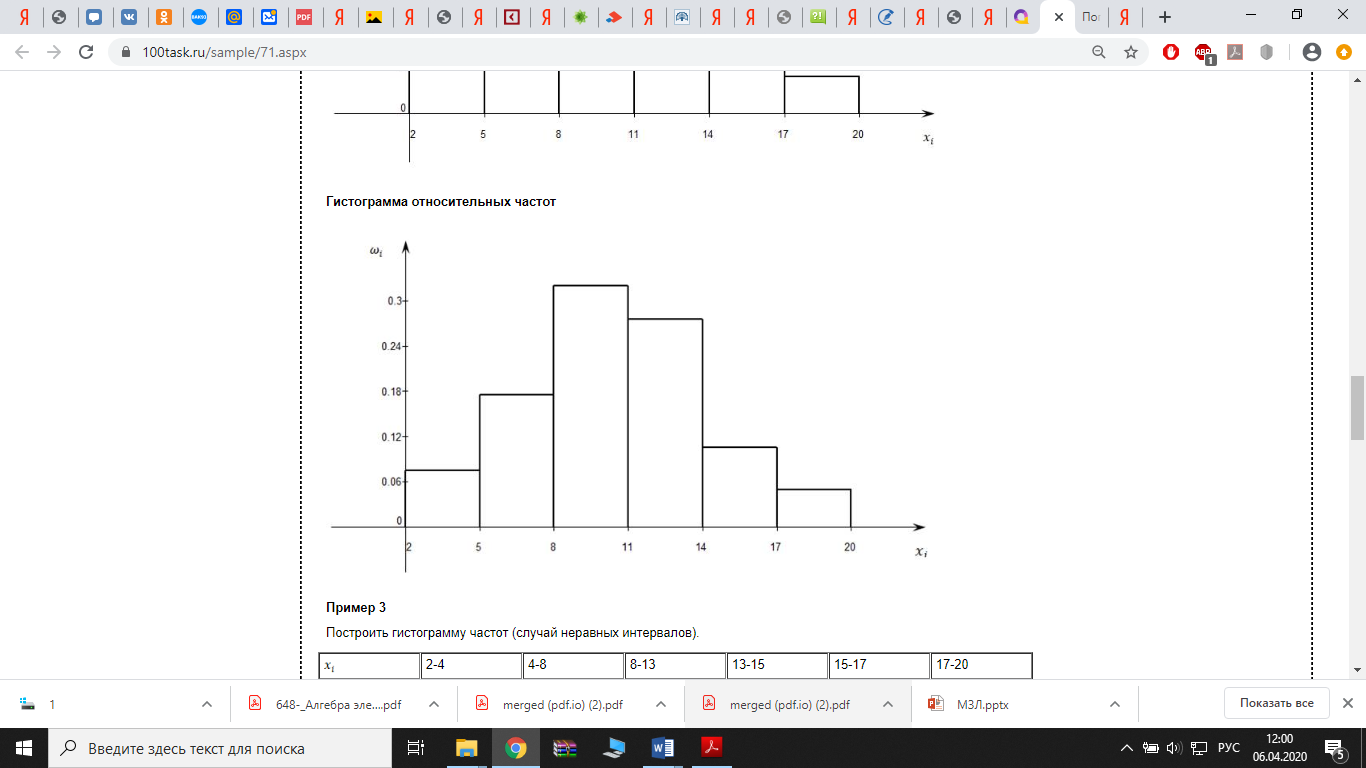
Задача 3
Построить гистограмму частот (случай неравных интервалов).
|
2-4 |
4-8 |
8-13 |
13-15 |
15-17 |
17-20 |
|
|
15 |
35 |
64 |
55 |
21 |
10 |
Вычислим плотности частоты:
|
Интервалы, |
Длина интервала, |
Плотность частоты, |
|
|
2 – 4 |
15 |
2 |
7,500 |
|
4 – 8 |
35 |
4 |
8,750 |
|
8 – 13 |
64 |
5 |
1,800 |
|
13 – 15 |
55 |
2 |
27,500 |
|
15 – 17 |
21 |
2 |
10,500 |
|
17 – 20 |
10 |
3 |
3,333 |
|
Итого |
200 |
— |
— |
Гистограмма частот
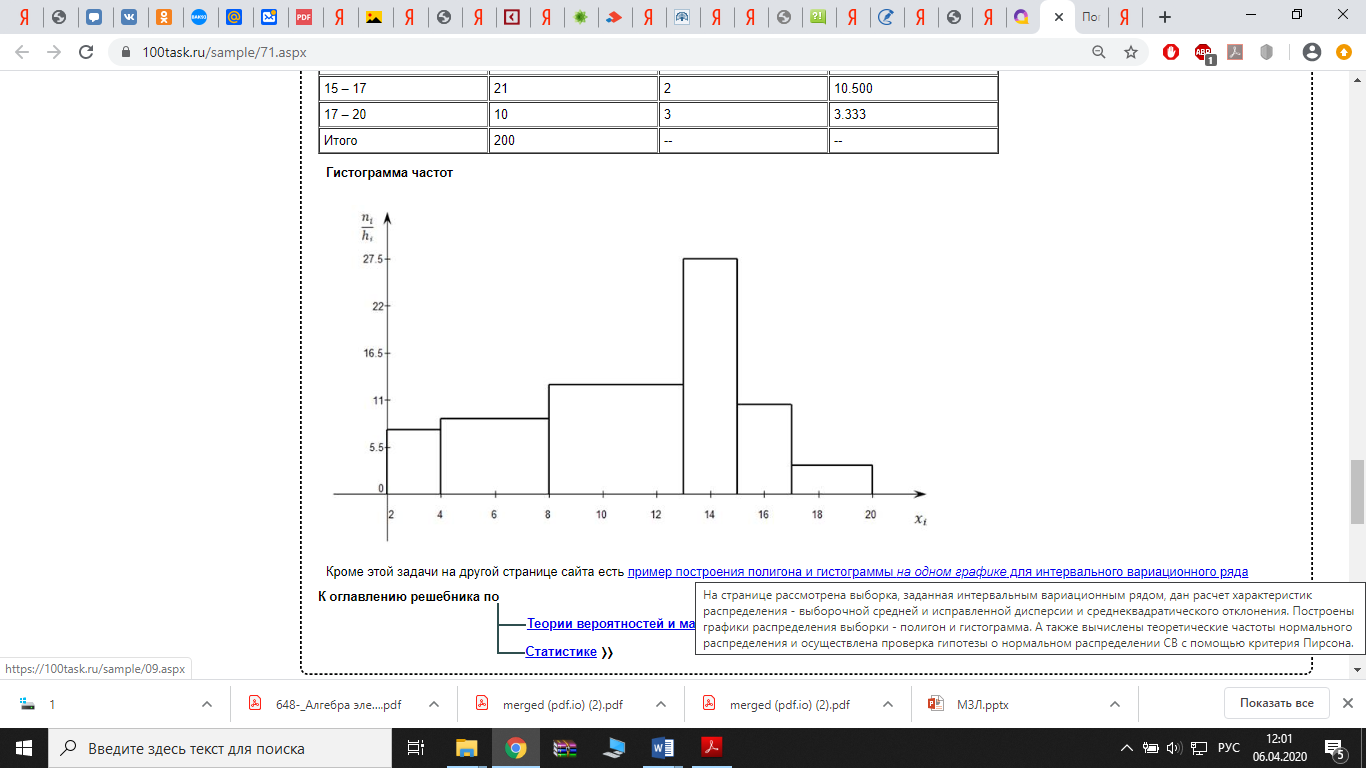
Круговая (секторная) диаграмма
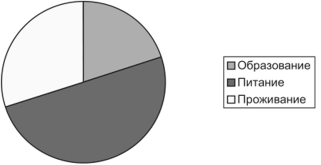
Круговая (секторная) диаграмма — это вид диаграммы, в которой площадь круга принимается за величину всей изучаемой совокупности, а площадь отдельных секторов соответствует удельному весу ее частей. Такая диаграмма требует подсчета частостей. Круговая диаграмма удобна для изображения структуры (состава) явления.
Задача 4. Построить круговую диаграмму распределения индивидуального дохода (рис. 3) на основании следующих данных: питание — 50 % дохода; образование — 20 % дохода; проживание — 30 % дохода.
Произведите конспект примера со страницы 24.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ И РЕШЕНИЯ ДОМАШНЕГО ЗАДАНИЯ.
Решите задачи из учебника Уч. пособие “Алгебра. Элементы статистики и теории вероятностей” авторов Ю.Н. Макарычева и Н.Г. Миндюк. (страница 27-28)
№1 – 8.16
№2 – 8.19
№3 – 8.21
Вопросы для повторения материала
-
Назовите формулу для нахождения относительных частот.
-
Объясните принцип построения полигона частот.
-
Объясните принцип построения полигона относительных частот.
-
Что такое гистограмма?
-
Объясните принцип построения гистограммы частот.
-
Объясните принцип построения гистограммы относительных частот.
-
Что такое круговая диаграмма?
-
Объясните принцип круговой диаграммы.
