Закон распределения дискретной случайной величины
В задачах 12.1-12.10 требуется найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение дискретной случайной величины X по заданному закону её распределения, заданному таблично (в первой строке таблицы указаны возможные значения, во второй строке – вероятности возможных значений).
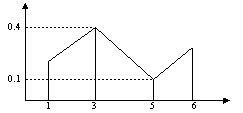
Закон распределения дискретной случайной величины можно изобразить графически. С этой целью на прямоугольной системе координат строят точки M1(x1; p1), M2(x2; p2), …, Mn(xn; pn), где xi – возможные значения случайной величины, а pi – соответствующие вероятности, и соединяют их последовательно отрезками прямых. Полученную фигуру называют многоугольником распределения. Построим многоугольник распределения дискретной случайной величины X, заданной следующим законом распределения:
| X | 1 | 3 | 5 | 6 |
| p | 0,2 | 0,4 | 0,1 | 0,3 |
Математическое ожидание:
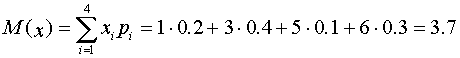
Дисперсия: 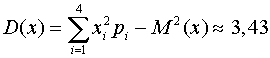 .
.
Среднее квадратическое отклонение: ![]() .
.
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 1
Построить полигон частот и
полигон относительных частот (частостей):
Решение
Вычислим относительные
частоты (частости):
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального
статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 2
Построить гистограмму
частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
Решение
Вычислим плотности
частоты:
Гистограмма частот
Кроме этой задачи на другой странице сайта есть
пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.
Пример 4
Построить кумулятивную
кривую:
Решение
Вычислим накопленные
частоты:
Кумулятивная кривая
Полигон распределения.
Для построения
полигона величина признака откладывается
на оси абсцисс, а частоты или относительные
частоты — на оси ординат. Из точек,
соответствующих значениям признака,
восстанавливаются перпендикуляры,
равные по высоте частотам. Вершины
перпендикуляров соединяются прямыми
линиями.
Для интервального
ряда ординаты, пропорциональные частоте
(или относительной частоте) интервала,
восстанавливаются перпендикулярно
оси абсцисс в точке, соответствующей
середине данного интервала.
Следующие
данные распределения рабочих в возрасте
до 24 лет по тарифным разрядам
(высококвалифицированные рабочие
сельхоз-машиностроения)15
дают возможность построить полигон
распределения (рис. 2):

Условно принято
крайние ординаты признака соединять с
серединами примыкающих интервалов (на
рис. 2 эти замыкающие линии нанесены
пунктиром). Однако для распределения,
где концентрация событий увеличивается
на концах полигона, такое изображение
может привести к ложным представлениям
о существе явления.
Кумулята.
Для графического
изображения вариационных рядов
используются также кумулятивные кривые.
При построении кумуляты, как и гистограммы,
на оси абсцисс откладываются границы
интервалов (либо значения дискретного
признака), а на оси ординат — накопленные
частоты (либо относительные частоты),
соответствующие верхним границам
интервалов. Таким образом, отличие
кумуляты от гистограммы в том, что на
графике кумуляты столбики,
пропорциональные частотам, последовательно
накладываются один на другой, так что
высота последнего столбика является
суммой высот столбиков гистограммы.
Кумулята округляет
индивидуальные значения признака в
пределах интервала и представляет
собой возрастающую ломаную линию.
Кумулята
позволяет быстро определить процент
лиц, находящихся ниже или выше заданной
величины признака. Например, по данным
табл. 3, процент семейств, в которых муж
старше cyпруги
не более чем на 5 лет, равен 65 (рис. 3, точка
А).

Вид (форма) кривых распределений.
Кривые, полученные
в результате графического представления
эмпирических данных, могут иметь
разнообразную форму. Среди них можно
выделить относительно небольшое
количество простых типов, Некоторые
возможные формы распределений приведены
на рис. 4, Анализ формы кривых иногда
помогает в выявлении внутренней, скрытой
структуры исследуемой совокупности.
Например, можно предположить, что форма
кривой обусловлена наложением двух
кривых: а и б, иначе говоря, предположить,
что существует третья скрытая переменная
(или группа переменных), детерминирующая
расчленение совокупности на две группы.
Существует множество
конкретных примеров того, как графический
анализ стимулирует дальнейшее развитие
исследовательской мысли.
Теоретическое распределение.
Сбор
эмпирической информации может быть
осуществлен двумя путями: исследованием
всей совокупности социальных объектов,
которые являются предметом изучения в
пределах, очерченных программой
социологического исследования, и
изучением лишь части этих объектов. В
первом случае исследование называется
сплошным, а множество социальных объектов
— генеральной совокупностью, во втором
исследование называется выборочным, а
выделенная часть объектов — выборкой16.
Одна из основных
задач статистики состоит в том, чтобы
по данным выборки оценить параметры
генеральной совокупности.
Гистограмма
и полигон распределения, построенные
на основу эмпирических данных выборки,
позволяют выявить лишь

приближенную
картину реального распределения в
генеральной совокупности.
При увеличении
выборочной совокупности и все большем
дроблении величины интервалов
эмпирическое распределение в виде
гистограммы или полигона все более
приближается к некоторой кривой,
называемой кривой распределения.
Если
группировочный признак является
непрерывной величиной, тo
в предельном случае при, постепенном
уменьшении величины интервала полигону
и гистограмме будет соответствовать
некоторая гладкая кривая (рис. 5).
Эта
кривая распределения, являющаяся
предельным случаем полигона данного
эмпирического распределения, называется
по установившейся терминологии кривой
плотности распределения. Обозначим
соответствующую функцию f(z).
В
терминах теории вероятностей плотность
распределения можно трактовать
следующим образом: вероятность (р) того,
что случайная величина (x)
примет значение из достаточно малого
интервала (XiXi+1),
равна произведению длины интервала на
высоту прямоугольника (f(xi)),
т. е.
![]()
Для интервала
произвольной длины суммированием этих
значений получим, что
![]()
Отсюда
приходим к определению фундаментального
понятия теории вероятностей — функции
распределения (F)
случайной величины (x),
которая по определению есть
![]()
Знание
функции
распределения дает
исчерпывающее представление о поведении
совокупности в отношении изучаемого
признака, поэтому определение типа
распределения признаков представляет
одну из задач исследования массовых
явлений.
Постройка полигона и гистограммы частот
Содержание:
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Определение
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),…, (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(W_i=frac{n_i}n)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Определение
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
(frac{n_ih}h=n_i)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Полигон частот и гистограмма частот
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Полигон частот
Пусть нам дан ряд распределения, записанный с помощью таблицы:
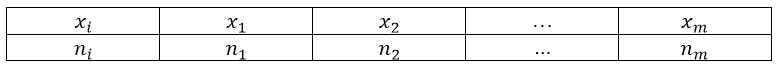
Рисунок 1.
Определение 1
Полигон частот — ломанная, которая соединяет точки $(x_m,n_m)$ ($m=1,2,dots ,m)$.
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие частоты. Полученные точки соединяют ломанной:
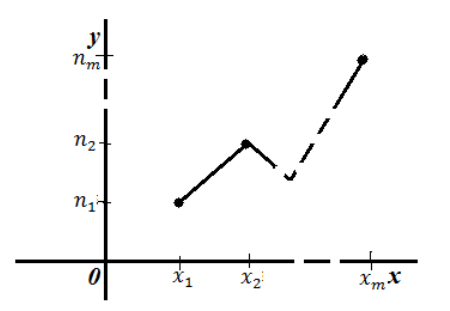
Рисунок 2. Полигон частот.
Помимо обычной частоты существует еще понятие относительной частоты.
Получаем следующую таблицу распределения относительных частот:
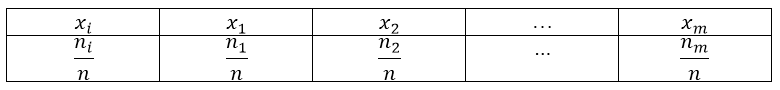
Рисунок 3.
Определение 2
Полигон относительных частот — ломанная, которая соединяет точки $(x_m,W_m)$ ($m=1,2,dots ,m)$.
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие относительные частоты. Полученные точки соединяют ломанной:
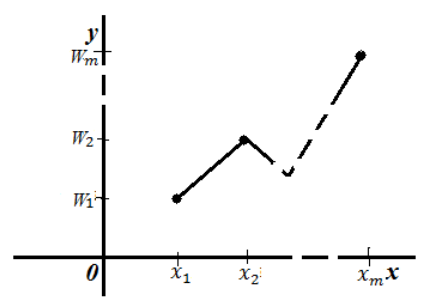
Рисунок 4. Полигон относительных частот.
Гистограмма частот
Помимо понятия полинома для непрерывных значений существует понятие гистограммы.
Определение 3
Гистограмма частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{n_i}{h}$:
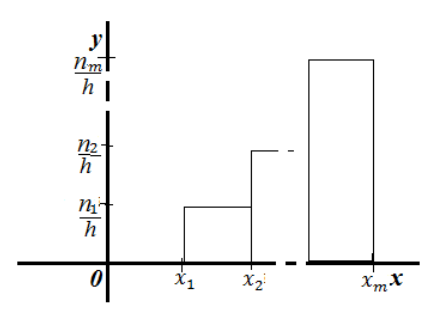
Рисунок 5. Гистограмма частот.
«Полигон частот и гистограмма частот» 👇
Заметим, что площадь одного такого прямоугольника $frac{n_ih}{h}=n_i$. Следовательно, площадь всей фигуры равна $sum{n_i}=n$, то есть равна объему выборки.
Определение 4
Гистограмма относительных частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{W_i}{h}$:
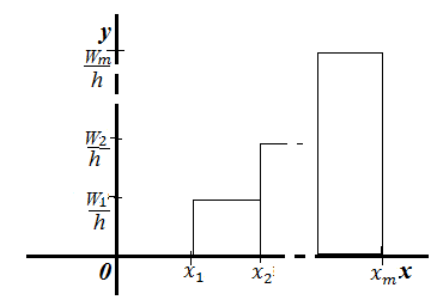
Рисунок 6. Гистограмма относительных частот.
Заметим, что площадь одного такого прямоугольника $frac{W_ih}{h}=W_i$. Следовательно, площадь всей фигуры равна $sum{W_i}=W=1$.
Примеры задачи на построение полигона и гистограммы
Пример 1
Пусть распределение частот имеет вид:

Рисунок 7.
Построить полигон относительных частот.
Решение.
Построим сначала ряд распределения относительных частот по формуле $W_i=frac{n_i}{n}$

Рисунок 8.
Получим следующий полигон относительных частот.
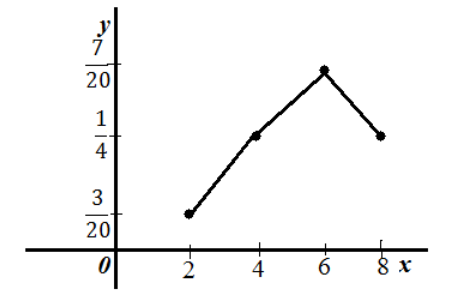
Рисунок 9.
Пример 2
Дан ряд непрерывного распределения частот:

Рисунок 10.
Решение.
Очевидно, что данном случае длина частичного интервала $h=2.$ Найдем высоты прямоугольников каждой точки разбиения.
При $x=1$: $frac{3}{2}=1,5$.
При $x=3$: $frac{5}{2}=2,5.$
При $x=6$: $frac{7}{2}=3,5.$
При $x=9$: $frac{9}{2}=4,5.$
Получаем следующую гистограмму частот:
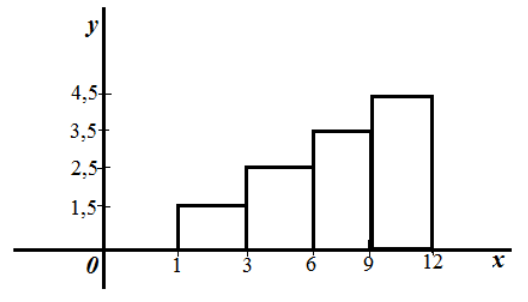
Рисунок 11.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 25.02.2023
