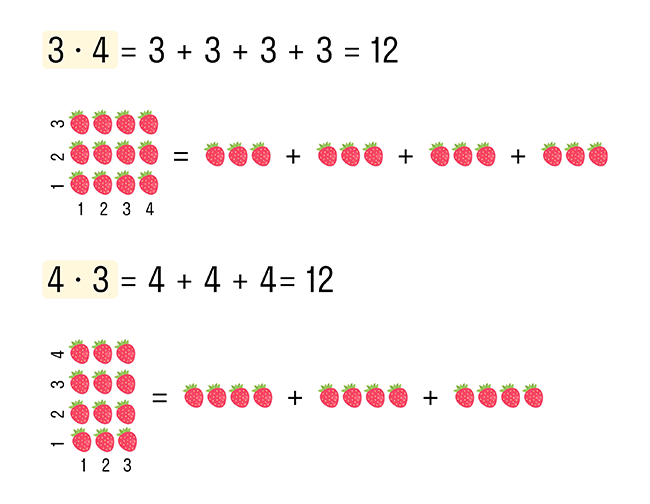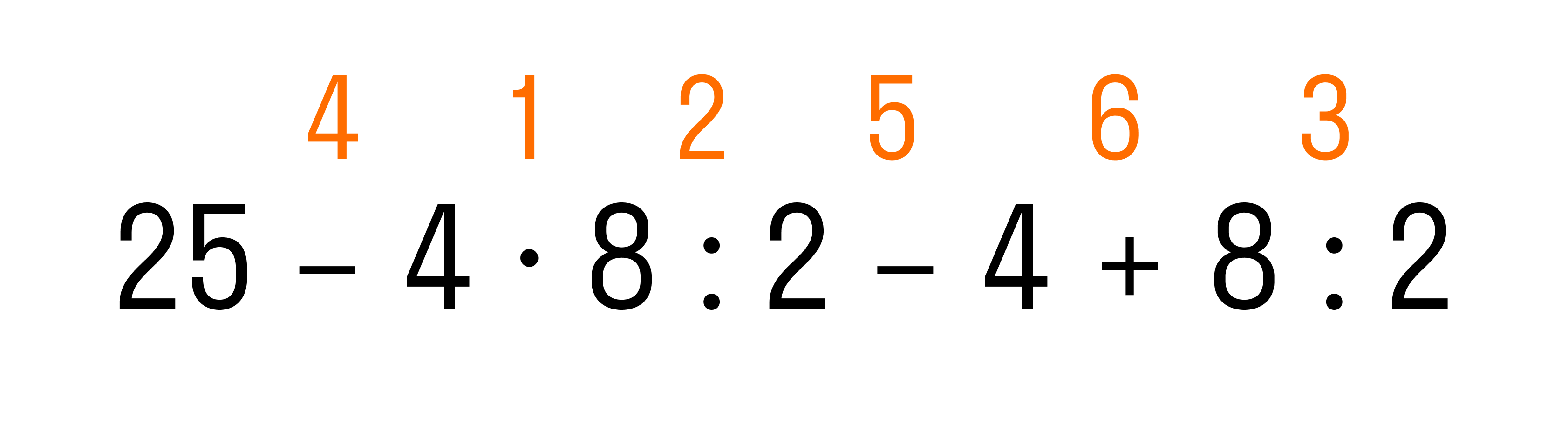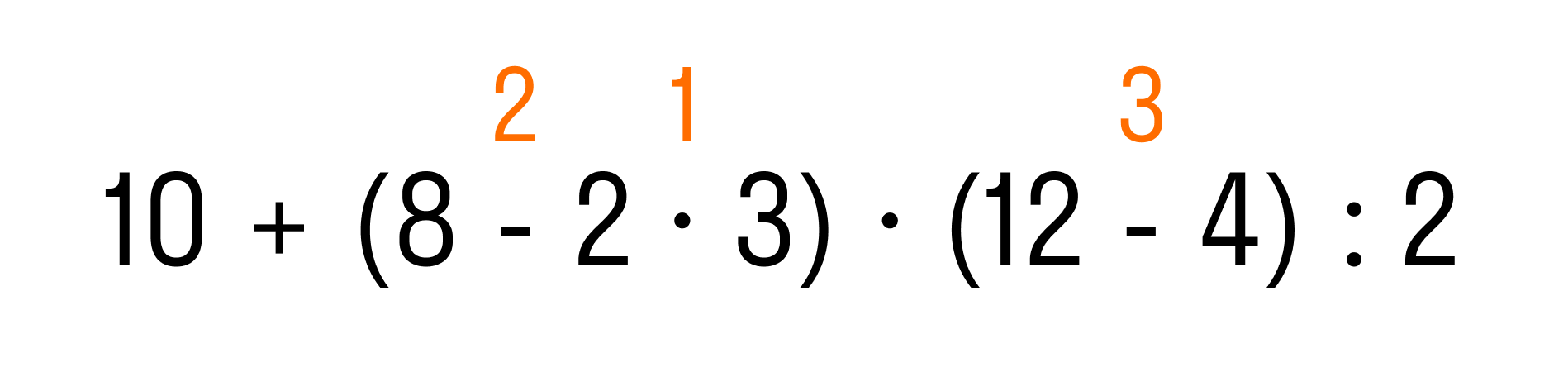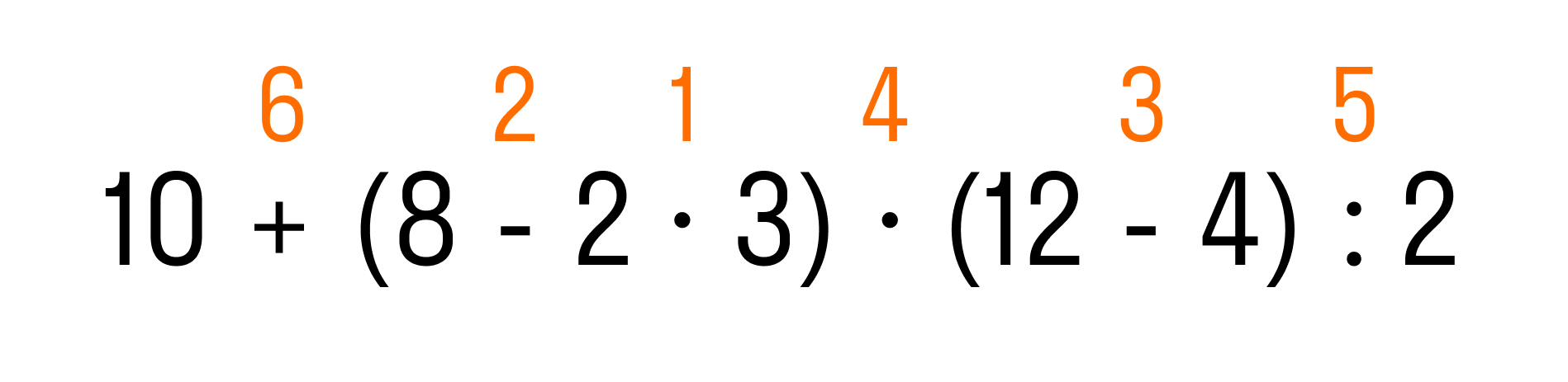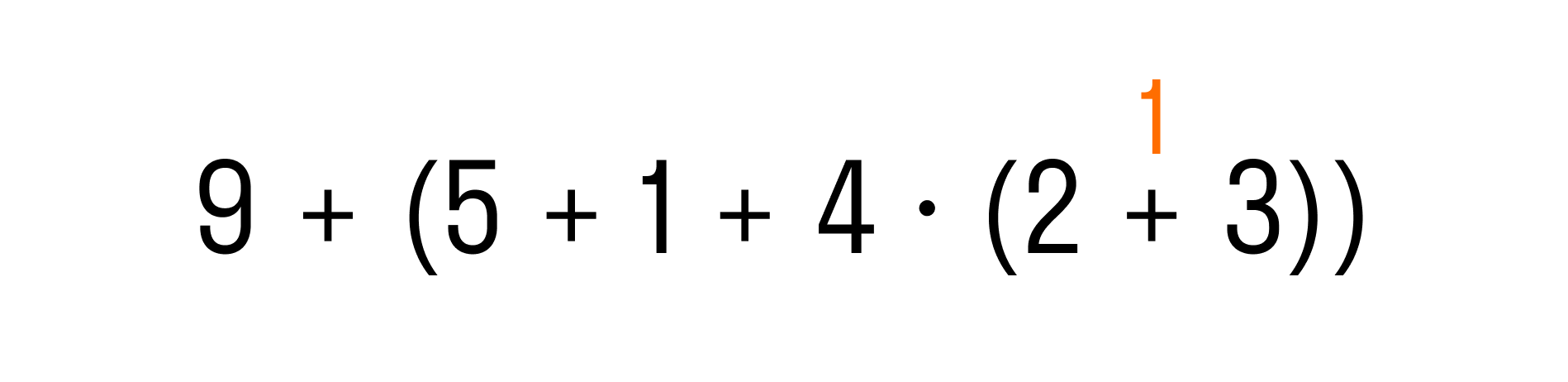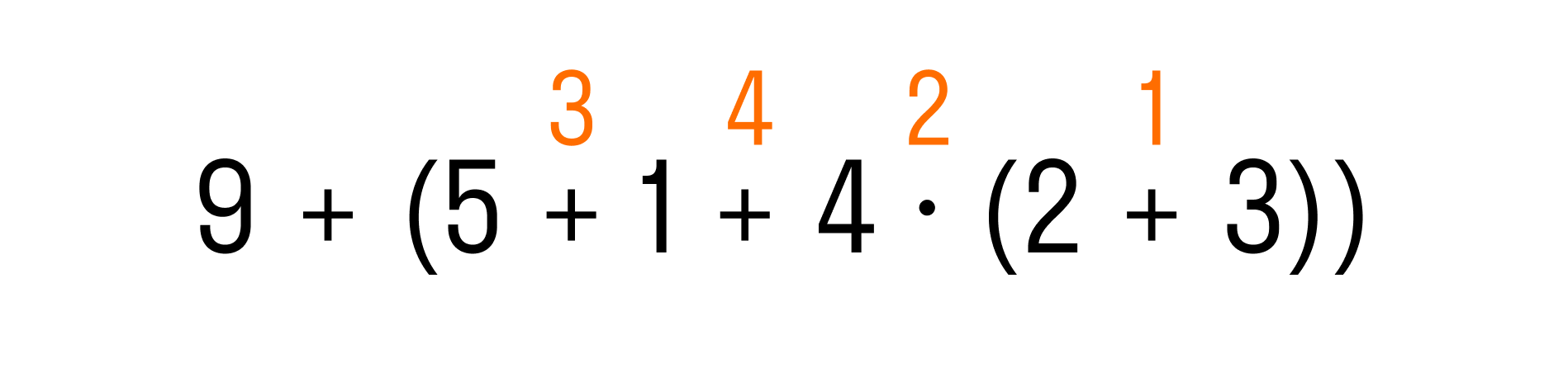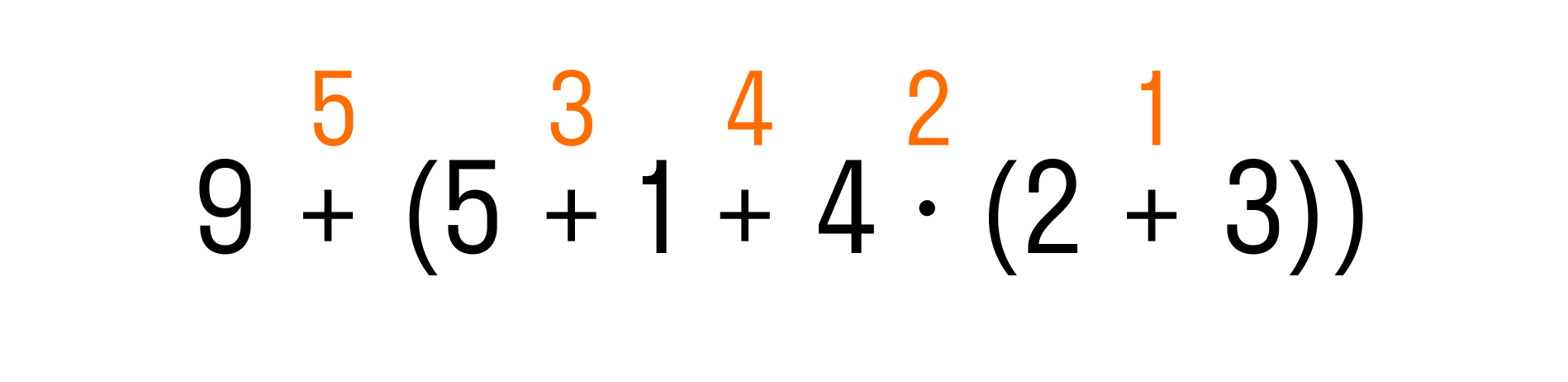Когда мы работаем с различными математическими выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий: деление и умножение, сложение и вычитание степеней и др. Когда нужно сделать расчет и преобразование или вычитание значение, очень важно соблюдать правильную очередность или расстановку этих действий. Другими словами, действия в арифметике имеют свой особый порядок выполнения. Порядок действий в математике и для любого математика крайне важен.
В этой не слишком длинной и сложной статье мы расскажем, какие действия должны делаться математически в первую очередь, а какие после (к примеру, сначала идет деление или умножение). Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения или символы, а также знаки деления, умножения, вычитания и сложения (к примеру, пять плюс ноль равно пять). Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует решать эти примеры по действиям. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах по действиям, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- Сперва мы выполняем деление и умножение, во вторую – вычитание и сложение (нужно прибавлять). Теперь понятен ответ на вопрос, что первое деление или умножение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности этого двойного правила несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро получить проверочные результаты.
Условие: вычислите, сколько будет 7−3+6.
Решение
В нашем выражении или высказывании, которое обычно решают средние классы, скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Вначале делаем минус три из семи, затем делаем плюс к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7−3+6=4+6=10
Ответ: 7−3+6=10.
Условие: в каком порядке будут выполняться вычисления в выражении 6:2·8:3?
Решение
Чтобы дать ответ на этот вопрос, что делается первым деление или умножение, перечитаем правило для выражений без кавычек (скобок), сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок того, что нужно вычесть, и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
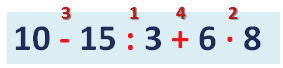
Условие: подсчитайте, сколько будет 17−5·6:3−2+4:2.
Решение
Сначала определим верный порядок действий (приоритетность), поскольку у нас здесь есть все основные компоненты арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо делить и перемножать. Что сначала деление или умножение? Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке слева направо. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:
17−5·6:3−2+4:2=17−10−2+2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17−10−2+2=7−2+2=5+2=7
Ответ: 17−5·6:3−2+4:2=7.
Пока порядок выполнения действий не заучен твердо, можно расставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
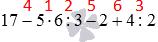
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
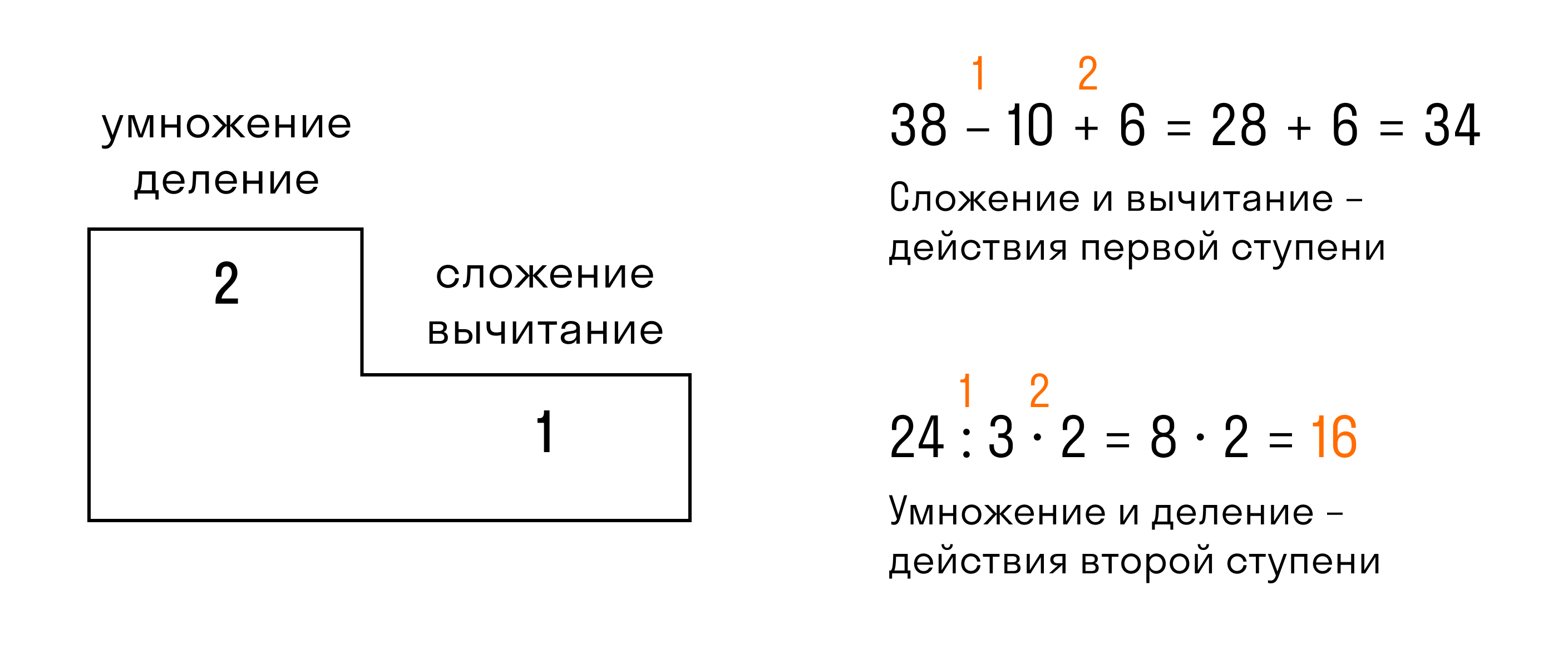
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся действия, где нужно вычитать и слагать, а ко второй – умножать и делить.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Решение примеров по действиям в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Условие: вычислите, сколько будет равно 5+(7−2·3)·(6−4):2.
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7−2·3. Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7−2·3=7−6=1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6−4=2.
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5+(7−2·3)·(6−4):2=5+1·2:2
Начнем с умножения и деления, потом выполним вычитание и получим:
5+1·2:2=5+2:2=5+1=6
На этом вычисления можно закончить.
Ответ: 5+(7−2·3)·(6−4):2=6.
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такое задание.
Условие: вычислите, сколько будет 4+(3+1+4·(2+3)).
Решение
У нас есть скобки в скобках. Начинаем с 3+1+4·(2+3), а именно с 2+3. Это будет 5. Значение надо будет подставить в выражение и подсчитать, что 3+1+4·5. Мы помним, что сначала надо умножать, а потом слагать: 3+1+4·5=3+1+20=24. Подставив найденные значения в исходное выражение, вычислим ответ: 4+24=28.
Ответ: 4+(3+1+4·(2+3))=28.
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4+(4+(4−6:2))−1)−1. Начинаем с выражения во внутренних скобках. Поскольку 4−6:2=4−3=1, исходное выражение можно записать как (4+(4+1)−1)−1. Снова обращаемся к внутренним скобкам: 4+1=5. Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Условие: найдите, сколько будет (3+1)·2+62:3−7.
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+36:3−7.
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание (слагаемое и вычитаемое).
(3+1)·2+36:3−7=4·2+36:3−7=8+12−7=13
Ответ: (3+1)·2+62:3−7=13.
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Порядок действий в математике
Какое действие выполнить в первую очередь: сложение или умножение? Простые для внимательного школьника примеры вида 2 + 2 × 2 не всякий взрослый решит правильно. Разберемся вместе, как без ошибок решать числовые выражения со скобками и без.
Решайте математические и логические задачи и примеры на ЛогикЛайк!
Выберите возраст для старта

Более 5500 увлекательных заданий для развития математических
способностей и логического мышления — в онлайн‑курсе ЛогикЛайк.
Для чего нужен порядок действий?
Большинство действий, которые мы выполняем в жизни имеют свой порядок. Согласитесь, чтобы пойти в магазин вы сначала одеваетесь, а затем выходите на улицу, а не наоборот. Так же и в математике, у арифметических действий есть своя очередность, которую необходимо соблюдать.
Вы уже решали простые примеры на сложение, вычитание, умножение или деление. Более сложные примеры называют числовыми выражениями, они содержат два, три и даже больше действий.
7 – 4 + 10
6 + 4 ∙ 5 – 3
60 – 24 : 8 + 2 × 4
Чтобы правильно решить подобные примеры, нужно знать какое действие выполняется раньше других.
Кто придумал порядок действий?
В 1560 году французский логик и математик Пьер де ла Раме в своей книге «Алгебра» впервые применил определенный способ выполнения последовательности действий.
Порядок действий в примерах и картинках
Вам задали решить длинный пример – не паникуйте, это проще простого, если знать порядок действий.
Порядок действий – это определенная последовательность выполнения цепочки арифметических действий.
В каком порядке выполнять действия?
Первыми всегда выполняются действия в скобках с учетом приоритетности. Приоритет действий: умножение или деление выполняются раньше, чем сложение или вычитание. При равном приоритете действия выполняются слева направо.
- Скобки (если они есть)
- Умножение или деление
- Сложение или вычитание
Порядок действий в выражениях без скобок
Вычислим значение выражения, применяя порядок выполнения действий.
Порядок выполнения равнозначных действий
- Умножение и деление равнозначны. Если умножение стоит слева от деления, то умножение выполняется первым. Если деление находится слева от умножения, сначала выполняется деление.
- Сложение и вычитание равнозначны. Если сложение стоит слева от вычитания, то сложение выполняется первым. Если вычитание находится слева от сложения, сначала выполняется вычитание.
Равнозначные действия выполняются по очереди слева направо.
Пример: 12 + 6 – 8
В данном выражении нет скобок и знаки равнозначные по очередности (сложение, вычитание), значит выполнять их мы будем по очереди слева направо.
12 + 6 – 8
18 – 8 = 10
Получаем результат 10.
Пример: 6 + 4 × 8 – 7
В данном выражении нет скобок, значит сначала мы будем выполнять умножение.
6 + 4 × 8 – 7
6 + 32 – 7
Когда остается два равнозначных действия, мы будем их выполнять слева направо по порядку. В данном случае сначала выполним сложение, а затем вычитание.
6 + 32 – 7
38 – 7
Получаем результат 31.
Если действия записаны в скобках, выполнение порядка действий сохраняется внутри скобок.
Как ЛогикЛайк может помочь родителям?
Выберите основную цель занятий
Порядок действий в выражениях со скобками
Пример: (4 + 3 × 2) ÷ (12 ÷ 4 – 3)
Начнем со скобок. В каждой скобке мы должны начинать с самой важной операции.
(4 + 3 × 2) ÷ (12 ÷ 4 – 3)
Если в примере две или более скобок – начинаем их решать слева направо. В левой скобке есть сложение и умножение. Начинаем с умножения, которое приоритетнее, «главнее» сложения.
(4 + 3 × 2) ÷ (16 ÷ 2 – 3)
В правой скобке в первую очередь выполним деление – оно приоритетнее, чем вычитание.
(4 + 6) ÷ (16 ÷ 2 – 3)
(4 + 6) ÷ (8 – 3)
Заканчиваем решение в каждой скобке.
(4 + 6) ÷ (8 – 3)
Остается только разделить.
10 ÷ 5 = 2
Получаем результат 2.
Решите выражения, расставляя порядок действий над знаками:
5 · 8 + 4 · 6 + 15 – 14 =
9 · 5 – 19 + 6 · 6 – 3 · 4 =
32 : 4 · 6 : 8 + 6 · 3 – 17 =
27 + 7 · 8 – 35 : 35 =
6 · 5 – 12 : 6 · 3 + 49 =
42 : 6 + 28 – 3 · 6 =
32 : 4 · 6 : 8 + 6 · 3 – 17 =
9 · 7 – 3 · 7 + 29 – 24 : 4 =
48 : 6 + 33 – 54 : 9 + 7 · 4 =
Подключайтесь к ЛогикЛайк!
Развивайте логику, интеллект и расширяйте
кругозор на сайте Logiclike.com.

Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
-
сложение (+);
-
вычитание (-);
-
умножение (*);
-
деление (:).
Операции отношения:
-
равно (=);
-
больше (>);
-
меньше (<);
-
больше или равно (≥);
-
меньше или равно (≤);
-
не равно (≠).
Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике
Привет! Это Макс, он хочет отпраздновать начало учебного года. Давай поможем Максу подготовиться к празднику
Жми на стрелки сверху, чтобы путешествовать в истории →
Макс делал домашку и потерял счёт времени. Он забыл, что Саша и Чак совсем скоро придут в гости →
Посчитай, сколько времени нужно Максу на все дела
Максу понадобится
13
12
14
15
минут, чтобы все успеть
Первое дело уже в работе! Для торта Максу в магазине нужно докупить продукты→
Максу надо докупить мармелад, сгущёнку и яйца
Cколько рублей надо заплатить Максу?
Ответ:
23 рубля
24 рубля
21 рубль
22 рубля
Макс купил муку, яйца, масло, сгущёнку и мармелад. Начинаем готовить торт! →
Рассчитай, сколько весят ингридиенты для торта
4 * 50 =
250
200
220
230
грамм весят 4 яйца
142 + 150 + 137 =
429
432
427
426
грамм весят 3 яблока
6 * 7 =
44
46
42
48
грамма весит полстакана сахара
32 : 4 =
6
4
8
10
столовых ложек муки в стакане
В домофон звонят Саша и Чак, а Макс забыл прибраться! У вас всего несколько минут
Макс уберёт книги перед тем, как пропылесосить, а посуду помоет после того, как пропылесосит. В каком порядке Макс сделает дела?
2
1
3
Супер! Благодаря тебе Макс сделал все дела.
Дальше узнаешь свои результаты →
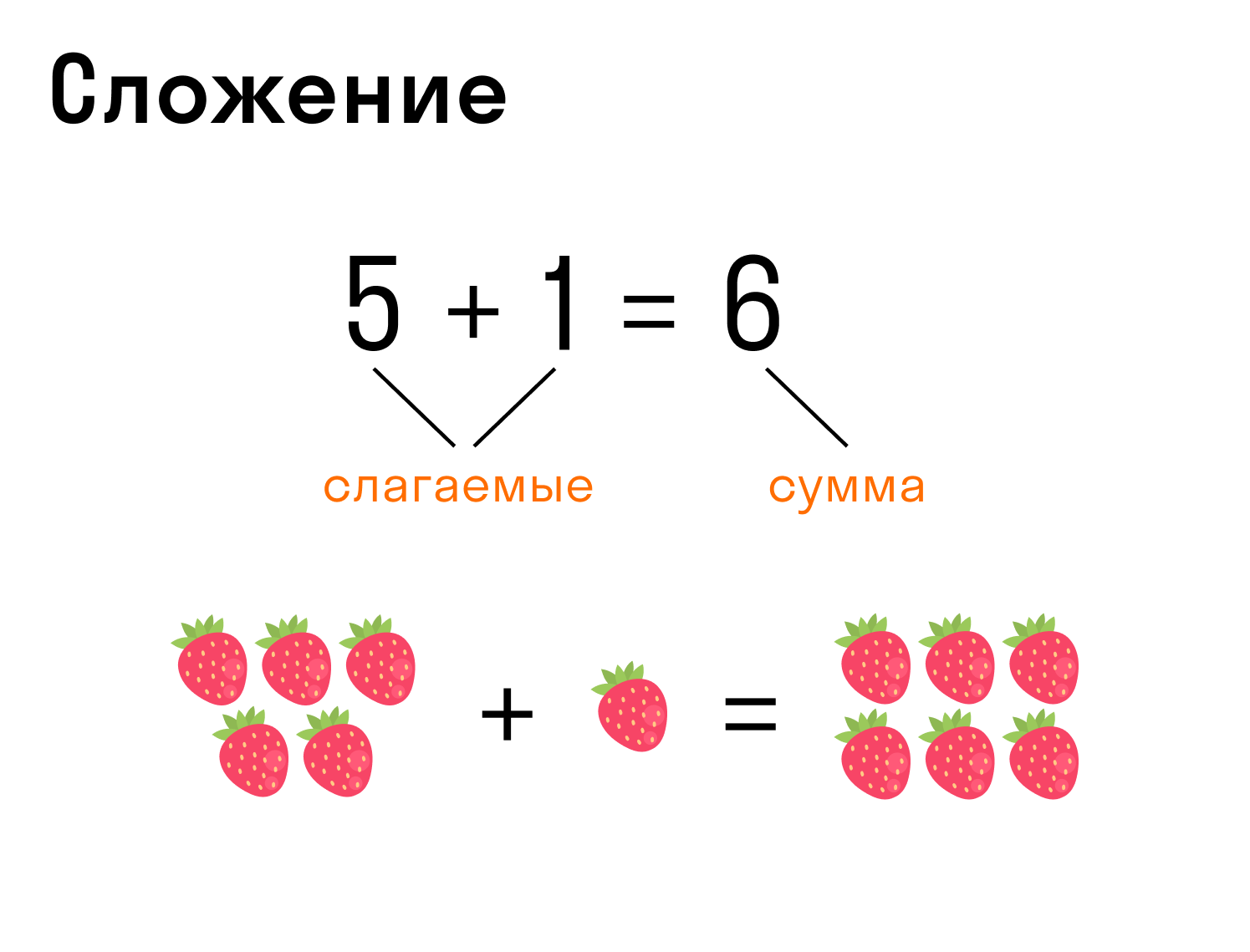
Сложение — операция, которая позволяет объединить два слагаемых.
-
Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.
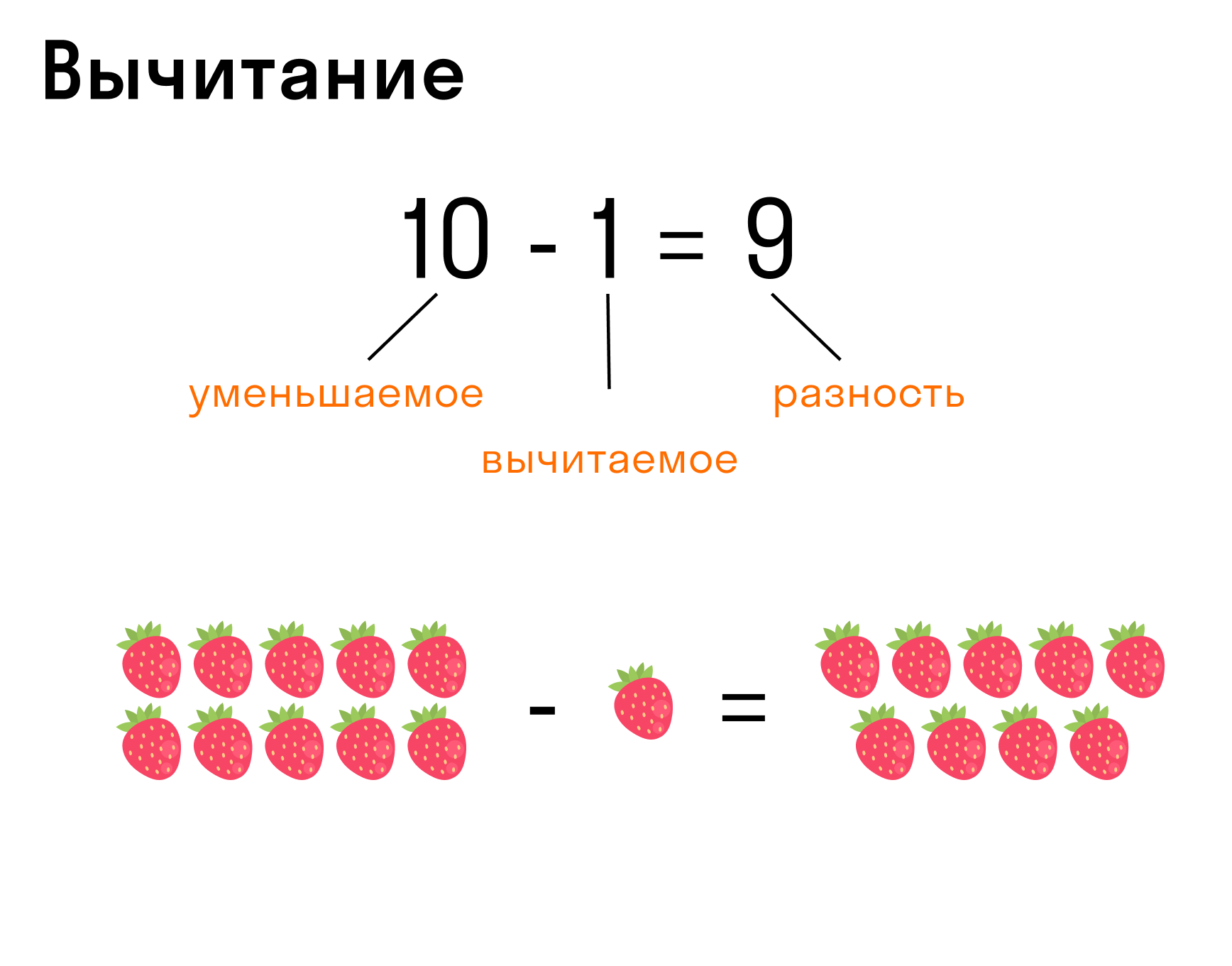
Вычитание — действие, обратное сложению.
-
Запись вычитания: 10 – 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 – 1 = 9.
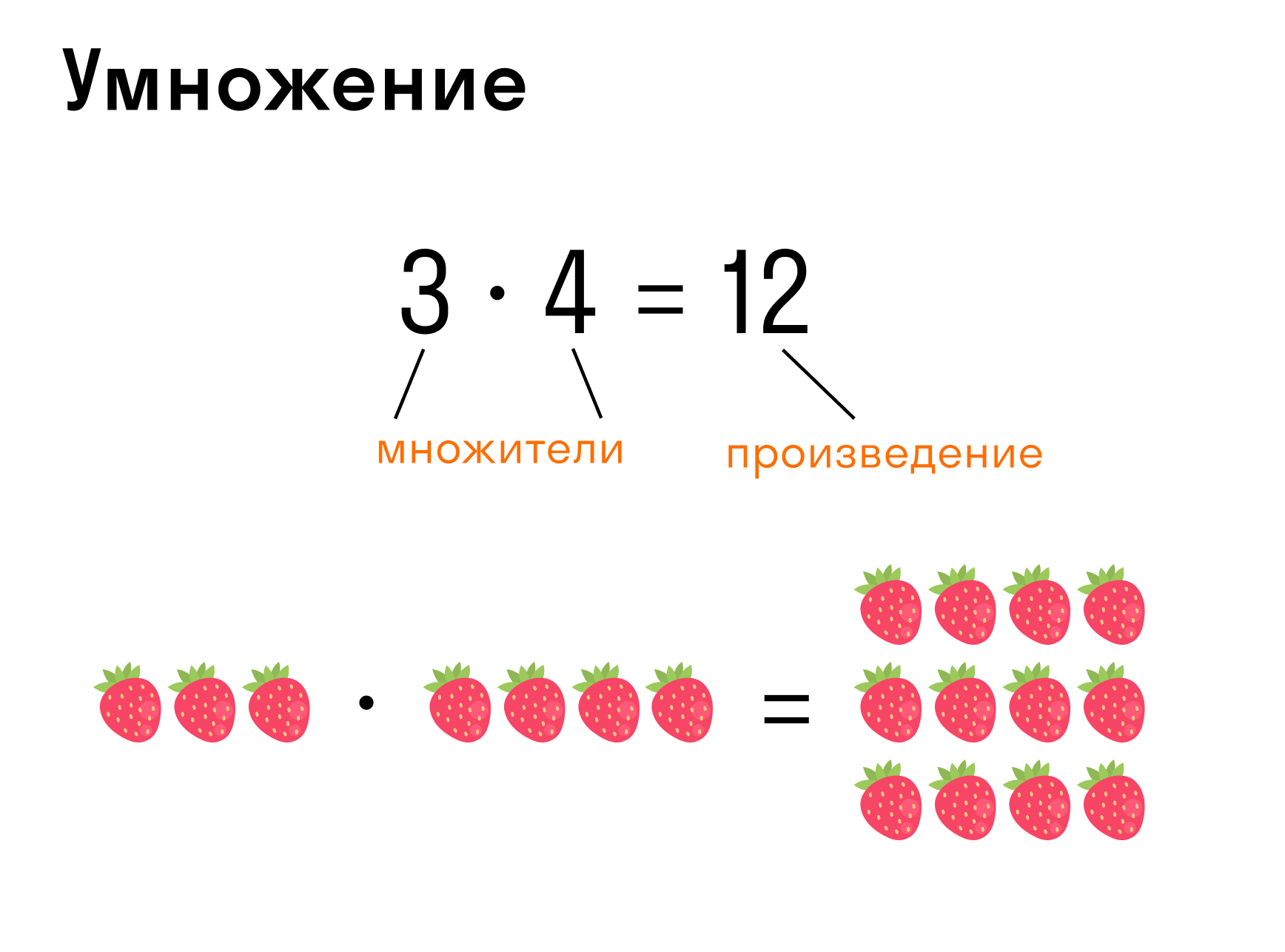
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
-
Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
-
3 × 4 = 3 + 3 + 3 + 3, то есть число 3 сложили 4 раза само с собой.
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 × 2 = 5 + 5 = 10 и 2 × 5 = 2 + 2 + 2 + 2 + 2 = 10.
Поэтому и множитель, и множимое называют сомножителями.
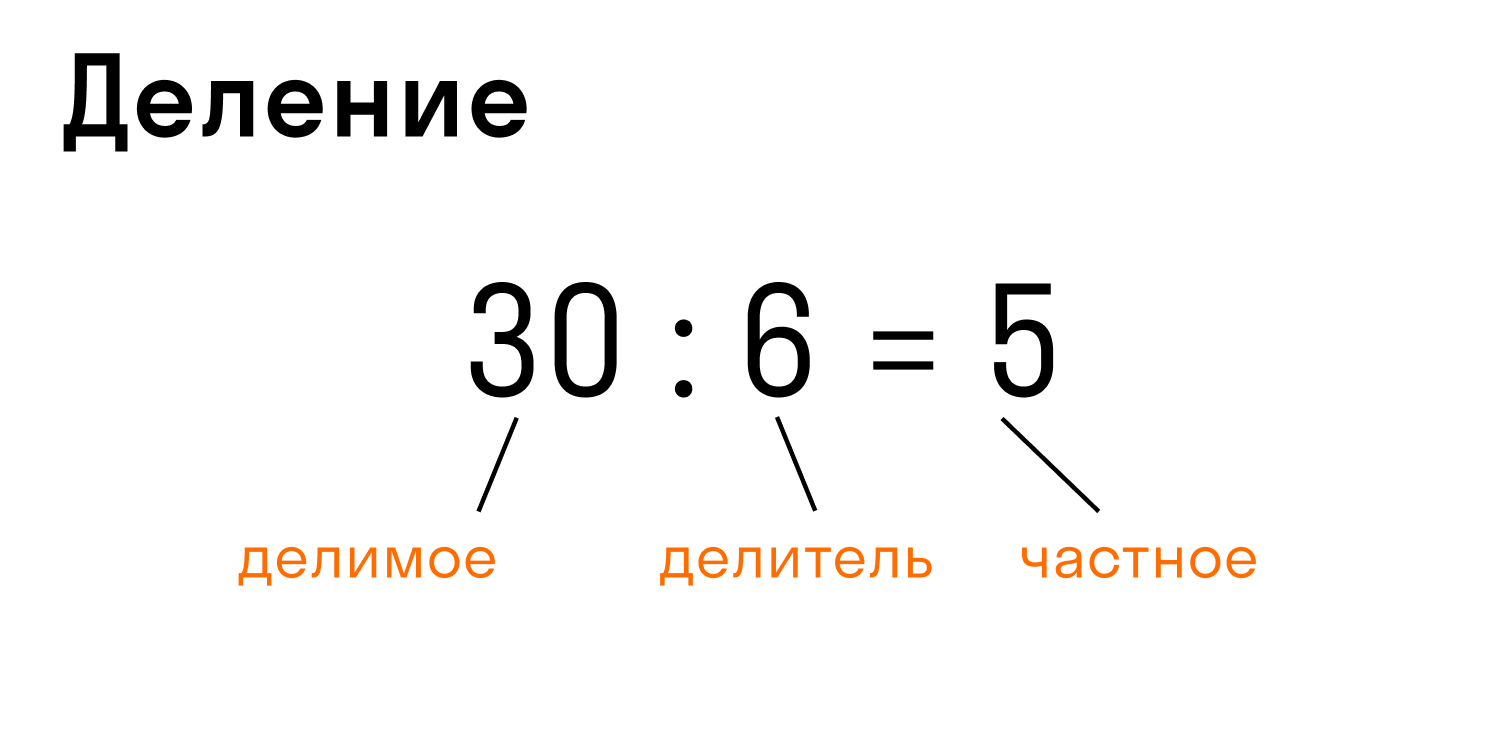
Деление — арифметическое действие обратное умножению.
-
Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5 в качестве проверки дает делимое 30.
Сложение и вычитание, умножение и деление попарно представляют обратные друг другу действия. А теперь давайте узнаем порядок выполнения арифметических действий.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
-
действия выполняются по порядку слева направо
-
сначала выполняется умножение и деление, а затем — сложение и вычитание.
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11 − 2 + 5.
Как решаем:
В нашем выражении нет умножения, деления и скобок, поэтому выполняем все действия слева направо. Сначала вычтем два из одиннадцати:
11 − 2 = 9
Затем прибавим к результату пять и в итоге получим четырнадцать:
9 + 5 = 14
Вот запись всего решения: 11 − 2 + 5 = 9 + 5 = 14.
Ответ: 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 × 7 : 5?
Как рассуждаем:
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два:
10 : 2 = 5
Теперь результат умножаем на семь:
5 × 7 = 35
И получившееся в число делим на пять:
35 : 5 = 7
Запись всего решения выглядит так: 10 : 2 × 7 : 5 = 5 × 7 : 5 = 35 : 5 = 7.
Ответ: 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
-
Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Пример 1. Вычислить: 10 + (8 − 2 × 3) × (12 − 4) : 2.
Как правильно решить пример:
Сначала определим порядок действий. Выражение содержит скобки, поэтому сначала будем выполнять действия в выражениях, которые заключены в эти скобки.
Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание.
Итак, мы определили первые три действия:
Когда выполнены все действия в скобках, по правилу дальше мы должны выполнить умножение и деление, и в последнюю очередь — сложение. Теперь мы знаем, в каком порядке решать пример:
Осталось решить пример по действиям:
- 2 × 3 = 6
- 8 − 6 = 2
- 12 − 4 = 8
- 2 × 8 = 16
- 16 : 2 = 8
- 10 + 8 = 18
На этом все действия выполнены.
Ответ: 10 + (7 − 2 × 3) × (12 − 4) : 2 = 18.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 × (2 + 3)).
Как решаем:
Для начала определим порядок действий
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 × (2 + 3). Но это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Теперь перейдем к выражению во внешних скобках. Первым действием по правилу будет умножение, а затем слева направо — две операции сложения:
И последним действием останется выполнить сложение:
Вычисляем по действиям:
-
2 + 3 = 5
-
4 × 5 = 20
-
5 + 1 = 6
-
6 + 20 = 26
-
9 + 26 = 35
Ответ: 4 + (3 + 1 + 4 × (2 + 3)) = 35.
Что мы узнали
-
Сначала мы вычисляем значения выражений в скобках (если они есть).
-
В выражениях без скобок мы выполняем действия слева направо.
-
Сложение и вычитание выполняем после умножения и деления.
-
Чтобы не запутаться, сначала стоит расставить порядок действий над примером, а затем решать его по действиям.
Закрепить на практике тему «Порядок действий» можно
на курсах по математике в Skysmart!
- Главная
- Справочники
- Справочник по математике для начальной школы
- Порядок выполнения действий
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Вычисляем:
1) 10 + 15 = 25
2) 25 – 6 = 19
3) 19 – 8 = 11
Полностью пример записываем так:
10 + 15 – 6 – 8 = 25 – 6 – 8 = 19 – 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Вычисляем:
1) 15 : 5 = 3
2) 3 • 4 = 12
3) 12 : 6 = 2
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
1)15 : 3 = 5
2) 6 • 8 = 48
3) 10 – 5 = 5
4) 5 + 48 = 53
Полностью пример записываем так:
10 – 15 : 3 + 6 • 8 = 10 – 5 + 6 • 8 = 10 – 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
1) 25 – 10 = 15
2) 15 : 3 = 5
3) 6 • 8 = 48
4) 5 + 48 = 53
Полностью пример записываем так:
(25 – 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
1) 12 : 4 = 3
2) 6 + 3 = 9
3) 18 : 9 = 2
4) 42 + 2 = 44
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Вывод:
Советуем посмотреть:
Скобки
Правило встречается в следующих упражнениях:
2 класс
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 68,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 12. Урок 4,
Петерсон, Учебник, часть 2
Страница 27. Урок 10,
Петерсон, Учебник, часть 2
Страница 42. Урок 16,
Петерсон, Учебник, часть 2
Страница 6. Урок 2,
Петерсон, Учебник, часть 3
Страница 102. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 69,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 43,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33. Урок 12,
Петерсон, Учебник, часть 1
Страница 99. Урок 38,
Петерсон, Учебник, часть 1
Страница 39. Урок 15,
Петерсон, Учебник, часть 2
Страница 67. Повторение,
Петерсон, Учебник, часть 3
Страница 71. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 75,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 9. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 81. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 115,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6. Урок 2,
Петерсон, Учебник, часть 1
5 класс
Задание 98,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 167,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 450,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 37,
Мерзляк, Полонский, Якир, Учебник
Номер 242,
Мерзляк, Полонский, Якир, Учебник
Номер 243,
Мерзляк, Полонский, Якир, Учебник
Номер 244,
Мерзляк, Полонский, Якир, Учебник
Номер 259,
Мерзляк, Полонский, Якир, Учебник
Номер 261,
Мерзляк, Полонский, Якир, Учебник
Номер 456,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 18,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 73,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 85,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 373,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 400,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 411,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 413,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 422,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 425,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 454,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Определение
Арифметика — это часть математики, которая занимается работой с числами.
Практически все умеют вычислять значения простых арифметических выражений, включающих сложение, вычитание, умножение или деление. Но при вычислении более сложных выражений, где есть два, три или более действия, многие испытывают затруднения в порядке выполнения в математике.
При работе с формулами и примерами, которые содержат цифры, переменные или буквы, необходимо выполнять правильный алгоритм.
Чтобы получить верный результат, необходимо выполнять действия в математике в определенной последовательности, то есть соблюдая правильный порядок.
Алгоритм выполнения действий первой и второй ступени
Во многих справочниках порядок арифметических действий делится на первоочередные и второстепенные. Чтобы понять это, необходимо сформулировать правило более точно.
К первоочередным относят сложение и вычитание, ко второй ступени относят деление и умножение.
Точнее записать это правило можно следующим образом:
- сначала выполнить умножение и деление в порядке слева направо;
- далее выполняем сложение и вычитание в том же порядке.
Рассмотрим несколько простых примеров на умножение и деление, сложение и вычитание с числовыми или переменными значениями. Также подробно рассмотрим формулы со скобками, содержащие степени, корни и пр.
Основной порядок выполнение действий для простых выражений
Для простых примеров, не имеющих скобок, существует единый порядок выполнения:
- вычисления выполняются слева направо;
- сначала делаем умножение и деление;
- затем выполняем сложение или вычитание.
Рассмотрим простейшие примеры математического порядка в выражениях с простыми вычислениями, которые легко можно сделать в уме, то есть без использования записи.
Пример 1
Поскольку в данном примере нет скобок, отсутствуют умножение и деление, поэтому выполнение действия производим по единому правилу.
Решение:
- из 7 вычитаем 3 (7 — 3 = 4);
- прибавляем 6 (4 + 6 = 10).
В итоге получается следующее выражение: 7 — 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10
Пример 2
Условие: необходимо вычислить выражение 6 : 2 ⋅ 8 : 3.
Порядок выполнения заключается в применении правил для примеров без скобок. Используется стандартный порядок вычисления, то есть слева направо.
Решение:
- делим 6 на 2 (6 : 2 = 3);
- умножаем результат на 8 (3 ⋅ 8 = 24);
- результат делим на 3 (24 : 3 = 8).
Получаем следующее: 6 : 2 ⋅ 8 : 3 = 3 ⋅ 8 : 3 = 24 : 3 = 8
Ответ: 6 : 2 ⋅ 8 : 3 = 8
Пример 3
Условие: необходимо вычислить, сколько будет 17 − 5 ⋅ 6 : 3 − 2 + 4 : 2.
В данном выражении присутствуют различные виды арифметических действий, включая умножение, деление, деление, вычитание.
Поэтому порядок в математике в данном примере будет следующий:
- выполняем деление и умножение в порядке слева направо;
- выполняем сложение и вычитание в обычном порядке.
Решение:
- 5 умножаем на 6 (5 ⋅ 6 = 30);
- делим 30 на 3 (30 : 3 =10);
- делим 4 на 2 (4 : 2 = 2);
- подставляем полученные цифры в исходное выражение (17 — 10 — 2 + 2 = 7).
В итоге расширенное решение данного примера выглядит следующим образом:
17 − 5 ⋅ 6 : 3 − 2 + 4 : 2 = 17 — 30 : 3 — 2 + 4 : 2 = 17 — 10 — 2 + 2 = 17 — 10 — 2 + 2 = 7 — 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 ⋅ 6 : 3 − 2 + 4 : 2 = 7
Если учеником порядок выполнения еще не усвоен, допускается использовать сверху цифры, полученные в результате промежуточных вычислений.
Правила выполнения действий для примеров с буквенными составляющими
Когда в выражении присутствуют буквы, применяется аналогичный порядок вычисления:
- делаем умножение и деление;
- выполняем сложение и вычитание.
Пример 4
Условие: необходимо обсчитать выражение 5х + 3х — 1х.
Порядок действий:
- выполняем сложение;
- делаем вычитание.
Решение:
- складываем 5х и 3х (5х + 3х = 8х);
- вычитаем 1х (8х — 1х = 7х).
В целом решение выглядит следующим образом: 5х + 3х — 1 = 8х — 1х = 7х
Ответ: 5х + 3х — 1х = 7х
Варианты записи процесса вычисления выражений
Процесс вычисления можно записывать несколькими способами.
Первый способ:
- Каждое действие записывается отдельно под своим номером по примеру.
- После выполнения последнего шага ответ обязательно сохраняется в исходном примере.
Примеры 5 — 6
Условие: необходимо вычислить выражение 50 — 23 + 2 ⋅ 4 — 30 : 6.
Решение:
2 ⋅ 4 = 8
30 : 6 = 5
50 — 23 = 27
27 + 8 = 35
35 — 5 = 30
Ответ: 50 — 23 + 2 ⋅ 4 — 30 : 6 = 30
При подсчете результатов операций с использованием двузначных и трехзначных чисел обязательно указывайте свои расчеты в соответствующей графе.
Условие: вычислите значение выражения 324 — 42 + 20 : 4 — 42
Решение:
20 : 4 + 5
324 — 42 = 282
282 + 5 = 287
287 — 42 = 245
Ответ: 324 — 42 + 20 : 4 — 42 = 245
Второй способ называется строковой записью, когда все расчеты выполняются точно в таком же порядке, но результаты записываются сразу после знака равенства.
Порядок действий в математике со скобками
Необходимо запомнить, если выражение содержит круглые скобки, порядок действий в скобках в математике немного изменяется:
- Действия внутри круглых скобок выполняются в первую очередь.
- Внутри скобок последовательность операций такая же, как и в примерах без скобок.
Действия в скобках делаем также в соответствии с порядком для простых примеров, то есть слева направо.
Пример 7
Условие: необходимо вычислить значение следующего выражения 25 — 3 + (6 ⋅ 3 — 12) — 7.
Используем порядок действий в математике со скобками:
- сначала выполняем работу в скобках;
- далее идем последовательно слева направо.
Решение:
- выполняем умножение в скобках, а затем вычитание (6 ⋅ 3 — 12 = 18 — 12 = 6);
- делаем последовательную работу за скобками (25 — 3 + 6 — 7 = 22 + 6 — 7 = 28 — 7 = 21).
В итоге решение данного выражения выглядит следующим образом:
25 — 3 + (6 ⋅ 3 — 12) — 7 = 25 — 3 + (18 — 12) — 7 = 25 — 3 + 6 — 7 = 22 + 6 — 7 = 28 — 7 = 21.
Ответ: 25 — 3 + (6 ⋅ 3 — 12) — 7 = 21
Если внутри круглых скобок есть еще несколько скобок, действия сначала выполняются внутри вложенных (внутренних) скобок. Для этого достаточно последовательно использовать основной принцип выполнения в выражениях со скобками.
Пример 8
Условие: вычислите значение выражения 60 — 2 ⋅ (30 — (7 + 3 ⋅ 4)) + 15.
Решение:
60 — 2 ⋅ (30 — (7 + 3 ⋅ 4)) + 15 = 60 — 2 ⋅ (30 — (7 + 12)) + 15 = 60 — 2 ⋅ (30 — 19) + 15 = 60 — 2 ⋅ 11 + 15 = 60 — 22 + 15 = 38 + 15 = 53
Ответ: 60 — 2 ⋅ (30 — (7 + 3 ⋅ 4)) + 15 = 53
Нет времени решать самому?
Наши эксперты помогут!
Процедура упрощения
Если пример содержит числовое или буквенное выражение в круглых скобках, которое нужно возвести в степень, то необходимо следовать таким правилам:
- Сначала делаем все вычисления внутри скобок.
- Затем вычисляем все скобки слева направо (от начала до конца примера).
- Все остальное делаем как обычно.
Пример 9
Условие: необходимо вычислить значение выражения 2³ ⋅ (4² − 12).
Выполняем вычисления в соответствие с порядком арифметических действий:
- рассчитываем значение в скобках;
- выполняем умножение.
Решение:
4² − 12 = 16 — 12 = 4
2³ ⋅ 4 = 8 ⋅ 4 = 32
Ответ: 2³ ⋅ (4² − 12) = 32
Порядок выполнения действий в сложных выражениях
Числовые и переменные примеры могут содержать символы различных арифметических операций. При преобразовании и вычислении значений таких примеров, все шаги выполняются в определенном порядке, который необходимо соблюдать.
Рассмотрим пример.
Пример 10
Рассчитайте значение 5 + (7 — 2 · 3) · (6 — 4) : 2.
Пример содержит круглые скобки, поэтому сначала выполним операции в заключенных в эти скобки.
- Начнем решение с выражения 7 − 2 · 3. В нем нужно сначала умножить, а потом вычесть: 7 − 2 · 3 = 7 − 6 = 1.
- Переходим ко второму выражению в скобках 6 — 4. Здесь только одно действие — вычитание: 6−4 = 2.
- Подставляем полученные значения в исходное выражение:
5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2 : 2.
В полученном значении сначала выполняем умножение и деление слева направо, а затем вычитание:
5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1= 6.
Все выполнено, мы сохранили следующий порядок их выполнения: 5 + (7 − 2 · 3) · (6 − 4) : 2.
Краткое решение: 5 + (7 −2 · 3) · (6 − 4) : 2 = 5 + 1 · 2 : 2 = 5 + 1 = 6.
Ответ: 5 + (7 — 2 · 3) · (6 — 4) : 2 = 6
Если ученик затрудняется в выполнении порядка арифметических действий, необходимо потренироваться на простейших примерах, которые содержат только сложение и вычитание. Только затем уже переходить к выражениям с умножением и делением.
Только после полного усвоения правил выполнения действий для простейших арифметических заданий, можно приступать к вычислению более сложных примеров со скобками.
Вычисление выражений, содержащих несколько скобок, возведение в степень или буквенные значения будет доступно только после того, как ученик легко будет справляться с простыми примерами.