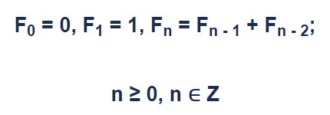Как составить последовательность фибоначчи - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 декабря 2022 года; проверки требуют 33 правки.

Черепица с квадратами, длина сторон которых является последовательными числами Фибоначчи: 1, 1, 2, 3, 5, 8, 13 и 21

Спираль Фибоначчи: приближение золотой спирали, созданной путём рисования круговых дуг, соединяющих противоположные углы квадратов в мозаике Фибоначчи;^[1] (см. предыдущее изображение)

Чи́сла Фибона́ччи (вариант написания — Фибона́чи^[2]) — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … (последовательность A000045 в OEIS),

в которой первые два числа равны 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел^[3]. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи)^[4].

Правда, в некоторых книгах, особенно в старых^{[каких?]}, член $F_{0}$ , равный нулю, опускается — тогда последовательность Фибоначчи начинается с ${displaystyle F_{1}=F_{2}=1}$ ^[5]^[6].

Говоря более формально, последовательность чисел Фибоначчи ${displaystyle {F_{n}}}$ задаётся линейным рекуррентным соотношением:

${displaystyle F_{0}=0,quad F_{1}=1,quad F_{n}=F_{n-1}+F_{n-2}}$

где

{displaystyle ngeqslant 2, nin mathbb {Z} }

Иногда числа Фибоначчи рассматривают и для отрицательных значений как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. Соответственно, члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: ${displaystyle F_{n}=F_{n+2}-F_{n+1}}$ :

n	…	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10	…
$F_{n}$	…	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55	…

Легко заметить, что ${displaystyle F_{-n}=(-1)^{n+1}F_{n}}$ .

Происхождение

Количество пар кроликов образуют последовательность Фибоначчи

Последовательность Фибоначчи была хорошо известна в древней Индии^[7]^[8]^[9], где она применялась в метрических науках (просодии, другими словами — стихосложении) намного раньше, чем стала известна в Европе^[8]^[10]^[11].

Образец длиной n может быть построен путём добавления S к образцу длиной n − 1, либо L к образцу длиной n − 2 — и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности^[9]. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Книга абака» (1202)^[12]^[13]. Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, где условия таковы: изначально дана новорождённая пара кроликов (самец и самка); со второго месяца после своего рождения кролики начинают спариваться и производить новую пару кроликов, причём уже каждый месяц; кролики никогда не умирают^[14]^[15], — а в качестве искомого выдвигает количество пар кроликов через год.

В начале первого месяца есть только одна новорождённая пара (1).
В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1).
В конце второго месяца первая пара рождает новую пару и опять спаривается (2).
В конце третьего месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара только спаривается (3).
В конце четвёртого месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5).

В конце -го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количеству новорождённых пар, которых будет столько же, сколько пар было два месяца назад, то есть ${displaystyle F_{n}=F_{n-2}+F_{n-1}}$ ^[16].
Возможно, эта задача также оказалась первой, моделирующей экспоненциальный рост популяции.

Название «последовательность Фибоначчи» впервые было использовано теоретиком XIX века Эдуардом Люка^[17].

Формула Бине

Формула Бине выражает в явном виде значение $F_{n}$ как функцию от n:

$F_{n}={frac {left({frac {1+{sqrt {5}}}{2}}right)^{n}-left({frac {1-{sqrt {5}}}{2}}right)^{n}}{sqrt {5}}}={frac {varphi ^{n}-(-varphi )^{-n}}{varphi -(-varphi )^{-1}}}={frac {varphi ^{n}-(-varphi )^{-n}}{2varphi -1}},$

где $varphi ={frac {1+{sqrt {5}}}{2}}$ — золотое сечение и varphi и ${displaystyle (-varphi )^{-1}=1-varphi }$ являются корнями характеристического уравнения $x^{2}-x-1=0.$
Вообще, аналогичная формула существует для любой линейной рекуррентной последовательности, какой служит и последовательность Фибоначчи.

Обоснование

^[18]

Преобразуем характеристическое уравнение ${displaystyle x^{2}-x-1=0}$ к виду ${displaystyle x^{2}=x+1,}$ умножим обе части на : ${displaystyle x^{3}=x^{2}+x}$ — и заменим в этой сумме $x^{2}$ на x+1 , что мы можем сделать в силу характеристического уравнения. Получим ${displaystyle x^{3}=x^{2}+x=(x+1)+x=2x+1.}$ Затем продолжим так же умножать на и преобразовывать $x^{2}$ , следуя первоначальному уравнению:

${displaystyle {begin{aligned}x^{4}&=2x^{2}+x=2(x+1)+x=\&=3x+2,\x^{5}&=3x^{2}+2x=3(x+1)+2x=\&=5x+3,\x^{6}&=5x^{2}+3x=5(x+1)+3x=\&=8x+5,\x^{7}&=8x^{2}+5x=8(x+1)+5x=\&=13x+8,\&cdots end{aligned}}}$

Таким образом образуется общее уравнение: ${displaystyle x^{n}=F_{n}x+F_{n-1}.}$ Чтобы это уравнение обратить в верное равенство и отсюда выразить сами числа Фибоначчи, нужно подставить корни varphi и ${displaystyle -varphi ^{-1}colon }$

${displaystyle {begin{cases}varphi ^{n}=F_{n}varphi +F_{n-1},\(-varphi )^{-n}=-F_{n}varphi ^{-1}+F_{n-1},end{cases}}}$

${displaystyle varphi ^{n}-(-varphi )^{-n}=F_{n}[varphi -(-varphi )^{-1}],qquad varphi ^{n}+(-varphi )^{-n}cdot varphi ^{2}=F_{n-1}(1+varphi ^{2}),}$

${displaystyle color {Black}{tfrac {1}{sqrt {5}}}left(({tfrac {1+{sqrt {5}}}{2}})^{n}-({tfrac {1-{sqrt {5}}}{2}})^{n}right)=F_{n},qquad {tfrac {1}{sqrt {5}}}left(({tfrac {1+{sqrt {5}}}{2}})^{n-1}-({tfrac {1-{sqrt {5}}}{2}})^{n-1}right)=F_{n-1}.}$

Следствие и обобщение

Из формулы Бине следует, что для всех число $F_{n}$ есть округление ${displaystyle {frac {varphi ^{n}}{sqrt {5}}},}$ то есть ${displaystyle F_{n}=leftlfloor {frac {varphi ^{n}}{sqrt {5}}}rightrceil .}$
В частности, при справедлива асимптотика ${displaystyle F_{n}sim {frac {varphi ^{n}}{sqrt {5}}}.}$

Формула Бине может быть аналитически продолжена следующим образом:

$F_{z}={frac {1}{sqrt {5}}}left(varphi ^{z}-{frac {cos {pi z}}{varphi ^{z}}}right).$

При этом соотношение $F_{z+2}=F_{z+1}+F_{z}$ выполняется для любого комплексного числа z.

Тождества

Иллюстрация формулы для суммы квадратов первых n чисел Фибоначчи^[19]

${displaystyle F_{1}+F_{2}+F_{3}+dots +F_{n}=F_{n+2}-1.}$ ^[20]

Доказательство

Докажем формулу индукцией по n:

База индукции:

${displaystyle F_{0}=F_{2}-1=0.}$

Шаг индукции: пусть утверждение для верно:

${displaystyle F_{1}+F_{2}+F_{3}+...+F_{n}=F_{n+2}-1.}$

Тогда надо доказать утверждение для

${displaystyle F_{1}+F_{2}+F_{3}+...+F_{n}+F_{n+1}=F_{n+3}-1.}$

Раскладываем ${displaystyle F_{n+3}}$

на ${displaystyle F_{n+2}}$

и ${displaystyle F_{n+1}colon }$

${displaystyle F_{1}+F_{2}+F_{3}+...+F_{n}+F_{n+1}=F_{n+2}+F_{n+1}-1}$

Сокращаем обе части на ${displaystyle F_{n+1}colon }$

${displaystyle F_{1}+F_{2}+F_{3}+...+F_{n}=F_{n+2}-1,}$

что и требовалось доказать. ∎

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}=F_{2n}.}$ ^[20]^[21]

Доказательство

Докажем формулу индукцией по n:

База индукции:

${displaystyle F_{1}=F_{2}=1.}$

Шаг индукции: Пусть утверждение для верно:

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}=F_{2n}.}$

Тогда надо доказать утверждение для

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}+F_{2n+1}=F_{2n+2}.}$

Раскладываем ${displaystyle F_{2n+2}}$

на ${displaystyle F_{2n+1}}$

и ${displaystyle F_{2n}colon }$

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}+F_{2n+1}=F_{2n+1}+F_{2n}.}$

Сокращаем обе части на ${displaystyle F_{2n+1}colon }$

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}=F_{2n}.}$

что и требовалось доказать. ∎

${displaystyle F_{2}+F_{4}+F_{6}+dots +F_{2n}=F_{2n+1}-1.}$ ^[20]^[22]

Это тождество можно доказать вычитанием первого из второго: ${displaystyle {begin{alignedat}{2}(F_{1}+F_{2}+dots +F_{{color {Red}2}n})-(F_{1}+F_{3}+dots +F_{2n-1})&=F_{{color {Red}2}n+2}-1-F_{2n},\F_{2}+F_{4}+dots +F_{2n}&=F_{2n+1}-1.\end{alignedat}}}$

И более общие формулы:

где матрицы имеют размер

и где i — мнимая единица.

$(-1)^{n}=F_{n+1}F_{n-1}-F_{n}^{2}.$

С равенством Кассини сопряжено более общее утверждение, названное в честь Эжена Каталана: ${displaystyle F_{n}^{2}-F_{n-r}F_{n+r}=(-1)^{n-r}F_{r}^{2}.}$

Свойства

Тринадцать ( ${displaystyle F_{7}}$ ) способов расположения длинных (красные) и коротких слогов (серые) в каденции^[en] длины шесть: пять ( $F_{5}$ ) заканчивается длинным слогом и восемь ( ${displaystyle F_{6}}$ ) — коротким

Последовательные наклоны плоскости и график приближений к золотому сечению, рассчитанному путём деления каждого числа Фибоначчи на предыдущее

на множестве неотрицательных целых чисел x и y^[30].

Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
Период чисел Фибоначчи по модулю натурального числа называется периодом Пизано и обозначается . Периоды Пизано образуют последовательность:

1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS).
Натуральное число является числом Фибоначчи тогда и только тогда, когда $5N^{2}+4$ или $5N^{2}-4$ является квадратом^[31].
Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи^[32].
Число Фибоначчи $F_{n+2}=F_{n+1}+F_{n}$ равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних единиц. При этом $F_{{n+1}}$ равно количеству таких кортежей, начинающихся с нуля, а $F_{n}$ — начинающихся с единицы.
Произведение любых подряд идущих чисел Фибоначчи делится на произведение первых чисел Фибоначчи.
Бесконечная сумма чисел, обратных числам Фибоначчи, сходится, его сумма («обратная постоянная Фибоначчи») равна 3,359884…

Вариации и обобщения

В других областях

Жёлтая ромашковая головка, показывающая расположение в 21 (синяя) и 13 (аква) спиралей. Такие схемы, включающие последовательные числа Фибоначчи, встречаются у самых разных растений

Число возможных предков на линии наследования Х-хромосомы в данном поколении предков следует последовательности Фибоначчи (Хатчисон Л. Растущее семейное древо: сила ДНК в восстановлении семейных отношений)^[33]

Иллюстрация модели Фогеля для n = 1 … 500

Существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространённый миф, который часто оказывается неточной подгонкой под желаемый результат^[34]^[35].

В природе

Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи, если листья (почки) на однолетнем приросте (побеге, стебле) имеют так называемое спиральное листорасположение. При этом число последовательно расположенных листьев (почек) по спирали плюс один, а также число совершенных при этом полных оборотов спирали вокруг оси однолетнего прироста (побега, стебля) выражаются обычно первыми числами Фибоначчи.
Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи^[36]^[37]^[38]^[39].

В искусстве

В поэзии чаще находят отношение «золотого сечения» (золотую пропорцию), связанное через формулу Бине с числами Фибоначчи. Например, в поэме Ш. Руставели «Витязь в тигровой шкуре» и на картинах художников^[40].

Однако числа Фибоначчи встречаются и непосредственно в поэзии и в музыке^[41]

В кодировании

В теории кодирования предложены устойчивые так называемые «коды Фибоначчи»^[42], причём основание этих кодов — иррациональное число.

См. также

Дерево Фибоначчи
Метод Фибоначчи с запаздываниями
Метод Фибоначчи поиска экстремума
Фибоначчи
Фибоначчиева система счисления
Числа Бине
Числа Леонардо
Таблица Витхоффа
Последовательность коров Нараяны
Золотое сечение
Пропорционирование

Примечания

↑ John Hudson Tiner. Изучение мира математики: от древних записей до новейших достижений в области компьютеров. — New Leaf Publishing Group, 200. — ISBN 978-1-61458-155-0.
↑ См., например, Т. В. Кропотова, В. Г. Подольский, П. Е. Кашаргин. Введение в высшую математику. — Казанский федеральный университет институт физики.
↑ Lucas, 1891, p. 3.
↑ Числа Фибоначчи // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Beck & Geoghegan (2010).
↑ Bóna, 2011, p. 180.
↑ Goonatilake, Susantha (1998), Toward a Global Science, Indiana University Press, с. 126, ISBN 978-0-253-33388-9, <https://books.google.com/books?id=SI5ip95BbgEC&pg=PA126>
↑ ¹ ² Singh, Parmanand (1985), The So-called Fibonacci numbers in ancient and medieval India, Historia Mathematica Т. 12 (3): 229—244, DOI 10.1016/0315-0860(85)90021-7
↑ ¹ ² Knuth, Donald (2006), The Art of Computer Programming, vol. 4. Generating All Trees – History of Combinatorial Generation, Addison–Wesley, с. 50, ISBN 978-0-321-33570-8, <https://books.google.com/books?id=56LNfE2QGtYC&pg=PA50&dq=rhythms>
↑ Knuth, Donald (1968), The Art of Computer Programming, vol. 1, Addison Wesley, с. 100, ISBN 978-81-7758-754-8, <https://books.google.com/books?id=MooMkK6ERuYC&pg=PA100>
↑ Livio, 2003, p. 197.
↑ Pisano, 2002, pp. 404—405.
↑ Fibonacci’s Liber Abaci (Book of Calculation). The University of Utah (13 декабря 2009). Дата обращения: 28 ноября 2018.
↑ Hemenway, Priya. Divine Proportion: Phi In Art, Nature, and Science (англ.). — New York: Sterling, 2005. — P. 20—21. — ISBN 1-4027-3522-7.
↑ Knott, Dr. Ron The Fibonacci Numbers and Golden section in Nature – 1. University of Surrey (25 сентября 2016). Дата обращения: 27 ноября 2018.
↑ Knott, Ron Fibonacci’s Rabbits. University of Surrey Faculty of Engineering and Physical Sciences.
↑ Gardner, Martin (1996), Mathematical Circus, The Mathematical Association of America, с. 153, ISBN 978-0-88385-506-5
↑ Art of Problem Solving. artofproblemsolving.com. Дата обращения: 9 мая 2021.
↑ Фибоначчи числа // Энциклопедический словарь юного математика / Сост. Савин А. П.. — 2-е изд. — М.: Педагогика, 1989. — С. 312—314. — 352 с. — ISBN 5715502187.
↑ ¹ ² ³ ⁴ ⁵ Теорема изложена в данном файле.
↑ Пункт 23.
↑ Пункт 24.
↑ Следствие из пункта 36.
↑ Пункт 30.
↑ 64.
↑ Пункт 55.
↑ proof of Cassini’s identity. planetmath.org. Дата обращения: 30 мая 2021.
↑ Тождество Кассини.
↑ J H E Cohn. Square Fibonacci Numbers Etc, С. 109—113. Архивировано 11 июля 2010 года. Дата обращения: 1 июля 2010.
↑ P. Ribenboim. The New Book of Prime Number Records. — Springer, 1996. — С. 193.
↑ Ira Gessel. Problem H-187 // Fibonacci Quarterly. — 1972. — Т. 10. — С. 417—419.
↑ В. Серпинский. Задача 66 // 250 задач по элементарной теории чисел. — М.: Просвещение, 1968. — 168 с.
↑ Hutchison, Luke. Growing the Family Tree: The Power of DNA in Reconstructing Family Relationships (англ.) // Proceedings of the First Symposium on Bioinformatics and Biotechnology (BIOT-04) : journal. — 2004. — September.
↑ Fibonacci Flim-Flam. Архивная копия от 23 апреля 2012 на Wayback Machine (англ.).
↑ The Myth That Will Not Go Away (англ.).
↑ Золотое сечение в природе.
↑ Числа Фибоначчи.
↑ Числа Фибоначчи.
↑ Акимов О. Е. Конец науки.
↑ Волошинов А. В. Математика и искусство. Москва: Просвещение, 2000. 400 с. ISBN 5-09-008033-X
↑ Математика в стихах и музыке
↑ Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. СПБ. Издательство: Питер, 2006. 320 с. ISBN 5-469-01369-3

Литература

Н. Н. Воробьёв. Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
А. И. Маркушевич. Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
А. Н. Рудаков. Числа Фибоначчи и простота числа 2¹²⁷ − 1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
Дональд Кнут. Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4.
Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7.
Грант Аракелян. Математика и история золотого сечения. — М.: Логос, 2014. — 404 с. — ISBN 978-5-98704-663-0.
Ball, Keith M (2003), 8: Fibonacci’s Rabbits Revisited, Strange Curves, Counting Rabbits, and Other Mathematical Explorations, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11321-0.
Beck, Matthias & Geoghegan, Ross (2010), The Art of Proof: Basic Training for Deeper Mathematics, New York: Springer, ISBN 978-1-4419-7022-0.
Bóna, Miklós (2011), A Walk Through Combinatorics (3rd ed.), New Jersey: World Scientific, ISBN 978-981-4335-23-2.
- Bóna, Miklós (2016), A Walk Through Combinatorics (4th Revised ed.), New Jersey: World Scientific, ISBN 978-981-3148-84-0.
Lemmermeyer, Franz (2000), Reciprocity Laws: From Euler to Eisenstein, Springer Monographs in Mathematics, New York: Springer, ISBN 978-3-540-66957-9.
Livio, Mario. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number (англ.). — First trade paperback. — New York City: Broadway Books (англ.) (рус., 2003. — ISBN 0-7679-0816-3.
Lucas, Édouard (1891), Théorie des nombres, vol. 1, Paris: Gauthier-Villars, Théorie des nombres в «Книгах Google», <https://archive.org/details/thoriedesnombr01lucauoft>.
Pisano, Leonardo (2002), Fibonacci’s Liber Abaci: A Translation into Modern English of the Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-0-387-95419-6

Ссылки

Первые 300 чисел Фибоначчи (англ.).
Числа Фибоначчи в природе (англ.).

Источник

Загрузить PDF

Последовательность Фибоначчи – это ряд чисел, в котором каждое последующее число равно сумме двух предыдущих чисел. Числовые последовательности часто встречаются в природе и искусстве в виде спиралей и «золотого сечения». Самый простой способ вычислить последовательность Фибоначчи – это создать таблицу, но такой метод не применим к большим последовательностям. Например, если нужно определить 100-й член последовательности, лучше воспользоваться формулой Бине.

1
Нарисуйте таблицу с двумя столбцами. Количество строк таблицы зависит от количества чисел последовательности Фибоначчи, которые нужно найти.
- Например, если нужно найти пятое число последовательности, нарисуйте таблицу с пятью строками.
- Используя таблицу, нельзя найти некоторое случайное число без вычисления всех предыдущих чисел. Например, если нужно найти 100-е число последовательности, нужно вычислить все числа: от первого до 99-ого. Поэтому таблица применима только для нахождения первых чисел последовательности.
2
В левом столбце напишите порядковые номера членов последовательности. То есть напишите цифры по порядку, начиная с единицы.
- Такие цифры определяют порядковые номера членов (чисел) последовательности Фибоначчи.
- Например, если нужно найти пятое число последовательности, в левой колонке напишите следующие цифры: 1, 2, 3, 4, 5. То есть нужно найти с первого по пятое число последовательности.
3
В первой строке правой колонки напишите 1. Это первое число (член) последовательности Фибоначчи.
- Имейте в виду, что последовательность Фибоначчи всегда начинается с 1. Если последовательность начинается с другого числа, вы неправильно вычислили все числа вплоть до первого.
4
К первому члену (1) прибавьте 0. Получится второе число последовательности.
- Запомните: чтобы найти любое число последовательности Фибоначчи, просто сложите два предыдущих числа.
- Чтобы создать последовательность, не забудьте о 0, который стоит перед 1 (первым членом), поэтому 1 + 0 = 1.
5
Сложите первый (1) и второй (1) члены. Получится третье число последовательности.
- 1 + 1 = 2. Третий член равен 2.
6
Сложите второй (1) и третий (2) члены, чтобы получить четвертое число последовательности.
- 1 + 2 = 3. Четвертый член равен 3.
7
Сложите третий (2) и четвертый (3) члены. Получится пятое число последовательности.
- 2 + 3 = 5. Пятый член равен 5.
8

Сложите два предыдущих числа, чтобы найти любое число последовательности Фибоначчи. Этот метод основан на формуле: $F_{{n}}=F_{{n-1}}+F_{{n-2}}$ .^[1] Эта формула не является замкнутой, поэтому при помощи этой формулы нельзя найти любой член последовательности без вычисления всех предыдущих чисел.

Реклама

1
2

В формулу подставьте порядковый номер числа (вместо ). – это порядковый номер любого искомого члена последовательности.
3

В формулу подставьте золотое сечение. Золотое сечение приблизительно равно 1,618034; подставьте в формулу это число.^[5]
4

Вычислите выражение в скобках. Не забывайте про правильный порядок выполнения математических операций, в котором выражение в скобках вычисляется в первую очередь:.
5

Возведите числа в степени. Возведите в соответствующие степени два числа, которые находятся в числителе.
6

Вычтите два числа. Перед тем как приступить к делению, вычтите числа, которые находятся в числителе.
7
Полученный результат разделите на квадратный корень из 5. Квадратный корень из 5 приблизительно равен 2,236067.
- В нашем примере: ${frac {11,180339}{2,236067}}=5,000002$ .
8
Полученный результат округлите до ближайшего целого числа. Последний результат будет десятичной дробью, которая близка к целому числу. Такое целое число представляет собой число последовательности Фибоначчи.
- Если в вычислениях использовать неокругленные числа, вы получите целое число. Работать с округленными числами намного легче, но в этом случае вы получите десятичную дробь.^[6]
- В нашем примере вы получили десятичную дробь 5,000002. Округлите ее до ближайшего целого числа и получите пятое число последовательности Фибоначчи, которое равно 5.
Реклама

Об этой статье

Эту страницу просматривали 27 660 раз.

Была ли эта статья полезной?

Источник

Числа Фибоначчи: циклом и рекурсией

Числа Фибоначчи – это ряд чисел, в котором каждое следующее число равно сумме двух предыдущих.

1, 1, 2, 3, 5, 8, 13, …

Иногда ряд начинают с нуля.

0, 1, 1, 2, 3, 5, 8, …

В данном случае мы будем придерживаться первого варианта.

Вычисление n-го числа ряда Фибоначчи с помощью цикла while

Присвоим переменным fib1 и fib2 значения двух первых элементов ряда, то есть единицы.

Получим от пользователя номер элемента, значение которого требуется вычислить. Присвоим номер элемента переменной n.

Поскольку значения первых двух элементов ряда Фибоначчи нам уже известны и вычисления начинаем с третьего, количество проходов по телу цикла должно быть на 2 меньше значения n, то есть n - 2.

Если пользователь вводит 1 или 2, тело цикла ни разу не выполняется, на экран выводится исходное значение fib2.

В теле цикла выполнять следующие действия:

Сложить fib1 и fib2, присвоив результат переменной для временного хранения данных, например, fib_sum.
Переменной fib1 присвоить значение fib2.
Переменной fib2 присвоить значение fib_sum.

После окончания работы цикла вывести значение fib2 на экран.

fib1 = 1
fib2 = 1
 
n = input("Номер элемента ряда Фибоначчи: ")
n = int(n)
 
i = 0
while i < n - 2:
    fib_sum = fib1 + fib2
    fib1 = fib2
    fib2 = fib_sum
    i = i + 1
 
print("Значение этого элемента:", fib2)

Пример выполнения программы:

Номер элемента ряда Фибоначчи: 10
Значение этого элемента: 55

Компактный вариант кода:

fib1 = fib2 = 1
 
n = input("Номер элемента ряда Фибоначчи: ")
n = int(n) - 2
 
while n > 0:
    fib1, fib2 = fib2, fib1 + fib2
    n -= 1
 
print("Значение этого элемента:", fib2)

Вывод ряда чисел Фибоначчи с помощью цикла for

В данном случае выводится не только значение искомого элемента ряда Фибоначчи, но и все числа до него включительно. Для этого вывод значения fib2 помещен в цикл.

fib1 = fib2 = 1
 
n = int(input())
 
print(fib1, fib2, end=' ')
 
for i in range(2, n):
    fib1, fib2 = fib2, fib1 + fib2
    print(fib2, end=' ')

Пример выполнения:

10
1 1 2 3 5 8 13 21 34 55

Рекурсивное вычисление n-го числа ряда Фибоначчи

Если n = 1 или n = 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
Во всех остальных случаях вызвать эту же функцию с аргументами n – 1 и n – 2. Результат двух вызовов сложить и вернуть в вызывающую ветку программы.

def fibonacci(n):
    if n in (1, 2):
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)
 
 
print(fibonacci(10))

Допустим, n = 4. Тогда произойдет рекурсивный вызов fibonacci(3) и fibonacci(2). Второй вернет единицу, а первый приведет к еще двум вызовам функции: fibonacci(2) и fibonacci(1). Оба вызова вернут единицу, в сумме будет два. Таким образом, вызов fibonacci(3) возвращает число 2, которое суммируется с числом 1 от вызова fibonacci(2). Результат 3 возвращается в основную ветку программы. Четвертый элемент ряда Фибоначчи равен трем: 1 1 2 3.

Больше задач в PDF

Источник

В этой статье вы узнаете, как определить пользовательский тип последовательности в Python и как реализовать последовательность Фибоначчи с помощью кастомного типа Sequence.

Иногда полезно реализовать собственный тип последовательности, у которого есть функции, аналогичные встроенным функциям для кортежей или списков.

Как вы уже знаете, последовательность может быть изменяемой или неизменяемой. В этой статье мы сосредоточимся на создании пользовательского неизменяемого типа последовательности.

У неизменяемой последовательность должно быть две основные возможности:

Возвращать количество элементов последовательности.
Возвращать элемент по заданному индексу или вызывать ошибку IndexError, если индекс выходит за границы последовательности.

Если объект удовлетворяет вышеуказанным требованиям, получится производить следующие действия:

Использовать синтаксис квадратных скобок [] для получения элемента по индексу.
Перебирать элементы последовательности: например, с помощью цикла for.

Чтобы реализовать перечисленные выше возможности, нужно создать следующие методы:

__getitem__ — возвращает элемент по заданному индексу.
__len__ — возвращает длину последовательности.

1) Метод getitem

У метода __getitem__ должен быть аргумент index, который является целым числом. Метод __getitem__ должен вернуть элемент из последовательности на основе указанного индекса.

Диапазон значений index: от нуля до length - 1. Если индекс выходит за границы, метод __getitem__ должен выдать исключение IndexError.

Метод __getitem__ может принимать объект среза для слайсинга.

2) The len method

Если у пользовательской последовательности есть метод __len__, вы можете использовать встроенную функцию len(), чтобы получить количество элементов последовательности.

Последовательность Фибоначчи

Последовательность Фибоначчи примерно в 1170 году открыл Леонардо Фибоначчи, итальянский математик.

В последовательности Фибоначчи каждое число является суммой двух предшествующих ему чисел. Например:

1, 1, 2, 3, 5, 8 , 13, 21, …

Последовательность Фибоначии можно задать следующей формулой:

f(1) = 1
f(2) = 1
f(n) = f(n-1) + f(n-2) если n > 2

В некоторые источниках сказано, что последовательность Фибоначчи начинается с нуля, а не с 1, как сейчас. То есть вот так:

0, 1, 1, 2, 3, 5, 8 , 13, 21, ...

Но мы будем придерживаться исходной последовательности Фибоначчи, которая начинается с единицы.

Чтобы вычислить число Фибоначчи в Python, нужно создать такую рекурсивную функцию:

def fib(n):
    if n < 2:
        return 1
    return fib(n-2) + fib(n-1)

В этой рекурсивной функции fib(1) и fib(2) всегда возвращают 1. А когда n больше 2, fib(n) = fib(n-2) – fib(n-1).

Добавим print() в начало функции, чтобы посмотреть, как она работает, и вызовем функцию fib() с аргументом 6.

def fib(n):
    print(f'Считаю {n} число Фибоначчи')
    if n < 2:
        return 1
    return fib(n-2) + fib(n-1)


fin(6)

Вывод

Считаю 6 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 5 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи

Как вы видите, функция fib() часто повторяется.

Например, ей приходится трижды вычислять 3 число Фибоначчи. Это неэффективно.

Чтобы решить эту проблему, в Python есть декоратор под названием lru_cache из модуля functools.

lru_cache позволяет кэшировать результат работы функции. Когда вы передаете тот же аргумент функции, функция просто получает результат из кэша вместо того, чтобы пересчитывать его.

Ниже показано, как использовать декоратор lru_cache для ускорения работы функции fib():

from functools import lru_cache


@lru_cache
def fib(n):
    print(f'Считаю {n} число Фибоначчи')
    if n < 2:
        return 1
    return fib(n-2) + fib(n-1)


fib(6)

Вывод

Считаю 6 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 5 число Фибоначчи

Как вы видите, количество вычислений значительно уменьшилось.

Создаем последовательность Фибоначии

1. Сначала определим класс, реализующий последовательность Фибоначчи:

class Fibonacci:
    def __init__(self, n):
        self.n = n

Метод __init__ принимает целое число n, которое задает длину последовательности.

2. Теперь определим статический метод, который вычисляет значение определенного числа Фибоначчи:

@staticmethod
@lru_cache(2**16)
def fib(n):
    if n < 2:
        return 1
    return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)

3. Реализуем метод __len__, чтобы мы могли использовать встроенную функцию len() для получения количества элементов из последовательности Фибоначчи:

def __len__(self):
    return self.n

4. Реализуем метод __getitem__ для поддержки индексации с помощью синтаксиса квадратных скобок []:

def __getitem__(self, index):
    if isinstance(index, int):
        if index < 0 or index > self.n - 1:
            raise IndexError

        return Fibonacci.fib(index)

Метод __getitem__ принимает целое число index. Метод __getitem__ проверяет, является ли индекс целым числом, используя функцию isinstance().

Если index выходит за границы последовательности, __getitem__ вызовет исключение IndexError. В противном случае он вернет число Фибоначчи индекса.

Соединим все вместе:

from functools import lru_cache


class Fibonacci:
    def __init__(self, n):
        self.n = n

    def __len__(self):
        return self.n

    def __getitem__(self, index):
        if isinstance(index, int):
            if index < 0 or index > self.n - 1:
                raise IndexError

            return Fibonacci.fib(index)

    @staticmethod
    @lru_cache(2**16)
    def fib(n):
        if n < 2:
            return 1
        return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)

Кастомная последовательность Фибоначчи в виде Python-класса готова. Однако вы не сможете просто сохранить этот код в модуле fibonacci.py и использовать его в другом скрипте.

Давайте разберемся, как использовать созданную последовательность.

Используем последовательность Фибоначии

Ниже показано, как использовать последовательность Фибоначчи из модуля fibonacci.py:

from fibonacci import Fibonacci

fibonacci = Fibonacci(10)

# используем []
print('Используем последовательность Фибоначчи с помощью []:')
print(fibonacci[0])
print(fibonacci[1])
print(fibonacci[2])

print('Используем последовательность Фибоначчи с помощью цикла for:')
# используем for
for f in fibonacci:
    print(f)

Вывод

Используем последовательность Фибоначии с помощью []:
1
1
2
Используем последовательность Фибоначчи с помощью цикла for:
1
1
2
3
5
8
13
21
34
55

Как это работает

Создаем новый экземпляр последовательности Фибоначчи, в котором содержится 10 элементов.
Получаем доступ к элементам последовательности Фибначчи с помощью квадратных скобок [].
Используем последовательность Фибоначии в цикле for.

Добавляем поддержку срезов

Чтобы можно было делать срезы нашей последовательности, как показано ниже,

fibonacci[1:5]

… нужно добавить соответсвующую логику, которая будет обрабатывать объект среза.

В fibonacci[1:5] аргументом index метода __getitem__ является объект среза, начало которого равно 1, а конец — 5.

Вы можете использовать метод indices() объекта среза, чтобы получить индексы элементов для возврата из последовательности:

indices = index.indices(self.n)

self.n — это длина последовательности, которая будет «нарезана». В данном случае это количество элементов в последовательности Фибоначчи.

Чтобы вернуть список Фибоначчи из среза, вы можете передать индексы в функцию range() и сделать вот так:

[Fibonacci.fib(k) for k in range(*indices)]

Соберем все вместе:

from functools import lru_cache


class Fibonacci:
    def __init__(self, n):
        self.n = n

    def __len__(self):
        return self.n

    def __getitem__(self, index):
        if isinstance(index, int):
            if index < 0 or index > self.n - 1:
                raise IndexError

            return Fibonacci.fib(index)
        else:
            indices = index.indices(self.n)
            return [Fibonacci.fib(k) for k in range(*indices)]

    @staticmethod
    @lru_cache
    def fib(n):
        if n < 2:
            return 1
        return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)

Теперь можно сделать срез последовательности следующим образом:

from fibonacci import Fibonacci

fibonacci = Fibonacci(10)
print(fibonacci[1:5])

Вывод

[1, 2, 3, 5]

Что нужно запомнить

Для создания кастомной последовательно нужно реализовать методы __len__ и __getitem__.
Метод __getitem__ должен возвращать элемент по заданному индексу или вызывать ошибку IndexError, если индекс выходит за границы последовательности.

Источник

Числа Фибоначчи — это числа такой последовательности, в которой первые два элемента — 0 и 1, а каждый последующий элемент равен сумме двух предшествующих. Выглядит это так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …

Примечание Иногда 0 опускается, и в этом случае ряд начинается с 1, но мы будем использовать последовательность с 0 на первой позиции.

Формула записывается следующим образом:

Вычисление ряда Фибоначчи — стандартная задача, которую задают на собеседованиях, чтобы проверить кандидата на понимание алгоритмов. Не так популярна, как сортировка, но всё же.

Давайте вычислим ряд и его отдельные элементы, использовав для этого язык Java.

Цикл
Рекурсия
Stream
Тест

Вычислить ряд Фибоначчи циклом

Предположим, что нам нужно вывести на экран первые десять чисел последовательности Фибоначчи. Мы помним, что:

первый элемент ряда — 0, второй — 1;
каждый последующий — сумма двух предыдущих.

Тогда наша последовательность будет иметь такой вид:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34

Но нам нужно вывести результат с использованием программы. Держите код с объяснениями в комментариях:

public class Main{
	public static void main(String[] args) {
	    
	        //Объявляем переменные при известных первых двух:
		int num0 = 0;
		int num1 = 1;
		int num2;
		
		//Первые две переменные выводим вне цикла:
		System.out.print(num0 + " " + num1 + " ");
		for(int i = 3; i <= 10; i++){
			num2 = num0 + num1;
			
			//Каждый следующий элемент выводим в цикле:
			System.out.print(num2 + " ");
			
			//Предыдущим двум переменным присваиваем новые значения:
			num0 = num1;
			num1 = num2;
		}
	}
}

Выполнение завершится на десятом элементе. Количество элементов при этом можно менять, изменив значение в условиях цикла.

Найти число Фибоначчи через рекурсию

Рекурсивная функция — это такая функция, которая вызывает саму себя. Она также неплохо отрабатывает в алгоритмических задачах вроде чисел Фибоначчи, но ей требуется больше времени.

Почему так происходит? Всё дело в том, что рекурсивная функция приводит к многоразовому вызову одних и тех же операций. Именно из-за этого её не рекомендуется использовать, но если уж на собеседовании прозвучит такая задача, вы будете готовы.

Рассмотрим пример, в котором нам нужно получить n-ое число в ряде Фибоначчи:

public int fibonacciValue(num) {
  if (num <= 1) {
     return 0;
  } else if (num == 2) {
     return 1;
  } else {
     return fibonacciValue(num - 1) + fibonacciValue(num - 2);
  }
}

Если в качестве num задать большое значение, программа зависнет.

Тип int в Java может хранить значения до 2147483647, так что вычислить получится лишь первые 46 чисел Фибоначчи. Тип long хранит до 9223372036854775807, а это 91 число Фибоначчи. Класс BigInteger призван работать с действительно большими значениями, вот только само выполнение программы это никак не ускорит.

Использовать для вычисления Stream

Stream в Java — это компонент для самостоятельной внутренней итерации своих же элементов. Подробнее о нём вы можете почитать в нашей статье о Java Stream API.

И, разумеется, Stream подходит для вычисления элементов последовательности Фибоначчи:

Stream.iterate(new int[]{0, 1}, arr -> new int[]{arr[1], arr[0]+ arr[1]})
    
   //Задаём лимит значений:
   .limit(num)
   
   //Отбираем по первому элементу каждого массива:
   .map(y -> y[0])
   
   //Выводим в консоль:
   .forEach(x -> System.out.println(x));

В данном примере метод iterate() будет возвращать упорядоченный поток, ограниченный лимитом в num значений и созданный с применением функции к начальному массиву arr. В консоль будет выведено следующее:

{0,1}
{1,1}
{1, 2}
{2, 3}
{3, 5}
{5, 8}
{8, 13}
{13, 21}
…

А так мы получим сумму чисел последовательности по элемент num включительно:

int fibonacciValuesSum = Stream.iterate(new int[]{0, 1}, arr -> new int[]{arr[1], arr[0]+ arr[1]})
     .limit(num)
     .map(y -> y[0])
     .mapToInt(Integer::intValue)
     .sum();
System.out.println(fibonacciValuesSum);

Математический тест

Любите математику? Попробуйте решить наш математический тест:

Источник

Происхождение

Формула Бине

Обоснование

Следствие и обобщение

Тождества

Свойства

Вариации и обобщения

В других областях

В природе

В искусстве

В кодировании

См. также

Примечания

Литература

Ссылки

Об этой статье

Была ли эта статья полезной?

Числа Фибоначчи: циклом и рекурсией

Вычисление n-го числа ряда Фибоначчи с помощью цикла while

Вывод ряда чисел Фибоначчи с помощью цикла for

Рекурсивное вычисление n-го числа ряда Фибоначчи

1) Метод __getitem__

2) The __len__ method

Последовательность Фибоначчи

Создаем последовательность Фибоначии

Используем последовательность Фибоначии

Как это работает

Добавляем поддержку срезов

Что нужно запомнить

Вычислить ряд Фибоначчи циклом

Найти число Фибоначчи через рекурсию

Использовать для вычисления Stream

Математический тест

Вам также может понравиться

Как правильно составить счет фактуры

Флеш карта только для чтения как исправить

Как найти в массиве одинаковые элементы javascript

Добавить комментарий Отменить ответ

1) Метод getitem

2) The len method