Этот метод построения далеко не новый, впервые он был предложен Евклидом в IV веке. Но у него есть весомое преимущество, которое заключается в том, что с его помощью можно строить фигуры большого размера. Для этого циркуль нужно заменить длинной ниткой, к концу которой привязан карандаш.
Шаг 1 из 9
На бумаге отметьте карандашом точку, в которой будет центр окружности. Установите острие циркуля в эту точку и нарисуйте любую окружность произвольного диаметра с центром в этой точке.
Шаг 2 из 9
Используя линейку и карандаш, проведите прямую линию через точку центра окружности. Линия будет пересекать окружность в двух диаметрально противоположных точках.
Шаг 3 из 9
Пересечение прямой и окружности отметьте карандашом. Это точка будет центром второй окружности.
Шаг 4 из 9
Установите острую сторону циркуля в эту точку и нарисуйте вторую окружность, длина радиуса которой равна длине радиуса первой окружности.
Полностью окружность вырисовывать не обязательно, достаточно получить две точки пересечения окружностей.
Шаг 5 из 9
Таким образом, у вас получится четыре точки. Отметьте их карандашом.
Шаг 6 из 9
Проведите прямую линию через центр первой окружности и верхнюю точку пересечения обеих окружностей.
Шаг 7 из 9
Аналогично, начертите прямую линию через нижнюю точку пересечения окружностей.
Шаг 8 из 9
Получилось шесть точек, каждая из которых будет вершиной углов шестиугольника.
Шаг 9 из 9
Соедините точки между собой фломастером. Ластиком сотрите нарисованные простым карандашом линии.
Загрузить PDF
Загрузить PDF
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
-
1
При помощи циркуля нарисуйте круг. Вставьте грифель карандаша в циркуль. Расширьте циркуль на желаемую ширину радиуса нужного круга. Радиус может быть от пары до десятка сантиметров шириной. Далее поставьте циркуль с грифелем на бумагу и нарисуйте круг.
- Иногда легче сначала нарисовать полкруга в одном направлении, а затем вторую половину — в другом.
-
2
Передвиньте иглу циркуля к краю круга. Поставьте ее на вершину круга. Не меняйте угол и расположение циркуля.
-
3
Сделайте небольшую отметку карандашом на окружности. Сделайте ее отчетливой, но не слишком темной, так как позже вы ее сотрете. Не забудьте сохранять угол, который вы установили для циркуля.
-
4
Переместите иглу циркуля на ту отметку, которую вы только что сделали. Поставьте иглу прямо на отметку.
-
5
Сделайте еще одну отметку карандашом на окружности. Таким образом вы сделаете вторую отметку на определенной дистанции от первой отметки. Продолжайте двигаться в одном направлении.
-
6
Тем же способом сделайте еще четыре отметки. Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.
-
7
Соедините отметки при помощи линейки. Шесть мест, где ваши отметки пересекаются с краем круга, — это шесть вершин шестиугольника. При помощи линейки и карандаша нарисуйте прямые линии, соединяя соседние отметки.
-
8
Сотрите все вспомогательные линии. Сотрите и круг, и отметки на краях круга, и другие метки, которые вы сделали. Поздравляем — вы нарисовали правильный шестиугольник.
Реклама
-
1
Обведите ободок стакана карандашом. Таким образом вы нарисуете круг. Очень важно рисовать именно карандашом, так как позже вам нужно будет стереть все вспомогательные линии. Вы также можете обвести перевернутую кружку, банку или что-либо еще, что имеет круглую основу.
-
2
Начертите горизонтальные линии через центр круга. Можете воспользоваться линейкой, книгой — чем угодно с прямым краем. Если у вас все же есть линейка, вы можете отметить середину, рассчитав вертикальную длину круга и разделив ее пополам.
-
3
Нарисуйте «Х» над половиной круга, разделив его на шесть равных секций. Так как вы уже провели линию через середину круга, «Х» должен быть больше в ширину, чем в высоту, чтобы части были равны. Представьте, что вы делите пиццу на шесть частей.
-
4
Сделайте из каждой секции треугольники. При помощи линейки нарисуйте прямую линию под изогнутой частью каждой секции, соединяя ее с другими двумя линиями, чтобы образовался треугольник. Сделайте это с оставшимися пятью секциями. Представьте, что формируете корочку вокруг кусков пиццы.
-
5
Сотрите все вспомогательные линии. К вспомогательным линиям относятся: круг, три линии, которыми круг разделен на секции, и другие отметки, которые вы делали в процессе.
Реклама
-
1
Нарисуйте горизонтальную линию. Чтобы нарисовать прямую линию без линейки, просто нарисуйте начальную и конечную точку горизонтальной линии. Затем поместите карандаш в начальную точку и протягивайте линию к концу. Длина этой линии может составлять лишь несколько сантиметров.
-
2
Нарисуйте две диагональные линии с концов горизонтальной. Диагональная линия с левой стороны должна быть направлена наружу так же, как и диагональная линия справа. Представьте, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
-
3
Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных прямых, нарисованных вовнутрь. Таким образом будет создано зеркальное отображение первых двух диагональных линий. Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания.
-
4
Нарисуйте еще одну горизонтальную линию, соединив нижние две диагональные линии. Таким образом вы нарисуете основу шестиугольника. В идеале эта линия должна быть параллельна верхней горизонтальной линии. Вот вы и завершили свой шестиугольник.
Реклама
Советы
- Если при использовании метода с циркулем вы соединили каждую отметку вместо всех шести, то получите равносторонний треугольник.
- Карандаш и циркуль должны быть острыми, чтобы минимизировать ошибки от слишком широких отметок.
- Не давите слишком сильно на карандаш или циркуль при рисовании шестиугольника, с тем чтобы у вас была возможность стереть лишние линии.
- Чтобы измерения были точными, измерьте углы шестиугольника.
Реклама
Предупреждения
- Циркуль — довольно острый инструмент, будьте с ним очень аккуратны.
Реклама
Принцип работы
- Каждый метод позволит нарисовать шестиугольник, образованный шестью равносторонними треугольниками с радиусом, равным длине всех сторон. Шесть нарисованных радиусов должны быть одинаковой длины, ровно как и все стороны шестиугольника, при условии что шаг циркуля не менялся. Благодаря тому, что шесть треугольников равносторонние, углы между их вершинами должны быть равны 60 градусам.
Что вам понадобится
- Бумага
- Карандаш
- Линейка
- Циркуль
- Что-нибудь, что можно подложить под бумагу, чтобы игла циркуля не соскальзывала
- Ластик
Об этой статье
Эту страницу просматривали 277 952 раза.
Была ли эта статья полезной?
Правильный шестиугольник и его свойства

Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
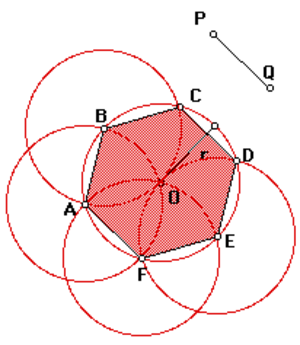
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
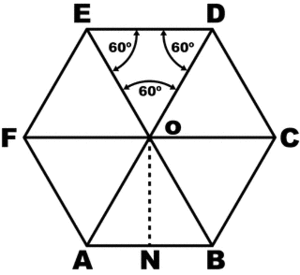
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Построение правильного шестиугольника и его свойства: углы, площадь и радиусы окружностей; интересные факты
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
- Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
- Пошаговая инструкция будет выглядеть так:
чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
- При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
- Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису.
Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность.
Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Газовый баллон для компрессора
- R=а.
- Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
- Ну а площадь этой окружности будет стандартная:
- S=πR²
Вписанная окружность
- Высота равностороннего треугольника вычисляется просто:
- h²=а²-(а/2)²= а²3/4, h=а(√3)/2
- А поскольку R=a и r=h, то получается, что
- r=R(√3)/2.
- Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
- Ее площадь будет составлять:
- S=3πa²/4,
- то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
- S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
- S=3R²(√3)/2
- Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Как прозвонить диод мультиметром на плате
- Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
- Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
- d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
Формула для нахождения площади правильного шестиугольника через сторону:
Через радиус описанной окружности
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Станок для заточки фуганочных ножей
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
- Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
- Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
- Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.
- При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt ) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
- Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
- Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
- Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
- Радиус вписанной окружности правильного шестиугольника равен апофеме:
- (r = m = alargefrac
ormalsize) - Радиус описанной окружности равен стороне правильного шестиугольника:
- Периметр правильного шестиугольника
- Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
- (S = pr = largefrac
ormalsize), - где (p) − полупериметр шестиугольника.
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90º и/или циркуля.
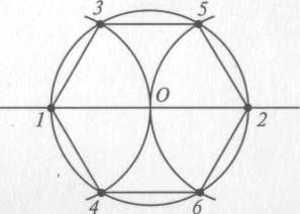
При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 2.24).
Последовательно соединив полученные точки, получают правильный вписанный шестиугольник.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 2.25). Соединив полученные точки, получают двенадцатиугольник.
2.2.5 Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 2.26.
Половину любого диаметра (радиус) делят пополам (рис. 2.26 а), получают точку А.Из точки А,как из центра, проводят дугу радиусом, равным расстоянию от точки Адо точки 1 до пересечения со второй половиной этого диаметра, в точке В(рис. 2.26 б). Отрезок 1Вравен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности.
Делая засечки на окружности (рис. 2.26, в) радиусом К,равным отрезку 1В,делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2 и 5 (рис. 2.26, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4.
Расстояние от точки 3 до точки 4 проверяют циркулем. Если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной.
Последовательно соединив найденные точки, получают пятиугольник (рис. 2.26, г).
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 2.26), но сначала делят окружность на пять частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 2.27, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник(рис. 2.27, б).
2.2.6 Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и
четырнадцатиугольника
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 2.28 и 2.29.
Из любой точки окружности, например точки А, радиусом заданной окружности проводят дугу (рис. 2.28, а) до пересечения с окружностью в точках В и D. Соединим точки Ви Dпрямой.
Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС,делают засечки на окружности в последовательности, показанной на рис. 2.28, б.
Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 2.28, в).
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 2.29, а).
Сначала окружность делится на семь равных частей от точки 1, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырнадцатиугольник (рис. 2.29, б).
- а) б)
- Рисунок 2.29
- Построение эллипса
- Изображение окружности в прямоугольной изометрической проекции во всех трех плоскостях проекций представляет собой одинаковые по форме эллипсы.
- Направление малой оси эллипса совпадает с направлением аксонометрической оси, перпендикулярной той плоскости проекций, в которой лежит изображаемая окружность.
При построении эллипса, изображающего окружность небольшого диаметра, достаточно построить восемь точек, принадлежащих эллипсу (рис. 2.30). Четыре из них являются концами осей эллипса (A, B, С, D),а четыре других (N1, N2, N3, N4) расположены на прямых, параллельных аксонометрическим осям, на расстоянии, равном радиусу изображаемой окружности от центра эллипса.
Урок по геометрии «Построение правильных многоугольников» 9 класс
- Тема: Построение правильных многоугольников.
- Этап ориентации.
- Оборудование: раздаточный тестовый материал, мультимедийный экран, компьютер, карточки с заданиями.
- Урок с использованием метода проектов, интерактивных технологий (работа в группах) предполагает класс разбить на 3 группы по интересам.
- Этап постановки цели урока.
-
Научить учеников строить правильные треугольники, четырёхугольники и шестиугольники;
Найти способ построения правильных 2n угольников;
Показать практическое применение данных построений в архитектуре и в быту;
Прививать каждому ученику вкус к самостоятельной, активной и творческой деятельности;
Развивать познавательный интерес к предмету.
Актуализация опорных знаний (2 вида тестов).
Мотивация учебной деятельности (презентации).
Изложение нового материала (использование программы «Живая геометрия»).
Итог урока. Заключительная презентация.
Этап организации выполнения плана действий.
Здравствуйте, сегодня у нас открытие банка «Созвездие». Наши гости выступают в роли акционеров банка «Созвездие». Я, как управляющая банком, собрала вас, акционеров, с целью донесения до вас новой информации и принятия решения.
Сегодня в наш банк «Созвездие» обратились первые представители трёх организаций (пчеловодов, архитекторов, дизайнеров интерьера), с целью оформить кредит в нашем банке.
И мы должны с вами принять решение о выдаче кредита (либо отказе) и о его сумме.
На повестке собрания —
1. Представители организаций должны убедить нас в необходимости и перспективности своих планов;
2. Информировать нас о своих финансовых возможностях.
3. А мы должны вынести решение о возможности (невозможности) кредитования.
Все финансовые операции будут производить бухгалтеры нашего банка и результаты заносить в векселя.
1 – Организация пчеловодов (разводят пчел). Кредит нужен для приобретения пасеки.
2 – Архитекторы (создают проекты зданий). Оформляют кредит для приобретения лицензионных программ с использованием трехмерного пространства.
3 – Дизайнеры интерьеров (создают эскизы паркета). Кредит – для поездки в Швейцарию. Цель поездки — обмен опытом.
2. Актуализация опорных знаний.
Необходимое условие кредитования — это заполнение анкетных данных всеми представителями организаций. На столах у вас лежат анкеты на синих и красных листах. Вы выбираете анкеты согласно своим возможностям.
- Решение тестовых заданий по уровням сложности:
- Фамилия_________________ Имя___________________
- Максимальное количество — 4 балл (4000 грн.)
1. Какая из ломанных является многоугольником?
2.Какой многоугольник выпуклый?
3. Многоугольник является правильным, если все его ….
1) углы равны; 2) углы и стороны равны; 3) стороны равны.
4. Соедините стрелочками соответствующие ячейки согласно формулам.
- Радиус окружности, описанной около правильного треугольника
- a
- ____
- 2
- Радиус окружности, вписанной в правильный четырёхугольник
- a
- Радиус окружности, описанной около правильного шестиугольника
- a
- ____
- √3
- Фамилия_________________ Имя___________________
- Максимальное количество — 8 баллов (8000 грн.)
1.Соедините стрелочками соответствующие ячейки согласно формулам.
- Радиус окружности, описанной около правильного треугольника
- a
- ____
- 2
- Радиус окружности, вписанной в правильный четырёхугольник
- a
- Радиус окружности, описанной около правильного шестиугольника
- a
- ____
- √3
- Радиус окружности, вписанной в правильный треугольник
- а
- ____
- 2√3
- Радиус окружности, вписанной в правильный шестиугольник
- a√3
- ____
- 2
- Радиус окружности, описанной около правильного четырёхугольника
- a
- ____
- 2sin 180
- n
- Радиус окружности, вписанной в правильный многоугольник
- а
- ____
- √2
- Радиус окружности, описанной около правильного многоугольника
- a
- ____
- 2tg 180
- n
2. Может ли пятиугольник иметь стороны длиной 3 см, 4 см, 8 см, 6см, 25 см?
3. В правильном n-угольнике сумма внутренних углов равна 3600. Сколько сторон у этого многоугольника?
- 1) 4; 2) 3; 3) 5.
- 4. У правильного пятиугольника внешний угол равен:
- 1) 360; 2) 45 0; 3) 72 0.
Тесты проверяют бухгалтеры и ответы помещают в векселя.
(Федоренко Б., Верескун Е., Фещенко Е.)
3. Мотивация учебной деятельности.
- Учитель.
- А теперь мы дадим возможность каждой из организаций презентовать свои проекты:
- Презентации 3х групп: (выступление авторов)
Пчеловоды; («Геометрия пчелиных сот») Полященко Вика
Архитекторы; (пентагон. ) Парубаева Вика
Дизайнеры интерьера (эскизы паркета) Полященко Влада.
- После презентаций делаем вывод:
- Что все организации столкнулись с необходимостью построения правильных многоугольников.
- Объявление практической темы собрания:
- Построение правильных многоугольников
- с помощью линейки и циркуля.
- Представители, какой организации могут дать нам историческую справку о создателе метода построения правильных многоугольников?
4.Исторический доклад — Брусниченко А
.
Первокурсник Геттингенского университета Карл Гаусс (1777–1855) решил задачу, перед которой математическая наука пасовала более 2 с лишним тысяч лет.
Еще древние греки нашли способы построения с помощью только циркуля и линейки правильных многоугольников с числом сторон 3, 4, 5, 15, а также с числом сторон, большим в 2 раза. Однако в отношении прочих правильных многоугольников царила полная неизвестность.
И вот будущий «король математиков» Гаусс догадался, как построить правильный 17-угольник. Это открытие стало поворотным пунктом в его жизни: ранее колебавшийся между филологией и математикой, теперь он твердо решил посвятить себя последней.
Это событие Гаусс посчитал столь значительным, что отметил его в «Дневнике» (запись от 30 марта 1796) и завещал высечь правильный 17-угольник на своём надгробии (воля Гаусса была исполнена).
5. Изложение нового материала.
- А теперь мы хотим выслушать ваше решение данной проблемы – «построение правильного многоугольника».
- Для построения правильных многоугольников будем использовать связь с окружностью.
- 1 группа – строит правильный шестиугольник (Кузьмина Е.)
- 3 группа — строит правильный треугольник; (Христолюбов А. )
- 2 группа — строит правильный пятиугольник; (Дударева Я.);
- Все участники чертят чертежи по очереди у себя в тетрадях по заранее готовым окружностям.
А наш банк предлагает вам альтернативное решение данной проблемы — с помощью программы «Живая геометрия» — платно!.
Четырёхугольник (восьмиугольник) – Набоков Д. на компьютере с помощью программы «Живая геометрия»
Вопрос ко всем присутствующим:
В чём преимущества построения правильных многоугольников с помощью программы «Живая геометрия»? И готовы ли вы будете её у нас приобрести?
После выполнения построения участники делают вывод, как построить правильный 2n-угольник, используя правильный n-угольник.
Банк даёт вам возможность увеличить сумму кредита – выполнение заданий самостоятельной работы (чем больше выполненных заданий, тем больше сумма кредита) (на разноцветных листах А4):
Задания для самостоятельной работы:
Чертежи выполняют на заранее приготовленных карточках:
Средний уровень – построить правильный восьмиугольник
Высокий уровень — построить правильный шестнадцатиугольник.
Достаточный уровень — построить правильный двенадцаугольник
Проверяют бухгалтеры и заносят баллы в векселя.
А теперь, пока бухгалтеры выполняют подсчёты, мы все вместе посмотрим презентацию «Правильные 4,5,6,7,8,9 – угольники в быту, технике, архитектуре, природе». В ходе просмотра данной презентации, мы, возможно, увидели потенциальных клиентов нашего банка.
Подводим итоги нашего собрания:
Построение правильных многоугольников
- Построить правильный шестиугольник, сторона которого равна данному отрезку.
- Дано: отрезок DC.
- Построить: правильный шестиугольник, сторона которого равна DC.
- Решение:
Для решения задачи воспользуемся тем, что сторона шестиугольника равна радиусу описанной около него окружности, т.е. (смотри формулу для вычисления стороны правильного многоугольника), где — радиус окружности описанной около правильного многоугольника. Нам нужно построить правильный шестиугольник со стороной DC, поэтому с помощью циркуля измеряем отрезок DC и строим окружность радиуса DC, и отмечаем на ней произвольную точку А1, центр окружности обозначаем буквой О.
Затем не меняя раствора циркуля, построим на этой окружности точки А2, А3, А4, А5, А6, так, чтобы выполнялись равенства
А1А2 = А2А3 = А3А4 = А4А5 = А5А6 = DC (т.е.
сначала строим окружность радиуса DC с центром в точке А1 (всю окружность строить необязательно, смотри выделенное красным), данная окружность пересечет окружность с центром О в точке А2, далее аналогично строим окружность радиуса DC с центром в точке А2, она пересечет окружность с центром О в точке А3 и т.д.).
Теперь соединяя последовательно построенные точки отрезками, получим искомый правильный шестиугольник А1А2А3А4А5А6.
Задача 2
Дан правильный -угольник. Построить правильный 2-угольник.
Дано: правильный -угольник А1А2А3…Аn.
- Построить: правильный 2-угольник.
- Решение:
- Пусть, например, нам дан шестиугольник А1А2А3А4А5А6, значит, построить нужно двенадцатиугольник.
Сначала опишем около данного шестиугольника А1А2А3А4А5А6 окружность. Для этого построим биссектрисы углов А1 и А2.
Чтобы построить биссектрису угла А1, строим окружность произвольного радиуса с центром в точке А1 (полностью окружность строить необязательно, смотри выделенное красным цветом), данная окружность пересечет стороны А1А2 и А1А6 угла А1 в точках Е и К. Затем строим две окружности с центрами в точках Е и К радиуса ЕК (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом), данные окружности пересекутся в точке Р. Далее проводим луч А1Р, который и будет биссектрисой угла А1.
- Аналогично строим биссектрису угла А2.
- Точку пересечения биссектрис углов А1 и А2 обозначаем буквой О и строим окружность радиуса ОА1 с центром О (окружность описанная около А1А2А3А4А5А6).
Далее нужно каждую из дуг А1А2, А2А3, А3А4, А4А5, А5А6, А6А1разделитьпополам. Чтобы разделить дугу А1А2 пополам, построим серединный перпендикуляр к отрезку А1А2.
Для этого строим две окружности с центрами в точках А1 и А2 радиуса А1А2 (полностью окружность строить необязательно, смотри выделенное красным цветом). Данные окружности пересекутся в двух точках, одну обозначим буквой М, а другая совпадет с точкой О, т.к.
у шестиугольника сторона равна радиусу (с другими многоугольниками совпадения с точкой О не будет) . Затем проводим прямую МО, данная прямая пересечет дугу А1А2 в точке В1, которая и разделит дугу А1А2 пополам.
Далее точку В1 соединяем с концами А1 и А2 дуги А1А2.
Аналогично находим точки В2, В3. Точки В4, В5, В6 в данном случае строить необязательно, они получаются автоматически при построении точек В1, В2, В3, т.к. шестиугольник симметричная фигура.
- Получили двенадцатиугольник А1В1А2В2А3В3А4В4А5В5А6В6 (смотри выделенное красным).
- Мы выполняли построения на примере правильного шестиугольника, если мы имеем произвольный правильный -угольник, то все построения выполняются аналогично.
Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный треугольник и пользуясь результатом задачи 2, можно построить правильный шестиугольник, затем правильный двенадцатиугольник и вообще 2k-угольник, где — любое целое число, больше двух.
Замечание
Не все правильные многоугольники можно построить с помощью циркуля и линейки. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.
Правильный шестиугольник ≪ Scisne?
Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
Все углы равны 120°. Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен: Площадь правильного шестиугольника рассчитывается по формулам: ,
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шахматная раскраска шестиугольного паркета
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — <6,3>, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости.
В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Наиболее плотная упаковка кругов на плоскости
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала). Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Построение правильного шестиугольника с помощью циркуля и линейки
Правильный шестиугольник в природе, технике и культуре
Пчелиные соты показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы, например графит, имеют гексагональную кристаллическую решётку.
Кристаллическая решетка графита
Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Гигантский гексагон — атмосферное явление на Сатурне.
Гигантский гексагон — устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер-1 и наблюдаемое снова в 2006 году аппаратом Кассини-Гюйгенс.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Вращение гексагона на северном полюсе Сатурна
Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса. Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м. Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Игровое поле зачастую составляют шестиугольники. Замощение плоскости правильными шестиугольниками является основой для гекса, гексагональных шахмат и других игр на клетчатом поле, полигексов, вариантов модели «Жизнь» и других двумерных клеточных автоматов, кольцевых флексагонов и т.п.
Гексагональные шахматы Глинского. Начальное положение фигур.
Сечение гайки имеет вид правильного шестиугольника.
Звезда Давида (гексаграмма) — шестиконечная звезда, образованная двумя правильными треугольниками, символ иудаизма.
- Пчелиные соты становятся шестиугольными без помощи пчёл Регулярный ячеистый рисунок можно сделать, если ячейки будут треугольными, квадратными или шестиугольными. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска. Впервые такую «экономность» пчёл заметили в IV веке н. э., и тогда же было высказано предположение, что пчёлы при постройке сотов «руководствуются математическим планом». Однако, полагают исследователи из Кардиффского университета, инженерная слава пчёл сильно преувеличена: правильная геометрическая форма шестигранных ячеек сотов возникает из-за, действующих на них физических сил, а насекомые тут лишь помощники.
- Почему стекло прозрачное?
- По своей структуре простейшие биосистемы и углеводородные кристаллы необыкновенно похожи. Если такой минерал дополнить компонентами белка, то мы получим реальный протоорганизм. Именно так видит начало начал кристаллизационная концепция происхождения жизни.
- Споры о структуре воды вот уже не одно десятилетие волнуют как научную общественность, так и людей, с наукой не связанных. Этот интерес не случаен: структуре воды порой приписывают целебные свойства, причём многие уверены, что этой структурой можно управлять каким-то физическим методом либо просто силой духа. А каково мнение учёных, которые не одно десятилетие занимаются изучением тайн воды в жидком и твёрдом состоянии?
- Используя опыт других исследователей и результаты собственных экспериментальных и клиническо-экспериментальных исследований, автор в пределах своих возможностей указывает на лечебные свойства пчелиного меда и на методы его применения в медицине. Желая придать этому труду более законченный вид, и чтобы читатель получил более целостное представление о хозяйственном и медицинском значении пчел, в книге кратко будут рассмотрены и другие продукты пчеловодства, неразрывно связанные с жизнью пчел, а именно: пчелиный яд, пчелиное маточное молочко, цветочная пыльца, воск и прополис, а также и отношение науки к этим продуктам.
- Каустики на плоскости и в пространстве Каустики — это вездесущие оптические поверхности и кривые, возникающие при отражении и преломлении света. Каустики можно описать как линии или поверхности, вдоль которых концентрируются световые лучи.
- Они повсюду: в каждом электроприборе, начиная с телевизора и заканчивая старыми тамагочами. Мы не знаем о них практически ничего, ведь воспринимаем их как данность. Но без них мир бы полностью изменился. Полупроводники. О том, что это такое и как они работают.
- Полет шмеля оказался устойчив к турбулентности Международный коллектив ученых выяснил, насколько легко приходится шмелям летать в сильно ветреную погоду. Оказалось, что даже в условиях значительной турбулентности особый механизм создания подъемной силы позволяет насекомым оставаться на лету с минимальными дополнительными затратами энергии.
- Испанские ученые открыли механизм, который может приводить к спонтанному образованию кристаллов карбонатов и силикатов очень сложной и необычной формы. Эти кристаллические новообразования напоминают биоморфы — неорганические структуры, полученные при участии живых организмов. А механизм, приводящий к такой мимикрии, на удивление прост — это всего лишь самопроизвольные колебания pH раствора карбонатов и силикатов на границе формирующегося твердого кристалла и жидкой среды.
- Ледяные узоры высокого давления
Шестиугольник и его свойства
Развернуть структуру обучения
Свернуть структуру обучения
Шестиугольник — это многоугольник, общее количество углов (вершин) которого равно шести.
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Чему равна сумма углов выпуклого шестиугольника? Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов. См. теорему о сумме углов многоугольника.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Правильный шестиугольник
Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- всі внутрішні кути рівні між собою
- кожен внутрішній кут правильного шестикутника дорівнює 120 градусам
- всі сторони рівні між собою сторона правильного шестикутника дорівнює радіусу описаного кола
- правильний шестикутник заповнює плоскість без пропусків і накладень
Формулы для правильного шестиугольника
(по порядку следования формул)
- Радиус описанной окружности (R) правильного шестиугольника равен его стороне (t)
- Все внутренние углы равны 120 градусам
- Радиус вписанной окружности (r) равен корню из трех, деленному на два и умноженному на длину стороны t (радиус описанной окружности R)
- Периметр правильного шестиугольника (P) равен шести радиусам описанной окружности (R) или четыре корня из трех, умноженным на радиус вписанной окружности (r)
- Площадь правильного шестиугольника равна трем корням из трех пополам, умноженным на квадрат радиуса описанной окружности (R) или квадрат стороны (t); либо площадь правильного шестиугольника равна двум корням из трех, умноженным на квадрат радиуса вписанной окружности (t)
Задача
Найти объем цилиндра, вписанного в правильную шестиугольную призму, каждое ребро которой равно t. Решение. Так как высота цилиндра Н равна высоте призмы и равна а, достаточно найти радиус основания цилиндра, который будет равен радиусу окружности, вписанной в правильный шестиугольник. Знайти об’єм циліндра, вписаного в правильну шестикутну призму, кожне ребро якої дорівнює t. Рiшення. Так як висота циліндра Н дорівнює висоті призми і дорівнює а, достатньо знайти радіус основи циліндра, який буде дорівнювати радіусу кола, вписаного в правильний шестикутник. Правильный многоугольник | Описание курса | Сумма углов многоугольника
2.4.2 Построение правильных многоугольников по данной стороне
Построение
квадрата по данной его стороне L (рисунок
34). На произвольной прямой откладывают
отрезокAB, равный
стороне квадратаL.Из любого
конца отрезка, например из точкиA,
восстанавливают перпендикуляр и на нем
откладывают отрезокAD = L. Затем
из точекB иDкак из центров
проводят дуги радиусомR = Lи на
пересечении их отмечают точкуС.Соединив прямыми точку Cс точкамиB иD, получают квадрат
с заданной сторонойL.Построение
правильного шестиугольника по данной
его сторонеL(рисунок 35).
Известно, что сторона правильного
шестиугольника равна радиусу окружности,
описанной вокруг него.Поэтому, построив
на произвольной прямой отрезокAB=L
(рисунок 35, а), из концов его как из центров
проводят две дуги радиусом R=L
до взаимного пересечения их в точке О.Приняв точку О
за центр, проводят окружность тем же
радиусом R=L
и делят ее на шесть равных частей. Точки
деления являются вершинами правильного
шестиугольника со стороной L
(рисунок 35, б).- а б
- Рисунок
35 - Построение
правильного шестиугольника с помощью
линейки и угольника с углами 60 и 30°
показано на рисунке 36.
Приближенный
способ построения правильных
многоугольников данной сторонеAB (рисунок 37). Изложенный ниже
способ заключается в том, что правильный
многоугольник строят как вписанный в
окружность.Из концов отрезкаАВрадиусом, равным этому отрезку, проводят
две дуги до взаимного пересечения их в
точкахОиО6.Из точекA иВк отрезкуAB восстанавливают перпендикуляры,
и на пересечении их с проведенными
дугами получают две вершины квадрата
(на рисунке 37 отмечена одна из них).ЦентрO4окружности, описанной около квадрата,
расположен в точке пересечения диагонали
квадрата с вертикальной прямойOO6.Для построения вписанного пятиугольника
отрезокO4O6делят пополам в точкеO5и из нее как из центра описывают окружность
радиусом, равным отрезкуO5A.
СторонаAB пять
раз уложится на этой окружности.2.4.3 Построение правильных многоугольников, описанных около окружности
Правильный
описанный треугольник строят следующим
образом(рисунок 38).Точки
деления А, В, С
являются вершинами правильного
треугольника, описанного около окружности
радиуса R1.Правильный
описанный четырехугольник (квадрат)можно построить с помощью циркуля и
линейки (рисунок 39). В заданной окружности
проводят два взаимно перпендикулярных
диаметра.Приняв точки пересечения
диаметров с окружностью за центры,
радиусом окружностиR описывают дуги до взаимного их
пересечения в точкахА, В, С,D.Для
построения правильного описанного
шестиугольниканеобходимо вначале
построить вершины описанного квадрата
указанным выше способом
(рисунок 40, а).Одновременно с определением
вершин квадрата заданную окружность
радиуса R делят
на шесть равных частей в точках 1,
2, 3, 4, 5, 6 и
проводят вертикальные стороны квадрата.Проведя через точки деления окружности
2–5
и 3–6
прямые до пересечения их с вертикальными
сторонами квадрата (рисунок 40, б), получают
вершины А, В, D, Е
описанного правильного шестиугольника.Построение правильного шестигранника
Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.
Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.
В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.
Способ вычерчивания шестиугольника циркулем, линейкой
Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.
Метод выглядит следующим образом:
Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 – углы, 0 – центр, D – радиус шестигранника.
- циркулем вычерчивается окружность – радиус является размером стороны;
- по линейке проводится радиус – точки пересечения этого отрезка будут углами многоугольника;
- находятся два угла многоугольника – циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
- находятся оставшиеся два угла – циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.
Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.
Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.
Способ вычерчивания шестиугольника без циркуля
Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины – специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.
Способ построения выглядит следующим образом:
Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 – углы, 0 – центр, D – радиус шестигранника.
- к одной стороне отрезка прикладывается угольник – короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
- на листе/заготовке вычерчивается линия – длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
- операция повторяется при развороте угольника – угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
- разворот угольника – теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
- уточнение размеров сторон – на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
- строительство двух оставшихся сторон – они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
- контроль параллельности – шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком
Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.
Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.
Третий способ вычерчивания шестиугольника циркулем: a – диаметр, b – сторона шестигранника.
В последнем случае удобнее несколько изменить технологию:
- после вычерчивания центрального отрезка по нему выравнивается рейсшина;
- инструмент откатывается вниз на произвольную величину;
- короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
- скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.
Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.
Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.
[spoiler title=”источники:”]
http://regionvtormet.ru/metally/postroenie-pravilnogo-shestiugolnika-i-ego-svojstva-ugly-ploshhad-i-radiusy-okruzhnostej-interesnye-fakty.html
http://moiinstrumenty.ru/standartnye/postroenie-shestigrannika.html
[/spoiler]
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
- Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
- Пошаговая инструкция будет выглядеть так:
чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
- При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
- Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису.
Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность.
Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Газовый баллон для компрессора
- R=а.
- Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
- Ну а площадь этой окружности будет стандартная:
- S=πR²
Вписанная окружность
- Высота равностороннего треугольника вычисляется просто:
- h²=а²-(а/2)²= а²3/4, h=а(√3)/2
- А поскольку R=a и r=h, то получается, что
- r=R(√3)/2.
- Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
- Ее площадь будет составлять:
- S=3πa²/4,
- то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
- S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
- S=3R²(√3)/2
- Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Как прозвонить диод мультиметром на плате
- Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
- Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
- d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
Формула для нахождения площади правильного шестиугольника через сторону:
Через радиус описанной окружности
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Станок для заточки фуганочных ножей
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
- Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
- Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
- Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.
- При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt ) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
- Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
- Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
- Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
- Радиус вписанной окружности правильного шестиугольника равен апофеме:
- (r = m = alargefrac
ormalsize) - Радиус описанной окружности равен стороне правильного шестиугольника:
- Периметр правильного шестиугольника
- Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
- (S = pr = largefrac
ormalsize), - где (p) − полупериметр шестиугольника.
Источник: https://MyTooling.ru/instrumenty/radius-pravilnogo-shestiugolnika-formula
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90º и/или циркуля.
При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 2.24).
Последовательно соединив полученные точки, получают правильный вписанный шестиугольник.

а) б)
Рисунок 2.24
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 2.25). Соединив полученные точки, получают двенадцатиугольник.

а) б)
Рисунок 2.25
2.2.5 Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 2.26.

а) б) в) г)
Рисунок 2.26
Половину любого диаметра (радиус) делят пополам (рис. 2.26 а), получают точку А.Из точки А,как из центра, проводят дугу радиусом, равным расстоянию от точки Адо точки 1 до пересечения со второй половиной этого диаметра, в точке В(рис. 2.26 б). Отрезок 1Вравен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности.
Делая засечки на окружности (рис. 2.26, в) радиусом К,равным отрезку 1В,делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2 и 5 (рис. 2.26, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4.
Расстояние от точки 3 до точки 4 проверяют циркулем. Если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной.
Последовательно соединив найденные точки, получают пятиугольник (рис. 2.26, г).
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 2.26), но сначала делят окружность на пять частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 2.27, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник(рис. 2.27, б).

а) б)
Рисунок 2.27
2.2.6 Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и
четырнадцатиугольника
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 2.28 и 2.29.
Из любой точки окружности, например точки А, радиусом заданной окружности проводят дугу (рис. 2.28, а) до пересечения с окружностью в точках В и D. Соединим точки Ви Dпрямой.
Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС,делают засечки на окружности в последовательности, показанной на рис. 2.28, б.
Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 2.28, в).
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 2.29, а).

а) б) в)
Рисунок 2.28
Сначала окружность делится на семь равных частей от точки 1, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырнадцатиугольник (рис. 2.29, б).

- а) б)
- Рисунок 2.29
- Построение эллипса
- Изображение окружности в прямоугольной изометрической проекции во всех трех плоскостях проекций представляет собой одинаковые по форме эллипсы.
- Направление малой оси эллипса совпадает с направлением аксонометрической оси, перпендикулярной той плоскости проекций, в которой лежит изображаемая окружность.
При построении эллипса, изображающего окружность небольшого диаметра, достаточно построить восемь точек, принадлежащих эллипсу (рис. 2.30). Четыре из них являются концами осей эллипса (A, B, С, D),а четыре других (N1, N2, N3, N4) расположены на прямых, параллельных аксонометрическим осям, на расстоянии, равном радиусу изображаемой окружности от центра эллипса.
Рисунок 2.30
Источник: https://infopedia.su/18x100b.html
Урок по геометрии «Построение правильных многоугольников» 9 класс
- Тема: Построение правильных многоугольников.
- Этап ориентации.
- Оборудование: раздаточный тестовый материал, мультимедийный экран, компьютер, карточки с заданиями.
- Урок с использованием метода проектов, интерактивных технологий (работа в группах) предполагает класс разбить на 3 группы по интересам.
- Этап постановки цели урока.
-
Научить учеников строить правильные треугольники, четырёхугольники и шестиугольники;
-
Найти способ построения правильных 2n угольников;
-
Показать практическое применение данных построений в архитектуре и в быту;
-
Прививать каждому ученику вкус к самостоятельной, активной и творческой деятельности;
-
Развивать познавательный интерес к предмету.
Этап проектирования.
-
Организационный момент.
-
Актуализация опорных знаний (2 вида тестов).
-
Мотивация учебной деятельности (презентации).
-
Исторический доклад.
-
Изложение нового материала (использование программы «Живая геометрия»).
-
Самостоятельная работа.
-
Итог урока. Заключительная презентация.
-
Домашнее задание.
Этап организации выполнения плана действий.
Учитель.
Здравствуйте, сегодня у нас открытие банка «Созвездие». Наши гости выступают в роли акционеров банка «Созвездие». Я, как управляющая банком, собрала вас, акционеров, с целью донесения до вас новой информации и принятия решения.
Сегодня в наш банк «Созвездие» обратились первые представители трёх организаций (пчеловодов, архитекторов, дизайнеров интерьера), с целью оформить кредит в нашем банке.
И мы должны с вами принять решение о выдаче кредита (либо отказе) и о его сумме.
На повестке собрания —
1. Представители организаций должны убедить нас в необходимости и перспективности своих планов;
2. Информировать нас о своих финансовых возможностях.
3. А мы должны вынести решение о возможности (невозможности) кредитования.
Все финансовые операции будут производить бухгалтеры нашего банка и результаты заносить в векселя.
Представление организаций.
1 – Организация пчеловодов (разводят пчел). Кредит нужен для приобретения пасеки.

2 – Архитекторы (создают проекты зданий). Оформляют кредит для приобретения лицензионных программ с использованием трехмерного пространства.
3 – Дизайнеры интерьеров (создают эскизы паркета). Кредит – для поездки в Швейцарию. Цель поездки — обмен опытом.
2. Актуализация опорных знаний.
Учитель.
Необходимое условие кредитования — это заполнение анкетных данных всеми представителями организаций. На столах у вас лежат анкеты на синих и красных листах. Вы выбираете анкеты согласно своим возможностям.
- Решение тестовых заданий по уровням сложности:
- Фамилия_________________ Имя___________________
- Максимальное количество — 4 балл (4000 грн.)
1. Какая из ломанных является многоугольником?

2.Какой многоугольник выпуклый?

3. Многоугольник является правильным, если все его ….
1) углы равны; 2) углы и стороны равны; 3) стороны равны.
4. Соедините стрелочками соответствующие ячейки согласно формулам.
- Радиус окружности, описанной около правильного треугольника
- a
- ____
- 2
- Радиус окружности, вписанной в правильный четырёхугольник
- a
- Радиус окружности, описанной около правильного шестиугольника
- a
- ____
- √3
- Фамилия_________________ Имя___________________
- Максимальное количество — 8 баллов (8000 грн.)
1.Соедините стрелочками соответствующие ячейки согласно формулам.
- Радиус окружности, описанной около правильного треугольника
- a
- ____
- 2
- Радиус окружности, вписанной в правильный четырёхугольник
- a
- Радиус окружности, описанной около правильного шестиугольника
- a
- ____
- √3
- Радиус окружности, вписанной в правильный треугольник
- а
- ____
- 2√3
- Радиус окружности, вписанной в правильный шестиугольник
- a√3
- ____
- 2
- Радиус окружности, описанной около правильного четырёхугольника
- a
- ____
- 2sin 180
- n
- Радиус окружности, вписанной в правильный многоугольник
- а
- ____
- √2
- Радиус окружности, описанной около правильного многоугольника
- a
- ____
- 2tg 180
- n
2. Может ли пятиугольник иметь стороны длиной 3 см, 4 см, 8 см, 6см, 25 см?
1) да; 2) нет.
3. В правильном n-угольнике сумма внутренних углов равна 3600. Сколько сторон у этого многоугольника?
- 1) 4; 2) 3; 3) 5.
- 4. У правильного пятиугольника внешний угол равен:
- 1) 360; 2) 45 0; 3) 72 0.

Тесты проверяют бухгалтеры и ответы помещают в векселя.
(Федоренко Б., Верескун Е., Фещенко Е.)
3. Мотивация учебной деятельности.
- Учитель.
- А теперь мы дадим возможность каждой из организаций презентовать свои проекты:
- Презентации 3х групп: (выступление авторов)
-
Пчеловоды; («Геометрия пчелиных сот») Полященко Вика
-
Архитекторы; (пентагон,..) Парубаева Вика
-
Дизайнеры интерьера (эскизы паркета) Полященко Влада.
- После презентаций делаем вывод:
- Что все организации столкнулись с необходимостью построения правильных многоугольников.
- Объявление практической темы собрания:
- Построение правильных многоугольников
- с помощью линейки и циркуля.
- Представители, какой организации могут дать нам историческую справку о создателе метода построения правильных многоугольников?
4.Исторический доклад — Брусниченко А
Первокурсник Геттингенского университета Карл Гаусс (1777–1855) решил задачу, перед которой математическая наука пасовала более 2 с лишним тысяч лет.
Еще древние греки нашли способы построения с помощью только циркуля и линейки правильных многоугольников с числом сторон 3, 4, 5, 15, а также с числом сторон, большим в 2 раза. Однако в отношении прочих правильных многоугольников царила полная неизвестность.
И вот будущий «король математиков» Гаусс догадался, как построить правильный 17-угольник. Это открытие стало поворотным пунктом в его жизни: ранее колебавшийся между филологией и математикой, теперь он твердо решил посвятить себя последней.
Это событие Гаусс посчитал столь значительным, что отметил его в «Дневнике» (запись от 30 марта 1796) и завещал высечь правильный 17-угольник на своём надгробии (воля Гаусса была исполнена).
5. Изложение нового материала.
- А теперь мы хотим выслушать ваше решение данной проблемы – «построение правильного многоугольника».
- Для построения правильных многоугольников будем использовать связь с окружностью.
- 1 группа – строит правильный шестиугольник (Кузьмина Е.)
- 3 группа — строит правильный треугольник; (Христолюбов А. )
- 2 группа — строит правильный пятиугольник; (Дударева Я.);
- Все участники чертят чертежи по очереди у себя в тетрадях по заранее готовым окружностям.
А наш банк предлагает вам альтернативное решение данной проблемы — с помощью программы «Живая геометрия» — платно!.
Четырёхугольник (восьмиугольник) – Набоков Д. на компьютере с помощью программы «Живая геометрия»
Вопрос ко всем присутствующим:
В чём преимущества построения правильных многоугольников с помощью программы «Живая геометрия»? И готовы ли вы будете её у нас приобрести?
После выполнения построения участники делают вывод, как построить правильный 2n-угольник, используя правильный n-угольник.
Банк даёт вам возможность увеличить сумму кредита – выполнение заданий самостоятельной работы (чем больше выполненных заданий, тем больше сумма кредита) (на разноцветных листах А4):
-
Задания для самостоятельной работы:
Чертежи выполняют на заранее приготовленных карточках:
Средний уровень – построить правильный восьмиугольник

Высокий уровень — построить правильный шестнадцатиугольник.

Достаточный уровень — построить правильный двенадцаугольник

Проверяют бухгалтеры и заносят баллы в векселя.
А теперь, пока бухгалтеры выполняют подсчёты, мы все вместе посмотрим презентацию «Правильные 4,5,6,7,8,9 – угольники в быту, технике, архитектуре, природе». В ходе просмотра данной презентации, мы, возможно, увидели потенциальных клиентов нашего банка.
Подводим итоги нашего собрания:
Источник: https://infourok.ru/material.html?mid=84363
Построение правильных многоугольников
- Построить правильный шестиугольник, сторона которого равна данному отрезку.
- Дано: отрезок DC.
- Построить: правильный шестиугольник, сторона которого равна DC.
- Решение:
Для решения задачи воспользуемся тем, что сторона шестиугольника равна радиусу описанной около него окружности, т.е. (смотри формулу для вычисления стороны правильного многоугольника), где — радиус окружности описанной около правильного многоугольника. Нам нужно построить правильный шестиугольник со стороной DC, поэтому с помощью циркуля измеряем отрезок DC и строим окружность радиуса DC, и отмечаем на ней произвольную точку А1, центр окружности обозначаем буквой О.
Затем не меняя раствора циркуля, построим на этой окружности точки А2, А3, А4, А5, А6, так, чтобы выполнялись равенства
А1А2 = А2А3 = А3А4 = А4А5 = А5А6 = DC (т.е.
сначала строим окружность радиуса DC с центром в точке А1 (всю окружность строить необязательно, смотри выделенное красным), данная окружность пересечет окружность с центром О в точке А2, далее аналогично строим окружность радиуса DC с центром в точке А2, она пересечет окружность с центром О в точке А3 и т.д.).

Теперь соединяя последовательно построенные точки отрезками, получим искомый правильный шестиугольник А1А2А3А4А5А6.

Задача 2
Дан правильный -угольник. Построить правильный 2-угольник.
Дано: правильный -угольник А1А2А3…Аn.
- Построить: правильный 2-угольник.
- Решение:
- Пусть, например, нам дан шестиугольник А1А2А3А4А5А6, значит, построить нужно двенадцатиугольник.
Сначала опишем около данного шестиугольника А1А2А3А4А5А6 окружность. Для этого построим биссектрисы углов А1 и А2.
Чтобы построить биссектрису угла А1, строим окружность произвольного радиуса с центром в точке А1 (полностью окружность строить необязательно, смотри выделенное красным цветом), данная окружность пересечет стороны А1А2 и А1А6 угла А1 в точках Е и К. Затем строим две окружности с центрами в точках Е и К радиуса ЕК (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом), данные окружности пересекутся в точке Р. Далее проводим луч А1Р, который и будет биссектрисой угла А1.
- Аналогично строим биссектрису угла А2.
- Точку пересечения биссектрис углов А1 и А2 обозначаем буквой О и строим окружность радиуса ОА1 с центром О (окружность описанная около А1А2А3А4А5А6).
Далее нужно каждую из дуг А1А2, А2А3, А3А4, А4А5, А5А6, А6А1разделитьпополам. Чтобы разделить дугу А1А2 пополам, построим серединный перпендикуляр к отрезку А1А2.
Для этого строим две окружности с центрами в точках А1 и А2 радиуса А1А2 (полностью окружность строить необязательно, смотри выделенное красным цветом). Данные окружности пересекутся в двух точках, одну обозначим буквой М, а другая совпадет с точкой О, т.к.
у шестиугольника сторона равна радиусу (с другими многоугольниками совпадения с точкой О не будет) . Затем проводим прямую МО, данная прямая пересечет дугу А1А2 в точке В1, которая и разделит дугу А1А2 пополам.
Далее точку В1 соединяем с концами А1 и А2 дуги А1А2.
Аналогично находим точки В2, В3. Точки В4, В5, В6 в данном случае строить необязательно, они получаются автоматически при построении точек В1, В2, В3, т.к. шестиугольник симметричная фигура.
- Получили двенадцатиугольник А1В1А2В2А3В3А4В4А5В5А6В6 (смотри выделенное красным).
- Мы выполняли построения на примере правильного шестиугольника, если мы имеем произвольный правильный -угольник, то все построения выполняются аналогично.
Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный треугольник и пользуясь результатом задачи 2, можно построить правильный шестиугольник, затем правильный двенадцатиугольник и вообще 2k-угольник, где — любое целое число, больше двух.
Замечание
Не все правильные многоугольники можно построить с помощью циркуля и линейки. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.
Источник: https://budu5.com/manual/chapter/3573
Правильный шестиугольник ≪ Scisne?
Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
.
Все углы равны 120°. Радиус вписанной окружности равен:
.
Периметр правильного шестиугольника равен: Площадь правильного шестиугольника рассчитывается по формулам: ,
.
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.

Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости.
В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Наиболее плотная упаковка кругов на плоскости
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала). Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Построение правильного шестиугольника с помощью циркуля и линейки
Правильный шестиугольник в природе, технике и культуре
Пчелиные соты показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы, например графит, имеют гексагональную кристаллическую решётку.
Кристаллическая решетка графита
Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Гигантский гексагон — атмосферное явление на Сатурне.
Гигантский гексагон — устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер-1 и наблюдаемое снова в 2006 году аппаратом Кассини-Гюйгенс.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Вращение гексагона на северном полюсе Сатурна
Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса. Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м. Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Игровое поле зачастую составляют шестиугольники. Замощение плоскости правильными шестиугольниками является основой для гекса, гексагональных шахмат и других игр на клетчатом поле, полигексов, вариантов модели «Жизнь» и других двумерных клеточных автоматов, кольцевых флексагонов и т.п.
Гексагональные шахматы Глинского. Начальное положение фигур.
Сечение гайки имеет вид правильного шестиугольника.
Звезда Давида (гексаграмма) — шестиконечная звезда, образованная двумя правильными треугольниками, символ иудаизма.
- Пчелиные соты становятся шестиугольными без помощи пчёл Регулярный ячеистый рисунок можно сделать, если ячейки будут треугольными, квадратными или шестиугольными. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска. Впервые такую «экономность» пчёл заметили в IV веке н. э., и тогда же было высказано предположение, что пчёлы при постройке сотов «руководствуются математическим планом». Однако, полагают исследователи из Кардиффского университета, инженерная слава пчёл сильно преувеличена: правильная геометрическая форма шестигранных ячеек сотов возникает из-за, действующих на них физических сил, а насекомые тут лишь помощники.
- Почему стекло прозрачное?
- По своей структуре простейшие биосистемы и углеводородные кристаллы необыкновенно похожи. Если такой минерал дополнить компонентами белка, то мы получим реальный протоорганизм. Именно так видит начало начал кристаллизационная концепция происхождения жизни.
- Споры о структуре воды вот уже не одно десятилетие волнуют как научную общественность, так и людей, с наукой не связанных. Этот интерес не случаен: структуре воды порой приписывают целебные свойства, причём многие уверены, что этой структурой можно управлять каким-то физическим методом либо просто силой духа. А каково мнение учёных, которые не одно десятилетие занимаются изучением тайн воды в жидком и твёрдом состоянии?
- Используя опыт других исследователей и результаты собственных экспериментальных и клиническо-экспериментальных исследований, автор в пределах своих возможностей указывает на лечебные свойства пчелиного меда и на методы его применения в медицине. Желая придать этому труду более законченный вид, и чтобы читатель получил более целостное представление о хозяйственном и медицинском значении пчел, в книге кратко будут рассмотрены и другие продукты пчеловодства, неразрывно связанные с жизнью пчел, а именно: пчелиный яд, пчелиное маточное молочко, цветочная пыльца, воск и прополис, а также и отношение науки к этим продуктам.
- Каустики на плоскости и в пространстве Каустики — это вездесущие оптические поверхности и кривые, возникающие при отражении и преломлении света. Каустики можно описать как линии или поверхности, вдоль которых концентрируются световые лучи.
- Они повсюду: в каждом электроприборе, начиная с телевизора и заканчивая старыми тамагочами. Мы не знаем о них практически ничего, ведь воспринимаем их как данность. Но без них мир бы полностью изменился. Полупроводники. О том, что это такое и как они работают.
- Полет шмеля оказался устойчив к турбулентности Международный коллектив ученых выяснил, насколько легко приходится шмелям летать в сильно ветреную погоду. Оказалось, что даже в условиях значительной турбулентности особый механизм создания подъемной силы позволяет насекомым оставаться на лету с минимальными дополнительными затратами энергии.
- Испанские ученые открыли механизм, который может приводить к спонтанному образованию кристаллов карбонатов и силикатов очень сложной и необычной формы. Эти кристаллические новообразования напоминают биоморфы — неорганические структуры, полученные при участии живых организмов. А механизм, приводящий к такой мимикрии, на удивление прост — это всего лишь самопроизвольные колебания pH раствора карбонатов и силикатов на границе формирующегося твердого кристалла и жидкой среды.
- Ледяные узоры высокого давления
Далее >>>
Источник: https://scisne.net/a-1926
Шестиугольник и его свойства
Развернуть структуру обучения
Свернуть структуру обучения
Шестиугольник — это многоугольник, общее количество углов (вершин) которого равно шести.
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Чему равна сумма углов выпуклого шестиугольника? Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов. См. теорему о сумме углов многоугольника.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Правильный шестиугольник
Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Свойства правильного шестиугольника
|
|
Формулы для правильного шестиугольника
(по порядку следования формул)
- Радиус описанной окружности (R) правильного шестиугольника равен его стороне (t)
- Все внутренние углы равны 120 градусам
- Радиус вписанной окружности (r) равен корню из трех, деленному на два и умноженному на длину стороны t (радиус описанной окружности R)
- Периметр правильного шестиугольника (P) равен шести радиусам описанной окружности (R) или четыре корня из трех, умноженным на радиус вписанной окружности (r)
- Площадь правильного шестиугольника равна трем корням из трех пополам, умноженным на квадрат радиуса описанной окружности (R) или квадрат стороны (t); либо площадь правильного шестиугольника равна двум корням из трех, умноженным на квадрат радиуса вписанной окружности (t)
Задача
| Найти объем цилиндра, вписанного в правильную шестиугольную призму, каждое ребро которой равно t. Решение. Так как высота цилиндра Н равна высоте призмы и равна а, достаточно найти радиус основания цилиндра, который будет равен радиусу окружности, вписанной в правильный шестиугольник. | Знайти об’єм циліндра, вписаного в правильну шестикутну призму, кожне ребро якої дорівнює t. Рiшення. Так як висота циліндра Н дорівнює висоті призми і дорівнює а, достатньо знайти радіус основи циліндра, який буде дорівнювати радіусу кола, вписаного в правильний шестикутник. |
0
Правильный многоугольник | Описание курса | Сумма углов многоугольника
Источник: https://profmeter.com.ua/communication/learning/course/course7/lesson669/
2.4.2 Построение правильных многоугольников по данной стороне
Построение
квадрата по данной его стороне L (рисунок
34). На произвольной прямой откладывают
отрезокAB, равный
стороне квадратаL.
Из любого
конца отрезка, например из точкиA,
восстанавливают перпендикуляр и на нем
откладывают отрезокAD = L. Затем
из точекBиDкак из центров
проводят дуги радиусомR = Lи на
пересечении их отмечают точкуС.
Соединив прямыми точкуCс точкамиBиD, получают квадрат
с заданной сторонойL.
Рисунок
34
Построение
правильного шестиугольника по данной
его сторонеL(рисунок 35).
Известно, что сторона правильного
шестиугольника равна радиусу окружности,
описанной вокруг него.
Поэтому, построив
на произвольной прямой отрезокAB=L
(рисунок 35, а), из концов его как из центров
проводят две дуги радиусом R=L
до взаимного пересечения их в точке О.
Приняв точку О
за центр, проводят окружность тем же
радиусом R=L
и делят ее на шесть равных частей. Точки
деления являются вершинами правильного
шестиугольника со стороной L
(рисунок 35, б).
- а б
- Рисунок
35 -
Построение
правильного шестиугольника с помощью
линейки и угольника с углами 60 и 30°
показано на рисунке 36.
Рисунок
36
Приближенный
способ построения правильных
многоугольников данной сторонеAB(рисунок 37).Изложенный ниже
способ заключается в том, что правильный
многоугольник строят как вписанный в
окружность.
Из концов отрезкаАВрадиусом, равным этому отрезку, проводят
две дуги до взаимного пересечения их в
точкахОиО6.
Из точекAиВк отрезкуABвосстанавливают перпендикуляры,
и на пересечении их с проведенными
дугами получают две вершины квадрата
(на рисунке 37 отмечена одна из них).
ЦентрO4окружности, описанной около квадрата,
расположен в точке пересечения диагонали
квадрата с вертикальной прямойOO6.
Для построения вписанного пятиугольника
отрезокO4O6делят пополам в точкеO5и из нее как из центра описывают окружность
радиусом, равным отрезкуO5A.
СторонаABпять
раз уложится на этой окружности.
Центры
окружностей, в которые сторонаABукладывается 8, 10, 12 и т. д. раз,
расположены в точках пересечения прямойOO6с окружностями соответственно радиусовO4A,О5А,О6Аи т. д.
Разделив пополам отрезкиO6O8,O8O10,O10O12и т.д., получают точкиO7,O9,
O11и т.
д., являющиеся центрами окружностей, в
которые сторонаABукладывается 7, 9, 11 и т. д. раз. Радиусы
этих окружностей равныO7A,
O9A,O11Aи т.д.
Рисунок
37
2.4.3 Построение правильных многоугольников, описанных около окружности
Правильный
описанный треугольник строят следующим
образом(рисунок 38).
Из центра
заданной окружности радиусаR1проводят
окружность радиусом R2
= 2R1
и делят ее на три равные части.
Точки
деления А, В, С
являются вершинами правильного
треугольника, описанного около окружности
радиуса R1.
Рисунок
38
Правильный
описанный четырехугольник (квадрат)можно построить с помощью циркуля и
линейки (рисунок 39). В заданной окружности
проводят два взаимно перпендикулярных
диаметра.
Приняв точки пересечения
диаметров с окружностью за центры,
радиусом окружностиRописывают дуги до взаимного их
пересечения в точкахА, В, С,D.
ТочкиA,B,C,Dи являются вершинами квадрата,
описанного около данной окружности.
Рисунок
39
Для
построения правильного описанного
шестиугольниканеобходимо вначале
построить вершины описанного квадрата
указанным выше способом
(рисунок 40, а).
Одновременно с определением
вершин квадрата заданную окружность
радиуса R делят
на шесть равных частей в точках 1,
2, 3, 4, 5, 6 и
проводят вертикальные стороны квадрата.
Проведя через точки деления окружности
2–5
и 3–6
прямые до пересечения их с вертикальными
сторонами квадрата (рисунок 40, б), получают
вершины А, В, D, Е
описанного правильного шестиугольника.
а б
Рисунок
40
Источник: https://studfile.net/preview/3636633/page:9/

- Определение и построение
- Свойства простые и интересные
- Описанная окружность и возможность построения
- Вписанная окружность
- Периметр и площадь
- Занимательные построения
- От теории к практике
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
180°(n-2),
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность

Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
S=3(2r/√3)²(√3)/2=r²(2√3)
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.





























 чертится прямая линия и на ней ставится точка;
чертится прямая линия и на ней ставится точка;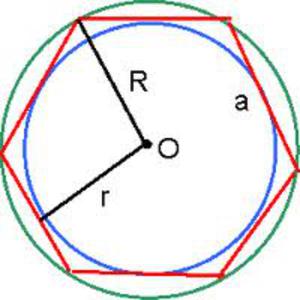 Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
 чертится прямая линия и на ней ставится точка;
чертится прямая линия и на ней ставится точка;

 Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.









