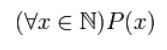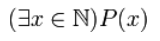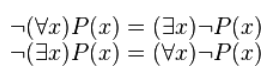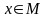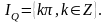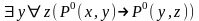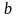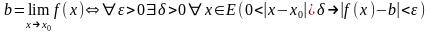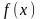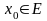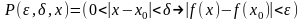Татьяна Шкляр
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Понятие предиката
Определение 1
Предикат – утверждение, которое содержит переменные, принимающие значение $1$ или $0$ (истинно или ложно) в зависимости от значений переменных.
Пример 1
Например, выражение $x=x^5$ является предикатом, т.к. оно является истинным при $x=0$ или $x=1$ и ложным при всех остальных значениях $x$.
Определение 2
Множество, на котором предикат принимает только истинные значения, называется множеством истинности предиката $I_p$.
Замечание 1
Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:
$P (x_1, dots, x_n)=1$
Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:
$P (x_1, dots, x_0)=0$
Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.
Т.к. предикаты могут принимать только два значения (истинно/ложно или $0/1$), то к ним можно применять все операции алгебры логики: отрицание, конъюнкция, дизъюнкция и т.д.
Примеры предикатов
Пусть предикат $R(x, y)$: $«x = y»$ обозначает отношение равенства, где $x$ и $y$ принадлежат множеству целых чисел. В этом случае предикат R будет принимать истинное значение для всех равных $x$ и $y$.
Другой пример предиката — РАБОТАЕТ($x, y, z$) для отношения «$x$ работает в городе y в компании $z$».
Еще один пример предиката — НРАВИТСЯ($x, y$) для «x нравится y» для $x$ и $y$, которые принадлежат $M$ — множеству всех людей.
Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.
«Предикаты и кванторы» 👇
Операции над предикатами
Рассмотрим применение операций алгебры логики к предикатам.
Логические операции:
Определение 3
Конъюнкция двух предикатов $A(x)$ и $B(x)$ — предикат , который принимает истинное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает истинное значение, а ложное значение — во всех остальных случаях. Множество истинности $T$ предиката — пересечение множеств истинности предикатов $A(x)$ и $B(x)$. Например: предикат $A(x)$: «$x$ — чётное число», предикат $B(x)$: «$x$ делится на $5$». Таким образом, предикатом будет выражение «$x$ — чётное число и делится на $5$» или «$x$ делится на $10$».
Определение 4
Дизъюнкция двух предикатов $A(x)$ и $B(x)$ — предикат , который принимает ложное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает ложное значение и принимает истинное значение во всех остальных случаях. Множество истинности предиката — объединение областей истинности предикатов $A(x)$ и $B(x)$.
Определение 5
Отрицание предиката $A(x)$ — предикат, который принимает истинное значение при всех значениях $x$ из $T$, при которых предикат $A(x)$ принимает ложное значение и наоборот. Множество истинности предиката $A(x)$ — дополнение $T’$ к множеству $T$ в множестве $x$.
Определение 6
Импликация предикатов $A(x)$ и $B(x)$ — предикат , который является ложным при тех и только тех значениях $x$ из $T$, при которых $A(x)$ — истинно, а $B(x)$ — ложно, и принимает истинное значение во всех остальных случаях. Читается: «Если $A(x)$, то $B(x)$».
Пример 2
Пусть $A(x)$: «Натуральное число $x$ делится на $3$»;
$B(x)$: «Натуральное число $x$ делится на $4$».
Составим предикат: «Если натуральное число $x$ делится на $3$, то оно делится и на $4$».
Множество истинности предиката — объединение множества истинности предиката $B(x)$ и дополнения к множеству истинности предиката $A(x)$.
Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.
Кванторы
Определение 7
Кванторы — логические операторы, применение которых к предикатам превращает их в ложные или истинные высказывания.
Определение 8
Квантор — логические операции, которые ограничивают область истинности предиката и создают высказывание.
Чаще всего используют кванторы:
-
квантор всеобщности (обозначается символом $forall x$) — выражение «для всех $x$» («для любого $x$»);
-
квантор существования (обозначается символом $exists x$) — выражение «существует $x$ такое, что… »;
-
квантор единственности и существования (обозначается $exists !x$) — выражение «существует точно одно такое $x$, что… ».
В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.
Примеры применения кванторов
Пусть — предикат «$x$ кратно $7$».
С помощью квантора всеобщности можно записать следующие ложные высказывания:
-
любое натуральное число делится на $7$;
-
каждое натуральное число делится на $7$;
-
все натуральные числа делятся на $7$;
который будет иметь вид:
Рисунок 1.
Для записи истинных высказываний используем квантор существования:
-
существуют натуральные числа, которые делятся на $7$;
-
найдётся натуральное число, которое делится на $7$;
-
хотя бы одно натуральное число делится на $7$.
Запись будет иметь вид:
Рисунок 2.
Пусть на множестве $x$ простых чисел задан предикат : «Простое число является нечетным». Поставив перед предикатом слово «любое», получим ложное высказывание: «Любое простое число является нечетным» (например, $2$ является простым четным числом).
Поставим перед предикатом слово «существует» и получим истинное высказывание: «Существует простое число , которое является нечетным» (например, $x=3$ ).
Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.
Операции над кванторами
Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:
Рисунок 3.
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:
Рисунок 4.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Логика предикатов
Предикаты вслед за высказываниями являются следующим важным предметом, исследуемым математической логикой. Понятие предиката обобщает понятие высказывания, а теория предикатов представляет собой более тонкий инструмент, по сравнению с теорией высказываний, для изучения закономерностей процессов умозаключения и логического следования, составляющих предмет математической логики. В настоящей главе рассматриваются основы теории предикатов.
Понятие предиката
В высказывании все четко: это — конкретное утверждение о конкретных объектах — истинное или ложное. Предикат — предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить, истинно оно или ложно. Дадим точное определение.
Определение 18.1. Определенным на множествах n-местным предикатом называется предложение, содержащее
переменных
, превращающееся в высказывание при подстановке вместо этих переменных любых конкретных элементов из множеств
соответственно.
Для n-местного предиката будем использовать обозначение . Переменные
называют предметными, а элементы множеств
, которые эти переменные пробегают, — конкретными предметами. Всякий n-местный предикат
, определенный на множествах
, представляет собой функцию п аргументов, заданную на указанных множествах и принимающую значения в множестве всех высказываний. Поэтому предикат называют также функцией-высказыванием.
Рассмотрим пример. Предложение “Река впадает в озеро Байкал” является одноместным предикатом, определенным над множеством всех названий рек. Подставив вместо предметной переменной
название “Баргузин”, получим высказывание “Река Баргузин впадает в озеро Байкал”. Это высказывание истинно. Подставив вместо предметной переменной
название “Днепр”, получим ложное высказывание “Река Днепр впадает в озеро Байкал”.
Другой пример. Предложение (выражение) “” является двухместным предикатом, заданным над множествами
. Множества, на которых задан двухместный предикат, совпадают (говорят, что “двухместный предикат задан на множестве
“). Пара действительных чисел 2, 2 превращает данный предикат в истинное высказывание: “
“, а пара чисел 2, 3 — в ложное: “
“.
Отметим еще один подход к понятию предиката. Как отмечалось, предикат , определенный на множествах
, превращается в конкретное высказывание
, если вместо предметных переменных
подставить в него конкретные предметы (элементы
) из множеств
соответственно. Это высказывание может быть либо истинным, либо ложным, т. е. его логическое значение равно 1 или 0. Следовательно, данный предикат определяет функцию
аргументов, заданную на множествах
принимающую значение в двухэлементном множестве
. Иногда эту функцию и называют предикатом.
Классификация предикатов
Определение 18.2. Предикат , заданный на множествах
, называется:
а) тождественно истинным, если при любой подстановке вместо переменных любых конкретных предметов
из множеств
соответственно он превращается в истинное высказывание
;
б) тождественно ложным, если при любой подстановке вместо переменных любых конкретных предметов из множеств
соответственно он превращается в ложное высказывание;
в) выполнимым (опровержимым), если существует по меньшей мере один набор конкретных предметов из множеств
соответственно, при подстановке которых вместо соответствующих предметных переменных в предикат
последний превратится в истинное (ложное) высказывание
.
Приведем примеры предикатов.
Одноместный предикат “Город расположен на берегу реки Волги”, определенный на множестве названий городов, является выполнимым, потому что существуют города, названия которых превращают данный предикат в истинное высказывание, или, иначе, удовлетворяют этому предикату (например, Ульяновск, Саратов и т. д.). Но данный предикат не будет тождественно истинным, потому что существуют города, названия которых превращают его в ложное высказывание, или, иначе, не удовлетворяют этому предикату (например, Прага, Якутск и т.д.). Этот же предикат являет собой пример опровержимого, но не тождественно ложного предиката (продумайте!).
В другом примере одноместный предикат ““, определенный на множестве действительных чисел, тождественно истинный. Наконец, двухместный предикат “
“, заданный также на множестве действительных чисел, является тождественно ложным предикатом, потому что любая пара действительных чисел превращает его в ложное высказывание (не удовлетворяет ему).
Отметим некоторые достаточно очевидные закономерности взаимосвязей между предикатами различных типов (рекомендуется осмыслить их):
1) каждый тождественно истинный предикат является выполнимым, но обратное неверно;
2) каждый тождественно ложный предикат является опровержимым, но обратное неверно;
3) каждый не тождественно истинный предикат будет опровержимым, но, вообще говоря, не будет тождественно ложным;
4) каждый не тождественно ложный предикат будет выполнимым, но, вообще говоря, не будет тождественно истинным.
Множество истинности предиката
Определение 18.3. Множеством истинности предиката , заданного на множествах
, называется совокупность всех упорядоченных n-систем
, в которых
, таких, что данный предикат обращается в истинное высказывание
при подстановке
. Это множество будем обозначать
. Таким образом,
Множество истинности “-местного предиката
представляет собой n-арное отношение между элементами множеств
. Если предикат
— одноместный, заданный над множеством
, то его множество истинности
является подмножеством множества
.
Например, множеством истинности двухместного предиката “Точка принадлежит прямой
“, заданного на множестве
всех точек плоскости и на множестве
всех прямых этой плоскости, является бинарное отношение принадлежности (инцидентности) между точками и прямыми плоскости. Другой пример. Множество истинности двухместного предиката
, заданного на множестве
, есть множество всех таких пар действительных чисел, которые являются координатами точек плоскости, образующими окружность с центром в начале координат и радиуса 3. Наконец, если
“
” — одноместный предикат над
, то
, или
.
В терминах множества истинности легко выразить понятия, связанные с классификацией предикатов (определение 18.2). В самом деле, n-местный предикат , заданный на множествах
, будет:
а) тождественно истинным тогда и только тогда, когда ;
б) тождественно ложным тогда и только тогда, когда ;
в) выполнимым тогда и только тогда, когда ;
г) опровержимым тогда и только тогда, когда .
На языке множеств истинности еще более отчетливо проясняются закономерности взаимосвязей между предикатами различных типов, отмеченные в конце предыдущего пункта. Проанализируйте их еще раз.
Равносильность и следование предикатов
Определение 18.4. Два n-местных предиката и
, заданных над одними и теми же множествами
, называются равносильными, если набор предметов (элементов)
превращает первый предикат в истинное высказывание
в том и только в том случае, когда этот набор предметов превращает второй предикат в истинное высказывание
.
Другими словами (на языке множеств истинности), предикаты и
равносильны тогда и только тогда, когда их множества истинности совпадают.
.
Утверждение о равносильности двух предикатов и
символически будем записывать так:
. Отношение равносильности предикатов является отношением эквивалентности, так что совокупность всех n-местных предикатов, определенных на множествах
, распадается на непересекающиеся классы равносильных предикатов (все они определяют одну и ту же функцию, заданную на множествах
и принимающую значения в двухэлементном множестве
). Переход от предиката
к равносильному ему предикату
называется равносильным преобразованием первого. Это понятие очень важно для школьной математики, потому что изучаемые в ней уравнения и неравенства представляют собой частные виды предикатов. Решение уравнения и неравенства есть поиск их множеств истинности. При таком поиске мы проделываем над уравнением и неравенством различные преобразования, и здесь важно, чтобы эти преобразования были равносильными, т. е. чтобы найденное множество оказалось бы множеством истинности именно исходного уравнения или неравенства. Аналогична ситуация при решении систем уравнений или неравенств.
Рассмотрим простой пример. Пусть требуется решить уравнение (найти множество истинности предиката): . Преобразуем его равносильным образом:
Ответ: — множество всех решений данного уравнения (множество истинности данного предиката).
Отметим следующее немаловажное обстоятельство: может быть так, что два предиката равносильны, если их рассматривать над одним множеством, и неравносильны, если их рассматривать над другим (в частности, объемлющим первое) множеством. Такова, например, ситуация с предикатами: и
.
Определение 18.5. Предикат , заданный над множествами
, называется следствием предиката
, заданного над теми же множествами, если он превращается в истинное высказывание на всех тех наборах значений предметных переменных из соответствующих множеств, на которых в истинное высказывание превращается предикат
.
Другими словами (в терминах множеств истинности), можно сказать, что предикат является следствием предиката
тогда и только тогда, когда
.
Утверждение о том, что предикат является следствием предиката
, будем символически записывать так:
.
Например, одноместный предикат, определенный на множестве натуральных чисел, “ делится на 3″ является следствием одноместного предиката, определенного на том же множестве, “
делится на 6″. Из двух предикатов, упомянутых перед последним определением, первый будет следствием второго, если считать, что оба предиката заданы на множестве
целых чисел.
Язык множеств истинности позволяет установить взаимосвязь между понятиями равносильности и следования предикатов: два предиката, определенные на одних и тех же множествах, равносильны тогда и только тогда, когда каждый из них является следствием другого. Кроме того, этот же язык дает возможность без труда установить следующие простые теоремы.
Теорема 18.6. Каждые два тождественно истинных (тождественно ложных) предиката, заданных на одних и тех же множествах, равносильны. Обратно, всякий предикат, равносильный тождественно истинному (тождественно ложному) предикату, сам является тождественно истинным (тождественно ложным) предикатом.
Теорема 18.7. Каждый тождественно истинный n-местный предикат является следствием любого другого n-местного предиката, определенного на тех же множествах. Каждый n-местный предикат является следствием любого тождественно ложного n-местного предиката, определенного на тех же множествах.
Теорема 18.8. Пусть и
— два n-местных предиката, определенные на одних и тех же множествах, такие, что
есть следствие
. Тогда:
а) если тождественно истинный (выполнимый), то и
тождественно истинный (выполнимый);
б) если тождественно ложный (опровержимый), то и
тождественно ложный (опровержимый).
Доказательство теоремы 18.8:
а) Поскольку , поэтому
. Если теперь
тождественно истинный предикат, то
(где
— множества, на которых определены n-местные предикаты
и
).
Но . Поэтому
, а, значит, предикат
— тождественно истинный предикат. Если же
— выполнимый предикат, то
. Но
. Тогда
и
— выполнимый предикат.
б) Пусть — тождественно ложный предикат. Тогда
. Но
, поэтому
. Следовательно, предикат
— тождественно ложный. Наконец, пусть
— опровержимый предикат. Тогда
. Поскольку, кроме того,
и
, то
.
Следовательно, предикат — опровержимый.
Отыщите самостоятельно в настоящем и предыдущем пунктах данной лекции утверждения, обосновывающие остальные сформулированные теоремы.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Предикаты и кванторы
- Понятие предиката
- Примеры предикатов
- Операции над предикатами
- Кванторы
- Примеры применения кванторов
- Операции над кванторами
Понятие предиката
Утверждения, содержащие в себе переменные, обладающие способностью принимать значения 0 или 1 (ложно или истинно) в зависимости от принимаемых переменными значений, называют предикатами.
В качестве примера может быть рассмотрено выражение x=x^5 представляет собой предикат, поскольку оно будет истинным исключительно в случае принятия переменной x значений 0 или 1 и будет ложным в случае присвоения переменной x всех стальных отличных от 0 и 1 значений.
Множеством истинности Ip любого предиката называют такое множество значений, которое может принимать переменная, позволяющих предикату принимает исключительно истинные значения.
В программировании предикатом принято считать функции, принимающие значения одного или большего числа аргументов и возвращающих значения логического (булевого) типа.
Тождественно-истинным называют предикат, способный принимать истинное значение в случае использования любого набора значений аргумента:
(P(x1,…,xn)=1)
Предикат, для которого использование любого набора значений аргумента приводит к принятию им ложного значения, называют тождественно-ложным:
(P(x1,…,xn)=0)
В случае если предикат приобретает истинное значение при использовании хотя бы одного набора значений аргумента, его считают выполненным.
Поскольку предикаты обладают способностью принимать исключительно значения двух видов – ложно или истинно (0 или 1), к ним могут быть применены все операции, относящиеся к алгебре логики: дизъюнкция, конъюнкция, отрицание и т.п.
Так и не нашли ответ на вопрос?
Просто напишите,с чем нужна помощь
Мне нужна помощь
Примеры предикатов
Допустим, что предикат, имеющий вид R(x,y): «x = y», где переменные x и y являются целыми числами, является обозначением отношения равенства. Принятие предикатом R истинного значения будет происходить исключительно в случае равенства всех x и y.
В качестве другого примера может быть рассмотрен предикат, имеющий вид ТРУДИТСЯ(x,y,z) образованный для отношения «x трудится в населённом пункте y на предприятии z».
Примером ещё одного вида может служить предикат – СИМПАТИЗИРУЕТ(x,y) характеризующий отношение «x симпатизирует y» для переменных x и y, принадлежащих к множеству М, включающему в себя всех людей.
На основании сказанного выше можно сделать вывод о том, что предикат представляет собой любое суждение об объекте, которое отрицается либо, утверждается.
Операции над предикатами
К предикатам могут быть применены операции, относящиеся к алгебре логики. Рассмотрим особенности применения подобных операций.
Операции логического характера:
Конъюнкцией предикатов A(x) и B(x) называют предикат нового вида, принимающий истинное значение исключительно при тех значениях переменной x из множества значений T, которые позволяют каждому из обоих предикатов приобретать истинное значение, в то время как ложное значение будет ими приниматься во всех иных случаях. Подобному предикату соответствует множество истинности T представляющее собой пересечение соответствующих заданным предикатам A(x) и B(x) множеств истинности. К примеру, если предикат A(x) характеризует отношение «x – число чётное», а предикат B(x) обозначает отношение «x делится на число 5», то конъюнкцией подобных предикатов станет предикат, характеризующий отношение следующего вида: «x – число чётное и кратно числу 5» или «x кратно 10».
Дизъюнкцией для предикатов A(x) и B(x) является предикат нового вида, принимающий ложное значение исключительно при тех значениях переменной x из множества значений T, которые позволяют каждому из обоих предикатов приобретать ложное значение, в то время как истинное значение будет ими приниматься во всех иных случаях. Ему соответствует множество истинности, представляющее собой пересечение соответствующих заданным предикатам A(x) и B(x) множеств истинности.
Отрицанием предиката A(x) является предикат нового вида, принимающий истинное значение в случае принятия переменной x всех значений из множества T, которые позволяют принимать предикату A(x) ложное значение или наоборот. Для подобного предиката множество истинности будет представлять собой дополнение T’ к соответствующему предикату A(x) множеству истинности.
Импликацией для предикатов A(x) и B(x) является предикат нового вида, принимающий ложное значение исключительно при тех значениях переменной x из множества значений T, которые позволяют предикату A(x) обретать истинное значение, в то время как предикат B(x) принимает значение ложное, принимая истинное значение во всех иных случаях. Запись подобной операции обычно имеет вид: «Если A(x), то B(x)».
Допустим, существуют предикаты A(x): «число x является натуральным и делится на 3» и B(x): «число x является натуральным и делится на 4».
Может быть составлен предикат определяющий отношение «если число x является натуральным и делится на 3, то такое число делится и на 4».
Для такого предиката множеством истинности будет иметь вид объединения множества истинности для B(x) и дополнения к множеству истинности для A(x).
Кроме операций логического характера над предикатами могут выполняться квантовые операции – это использование кванторов существования, всеобщности и т.п.
Лень читать?
Задай вопрос специалистам и получи ответ уже через 15 минут
Задать вопрос
Кванторы
Применяемые к предикатам логические операторы, превращающие их в высказывания, имеющие истинное или ложное значение, называются кванторами.
Существует другое определение кванторов, согласно которому, это логические операции, создающие высказывание и ограничивающие для предикатов, к которым они применяются, их область истинности.
Наиболее часто применяемыми являются следующие кванторы:
- обозначаемый символом ∀, квантор всеобщности, который соответствует выражениям, имеющим вид «для всех значений x», «для любого значения x» и т.п.;
- обозначаемый символом ∃, квантор существования, который соответствует выражению, имеющему вид «существует значение x такое, что…»;
- обозначаемый символом ∃!, квантор существования и единственности, который соответствует выражению имеющему вид «существует всего одно такое значение x, что…».
Процессу приписывания квантора к формуле в математической логике соответствует понятие квантификации или связывания.
Не нашли ответ?
Просто напиши,с чем тебе нужна помощь
Мне нужна помощь
Примеры применения кванторов
Допустим, существует предикат, описывающий отношение «x кратно 7».
Применяя квантор всеобщности, ложные высказывания могут быть записаны следующим образом:
- любое число, являющееся натуральным, делится на 7;
- каждое из чисел, являющихся натуральным, делится на 7;
- все существующие числа, являющиеся натуральными, способны делиться на 7.
Такой квантор будет иметь следующий вид:
- ( (∀x ∈ N)P(x) )
Применяя квантор существования, истинные высказывания в отношении этого же предиката могут быть записаны следующим образом:
- существуют числа, являющиеся натуральными, которые делятся на число 7;
- может быть найдено натуральное число, кратное числу 7;
- существует хотя бы одно число, являющееся натуральным, способное делиться на число 7.
Запись данного квантора приобретёт вид:
- ( (∃x ∈ N)P(x) )
Допустим, для множества некоторых простых чисел x образован предикат, описывающий отношение «простое число является числом нечётным». Если перед предикатом вставить слово «любое» получим в результате ложное высказывание, имеющее вид: «любое простое число одновременно является числом нечётным» (число 2, например, будучи числом простым, являясь при этом чётным числом).
Если перед предикатом вставить слово «существует» получим в результате истинное высказывание в виде: «существует простое число, одновременно являющееся нечётным» (x=3, к примеру).
На основании сказанного выше можно заключить, что предикат может быть превращён в высказывание путём присоединения квантора перед ним.
Лень читать?
Задай вопрос специалистам и получи ответ уже через 15 минут
Задать вопрос
Операции над кванторами
Применяемым для образования отрицания высказываний, содержащих кванторы, является правило отрицания кванторов, имеющее вид:
( ¬(∀x)P(x) = (∃x)¬P(x) )
( ¬(∃x)P(x) = (∀x)¬P(x) )
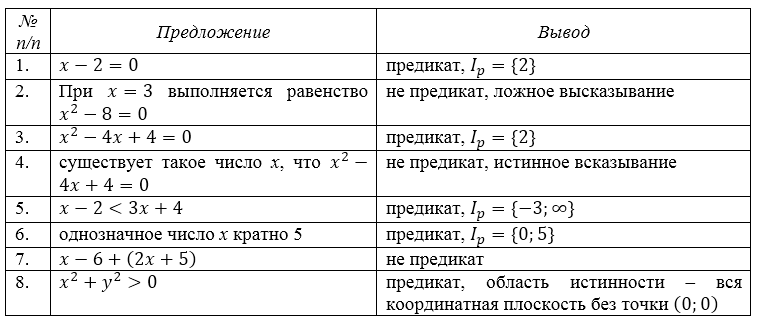
Для примера рассмотрим некоторые предложения, определив среди них предикаты и область истинности для них:
- предложение x – 2 = 0 – представляет собой предикат с множеством истинности Ip = {2};
- выполняемое при x=3 равенство x^2 – 8 = 0 – не является предикатом, являясь ложным высказыванием;
- предложение x^2 – 4 x + 4 = 0 – является предикатом с множеством истинности Ip = {2};
- существует такое значение переменной x при котором x^2 – 4 x + 4 = 0 – не является предикатом, являясь истинным высказыванием;
- предложение x – 2 < 3x + 4 – является предикатом с множеством истинности Ip = {-3;∞};
- однозначное число x кратно 5 – предикат с множеством истинности Ip = {0;5};
- предложение x – 6 + (2x + 5) – не является предикатом;
- предложение x^2 + y^2 > 0 – является предикатом, для которого область истинности это вся плоскость координат за исключением точки с координатами (0;0).
Логика
предикатов
Понятие
предиката. Значение
формулы логики предикатов.
Общезначимость и выполнимость формул.
Проблема разрешимости.
Применение
языка логики предикатов для записи
математических предложений, определений,
построения отрицания предложений.
Доказательство
теорем методом от противного
Понятие
предиката
В
алгебре логики высказывания рассматриваются
как нераздельные целые и только с точки
зрения их истинности или ложности.
Ни
структура высказываний, ни, тем более,
их содержание не затрагиваются. В то же
время и в науке, и в практике используются
заключения, существенным образом
зависящие как от структуры, так и от
содержания используемых в них высказываний.
Например,
в рассуждении “Всякий ромб –
параллелограм; АВСD – ромб; следовательно,
АВСD – параллелограм ” посылки и заключение
являются элементарными высказываниями
логики высказываний и с точки зрения
этой логики рассматриваются как целые,
неделимые, без учета их внутренней
структуры. Следовательно, алгебра
логики, будучи важной частью логики,
оказывается недостаточной в анализе
многих рассуждений.
В
связи с этим возникает необходимость
в расширении логики высказываний, в
построении такой логической системы,
средствами которой можно было бы
исследовать структуру тех высказываний,
которые в рамках логики высказываний
рассматриваются как элементарные.
Такой
логической системой является логика
предикатов, содержащая всю логику
высказываний в качестве своей части.
Логика
предикатов, как и традиционная формальная
логика, расчленяет элементарное
высказывание на
субъект
(буквально
– подлежащее, хотя оно может играть и
роль дополнения) и предикат
(буквально – сказуемое, хотя оно может
играть и роль определения).
Субъект
– это то, о чем что-то утверждается в
высказывании;
предикат
– это то, что утверждается о субъекте.
Например,
в высказывании “7 – простое число”, “7”
– субъект, “простое число” – предикат.
Это высказывание утверждает, что “7”
обладает свойством “быть простым
числом”.
Если
в рассмотренном примере заменить
конкретное число 7 переменной х из
множества натуральных чисел, то получим
высказывательную
форму “х – простое число”. При одних
значения х (например, х=13, х=17) эта форма
дает истинные высказывания, а при других
значениях х (например, х=10, х=18) эта форма
дает ложные высказывания.
Ясно,
что эта высказывательная форма определяет
функцию одной переменной х, определенной
на множестве N, и принимающую значения
из множества {1;0}. Здесь предикат становится
функцией субъекта и выражает свойство
субъекта.
Областью значений предиката
является двухэлементное множество
B={true, false}. При этом сами переменные
x1,…,x n называются предметными
переменными, т.е. их значения не являются
логическими ( не принадлежат множеству
B).
Понятие “предикат” обобщает понятие
“высказывание”. Неформально говоря,
предикат – это высказывание, в
которое можно подставлять аргументы.
Если аргумент один – то предикат выражает
свойство аргумента, если больше – то
отношение между аргументами.
Так как значениями предикатов
являются true или false, то сами предикаты
можно рассматривать как логические
переменные. Из них можно составлять
сложные логические выражения, образованные
из простых предикатов с помощью знаков
логических операций. После подстановки
в такое составное выражение конкретных
значений предметных переменных получается
сложное высказывание, значение которого
определяется истинностью или ложностью
входящих в него простых высказываний
и логическими операциями.
Определение 1. Логика
предикатов, раздел
математической логики,
изучающий логические законы, общие для
любой области объектов исследования
(содержащей хоть один объект) с заданными
на этих объектах предикатами (т. е.
свойствами и отношениями).
В результате формализации
логика предикатов принимает вид
различных исчислений.
Простейшими логическими исчислениями
являются исчисления высказываний. В
более сложных исчислениях предикатов
описываются логические законы, связывающие
объекты исследования с отношениями
между этими объектами.
В классическом исчислении
предикатов употребляются следующие
знаки: 1) т. н. предметные переменные —
буквы х, у, z,…, которые содержательно
рассматриваются как неопределённые
имена объектов исследования теории; 2)
предикатные переменные — знаковые
комплексы вида Pm, Qn, Rl,…
(m, n, l — натуральные числа), причём,
например, Qn означает произвольное
n-местное отношение между объектами; 3)
знаки для логических связок: конъюнкции
&, дизъюнкции
,
импликации , отрицания
, означающие
соответственно «… и…», «… или…»,
«если…, то…», «неверно, что…»; 4) знаки
для кванторов
(квантор
всеобщности),
(квантор существования), означающие
соответственно «для всех…» и «существует…
такое, что…»; 5) запятая, скобки (для
уточнения строения формул).
Определение 2 Квантор
(от лат. quantum — сколько), логическая
операция, дающая количественную
характеристику области предметов, к
которой относится выражение, получаемое
в результате её применения.
В обычном языке носителями
таких характеристик служат слова типа
«все», «каждый», «некоторый», «существует»,
«имеется», «любой», «всякий», «единственный»,
«несколько», «бесконечно много»,
«конечное число», а также все количественные
числительные. В формализованных
языках, составной частью
которых является исчисление
предикатов, для выражения
всех подобных характеристик оказывается
достаточным кванторов двух видов:
Квантор всеобщности (оборот «для всех
х», обозначается через x,
и Квантор существования («для некоторых
х», обозначения: x.
С помощью кванторов можно
записать четыре основных формы суждений
традиционной логики: «все А суть В»
записывается в виде x
[A (x) B
(x)], «ни одно A не есть B» —
в виде x [A
(x)
B
(x)], «некоторые А суть B» —
в виде x [A (x)B
(x)], «некоторые А не суть В»
— в виде x [A
(x)
B
(x)] (здесь А (х) означает,
что х обладает свойством A).
Часть формулы, на которую
распространяется действие каких-либо
Квантора, называется областью действия
этого Квантора (её можно указать с
помощью скобок). Применение Квантора
уменьшает число свободных переменных
в логическом выражении и превращает
(если Квантор не «фиктивный», т. е.
относится к переменной, действительно
входящей в формулу) трёхместный предикат
в двухместный, двухместный — в одноместный,
одноместный — в высказывание.
Определение
3. Одноместным предикатом Р(x)
называется произвольная функция
переменной x, определенная на множестве
M и принимающая значение из множества
{1; 0}.
Определение
4. Множество
М, на котором определен предикат Р(x),
называется
областью определения предиката Р(x).
Множество
всех элементов
,
при которых предикат принимает значения
“истина” (1), называется множеством
(областью) истинности предиката Р(x),
т.е. множество истинности предиката
Р(х)- это множество
или иначе:
или так:
Так, например, предикат Р(x) – “x – простое
число” определен на множестве N, а
множество истинности IP
для него есть множество всех простых
чисел.
Предикат
Q(x) – “sin(x)=0” определен на множестве R,
а его множеством истинности является
Предикат
F(x) – “диагонали параллелограма x взаимно
перпендикулярны” определен на множестве
всех параллелограмов, а его множеством
истинности является множество всех
ромбов.
Из
приведенных примеров видим, что
одноместные предикаты выражают свойства
предметов (субъектов).
Определение
5. Предикат
Р(х), определенный на множестве М,
называется
тождественно истинным,
если его множество истинности совпадает
с областью определения, т. е. Ip=M.
Определение
6. Предикат
Р(х), определенный на множестве М,
называется тождественно
ложным,
если его множество истинности является
пустым множеством, т. е. Ip=0.
Естественным
обобщением понятия одноместного
предиката является понятие многоместного
предиката,
с помощью которого выражаются отношения
между
предметами.
Примером
бинарного отношения, т. е. отношения
между двумя предметами, является
отношение “меньше ”. Пусть это отношение
введено на множестве Z целых чисел. Оно
может быть охарактеризовано высказывательной
формой “х<y”, где
,
то–есть является функцией двух переменных
Р(х,y), определенной на множестве
упорядоченных пар целых чисел ZхZ=Z2
c множеством значений {1;0}.
Определение
7. Двухместным предикатом Р(x,y)
называется функция двух переменных x
и y, определенная на множестве М=М1хМ
2 и
принимающая значения из множества
{1;0}.
В
числе примеров двухместных предикатов
можно назвать такие предикаты: Q(x,
y) – “x=y” – предикат равенства, определенный
на множестве RхR=R2;
F(x,y) – “х параллелен y”, “прямая х
параллельна прямой y”, определенный на
множестве прямых, лежащих на данной
плоскости.
Совершенно
аналогично вводится понятие трехместного
предиката. Приведем пример трехместного
предиката (функции трех переменных):
S(x,y,z) – “x+y=z”. Подстановка в него х=3
превращает его в двухместный предикат:
S(y,z) – “3+y=z”, а подстановка х=3, z=2
– в одноместный предикат S(y) –
“3+y=2”.Подстановка же S(2,3,5) превращает
его в истинное высказывание, а S(1,7,4)– в
ложное.
Аналогично
определяется и n-местный предикат
(функция n переменных). Пример п- местного
предиката:
R(x1,
x2,…,xn):
a1
x1+…+anxn=0,
который,
как видим, представляет собой алгебраическое
уравнение с n
неизвестными.
При
n=0
будем иметь нульместный
предикат –
это логическая (пропозициональная)
переменная, принимающая значения из
множества {1;0}.
Исторически понятие о
предикате явилось следствием логического
анализа высказываний естественного
языка, т. е. выяснения их логической
структуры, выяснения того, какой логикой
может быть выражен (формализован) смысл
этих высказываний. Идея выделения
логической структуры речи, в отличие
от грамматической, для нужд логической
дедукции принадлежит Аристотелю. В
аристотелевской и в последующей
«традиционной» логике П. понимался в
узком смысле как один из двух терминов
суждения, а именно тот, в котором нечто
говорится о предмете речи — субъекте.
Форма сказывания — предикативная связь
— сводилась при этом к атрибутивной
связи, т. е. выражала «присущность»
предмету некоторого признака. Аристотель
выделял 4 типа признаков, способных
играть роль предиката.: родовые, видовые,
собственные и случайные. Это т. н.
предикабилии — типы сказуемых.
Основой для «функциональной»
точки зрения на предикат служат в
естественных и в искусственных (точных)
языках выражения вида повествовательных
предложений, содержащие неопределённые
термины — неопределённые имена предметов:
переменные (параметры) в записи утверждений
в математическом языке, например х
+ 2 = 4; слова «нечто», «некто», «кто-либо»
и пр., играющие в естественном языке
роль переменных в выражениях типа:
«Некто человек», «Кто-то любит кого-то»,
«Если кто-либо человек, то он смертен»
и т.п. Записав эти выражения некоторым
единым способом, например заменяя
неопределённые термины пробелами,
аналогично тому, как это делается в
опросных бланках, «—+ 2 = 4», «—человек»,
«— любит —», «Если — человек, то —
смертен», или же принимая запись с
помощью переменных в качестве основной,
«x + 2 = 4», «x человек», «х
любит у», «Если х человек, то х
смертен», легко заметить нечто общее
между ними. Во-первых, наличие неопределённых
терминов делает эти и подобные им
выражения, вообще говоря, неопределёнными
как в смысле того, что в них утверждается,
так и в смысле их истинностного
значения; во-вторых, всякое
подходящее указание на область значений
неопределённых терминов и одновременная
квантификация или замена неопределённых
терминов их значениями преобразует
соответствующие выражения в осмысленные
высказывания. В современной логике
выражения, имеющие вид повествовательных
предложений и содержащие неопределённые
термины, получили общее название
пропозициональных функций, или, сохраняя
традиционный термин, предикатов. Как и
числовые функции, предикаты. являются
соответствиями. Неопределённые термины
играют в них обычную роль аргументов
функции, но, в отличие от числовых
функций, значениями предикатов. служат
высказывания. В общем случае, отвлекаясь
от какого-либо определённого языка и
сохраняя только функциональную форму
записи, предикат от n переменных (от
n неопределенных терминов) выражают
формулой P (x1,…, xn),
где n 0. При
n = 0 предикат совпадает с высказыванием,
при n = 1 предикат будет свойством в
узком смысле (1-местным предикатом), при
n = 2 — свойством «пары» (2-местным
предикатом, или бинарным отношением),
при n = 3 — свойством «тройки»
(3-местным предикатом, или тернарным
отношением) и т.д.
Примеры предикатов:
1. Возьмём высказывания: “Сократ
– человек”, “Платон
– человек”. Оба эти высказывания
выражают свойство “быть человеком”.
Таким образом, мы можем рассматривать
предикат “быть
человеком” и говорить, что он
выполняется для С0ократа
и Платона.
2. Возьмём высказывание: “расстояние
от Иркутска до Москвы 5 тысяч километров”.
Вместо него мы можем записать предикат
“расстояние”
(означающий, что первый и второй аргумент
этого предиката находятся на расстоянии,
равном третьему аргументу) для аргументов
“Иркутск”,
“Москва”
и “5
тысяч километров”.
3. Высказывание “у каждого
человека есть отец” можно записать:
x
y
(человек(x) отец(y,x))
3. Выражение “Джон владеет
красной машиной” записывается,
например, так:
x
( владеет(Джон, x) машина(x)
&красный(x))
4. Выражение «все простые
числа больше чем x» можно записать
y(P (y)
Q(x, y)). , где
-
P(x) выражает условие “x является
простым числом”, -
Q(x,
y) выражает условие “x меньше чем y”.
5. Выражение “у всех людей общий отец”.
y
x
(человек(x)
отец(y,x))
Значение формулы логики предикатов
О
логическом значении формулы логики
предикатов можно говорить лишь тогда,
когда задано множество M, на котором
определены входящие в эту формулу
предикаты. Логическое значение формулы
логики предикатов зависит от значений
трех видов переменных: 1) значений
входящих в формулу переменных высказываний,
2) значений свободных предметных
переменных из множества М, 3) значений
предикатных переменных.
При
конкретных значениях каждого из трех
видов переменных формула логики
предикатов становится высказыванием,
имеющим истинное или ложное значение.
В
качестве примера рассмотрим формулу
,
(1) в которой двухместный предикат Р(x,
y) определен на множестве MхM, где
M={0,1,2,…,n,…},
т.е. MхM=NхN.
В
формулу (1) входит переменный предикат
P(x,y), предметные переменные x,y,z, две из
которых y и z – связанные кванторами, а
x – свободная.
Возьмем
за конкретное значение предиката P(x,y)
фиксированный предикат P0(x,y):
“x<y”,
а свободной переменной х придадим
значение
.
Тогда при значениях y, меньших x0=5,
предикат P0(x0,y)
принимает значение “ложь”, а импликация
при всех
принимает значение “истина”, т.е.
высказывание
имеет значение “истина”.
Применение
языка логики предикатов для записи
математических предложений, определений,
построения отрицания предложений
Язык
логики предикатов удобен для записи
математических предложений и определений.
Он дает возможность выражать логические
связи между понятиями, записывать
определения, теоремы, доказательства.
Приведем несколько примеров таких
записей.
Пример
1. Определение
предела “
”
функции ƒ(х), определенной в области E,
в точке x0:
.
Используя трехместный предикат
,
запишем:
,
где
.
Пример
8. Определение
непрерывности функции в точке.
Функция
,
определенная на множестве E,
непрерывна в точке
,
если
,
где
.
Построение
противоположный утверждений
Пусть
дано некоторое математическое утверждение
А. Ему будет противоположным будет
утверждение
.
Логика
предикатов позволяет путем равносильных
преобразований формулы
придать ей хорошо обозримый вид.
Определение
неограниченной функции мы получим, беря
отрицание этой формулы и проводя
равносильные преобразования:
.
Последняя
формула дает не негативное, а положительное
определение неограниченной функции.
Из
приведенного определения видно, что
для построения противоположного
утверждения к утверждению, заданному
формулой логики предикатов, содержащей
все кванторы впереди, необходимо заменить
все кванторы на противоположные и взять
отрицание от предиката, стоящего под
знаком кванторов.
Логика предикатов — это расширение логики пропозиций, которую мы рассматривали ранее в курсе.
Это следующая ступень, на которой появляются два новых понятия — предикаты и квантификаторы. Эти понятия помогают лучше передать смысл утверждений, которые сложно выразить в пропозициональной логике.
Предикаты
Предикаты (
) можно рассматривать как функции, которые определяют истинность высказывания
при разных значениях
. Проще говоря, предикат помогает определить, истинно высказывание или ложно.
Рассмотрим утверждение
. Оно состоит из двух частей:
-
Переменная
— переменная высказывания
-
Высказывание
— предикат. Он обозначает свойство, которым может обладать переменная
Высказывание «
больше
» можно записать как
. В таком случае
будет обозначать переменную, а
— предикат «больше
».
Как только переменной
присваивается значение, высказывание
становится пропозицией. У него появляется значение истинности или ложности.
Возьмем конкретное значения для
и проверим, как это работает. Для примера возьмем значение
и подставим его в
. В итоге мы получим
. Это истина, ведь
действительно больше
.
Изучим еще один пример:
-
Представим, что предикат
— это высказывание
-
Присвоим переменной
значение
-
Так как мы присвоили
конкретное значение, высказывание
становится пропозицией. Теперь можно определить, истинно оно или ложно
-
Подставим значение и проверим, истинно или ложно высказывание
. Получается, что для
предикат
— это истина
-
А теперь поменяем значение
с
на
-
Высказывание
снова становится пропозицией, и теперь можно определить, истинно оно или ложно
-
Подставим значение и проверим, истинно или ложно высказывание
. Получается, что для
предикат
— это ложь, ведь
, а не
Высказывание, которое включает в себя
переменных
1,
2,
3,
,
n:
Обратите внимание, что в примере выше
, потому что мы рассматривали
значения:
1
,
2
. Это можно обозначить так:
В этом случае
называется n-арным предикатом.
Квантификаторы
Часто у нас возникает необходимость проверить истинность высказывания не с конкретным значением, а сразу на диапазоне значений. В этом и помогают квантификаторы.
Рассмотрим два высказывания:
-
Вася любит вкусную еду
-
Каждый человек любит вкусную еду
В обоих высказываниях есть критерий: любит вкусную еду. В первом высказывании Вася — это конкретное значение. Во втором случае слово каждый указывает, что в качестве переменной мы рассматриваем много людей, то есть диапазон значений.
Само слово каждый — это квантификатор, а подобное выражение называется квантифицированным.
В логике квантификатор — это способ утверждать, что определенное количество элементов удовлетворяет каким-то определенным критериям.
В этом уроке мы рассмотрим три вида квантификаторов:
-
Универсальные
-
Экзистенциальные
-
Квантификаторы единственности
Универсальная квантификация
Иногда в математических высказываниях утверждается, что любое значение переменной удовлетворяет критерию. Такое утверждение называется универсальной квантификацией.
Универсальный квантификатор обозначается символом
, который похож на перевернутую букву
и обозначает для всех или для любого.
Универсальная квантификация
— это предложение, которое утверждает, что
истинно для всех значений
.
Возьмем для примера такое выражение:
Разделим его на отдельные части и переведем на естественный язык:
-
— для любого значения
-
— квадрат
не отрицателен
Объединяем части и получаем понятное высказывание: «Квадрат любого числа не отрицателен».
Экзистенциальная квантификация
Некоторые математические высказывания утверждают, что элемент с определенным свойством существует — это экзистенциальная квантификация.
Экзистенциальный квантификатор обозначается символом
, который похож на перевернутую букву
.
С помощью экзистенциальной квантификации можно сформировать предложение, которое истинно, только если
истинно хотя бы для одного значения
в области.
Вернемся к примеру выше:
Превратим его в экзистенциальную квантификацию. Для этого разделим на части и переведем на естественный язык:
-
— существует значение
-
— квадрат
не отрицателен
В итоге получаем такое высказывание: «Существует такое число
, квадрат которого не отрицателен».
Теперь вспомним высказывание из начала урока:
Каждый человек имеет право водить машину, если он достиг восемнадцатилетнего возраста
Попробуем применить логику предикатов и преобразовать это высказывание в математическое утверждение. Получим такой результат:
В выражении выше мы видим:
-
— это утверждение «
старше 18 лет»
-
— это утверждение «
имеет право водить машину»
Объединяем и получаем: «Любой
старше 18 лет имеет право водить машину».
Квантификатор единственности
Универсальные и экзистенциальные квантификаторы являются самыми важными в математике и информатике, но есть и другие. Из остальных возможных квантификаторов чаще всего встречается квантификатор единственности, которые обозначается
.
Например, высказывание «Существует единственный
, при котором
истинно» можно записать в виде нотации
.