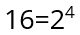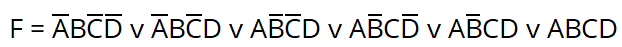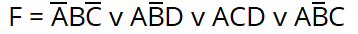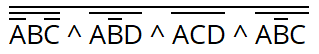Построение логической схемы по произвольной таблице истинности
Любая логическая схема без памяти полностью описывается таблицей истинности. При этом не обязательно чтобы все комбинации входных сигналов были полезными. Возможна ситуация, когда только часть комбинаций входных сигналов является полезной. В этом случае выходные сигналы для оставшихся комбинаций входных сигналов могут быть доопределены произвольно. Обычно при этом стараются выбирать выходные сигналы таким образом, чтобы схема получилась простейшей.
Для реализации логических схем с произвольной таблицей истинности используется сочетание простейших логических элементов «И» «ИЛИ» «НЕ». Существует два способа синтеза логических схем, реализующих произвольную таблицу истинности. Это СКНФ (логическое произведение суммы входных сигналов) и СДНФ (сумма логических произведений входных сигналов).
При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) отдельно. В настоящее время наиболее распространены микросхемы, совместимые с ТТЛ технологией, а в этой технологии проще всего получить элементы «И». Поэтому первым рассмотрим способ реализации произвольной таблицы истинности основанный на СДНФ.
Для реализации таблицы истинности при помощи логических элементов «И» достаточно рассмотреть только те строки таблицы истинности, которые содержат логические «1» в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую «1», реализуется схемой логического «И» с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.
Входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим нулем, подаются на вход этой же схемы «И» через инверторы. Объединение сигналов с выходов схем «И», реализующих отдельные строки таблицы истинности, производится при помощи схемы логического «ИЛИ». Количество входов в схеме «ИЛИ» определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 1:
Рисунок 1. Произвольная таблица истинности
Для построения схемы, реализующей сигнал Out0, достаточно рассмотреть строки, выделенные красным цветом. В таблице истинности три строки, содержащие единицу в выходном сигнале Out0, поэтому в формуле СДНФ будет содержаться три произведения входных сигналов:
Полученная формула реализуются микросхемой D2 на рисунке 2. Как и в формуле каждая строка реализуется своей схемой «И», затем выходы этих схем объединяются схемой «ИЛИ». Количество входов элемента «И» однозначно определяется количеством входных сигналов в таблице истинности. Количество этих элементов, а значит и количество входов в логическом элементе «ИЛИ» определяется количеством строк с единичным сигналом на реализуемом выходе схемы.
Рисунок 2. Принципиальная схема, реализующая таблицу истинности, приведенную на рисунке 1
Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше. В таблице истинности присутствуют всего три строки, содержащие единицу в выходном сигнале Out1, поэтому в формуле СДНФ выхода ‘Out1’ будет содержаться три произведения входных сигналов:
Обычно при построении цифровых схем после реализации таблицы истинности производится минимизация схемы, но для упрощения понимания материала минимизация производиться не будет. Это оправдано еще и с той точки зрения, что неминимизированные схемы обычно обладают максимальным быстродействием. При реализации схемы на ТТЛ микросхемах быстродействие всего узла будет равно быстродействию одиночного инвертора (см описание ТТЛ микросхем).
Применение СКНФ оправдано при большом количестве единиц в выходном сигнале, как, например, в таблице истинности, приведенной в таблице 2.
Для реализации таблицы истинности при помощи логических элементов «ИЛИ» достаточно рассмотреть только те строки таблицы истинности, которые содержат логические «0» в выходном сигнале. Строки, содержащие в выходном сигнале логическую 1 в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логический «0», реализуется схемой логического «ИЛИ» с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.
Входные сигналы, описанные в таблице истинности логическим нулём, подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этой же схемы «ИЛИ» через инверторы. Объединение сигналов с выходов схем «ИЛИ», реализующих отдельные строки таблицы истинности, производится при помощи схемы логического «И». Количество входов в схеме «И» определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.
Таблица 2. Пример таблицы истинности 2
| Входы | Выходы | |||||
|---|---|---|---|---|---|---|
| № комбинации | 8 | 4 | 2 | 1 | a | b |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 |
Для построения схемы, реализующей сигнал Out0, достаточно рассмотреть строки, выделенные курсивом. В рассматриваемой таблице истинности имеются всего две строки, содержащие логический ноль в выходном сигнале a, поэтому в формуле СКНФ будет содержаться две суммы входных сигналов:
Полученная формула в схеме на рисунке 9 реализуются микросхемой D2.
Для построения схемы, реализующей сигнал b, достаточно рассмотреть строки, выделенные жирным шрифтом. Эти строки в схеме на рисунке 9 реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше. В таблице истинности присутствуют всего две строки, содержащие ноль в выходном сигнале b, поэтому в формуле СКНФ выхода b будет содержаться две суммы входных сигналов:
Понравился материал? Поделись с друзьями!
Вместе со статьей «Построение логической схемы по произвольной таблице истинности» читают:
Источник
Логические элементы в электрических схемах

Устройства, оперирующие дискретными сигналами, называют дискретными. Работа таких устройств анализируется с помощью понятий булевой алгебры — алгебры логики.
Основные положения алгебры логики
Логической переменной называют входную величину, которая может принимать только два противоположных значения: х = 1 или х = 0. Логической функцией называют зависимость выходной величины от входных, и сам выходной сигнал, который тоже может принимать только два значения: у = 1 или у = 0. Логическая операция — это действие, которое совершает логический элемент с логическими переменными в соответствии с логической функцией. Значения 1 и 0 взаимно противоположны (инверсны): 1 = 0, 0 = 1. Черточкой обозначается отрицание (инверсия).
Принимается, что 0 • 0 = 0, 0 + 0 = 0, 1 — 0 = 0, 1 + 0 = 1, 1 • 1 = = 1, 1 + 1 = 1.
При преобразовании формул алгебры логики сначала выполняют операции инверсии, затем умножения, сложения и затем все остальные.
Основные логические операции рассмотрены здесь: Логические устройства
Логические элементы в виде релейно-контактных схем
Логические элементы могут быть представлены в виде релейно-контактной схемы (рис. 1).
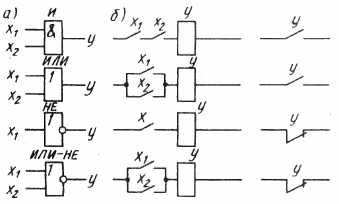
Рис. 1. Основные логические элементы (а) и релейно-контактный эквивалент (б)
Если считать, что замкнутые контакты соответствуют единичному сигналу, а разомкнутые — нулевому, то элемент И можно представить соединенных контакта х1 и х2 и реле у. Если оба контакта замкнуты, то по катушке пойдет ток, реле сработает и его контакты замкнутся.
Элемент ИЛИ можно представить как два замыкающих контакта, соединенных параллельно. При замыкании или первого или второго из них реле срабатывает и замыкает свои контакты, через которые пойдет сигнал.
Элемент НЕ можно представить как один замыкающий контакт х и один размыкающий у. Если сигнал на вход не подавать (х = 0), то реле не срабатывает и контакты у остаются замкнутыми, ток через них проходит. Если же замкнуть контакты х, реле сработает и разомкнет свои контакты, тогда сигнал на выходе будет равен нулю.
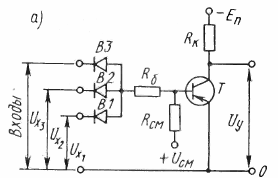
На рис. 2 изображена схема, выполняющая операцию ИЛИ — НЕ. Если ни на один из входов не подавать сигнал, то транзистор останется закрытым, ток через него не потечет, а напряжение на выходе будет равно ЭДС источника Uy = Uc, т. е. у= 1.
Рис. 2. Схема логического элемента ИЛИ — НЕ, выполняющего логические операции
Если хотя бы на один из входов подать напряжение, то сопротивление транзистора упадет от ∞ до 0 и по цепи эмиттер — коллектор потечет ток. Падение напряжения на транзисторе станет равным нулю (Uy = 0). Это означает, что сигнала на выходе нет, т. е. у = 0. Для нормальной работы элемента необходимо создавать смещение потенциала базы относительно общей точки, это достигается специальным источником Uсм и резистором Rсм. Резистор R6 ограничивает ток база — эмиттер.
Логические элементы, построенные на электромагнитных реле, транзисторах, магнитных сердечниках, электронной лампе, пневматических реле, имеют слишком большие размеры, поэтому сейчас применяют интегральные микросхемы. Логические операции в них происходят на уровне кристаллов.
Примеры использования логических элементов в схемах
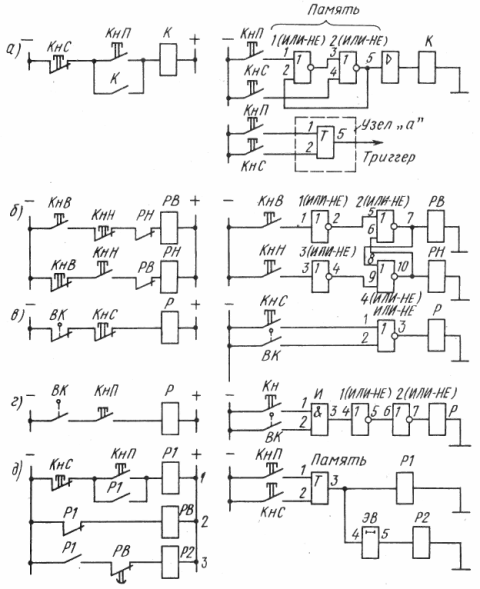
Рассмотрим несколько узлов электрических схем, наиболее часто встречающихся в электроприводе. На рис. 3, а показан узел питания катушки контактора К.
Рис. 3. Узлы схем с логическими элементами: 1 — 8 — номера входа и выхода
При нажатии кнопки КнП ток проходит по линии и срабатывает контактор. Его главные контакты (на схеме не показаны) подключают двигатель к сети, а контакты К, замыкаясь, шунтируют кнопку КнП. Теперь ток будет протекать по этим контактам, а кнопку КнП можно отпустить. Под действием пружины она размыкает свои контакты, но катушка будет продолжать питаться через контакты К. При нажатии кнопки КнС линия разрывается и контактор отпускается.
Этот узел можно выполнить на логических элементах. В схему входят катушка контактора К, кнопки КнП и КнС, два логических элемента ИЛИ — НЕ и усилитель. Исходное состояние х1 = 0 и х2 = 0, тогда на выходе элемента 1 получим у1 = х1 + х2 = 0 + 0 = 1. На выходе элемента 2 — у5 = х3 + х4 = 1 + 0 = 0, т. е. катушка обесточена, реле не срабатывает.
Если нажать КнП, то y1 = x1 + х2 = 1 + 0 = 0. На выходе элемента 2 у5 = x3 + х4 = 0 + 0 = 1. По катушке проходит ток и контактор срабатывает. Сигнал у2 подается на вход х2 но у1 от этого не меняется, так как у1 = x1 + х2 = 1 + 1 = 0. Таким образом, катушка контактора находится под током.
Если нажать кнопку КнС, то на вход второго элемента будет подаваться сигнал х4 = 1, тогда у2 = х3 + х4 = 0 + 1 = 0 и контактор отпускается.
Рассмотренная схема способна «запоминать» команды: сигнал у2 остается неизменным, даже если отпустить кнопку.
Такую же функцию памяти можно осуществить с помощью триггера. Если на вход подать сигнал х1 = 1, то на выходе появится сигнал у = 1 и будет оставаться неизменным до тех пор, пока не нажмем кнопку КнС. Тогда триггер переключается и на выходе появляется сигнал у = 0. Он будет оставаться без изменения до тех пор, пока снова не нажмем кнопку КнП.
На рис. 3, б показан узел электрической блокировки двух реле РВ (вперед) и РН (назад), исключающий их одновременное срабатывание, так как это приведет к короткому замыканию. Действительно, при нажатой кнопке КнВ срабатывает реле PB, а его блок-контакты размыкаются и катушка РН не сможет оказаться под током, даже если нажать кнопку КнН. Отметим, что шунтирование замыкающих контактов кнопок здесь не предусмотрено, т. е. узел памяти отсутствует.
В схеме с логическими элементами при нажатии кнопки КнВ на первом элементе получим х1 = 1, у2 = х1 = 0. На втором элементе y7 = х5 + х6 = y2 + х6 = 0 + 0 = 1
Реле РВ срабатывает и сигнал y 7 подается на вход элемента 4 ( y 7 — х8 = 1). На входе элемента 3 сигнал отсутствует (х2 = 0), тогда у4 = х2 = 1. На четвертом элементе: y10 = х8 + х9 = х8 + y4 = 1 + 1 = 0, т. е. реле РН сработать не может, даже если нажать кнопку КнН. Тогда получим такой же результат: у 1 0 = х8 + х9 = = х8 + y4 = 1 + 0 = 0.
На рис. 3, в показан узел отпускания реле в случае нажатия кнопки КнС или размыкания контактов конечного выключателя ВК. В схеме с логическими элементами в исходном положении у3 = х1 + х2 = 0 + 0 = 1, т. е. катушка реле находится под током. При нажатии кнопки КнС получим y3 = x 1 + х2 = 1 + 0 = 0 и реле отпускается.
На рис. 3, г показан узел включения реле в случае нажатия кнопки КнП при замкнутом контакте ВК. В схеме с логическими элементами в нормальном состоянии контактов получим у7 = х 6 = у 6 = х 4 = у3 = х1х2 = 0 • 0 = 0. Если нажата только кнопка КнП, то у7 = х1х2 = 1 • 0 = 0. Если замкнут только контакт ВК, то у7 = = х1х2 = 0 • 1 = 0. При замыкании КнП и ВК получим у7 = х1х2 = 1 • 1 = 1. Это означает, что реле срабатывает.
На рис. 3, д показана схема управления двумя реле Р1 и Р2. При подаче напряжения на цепь срабатывает реле времени РВ, его контакты в линии 3 размыкаются мгновенно. Схема готова к работе. При нажатии кнопки КнП срабатывает реле Р1, его контакты замыкаются, шунтирут кнопку. Другие контакты в линии 2 размыкаются, а в линии 3 замыкаются. Реле РВ отпускается и его контакты с выдержкой времени замыкаются, срабатывает реле Р2. Таким образом, после нажатия кнопки КнП реле Р1 срабатывает сразу, а Р2 — через некоторое время.
В схеме с логическими элементами узел «Память» построен на триггере. Пусть на выходе у него сигнал отсутствует (у3 = 0), реле Р1 и Р2 обесточены. Нажимаем кнопку КнП, появляется сигнал на выходе триггера. Срабатывает реле Р1 и начинает отсчет времени элемент ЭВ.
Когда появится сигнал у5 = 1, срабатывает реле Р2. При нажатии кнопки КнС триггер переключается и тогда у3 = 0. Реле Р1 и Р2 отпускаются.
Типовые узлы с логическими элементами широко применяют в более сложных схемах, причем такие схемы гораздо проще, чем схемы на релейно-контакторной аппаратуре.
Источник
Лекция
Тема: Построение
логических схем с помощью базовых логических элементов
План
1. Логические
элементы.
2. Построение
логических схем.
Логическим элементом
называется дискретный преобразователь, который после обработки входных двоичных
сигналов выдает на выходе сигнал, являющийся значением одной из логических
операций.
Поскольку любая логическая операция может быть
представлена в виде комбинаций трех основных, любые устройства компьютера,
производящие обработку или хранение информации, могут быть собраны из базовых
логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют сигналами,
представляющими собой электрические импульсы. Есть импульс – логический смысл
сигнала – 1, нет импульса – 0. На входы логического элемента поступают
сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается
таблицей состояния, которая фактически является таблицей истинности,
соответствующей логической функции.
Рассмотрим условные обозначения (схемы) базовых
логических элементов, реализующих логическое умножение (конъюнктор), логическое
сложение (дизъюнктор) и отрицание (инвертор).
Логический
элемент «ИЛИ»:

Логический
элемент «НЕ»:

Логический
элемент «И»:
например,
ИЛИ ДРУГОЙ ВИД ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
|
Инверсия |
|
|
Конъюнкция |
|
|
Дизъюнкция |
|
Устройства компьютера (сумматоры в процессоре, ячейки
памяти в оперативной памяти и др.) строятся на основе базовых логических
элементов.
Если элемент имеет входное напряжение от 0 до 0,4В, то
оно рассматривается как логический 0, если напряжение в пределах от 0,7 до
1,5В, то оно рассматривается как 1. Примерно такие же характеристики имеет
выходное напряжение.
I.
Построить
схемы
Пример 1. Составить схему
Результат:
Пример 2. Составить схему
Результат:
Пример 3. Составить
схему
Результат:
Пример 4. Составить схему
Результат:
Пример 5. Составить
схему
Результат:
Пример 6. Составить схему
Результат:
Пример 7. Составить
схему
Результат:
II. Выполним задачу
обратную данной. Составим логическое выражение по заданной логической схеме:
Данное логическое
выражение можно упростить.
Операция И – логическое
умножение, ИЛИ – сложение. Запишем выражение, заменяя знаки & и U на * и +
соответственно.
Упростим
, затем
запишем
)
и тогда
логическая схема примет вид:
Вывод: Логические схемы, содержащие минимальное
количество элементов, обеспечивают большую скорость работы и увеличивают
надёжность устройства.
Алгебра логики дала конструкторам мощное средство
разработки, анализа и совершенствования логических схем. Проще, и быстрее
изучать свойства и доказывать правильность работы схемы с помощью выражающей её
формулы, чем создавать реальное техническое устройство.
По заданной логической функции построить логическую
схему.
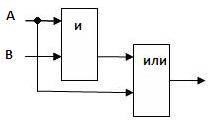
Наше построение схемы, мы начнем с логической
операции, которая должна выполняться последней. В нашем случае такой операцией
является логическое сложение, следовательно, на выходе логической схемы должен
быть дизъюнктор. На него сигналы будут подаваться с двух конъюнкторов, на
которые в свою очередь подаются один входной сигнал нормальный и один
инвертированный (с инверторов).
Пример 2. Выписать
из логической схемы соответствующую ей логическую формулу:
|
А |
В |
F |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Решение:
2.
Построение
логических схем.
Вариант
1.
По
заданной логической функции построить
логическую схему и таблицу истинности.
Решение:
2.
Выписать из логической схемы соответствующую ей логическую формулу:
|
А |
В |
F |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Решение:
Вариант
2.
1.
По заданной логической функции построить
логическую схему и таблицу истинности.
Решение:
2.
Выписать из логической схемы соответствующую ей логическую формулу:
|
А |
В |
F |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Решение:
По
заданной логической функции построить
логическую схему и таблицу истинности.
Контрольные
вопросы:
1. Перечислите
основные логические операции.
2. Что такое
логическое умножение?
3. Что такое
логическое сложение?
4. Что такое
инверсия?
5. Что такое
таблица истинности?
6. Что такое
сумматор?
7. Что такое
полусумматор?
Литература,
ЭОР:
1.
Информатика
и информационные технологии. Учебник для 10-11 классов,Н. Д. Угринович –
2007г.;
2. Практикум по
информатике и информационным технологиям. Учебное пособие для
общеобразовательных учреждений, Н. Д. Угринович, Л. Л. Босова, Н. И. Михайлова
– 2007г.
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
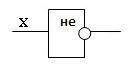
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
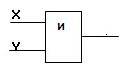
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
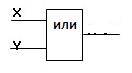
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx
Пример 1.
Составьте логическую схему для логического выражения: F=A / B / A.
1. Две переменные – А и В.
2. Две логические операции: 1-/, 2-/.
3. Строим схему:
Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/В/ ¬(В/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: / и две /; А/В/ ¬ (В/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
4. Вычислим значение выражения: F=1 / 0 / ¬(0 / 1)=0
Исследование логических элементов и синтез логических схем
Цель работы.
Ознакомление с основными функциями и
законами алгебры логики, характеристиками
логических микросхем, основами анализа
и синтеза простых и сложных логических
схем.
Краткие
теоретические сведения.
Анализ работы
цифровых устройств и синтез логических
цепей производится на основе
математического аппарата алгебры
логики или «булевой» алгебры, оперирующей
только двумя понятиями: истинным
(логическая «1») и ложным (логический
«0»). Функции, отображающие такую
информацию, а также устройства,
формирующие функции алгебры логики,
называются логическими. Логические
функции нескольких переменных определяют
характер логических операций, в
результате которых набору входных
переменных
x0,
x1,…,
xn-1
ставится в соответствие выходная
переменная F
F
= f(x0,
x1,…,
xn-1).
Функция преобразования
характеризуется таблицей, в которой
каждой комбинации входных переменных
соответствует значение выходной
переменной F.
Ее называют таблицей истинности.
Основными функциями
алгебры логики, с помощью которых можно
осуществлять любые логические
преобразования, являются логическое
умножение (конъюнкция), логическое
сложение (дизъюнкция) и логическое
отрицание (инверсия).
Алгебра логики
позволяет преобразовывать формулы,
описывающие сложные логические
зависимости, с целью их упрощения. Это
помогает в конечном итоге определять
оптимальную структуру того или иного
цифрового автомата, реализующего любую
сложную функцию. Под оптимальной
структурой принято понимать такое
построение автомата, при котором число
входящих в его состав элементов
минимально.
Основные законы
алгебры логики.
Переместительный
закон:
a
+ b
= b
+ а; ab
= ba.
Сочетательный
закон:
(a + b)
+ c = a + (b + c); (ab)c = a(bc).
Распределительный
закон:
a(b + c) = ab + ac; a + bc
= (a + b)(a +c).
Закон поглощения:
a + ab = a(1 + b) = a; a(a
+ b) = a + ab = a.
Закон
склеивания:
ab
+ a
= a;
(a
+ b)(a
+)
= a.
Закон отрицания:
или
.
Логические
элементы.
Логические элементы используют в
качестве значений входных и выходных
напряжений лишь два уровня: «высокий»
и «низкий». Если логическому «0»
соответствует напряжение низкого
уровня, а логической «1» – высокого, то
такую логику называют положительной,
и наоборот, если за логический «0»
принимают напряжение высокого уровня,
а за логическую «1» – напряжение низкого
уровня, то такую логику называют
отрицательной. В транзисторно-транзисторной
логике (ТТЛ) напряжение логического
«0» – U0
составляет десятые доли вольт
(менее 0,4 В), а напряжение логической
«1» – U1
>2,4 В. Логические элементы реализуют
простейшие функции или систему функций
алгебры логики.
|
Таблица |
|
|
|
|
|
0 |
1 |
|
1 |
0 |
П

функцией алгебры логики является
функция НЕ. Она реализуется с помощью
инвертора, условное графическое
обозначение которого приведено на рис.
1. На вход инвертора подается величинаX,
которая может принимать два значения:
«0» и «1». Выходная величина Y,
при этом тоже принимает два значения:
«1» и «0». Взаимно однозначное соответствие
X
и Y
дается таблицей истинности (табл. 1),
причем значение выходной величины Y
зависит не от предыдущих значений, а
лишь от текущего значения входной
величины X:
Y
=
.
Это справедливо
для всех логических элементов, не
имеющих памяти, у которых в таблице
истинности значение Y
не зависит от порядка строк.
|
Таблица |
||
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Л

элементами, реализующими функции
логического сложения и логического
умножения, являются элементы ИЛИ и И.
Таблицы истинности для этих элементов
однозначно связывают значение выходной
величиныY
со значениями двух (или более) входных
величин хl,
х2,
… xn.
Условные графические обозначения
логических элементов ИЛИ и И приведены
соответственно на рис. 2 и 3, а их таблицы
истинности – в таблицах 2 и 3. Например,
для логического элемента 2-ИЛИ,
реализующего дизъюнкцию
Y
= хl
+ х2
или Y
= хl
х2,
а для элемента
2-И, реализующего конъюнкцию
Y
= хl
х2
или Y
= хl
х2.
|
Таблица |
||
|
|
|
|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Н

наборе логических элементов И,
ИЛИ, НЕ можно реализовать любую сколь
угодно сложную логическую функцию,
поэтому данный набор элементов
называют функционально полным.
На практике часто
используется расширенный набор
логических элементов, позволяющих
также составлять функционально полные
системы. К ним относятся элементы:
ИЛИ-НЕ (элемент
Пирса), реализующий функцию
;
И-НЕ (элемент
Шеффера), реализующий функцию
.
Их обозначения и
таблицы истинности приведены на рис.
4 и в табл. 4.
|
Таблица |
|||
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
Рис. 4
В частности
функционально полные системы могут
состоять из элементов только
одного типа, например, реализующих
функцию И-НЕ либо ИЛИ-НЕ.
Комбинационные
логические цепи – это такие цепи,
выходные сигналы которых однозначно
определяются сигналами, присутствующими
на их входах в рассматриваемый момент
времени и не зависят от предыдущего
состояния.
Набор логических
элементов, входящих в состав учебного
стенда по основам цифровой техники не
содержит элементов, реализующих функцию
ИЛИ-НЕ, что ограничивает число вариантов
построения логических схем при их
синтезе и позволяет составлять схемы
только в базисе элементов И-НЕ.
Прежде чем перейти
к вопросам анализа и синтеза логических
устройств в заданном базисе элементов
(И-НЕ), необходимо составить таблицу, в
которую будут сведены все возможные
формы представления выходных сигналов
указанных элементов при условии, что
на их входы поданы логические переменные
хl
и х2.
При синтезе схем можно использовать
два технических приема: двойное
инвертирование входного исходного
выражения или его части и применение
теорем Де-Моргана. При этом функция
преобразуется к виду, содержащему
только операции логического умножения
и инверсии, и переписывается через
условные обозначения операции И-НЕ и
НЕ.
Последовательность
проведения анализа и синтеза комбинационных
логических цепей:
-
Составление
таблицы функционирования логической
цепи (таблицы истинности). -
Запись логической
функции. -
Минимизация
логической функции и преобразование
ее к виду, удобному для реализации в
заданном базисе логических элементов
(И-НЕ, НЕ).
Пример проведения
анализа и синтеза логических цепей
[1].
Пусть необходимо
построить мажоритарную ячейку (ячейку
голосования) на три входа, т.е. такую
ячейку, у которой сигнал на выходе равен
единице тогда, когда на двух или трех
входах цепи присутствует сигнал единицы,
в противном случае выходной сигнал
должен быть равен нулю.
Вначале заполним
таблицу истинности (табл. 5). Поскольку
в данном случае имеются три входных
сигнала х1,
х2,
х3,
каждый из которых может принимать одно
из двух возможных значений (0 или 1), то
всего может быть восемь различных
комбинаций этих сигналов. Четырем из
этих комбинаций будет соответствовать
выходной сигнал F,
равный единице.
Таблица
5
|
N |
x1 |
x2 |
x3 |
F |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
Пользуясь данными табл.
5, можно записать логическую функцию,
которую должна реализовать
синтезируемая цепь. Для этого нужно
представить эту функцию в виде суммы
логических произведений, соответствующих
тем строкам табл. 5 (3, 5-7), для которых
функция F
равна единице. Аргументы записываются
без инверсии, если они равны единице и
с инверсией, если равны нулю.
Если в синтезируемой
таблице истинности выходная величина
чаще принимает значение «1», то
синтезируются строки, в которых выходная
величина равна «0».
При выполнении
заданной процедуры получим функцию
F=. (1)
Для минимизации
(упрощения) данной функции нужно
применить основные законы алгебры
логики. Возможна следующая последовательность
преобразований, например, с применением
закона склеивания (теоремы Де-Моргана):
F
=
=
+
=. (2)
Как видно, полученное
конечное выражение гораздо проще
исходного.
Аналогично
проводится анализ (составление таблиц
истинности) и более сложных логических
схем.
Для выполнения
задания предлагается набор наиболее
распространенных логических элементов
(рис. 5).

5. Набор логических элементов для
выполнения задания
Задание к
лабораторной работе
1. Составить таблицы
истинности для всех логических элементов,
приведенных на рис. 5.
2. Для каждого
логического элемента из набора
представленных на рис. 5. составить
логические выражения, реализующие их
функции в базисе логических элементов
НЕ и И-НЕ и начертить полученные
тождественные схемы.
3. Собрать
рассмотренные схемы на стенде и, путем
перебора комбинаций входных сигналов,
составить их таблицы истинности.
4. Используя законы
отрицания (теоремы Де-Моргана) произвести
преобразование минимизированной
функции (2) для реализации ее в базисе
логических элементов НЕ и И-НЕ и начертить
полученную тождественную схему.
5. Собрать
представленную схему на стенде и, путем
перебора комбинаций входных сигналов,
проверить соответствие ее работы
таблице истинности (табл. 5).
Контрольные
вопросы
-
Что
такое функционально полная система и
базис логических элементов? -
В чем
особенности синтеза логических
устройств? -
В чем
заключаются принципы минимизации
логических устройств? -
Назовите основные
операции булевой алгебры. -
Что
отражают теоремы булевой алгебры?
Сформулировать теоремы Де-Моргана:
поглощения и склеивания. -
Какие
цифровые устройства называются
комбинационными?
ЛАБОРАТОРНАЯ
РАБОТА № 6
Соседние файлы в предмете Электроника
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример проектирования цифрового устройства «на пальцах»
Время на прочтение
3 мин
Количество просмотров 23K
Привет, Хабр! Это начало небольшого цикла из двух статей с пошаговым проектированием цифрового устройства с уклоном на практику. Минимум «воды» и максимум практики!
Для начала работы возьмем следующие выходные параметры: 0000110001110001
Примечание: существует множество способов и программ для проектирования цифровых устройств. Показанное в статье может отличаться от привычных вам. Это нормально.
Инструменты, материалы и прочее:
- Electronics Workbench
- Линейка, ручка и листок (для общих расчетов)
- Базовые знания дискретной математики, цифровой схемотехники и принципа работы представленных программ
- Условное графическое обозначение микросхем 7404 (аналог К155ЛН1), 7410 (аналог К155ЛА4), 7410 (аналог К155ЛА4) и 7420 (аналог К155ЛА1)
- Фактическое изображение микросхем 7404 (аналог К155ЛН1), 7410 (аналог К155ЛА4), 7410 (аналог К155ЛА4) и 7420 (аналог К155ЛА1)
Начало работы
1. Построение таблицы истинности и нахождение совершенной дизъюнктивной нормальной формы (СДНФ)
Первым делом необходимо составить таблицу истинности по формуле
где N – количество возможных вариантов, а i – количество выходных сигналов.
В представленном случае это будет выглядеть так:
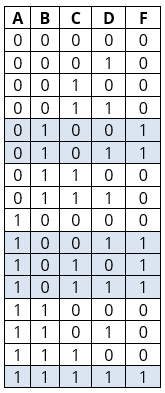
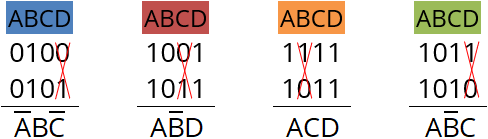
На основе полученных данных можно перейти к построению таблицы истинности. Для наглядности входные сигналы были обозначены как A, B, C и D, выходной как F.
После построения таблицы истинности можно приступать к получению СДНФ. Это выполняется в два шага:
- Выделяются строчки таблицы истинности, в которых F=1.
- Выписывается конъюнкция переменных у всех выделенных строк по следующей формуле: если значение переменной равно 1, то в конъюнкцию включается сама переменная. Если значение равно 0, то включается отрицание переменной. Полученные конъюнкции нужно связать в дизъюнкцию.
По итогу выходит такая СДНФ:
Более наглядно:
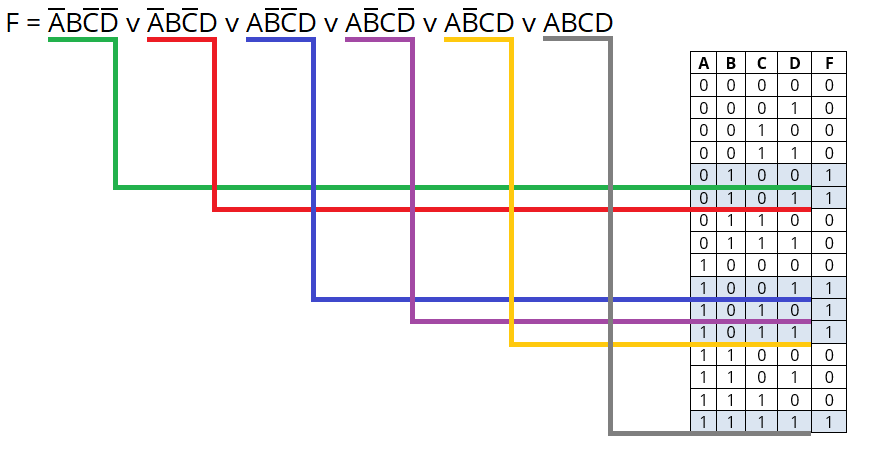
2. Создание карты Карно, минимизация и приведение к базису И-НЕ
Полученную СДНФ необходимо сократить при помощи карт Карно.
Три шага для построения карт Карно:
- так как используются четыре переменные (A, B, C и D), то строится таблица 5×5 клеток;
- таблица заполняется на основе «координат» из таблицы истинности (из строк, в которых F=1) или СДНФ (суть одна. Просто кому как удобнее);
- в заключение смежные клетки объединяются в группы. Группы не должны содержать нули. Группы должны быть кратны двум. Группы могут пересекаться.
В итоге получилось 4 группы:
Более наглядно:

Следующее действие — минимизация полученных групп. Общий принцип можно свести к следующему:
Если 11 — значение не меняется;
Если 00 — присваивается отрицание;
Если 01 (или 10) — вычеркивается.
Полученные произведения связываются в дизъюнкцию:
После чего составленное выражение приводится к базису И-НЕ при помощи закона де Моргана (отрицание конъюнкции есть дизъюнкция отрицаний, отрицание дизъюнкции есть конъюнкция отрицаний):
Обратите внимание на изменения — появилось двойное отрицание (по одной на «группу» и одно общее) и изменились знаки.
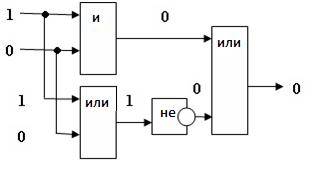
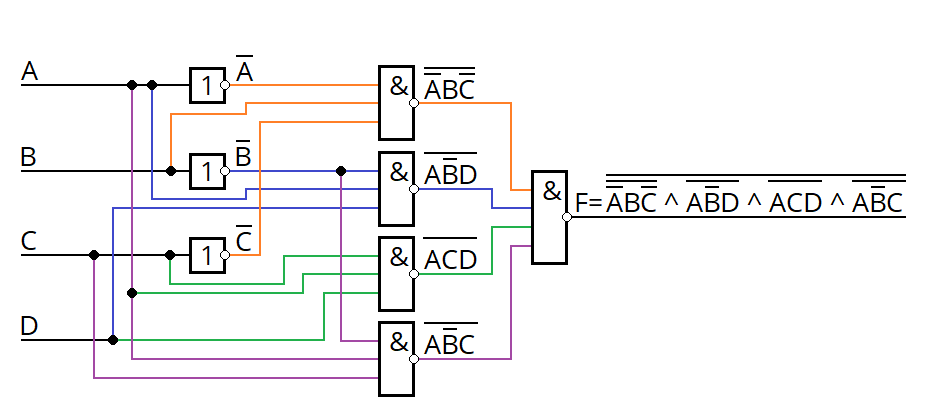
По желанию также можно составить логическую схему. Почему по желанию? Потому что дальше будет составление электронной схемы на основе логических элементов, а она, по своей сути, является той же самой логической схемой, но с возможностью проверки работоспособности.
Пример логической схемы:
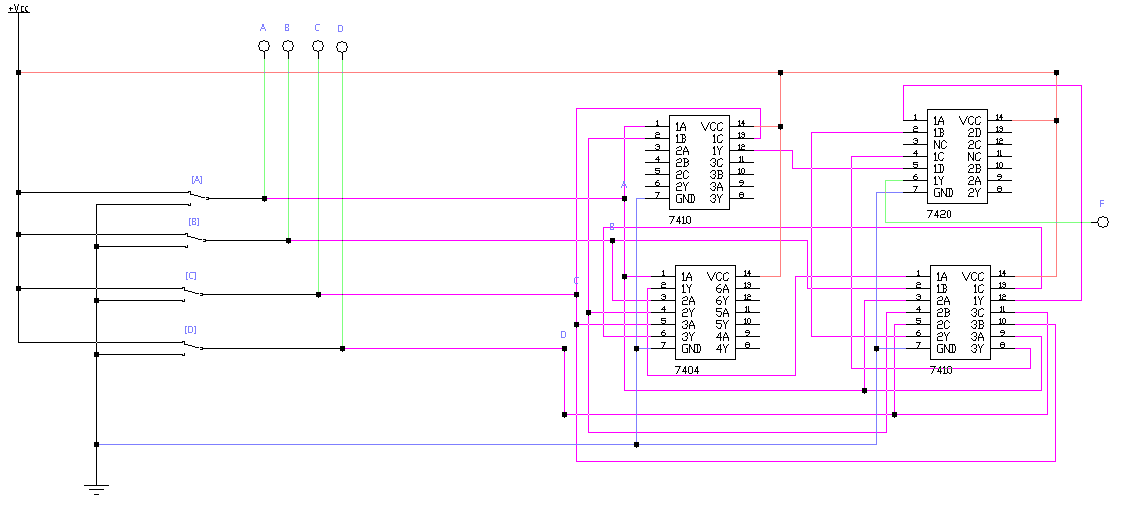
3. Электронная схема на основе логических элементов
Основные расчеты завершены. Теперь можно отложить листок с ручкой и линейкой. Переходим в Electronics Workbench.
В данном случае этот этап выступает «промежуточным» и упрощает процесс перехода от выражения в базисе И-НЕ к электронной схеме на основе микросхем.
Более наглядно:
1 — Питание;
2 — Переключатели, используемые для подачи сигналов;
3 — Индикаторы (применяются для наглядной проверки работоспособности);
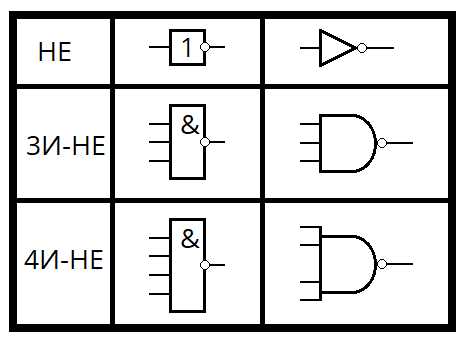
4 — Логические элементы типа «НЕ»;
5 — Логические элементы типа «3И-НЕ»;
6 — Логический элемент типа «4И-НЕ»;
7 — Заземление.
Как можно заметить, логические элементы электронной схемы внешне отличаются от тех, что были представлены ранее (в логической схеме). Это связано с тем, что в Electronics Workbench условное графическое обозначение логических элементов выполнено по стандартам ANSI, тогда как показанная ранее логическая схема была выполнена в соответствии ГОСТ 2.743-91.
Идем дальше.
Работоспособность электронной схемы проверяется по таблице истинности. Для этого нужно нажать кнопку запуска
и начать производить переключения, проводя сравнение с таблицей истинности.
Пример:
ВАЖНО: нужно проверять каждую строчку. Выборочная проверка ничего не даст.
4. Электронная схема на основе микросхем
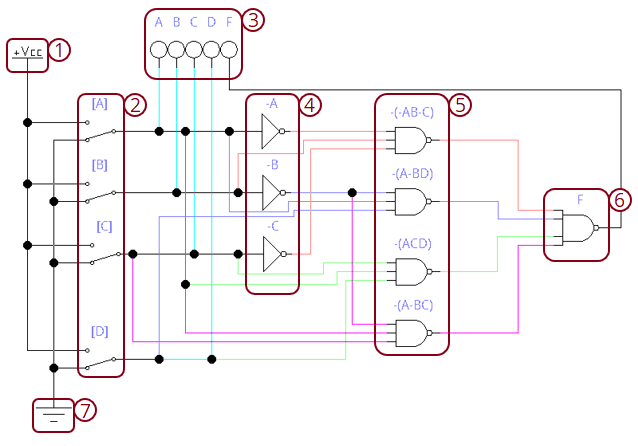
На базе имеющихся данных производится построение электронной схемы на основе микросхем (также по полученной схеме можно будет ориентироваться во время проектирования печатной платы).
Как можно заметить, в полученной электронной схеме использовано 4 микросхемы — 7404 (аналог К155ЛН1), 7410 (аналог К155ЛА4), 7410 (аналог К155ЛА4) и 7420 (аналог К155ЛА1). Для того чтобы понять, как происходит подключение, следует обратиться к фактическому изображению микросхем.
Сначала это может показаться сложным, но со временем вы поймете, что это не так уж и трудно.
ВАЖНО: не забывайте делать проверку.