Практическая работа № 7
Тема: Программная реализация вывода графических изображений на экран.
Цель: Научиться создавать программы для построения графических изображений на экране.
Оборудование: ПК, система программирования Qbasic.
Ход работы
1. Изучить основные сведения по теме.
Основные сведения
При запуске среды QBasic экран монитора автоматически устанавливается в текстовый режим. Чтобы переключить экран в графический режим используется оператор SCREEN.
Формат: SCREEN <номер графического режима>
Номер графического режима указывает, на какое количество пикселей будет разбит экран.В графическом режиме на экран монитора выводится изображение (рисунок).
Рисунок – это совокупность точек различного цвета. Эти точки называются пикселями. Экран монитора состоит из точек – пикселей.
В графическом режиме изображение на экране строится по точкам. Каждая точка имеет определенные координаты (х, у) и цвет. Начало координат находится в левом верхнем углу экрана.
Оператор SCREEN 9 включает графический режим работы экрана. В этом режиме экран разбивается на 640 точек по горизонтали (ось Х) и 340 точек по вертикали (ось У).
Для рисования точки определенного цвета используется оператор PSET
PSET – оператор построения точки (высвечивание экранной точки с заданными координатами и заданным цветом)
Формат: PSET (X,Y), N
(X,Y) – координаты экранной точки в пикселях
N – целое число, которое указывает номер цвета из активной палитры
Номер цвета можно не указывать, в этом случае изображение будет белым.

Для рисования прямых линий используется оператор LINE.
LINE – оператор построения отрезка.
Формат: LINE (X1,Y1) – (X2,Y2), N
(X1,Y1) – координаты начала отрезка
(X2,Y2) – координаты конца отрезка
N – номер цвета
Для рисования прямоугольников используется специальная форма оператора LINE. При этом задаются две противоположно лежащие точки и на них, как на диагонали, строится прямоугольник (например, координаты левого верхнего угла прямоугольника и координаты правого нижнего угла прямоугольника)
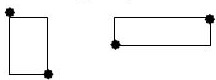
Формат: LINE (X1,Y1) – (X2,Y2), N, B
(X1,Y1) – координаты начала диагонали
(X2,Y2) – координаты конца диагонали
N – номер цвета
B – служебное слово, обозначающее прямоугольник (box)
Для рисования закрашенных прямоугольников вместо служебного слова В используется служебное слово BF
Формат: LINE (X1,Y1) – (X2,Y2), N, BF
N – номер цвета контура и заливки
Чтобы нарисовать окружность необходимо знать радиус и центр окружности. Для рисования окружностей используется оператор CIRCLE.
CIRCLE – оператор построения окружности
Формат: CIRCLE (X,Y), R, N
(X,Y) – координаты центра окружности
R – радиус окружности (длина радиуса в пикселях)
N – номер цвета
Для рисования овалов используется специальная форма оператора CIRCLE:
Формат: CIRCLE (X,Y), R, N, , , К (три запятые после номера цвета ОБЯЗАТЕЛЬНЫ)
К – коэффициент сжатия первоначальной окружности.
Если К>1, то сжатие по горизонтали
Если 0<К<1, то сжатие по вертикали
![]()
Для рисования дуги окружности используется специальная форма оператора CIRCLE:
Формат: CIRCLE (X,Y), R, N, a, b
a – угол, от которого начинается дуга (значение угла задается в радианах)
b – угол, где дуга заканчивается (значение угла задается в радианах)
Правило рисования дуг: дуга строится от угла a к углу b против часовой стрелки.
Формула перевода углов из градусной меры в радианы: 1° × 3,14/180 = 0,01745 рад
Бейсик позволяет использовать в качестве операндов в своих командах арифметические выражения. Поэтому, если вы затрудняетесь определить угол начала или окончания дуги на тригонометрической окружности (знаете, например, его значение в градусах 300, но не знаете значение в радианах), то можете в соответствующем месте оператора дуги написать 3,14*30/180 и пусть компьютер сам считает.
На рисунке можно закрашивать замкнутые области, ограниченные линиями одного цвета. Для закраски замкнутых областей применяется оператор PAINT. Закрашивать можно ТОЛЬКО замкнутые области.
PAINT – оператор заливки
Формат: PAINT (X,Y), N1, N2
(X,Y) – координаты точки внутри замкнутой области
N1 – цвет заливки
N2 – цвет контура (линии, ограничивающей область)
Для рисования некоторых фигур можно использовать ломаную линию.
DRAW – оператор построения ломаной линии.
Формат: DRAW “направления”
Возможные направления линий:
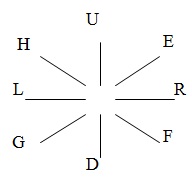
Примеры использования операторов:
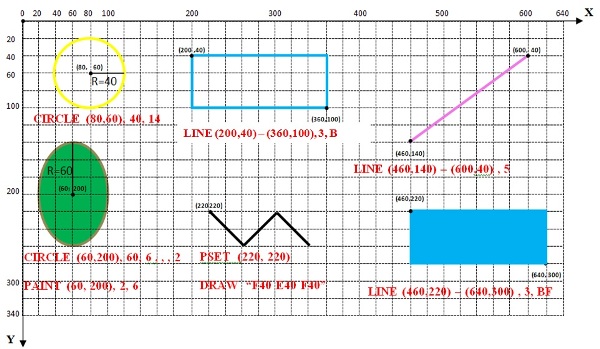
2.Выполнить задания по теме.
Задание 1.
1. На рабочем столе найдите ярлык программы qbasic2. Запустите программу. Создайте новый файл.
2. Введите в программу примеры построчно. Вводите одну строку, запустите на выполнение (Run-Start или F5), посмотрите, что произошло на экране, введите вторую строку, запустите на выполнение и т.д.
SCREEN 9
PSET (240,180), 10
LINE (460,140) – (600,40), 5
LINE (200,40) – (360,100), 3,B
LINE (460,220) – (620,300), 3,BF
CIRCLE (80,60), 40, 14
CIRCLE (160,140), 30, 14, , , 3
CIRCLE (240,160), 25, 14, , , 0.5
CIRCLE (60,200), 60, 6, , , 2
PAINT (62,203), 2, 6
PAINT (84,65), 14, 3
Удалите последнюю строчку, посмотрите на изменения
PAINT (84,65), 14, 14
PSET (220,200), 12
DRAW “F40 E40 F40”
3. Сохраните программу под именем grafika.bas
Задание 2.
1. Начертите в тетради систему координат XY, выбрав начало координат в верхнем левом углу страницы, горизонтальная ось Х, единичный отрезок 1 клеточка – 20пт, вертикальная ось Y, единичный отрезок 1 клеточка – 10пт.
2. Нарисуйте в этой системе координат (В ТЕТРАДИ) рисунок с домиком строго по клеточкам:

3. Составить программу после выполнения которой на экране появится это изображение.
4. Изменить программу, добавив новые элементы в рисунок и раскрасить его различными цветами.
Задание 3.
1. Используя оператор DRAW нарисуйте на экране свое имя.
3. Работа над контрольными вопросами.
Контрольные вопросы
- Как включить графический режим работы экрана?
- Какой оператор используется для построения отрезка? Какие точки нужно указывать при построении отрезка?
- Какой оператор используется для построения прямоугольника? Какие точки нужно указывать при построении прямоугольника?
- Какой оператор используется для построения окружности, овала? Что нужно задать, чтобы построить окружность?
- Какой оператор используется для построения закрашенного прямоугольника?
- Какой оператор используется для построения ломаной линии?
- Какой оператор используется для окрашивания фигур? Какие области нельзя окрасить с помощью этого оператора?
Презентация к уроку “Программная реализация вывода графических изображений на экран”
Помогаю со студенческими работами здесь
 Разработать алгоритм и составить программу для построения на экране изображения
Разработать алгоритм и составить программу для построения на экране изображения
Разработать алгоритм и составить программу для построения на экране изображения
В качестве…
 Разработать алгоритм и составить программу для построения на экране изображения
Разработать алгоритм и составить программу для построения на экране изображения
Разработать алгоритм и составить программу для построения на экране изображения
В качестве…
Составить программу для построения геометрического изображения пространственной фигуры
Составить программу для построения геометрического изображения пространственной…
 Составить программу построения изображения n квадратов
Составить программу построения изображения n квадратов
Составить программу построения изображения n квадратов: квадраты вписаны друг в друга так, что…
Составить программу построения изображения в плоском зеркале с анимацией
Составить программу построения изображения в плоском зеркале с анимацией
Разработать программу для построения изображения.
Разработать программу для построения изображения..
Закрасить и заштриховать изображение!!!…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
Семинары
N7
и N8
МАШИННАЯ ГРАФИКА.
Семинар
N7
Построение
плоских изображений и создание анимации
Компьютерная
графика – совокупность методов и средств
для преобразования данных в графическую
форму представления и обратно с помощью
ЭВМ.
Компьютерная
графика находит самое широкое применение
в различных отраслях науки и техники,
промышленности, экономике, учебном
процессе, органах управления, быту.
Для
построения изображений необходимо
иметь специальные технические и
программные средства, называемые
средствами компьютерной графики.
Основным техническим устройством
является графический дисплей, основу
которого сегодня может представлять
электронно-лучевая трубка, плазменная
панель или жидкокристаллическая матрица.
Однако в каждом из этих трех случаев
поверхность, на которой формируется
изображение, представляет собой
совокупность отдельных светящихся
элементов, т.е. имеет дискретную природу,
в то время как выводимые геометрические
объекты имеют непрерывный характер.
Изображение
на поверхности дисплея формируется в
виде совокупности отдельных светящихся
точек, поэтому для построения сколь
угодно сложного графического изображения
достаточно знать цвет каждой точки
экрана, т.е. изображение фактически
представляет собой мозаику. Однако
разная природа исходных и визуализированных
объектов порождает целый ряд проблем,
прежде всего, требует разработки и
применения соответствующих алгоритмов
построения отрезков, окружностей, других
кривых, заполнения областей на поверхности
экрана.
Изображение,
подлежащее выводу на экран дисплея,
может быть представлено совокупностью
простейших геометрических фигур
(отрезков, прямоугольников, окружностей,
эллипсов и т.д.), для высвечивания которых
имеются, как правило, готовые языковые
средства. Однако для правильного
использования готовых методов классов,
обеспечивающих построение геометрических
фигур, следует знать параметрическое
число каждого из таких объектов.
Параметрическим числом объекта называется
минимальное количество параметров,
задающих этот геометрический объект.
Например, параметрическое число отрезка
– четыре, прямоугольника, эллипса – пять.
Однако
при использовании методов классов
Delphi
требуется задавать меньшее количество
параметров. Это свидетельствует о том,
что данные методы обеспечивают вывод
фигур частного положения. Например,
отрезок строится из текущего положения
графического курсора в точку с заданными
координатами, прямоугольник – со
сторонами, параллельными координатным
осям, эллипс – с осями, также параллельными
координатным осям. Данные ограничения
следует принимать во внимание при
написании программ, в частности, в том
случае, когда строится преобразованное
(повернутое) изображение, так как в этом
случае геометрические фигуры приобретают
произвольную ориентацию на плоскости.
В этом случае необходимо самостоятельно
написать фрагмент программы, обеспечивающей
построение требуемого изображения.
Вывод прямоугольника удобно осуществлять,
зная координаты его четырех вершин, а
построение кривых обычно производится
по точкам, принадлежащим кривой, которые
соединяются отрезками прямых.
При
написании программы вывода графического
изображения целесообразно составить
выражения для вычисления координат
точек, используемых при обращении к
методам вывода геометрических объектов.
При этом определенную точку изображения
принимают за базовую, а координаты
остальных точек вычисляют по отношению
к этой базовой точке. Такой подход делает
программу достаточно гибкой и
универсальной, так как при изменении
положения базовой точки автоматически
пересчитываются координаты других
точек. Размеры фрагментов изображения
не следует задавать в абсолютных
значениях, а лучше задавать в долях от
размеров поля вывода (разрешающей
способности), так как в этом случае при
изменении размеров поля вывода
пропорционально изменятся и размеры
выводимого изображения и не придется
заново вычислять новые размеры и
координаты точек.
Под
разрешающей способностью экрана понимают
количество растра, приходящихся на
единицу измерения длины, вдоль координатных
осей.
Среда
визуального программирования Delphi
в полной мере предоставляет пользователю
возможность разрабатывать программы,
с помощью которых можно получить
графические изображения: схемы, чертежи,
текст и иллюстрации. Богатство графических
возможностей Windows
связано с так называемым дескриптором
контекста графического устройства DC
(Device
Context)
и тремя входящими в него инструментами
– шрифтом, пером и кистью. В Delphi
созданы
классы-надстройки, упрощающие
использованием графических инструментов
Windows:
для контекста – класс TCanvas,
для шрифта – TFont,
для пера – TPen,
для кисти – TBrush.
Связанные с этими классами объекты
автоматически создаются для всех видимых
элементов и становятся доступны программе
через свойства Canvas,
Font,
Pen,
Brush.
В
Delphi
существует ряд специальных компонентов
для вывода готовых изображений (рисунков
или фотографий) из графических файлов
(компонент Image),
некоторых геометрических фигур (компонент
Shape),
графиков и диаграмм (компонент Chart)
и др. Например, с помощью компонента
Shape
(он расположен на странице Additional
палитры компонентов) можно изобразить
на форме круг, эллипс, квадрат, прямоугольник
или прямоугольник с закругленными
углами. Для этого достаточно поместить
на форму компонент Shape
и
настроить его с помощью соответствующих
свойств (свойство Shape
позволяет выбрать фигуру, свойство
Brush
отвечает за её фоновый цвет, а свойство
Pen
–
за толщину и цвет её границы).
Основным
классом, позволяющим использовать
обширные графические возможности Delphi
является
класс TСanvas.
Этот класс имеет множество свойств и
методов. Объект Canvas
(канва, холст) этого класса является
свойством формы и многих графических
компонентов (Image,
PaintBox, BitMap и
др.). Он представляет собой область
компонента, на которой можно рисовать
или отображать готовые изображения.
Канва содержит свойства и методы,
существенно упрощающие графику Delphi.
Каждая
точка канвы имеет координаты Х
и Y.
Система координат канвы, как и везде в
Delphi,
имеет
началом левый верхний угол канвы.
Координата Х
возрастает при перемещении слева
направо, а координата Y
– при перемещении сверху вниз. Координаты
измеряются в пикселах. Важнейшее свойство
пиксела – его цвет. Для описания цвета
используется тип TColor.
Цвет встречается практически в каждом
компоненте. В Delphi определено множество
констант типа TСolor.
Одни из них непосредственно определяют
цвета (например, clBlue
– синий), другие определяют цвета элементов
окон, которые могут меняться в зависимости
от выбранной пользователем палитры
цветов Windows
(например, clBtnFace
– цвет поверхности кнопок).
Таблица 1
Константы свойства Color
|
Константа |
Цвет |
Константа |
Цвет |
|
clBlack |
Черный |
clSilver |
Серебристый |
|
clMaroon |
Каштановый |
clRed |
Красный |
|
clGreen |
Зеленый |
clLime |
Салатный |
|
clOlive |
Оливковый |
clBlue |
Синий |
|
clNavy |
Темно-синий |
clFuchsia |
Ярко-розовый |
|
clPurple |
Розовый |
clAqua |
Бирюзовый |
|
clTeal |
Зелено-голубой |
clWhite |
Белый |
|
clGray |
Серый |
clYellow |
Желтый |
У
канвы имеется свойство Pen
– перо. Оно, в свою очередь, имеет ряд
свойств. Одно из них – уже известное
свойство Color
– цвет, которым наносится рисунок. Второе
свойство – Width
(ширина линии). Она задается в пикселах.
По умолчанию ширина линии равна 1. Третье
свойство Style
определяет вид линии. Это свойство может
принимать следующие значения:
Таблица
2
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
10.02.201514.6 Mб46marochnik-staley-i-splavovov-zsorokinu-hocre.djvu
- #
- #
- #
- #
- #
- #
18

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ ДЕТЕЙ
«СТАНЦИЯ ЮНЫХ ТЕХНИКОВ ГОРОДА ЕВПАТОРИИ РЕСПУБЛИКИ КРЫМ»
(МБОУДОД “СЮТ”)

297402, Российская Федерация, Республика Крым, город Евпатория, ул. Революции, д. 75, тел. (06569) 3-03-30,
е-mail: [email protected]
План-конспект учебного занятия
кружок «Компьютер и информационные технологии», группа 2 – А
Тема учебного занятия: «Построение графических изображений в среде Turbo Pascal».
Цель учебного занятия: формирование у детей знаний и умений работы с языком программирования Pascal, организация работы по усвоению детьми основных понятий, принципов работы с данным языком.
Задачи учебного занятия:
Образовательная:
-
проконтролировать степень усвоения основных понятий, принципов работы с языком программирования Pascal, изученных и сформированных на предыдущих занятиях;
-
обеспечить усвоение основных задач, входящих в содержание темы учебного занятия;
-
научить составлять программы с использованием графических процедур и функций в среде Turbo Pascal;
-
формировать умение правильно и грамотно выражать свои мысли.
Развивающая:
-
развивать творческие способности, память, мышление обучающихся, навыки индивидуальной практической деятельности.
Воспитательная:
-
воспитывать аккуратность, внимательность, вежливость, дисциплинированность и бережное отношение к вычислительной технике.
Тип учебного занятия: формирование новых знаний, навыков и умений.
Методы работы: объяснительно-иллюстративный, практическая работа.
Формы работы: индивидуальная, групповая.
Оборудование: персональные компьютеры, доска, мел.
Дидактические материалы: карточки с заданиями.
Ход учебного занятия.
-
Организационный момент;
-
ТБ при работе за компьютером;
-
Актуализация опорных знаний:
-
Мотивация учебной деятельности обучающихся:
-
Выполнение практической работы;
-
Физкультминутка;
-
Итоги учебного занятия:
-
Вы научились составлять программы с использованием графических процедур и функций в среде Turbo Pascal.
1. Организационный момент.
Приветствие, проверка присутствующих. Объяснение хода учебного занятия.
2. ТБ при работе за компьютером.
3. Актуализация опорных знаний:
Основные принципы работы с языком Pascal.
Pascal – один из самых известных языков программирования. Создан в 1968 – 1969 годах швейцарским ученым Никлаусом Виртом, был назван в честь французского математика и физика Блеза Паскаля, и используется для обучения программированию по сей день.
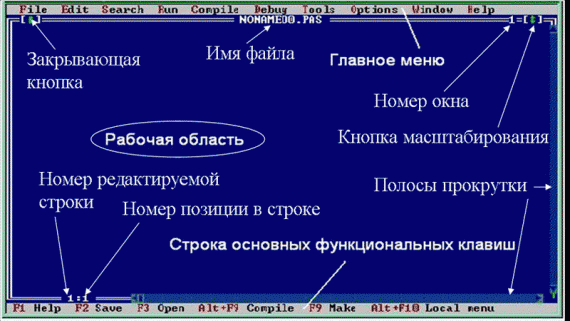
Перед началом работы следует напомнить, что язык Pascal – это совокупность трёх составляющих: алфавита, синтаксиса (правил написания объектов языка) и семантики (правил использования этих объектов).
Алфавит Pascal состоит из:
-
Прописных и строчных букв латиницы: A…Z, a…z;
-
Цифр: 0…9;
-
Специальных символов: + — * / = .,:; ‘ # ( ) { } [ ] и их комбинаций: «=» «
Задача же синтаксиса и семантики состоит в том чтобы, правильно написать раздел программы и правильно составить ее структуру, в противном же случае ваша программа будет работать неправильно (или же не работать вовсе!).
Структура программы выглядит так:
Program «имя программы»; — заголовок программы;
(Примечание: в конце строки ставится точка с запятой, не во всех, но в большинстве)
Uses (название библиотеки); здесь подключаются библиотеки, которые дают дополнительные возможности при создании программ;
Label (имя метки); здесь, если необходимо, прописываются метки, позволяющие переходить в разные места программы (о них позже);
Const тут указываем переменные с постоянной величиной, например, p=3.14;
Var тут через запятую перечисляем все переменные, а затем, указываем тип данных (Пример: Var: K, L, M: integer; N, O: real; (если несколько типов));
Begin (здесь без точки с запятой)
Дальше следует основной блок программы;
end. – конец программы (обязательно после “end” точка, если только это конец программы, а не операторные скобки).
Следует заметить, что из вышеперечисленных разделов обязательными есть только «Var», «Begin» и «end», остальные же могут применяться, если это требуется в ходе выполнения поставленной задачи.
Для использования графических возможностей Турбо Паскаля необходимо в блоке описания uses подключить графический модуль Graph. Перечислим набор графических функций и процедур, основные из которых рассмотрены ниже.
Модуль Graph
ТР обладает достаточно разнообразными средствами для работы со стандартным VGA экраном (возможно также использование и и других типов видеоадаптеров).
VGA адаптер имеет разрешение 640х480 пиксель (точка (0,0) в левом верхнем углу экрана), 16 цветов.
Перед началом работы с графикой необходимо ее инициализировать, а по окончании – “закрыть”. Все графические процедуры и функции находятся в модуле Graph, поэтому также необходимо его подключение.
Общая структура графической программы:
Uses crt, graph;
var Gd, Gm: Integer;
begin
Gd: = Detect;
InitGraph (Gd, Gm, ‘c: bpbgi’);
…
{Здесь построение изображения}
…
ReadKey;
CloseGraph;
end.
Путь c: bpbgi указывает расположение файла egavga. bgi (драйвер графического адаптера). На разный компьютерах этот путь может быть разным. Если файл egavga. bgi поместить в каталог с программой, то путь можно не указывать.
Основные графические процедуры и функции:
Построение фигур
PutPixel (x,y,c) – отображает на экране точку с координатами (x,y) и цветом c
Line (x1,y1,x2,y2) – рисует линию с началом в точке (x1,y1) и концом – (x2,y2)
Rectangle (x1,y1,x2,y2) – рисует контур прямоугольника с диагональю (x1,y1) – (x2,y2)
Bar (x1,y1,x2,y2) – рисует закрашенный прямоугольник с диагональю (x1,y1) – (x2,y2)
Circle (x,y,r) – рисует окружность с центром (x,y) и радиусом r
Ellipse (x,y,ba,ea,xr,yr) – рисует дугу эллипса с центром в (x,y), горизонтальным и вертикальным радиусом xr и yr, и начальным и конечным углом ba и ea
FillEllipse (x,y,xr,yr) – рисует закрашенный эллипс с центром в (x,y), горизонтальным и вертикальным радиусом xr и yr
Определение цветов и стилей
GetPixel (x,y) – возвращает цвет пиксела с координатами (x,y)
SetColor (c) – устанавливает цвет изображения (для линий)
SetFillStyle (p,c) – устанавливает текущий стиль и цвет c (для “закрашенных” фигур)
FloodFill (x,y,b) – закрашивает замкнутую область с внутренней точкой (x,y) и цветом контура b
Работа с текстом
OutTextXY (x,y,st) – выводит на экран строку st с позиции (x,y)
SetTextStyle (f,d,s) – устанавливает шрифт f, его направление d и размер
Сообщения об ошибках.
function GraphErrorMsg (ErrorCode: integer): String; Возвращает строку сообщения об ошибке для заданного кода ErrorCode.
function GraphResult: integer; Возвращает код ошибки для последней графической операции.
Графические процедуры
Arc (x,y: integer; St,En,R: word);{рисование дуги, где x,y – коорд. центра дуги, R – радиус, St, En – нач. и конечный углы. }
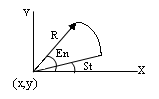
ClearDevice; {очистка экрана}
Circle (x,y: integer; R: word);{окружность радиуса R
cцентром в точке (x,y) }
CloseGraph; {закрытие графики}
InitGraph (gd,gm: integer; Path: string);{инициализация графики, где
gd – графический драйвер,
gm – графический режим,
Path – путь размещения файла
с расширением. bgi. }
Line (x1,y1,x2,y2: integer); {рисование линии, проходящей через две точки:
с координатами (x1,y1) и (x2,y2) }
LineRel (dx,dy: integer);{рисование линии: dx, dy– приращения
координат к координатам текущей позиции курсора}
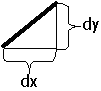
LineTo (x,y: integer);{рисование линии, проходящую через текущую позицию курсора и точку с координатами (x,y) }
Moveto (x,y: integer);{задание координат текущей точки}
OutText (T: string);{вывод текста в текущую точку}
OutTextXY (x,y: integer; T: string);{вывод текста в точку с координатами х, у}
Rectangle (x1,y1,x2,y2: integer);{рисование прямоугольника: (x1,y1) и (x2,y2) – координаты противоположных вершин}
PutPixel (x,y: integer; c: word);{выводит точку с координатами (х, у) цветом с}
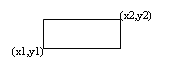
Графические функции
GetMaxX – определяет максимальный размер экрана по оси x.
GetMaxY – определяет максимальный размер экрана по оси y.
GetX – координата текущей позиции курсора по оси x.
GetY – координата текущей позиции курсора по оси y.
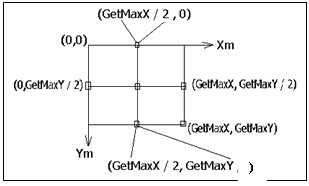
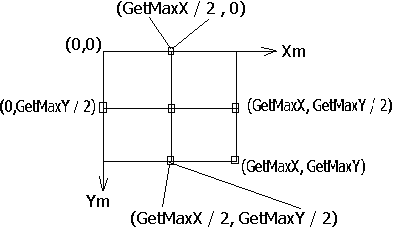
Машинные координаты.
Начало машинной системы координат, направление осей, а также максимальные значения координат монитора показаны на рисунке
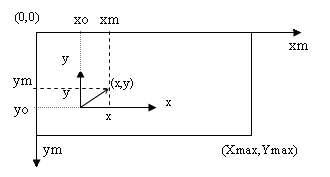
На рисунке приведена также машинная (xm, ym) и физическая (x,y) системы координат. Для изображения на экране точки с физическими координатами (x,y) необходимо определить ее машинные координаты (xm, ym). Расчетные формулы имеют следующий вид (попробуйте самостоятельно получить эти формулы):
xm=x0+x*Mx,
ym=y0-y*My,
где Mx, My-масштабы соответственно по осям x и y, которые показывают число пикселей в одной физической единице,
x, y – физические координаты точки,
xm, ym – машинные координаты точки,
x0, y0 – машинные координаты начала физической системы координат.
Пример. Нарисовать через весь экран горизонтальную и вертикальную линии, пересекающиеся в центре монитора.
Этапы разработки программы сведены в таблицу.
Таблица
|
N |
Этапы программирования |
Выполнение |
|
1. |
Постановка задачи |
Нарисовать через весь экран горизонтальную и вертикальную линии, пересекающиеся в центре монитора. |
|
2. |
Математическое описание |
Изобразим вид экрана с указанием координат требуемых линий
|
|
3. |
Разработка структограммы |
|
|
4. |
Написание программы |
Program P5; Uses graph; {подключениеграф. модуля} Var gd,gm: integer; Begin gd: =detect; {определениеграф. драйвера} InitGraph (gd,gm,’ ‘); {инициализация графики} Line (0, round (GetMaxY/2), GetMaxX, Round (GetMaxY/2)); {гориз. лин. } Line (round (GetMaxX/2),0,Round (GetMaxX/2), GetMaxY); {вертик. лин. } Readln; {пустойввод} CloseGraph; {закрытие графики} End. |
|
5. |
Отладка и получение результатов |
Выполнить самостоятельно |
Пример. Написать программу построения графика функции y=x2 для xϵ [-1; 1].
Этапы разработки программы сведены в таблицу.
Таблица
|
N |
Этапы программирования |
Выполнение |
|
1. |
Постановка задачи |
Построить график функции y=x2 для x∈ [-1; 1]. |
|
2. |
Математическое описание |
Изобразим вид экрана, который мы хотели бы получить после выполнения программы.
|
|
3. |
Разработка структограммы |
|
|
4. |
Написание программы |
Program P6; Uses graph; Var gd,gm: integer; x,y: real; x0,y0,xm,ym,Mx,My: integer; begin gd: =detect; InitGraph (gd,gm,’ ‘); Mx: =300; x0: =320; My: =440; y0: =460; {выбраны для монитора 640×480 пикс. } For xm: =20 to 620 do Begin x: = (xm-x0) /Mx; y: =sqr (x); ym: =round (y0-y*My); PutPixel (xm,ym,1); End; Readln; CloseGraph; End. |
|
5. |
Отладка и получение результатов |
Выполнить самостоятельно |
4. Мотивация учебной деятельности обучающихся:
Создавая Паскаль, Вирт преследовал 2 цели:
-
во-первых, разработать язык, пригодный для обучения программированию как систематической дисциплине;
-
во-вторых, реализация языка должна быть эффективной и надежной на существующих вычислительных машинах.
Одним из достоинств языка Pascal является то, что он воплотил в себе идею структурного программирования, суть которой заключается в том, что с помощью нескольких конструкций можно выразить в принципе любые алгоритмы: линейные, ветвление, циклические конструкции.
Это был самый первый простой язык (ord pascal) для программирования, помогающий решить множество практических задач прошлого столетия (1970 год). Он был разработан группой ученых. С расширением платформ были созданы новые версии этой программы, а Pascal стал классическим языком программирования.
5. Выполнение практической работы.
Линейные алгоритмы в графике.
I. Рисунки, построенные из простейших геометрических фигур.
Один из самых простых способов построения графического изображения основан на использовании элементарных геометрических фигур – отрезков прямых, окружностей, прямоугольников, дуг, эллипсов и т. п.
Построенное изображение часто напоминает детские рисунки или картинки для игры в мозаику.
Программировать такие картинки несложно, однако, требуется предварительная кропотливая работа по определению размеров фигур и их размещение на экране.
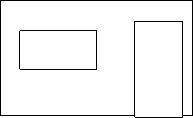
Пример 1. Следующая программа позволяет получить на экране изображение домика.
|
|
|
|
uses graph;
var dr, mode:integer;
begin
dr:=detect;
initgraph(dr, mode,’c:bpbgi’);
rectangle(40,280,460,520);
rectangle(80,320,200,440);
rectangle(280,320,400,520);
line(40,280,240,120);
line(240,120,460,280);
circle(240,200,40);
readln;
closegraph;
end.
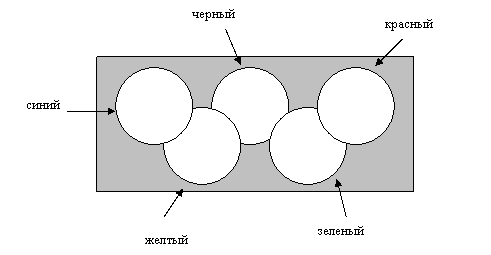
Пример 2. Данная программа выводит на экран флаг Олимпийских игр.
|
|
uses graph;
var dr, mode:integer;
begin
dr:=detect;
initgraph(dr, mode,’c:bpbgi’);
setfillstyle(solidfill, lightgray);
bar(80,80,200,135);
setcolor(green);
circle(100,100,15);
setcolor(black);
circle(140,100,15);
setcolor(red);
circle(180,100,15);
setcolor(yellow);
circle(120,115,15);
setcolor(blue);
circle(160,115,15);
readln;
closegraph;
end.
II. Построение сечений в пространственных геометрических фигурах.
Для развития пространственного воображения и ознакомления с основными геометрическими телами можно предложить учащимся написать программы, выводящие на экран компьютера изображения призм, пирамид, конусов и т. п. с построением различного рода сечений.
Пример 1. В результате выполнения следующей программы, в треугольной пирамиде будет построено сечение, проходящее через боковое ребро и медиану основания.

uses graph;
const
tr:array[1..5] of pointtype=((x:320;y:80),(x:440;y:360),(x:320;y:440),
(x:160;y:400),(x:320;y:80));
var
driver, mode, e,xc, yc:integer;
begin
driver:=detect;
initgraph(driver, mode,’c:bpbgi’);
drawpoly(5,tr);
line(160,400,440,360);
xc:=(320+160) div 2;
yc:=(400+440) div 2;
line(320,80,xc, yc);
line(xc, yc,440,360);
setfillstyle(2,14);
floodfill(420,320,15);
floodfill(xc+1,yc-1,15);
line(320,80,320,440);
readln;
closegraph;
end.
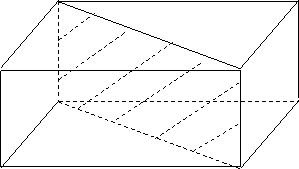
Пример 2. Следующая программа решает задачу: в прямоугольном параллелепипеде провести диагональное сечение.
|
|
uses graph;
var driver, mode:integer;
font:word;
begin font:=installuserfont(‘goth’);
driver:=detect;
initgraph(driver, mode,’c:bpbgi’);
setfillstyle(0,0);
bar3d(120,120,480,360,80,true);
line(120,360,200,300);
line(200,300,200,62);
line(200,300,560,300);
line(200,300,480,360);
line(200,62,480,120);
setfillstyle(3,15);
floodfill(202,70,15);
floodfill(202,130,15);
floodfill(475,340,15);
settextstyle(font,0,4);
outtextxy(220,420,’parallepiped’);
readln;
closegraph;
end.
Примеры решения задач с использованием операторов графики и циклических операторов:
Задача1.: Составить программу, осуществляющую движение отрезка, концы которого вращаются по двум заданным окружностям.
Листинг решение:
uses crt,graph;
var x1,y,x2,x3,y3,x4,y4:integer;
u:real;
begin
initgraph(x1,y,”);
x1:=20;
y:=getmaxY div 2;
x2:=100;
u:=pi/2;
repeat
setcolor(14);
setlinestyle(0,0,1);
circle(x1,y,20);
circle(x2,y,20);
x3:=x1+round(20*cos(u));
y3:=y-round(20*sin(u));
x4:=x2+round(20*cos(u));
y4:=y-round(20*sin(u));
setcolor(11);
setlinestyle(0,0,3);
line(x3,y3,x4,y4);
delay(100);
setcolor(0);
circle(x1,y,20);
circle(x2,y,20);
setlinestyle(0,0,3);
line(x3,y3,x4,y4);
x1:=x1+5;
x2:=x2+5;
u:=u-0.1;
until x1=getmaxX;
setcolor(12);
settextstyle(0,0,3);
outtextXY(getmaxX div 2-60,y,’Okonchanie rabotu programmu’);
readln
end.
Сохраните Вашу работу и покажите её педагогу.
6. Физкультминутка.
7. Итоги учебного занятия
Ответьте на следующие вопросы:
-
Что нового Вы узнали, решив задания на учебном занятии?
-
Задания были сложными? Задания были интересными?
-
Над изучением каких тем в разделе «Изучение языка программирования Pascal» Вы хотели бы ещё поработать?
18