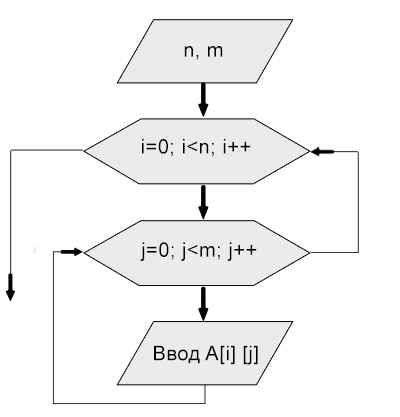
Общая часть
Во всех задачах будем считать, что матрица описана следующим образом:
const SzM = 10; SzN = 10; type Matrix = array [1..SzM,1..SzN] of integer;
Кроме того, во всех задачах будем использовать следующие процедуры для заполнения и вывода:
procedure FillMatrixByRandom(var a: Matrix; m,n: integer); // Заполнение случайными begin for var i:=1 to M do for var j:=1 to N do a[i,j] := Random(10); end; procedure PrintMatrix(const a: Matrix; m,n: integer); // Вывод матрицы begin for var i:=1 to M do begin for var j:=1 to N do write(a[i,j]:4); writeln; end; end;
Данные участки кода следует писать в начале каждой программы, приводимой в этом пункте.
Заполнение матрицы случайными числами и вывод
var a: Matrix; begin var m := 4; var n := 5; FillMatrixByRandom(a,m,n); writeln('Элементы матрицы: '); PrintMatrix(a,m,n); end.
Перемена местами двух строк
var a: Matrix; begin var m := 5; var n := 9; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); var k1 := 2; // поменять местами строки с номерами k1 и k2 var k2 := 4; for var j:=1 to n do Swap(a[k1,j],a[k2,j]); writeln('Преобразованная матрица: '); PrintMatrix(a,m,n); end.
Поиск минимумов в строках
var a: Matrix; mins: array [1..SzN] of integer; begin var m := 5; var n := 9; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); for var i:=1 to m do begin var min := a[i,1]; for var j:=2 to n do if a[i,j]<min then min := a[i,j]; mins[i] := min; end; writeln('Минимумы в строках: '); for var i:=1 to m do write(mins[i]:4); end.
Поиск максимумов в столбцах
var a: Matrix; maxs: array [1..SzN] of integer; begin var m := 5; var n := 9; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); for var j:=1 to n do begin var max := a[1,j]; for var i:=2 to m do if a[i,j]>max then max := a[i,j]; maxs[j] := max; end; writeln('Максимумы в столбцах: '); for var j:=1 to n do write(maxs[j]:4); end.
Поиск сумм в строках
var a: Matrix; sums: array [1..SzM] of integer; begin var m := 4; var n := 5; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); for var i:=1 to m do begin var sum := 0; for var j:=1 to n do sum += a[i,j]; sums[i] := sum; end; writeln('Суммы в строках: '); for var i:=1 to m do write(sums[i]:4); end.
Поиск произведений в столбцах
var a: Matrix; products: array [1..SzN] of integer; begin var m := 3; var n := 4; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); for var j:=1 to n do begin var p := 1; for var i:=1 to m do p *= a[i,j]; products[j] := p; end; writeln('Произведения в столбцах: '); for var j:=1 to n do writeln(products[j]:4); end.
Наличие нуля в матрице
var a: Matrix; HasZero: boolean; label 1; begin var m := 3; var n := 4; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); HasZero := False; for var i:=1 to m do for var j:=1 to n do if a[i,j]=0 then begin HasZero := True; goto 1; end; 1: if HasZero then writeln('В матрице есть нули') else writeln('В матрице нулей нет') end.
Сумма чисел на главной диагонали
var a: Matrix; sum: integer; begin var m := 5; var n := m; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); sum := 0; for var i:=1 to m do sum += a[i,i]; writeln('Сумма элементов главной диагонали: ',sum); end.
Сумма чисел на побочной диагонали
var a: Matrix; sum: integer; begin var m := 5; var n := m; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); sum := 0; for var i:=1 to m do sum += a[i,m-i+1]; writeln('Сумма элементов побочной диагонали: ',sum); end.
Заполнение нулями ниже главной диагонали
var a: Matrix; sum: integer; begin var m := 5; var n := m; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); for var i:=2 to m do for var j:=m-i+2 to m do a[i,j] := 0; writeln('Преобразованная матрица: '); PrintMatrix(a,m,n); end.
Заполнение нулями выше побочной диагонали
var a: Matrix; sum: integer; begin var m := 5; var n := m; FillMatrixByRandom(a,m,n); writeln('Исходная матрица: '); PrintMatrix(a,m,n); for var i:=1 to m-1 do for var j:=i+1 to m do a[i,j] := 0; writeln('Преобразованная матрица: '); PrintMatrix(a,m,n); end.
Ссылки
- Программы для начинающих
- Сайт PascalABC.NET: Программы и алгоритмы для начинающих
Функциональное программирование на примере работы с матрицами из теории линейной алгебры
Время на прочтение
11 мин
Количество просмотров 12K
Вступление
В основе работы с матрицами (в данной статье мы будем рассматривать только двумерные матрицы) лежит мощная математическая теория из области линейной алгебры. Одно определение или действие следует из другого, одна функция вызывает другую. Поэтому для программной реализации функционала математических операций над матрицами функциональные языки подходят очень хорошо. В рамках данной статьи мы рассмотрим конкретные примеры на языке F# и дадим подробные комментарии, как это работает. Так как F# входит в семейство .NET, то полученный функционал можно без каким либо проблем использовать в других императивный языках, например C#.
Определение матрицы и реализация на F#
Матрицы являются базовой и важнейшей частью линейной алгебры. Матрицы часто используются в программировании, например в 3D-моделировании или гейм-девелопинге. Разумеется, велосипед уже давно изобретен и необходимые фреймворки для работы с матрицами уже готовы, и их можно и нужно использовать. Данная статья не ставит своей целью изобретение нового фреймворка, но показывает реализацию базовых математических операций для работы с матрицами в функциональном стиле с использованием языка программирования F#. По мере рассмотрения материала мы будем обращаться к математической теории матриц и смотреть, как ее можно реализовать в коде.
Для начала вспомним, что такое матрица? Теория говорит нам следующее
Прямоугольная таблица чисел, содержащая m строк и n столбцов, называется матрицей размера m x n
Матрицы, как правило, обозначаются прописными буквами латинского алфавита и записываются в виде
Или коротко
Для работы с матрицами в F# создадим запись, основанную на двумерной таблице, которую в дальнейшем будем расширять полезными методами для того, чтобы совершать необходимые математические операции над ней.
type Matrix = { values: int[,] }
with
// здесь будем добавлять методы
end
Добавим вспомогательный метод для инициализации записи двумерным массивом
static member ofArray2D (values: int [,]) =
{ values = values }
Входным аргументом функции будет двумерный массив, а на ее выходе — запись типа Matrix. Ниже приведем пример инициализации записи.
let a = array2D [[1;0;2]
[3;1;0]]
let A = Matrix.ofArray2D a
Две матрицы A=(aij) и B=(bij) называются равными, если они совпадают поэлементно, т.е. aij=bij для всех i=1,2…,m и j=1,2…n
Для реализации этого правила будем использовать переопределенный оператор == и добавим пару полезных функций, которые также понадобятся нам в дальнейшем.
static member sizes matrix =
let rows = matrix.values.[*,0].Length
let cols = matrix.values.[0,*].Length
(rows, cols)
static member isEquallySized matrix1 matrix2 =
let dim1 = Matrix.sizes matrix1
let dim2 = Matrix.sizes matrix2
(dim1 = dim2)
static member (==) (matrix1, matrix2) =
if not (Matrix.isEquallySized matrix1 matrix2) then false
else
not (matrix1.values
|> Array2D.mapi (fun x y v -> if matrix2.values.[x, y] <> v then false else true)
|> Seq.cast<bool>
|> Seq.contains false)
Давайте подробнее рассмотрим код выше. Как можно заметить, здесь есть три функции. Первая функция sizes возвращает размерность матрицы в виде кортежа. Так как мы работаем только с прямоугольными матрицами, то для получения количества строк мы берем полный срез первой колонки и возвращаем ее длину.
let rows = matrix.values.[*,0].Length
Аналогичным способом работает определение количества колонок — получаем полный срез первой строки и возвращаем ее длину.
Следующая функция isEquallySized сравнивает размерность двух матриц и возвращает true если они равны. Для этого она использует уже готовую функцию sizes и просто сравнивает результаты.
Оператор == для поэлементного сравнения двух матриц кажется сложнее, но сейчас вы увидите, что он также простой.
Перед тем, как сравнивать две матрицы, сравним их размерность. Если они не равны, то нет дальше смысла проводить проверку, так как уже понятно, что и матрицы будут не равны.
if not (Matrix.isEquallySized matrix1 matrix2) then false
Далее, на основе исходных матриц matrix1 и matrix2 мы формируем новую матрицу, заполненную true или false, в зависимости от того, совпадают ли соответствующие ячейки обеих матриц.
matrix1.values
|> Array2D.mapi (fun x y v -> if matrix2.values.[x, y] <> v then false else true
Функция Array2D.mapi перебирает все элементы matrix1 и передает в обработчик три параметра
x — индекс строки
y — индекс колонки
v — содержимое ячейки
Содержимое ячейки v мы сравниваем с соответствующей ячейкой matrix2 и если они равны, то пишем true, иначе — false.
Если есть хоть одна ячейка с элементом false, то это означает, что матрицы не равны между собой.
Так как Array2D не содержит в себе методов для фильтрации или поиска, то реализуем это сами. Для этого разложим матрицу в линейный список
|> Seq.cast<bool>
И найдем хоть одно несовпадение
|> Seq.contains false
Функция Seq.contains вернет true если в разложенном списке будет найдено хоть одно значение false. Поэтому нам нужно инвертировать полученный результат, чтобы оператор == работал так, как мы хотим
else
not (matrix1.values
|> Array2D.mapi (fun x y v -> if matrix2.values.[x, y] <> v then false else true)
|> Seq.cast<bool>
|> Seq.contains false)
Матрица O называется нулевой или нуль-матрицей, если все ее элементы равны нулю.
static member O rows cols =
let array2d = Array2D.zeroCreate rows cols
{ values = array2d }
Пример использования этой функции
let AO = Matrix.O 5 5
Полагаю, что здесь нет ничего сложного, что требует пояснений, поэтому продолжаем.
Матрица, число строк которой равно числу столбцов и равно n, называется квадратной матрицей порядка n
Таким образом, квадратная матрица имеет вид.
В рамках этого правила мы создадим функцию, которая прямоугольную матрицу трансформирует в квадратную путем отсечения всех элементов, которые не попадают в квадрат.
static member toSquare matrix =
// получаем размерность исходной матрицы
let dim = Matrix.sizes matrix
// получаем количество колонок
let colCount: int = snd dim
// получаем количество строк
let rowCount: int = fst dim
// находим размер минимальной стороны
let length = System.Math.Min (colCount, rowCount)
// создаем пустой квадратный массив с размерностью
// равной наименешей стороне исходной матрицу
let zero = Array2D.zeroCreate length length
// копируем исходную матрицу в квадратную
let square = zero |> Array2D.mapi (fun x y _ -> matrix.values.[x, y])
// позвращаем полученную матрицу
{ values = square }
Комментариев в исходном коде поясняют принцип работы функции, поэтому продолжим.
Квадратная матрица называется треугольной, если все ее элементы ниже главной диагонали равны нулю, т.е. треугольная матрица имеет вид
Ниже приведен код функции, который преобразует исходную матрицу в треугольную. Но в нашей функции мы будем работать с прямоугольной матрицей, то есть она может быть не квадратной. Читатель легко может модифицировать код функции так, чтобы она возвращала квадратную треугольную матрицу, используя функцию, которую мы рассмотрели ранее.
static member T matrix =
let values = matrix.values |> Array2D.mapi (fun x y v -> if y < x then 0 else v)
{ values = values }
Функция Array2D.mapi преобразовывает исходный двумерный массив в новый при помощи обработчика, который принимает три параметра
x — номер строки
y — номер колонки
v — содержимое ячейки
if y < x then 0 else v
Здесь мы делаем проверку, находится ли элемент ниже главной диагонали и если да, то заполняем ячейку 0. В противном случае — исходным значение из входной матрицы.
Ниже приведен пример использования этой функции.
let a = array2D [[1;2;3]
[4;5;6]
[7;8;9]
[10;11;12]]
let A = Matrix.ofArray2D a
let R = Matrix.triangular A
printfn "origin = n %A" A.values
printfn "triangular = n %A" R.values
Получаем следующий результат
origin =
[[1; 2; 3]
[4; 5; 6]
[7; 8; 9]
[10; 11; 12]]
triangular =
[[1; 2; 3]
[0; 5; 6]
[0; 0; 9]
[0; 0; 0]]
Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю
static member D matrix =
let diagonal = matrix.values |> Array2D.mapi (fun x y v -> if x <> y then 0 else v)
{ values = diagonal }
Эта функция очень похожа на предыдущую, отличается только условие проверки. Ниже пример использования
let a = array2D [[1;2;3]
[4;5;6]
[7;8;9]
[10;11;12]]
let A = Matrix.ofArray2D a
let R = Matrix.D A
printfn "origin = n %A" A.values
printfn "diagonal = n %A" R.values
origin =
[[1; 2; 3]
[4; 5; 6]
[7; 8; 9]
[10; 11; 12]]
diagonal =
[[1; 0; 0]
[0; 5; 0]
[0; 0; 9]
[0; 0; 0]]
Диагональная матрица является единичной и обозначается E, если все ее элементы, расположенные на главной диагонали, равны единице
Реализация такой матрицы на F# выглядит так
static member E rows cols =
let array2d = Array2D.init rows cols (fun x y -> if x = y then 1 else 0)
{ values = array2d }
Операции над матрицами при помощи F#
Над матрицами, как и над числами, можно производить ряд действий, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.
Суммой двух матриц Amn=(aij)и Bmn=(bij)одинаковых размеров называется матрица того же размера A+B=Cmn=(cij), элементы которой равны сумме элементов матриц A и B, расположенных на соответствующих местах
Пример, для заданных матриц A и B находим сумму A+B
Рассмотрим код для сложения двух матриц
static member (+) (matrix1, matrix2) =
if Matrix.isEquallySized matrix1 matrix2 then
let array2d = matrix1.values |> Array2D.mapi (fun x y v -> matrix2.values.[x, y] + v)
{ values = array2d }
else failwith "matrix1 is not equal to matrix2"
Перед тем, как складывать матрицы, нужно убедиться, что их размерность совпадает, в противном случае функция генерирует исключение. Ниже приведем пример использования данной функции
let a = array2D [[2;3]
[1;-5]
[0;6]]
let A = Matrix.ofArray2D a
let b = array2D [[-3;3]
[1;7]
[2;0]]
let B = Matrix.ofArray2D b
let R = A+B
printfn "A+B =n %A" R.values
A+B =
[[-1; 6]
[2; 2]
[2; 6]]
Произведением матрицы A=(aij) на число k называется матрица kA=(kaij) такого же размера, что и матрица A, полученная умножением всех элементов матрицы A на число k
Пример, для заданной матрицы A находим матрицу 3A
static member (*) (value, matrix) =
let array2d = matrix.values |> Array2D.mapi (fun _ _ v -> v * value)
{ values = array2d }
Матрицу -A=(-1)*A будем называть противоположной матрице A. Из этого определения плавно переходим к следующему
Разностью матриц A и B одинаковых размеров называется сумма матрицы A и матрицы, противоположной к B
static member (-) (matrix1: Matrix, matrix2: Matrix) =
if Matrix.isEquallySized matrix1 matrix2 then
matrix1 + (-1)*matrix2
else failwith "matrix1 is not equal to matrix2"
Две матрицы называются согласованными, если число столбцов первой равны числу строк второй
static member isMatched matrix1 matrix2 =
let row1Count = matrix1.values.[0,*].Length
let col2Count = matrix2.values.[*,0].Length
row1Count = col2Count
Проверка согласованности матриц требуется для их перемножения.
Произведением AB согласованных матриц Amn=(aij) и Bnp=(bjk) называется матрица Cmn=(cik), элемент cik которой вычисляется как сумма произведений элементов i-й строки матрицы A и соответствующих элементов k-го столбца матрицы B
Вычислить произведение матриц
Решение по определению произведения матриц
Рассмотрим код для умножения двух матриц
static member (*) (matrix1, (matrix2: Matrix)) =
if Matrix.isMatched matrix1 matrix2 then
let row1Count = matrix1.values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
let values = Array2D.zeroCreate row1Count col2Count
for r in 0..row1Count-1 do
for c in 0..col2Count-1 do
let row = Array.toList matrix1.values.[r,*]
let col = Array.toList matrix2.values.[*,c]
let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col
values.[r,c] <- cell
{ values = values }
else failwith "matrix1 is not matched to matrix2"
Давайте разберемся с кодом подробнее.
Перед умножением нужно убедиться, что матрицы являются согласованными
if Matrix.isMatched matrix1 matrix2 thenИтоговая матрица будет иметь размерность, в которой количество строк такое же, как у первой матрицы и количество столбцов такое же, как у второй матрицы
let row1Count = matrix1.values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
// формируем пустой двумерный массив для сохранения результатов умножения
let values = Array2D.zeroCreate row1Count col2Count
После этого мы последовательно перебираем все строки и все столбцы исходных матриц
for r in 0..row1Count-1 do
for c in 0..col2Count-1 do
let row = Array.toList matrix1.values.[r,*]
let col = Array.toList matrix2.values.[*,c]
Вычисляем итоговое значение каждой ячейки
let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col
Функция List.fold2 на вход получает два списка (строку и колонку) и передает в обработчик следующие параметры
acc — аккумулятор, содержащий результат предыдущего вычисления
val1 — содержимое ячейки из первого массива. В нашем случае это строка из первой матрицы
val2 — содержимое ячейки из второго массива, то есть колонки второй матрицы
Так как матрицы являются согласованными, то мы уверены, что у нас не произойдет выхода за пределы массивов.
Обработчик добавляет к аккумулятору произведение ячеек из строк и столбца и полученное значение будет передано следующей итерации. Таким образом конечным итогом работы функции List.fold2 будет итоговое значение произведений двух матриц. Остается только заполнить им предварительно созданную пустую матрицу
values.[r,c] <- cellКоторая вернется как результат
{ values = values }Ниже приведем пример использования данной функции
let a = array2D [[1;0;2]
[3;1;0]]
let A = Matrix.ofArray2D a
let b = array2D [[-1;0]
[5;1]
[-2;0]]
let B = Matrix.ofArray2D b
let R = A*B
printfn "A*B =n %A" R.values
A1*B1 =
[[-5; 0]
[2; 1]]
Если k ∈ N, то k-й степенью квадратной матрицы Aназывается произведение k матриц A
Рассмотрим код на F# для произведения матрицы в степень. Здесь будет использоваться хвостовая рекурсия для того, чтобы не переполнить стек при больших значениях степеней. Хвостовая рекурсия — это такая рекурсия, которая компилятором в итоге преобразуется в цикл. По возможности рекомендуется всегда использовать именно хвостовую рекурсию вместо обычной, но для этого нужно чтобы каждый кадр рекурсии возвращал итоговое вычисленное значение. Это значение обычно называется аккумулятором и передается в следующий кадр рекурсии. То есть, в отличие от обычной рекурсии, которая возвращает вычисленное значение вверх по стеку, хвостовая рекурсия передает вычисленное значение вниз по стеку. Каждый новый кадр рекурсии делает свои вычисления и добавляет их к уже ранее вычисленному значению, которое хранится в аккумуляторе. После того, как последний кадр рекурсии отработал, в аккумуляторе уже есть вычисленное значение, которое просто возвращается как результат.
Таким образом, компилятор может оптимизировать код и преобразовать его в обычный цикл.
// возводим матрицу в степень
// matrix - исходная матрица
// value - значение степени
static member (^^) (matrix, value) =
// внутренняя функция, которая реализует хвостовую рекурсию
// m - матрица
// p = значение степени
let inRecPow m p =
// рекурсивная функция
// acc - накопленный аккумулятор. имеет тип Matrix
// p - значение степени для текущего кадра
// с каждым кадром рекурсии это значение уменьшается на единицу
let rec recPow acc p =
// сравниваем текущую степень
match p with
| x when x > 0 ->
// вычисляем новое значение аккумулятора
// умножаем исходную матрицу на старый аккумулятор, то есть возводим в следующую степень
let nextAcc = acc*m
// рекурсивно вызываем функцию и передаем ей уменьшенное на единицу значение степени
recPow nextAcc (x-1)
// если степень достигла нуля, то возвращаем вычисленный аккумулятор
| _ -> acc
// создаем единичную матрицу, чтобы передать ее в качестве аккумулятор для вычисления степени
let dim = Matrix.sizes matrix
let colCount = snd dim
let rowCount = fst dim
let u = Matrix.E rowCount colCount
// вызываем рекурсивную функцию и передаем ей единичную матрицу в качестве аккумулятора
recPow u p
// вызываем функцию, реализующую хвостовую рекурсию для получения результата
let powMatrix = inRecPow matrix value
// возвращаем итоговую матрицу
{ values = powMatrix.values }
Код содержит подробные комментарии о том, как он работает. Требует небольшого пояснения, зачем используется единичная матрица? Она нужна для первого кадра рекурсии и служит в качестве базового значения аккумулятора, в котором будет накапливаться итоговый результат.
Ниже рассмотрим пример использования нашей функции
Вычислим следующее произведение
Где E — это единичная матрица. Так как мы не можем к матрице прибавить число, то мы должны прибавлять 3E.
// возвращает сумму матрицы и числа
static member (+) (matrix, (value: int)) =
let dim = Matrix.sizes matrix
let r = fst dim
let c = snd dim
// создаем единичную матрицу
let unit = Matrix.E r c
// умножаем единичную матрицу на число и прибавляем к входной матрице
value*unit + matrix
let a = array2D [[1;0]
[2;-1]]
let A = Matrix.ofArray2D a
let R = 2*(A^^3) - 4*(A^^2) + 3
printfn "2*A^3 - 4*A^2 + 3 =n %A" R.values
2*A5^3 - 4*A5^2 + 3 =
[[1; 0]
[4; -3]]
Матрица AT, столбцы которой составлены из строк матрицы A с теми же номерами и тем же порядком следования элементов, называется транспонированной к матрице A
static member transpose matrix =
let dim = Matrix.sizes matrix
let rows = fst dim
let cols = snd dim
// создаем нулевую матрицу для вычисления результатов
let tMatrix = Matrix.O cols rows
// копируем в нее данные из исходной матрицы
matrix.values |> Array2D.iteri(fun x y v -> tMatrix.values.[y, x] <- v)
// возвращаем результат
tMatrix
Пример использования
let a = array2D [[1;2;3]
[4;5;6]
[7;8;9]
[10;11;12]]
let A = Matrix.ofArray2D a
let R6 = Matrix.T A
printfn "origin = n %A" A.values
printfn "transpose = n %A" R.values
origin =
[[1; 2; 3]
[4; 5; 6]
[7; 8; 9]
[10; 11; 12]]
transpose =
[[1; 4; 7; 10]
[2; 5; 8; 11]
[3; 6; 9; 12]]
Итоги
В этот статье мы рассмотрели примеры реализации и использования матриц из теории линейной алгебры. А также основных математических операций над ними, с использованием функционального подхода на языке F#. Я надеюсь, что читатель смог оценить ту гибкость, которую дают функциональные языки.
Полный исходный код модуля матриц, фрагменты которого были рассмотрены в рамках статьи, вы сможете найти на гитхабе.
Github Matrix.fs

Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus 300
for i:=1 to StringGrid1.RowCount-1 do
for j:=1 to StringGrid1.ColCount-1 do StringGrid1.Cells[j,i]:=”;
был использован оператор with StringGrid1 do
for i:=1 to RowCount-1 do for j:=1 to ColCount-1 do
Cells[j,i]:=”;
Рассмотрим несколько задач обработки матриц. Для их решения напомним читателю некоторые свойства матриц (рис. 6.12):
Рисунок 6.12: Свойства элементов матрицы
●если номер строки элемента совпадает с номером столбца (i=j), это означает что элемент лежит на главной диагонали матрицы;
●если номер строки превышает номер столбца (i>j), то элемент
находится ниже главной диагонали;
●если номер столбца больше номера строки (i<j), то элемент находится выше главной диагонали;
●элемент лежит на побочной диагонали, если его индексы удовлетворяют равенству i+j–1=n;
●неравенство i+j–1<n характерно для элемента, находящегося выше побочной диагонали;
●соответственно, элементу, лежащему ниже побочной диагонали, соответствует выражение i+j–1>n.
Рассмотри несколько примеров решения задач обработки матриц.
ЗАДАЧА 6.3. Найти сумму элементов матрицы, лежащих выше главной диагонали (см. рис. 6.13).

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
301 |
|
Рассмотрим два алгоритма решения данной |
||
|
задачи. Первый алгоритм (см. рис. 6.14) по- |
||
|
строен следующим образом: вначале перемен- |
||
|
ная S для накапливания суммы обнуляется |
||
|
(S:=0). Затем с помощью двух циклов (первый |
||
|
по строкам, второй по столбцам) перебираются |
||
|
Рисунок 6.13: |
все элементы матрицы, но накапливание суммы |
|
|
происходит только в том случае, если этот эле- |
||
|
Иллюстрация |
||
|
мент находится выше главной диагонали (если |
||
|
к задаче 6.3 |
||
|
выполняется свойство i<j). |
||
|
Текст консольного приложения |
||
|
с комментариями: |
||
|
var |
||
|
a:array [1..15,1..10] |
||
|
of real; |
||
|
i,j,n,m: integer; |
||
|
s: real; |
|
begin |
|
|
write(‘Введите размеры’); |
|
|
writeln(‘матрицы’); |
|
|
write(‘n – количество’); |
|
|
writeln(‘строк: ‘); |
|
|
readln (n); |
|
|
write(‘m — количество’); |
|
|
writeln(‘столбцов: ‘); |
|
|
readln (m); |
Рисунок 6.14: Блок-схема |
|
writeln(‘Матрица A:’); |
задачи 6.3 (алгоритм 1) |
for i:=1 to n do for j:=1 to m do
read(a[i,j]);
s:=0;
for i:=1 to n do for j:=1 to m do
{Если элемент лежит выше главной диагонали,то} if j>i then
s:=s+a[i,j];{ накапливаем сумму. }
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
302 |
writeln(‘матрица А’); for i:=1 to n do begin
for j:=1 to m do {Здесь формат важен,
особенно общая ширина поля!} write(a[i,j]:8:3,’ ‘);
writeln end;
writeln(‘сумма элементов матрицы’, s:8:3); end.
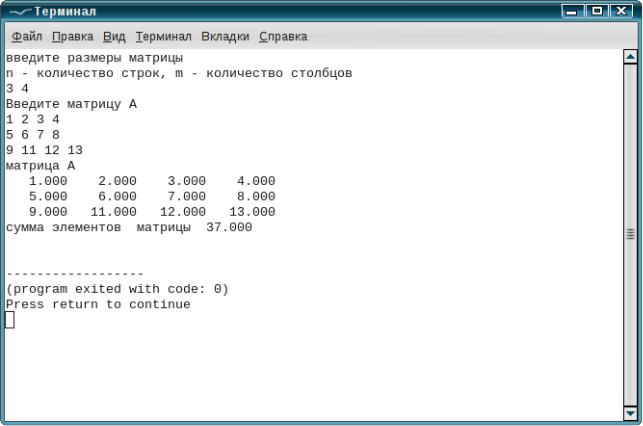
Результаты работы программы представлены на рис. 6.15.
Рисунок 6.15: Результаты работы программы решения задачи 6.3
Второй алгоритм решения этой задачи представлен на рис. 6.16. В нем проверка условия i<j не выполняется, но, тем не менее, в
нем так же суммируются элементы матрицы, находящиеся выше главной диагонали. Для пояснения функционирования алгоритма обратимся к рисунку 6.13.

AN , N
A1,1
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
303 |
Рисунок 6.16: Блок-схема задачи 6.3 (алгоритм 2)
В первой строке заданной матрицы необходимо сложить все элементы, начиная со второго. Во второй – все, начиная с третьего, в i–й строке процесс суммирова-
ния начнется с (i+1)–го элемента
и так далее. Таким образом, первый цикл работает от 1 до N, а
второй от i+1 до M.
Предлагаем читателю самостоятельно составить программу, соответствующую описанному алгоритму.
ЗАДАЧА 6.4. Вычислить количество положительных элементов квадратной матрицы A, расположенных по ее периметру и на диагоналях.
В квадратной матрице число строк равно числу столбцов. Прежде чем приступить к решению задачи, рассмотрим рисунок 6.17, на котором изображена схема диагоналей квадратных матриц различной размерности.
Из рисунка видно, что нет необходимости рассматривать все элементы матрицы. Достаточно рассмотреть элементы, расположенные в первой и последней строках, в первом и последнем столбцах, а также на диагоналях квадратной матрицы. Все эти элементы отмечены на рис. 6.17, причем черным цветом выделены элементы, которые принадлежат строкам, столбцам и диагоналям. Например, элемент принадлежит первой строке, первому столбцу и главной диагонали матрицы, элемент находится в последней строке, последнем столбце и принадлежит главной диагонали. Кроме того, если N – чис-
ло нечетное (на рисунке 6.17 эта матрица расположена слева), то существует элемент с индексом (N div 2 +1, N div 2 +1), который
находится на пересечении главной и побочной диагоналей. При четном значении N (матрица справа на рис. 6.17) диагонали не пересе-
каются.

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
304 |
Рисунок 6.17: Рисунок к условию задачи 6.4
Рассмотрим алгоритм решения задачи. Для обращения к элементам главной диагонали вспомним, что номера строк этих элементов всегда равны номерам столбцов. Поэтому, если параметр i изменяется циклически от 1 до N, то Ai , i — элементы расположенные на глав-
ной диагонали. Воспользовавшись свойством, характерным для эле-
ментов побочной диагонали, получим: i+j-1=N → j=N-i+1,
следовательно, для строк i=1,2,…,N элемент Ai , N−i 1 — элемент побочной диагонали. Элементы, находящиеся по периметру матрицы,
|
записываются следующим образом: |
A1,i |
— элементы, расположен- |
|
|
ные в первой строке (i=1,2,…,N), |
AN ,i |
— элементы, расположен- |
|
|
ные в последней строке (i=1,2,…,N) и соответственно |
Ai ,1 — эле- |
||
|
менты, расположенные в первом столбце (i=1,2,…,N), |
Ai , N — в |
||
|
последнем столбце (i=1,2,…,N). |
Алгоритм обработки построим следующим образом, сначала обработаем элементы, расположенные на диагоналях квадратной матрицы. Для этого необходимо в каждой строке (i=1,2,…,N) проверять
|
знак элементов Ai , i и Ai , N−i 1 . |
|
|
for i:=1 to N do |
|
|
begin |
k:=k+1; |
|
if (a[i,i]>0) then |
|
|
if a[i,N-i+1]>0 then |
k:=k+1; |
|
end; |
Так как при проверке диагональных элементов матрицы угловые элементы были учтены, то при обработке элементов, расположенных по периметру матрицы, угловые элементы учитывать не нужно.

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
305 |
Поэтому надо перебрать элементы со второго до предпоследнего в
первой и последней строках, в первом и последнем столбцах. for i:=2 to N-1 do
begin
{ Если элемент находится в первой строке. } if (a[1,i]>0) then k:=k+1;
{ Если элемент находится в последней строке. }
|
if (a[N,i]>0) |
then |
k:=k+1; |
|
{ Если элемент находится в первом столбце. } |
||
|
if (a[i,1]>0) |
then |
k:=k+1; |
{ Если элемент находится в последнем столбце. }
|
if (a[i,N]>0) then |
k:=k+1; |
|
end; |
Затем надо проверить, не был ли элемент, находящийся на пересечении диагоналей, подсчитан дважды. Это могло произойти только в том случае, если N – нечетно и элемент, расположенный на пересече-
нии диагоналей70, положителен.
if (N mod 2 <>0) and (a[n div 2+1,n div 2+1]>0) then k:=k-1;
Ниже приведен полный текст консольного приложения решения задачи 6.4 с комментариями. На рис. 6.18 представлены результаты
работы программы решения задачи 6.4. var
a:array [1..10,1..10] of integer; i,j,N,k:integer;
begin write(‘N=’); readln(N);
//Ввод исходной матрицы. writeln(‘Введите матрицу A’); for i:=1 to N do
for j:=1 to N do read(a[i,j]);
//Вывод исходной матрицы. writeln(‘Была введена матрица A:’);
70 На пересечении диагоналей находится элемент с индексами (N div 2 +1, N div 2 +1)

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
306 |
Рисунок 6.18: Результаты решения задачи 6.4 for i:=1 to N do
begin
for j:=1 to N do write(a[i,j],’ ‘);
writeln;
end;
k:=0;
//Обработка элементов, расположенных //на диагоналях матрицы.
for i:=1 to N do begin
if (a[i,i]>0) then k:=k+1; if a[i,N-i+1]>0 then k:=k+1;
end;
//Обработка элементов, расположенных //по периметру матрицы.
for i:=2 to N-1 do begin
if (a[1,i]>0) then k:=k+1; if (a[N,i]>0) then k:=k+1; if (a[i,1]>0) then k:=k+1;

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
307 |
if (a[i,N]>0) then k:=k+1;
end;
{ Если элемент, находящийся на пересечении диагоналей, подсчитан дважды, то уменьшить вычисленное значение k на один. }
if (n mod 2<>0) and (a[N div 2+1,N div 2+1]>0) then
k:=k-1; writeln(‘k=’,k); end.
ЗАДАЧА 6.5. Проверить, является ли заданная квадратная матрица единичной.
Единичной называют матрицу, у которой элементы главной диагонали – единицы, а все остальные – нули. Например,
|
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
Решать задачу будем так. Предположим, что матрица единичная, (pr:=true) и попытаемся доказать обратное. В двойном цикле по
строкам (i:=1,2,…,N) и по столбцам (j:=1,2,…,N) переби-
раем все элементы матрицы. Если диагональный элемент ( i= j ) не равен единице или элемент, расположенный вне диагонали ( i≠ j ), не равен нулю71, то в логическую переменную pr записываем значе-
ние false и прекращаем проверку (аварийно покидаем цикл). После цикла проверяем значение pr, если переменная pr попрежнему равна
true, то матрица единична, иначе она такой не является. var a:array[1..10,1..10] of real; i,j,n:integer;
pr:boolean; begin
writeln(‘Введите размер матрицы’); readln(n);
writeln(‘Введите матрицу’); for i:=1 to n do
71 Воспользовавшись логическими операциями and и or, это сложное условие можно записать так if ((i=j) and (a[i,j]<>1)) or ((i<>j) and (a[i,j]<>0)) then

Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus 308
for j:=1 to n do read(a[i,j]);
{Предположим, что матрица единичная, и присвоим логической переменной значение
истина. Если значение этой переменной при выходе из цикла не изменится, это будет означать, что матрица единичная.} pr:=true;
for i:=1 to n do for j:=1 to n do
if ((i=j) and (a[i,j]<>1)) or ((i<>j) and (a[i,j]<>0)) then
{Если элемент лежит на главной диагонали и не равен единице или элемент лежит вне главной диагонали и не равен нулю , то }
begin
{логической переменной присвоить значение ложь, это будет означать, что матрица не единичная.}
pr:=false; { выйти из цикла. }
break;
end;
{Проверка значения логической переменной и печать результата.}
if pr then
writeln(‘Матрица единичная’)
else
writeln(‘Матрица не является единичной’);
end.
ЗАДАЧА 6.6. Преобразовать исходную матрицу так, чтобы последний элемент каждого столбца был заменен разностью минимального и максимального элемента в этом же столбце.
Для решения данной задачи необходимо в каждом столбце найти максимальный и минимальный элементы, после чего в последний элемент столбца записать их разность. Блок-схема алгоритма решения приведена на рис. 6.19.
Ниже приведен текст консольного приложения с комментариями.

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
309 |
Рисунок 6.19: Блок-схема алгоритма решения задачи 6.6
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus 310
var a:array[1..25,1..25] of real; i,j,n,m:integer;
max,min:real; begin
{Ввод размеров матрицы.} writeln(‘Введите размеры матрицы’); readln(n,m);
{Ввод исходной матрицы.} writeln(‘Введите матрицу’); for i:=1 to n do
for j:=1 to m do read(a[i,j]);
{Последовательно перебираем все столбцы матрицы.}
for j:=1 to m do begin
{Максимальным и минимальным объявляем первый элемент текущего (j-го) столбца матрицы.}
max:=a[1,j];
min:=a[1,j];
{Последовательно перебираем все элементы в текущем (j-м) столбце матрицы.}
for i:=2 to n do begin
{Если текущий элемент больше максимального, то его и объявляем максимальным.}
if a[i,j]>max then max:=a[i,j];
{Если текущий элемент меньше минимального, то его и объявляем минимальным.}
if a[i,j]<min then min:=a[i,j]; end;
{В последний элемент столбца записываем разность между максимальным и минимальным элементами столбца.}
a[n,j]:=max-min; end;
{Вывод преобразованной матрицы.} writeln(‘Преобразованная матрица’);

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
311 |
for i:=1 to n do begin
for j:=1 to m do write(a[i,j]:7:3,’ ‘);
writeln;
end;
end.
Теперь давайте создадим визуальное приложение, реализующее рассмотренный алгоритм. За основу возьмем форму (рис. 6.9) и проект транспонирования матрицы A(N,M), разработанные для зада-
чи 6.2. Окно формы несколько изменим. Кнопку Транспонирование переименуем в Преобразование матрицы, а свойство Caption метки label5 установим Преобразованная матрица A. Кроме того изменим свойство Caption формы. Окно измененной формы представлено на рис. 6.20.
Рисунок 6.20: Окно формы решения задачи 6.6
Обработчики кнопок Ввод, Очистить, Выход из программы
изменятся мало. Рассмотрим алгоритм работы обработчика кнопки Преобразование матрицы. В этом обработчике будет считывание
матрицы из компонента StringGrid1, преобразование матрицы A
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
312 |
по алгоритму, представленному на рис. 6.19, вывод преобразованной матрицы в компонент StringGrid2.
Текст модуля визуального приложения решения задачи 6.6 с комментариями приведен ниже.
|
unit Unit1; |
|||
|
{$mode objfpc}{$H+} |
|||
|
interface |
|||
|
uses |
SysUtils, |
LResources, |
Forms, |
|
Classes, |
Controls, Graphics, Dialogs, StdCtrls,Grids; //Описание формы
type
{ TForm1 }
TForm1 = class(TForm) Button1: TButton; Button2: TButton; Button3: TButton; Button4: TButton; Edit1: TEdit;
Edit2: TEdit;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel; StringGrid1: TStringGrid; StringGrid2: TStringGrid;
procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); procedure Button3Click(Sender: TObject); procedure Button4Click(Sender: TObject); private
{private declarations } public
{public declarations } end;
var
A:array[1..25,1..25] of real;
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
313 |
N,M:integer; Form1: TForm1; implementation { TForm1 }
//Обработчик кнопки «Выход из программы». procedure TForm1.Button4Click(Sender: TObject); begin
Close;
end;
//Обработчик первой кнопки — кнопки //ввода размерности матрицы.
procedure TForm1.Button1Click(Sender: TObject); var i:byte;kod_n,kod_m,kod:integer;
begin
//Ввод размерности матрицы.
//Символьная информация преобразовывается
//в числовую и записывается в переменные N и M. Val(Edit1.Text,N,kod_m); Val(Edit2.Text,M,kod_n);
//Если преобразование прошло успешно //и введенные размеры удовлетворяют //писанию матриц A и B,
if (kod_n=0) and (kod_m=0) and (N>0) and (N<26) and (M>0) and (M< 26) then
//то begin
//визуализируется первая матрица, StringGrid1.Visible:=true;
//соответствующая ей надпись, Label4.Visible:=true;
//кнопки Очистить Button2.Visible:=true;
//и преобразование матрицы. Button3.Visible:=true; with StringGrid1 do begin
ColCount:=M+1;
RowCount:=N+1;
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
314 |
||
|
//и нумеруются строки и |
|||
|
for i:=1 to RowCount-1 do |
|||
|
Cells[0,i]:=IntToStr(i); |
|||
|
//столбцы первой таблицы. |
|||
|
for i:=1 to ColCount-1 do |
|||
|
Cells[i,0]:=IntToStr(i); |
|||
|
end; |
|||
|
StringGrid2.ColCount:=M+1; |
|||
|
StringGrid2.RowCount:=N+1; |
|||
|
end |
|||
|
else |
|||
|
begin |
|||
|
//При некорректном вводе выдается |
|||
|
//соответствующее сообщение. |
введены |
не |
|
|
MessageDlg(‘Размеры матрицы |
|||
|
верно!’,MtInformation,[mbOk],0); |
|||
|
//Устанавливаются стартовые параметры |
|||
|
//в поля ввода. |
|||
|
Edit1.Text:=’4′; |
|||
|
Edit2.Text:=’3′; |
|||
|
end; end; |
|||
|
//Обработчик кнопки «Преобразование матрицы». |
|||
|
procedure TForm1.Button2Click(Sender: TObject); |
|||
|
var i,j:integer; |
|||
|
max,min:real; |
|||
|
begin |
|||
|
StringGrid2.Visible:=true; |
|||
|
label5.Visible:=true; |
|||
|
for i:=1 to N do |
//Цикл по номерам строк. |
||
|
for j:=1 to M do |
//Цикл по номерам столбцов. |
||
|
//Считывание элементов матрицы A |
|||
|
//из компонента StringGrid1. |
|||
|
A[i,j]:=StrToFloat(StringGrid1.Cells[j,i]); |
|||
|
with StringGrid2 do |
|||
|
begin |
|||
|
for i:=1 to RowCount-1 do //Нумеруются |
|||
|
Cells[0,i]:=IntToStr(i); |
//строки и |
||
|
//столбцы 2-й матрицы. |
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
315 |
for i:=1 to ColCount-1 do Cells[i,0]:=IntToStr(i);
end;
//Решение задачи 6.6. for j:=1 to m do begin
{Максимальным и минимальным объявляем первый элемент текущего (j-го) столбца матрицы.}
max:=a[1,j];
min:=a[1,j];
{Последовательно перебираем все элементы в текущем (j-м) столбце матрицы.}
for i:=2 to n do begin
{Если текущий элемент больше максимального, то его и объявляем максимальным.}
if a[i,j]>max then max:=a[i,j];
{Если текущий элемент меньше минимального, то его и объявляем минимальным.}
if a[i,j]<min then min:=a[i,j]; end;
{В последний элемент столбца записываем разность между максимальным и минимальным элементами столбца.}
a[n,j]:=max-min; end;
//Элементы преобразованной матрицы A выводятся
|
в ячейки |
|
|
//таблицы на форме. |
//Цикл по номерам строк. |
|
for i:=1 to N do |
|
|
for j:=1 to M do |
//Цикл по номерам столбцов. |
//Запись элемента преобразованной матрицы A в ячейку StringGrid2.
StringGrid2.Cells[j,i]:=FloatToStr(A[i,j]); //Делаем первую кнопку невидимой. Button1.Visible:=False;
end;
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
316 |
//Обработчик кнопки «Очистить».
procedure TForm1.Button3Click(Sender: TObject); var i,j:integer;
begin
//Очистка компонента StringGrid1. with StringGrid1 do
for i:=1 to RowCount-1 do for j:=1 to ColCount-1 do
Cells[j,i]:=”; //Очистка компонента StringGrid2. with StringGrid2 do
for i:=1 to RowCount-1 do for j:=1 to ColCount-1 do
Cells[j,i]:=”; //Делаем невидимыми компоненты
//StringGrid1, StringGrid2,labe4, label5. StringGrid1.Visible:=False; StringGrid2.Visible:=False; label4.Visible:=False; label5.Visible:=False;
//Делаем невидимыми кнопки //«Преобразование матрицы» и «Очистить». Button2.Visible:=False; Button3.Visible:=False;
//Делаем видимой кнопку «Ввод». Button1.Visible:=True;
//Запись начальных значений размеров //матрицы (N=4, M=3). Edit1.Text:=’4′;
Edit2.Text:=’3′;
end; initialization {$I unit1.lrs} end.
На рис. 6.21 представлено окно с результатами решения задачи.

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
317 |
Рисунок 6.21: Результаты решения задачи 6.6
ЗАДАЧА 6.7. Поменять местами n-й и r-й столбцы матрицы A(K,M).
Задача сводится к обмену n-го и r-го элементов во всех строках матрицы. Блоксхема приведена на рис. 6.22.
Ниже приведен листинг консольного приложения с комментариями.
Результаты работы программы приведе-
ны на рис. 6.23. type matrica=
array [1..15,1..15] of real; var
a:matrica; b:real; i,j,k,m,n,r:byte;
begin
//Ввод размеров матрицы. write (‘k=’);readln(k); write (‘m=’);readln(m); //Ввод матрицы A.
Рисунок 6.22: Блок-схема алгоритма
решения задачи 6.7

Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus 318
writeln(‘Матрица A’); for i:=1 to k do
for j:=1 to m do read(a[i,j]); //Ввод номеров столбцов матрицы, //подлежащих обмену.
repeat write(‘n=’);readln(n); write(‘r=’);readln(r);
{Ввод считается верным, если n и r не больше m и не равны друг другу.} until (n<=m) and (r<=m) and (n<>r);
Рисунок 6.23: Результаты решения задачи 6.7
{Элементы столбца с номером r заменить элементами столбца с номером n.}
for i:=1 to k do begin
b:=a[i,n];
a[i,n]:=a[i,r];
a[i,r]:=b
end;
writeln(‘Преобразованная матрица A’); for i:=1 to k do
begin
for j:=1 to m do

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
319 |
write(a[i,j]:7:3,’ ‘); writeln;
end;
end.
ЗАДАЧА 6.8. Преобразовать матрицу A(m,n) так, чтобы строки с нечетными индексами были упорядочены по убыванию, c четными – по возрастанию.
Каждая строка матрицы является одномерным массивом. Поэтому для упорядочивания строки или столбца можно использовать обычные алгоритмы сортировки массивов. При решении задачи необходимо последовательно просматривать все строки матрицы, если номер строки нечетен, то сортируем строку методом пузырька по убыванию, иначе — по возрастанию.
Блок-схема этого алгоритма представлена на рис. 6.24. Ниже представлено консольное приложение решения этой задачи с комментариями.
На рис. 6.25 приведены результаты работы программы. var
a:array [1..15,1..15] of real; j,i,k,m,n:byte;
b:real; begin
//Ввод размеров матрицы. writeln(‘введите m и n’); readln(m,n);
//Ввод матрицы. writeln(‘Матрица А’); for i:=1 to m do
for j:=1 to n do read(a[i,j]);
//Преобразование матрицы. for i:=1 to m do
if (i mod 2)=0 then
{Если номер строки четный, то } begin
{упорядочить ее элементы по возрастанию. }

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
320 |
Рисунок 6.24: Блок-схема алгоритма решения задачи 6.8

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
321 |
{Упорядочивание строки матрицы методом пузырька по возрастанию.}
for k:=1 to n-1 do for j:=1 to n-k do
if a[i,j] > a[i,j+1] then begin
b:=a[i,j];
a[i,j]:=a[i,j+1];
a[i,j+1]:=b;
end
end
else { Если номер строки нечетный,
то упорядочить ее элементы по убыванию.}
Рисунок 6.25: Результаты решения задачи 6.8
{Упорядочивание строки матрицы методом пузырька по убыванию.}
for k:=1 to n-1 do for j:=1 to n-k do
if a[i,j] < a[i,j+1] then begin
b:=a[i,j];
a[i,j]:=a[i,j+1];
a[i,j+1]:=b;
end;

Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus 322
//Вывод преобразованной матрицы. writeln(‘преобразованная матрица A’); for i:=1 to m do
begin
for j:=1 to n do
write (a[i,j]:7:3,’ ‘); writeln
end end.
ЗАДАЧА 6.9. Задана матрица целых положительных чисел A(n,m). Сформировать вектор P(n), в который записать сумму простых чисел каждой строки матрицы в четверичной системе счисления, если в строке нет простых чисел, в соответствующий элемент массива записать число 0.
Для решения этой задачи нам понадобятся функции: проверки, является ли число простым, и перевода целого числа в четверичную систему счисления. Функция проверки, является ли число простым, подробно рассматривалась в пятой главе при решении задачи 5.7.
Поэтому здесь просто приведем ее текст.
function prostoe(N:integer):boolean; var i:integer; pr:boolean;
begin
if N<1 then pr:=false else
begin pr:=true;
for i:=2 to N div 2 do if (N mod i = 0) then begin
pr:=false;
break;
end;
end;
prostoe:=pr;
end;
Кроме того в пятой главе мы рассматривали алгоритм (рис. 5.45) и функцию перевода
function perevod(N:real;P:word;kvo:word):real;
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
323 |
вещественного числа в p-чную систему счисления (задача 5.10). Нужная нам функция перевода целого числа в четверичную систему счисления является частным случаем рассмотренной ранее функции perevod. Ниже приведен текст функции perevod4 , которая пере-
водит целое положительное число в четверичную систему счисления.
{Функция перевода целого числа N в четверичную систему счисления.}
function perevod4(N:word):word; var
s1,i ,q, ost: word; begin
{В переменной s1 мы будем собирать число в четверичной системе счисления.}
s1:=0;
{В переменной q будем последовательно хранить степени десяти, вначале туда записываем 1 — десять в 0 степени, а затем последовательно в цикле будем умножать q на 10.}
q:=1;
{Перевод целого числа. Пока число не станет равным 0.}
while (N<>0) do begin
{Вычисляем ost — очередной разряд числа, как остаток от деления N на 4 (основание системы счисления).}
ost:=N mod 4;
{Очередной разряд числа умножаем на 10 в степени i и добавляем к формируемому числу s1.}
s1:=s1+ost*q;
{Уменьшаем число N в 4 раза путем целочисленного деления на 4.}
N1:=N1 div 4;
{Формируем следующую степень десятки.} q:=q*10;
end;
{Возвращаем число в четверичной системе счисления.}

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
324 |
perevod:=s1;
end;
В каждой строке надо найти сумму простых чисел, а затем полученное число перевести в четверичную систему счисления. Поэтому необходимо для каждой строки (i:=1,2,..,n) выполнить следую-
щее: обнулить сумму S (S:=0), организовать цикл по элементам строки (j:=1,2,…,m), внутри которого проверять, является ли текущий элемент Ai , j простым и, если является, добавлять его к сумме S. После выхода из цикла по j необходимо проверить, были ли в строке с номером i простые числа (S>0), и, если были, перевести S в
четверичную систему счисления и сформировать соответствующий элемент массива P (P[i]:=perevod4(S)).
Блок-схема алгоритма приведена на рис. 6.26.
Рисунок 6.26: Блок-схема алгоритма решения задачи 6.9
Полный текст консольного приложения: function prostoe(N:integer):boolean;
var i:integer; pr:boolean; begin
if N<1 then pr:=false
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus 325
else begin pr:=true;
for i:=2 to N div 2 do if (N mod i = 0) then begin
pr:=false; break; end;
end;
prostoe:=pr;
end;
function perevod4(N:word):word; var s1,q, ost: word;
begin
{В переменной s1 мы будем собирать число в четверичной системе счисления.}
s1:=0;
{В переменной q будем последовательно хранить степени десяти, вначале туда записываем 1 — десять в 0 степени, а затем последовательно в цикле будем умножать q на 10.}
q:=1;
{Перевод целого числа.
Пока число не станет равным 0.} while (N<>0) do
begin
{Вычисляем ost — очередной разряд числа, как остаток от деления N на 4 (основание системы счисления).}
ost:=N mod 4;
{Очередной разряд числа умножаем на 10 в степени i и добавляем к формируемому числу s1.}
s1:=s1+ost*q;
{Уменьшаем число N в 4 раза путем целочисленного деления на 4.}
N:=N div 4;
{Формируем следующую степень десятки.} q:=q*10;
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
326 |
end;
{Возвращаем число в 4-ной системе счисления.} perevod4:=s1;
end;
var S,i,j,n,m: word; a:array[1..25,1..25] of word; p:array[1..25] of word;
begin
//Ввод размеров матрицы. writeln(‘Введите размеры матрицы’); readln(n,m);
writeln(‘Введите матрицу A’);{Ввод матрицы.} for i:=1 to n do
for j:=1 to m do read(A[i,j]); {Последовательно перебираем все строки матрицы
для формирования суммы простых чисел каждой строки.}
for i:=1 to n do begin
S:=0;{Вначале сумма равна нулю.} {Перебираем все элементы в i-й строке матрицы.}
for j:=1 to m do
{Если очередной элемент в i-й строке матрицы — простое число, то добавляем его к сумме.}
if prostoe(A[i,j]) then s:=s+A[i,j];
{Если в строке были простые числа, то их сумму переводим в четверичную систему счисления и записываем в p[i].}
if s>0 then p[i]:=perevod4(s)
{Если в строке не было простых чисел, то p[i]:=0.}
else p[i]:=0; end;
//Вывод сформированного массива P. writeln(‘Массив P’);
for i:=1 to n do write(P[i],’ ‘); writeln; end.

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
327 |
Результаты работы программы представлены на рис. 6.27.
Рисунок 6.27: Результаты работы программы решения задачи 6.9
ЗАДАЧА 6.10. Написать программу умножения двух матриц A(N,M) и B(M,L).
Напомним некоторые сведения из курса математики.
Умножать можно только матрицы, у которых количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Матрица-произведение имеет столько строк, сколько было в первой матрице и столько столбцов, сколько было во второй. Таким образом, при умножении матрицы A(N,M) на матрицу B(M,L) получа-
ется матрица C(N,L). Каждый элемент матрицы Ci , j является скалярным произведением i-й строки матрицы A и j-го столбца матрицы B. В общем виде формула для нахождения элемента Ci , j матрицы имеет вид:
M
Ci , j= ∑ Aik Bkj , где i = 1,N и j = 1,L. (6.1)
k =1
Рассмотрим более подробно формирование матрицы C(3,2) как произведение матриц A(3,3) и B(3,2).
|
C11 |
C12 |
a11 b11 a12 b21 a13 b31 |
|
|
C21 |
C 22 |
= a21 b11 a22 b21 a23 b31 |
|
|
C31 |
C32 |
a31 b11 a32 b21 a33 b31 |
a11 b12 a12 b22 a13 b32 a21 b12 a22 b22 a23 b32 . a31 b12 a32 b22 a33 b32
Следует помнить, что A B≠B A .
Блок-схема, реализующая расчет каждого элемента матрицы C по

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
328 |
формуле (6.1), приведена на рис. 6.28. Далее приведен текст программы умножения двух матриц с комментариями. Результат работы представлен на рис. 6.29.
|
Рисунок 6.28: Блок-схема |
Рисунок 6.29: Результаты работы |
|
|
программы умножения матриц |
||
|
умножения двух матриц |
||
//Умножение двух матриц.
type matrica=array [1..15,1..15] of real; var a,b,c:matrica; i,j,M,N,L,k:byte; begin
//Ввод размеров матриц.
writeln(‘введите n,m и l’); readln(N, M, L); writeln(‘Матрица A’);//Ввод матрицы A.
for i:=1 to N do
for j:=1 to M do read(a[i,j]); writeln(‘Матрица B’);//Ввод матрицы B. for i:=1 to M do
for j:=1 to L do read(b[i,j]);
for i:=1 to N do //Формирование матрицы C. for j:=1 to L do
begin

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
329 |
{В C[i,j] хранится результат скалярного произведения i-й строки на j-й столбец.}
c[i,j]:=0;
for k:=1 to M do c[i,j]:=c[i,j]+a[i,k]*b[k,j];
end;
writeln(‘матрица C=A*B’);//Вывод матрицы C=AB. for i:=1 to N do
begin
for j:=1 to L do write(c[i,j]:7:3,’ ‘);
writeln;
end;
end.
ЗАДАЧА 6.11 В матрице натуральных чисел A(N,M) найти строки, где находится максимальное из простых чисел. Элементы в них упорядочить по возрастанию. Если в матрице нет простых чисел, то оставить ее без изменений.
Перед решением задачи отметим некоторые ее особенности72. В матрице может не быть простых чисел, максимальных значений может быть несколько, и при этом некоторые из них будут находиться в одной строке.
При решении задачи нам понадобятся следующие подпрограммы: 1. Функция Prostoe, которая проверяет, является ли число P
типа word простым. Она возвращает значение true, если число P –
простое и false – в противном случае. Заголовок функции имеет вид
Function Prostoe (P:word):Boolean;
2. Процедура Udal, которая из массива чисел X удаляет значения,
встречающиеся более одного раза. У процедуры два параметра: массив X и его размер N, оба – параметры переменные. Заголовок проце-
дуры имеет вид:
Procedure Udal(var X:massiv; var N:word);
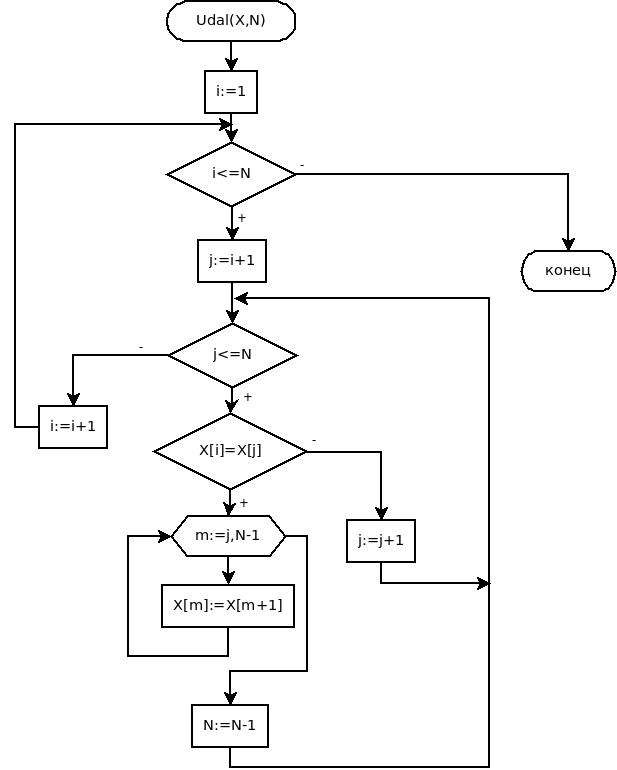
Перед описанием процедуры следует описать тип данных massiv (например, massiv = array [1..200] of word). Блок-схема
процедуры Udal представлена на рис. 6.30.
72 Авторы рекомендуют читателям внимательно изучить этот пример, в нем сконцентрированы практически все основные моменты, рассмотренные нами до сих пор.
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
330 |
Рисунок 6.30: Блок-схема процедуры Udal
Удаление повторяющихся элементов происходит следующим образом. Просматриваются все элементы, начиная с первого, i-й эле-
мент сравнивается со всеми последующими . Если xi=x j , то встретился повторяющийся элемент, и мы удаляем из массива элемент с но-

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
331 |
мером j. Алгоритм удаления был подробно рассмотрен в пятой главе. 3. Функция Nalichie возвращает true, если число a присутствует в массиве b, и false – в противном случае. Заголовок проце-
дуры имеет вид:
Function Nalichie(a:word; b:massiv; N:word);
Блок-схема функции представлена на рис. 6.31. 4. Процедура Vozr упорядочения масси-
ва х по возрастанию.
Алгоритмы упорядочения рассматривались в пятой главе. Здесь авторами использовался алгоритм сортировки методом пузырька.
У процедуры Vozr два параметра: массив х (параметр-переменная) и его размер N
(параметр-значение). Заголовок процедуры
имеет вид:
Procedure Vozr(var x:massiv; N:word);
Рассмотрим более подробно алгоритм решения задачи 6.11, который приведен на рис. 6.32-6.33. После ввода матрицы (блоки 1-4) предполагаем, что простых чисел нет.
В логическую переменную Pr записываем false, как только встретится простое число, в переменную Pr запишем true.
Количество максимальных значений среди простых чисел равно 0 (k:=0) (блок 5).
Рисунок 6.31: Блок-схема функции
Nalichie
Для проверки, является ли простым числом каждый элемент матрицы, обращаемся к функции Prostoe. Если число простое (блок 8),
проверяем, первое ли это простое число в матрице (блок 9).
Если это первое простое число, то переписываем его в переменную max, в переменную k записываем число 1 (количество максиму-
мов равно 1), номер строки, в которой находится максимум, записы-

|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
332 |
ваем в массив mas под номером k73. В связи с тем что в матрице есть простые числа, в переменную Pr записываем true (блок 10).
Если это не первое простое число, сравниваем Aij с переменной max. Если Aij max (блок 11), то в переменную max запишем Aij , в переменную k запишем 1 (есть один максимум), в mas[k] записываем i – номер строки, где находится максимальный элемент (блок
12). Если Aij=max (блок 13), то встретилось число, равное переменной max. В этом случае значение k увеличиваем на 1 и в mas[k] записываем номер строки, где находится элемент, равный max.
В результате двойного цикла обработки всех элементов матрицы (блоки 6-14) в переменной max будет храниться максимальное из про-
стых чисел, в переменной k – количество максимумов, в массиве mas из k элементов будут храниться номера строк, где находятся максимальные значения среди простых чисел матрицы. В переменной Pr хранится true, если в матрице есть простые числа, false – в про-
тивном случае.
Если в матрице нет простых чисел (блок 15), выводим соответствующее сообщение (блок 16), в противном случае – с помощью процедуры Udal (блок 17) удаляем из массива mas элементы, встре-
чающиеся более одного раза74. Затем просматриваем все строки матрицы (цикл начинается блоком 18), если номер этой строки присутствует в массиве mas (блок 19), то переписываем текущую строку
матрицы в массив b (блоки 20-21) и обращаемся к процедуре упорядочивания массива по возрастанию Vozr (блок 22).
Упорядоченный массив b переписываем в i-ю строку матрицы А (блоки 23-24). На последнем этапе выводим на экран матрицу А после
преобразования (блоки 25-27).
Ниже приведен листинг всей программы с подробными комментариями.
73В массиве mas будут храниться номера строк, где находится максимум.
74Если некоторые максимальные элементы находятся в одной строке, то в массиве mas есть повторяющиеся элементы.
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
333 |


|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
334 |
Рисунок 6.33: Блок-схема решения задачи 6.11 (продолжение)
{Тип данных massiv будет использоваться при описании процедур. }
type massiv=array[1..200] of word;
{ Функция prostoe проверяет, является ли число N простым (true) или нет (false). } function prostoe(N:word):boolean;
var pr:boolean;i:word; begin
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus 335
if N>0 then begin
{Предполагаем, что число N – простое (pr=true)} pr:=true;
{Проверяем, делится ли число N на какое-либо из чисел от 2 до N/2.}
for i:=2 to n div 2 do
{Если встречается число i, на которое делится N, то}
if N mod i =0 then begin
{число N не является простым (pr=false) и } pr:=false;
{выходим из цикла. }
break;
end
end
else pr:=false;
{ Имени функции присваиваем значение переменной pr. }
prostoe:=pr;
end;
{Процедура udal удаляет из массива x элементы, которые встречаются более одного раза. Х, N являются параметрами-переменными, так как эти значения возвращаются в головную программу при вызове процедуры udal.}
procedure udal(var x:massiv; var n:word); var i,j,m:word;
begin i:=1;
{Просматриваем все элементы, начиная с первого i=1,2,…,N;i-й элемент сравниваем с последующими j=i+1,i+2,…,n. }
while(i<=n) do begin
j:=i+1; while(j<=N) do
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
336 |
{Если x[i] равно x[j], то встретился повторяющийся элемент}
if x[i]=x[j] then begin
{и удаляем его (x[j]) из массива. }
for m:=j to N-1 do x[m]:=x[m+1];
{После удаления элемента количество элементов уменьшаем на 1, при этом не переходим к следующему элементу, так как после удаления под j-м номером находится уже другой элемент. }
N:=N-1;
End
{Если x[i] не равно x[j], то переходим к следующему элементу. }
else j:=j+1; i:=i+1;
end;
end;
{Функция nalichie возвращает true, если число a встречается в массиве b, false – в противном случае. }
function nalichie(a:word;b:massiv;n:word):boolean;
var pr:boolean; i:word; begin
{Предполагаем, что в массиве b не встречается значение a, в pr=false}
pr:=false;
{Перебираем все элементы массива. }
for i:=1 to N do
{Если очередной элемент массива b равен значению a, то в pr записываем true}
if b[i]=a then begin
pr:=true;
{и выходим из цикла. }
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
337 |
break end;
{Имени функции присваиваем значение переменной
pr. } nalichie:=pr end;
{Процедура vozr упорядочивает массив x по возрастанию. }
procedure vozr(var x:massiv; n:word);
{X является параметром-переменной, именно массив и возвращается в головную программу при вызове процедуры vozr. }
var i, j, b :word; begin
for i:=1 to N-1 do for j:=1 to N-i do
if x[j]>x[j+1] then begin
b:=x[j];
x[j]:=x[j+1];
x[j+1]:=b;
end
end;
//Начинается основная программа var
N, M, i, j, k, max :word; A:array[1..20,1..20] of word; pr, L: boolean;
mas, b:massiv; begin
{Вводим элементы матрицы А. } write(‘N=’);readln(N); write(‘M=’);readln(M);
writeln(‘ Matrica A’); for i:=1 to N do
for j:=1 to M do read(A[i,j]);
{ Предполагаем, что в матрице нет простых чи-
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
338 |
сел. } Pr:=false;
{Количество элементов, равных максимальному, равно 0. }
k:=0;
{Перебираем все элементы в матрице. }
for i:=1 to N do for j:=1 to M do begin
{Обращаемся к функции, которая проверяет, является ли число A[I,j] простым. }
L:=Prostoe(A[i,j]);
{Если число простое и }
if L then
{если простое число встретилось первый раз,} if not Pr then
begin
{записывем в pr true,}
Pr:=true;
{увеличиваем количество максимумов на 1, можно было просто написать k:=1}
k:=k+1;
{Это число записываем в переменную max, это первое простое число, и предполагаем, что оно максимальное. }
max:=A[i,j];
{В mas[k] записываем номер строки, где хранится число A[I,j]}
mas[k]:=i
end else
{Если A[i,j] не первое простое число, то сравниваем max и текущее простое значение матрицы А. }
if A[i,j]>max then
{Если A[I,j]> max, то }
Begin
{ количество максимумов равно 1, т.к. встретился наибольший в данный момент элемент. }
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus |
339 |
k:=1;
{ в переменную max записываем A[i,j], } max:=A[i,j];
{ в mas[k] записываем номер строки, где хранится число A[I,j]}
mas[k]:=i
end else
{ Если A[i,j]=max (встретился элемент, равный максимуму), то }
if A[i,j]=max then begin
{ количество максимумов увеличиваем на 1. } k:=k+1;
{ в mas[k] записываем номер строки, где хранится число A[I,j]}
mas[k]:=i
end
end;
{Если в pr осталось значение false,то выводим сообщение, что в матрице нет простых чисел, }
if not Pr then writeln(‘В матрице A нет простых чисел’)
else begin
{ иначе удаляем из массива mas, номера строк, где хранятся максимумы, повторяющиеся элементы. }
Udal(mas,k);
{Перебираем все строки матрицы. } for i:=1 to N do
begin L:=Nalichie(i,mas,k);
{Если номер строки присутствует в массиве mas,} if L then
begin
{то переписываем строку в массив b} for j:=1 to M do
b[j]:=A[i,j];

Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus 340
{упорядочиваем массив b по возрастанию. } Vozr(b,M);
{ упорядоченный массив записываем на место i-й строки матрицы A. }
for j:=1 to M do A[i,j]:=b[j];
end end;
writeln(‘Преобразованная матрица A’); for i:=1 to N do
begin
for j:=1 to M do write(A[i,j],’ ‘); writeln;
end
end end.
Результаты работы программы приведены на рис. 6.34.
Рисунок 6.34: Результаты решения задачи 6.11
Авторы рекомендуют читателю по рассмотренным алгоритмам и консольным приложениям задач 6.7-6.11 разработать визуальные приложения, аналогичные тем, которые были разработаны для задач 6.2, 6.6.
Матрица — это двумерный массив, каждый элемент которого имеет два индекса: номер строки и номер столбца, поэтому для работы с элементами матрицы необходимо использовать два цикла. Если значениями параметра первого цикла будут номера строк матрицы, то значениями параметрами второго — столбцы (или наоборот). Обработка матрицы заключается в том, что вначале поочередно рассматриваются элементы первой строки (столбца), затем второй и т.д. до последней.
Перед тем, как приступить к изучению алгоритмов обработки матриц, давайте рассмотрим, как описываются матрицы в C++. Двумерный массив можно объявить так:
тип имя_переменной [n] [m];
Здесь тип определяет тип элементов массива, имя_переменной — имя матрицы, n — количество строк, m — количество столбцов. Строки нумеруются от 0 до n-1, столбцы от 0 до m-1.
Например int h[10] [15];
Выше матрица целых чисел h, состоящая из 10 строк и 15 столбцов (строки нумеруются от 0 до 9, столбцы от 0 до 14).
Для обращения к элементу матрицы необходимо указать ее имя и в квадратных скобках номер строки, затем номер столбца. Например, h[2] [5].
Ввод-вывод матриц
Матрицы, как и одномерные массивы, нужно вводить (выводить) поэлементно. Блок-схема ввода элементов матрицы A[n] [m] изображена ниже:
Код программы на Visual C++ вода-вывода матрицы будет иметь примерно такой вид:
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
setlocale (LC_ALL, "RUS");
int i,j,N,M,a[20][20];
cout<<"N="; //ввод количества строк
cin>>N;
cout<<"M="; //ввод количества столбцов
cin>>M;
cout<<"Input matrix A n";
//цикл по переменной i, в которой перебираем строки матрицы
for (i=0; i<N; i++)
//цикл по переменной j, в котором перебираем элементы внутри строки
for (j=0; j<M; j++)
cin>>a[i][j]; //ввод очередного элемента матрицы
cout<<"matrix A n";
for (i=0; i<N; i++)
{
//цикл по переменной i, в котором перебираем строки матрицы
for (j=0; j<M; j++)
cout<<a[i][j]<<"t"; //вывод очередного элемента матрицы
cout<<endl; //переход на новую строку после вывода всех элементов строки
}
system("pause");
return 0;
}
Результат работы программы:
Теперь, давайте рассмотрим некоторые свойства матриц:
- если номер строки элемента совпадает с номером столбца (i = j), это означает , что элемент лежит на главной диагонали матрицы;
- если номер строки превышает номер столбца (i > j), то элемент находиться ниже главной диагонали;
- если номер столбца больше номера строки (i < j), то элемент находиться выше главной диагонали;
- элемент лежит на побочной диагонали, если его индексы удовлетворяют равенству i+j+1=n;
- неравенство i+j+1<n характерно для элемента, находящегося выше побочной диагонали;
- соответственно, элементу, лежащему ниже побочной диагонали, соответствует выражение i+j+1>n.
Примеры задач обработки матриц
Задача 1
Найти сумму элементов матрицы, лежащих выше главной диагонали (рис. ниже)
Алгоритм решения данной задачи можно построить следующим образом: обнулить ячейку для накапливания суммы (переменная S). Затем с помощью двух циклов просмотреть каждый элемент матрицы, суммировать элементы при условии, что элемент находиться выше главной диагонали. Текст решения задачи:
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
setlocale (LC_ALL, "RUS");
int S, i, j, N, M, a[20][20];
cout<<"N="; cin>>N;
cout<<"M="; cin>>M;
cout<<"Введите матрицу А n";
for (i=0; i<N; i++)
for (j=0; j<M; j++)
cin>>a[i][j];
for (S=i=0; i<N; i++)
for (j=0; j<M; j++)
//если элемент лежит выше главной диагонали, то наращиваем сумму
if (j>i) S+=a[i][j];
cout<<"S="<<S<<endl;
system("pause");
return 0;
}
Задача 2
Проверить, является ли заданная квадратная матрица единичной. Единичной называют матрицу, у которой элементы главной диагонали — единицы, а все остальные — нули. Например:
Решать задачу будем так. Предположим, что матрица единичная и попытаемся доказать обратное. Если окажется, что хотя бы один диагональный элемент не равен единице или любой из элементов вне диагонали не равен нулю, то матрица единичной не является. Воспользовавшись логическими операциями языка C++, все эти условия можно соединить в одно и составить программу:
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
setlocale (LC_ALL, "RUS");
int pr, i, j, N, a[20][20];
cout<<"N="; cin>>N;
cout<<"Введите матрицу А n";
for (i=0; i<N; i++)
for (j=0; j<N; j++)
cin>>a[i][j];
//предположим, что матрица единичная, и присвоем переменной pr значение 1
//если значение этой переменной при выходе из цикла не измениться,
//это будет означать, что матрица действительно единичная
for (pr=1, i=0; i<N; i++)
for (j=0; j<N; j++)
if (((i==j) && (a[i][j]!=1)) || ((i!=j) && (a[i][j]!=0)))
//если элемент лежит на главной диагонали и не равен единице или
//элемент лежит вне главной диагонали и не равен нулю, то
{
//переменной pr присвоить значение 0, это будет означать, что
//матрица единичной не является, и выйти из цикла.
pr=0;
break;
}
//проверка значения переменной pr и вывод соответствующего сообщения
if (pr) cout<<"Single matrix"<<endl;
else cout<<"No single matrix"<<endl;
system("pause");
return 0;
}
Задача 3
Преобразовать исходную матрицу так, чтобы нулевой элемент каждый строки был заменен среднем арифметическим элементом этой строки.
Для решения задачи необходимо найти в каждой строке сумму элементов, которую разделить на их количество. Полученный результат записать в нулевой элемент соответствующей строки.
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
setlocale (LC_ALL, "RUS");
int i, j, N, M;
double S, a[20][20];
cout<<"N="; cin>>N;
cout<<"M="; cin>>M;
cout<<"Введите матрицу А n";
for (i=0; i<N; i++)
for (j=0; j<M; j++)
cin>>a[i][j];
for (i=0; i<N; a[i][0]=S/M, i++)
//цикл по i завершается записью среднего значения в нулевой элемент
//строки и наращиванием i
for (S=j=0; j<M; j++)
//вычисление суммы жлементов строки
S+=a[i][j];
cout<<"выход матрицы A"<<endl;
for (i=0; i<N; cout<<endl, i++)
for (j=0; j<M; j++)
cout<<a[i][j]<<endl;
system("pause");
return 0;
}
( 2 оценки, среднее 5 из 5 )
uses crt;
const nmax=20;
type matr=array[1..nmax,1..nmax] of integer;
procedure Vvod(var a:matr;var x,y:byte);
var i,j:byte;
begin
repeat
write('Количество строк до ',nmax,' =');
readln(x);
until x in [1..nmax];
repeat
write('Количество столбцов до ',nmax,' =');
readln(y);
until y in [1..nmax];
for i:=1 to x do
for j:=1 to y do
a[i,j]:=random(20)+1;
end;
procedure Vyvod(var a:matr;x,y:byte);
var i,j:byte;
begin
for i:=1 to x do
begin
for j:=1 to y do
write(a[i,j]:4);
writeln;
end;
writeln;
end;
function MaxMin(a:matr;x,y,k:byte):integer;
var i,j:byte;
mn,mx:integer;
begin
mn:=a[1,1];mx:=a[1,1];
for i:=1 to x do
for j:=1 to y do
if a[i,j]<mn then mn:=a[i,j]
else if a[i,j]>mx then mx:=a[i,j];
if k=1 then MaxMin:=mx else MaxMin:=mn;
end;
procedure SumRaz(var a:matr;x,y,k:byte;m:integer);
var i,j:byte;
begin
for i:=1 to x do
for j:=1 to y do
if k=1 then a[i,j]:=a[i,j]-m
else a[i,j]:=a[i,j]+m;
end;
var a:matr;
m,n,w:byte;
x:integer;
begin
clrscr;
randomize;
Vvod(a,n,m);
writeln('Исходная матрица:');
Vyvod(a,n,m);
writeln('Выберите действие:');
writeln('1-Найти максимум');
writeln('2-Найти минимум');
repeat
readln(w);
until w in [1..2];
x:=MaxMin(a,n,m,w);
if w=1 then
begin
writeln('Максимальный элемент=',x);
writeln;
writeln('Матрица разностей с максимальным элементом:');
end
else
begin
writeln('Минимальный элемент=',x);
writeln;
writeln('Матрица сумм с минимальным элементом:');
end;
SumRaz(a,n,m,w,x);
Vyvod(a,n,m);
readln
end.