Как составить программу для вычисления площади треугольника – Сайт, где вы сможете решить свои вопросы

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given the sides of a triangle, the task is to find the area of this triangle.

Examples :

Input : a = 5, b = 7, c = 8
Output : Area of a triangle is 17.320508


Input : a = 3, b = 4, c = 5
Output : Area of a triangle is 6.000000

Approach: The area of a triangle can simply be evaluated using following formula.

where a, b and c are lengths of sides of triangle, and
s = (a+b+c)/2

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>

using namespace std;

float findArea(float a, float b, float c)

{

if (a < 0 || b < 0 || c < 0 ||

(a + b <= c) || a + c <= b ||

b + c <= a)

{

cout << "Not a valid triangle";

exit(0);

}

float s = (a + b + c) / 2;

return sqrt(s * (s - a) *

(s - b) * (s - c));

}

int main()

{

float a = 3.0;

float b = 4.0;

float c = 5.0;

cout << "Area is " << findArea(a, b, c);

return 0;

}

C

#include <stdio.h>

#include <stdlib.h>

float findArea(float a, float b, float c)

{

if (a < 0 || b < 0 || c <0 || (a+b <= c) ||

a+c <=b || b+c <=a)

{

printf("Not a valid triangle");

exit(0);

}

float s = (a+b+c)/2;

return sqrt(s*(s-a)*(s-b)*(s-c));

}

int main()

{

float a = 3.0;

float b = 4.0;

float c = 5.0;

printf("Area is %f", findArea(a, b, c));

return 0;

}

Java

class Test

{

static float findArea(float a, float b, float c)

{

if (a < 0 || b < 0 || c <0 || (a+b <= c) ||

a+c <=b || b+c <=a)

{

System.out.println("Not a valid triangle");

System.exit(0);

}

float s = (a+b+c)/2;

return (float)Math.sqrt(s*(s-a)*(s-b)*(s-c));

}

public static void main(String[] args)

{

float a = 3.0f;

float b = 4.0f;

float c = 5.0f;

System.out.println("Area is " + findArea(a, b, c));

}

Python3

def findArea(a,b,c):

if (a < 0 or b < 0 or c < 0 or (a+b <= c) or (a+c <=b) or (b+c <=a) ):

print('Not a valid triangle')

return

s = (a + b + c) / 2

area = (s * (s - a) * (s - b) * (s - c)) ** 0.5

print('Area of a triangle is %f' %area)

a = 3.0

b = 4.0

c = 5.0

findArea(a,b,c)

C#

using System;

class Test {

static float findArea(float a, float b,

float c)

{

if (a < 0 || b < 0 || c <0 ||

(a + b <= c) || a + c <=b ||

b + c <=a)

{

Console.Write("Not a valid triangle");

System.Environment.Exit(0);

}

float s = (a + b + c) / 2;

return (float)Math.Sqrt(s * (s - a) *

(s - b) * (s - c));

}

public static void Main()

{

float a = 3.0f;

float b = 4.0f;

float c = 5.0f;

Console.Write("Area is " + findArea(a, b, c));

}

PHP

<?php

function findArea($a, $b, $c)

{

if ($a < 0 or $b < 0 or

$c < 0 or ($a + $b <= $c) or

$a + $c <= $b or $b + $c <= $a)

{

echo "Not a valid triangle";

exit(0);

}

$s = ($a + $b + $c) / 2;

return sqrt($s * ($s - $a) *

($s - $b) * ($s - $c));

}

$a = 3.0;

$b = 4.0;

$c = 5.0;

echo "Area is ", findArea($a, $b, $c);

?>

Javascript

<script>

function findArea( a, b, c)

{

if (a < 0 || b < 0 || c < 0 ||

(a + b <= c) || a + c <= b ||

b + c <= a)

{

document.write( "Not a valid triangle");

return;

}

let s = (a + b + c) / 2;

return Math.sqrt(s * (s - a) *

(s - b) * (s - c));

}

let a = 3.0;

let b = 4.0;

let c = 5.0;

document.write( "Area is " + findArea(a, b, c));

</script>

Time Complexity: O(log₂n)
Auxiliary Space: O(1), since no extra space has been taken.

Given the coordinates of the vertices of a triangle, the task is to find the area of this triangle.

Approach: If given coordinates of three corners, we can apply the Shoelace formula for the area below.

$Area = frac{sum_{i=1}^{n-1} (x_i y_{(i+1)}+x_ny_{1}) - sum_{i=1}^{n-1}(x_{(i+1)}y_i-x_1y_n)}{2}$

$= frac{(x_{1}y_{2} + x_{2}y_{3} + ... + x_{n-1}y_{n} + x_{n}y_{1}) -(x_{2}y_{1} + x_{3}y_{2} + ... + x_{n}y_{n-1} + x_{1}y_{n})}{2}$

C++

#include <bits/stdc++.h>

using namespace std;

double polygonArea(double X[], double Y[], int n)

{

double area = 0.0;

int j = n - 1;

for (int i = 0; i < n; i++)

{

area += (X[j] + X[i]) * (Y[j] - Y[i]);

j = i;

}

return abs(area / 2.0);

}

int main()

{

double X[] = {0, 2, 4};

double Y[] = {1, 3, 7};

int n = sizeof(X)/sizeof(X[0]);

cout << polygonArea(X, Y, n);

}

Java

import java.io.*;

import java.math.*;

class GFG {

static double polygonArea(double X[], double Y[], int n)

{

double area = 0.0;

int j = n - 1;

for (int i = 0; i < n; i++)

{

area += (X[j] + X[i]) * (Y[j] - Y[i]);

j = i;

}

return Math.abs(area / 2.0);

}

public static void main (String[] args)

{

double X[] = {0, 2, 4};

double Y[] = {1, 3, 7};

int n = X.length;

System.out.println(polygonArea(X, Y, n));

}

Python3

def polygonArea(X,Y, n) :

area = 0.0

j = n - 1

for i in range( 0, n) :

area = area + (X[j] + X[i]) * (Y[j] - Y[i])

j = i

return abs(area // 2.0)

X = [0, 2, 4]

Y = [1, 3, 7]

n = len(X)

print(polygonArea(X, Y, n))

C#

using System;

class GFG {

static double polygonArea(double []X,

double []Y, int n)

{

double area = 0.0;

int j = n - 1;

for (int i = 0; i < n; i++)

{

area += (X[j] + X[i]) *

(Y[j] - Y[i]);

j = i;

}

return Math.Abs(area / 2.0);

}

public static void Main ()

{

double []X = {0, 2, 4};

double []Y = {1, 3, 7};

int n = X.Length;

Console.WriteLine(

polygonArea(X, Y, n));

}

PHP

<?php

function polygonArea( $X, $Y, $n)

{

$area = 0.0;

$j = $n - 1;

for ( $i = 0; $i < $n; $i++)

{

$area += ($X[$j] + $X[$i]) *

($Y[$j] - $Y[$i]);

$j = $i;

}

return abs($area / 2.0);

}

$X = array(0, 2, 4);

$Y = array(1, 3, 7);

$n = count($X);

echo polygonArea($X, $Y, $n);

?>

Javascript

<script>

function polygonArea(X, Y, n)

{

let area = 0.0;

let j = n - 1;

for (let i = 0; i < n; i++)

{

area += (X[j] + X[i]) * (Y[j] - Y[i]);

j = i;

}

return Math.abs(area / 2.0);

}

let X = [0, 2, 4];

let Y = [1, 3, 7];

let n = X.length;

document.write(polygonArea(X, Y, n));

</script>

Time Complexity: O(n)
Auxiliary Space: O(1)

Last Updated :
16 Feb, 2023

Like Article

Save Article

Источник

В прошлых уроках мы разобрались с такими понятиями, как переменные и типы данных (смотрите список предыдущих уроков курса в конце статьи).

Чтобы закрепить эти знания, напишем простую программу, а заодно рассмотрим типичные ошибки, которые могут возникнуть при написании даже простейших программ.

Но прежде чем продолжить далее, отмечу, что можете посмотреть видео (в нем больше информации, по понятным причинам), или прочитать текстовую версию чуть ниже.

Задача

Напишем программу, которая считает площадь треугольника.

Для тех, кто забыл геометрию, напомню, что площадь треугольника вычисляется по формуле:

S = 0.5 * a * h

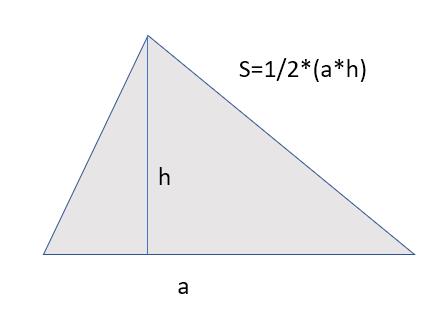
Площадь треугольника

где:

a — основание треугольника
h — высота треугольника
S — площадь треугольника

Что любопытно

Несмотря на то, что задача элементарная, мы сразу повторим несколько базовых концепция программирования.

Ввод и вывод данных.
Работа с переменными.
Работа с нужными типами данных.

Что делаем наша программа?

Программа должна запрашивать два числа у пользователя. Это высота и основание треугольника.
Программа выводит результат на экран, после того, как посчитает площадь треугольника.

Единственное, что мы пока не умеем делать — это запрашивать данные от пользователя.

Для этого нам понадобится использовать функцию input().

Вот код нашей программы с комментариями.

print("Площадь треугольника")
print("Введите основание треугольника:")
a = float(input())  # ввод данных от пользователя
print("Введите высоту треугольника:")
h = float(input()) # ввод данных от пользователя
s = 0.5*a*h # вычисление площади по формуле
print("Площадь треугольника = :", s) # вывод результата

Как это выглядит на компьютере:

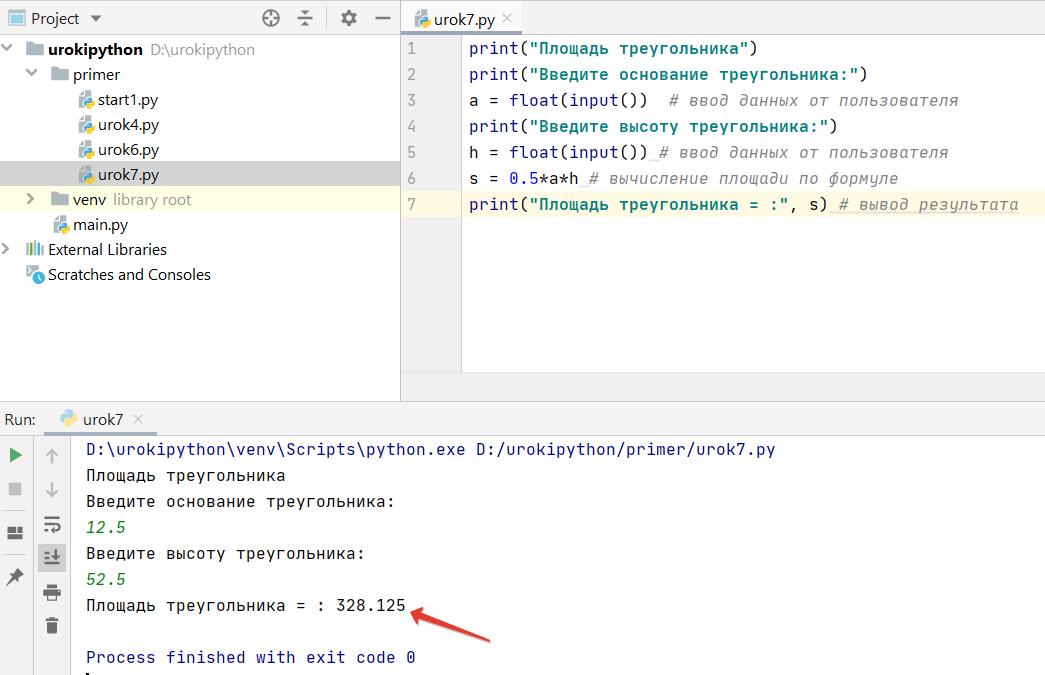
Пример программы на Python

Как видите, ничего сложного нет. Единственное, что нужно сразу предусмотреть — это использование для переменных типа данных float. Если выбрать тип данных int, то мы сможем считать площадь треугольника только с целыми числами для высоты и основания.

Поэтому, сразу выбираем float.

Уроки по Python 3:

Урок №1. Стоит ли изучать Python? Почему он стал лучшим «первым» языком программирования для начинающих?
Урок №2: Как установить Python 3 в Windows и проверка установки в Linux
Урок №3: PyCharm: пошаговая инструкция по установке IDE для изучения Python
Урок №4: Переменные в Python: что это такое, как их называть и использовать?
Урок №5: Комментирование кода в Python
Урок №6: 3 основных типа данных в Python, с которыми начнем работать сразу: int, float, str
Урок №7: Числа и операции с ними в Python
Урок №8: Ввод и вывод данных в Python. Пишем первую программу

Источник

Ученик

(119),
на голосовании

11 лет назад

Голосование за лучший ответ

Константин Григорьев

Мыслитель

(5799)

11 лет назад

держи, тут писать то 5 минут
program a2;{ вычисление площади треугольника}
uses crt;
var a,h,s:real;
procedure dd;
begin
writeln(‘Введите значение стороны треугольника == >’);
readln(a);
writeln(‘Введите значение высоты треугольника == >’);
readln(h);
s:=(a*h*0.5);
if a > 0 then
writeln(‘Площадь треугольника равна ==>’,s:8:3,’ квадратных едениц’)
else writeln(‘Сторона не может быть отрицательной’);
end;
begin
clrscr;
writeln(‘Расчёт площади треугольника, ввод вручную’);
dd;
readln;
readkey;
end.

Источник: паскаль

Леонид Сидоренко

Ученик

(148)

6 лет назад

нина кутявина

Ученик

(120)

4 года назад

var a,b,s,h: real;
begin
write (‘введите длину основания’);
read (b);
write (‘введите длину высоты’);
read (h);
s:=1/2*b*h;
a:=sqrt(sqr(b)/2);
writeln (‘Площадь =’,s);
writeln (‘Боковые стороны равны =’,a);
end.

Источник

Площадь треугольника по формуле Герона

📐 Площадь прямоугольного треугольника. Вычислить площадь и периметр прямоугольного треугольника по двум сторонам. Четыре варианта решения задач.

🟩 Вычисление периметра и площади квадрата. Четыре варианта решения задачи. В том числе вариант решения на PascalABC.NET, без использования устаревших конструкций (с точки зрения этой версии).

Даны три стороны треугольника ABC. Напишите программу вычисления площади треугольника по формуле Герона

Задачи по информатике, программирование на Паскале. Во втором примере используется оператор перехода GOTO. Третий пример написан, с учётом рекомендаций PascalABC.NET (“здоровье кода” составляет 144%).

Задача №1

Задание:
Вычислить площадь треугольника по формуле Герона S = √(p·(p – a)·(p – b)·(p – c))

Program Heron;
Var p, St, A, B, C : Real;
begin
writeln(‘Площадь треугольника по формуле Герона ‘);
write(‘Введите стороны треугольника ‘);
readln(A, B, C);
if (A+B>C) AND (A+C>B) AND (B+C>A) then begin
p := (A + B + C) / 2;
St := Sqrt(p * (p – a) * (p – b) * (p – c));
writeln(‘Площадь треугольника ‘, St:8:5)
end
else writeln(‘Треугольник с такими сторонами не существует’)
end.

Замечание:
В процедуре вывода writeln используется форматированный вывод переменной. St:8:5 обозначает, что для вывода значения переменной S будет использоваться 8 позиций, в том числе 5 после запятой. При этом если целая часть числа будет трёхзначной, то после запятой всё равно будет 5 знаков, а всё число будет занимать 9 позиций.

Задача №2

Задание:
1. Вычислить площадь треугольника по формуле Герона S = √(p·(p – a)·(p – b)·(p – c))
2. Спросить у пользователя “Заверить программу или продолжить выполнение”.

Program Heron;
Label 1;
Var
p, St, A, B, C : Real;
YN : Char;
begin
writeln(‘Площадь треугольника по формуле Герона ‘);
1:
write(‘Введите стороны треугольника ‘);
readln(A, B, C);
if (A+B>C) AND (A+C>B) AND (B+C>A) then begin
p := (A + B + C) / 2; { Найти полупериметр треугольника }
St := Sqrt(p * (p – a) * (p – b) * (p – c));
writeln(‘Площадь треугольника ‘, St:8:5)
end
else writeln(‘Треугольник с такими сторонами не существует’);
write(‘Продолжить выполнение программы? Y / N ‘);
readln(YN);
if (YN = ‘Y’) OR (YN = ‘y’) then GOTO 1
else writeln (‘Вы закончили работу с программой’);
end.

Вычислить площадь треугольника по формуле Герона. Вариант решения на PascalABC.NET

Задание:
Найти площадь треугольника. При решении задачи использовать синтаксис, рекомендуемый в PascalABC.NET.

begin
Println(‘Площадь треугольника по формуле Герона ‘);
Print(‘Введите стороны треугольника ‘);
var (A, B, C) := ReadReal3; // Возвращает кортеж из трёх значений типа real, введенных с клавиатуры.
if (A+B>C) AND (A+C>B) AND (B+C>A) then begin // Проверить существует ли треугольник с такими сторонами.
var p := (A + B + C) / 2; // Найти полупериметр треугольника.
var St := Sqrt(p * (p – a) * (p – b) * (p – c)); // Вычислить площадь. Функция Sqrt – возвращает квадратный корень числа.
Println(‘Площадь треугольника ‘, St)
end
else Println(‘Треугольник с такими сторонами не существует’)
end.

Рекламный блок

Информационный блок

Источник

На языке программирования Питон можно решить много разных задач, в том числе и по математике. Для начинающих изучать этот язык будет полезно решить задание на вычисление площади треугольника. Одним из способов вычисления этой величины является применение формулы Герона.

Математическая часть задачи

Из школьного курса математики вы знаете, что площадь треугольника можно вычислить по данным длинам трёх его сторон по формуле Герона:

где

p – полупериметр треугольника.

Решение задачи на Питоне

На вход программе подаются целые числа, выводом программы должно являться вещественное число, соответствующее площади треугольника.

Для ввода целых чисел используем функцию int().

Для решения задачи нам необходимо подключить библиотеку с математическими функциями. Делаем это с помощью строки импорта:


import math

Функция для извлечения квадратного корня в этой библиотеке записывается так:

math.sqrt()

Код программы для вычисления площади треугольника

import math  #подключаем библиотеку математических функций

a=int(input("Введите сторону a="))

b=int(input(Введите сторону b=))

c=int(input(Введите сторону c=))

p=(a+b+c)/2

s=math.sqrt(p*(p-a)*(p-b)*(p-c))

print(s)

Результат выполнения кода программы


Python 3.5.2 (default, Dec 2015, 13:05:11)

[GCC 4.8.2] on Linux

 12

 13

 14

72.30793524918272

Второй вариант решения задачи

Также можно воспользоваться стандартной функцией возведения числа в степень. Дело в том, что квадратный корень – это возведение в степень 1/2.

Синтаксис функции такой:

pow(x,y)

где x – число, возводимое в степень, а y – сама степень.

Вот так это запишется по формуле:


s=pow((p*(p-a)*(p-b)*(p-c)),1/2)

Результат выполнения кода:


Python 3.5.2 (default, Dec 2015, 13:05:11)

[GCC 4.8.2] on linux

 12

 13

 14

72.30793524918272

Третий вариант решения задачи

Вместо извлечения корня можно возвести в степень 1/2 или 0,5. При этому функцию использовать не нужно.


s=(p*(p-a)*(p-b)*(p-c))**0.5

Как видим, результат выполнения программы точно такой же.

Python 3.5.2 (default, Dec 2015, 13:05:11)

[GCC 4.8.2] on linux

 12

 13

 14

72.30793524918272

Нахождение натуральных чисел с условием Вычисление площади фигур

Источник

Given the sides of a triangle, the task is to find the area of this triangle.

C++

C

Java

Python3

C#

PHP

Javascript

Given the coordinates of the vertices of a triangle, the task is to find the area of this triangle.

C++

Java

Python3

C#

PHP

Javascript

Задача

Что любопытно

Что делаем наша программа?

Как это выглядит на компьютере:

Уроки по Python 3:

Площадь треугольника по формуле Герона

Даны три стороны треугольника ABC. Напишите программу вычисления площади треугольника по формуле Герона

Задача №1

Задача №2

Вычислить площадь треугольника по формуле Герона. Вариант решения на PascalABC.NET

Рекламный блок

Информационный блок

Математическая часть задачи

Решение задачи на Питоне

Второй вариант решения задачи

Третий вариант решения задачи

Вам также может понравиться

Как найти компанию для нового года

Как найти частоту колебаний заряда

Как проверить слово исправить букву с

Добавить комментарий Отменить ответ