Просмотров 17.2к. Обновлено 23 ноября 2020
Урок из серии: «Программирование на языке Паскаль»
Процесс обработки и поиска информации при решении многих задач проходит быстрее и эффективнее, если данные расположены в определенном порядке. Например, различные списки студентов, учащихся, сотрудников — в алфавитном порядке, числовые данные от большего значения к меньшему (или наоборот) и т.д.
Существует довольно много различных методов сортировки массивов, отличающихся друг от друга степенью эффективности, под которой понимается количество сравнений и количество обменов, произведенных в процессе сортировки. Рассмотрим подробно некоторые из них.
Сортировка массива методом простого выбора
При сортировке массива методом выбора применяется базовый алгоритм поиска максимального (минимального) элемента и его номера.
Алгоритм сортировки массива методом выбора:
- Для исходного массива выбрать максимальный элемент.
- Поменять его местами с последним элементом (после этого самый большой элемент будет стоять на своем месте).
- Повторить п.п. 1-2 с оставшимися n-1 элементами, то есть рассмотреть часть массива, начиная с первого элемента до предпоследнего, найти в нем максимальный элемент и поменять его местамис предпоследним (n-1)- м элементом массива, затем с оставшиеся (n-2)-мя элементами и так далее, пока не останется один элемент, уже стоящий на своем месте.
Для упорядочения массива потребуется (n-1) просмотров массива. В процессе сортировки будет увеличиваться отсортированная часть массива, а неотсортированная, соответственно, уменьшаться.
При сортировке данных выполняется обмен содержимого переменных. Для обмена необходимо создавать временную переменную, в которой будет храниться содержимое одной из переменных. В противном случае ее содержимое окажется утерянным.
Задача 1. Массив из 10 элементов отсортировать по возрастанию методом простого перебора.
Решение
Напишем процедуру. Входным параметром для неё будет массив. Он же будет и выходным параметром. Поэтому описываем его как параметр-переменная (с ключевым словом var).
В процедуре внешний цикл по i — определяет длину рассматриваемой части массива. Она будет изменяться от n до 2.
Внутренний цикл по j используется для поиска максимального элемента и его номера. В качестве начального значения максимума разумно взять значение последнего элемента рассматриваемой части массива.
Программный код процедуры:
Procedure sorting1(var a:myarray);
{Сортировка по возрастанию методом простого выбора}
var i,j:integer;
k,m:integer; {номер и значение максимального элемента}
begin
for i:= n downto 2 do{задаем длину рассматриваемой части массива}
begin
{ищем максимальный элемент и его номер}
k:=i; m:=a[i]; for j:= 1 to i-1 do
if a[j] > m then begin k:=j; m:=a[k] end;
{меняем местами найденный элемент и последний}
if k <> i then
begin a[k]:=a[i]; a[i]:= m; end;
end;
end;
end;
Программный код основной программы:
program primer_1;
const n = 10;
type myarray = array[1..n] of integer;
var a:myarray;
Procedure sorting1(var a:myarray);
{Линейная сортировка (сортировка отбором)}
...
begin {main}
writeln('Введите исходный массив:');
for i:=1 to n do read(a[i]);
sorting1(a);
writeln('Отсортированный массив:');
for i:=1 to 10 do write(a[i],' ');
writeln;
end.
Процесс упорядочения элементов в массиве по возрастанию методом отбора:
| Номер элемента | 1 | 2 | 3 | 4 | 5 |
| Исходный массив | 8 | 7 | 5 | 4 | 2 |
| Первый просмотр | 2 | 7 | 5 | 4 | 8 |
| Второй просмотр | 2 | 4 | 5 | 7 | 8 |
| Третий просмотр | 2 | 4 | 5 | 7 | 8 |
| Четвертый просмотр | 2 | 4 | 5 | 7 | 8 |
При упорядочивании массива по убыванию необходимо перемещать минимальный элемент. Для чего в алгоритме нахождения максимального элемента достаточно знак «>» поменять на знак «<«.
Сортировка массива методом простого обмена (методом пузырька)
Наиболее известным методом сортировки является сортировка пузырьковым методом. Его популярность объясняется запоминающимся названием и простым алгоритмом.
Метод основан на том, что в процессе исполнения алгоритма более «легкие» элементы массива постепенно «всплывают».
Особенностью данного метода является сравнение не каждого элемента со всеми, а сравнение в парах соседних элементов. Выполняется несколько последовательных просмотров массива от начала к концу. Если соседние элементы расположены «неправильно», то они меняются местами.
Алгоритм сортировки массива по возрастанию методом простого обмена:
- Начнем просмотр с первой пары элементов ( a[1] и a[2] ). Если первый элемент этой пары больше второго, то меняем их местами, иначе оставляем без изменения. Затем берем вторую пару элементов ( a[2] и a[3] ), если второй больше третьего, то также меняем их, далее сравниваем третий и четвертый, и если третий больше четвертого, меняем их местами, и т.д. Последними сравниваем (n-1)-ый и n-ый элементы.При первом обходе массива будут просмотрены все пары элементов массива a[i] и a[i+1] для i от 1 до (n-1). В результате максимальный элемент массива переместится в конец массива.
- Поскольку самый большой элемент находится на своем месте, рассмотрим часть массива без него, то есть с первого до (n-1) — го элемента.Повторим предыдущие действия для этой части массива, в результате чего второй по величине элемент массива переместится на последнее место рассматриваемой части массива, то есть на ( n-1 ) — е место во всем массиве.
- Эти действия продолжают до тех пор, пока количество элементов в текущей части массива не уменьшится до двух. В этом случае необходимо выполнить последнее сравнение и упорядочить последние два элемента.
Нетрудно заметить, что для преобразования массива, состоящего из n элементов, необходимо просмотреть его n–1 раз, каждый раз уменьшая диапазон просмотра на один элемент.
Ниже приведен текст процедуры сортировки массива по возрастанию методом пузырька.
procedure sorting2(var a:myarray);
var k,i,t:integer;
begin
for k := 1 to n-1 do {цикл по номеру просмотра}
for i:=1 to n-k do
{Если текущий элемент больше следующего, поменять местами}
if a[i] > a[i+1] then
begin
t:=a[i];
a[i]:=a[i+1];
a[i+1]:=t;
end;
end;
Для упорядочения элементов массива по убыванию их значений необходимо при сравнении элементов массива знак «>» заменить на «<«.
Процесс упорядочения элементов в массиве по возрастанию методом обмена:
| Номер элемента | 1 | 2 | 3 | 4 | 5 |
| Исходный массив | 8 | 7 | 5 | 4 | 2 |
| Первый просмотр | 7 | 5 | 4 | 2 | 8 |
| Второй просмотр | 5 | 4 | 2 | 7 | 8 |
| Третий просмотр | 4 | 2 | 5 | 7 | 8 |
| Четвертый просмотр | 2 | 4 | 5 | 7 | 8 |
Что такое сортировка и зачем она нужна
Сортировка распределяет элементы в порядке, удобном для работы. Если отсортировать массив чисел в порядке убывания, то первый элемент всегда будет наибольшим, а последний наименьшим. Поэтому желательно хранить информацию упорядочено, чтобы было проще проводить над ней операции.
В данной статье вы научитесь разным техникам сортировок на языке С++. Мы затронем 7 видов:
- Пузырьковая сортировка (Bubble sort);
- Сортировка выбором (Selection sort);
- Сортировка вставками (Insertion sort);
- Быстрая сортировка (Quick sort);
- Сортировка слиянием (Merge sort);
- Сортировка Шелла (Shell sort);
- Сортировка кучей (Heap sort).
Знание этих техник поможет получить работу. На площадке LeetCode содержится более 200 задач, связанных с сортировками. 19 из них входят в топ частых вопросов на собеседованиях по алгоритмам.
1. Пузырьковая сортировка
В пузырьковой сортировке каждый элемент сравнивается со следующим. Если два таких элемента не стоят в нужном порядке, то они меняются между собой местами. В конце каждой итерации (далее называем их проходами) наибольший/наименьший элемент ставится в конец списка.
Прежде чем писать код, разберем сортировку визуально на примере массива из пяти элементов. Отсортируем его в порядке возрастания.

Проход №1
Оранжевым отмечаются элементы, которые нужно
поменять местами. Зеленые уже стоят в нужном порядке.

Наибольший элемент — число 48 — оказался в конце
списка.
Проход №2

Наибольший элемент уже занимает место в конце
массива. Чтобы поставить следующее число по убыванию, можно пройтись лишь до 4-й позиции, а не пятой.
Проход №3

Проход №4

После четвертого прохода получаем
отсортированный массив.
Функция сортировки в качестве параметров будет принимать указатель на массив и его размер. Функцией swap() элементы
меняются местами друг с другом:
#include <iostream>
using namespace std;
void bubbleSort(int list[], int listLength)
{
while(listLength--)
{
bool swapped = false;
for(int i = 0; i < listLength; i++)
{
if(list[i] > list[i + 1])
{
swap(list[i], list[i + 1]);
swapped = true;
}
}
if(swapped == false)
break;
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
bubbleSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в лучшем случае: O(n).
Сложность в среднем случае: O(n2).
Сложность в худшем случае: O(n2).
2. Сортировка выбором
Ищем наименьшее значение в массиве и ставим
его на позицию, откуда начали проход. Потом двигаемся на следующую позицию.
Возьмем тот же массив из пяти элементов и отсортируем его.
Проход №1

Зеленым отмечается наименьший элемент в
подмассиве — он ставится в начало списка.
Проход №2
Число 4 — наименьшее в оставшейся части массива.
Перемещаем четверку на вторую позицию после числа 0.

Проход №3

Проход №4

Напишем функцию поиска наименьшего элемента и
используем ее в сортировке:
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
#include <iostream>
using namespace std;
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
void selectionSort(int list[], int listLength)
{
for(int i = 0; i < listLength; i++)
{
int smallestPosition = findSmallestPosition(list, i, listLength);
swap(list[i], list[smallestPosition]);
}
return;
}
int main ()
{
int list[5] = {12, 5, 48, 0, 4};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
selectionSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в любом случае: O(n2).
3. Сортировка вставками
В сортировке вставками начинаем со второго
элемента. Проверяем между собой второй элемент с первым и, если надо, меняем местами.
Сравниваем следующую пару элементов и проверяем все пары до нее.
Проход №1. Начинаем со второй позиции.

Число 12 больше 5 — элементы меняются местами.
Проход №2. Начинаем с третьей позиции.
Проверяем вторую и третью позиции. Затем
первую и вторую.

Проход №3. Начинаем с четвертой позиции.

Произошло три смены местами.
Проход №4. Начинаем с последней позиции.

Получаем отсортированный массив на выходе.
#include <iostream>
using namespace std;
void insertionSort(int list[], int listLength)
{
for(int i = 1; i < listLength; i++)
{
int j = i - 1;
while(j >= 0 && list[j] > list[j + 1])
{
swap(list[j], list[j + 1]);
cout<<"ndid";
j--;
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
insertionSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n).
Сложность в худшем случае: O(n2).
4. Быстрая сортировка
В основе быстрой сортировки лежит стратегия
«разделяй и властвуй». Задача разделяется на более мелкие подзадачи. Подзадачи
решаются отдельно, а потом решения объединяют. Точно так же, массив разделяется
на подмассивы, которые сортируются и затем сливаются в один.
В первую очередь выбираем опорный элемент.
Отметим его синим. Все значения больше опорного элемента ставятся после него,
остальные — перед.

На иллюстрации массив разделяется по опорному
элементу. В полученных массивах также выбираем опорный элемент и разделяем по
нему.
Опорным может быть любой элемент. Мы выбираем
последний в списке.
Чтобы расположить элементы большие — справа от
опорного элемента, а меньшие — слева, будем двигаться от начала списка. Если
число будет больше опорного, то оно ставится на его место, а сам опорный на
место перед ним.


Напишем функцию разделения partition(),
которая возвращает индекс опорного элемента, и используем ее в сортировке.
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
#include <iostream>
using namespace std;
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
void quickSort(int list[], int start, int end)
{
if(start < end)
{
int pivot = partition(list, start, end);
quickSort(list, start, pivot - 1);
quickSort(list, pivot + 1, end);
}
}
int main()
{
int list[6]={2, 12, 5, 48, 0, 4};
cout<<"Input array ...n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
quickSort(list, 0, 6);
cout<<"nnSorted array ... n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n*logn).
Сложность в худшем случае: O(n2).
5. Сортировка слиянием
Сортировка слиянием также следует стратегии
«разделяй и властвуй». Разделяем исходный массив на два равных подмассива.
Повторяем сортировку слиянием для этих двух подмассивов и объединяем обратно.

Цикл деления повторяется, пока не останется по
одному элементу в массиве. Затем объединяем, пока не образуем полный список.
Алгоритм сортировки состоит из четырех этапов:
- Найти середину массива.
- Сортировать массив от
начала до середины. - Сортировать массив от
середины до конца. - Объединить массив.
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
Для объединения напишем отдельную функцию
merge().
Алгоритм объединения массивов:
- Циклично проходим по
двум массивам.. - В объединяемый ставим тот элемент, что меньше.
- Двигаемся дальше, пока не дойдем до конца
обоих массивов.
#include <iostream>
using namespace std;
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
void merge(int list[],int start, int end, int mid)
{
int mergedList[8];
int i, j, k;
i = start;
k = start;
j = mid + 1;
while (i <= mid && j <= end) {
if (list[i] < list[j]) {
mergedList[k] = list[i];
k++;
i++;
}
else {
mergedList[k] = list[j];
k++;
j++;
}
}
while (i <= mid) {
mergedList[k] = list[i];
k++;
i++;
}
while (j <= end) {
mergedList[k] = list[j];
k++;
j++;
}
for (i = start; i < k; i++) {
list[i] = mergedList[i];
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
mergeSort(list, 0, 7);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в любом случае: O(n*logn).
6. Сортировка Шелла
Алгоритм включает в себя сортировку вставками.
Исходный массив размером N разбивается на подмассивы с шагом N/2. Подмассивы
сортируются вставками. Затем вновь разбиваются, но уже с шагом равным N/4. Цикл
повторяется. Производим целочисленное деление шага на два каждую итерацию.
Когда шаг становится равен 1, массив просто сортируется вставками.
У массива размером с 8, первый шаг будет равен 4.

Уменьшаем шаг в два раза. Шаг равен 2.
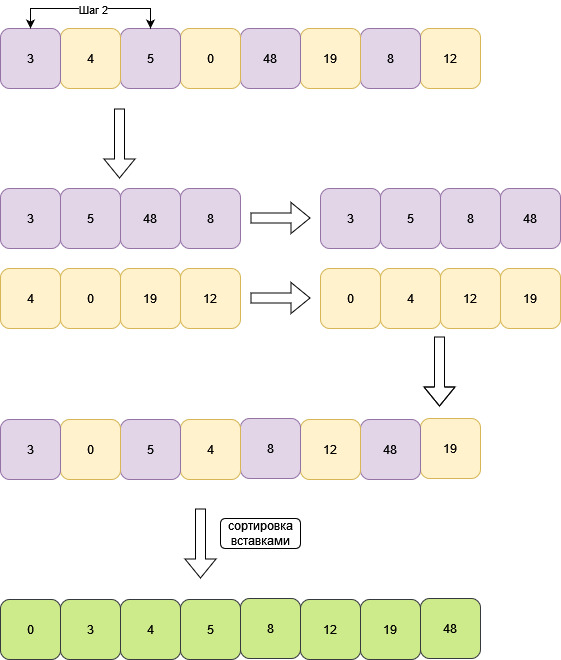
#include <iostream>
using namespace std;
void shellSort(int list[], int listLength)
{
for(int step = listLength/2; step > 0; step /= 2)
{
for (int i = step; i < listLength; i += 1)
{
int j = i;
while(j >= step && list[j - step] > list[i])
{
swap(list[j], list[j - step]);
j-=step;
cout<<"ndid";
}
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
shellSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в лучшем и среднем случае:
O(n*logn).
Сложность в худшем случае: O(n2).
Исходный массив представляем в виде структуры
данных кучи. Куча – это один из
типов бинарного дерева.
У кучи есть следующие свойства:
- Родительский узел
всегда больше дочерних; - На i-ом слое 2i
узлов, начиная с нуля. То есть на нулевом слое 1 узел, на первом – 2 узла, на
втором – 4, и т. д. Правило для всех слоев, кроме последнего; - Слои заполняются слева направо.
После формирования кучи будем извлекать самый
старший узел и ставить на конец массива.
Алгоритм сортировки кучей:
- Формируем бинарное
дерево из массива. - Расставляем узлы в
дереве так, чтобы получилась куча (методheapify()). - Верхний элемент
помещаем в конец массива. - Возвращаемся на шаг 2, пока куча не опустеет.
Обращаться к дочерним узлам можно, зная, что
дочерние элементы i-го элемента находятся на позициях 2*i + 1 (левый узел) и
2*i + 2 (правый узел).
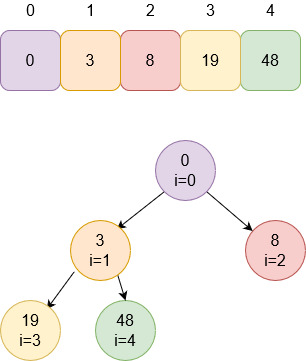
Изначальная куча:

Индекс с нижним левым узлом определим по
формуле n/2-1, где n – длина массива. Получается 5/2 – 1 = 2 – 1 = 1. С этого
индекса и начинаем операцию heapify(). Сравним дочерние узлы 1-й позиции.

Дочерний узел оказался больше. Меняем местами
с родителем.

Теперь проверяем родительский узел от позиции
1.

48 больше 3. Меняем местами.

После смены проверяем все дочерние узлы
элемента, который опустили. То есть для числа 3 проводим heapify(). Так как 3
меньше 19, меняем местами.

Наибольший элемент оказался наверху кучи.
Осталось поставить его в конце массива на позицию 4.

Теперь продолжаем сортировать кучу, но последний элемент игнорируем. Для
этого просто будем считать, что длина массива уменьшилась на 1.

Повторяем алгоритм сортировки, пока куча не
опустеет, и получаем отсортированный массив.
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
#include <iostream>
using namespace std;
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
void heapSort(int list[], int listLength)
{
for(int i = listLength / 2 - 1; i >= 0; i--)
heapify(list, listLength, i);
for(int i = listLength - 1; i >= 0; i--)
{
swap(list[0], list[i]);
heapify(list, i, 0);
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout<<"Input array ..."<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
heapSort(list, 5);
cout << "Sorted array"<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность алгоритма в любом случае: O(n*logn).
***
В этой статье мы познакомились с семью видами
сортировок, рассмотрели их выполнение и написание на С++. Попробуйте применить
новые знания в решении задачек на LeetCode или Codeforces. Понимание подобных
алгоритмов поможет в будущем пройти собеседование.
Источники:
- https://www.softwaretestinghelp.com/sorting-techniques-in-cpp/
- https://medium.com/@ssbothwell/sorting-algorithms-and-big-o-analysis-332ce7b8e3a1
- https://www.programiz.com/dsa/shell-sort
- https://www.happycoders.eu/algorithms/sorting-algorithms/
***
Материалы по теме
- Какая сортировка самая быстрая? Тестируем алгоритмы
- Пузырьковая сортировка на JavaScript
- Вводный курс по алгоритмам: от сортировок до машины Тьюринга
***
Мне сложно разобраться самостоятельно, что делать?
Алгоритмы и структуры данных действительно непростая тема для самостоятельного изучения: не у кого спросить и что-то уточнить. Поэтому мы запустили курс «Алгоритмы и структуры данных», на котором в формате еженедельных вебинаров вы:
- изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
- научитесь применять алгоритмы и структуры данных при разработке программ;
- подготовитесь к техническому собеседованию и продвинутой разработке.
Курс подходит как junior, так и middle-разработчикам.
В практике программиста часто случается так, что нужно разместить какие-либо данные в определенном порядке. В Паскале для таких случаев предусмотрена сортировка. Существует два основных алгоритма сортировки. Первый из них — метод прямого выбора. Ее смысл заключается в том, что за счет вложенности циклов каждый элемент массива сравнивается с остальными.
То есть, если у нас 10 чисел, то сначала первое из них будет сравниваться до тех пор, пока не будет найдено другой, например, большее его (если мы сортируем просто по возрастанию). Далее так же будет сравниваться 2, 3, 4 … элементы с последующими, но не с теми, которые уже отсортированы.
Прелесть этого вида сортировки заключается в том, что она очень проста для начинающего программиста, и все обычно начинают именно с неё. Давайте же рассмотрим пример. Пусть нам дан массив из 20 элементом и нам нужно отсортировать по убыванию.
Program SortMas;
var
i, j, k: integer;
mas: array[1..20] of integer;
Begin
randomize;
for i := 1 to 20 do mas[i] := random(100);
writeln;
writeln('массив до сортировки');
for i := 1 to 20 do write(mas[ i], ' ');
for i := 1 to 19 do
for j := i + 1 to 20 do
if mas[i] < mas[j] then
begin
k := mas[i];
mas[i] := mas[j];
mas[j] := k;
end;
writeln('массив после сортировки');
for i := 1 to 20 do write(mas[ i], ' ');
End.
Обратите внимание на 2 первые строки после Begin. Здесь мы вызываем процедуру генерации случайных чисел. То есть просто заполняем наш массив числами от 1 до 100. Далее в цикле выводится для пользователя первоначальный массив.
Далее следует сам алгоритм сортировки, для новичков объясним, что это 2 цикла for, первый из них, в данной случае, идет с самого начала и до N-1 (1 первого до предпоследнего элемента).
Далее вложенный for, где используется уже другой счетчик j. Он изменяется от текущего i-того, увеличенного на 1 и до конца. И далее мы проверяем 2 элемента массива в условии и, если все нас устраивает, то производим обмен переменными. В последнем цикле мы выводим отсортированный массив.
Заметим, что первоначальный массив при сортировке не сохраняется. Кроме того хочу вам показать, как можно сделать так, чтобы первая половина массива была отсортирована по возрастанию, а вторая — по убыванию.
Program SortPopolam;
var
i, j, k: integer;
mas: array[1..10] of integer;
begin
randomize;
for i := 1 to 10 do mas[i] := random(101);
writeln('массив до сортировки');
for i := 1 to 10 do write(mas[ i], ' ');
for i := 1 to 4 do
for j := i + 1 to 5 do
if mas[ i] > mas[ j] then
begin
k := mas[ i];
mas[i] := mas[j];
mas[j] := k;
end;
for i := 5 to 9 do
for j := i + 1 to 10 do
if mas[ i] < mas[ j] then
begin
k := mas[ i];
mas[ i] := mas[j];
mas[j] := k;
end;
writeln;
writeln('массив после сортировки');
for i := 1 to 10 do write(mas[ i], ' ');
end.
Надеюсь, что вы заметили, что здесь 2 алгоритма сортировки, первый идет с первого элемента по 5, а второй — с 5 по 10. Они отличаются только условиями, в этом и заключается этот нехитрый способ.
Как видите, здесь нет ничего особенного. И еще один пример по сортировке выбором. Пусть нудно отсортировать массив таким образом, чтобы числа в нем располагались в порядке возрастания своих последних разрядов. Допустим, если у нас массив 17 23 18 70, то после сортировки он должен выглядеть так: 70 23 17 18. Вот код этой программы.
Program SortOstatok;
var
a: array[1..10] of Integer;
i, j, k: Integer;
begin
randomize;
for i := 1 to 10 do a[ i] := random(100);
writeln('массив до сортировки');
for i := 1 to 10 do write(a[ i], ' ');
for i := 1 to 9 do
for j := i + 1 to 10 do
if a[i] mod 10 > a[j] mod 10 then begin
k := a[i];
a[i] := a[j];
a[j] := k;
end;
writeln('массив после сортировки');
for i := 1 to 10 do write(a[i], ' ');
end.
Эта программа схожа с первой, их отличие лишь в том, что разное условие для перестановки элементов массива. В первой это «if mas[i] < mas[j] then «, а во втрой «if a[i] mod 10 > a[j] mod 10 then» То есть мы располагаем наши элементы в таком необычном порядке благодаря тому, что просто проверяем остатки их деления на 10, то есть и сравниваем их последние цифры.
Теперь подробнее о сортировке пузырьком. Его сущность заключается в том, что мы сравниваем соседние элементы парами : 1 и 2, 2и 3,3 и 4,4 т.д. И если наш элемент удовлетворяет условию сортировки, то мы его проталкиваем в конец массива, он как бы всплывает, прямо как «пузырек». От этого и название этого алгоритма.
Вот пример программы с этим алгоритмом.
Program SortPusirkom;
var
mas: array[1..20] of integer;
i, j, k: integer;
begin
randomize;
for i := 1 to 20 do mas[i] := random(100);
writeln('массив до сортировки');
for i := 1 to 20 do write(mas[ i], ' ');
for i := 1 to 19 do
for j := 1 to 20 - i do
if mas[j] > mas[j + 1] then begin
k := mas[j];
mas[j] := mas[j + 1];
mas[j + 1] := k;
end;
writeln;
writeln('Отсортированный массив: ');
for i := 1 to 20 do
write(mas[i], ' ');
end.
Ее алгоритм чем-то похож на сортировку выбором. Здесь так же 2 цикла for, но второй цикл идет с 1 до 20 — i.
Кроме того существует второй, не менее известный алгоритм сортировки «пузырьком» с флагом. Флаг — это переменная типа boolean. Из-за этого меняется структура алгоритма, но сущность остается прежней. Вот он.
program SotrSFlagom;
var
a: array[1..20] of integer;
i, j, L: integer;flag: boolean;
begin
randomize;
for i := 1 to 20 do
a[i] := random(100);
writeln('массив до сортировки');
for i := 1 to 20 do write(a[i], ' ');
i:=0;
repeat
i := i + 1;
flag:=false;
for j := 19 downto i do
if a[j] < a[j + 1] then begin
L := a[j]; a[j] := a[j + 1]; a[j + 1] := L;
flag := true;
end;
until not flag;
writeln;
writeln('массив после сортировки');
for i := 1 to 20 do write(a[i], ' ');
end.
Этот алгоритм наиболее сложный для запоминания, но уверяю Вас, что его и не нужно зазубривать, а понимать, что за чем идет. Здесь используется внешний цикл repeat … until not flag; Он существует до тех пор, пока флаг не окажется истинным, то есть flag := true; А это может произойти, если наше условие сортировки выполняется. И наш элемент тоже всплывает, как пузырек.
Итак, надеюсь, что вы поняли, в чем отличие этих 2 алгоритмов сортировок и теперь сможете отсортировать любой массив так, как Вам нужно.
Здравствуй, дорогой гость. В этой статье я расскажу об алгоритме сортировки массива методом пузырька.

Элементы массива, как пузырьки
Алгоритм пузырьковой сортировки — это довольно простой в реализации алгоритм для сортировки массивов. Можно встретить и другие названия: пузырьковая сортировка, Buble sort или сортировка простыми обменами — но все они будут обозночать один и тот же алгоритм. Назван так, потому что большее или меньшее значение «всплывает» (сдвигается) к краю массива после каждой итерации, это будет видно в примере.
Сложность этого алгоритма выражается формулой О(n^2) (n в степени 2). Алгоритм работает медленно с большими массивами, а поэтому малоэффективен и на практике используется редко, чаще всего в учебных целях. Для сортировки массивов на практике используют другие более быстрые алгоритмы, один из них — QuickSort(быстрая сортировка). Функция для быстрой сортировки включена во многие стандартные библиотеки языков программирования, например в языке C функция qsort() из стандартной библиотеки.
Алгоритм работает очень просто. Программа проходит по всем элементами массива по порядку. Каждый текущий элемент сравнивается с соседним и, если он меньше/больше(если сортируем по убыванию/возрастанию соответственно) меняется местами с соседним.
Пример работы алгоритма пузырьковой сортировки
Рассмотрим пример работы алгоритма с массивом, состоящим из четырех элементов.
Имеется массив [4, 5, 2, 6]. Сортировать его будем по убыванию.
N — количество элементов в массиве. i — номер прохода. Алгоритм будет делать проходы по массиву, всего N-1 проходов до N-i ячейки в каждой итерации для любого массива.
Первый проход циклом от первого до N-1 элемента, сравнение условием и перемена местами в случае удовлетворения условия — если левый элемент меньше правого.
4 5 2 6
Сравниваем 4 и 5, 4 меньше 5, а значит мы их меняем местами.
Следующий проход.
5 4 2 6
Сравниваем 4 и 2, 4 не меньше 2, а значит пропускаем и идем дальше.
5 4 2 6
Сравниваем 2 и 6, 4 меньше 6, а значит мы их меняем местами.
Теперь мы у нас массив [5, 4 ,6, 2]. Как видно, он еще не упорядочен до конца. После первого прохода в конец массива передвинулось самое маленькое значение, теперь нам нужно сделать еще проход до элемента N-2 (ведь идет 2-ая итерация).
Делаем проход, начиная с первого элемента.
5 4 6 2
Сравниваем 5 и 4, 5 не меньше 4, а значит пропускаем и идем дальше.
5 4 6 2
Сравниваем 6 и 4, 6 меньше 4, а значит мы их меняем местами. Мы достигли элемента N-2, завершаем итерацию.
Теперь мы имеем массив [5, 6, 4, 2]. 2 последних элемента упорядочены как нужно. Для завершения нужно выполнить еще один проход до N-3.
5 6 4 2
Сравниваем 5 и 6, 5 меньше 6, а значит мы их меняем местами. Мы достигли элемента N-3, завершаем итерацию.
В итоге на выходе мы получили массив упорядоченный по убыванию — [6, 5, 4, 2].
Реализация алгоритма на языке C++
Программа выполнит последовательно следующие действия:
- Установит размер массива, прося пользователя ввести числовое значение.
- Заполнит массив значениями, введенными пользователем для каждого элемента массива.
- Выведет исходный массив.
- Отсортирует массив по убыванию.
- Выведет отсортированный массив.
Теперь собственно код по каждому из пунктов.
1. Объявим переменную и инициализируем её значение данными, введенными пользователем.
/* Установим размер массива */ int n; // Кол-во элементов cout << "Количество элементов: "; cin >> n;
2. Объявим массив из количества элементов, которое ввел пользователь. А то есть объявим массив из n элементов. После запустим цикл и попросим пользователя ввести значение каждого элемента.
/* Заполним массив значениями */
int mass[n];
for(int i = 0; i < n; ++i)
{
cout << i+1 << "-ый элемент: ";
cin >> mass[i];
}
3. Выведем значения всех элементов массива, используя цикл.
/* Выведем исходный массив */
cout << "Исходный массив: ";
for(int i = 0; i < n; ++i)
{
cout << mass[i] << " "; // Вывод i-го элемента
}
cout << endl;
4. Отсортируем массив по убыванию. Здесь нам понадобятся 2 цикла. Первый будет выполнять количество итераций n-1, как в примере выше, который мы разобрали. Второй цикл будет осуществлять проходы по элементам массива (таких проходов n-i) и сравнивать соседние элементы. Элементы сравниваются условием, если i-ый элемент меньше правого соседа, то они меняются местами, таким образом самый маленький элемент будет в правой крайней части.
/* Отсортируем массив по убыванию */
for(int i = 1; i < n; ++i)
{
for(int r = 0; r < n-i; r++)
{
if(mass[r] < mass[r+1])
{
// Обмен местами
int temp = mass[r];
mass[r] = mass[r+1];
mass[r+1] = temp;
}
}
}
5. Выведем отсортированный массив, используя цикл, как в 3-ем действии.
/* Выведем отсортированный массив */
cout << "Отсортированный массив: ";
for(int i = 0; i < n; ++i)
{
cout << mass[i] << " ";
}
cout << endl;
Весь код программы
#include <iostream>
using namespace std;
int main()
{
/* Установим размер массива */
int n; // Кол-во элементов
cout << "Количество элементов: ";
cin >> n;
/* Заполним массив значениями */
int mass[n];
for(int i = 0; i < n; ++i)
{
cout << i+1 << "-ый элемент: ";
cin >> mass[i];
}
/* Выведем исходный массив */
cout << "Исходный массив: ";
for(int i = 0; i < n; ++i)
{
cout << mass[i] << " ";
}
cout << endl;
/* Отсортируем массив по убыванию */
for(int i = 1; i < n; ++i)
{
for(int r = 0; r < n-i; r++)
{
if(mass[r] < mass[r+1])
{
// Обмен местами
int temp = mass[r];
mass[r] = mass[r+1];
mass[r+1] = temp;
}
}
}
/* Выведем отсортированный массив */
cout << "Отсортированный массив: ";
for(int i = 0; i < n; ++i)
{
cout << mass[i] << " ";
}
cout << endl;
return 0;
}
Обратите внимание, что в коде программы использовались русские символы, если у вас их отображение некорректно, то почитайте статью про решение проблемы с отображением русских символов в консоли.
Написание программы завершено, теперь проверим результаты. А для этого введем в программу массив, сортировку которого мы произвели, рассматривая пример работы алгоритма немного выше в этой статье.
После ввода данных и выполнения программы мы получили результат.

Результат сортировки массива методом пузырька
Как видно на картинке, массив отсортирован по убыванию. Программа работает.
Как я отмечал ранее, алгоритм работает очень медленно с большим объемом данных, а потому непригоден для использования на практике, а пригоден лишь в обучающих и ознакомительных целях. Посмотрите на решения других задач по программированию.
Содержание
- Задача
- Алгоритм «Сортировка выбором»
- Реализация алгоритма сортировки выбором в C#
- Программа сортировки массива C# выбором
- Собираем массив целых чисел
- Выводим неотсортированный массив в консоль
- Сортируем массив, используя алгоритм «Сортировка выбором» и показываем результат
- Результат работы программы
- Исходный код программы
- Итого
уважаемые посетители блога, если Вам понравилась, то, пожалуйста, помогите автору с лечением. Подробности тут.
На данный момент у нас уже хватает знаний, чтобы попробовать написать простейшую программу в C#. Но, простейшая — не значит бесполезная. Наша программа будет сортировать массив C#. При написании различных программ нам часто приходится сталкиваться с таким понятием как сортировка. Например, необходимо отсортировать список людей по алфавиту или произвести сортировку оценок учащихся по возрастанию. И для того, чтобы максимально эффективно решить такую задачу мы должны знать не только сам язык программирования, но и алгоритмы сортировки — их сложность, как они реализуются на практике и так далее. Сегодня мы рассмотрим самый простой алгоритм сортировки массива C# — сортировку выбором.
Задача
Пользователь вводит с клавиатуры целые числа, разделенные запятой. Программа должна собрать из этих чисел массив и отсортировать его по возрастанию.
В консоль программа выведет неотсортированный и отсортированный массивы.
Алгоритм «Сортировка выбором»
Этот алгоритм является одним из самых простейших алгоритмов сортировки массива. Его смысл заключается в том, чтобы, чтобы идти по массиву, например слева направо, каждый раз искать минимальный элемент массива и обменивать его с первым элементом неотсортированной части массива. Шаги алгоритма можно представить следующим образом:
- Находим минимальный элемент в массиве.
- Меняем местами минимальный и первый элемент местами.
- Ищем минимальный элемент в неотсортированной части массива, т.е., начиная уже со второго элемента массива.
- Меняем местами второй элемент массива и найденный минимальный.
- Ищем минимальный элемент в массиве, начиная с третьего, меняем местами третий и минимальный элементы.
- Продолжаем алгоритм до тех пор пока не дойдем то конца массива.
Вначале приведу реализацию алгоритма сортировки массивы выбором в C#. Код постарался максимально пояснить с помощью комментариев:
//intArray - это массив целых чисел
int indx; //переменная для хранения индекса минимального элемента массива
for (int i = 0; i < intArray.Length; i++) //проходим по массиву с начала и до конца
{
indx = i; //считаем, что минимальный элемент имеет текущий индекс
for (int j = i; j < intArray.Length; j++) //ищем минимальный элемент в неотсортированной части
{
if (intArray[j] < intArray[indx])
{
indx = j; //нашли в массиве число меньше, чем intArray[indx] - запоминаем его индекс в массиве
}
}
if (intArray[indx] == intArray[i]) //если минимальный элемент равен текущему значению - ничего не меняем
continue;
//меняем местами минимальный элемент и первый в неотсортированной части
int temp = intArray[i]; //временная переменная, чтобы не потерять значение intArray[i]
intArray[i] = intArray[indx];
intArray[indx] = temp;
}
Проверить работу алгоритма нам поможет небольшая консольная программка в C#, которую мы сейчас и напишем.
Программа сортировки массива C# выбором
По условию задачи пользователь может ввести любое количество целых чисел, разделенных запятыми. Нам необходимо прочитать эти числа, составить из полученных чисел массив, вывести его в консоль, отсортировать массив приведенным выше алгоритмом и вернуть в консоль отсортированный массив. Все эти шаги реализуются достаточно просто.
Собираем массив целых чисел
Console.WriteLine("Введите через запятую целые числа и нажмите Enter");
string[] nums = Console.ReadLine().Split(new char[] { ',' });
int[] intArray = new int[nums.Length];
for (int i = 0; i < nums.Length; i++)
{
intArray[i] = int.Parse(nums[i]);
}
В первой строке мы предлагаем пользователю ввести целые числа. После того, как пользователь введет любое количество чисел и нажмет Enter, программа переходит к следующему шагу — разделит полученную от пользователя строку на массив строк:
string[] nums = Console.ReadLine().Split(new char[] { ',' });
здесь nums — это массив строк.
Метод Console.ReadLine() возвращает нам последнюю строку из консоли.
Метод Split(new char[] { ',' })— это метод для типа string, который возвращает массив строк, созданный из исходной строки. В качестве аргумента этот метод принимает массив символов по которым будет делиться строка. Так как у нас, по условиям задачи, разделитель всего один — запятая, то и массив разделителей в методе Split() содержит всего один элемент.
На следующем шаге мы создаем массив целых чисел размер которого совпадает с размером массива nums.
int[] intArray = new int[nums.Length]
Далее, в цикле for мы наполняем наш созданный массив числами, используя метод Parse() у типа данных int, который возвращает нам целое число из строки.
for (int i = 0; i < nums.Length; i++)
{
intArray[i] = int.Parse(nums[i]);
}
Выводим неотсортированный массив в консоль
Вывести неотсортированный массив пользователю проще простого, если воспользоваться циклом foreach:
Console.WriteLine("Неотсортированный массив:");
foreach (int value in intArray)
{
Console.Write($"{value} ");
}
Сортируем массив, используя алгоритм «Сортировка выбором» и показываем результат
Для этого используем реализацию алгоритма, которая представленная выше. Чтобы вывести отсортированный массив пользователю снова используем цикл foreach.
Console.WriteLine("rnОтсортированный массив:");
foreach (int value in intArray)
{
Console.Write($"{value} ");
}
так как для неосортированного массива мы использовали метод Console.Write(), которые не производит переход на следующую строку, то здесь, в методе Console.WriteLine() мы использовали управляющие символы C# /r/n для перехода на новую строку и возврат каретки в начало строки.
Результат работы программы
В результате работы программы можно получить, например, вот такой вывод в консоли:
Введите через запятую целые числа и нажмите Enter
0,100,999,345,-100,1,0,9,7,6,5,4,3,2,1,67,88
Неотсортированный массив: 0 100 999 345 -100 1 0 9 7 6 5 4 3 2 1 67 88
Отсортированный массив: -100 0 0 1 1 2 3 4 5 6 7 9 67 88 100 345 999
Как видите, алгоритм успешно справляется с сортировкой массива и все заданные числа были отсортированы от меньшего к большему.
Исходный код программы
Ниже приведен весь исходный код программы C# для сортировки массива:
using System;
namespace SelectSort
{
class Program
{
static void Main(string[] args)
{
Console.WriteLine("Введите через запятую целые числа и нажмите Enter");
string[] nums = Console.ReadLine().Split(new char[] { ',' });
int[] intArray = new int[nums.Length];
for (int i = 0; i < nums.Length; i++)
{
intArray[i] = int.Parse(nums[i]);
}
Console.WriteLine("Неотсортированный массив:");
foreach (int value in intArray)
{
Console.Write($"{value} ");
}
int indx; //переменная для хранения индекса минимального элемента массива
for (int i = 0; i < intArray.Length; i++) //проходим по массиву с начала и до конца
{
indx = i; //считаем, что минимальный элемент имеет текущий индекс
for (int j = i; j < intArray.Length; j++) //ищем минимальный элемент в неотсортированной части
{
if (intArray[j] < intArray[indx])
{
indx = j; //нашли в массиве число меньше, чем intArray[indx] - запоминаем его индекс в массиве
}
}
if (intArray[indx] == intArray[i]) //если минимальный элемент равен текущему значению - ничего не меняем
continue;
//меняем местами минимальный элемент и первый в неотсортированной части
int temp = intArray[i]; //временная переменная, чтобы не потерять значение intArray[i]
intArray[i] = intArray[indx];
intArray[indx] = temp;
}
Console.WriteLine("rnОтсортированный массив:");
foreach (int value in intArray)
{
Console.Write($"{value} ");
}
}
}
}
Также, Вы можете загрузить исходный код приложения из нашего репозитория на Github.
Итого
Сегодня мы написали своё первое полноценное приложение на C# для сортировки массива. Как видите, для этого нам пригодилось всё, что мы изучали ранее — переменные, работа с массивами, литералы, циклы и так далее. Постепенно, наши программы будут «обрастать» новыми возможностями, станут более устойчивыми к различным ситуациям (например, сегодня я даже не пытался проверить то, что ввел пользователь, хотя такую проверку необходимо проводить). Но всё это будет делаться постепенно, по мере изучения возможностей C#.
уважаемые посетители блога, если Вам понравилась, то, пожалуйста, помогите автору с лечением. Подробности тут.
