Производящие
функции и рекуррентные соотношения
Теория производящих
функций тесно связана с рекуррентными
соотношениями. Обратимся к делению
многочленов. Пусть функции f(x)
иg(x)
разложены в степенные ряды,
–
два многочлена, причем
.
Мы будем, кроме того, предполагать, что,
то есть, что алгебраическая дробьправильна (в противном случае мы всегда
можем выделить из нее целую часть). Мы
знаем, что если
(2.0)
то
Раскроем
в правой части этого равенства скобки
и сравним коэффициенты при одинаковых
степенях
слева и справа. Сначала мы получим
соотношений такого вида:

(если
,
то мы считаем, что).
А дальше все соотношения имеют один и
тот же вид:
(2.2)
(ведь
в
нет членов, содержащих
и т.д.). Таким образом, коэффициенты
ряда (2. 0) удовлетворяют рекуррентному
соотношению (2.2). Коэффициенты этого
соотношения зависят лишь от знаменателя
дроби. Числитель же дроби нужен для
нахождения первых членоврекуррентной последовательности.
Обратно,
если дано рекуррентное соотношение
(2.2) и заданы члены
,
то мы сначала по формулам (2.1) вычислим
значения.
А тогда производящей функцией для
последовательности чиселявляется алгебраическая дробь
(2.3)
На
первый взгляд кажется, что мы мало
выиграли при замене рекуррентного
соотношения производящей функции. Ведь
все равно придется делить числитель на
знаменатель, а это приведет к тому же
самому рекуррентному соотношению (2.2).
Но дело в том, что над дробью (2.3) можно
выполнять некоторые алгебраические
преобразования, а это облегчит отыскание
чисел
.
Об
едином нелинейном рекуррентном
соотношении
При
решении задачи о разбиении последовательности
мы пришли к рекуррентному соотношению
(2.4)
где
.
Покажем, как решить соотношение (2.4). Для
этого составим производящую функцию.
(2.5)
Положим
(2.6)
и
возведем
в квадрат. Мы получим, что
Но
по рекуррентному соотношению (2.4),
Значит,
Полученный
ряд есть не что иное, как
;
поскольку,
он равен
Для
функции
получилось квадратное уравнение (2.7).
Решая его, находим, что
Мы
выбрали перед корнем знак минус, так
как в противном случае при
мы имели бы
,
а из разложения (2.6) видно, что.
Начальным
моментом k-го
порядка случайной величины Xназывается математическое ожиданиеk-й степени случайной
величины [8] :
.
(2.7)
Центральным
моментом k-го
порядка случайной величины Xназывается математическое ожиданиеk-й степени отклонения случайной величины
от своего математического ожидания:
.
(2.8)
Справедливы
следующие выражения для центральных
моментов:
;
(2.9)
;
(2.10)
;
(2.11)
;
(2.12)
.
(2.13)
Производящей
функцией случайной величины Xназывается функция от параметра (вообще
говоря, комплексного), равная
.
(2.14)
Как
и раньше, если известно, о какой случайной
величине идёт речь, то индекс, обозначающий
эту случайную величину, опускается:
.
Начальные
моменты случайной величины Хвыражаются через производные её
производящей функции:
для всех k
= 0, 1, 2 K:, (2.15)
где
–k-я производная
функции.
Если
(где
),
то производящая функция переходит вхарактеристическую функцию, широко
используемую в фундаментальной теории
вероятностей и теории меры.
Производящая
функция случайной величины обладает
следующими свойствами:
;
(2.16)
(2.17)
(здесь
X, Y
– независимые случайные величины,c-неслучайная постоянная).
В
качестве показателя центра группирования
значений случайной величины, наряду с
математическим ожиданием, используются
также медиана и мода.
Медианой
абсолютно непрерывной случайной величиныХназывается такое число , что
.
(2.18)
Медиана
дискретной случайной величиныX– это любое число, которое находится на
отрезке,
определяемом из условий
,
(2.19)
и
называемом медианным. В качестве
медианыобычно используют значение, получаемое
линейной аппроксимацией:
(2.20)
Модой
абсолютно непрерывной случайной величины
Xназывается точка
локального максимума плотности
распределения:
.
(2.21)
Модой
дискретной случайной величины Xназывается значение этой случайной
величины, соответствующее наибольшей
вероятности:
,
такое, что
.
(2.22)
Распределения,
имеющие одну моду, называются
одномодальными.
Коэффициент
асимметриислучайной величины Xхарактеризует скошенность кривой
распределения этой случайной величины
относительно её математического ожидания
и вычисляется по формуле
.
(2.23)
Обычно
.
Для симметричных распределений
, если левая ветвь кривой распределения
длиннее правой, то,
если же левая ветвь кривой распределения
короче правой, то.
Эксцесс
случайной величины Xхарактеризует островершинность кривой
распределения этой случайной величины
по сравнению с кривой нормального
распределения и вычисляется по формуле
.
(2.24)
Обычно
.
Для нормального распределения;
если кривая распределения случайной
величиныXимеет менее
острую вершину, чем кривая нормального
распределения, то;
если кривая распределения случайной
величиныXимеет более
острую вершину, чем кривая нормального
распределения, то.
Левосторонней
критической границей (или квантилью)уровняслучайной величиныX
называется такое число,
что
,
(2.25)
т.
е.
.
Правосторонней
критической границейуровняaслучайной величиныX
называется такое число,
что
,
(2.26)
т.
е.
.
Левосторонняя
и правосторонняя критические границы
одного и того же уровня a
связаны между собой соотношением
.
(2.27)
Двусторонними
критическими границамиуровняaслучайной величиныXназываются такие числа,
что
,
(2.28)
т.
е.
.
Между
односторонними и двусторонними
критическими границамислучайной
величины Xсуществуют
следующие соотношения
.
(2.29)
Для
стандартного нормального распределения
двусторонние критические границы уровняaсимметричны и имеют
специальные обозначения,
при этом
.
(2.30)
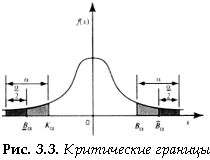
На
рис. 3.3 указаны левосторонняя, правосторонняя
и двусторонние критические границы для
некоторого распределения.
Рис.
3.3. Критические границы
Тема
9. Теория
автоматов. Основные понятия теории
конечных автоматов. Способы задания
абстрактных автоматов: таблица переходов,
граф переходов, матрица переходов.
Автоматы Мили и Мура. Частичный автомат.
Основные
понятия теории конечных автоматов.
Дискретный
автомат можно охарактеризовать как
устройство, имеющее входной и выходной
каналы и находящееся в каждый из
дискретных моментов времени, называемых
тактовыми моментами, в одном из состояний.
В том случае, когда устройство принимает
состояния из конечного множества,
автомат называется конечным. При этом,
как правило, входные и выходные переменные
принимают значения из конечных множеств.
В общем случае выходные переменные
могут зависеть от значений входных
переменных не только в данный момент,
но от их предыдущих значений. Иначе
говоря, значение выходных переменных
определяется последовательностью
значений входных переменных, в связи с
чем схемы с такими свойствами называют
последовательными. Особое внимание
заслуживают конечные автоматы, входные
и выходные переменные которых представляют
собой двоичные коды, а зависимость между
ними выражается булевыми функциями. Их
значение обусловлено тем, что любая
информация может быть представлена в
двоичных кодах (двоично-десятичные коды
чисел, телетайпный код в технике связи,
двоичное представление информации при
обработке ее в электронных вычислительных
машинах, устройствах числового
программного управления и т.п.). В то же
время при технической реализации
автоматов используются преимущественно
двоичные элементы и двузначная логика.
В реальных условиях сигналы представляются
непрерывными функциями времени, поэтому
для их надежного различения требуется,
чтобы новые значения на входах автоматов
появлялись после окончания переходных
процессов, связанных с предыдущими
значениями. При рассмотрении логической
структуры автоматов обычно отвлекаются
от существа этих процессов и считают,
что переменные изменяются не непрерывно,
а мгновенно в некоторые моменты времени,
называемые тактами. Интервалы между
тактами могут быть различными, но без
потери общности их можно считать равными
Δt. Предполагается, что тактовые моменты
th+1 =th+Δt определяются синхронизирующими
сигналами. Таким образом, вводиться
понятие дискретного автоматного времени
th (h= 1,2,3…), причем переменные зависят не
от физического времени, а от номера
такта, т.е. вместо непрерывной функции
x(t) рассматриваются ее дискретные
значения x(h). Кроме входных и выходных
переменных, в автомате можно выделить
некоторую совокупность промежуточных
переменных, которые связаны с внутренней
структурой автомата и характеризуют
его внутренние состояния. Отсюда ясно,
что последовательные автоматы должны
обладать способностью сохранять
предыдущее состояние до следующего
такта, в связи с чем их называют также
автоматами с памятью, или последовательными
машинами. В качестве памяти могут
использоваться элементы задержки, на
выходах которых повторяются входные
воздействия со сдвигом во времени на
интервал между тактами Δt. Широко
применяются и различные запоминающие
элементы, например, электромеханические
устройства, способные сохранять состояние
на выходах до тех пор, пока оно не
изменится в результате воздействия на
их входах [З].
Автоматы
Мили и Мура.
По
способу формирования функций выходов
выделяют автоматы Мили и Мура. В автомате
Мили функция выходов λопределяет значение выходного символа
по классической схеме абстрактного
автомата. Математическая модель автомата
Мили и схема рекуррентных соотношений
не отличаются от математической модели
и схемы рекуррентных соотношений
абстрактного автомата. Таким образом,
можно дать следующее определение:
Конечным
детерминированным автоматом типа Милиназывается совокупность пяти объектов
,
где
S,XиY— конечные непустые множества, аδиλ— отображения вида:
и
со
связью элементов множеств S,XиYв
абстрактном времениT=
{0, 1, 2, …} уравнениями:
,
(Отображения
δиλполучили
названия, соответственно функции
переходов и функции выходов автоматаA).
Особенностью
автомата Мили является то, что функция
выходов является двухаргументной и
символ в выходном канале y(t)
обнаруживается только при наличии
символа во входном каналеx(t).
Функциональная схема не отличается от
схемы абстрактного автомата.
Зависимость
выходного сигнала только от состояния
представлена в автоматах типа Мура. В
автомате Мура функция выходов определяет
значение выходного символа только по
одному аргументу — состоянию автомата.
Эту функцию называют также функцией
меток, так как она каждому состоянию
автомата ставит метку на выходе.
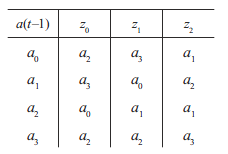
В
таблице 3, 4 приведены примеры соответственно
функций переходов и выходов автомата
Мили.
Таблица
3 Таблица 4
Граф
переходов указан на рисунке 3.
Рисунок 3 – Граф
переходов автомата Мили.
Конечным
детерминированным автоматом типа Мураназывается совокупность пяти объектов:
,
где
S,X,Yиδ— соответствуют
определению автомата типа Мили, аμявляется отображением вида:μ:S→Y, с
зависимостью состояний и выходных
сигналов во времени уравнением:
Особенностью
автомата Мура является то, что символ
y(t) в выходном
канале существует все время пока автомат
находится в состоянииs(t).
Интересно
выделить особые классы автоматов,
математические модели которых опираются
только на два носителя алгебры.
Пусть
|X| = 1. Тогда математическая
модель и система рекуррентных соотношений
имеют вид:
где
SиY—
конечные непустые множества состояний
и входных сигналов, а
и
— отображения выше указанного вида.
Особенностью функционирования такого
автомата является генерация
последовательности символов выходного
слова только в зависимости от
последовательности состояний автомата.
Такой автомат получил название автономного
конечного детерминированного автомата.
Для
каждых начального состояния
и
натурального числаtавтоматBопределяет две
последовательности:
,
Функциональная
схема автомата Мура
В
таблице 5, 6 приведены примеры соответственно
функций переходов и выходов автомата
Мура.
Таблица 5
Таблица 6
Граф
переходов указан на рисунке 4.
Рисунок 3 – Граф
переходов автомата Мура.
Частичный
автомат.
Частичным
автоматом называется абстрактный
автомат, у которого функция переходов
или функция выходов ( обычная или
сдвинутая), или обе эти функции, определены
не для всех пар значений своих аргументов
а их.
Беря
соответствующий частичный автомат, где
эти переходы и выходы не определены
вовсе, мы тем самым оставляем за собой
право определить их впоследствии так,
как это нам будет удобно.
Для
частичных автоматов употребляются те
же способы задания, что и для вполне
определенных автоматов. В тех местах
таблицы переходов или таблицы выходов
( обычной или сдвинутой), в которых
изображаемые ими функции не определены,
мы будем ставить черточки. Граф частичного
автомата чможет иметь вершины, из которых
не выходят стрелки, обозначенные теми
или иными входными сигналами.
Для
частичных автоматов Мура естественно
считать запрещенными все состояния,
для которых сдвинутая функция выходов
не определена. Легко понять, что перейти
из начального состояния в запрещенное
под воздействием непустого слова автомат
Мура может лишь в том случае, когда это
слово – запрещенное.
Для
частичных автоматов Мили и Мура в
рассмотренных таблицах на месте
неопределенных состояний и выходных
сигналов ставится прочерк.
В
случае частичных автоматов помимо
эквивалентности и изоморфизма автоматов
часто используются понятия эквивалентного
и изоморфного продолжения автоматов.
Сущность
задачи минимизации частичных автоматов
состоит в следующем: дан частичный
автомат ( Мура или Мили) А, индуцирующий
частичное автоматное отображение ф,
определенное на некотором множестве М
слов входного алфавита. Требуется
построить частичный автомат ( Мура или
соответственно Мили) В, который индуцирует
частичное автоматное отображение,
совпадающее на множестве М с отображением
ф, и имеет наименьшее число внутренних
состояний среди всех автоматов ( Мура
или Мили), удовлетворяющих этому условию.
В
отличие от частичных автоматов,
рассматривавшиеся ранее автоматы
называются вполне определенными.
Для
случая же частичных автоматов свойство
транзитивности для отношения / –
совместимости, вообще говоря, не
выполняется.
В
случае же частичных автоматов дело
обстоит гораздо сложнее: с построением
ос-классов и нормальной формы процесс
минимизации, вообще говоря, не
заканчивается.
Если
функцию переходов произвольного
частичного автомата Мили А рассматривать
не заданной во всех точках, в которых
не задана его функция выходов то возникший
таким образом новый частичный автомат
Мили В будет, индуцировать то же самое
частичное отображение, что и автомат
А.
Не
изменяя индуцируемого частичным
автоматом Мура частичного отображения,
можно считать функцию переходов этого
автомата неопределенной всякий раз,
когда она принимает запрещенное значение.
Подобно
вполне определенным автоматам частичные
автоматы также делятся на автоматы
первого и второго рода, автоматы Мили
и автоматы Мура. Изоморфизм частичных
автоматов предусматривает, чтобы
соответствующее изоморфное отображение
переводило множества значений, в которых
не определены функции переходов или
выходов ( обычная или сдвинутая) одного
автомата, в множества значений, в которых
не определены соответствующие функции
другого автомата.
Отметим,
что синтез частичных автоматов не
отличается от изложенного выше. При тех
комбинациях входных сигналов и внутренних
состояний частичного автомата, которые
не входят в кодированные таблицы
переходов и выходов, значения функций
возбуждения можно выбирать произвольно.
Рассмотрим
отображение, индуцируемое частичным
автоматом. Будем подавать на вход
автомата, установленного предварительно
в начальное состояние, различные слова
входного алфавита. В этом случае говорят,
что входное слово р является запрещенным
для данного частичного автомата.
Совокупность всех запрещенных слов
образует область запрета данного
автомата. Слова, не являющиеся запрещенными,
называются допустимыми, а их совокупность
– множеством допустимых слов автомата.
Наряду
с полностью определенными рассматривает
частичные автоматы, у которых область
определения функций б ( a, z) или К ( a, z)
отлична от Ay Z. Моменты переходов автомата
из состояния в состояние могут разделяться
равными или неравными промежутками.
Наконец,
совершаем переход к частичному автомату.
Из
определения допустимых слов ( для любого
данного частичного автомата А) вытекает,
что в случае, когда входное словоpxtix –
L… Обычно к числу начальных отрезков
слова р причисляют само это слово, а
также пустое слово, не содержащее ни
одной буквы. Сделанное замечание
позволяет сформулировать следующее
предложение.
На
практике обычно пользуются следующим
приемом минимизации частичных автоматов:
мысленно заполняя прочеркнутые места
в таблицах переходов и выходов данного
частичного автомата А, объединяют
состояния в i-классы и минимизируют по
тем же самым правилам, что и в случае
обычных ( всюду определенных) автоматов.
Все или некоторые из возникающих
вариантов объединения состояний в
классы проверяются, и из полученных
канонических минимизаций выбирают ту,
которая имеет наименьшее число состояний.
Несколько
сложнее обстоит дело с понятием
эквивалентности частичных автоматов.
Для того чтобы определить это понятие,
необходимо прежде всего установить,
что следует понимать под отображением,
индуцируемым данным частичным автоматом
А. Для этой цели, как и прежде, мы будем
подавать на вход частичного автомата
( приведенного предварительно в начальное
состояние) различные входные слова. А,
мы можем столкнуться с положением, когда
соответствующий ей выходной сигнал не
определен.
Еще
одно замечание касается способов
практического использования понятия
частичного автомата. Обычно все реально
существующие автоматы являются вполне
определенными. Однако они могут быть
поставлены в такие условия, что некоторые
слова их входного алфавита никогда не
подаются на их вход.
Уже
на этом примере видно, что для частичных
автоматов / – классы, вообще говоря,
пересекаются между собой. То же самое
имеет место и для оо-классов.
Сущность
задачи минимизации частичных автоматов
состоит в следующем: дан частичный
автомат ( Мура или Мили) А, индуцирующий
частичное автоматное отображение ф,
определенное на некотором множестве М
слов входного алфавита. Требуется
построить частичный автомат ( Мура или
соответственно Мили) В, который индуцирует
частичное автоматное отображение,
совпадающее на множестве М с отображением
ф, и имеет наименьшее число внутренних
состояний среди всех автоматов ( Мура
или Мили), удовлетворяющих этому условию.
В
структурной теории принято несколько
отличное от абстрактной теории понимание
частичных автоматов.
Отображение
ф множества входных слов в множество
выходных слов, индуцируемое частичным
автоматом А, является, таким образом,
частичным отображением, областью
определения которого служит множество
всех допустимых слов данного автомата.
Образ ф ( р) любого допустимого слова
при этом отображении определяется точно
так же, как и для вполне определенных
автоматов.
Определим
понятие связного автомата, которое
играет важную роль при изучении частичных
автоматов.
Рассмотрим
теперь некоторые соотношения между
областями определений функций переходов
и выходов в частичном автомате.
Предположим, что мы имеем частичный
автомат Мили А, и пусть для некоторого
состояния ai и входного сигнала х его
функция выходов не определена. Это
означает, очевидно, что переход автомата
из состояния а ( в новое состояние под
воздействием входного сигнала Xj
реализуется лишь при подаче на вход
автомата запрещенных входных слов.
Если
отображение ф множества слов в алфавите
Ж в множество слов в алфавите 3) задается
частичным автоматом, то оно будет,
разумеется, лишь частичным отображением,
определенным не на всех словах. Однако
для него по-прежнему будут выполняться
оба условия автоматности при дополнительном
предположении, что ф ( /) существует.
Запрещенными
здесь и далее будем называть все слова
во входном алфавите, которые при подаче
их на вход данного частичного автомата
приведут хотя бы для одного составляющего
их входного сигнала к не определенному
в автомате выходному сигналу.
На
практике обычно пользуются следующим
приемом минимизации частичных автоматов:
мысленно заполняя прочеркнутые места
в таблицах переходов и выходов данного
частичного автомата А, объединяют
состояния в i-классы и минимизируют по
тем же самым правилам, что и в случае
обычных ( всюду определенных) автоматов.
Все или некоторые из возникающих
вариантов объединения состояний в
классы проверяются, и из полученных
канонических минимизаций выбирают ту,
которая имеет наименьшее число состояний.
Возникающий
здесь параллелизм имеет, однако, место
не при минимизации обычных всюду
определенных автоматов, а при переходе
к более общей задаче минимизации
частичных автоматов.
Соответствующий
автомат полностью определен, если фг (
а, q) 1 при любых а е А и q Q, в противном
случае имеем частичный автомат. Легко
заметить, что область определения
частичного автомата всегда представляет
собой конечно перечислимое множество.
Если
функцию переходов произвольного
частичного автомата Мили А рассматривать
не заданной во всех точках, в которых
не задана его функция выходов то возникший
таким образом новый частичный автомат
Мили В будет, индуцировать то же самое
частичное отображение, что и автомат
А.
Нетрудно
видеть, что в силу определения событий,
представленных в автомате, введенное
таким образом частичное отображение ф
как раз и будет тем частичным отображением,
которое индуцируется заданным частичным
автоматом А.
Если
операция умножения применяется к вполне
определенным автоматам, то в результате
получаем вполне определенный автомат,
если же хотя бы один из исходных автоматов
частичный, то в результате получим
частичный автомат.
Основные
виды соединений автоматов.
Параллельное
соединение
Параллельное
соединение двух автоматов иллюстрируется
на следующем рисунке:
Здесь
Результирующим
автоматом параллельного соединения
двух автоматов S1 иS2
назовем автомат
,
у которого:
Последовательное
соединение
Результирующим
автоматом последовательного соединения
двух автоматов S1 иS2
назовем автомат
,
у которого:
Соединение
с обратной связью
Пример.
Соединение
с выходной функцией
Пример.
Соединение
в сеть
Определение:
Компонентный
автомат ( полуавтомат Мура ) это автомат
Мура, в котором обеспечена полнота
выходов, означающая, что каждому состоянию
поставлен в соответствие свой выходной
сигнал, отличный от выходных сигналов
других состояний.
Определение:
Сетью
автоматов назовем шестерку
,
где
:
Z- множество входов автомата-сети,
W- множество выходов автомата-сети,
Si- компонентный автоматcети
с алфавитом входовZi,
образующийся из алфавита внутренних
входовZi’ и алфавита
внешних входовZi”, с
алфавитом выходовAi,
,
n
– количество компонентых автоматов.
Эквивалентная
схема:
Перед
вами схемы трех автоматов.
Блокировочное
соединение автоматов.
Блокировочное
Соединение или блокировка семейства Nконечных автоматов
,
определяется заданием множестваNпредикатов блокировки переходов этих
автоматов:
,
где
– множество состояний автомата
.
Предикаты блокировки
,
выражают взаимные ограничения на
переходы автоматов, связанных блокировочным
соединением.
Если
,
где
,
то автомат
«заблокирован»
набором состояний
остальных автоматов: все переходы
автомата
«запрещены», любой входной сигнал
автомата
заменяется тождественным входным
сигналом.
Если
,
то переходы автомата
не зависят от состояний других автоматов:
все переходы автомата
«разрешены», автомат
ведет себя в соответствии с собственными
функциями переходов и выходов.
Разрешающие
и запрещающие состояния.
Если
N=2, то блокировочное
соединение
автоматов
и
определяется парой предикатов блокировки
и
.
Обозначим:
– множество всех
таких
,
что;
– множество всех
таких
,
что;
– множество всех
таких
,
что;
– множество всех
таких
,
что;
Элементы
множеств
и
называются разрешающими состояниями
автоматов
и
соответственно, элементы множеств
и
запрещающими состояниями автоматов
и
.
Если
один из двух автоматов
или
находится в разрешающем состоянии, то
другой работает как бы «сам по себе»,
как предписывают его собственные функции
переходов и выходов. Если же один автомат
находится в запрещающем состоянии, то
работа другого автомата полностью
блокируется: каждый его входной сигнал
заменяется тождественным.
Односторонние
и взаимные блокировки.
Если
одно из множеств запрещающих состояний
или
пусто, то блокировка
называется односторонней. В противном
случае – двусторонней или взаимной.
При односторонней блокировке работа
только одного из соединяемых автоматов
зависит от состояния другого.
Односторонняя
блокировка есть частный случай каскадного
соединения автоматов. Взаимная блокировка
не является частным случаем каскадного
соединения.
Односторонняя
блокировка автомата
автоматом
называется максимальной, если множество
содержит ровно один элемент. При
максимальной односторонней блокировке
автомат
работает (в соответствии со своими
функциями переходов и выходов) только
при одном состоянии автомата
.
Все остальные состояния автомата
являются блокирующими для автомата
.
Автомат
группы сильно связен точно тогда, когда
его группа транзитивна. Группа автомата
максимальной односторонней блокировки
перестановочного автомата
сильно связным перестановочным автоматом.
есть подстановочное
сплетение групп автоматов
и
.
Обратно, подстановочное сплетение
конечной группыи транзитивной конечной группы
изоморфно группе максимальной
односторонней блокировки перестановочного
автомата
,
группа которого есть,
перестановочным автоматом
,
группа которого есть.
Взаимная
блокировка автоматов
и
называется максимальной, если их
множества разрешающих состоянийи
содержат ровно по одному элементу.
Группа максимальной взаимной блокировки
двух сильно связных перестановочных
автоматов
и
,
число состояний которых равнои
соответственно, есть либо симметрическая
группа
,
либо знакопеременная группа
.
Второй случай имеет место тогда и только
тогда, когда группы обоих автоматов
и
содержат только четные подстановки.-
Производя́щая фу́нкция после́довательности — алгебраическое понятие, которое позволяет работать с разными комбинаторными объектами аналитическими методами. Они дают гибкий способ описывать соотношения в комбинаторике, а иногда помогают вывести явные формулы для числа комбинаторных объектов определённого типа.
Если дана последовательность 

,
который называется производящей функцией 
Близким понятием является экспоненциальная производящая функция последовательности 
,
у которого коэффициент перед 

Замечания[править | править код]
Зачастую производящая функция последовательности чисел является рядом Тейлора некоторой аналитической функции, что может использоваться для изучения свойств самой последовательности. Однако, в общем случае производящая функция не обязана быть аналитической. Например, оба ряда
и
имеют радиус сходимости ноль, то есть расходятся во всех точках, кроме нуля, а в нуле оба равны 1, то есть как функции они совпадают; тем не менее, как формальные ряды они различаются.
Свойства[править | править код]
- Производящая функция суммы (или разности) двух последовательностей равна сумме (или разности) соответствующих производящих функций.
Примеры использования[править | править код]
В комбинаторике[править | править код]
- Число композиций
Пусть 





При фиксированном m производящей функцией последовательности 
Поэтому число 


- Число связных графов
Обозначим через 


Заметим, что 
Рассмотрим экспоненциальные производящие функции этих последовательностей:
Оба ряда расходятся при 
из которого следует простое рекуррентное соотношение для 
В теории вероятностей[править | править код]
- Если
— положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
то её математическое ожидание может быть выражено через производящую функцию последовательности 
как значение первой производной в единице: ![M[X]=P'(1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce30edda666becbc81b6d7501b079d25533b2a91)

При подстановке 



![P'(1)=M[X]=infty](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c518b607b588af4022fd7a010fab539599ce3fa)
Эта производящая функция связана с определённой ранее функцией 


Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:
Чтобы получить дисперсию ![D[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa482bb7dcd759ae8e7e38fa47bea024feb50892)
![M[X]-M^{2}[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5feafe81b4c40e4badf9b77886a9391d159f629d)
.
В случае бесконечной дисперсии 
Вариации и обобщения[править | править код]
Производящая функция Дирихле[править | править код]
Производящая функция Дирихле последовательности 
.
- Производящей функцией Дирихле последовательности единиц 1,1,… является дзета-функция Римана:
История[править | править код]
Метод производящих функций был разработан Эйлером в 1750-х годах; классическим примером служит пентагональная теорема Эйлера.
Примечания[править | править код]
- ↑ Харари Ф., Палмер Э. Перечисление графов. — Мир, 1977.
Литература[править | править код]
- Бронштейн Е. М. Производящие функции // Соросовский Образовательный Журнал. — 2001. — Т. 7, № 2. — С. 103—108.
- Воронин С., Кулагин А. Метод производящих функций // Квант. — 1984. — № 5.
- Ландо С. К. Лекции по комбинаторике. — МЦНМО, 1994.
- Ландо С. К. Лекции о производящих функциях. — 3-е изд., испр.. — М.: МЦНМО, 2007. — 144 с. — ISBN 978-5-94057-042-4. (недоступная ссылка)
- Табачников С.Л., Фукс Д.Б. Математический дивертисмент. — МЦНМО, 2011. — ISBN 978-5-94057-731-7.
- Рыбников К.А. Введение в комбинаторный анализ. — МГУ, 1972.
- В. Феллер. Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons / Пер. с англ. Р. Л. Добрушина, А. А. Юшкевича, С. А. Молчанова; С предисловием А. Н. Колмогорова; Под ред. Е. Б. Дынкина. — 2-е изд. — М.: Мир, 1964. — С. 270—272.
- Herbert S. Wilf. Generatingfunctionology. — Academic Press, 1994. — ISBN 0-12-751956-4.
Ссылки[править | править код]
- Производящие функции
| Определение: |
| Производящая функция (англ. generating function) — это формальный степенной ряд вида , порождающий (производящий) последовательность . |
Метод производящих функций был разработан Эйлером в 1750-х годах.
Содержание
- 1 Применение
- 2 Примеры производящих функций
- 3 Примеры решений задач методом производящих функций
- 3.1 Решение рекуррентных соотношений
- 3.2 Расчет дисперсии геометрического распределения
- 3.3 Пример задачи на нахождение производящей функции
- 4 Приложения
- 4.1 Примеры простых производящих функций
- 5 См. также
- 6 Примечания
- 7 Источники информации
Применение
Производящая функция используется для:
- Компактной записи информации о последовательности.
- Нахождения зависимости для последовательности , заданной рекуррентным соотношением. Например, для чисел Фибоначчи.
- Нахождения рекуррентного соотношения для последовательности — вид производящей функции может помочь найти формулу.
- Исследования асимптотического поведения последовательности.
- Доказательства тождеств с последовательностями.
- Решения задачи подсчета объектов в комбинаторике. Например, в доказательстве пентагональной теоремы или в задаче нахождения количества расстановок ладей на доске .
- Вычисления бесконечных сумм.
Примеры производящих функций
Рассмотрим производящие функции для различных комбинаторных последовательностей:
- — производящая функция для разности количества разбиений числа в четное и нечетное число различных слагаемых. Например, коэффициент при равен , потому что существует два разбиения на четное число различных слагаемых и одно на нечетное (). Правильность этого легко осознать, если понять, что каждая скобка представляет какое-то слагаемое и мы можем его взять (второе слагаемое — ) или не взять (первое — ). Эта производящая функция используется в комбинаторном доказательстве пентагональной теоремы.
- — производящая функция для последовательности , где — число разбиений числа на слагаемые.
- — производящая функция для последовательности , где — число разбиений на различные слагаемые.
- — производящая функция для последовательности , где — число разбиений на нечётные слагаемые. С помощью метода производящих функций можно доказать, что производящие функции последовательностей равны, соответственно :
Примеры решений задач методом производящих функций
Решение рекуррентных соотношений
Существует целый класс последовательностей, задаваемых рекуррентным соотношением, например, — числа Фибоначчи или —
числа Каталана. Метод производящих функций позволяет получить выражение для через номер элемента в последовательности в замкнутом виде, то есть в таком виде, что выражение можно вычислить, предполагая, что достаточно мало.
Пусть последовательность удовлетворяет некоторому рекуррентному соотношению. Мы хотим получить выражение для (при ) в замкнутом виде. Алгоритм получения замкнутого выражения для чисел , удовлетворяющих рекуррентному соотношению, с помощью производящих функций состоит из 4 шагов:
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен , то есть количество предшествующих элементов, требуемых для вычисления элемента с номером , равно ):
- Домножить каждую строчку на в соответствующей степени и просуммировать строчки для всех .
- В полученном уравнении привести все суммы к замкнутому виду. Получить уравнение для производящей функции.
- Выразить в явном виде (решить уравнение, полученное на предыдущем шаге) и разложить производящую функцию в ряд по степеням .
Для демонстрации универсальности метода рассмотрим довольно произвольное рекуррентное соотношение:
Запишем производящую функцию для этой последовательности и преобразуем правую часть:
Для того, чтобы замкнуть последнюю сумму воспользуемся очень важным приемом, который используется при преобразовании производящих функций. Фактически мы имеем дело с последовательностью (в нашем случае последовательность ). Такая последовательность получается путём дифференцирования функции , производящей для , с последующим умножением результата на :
Тогда замкнем последнее слагаемое следующим образом:
Таким образом, наше последнее слагаемое примет вид:
Это уравнение для производящей функции. Из него выражаем :
Разложим знаменатель на множители и разобьём дробь на сумму простых дробей [1]:
Разложим первое слагаемое в ряд, используя расширенные биномиальные коэффициенты [2]:
Расчет дисперсии геометрического распределения
Метод производящих функций также используется для нахождения математического ожидания и дисперсии различных распределений в теории вероятностей. Например, в геометрическом распределении [3] для нахождения дисперсии нужно найти два мат. ожидания:
которые фактически являются производящими функциями последовательностей и :
.
Тогда:
Пример задачи на нахождение производящей функции
| Задача: |
| Рассмотрим множество путей на прямой, состоящих из шагов длины вправо и влево. Найдите производящую функцию для числа таких путей из шагов, начинающихся в и оканчивающихся в . |
Заметим, что для того, чтобы закончить путь в , необходимо совершить равное число шагов вправо и влево. Тогда задача сводится к тому, чтобы выбрать позиций для, например, шагов вправо из всего шагов. Тогда ответом будет сумма от нуля до бесконечности по всех . То есть:
Рассмотрим , где — число Каталана. Тогда, заметим что . Так как , то справедливо равенство:
Мы знаем, что производящая функция для чисел Каталана равна . Найдем .
Соответственно, ответом будет производящая функция вида:
| Задача: |
| Рассмотрим множество путей на прямой, состоящих из шагов длины вправо и влево. Найдите производящую функцию для числа таких путей из шагов, начинающихся и оканчивающихся в и не заходящих в отрицательную полупрямую. |
Заметим, что задача аналогична Правильной скобочной последовательности. Тогда производящей функцией для нашей задачи будет производящая функция для правильной скобочной последовательности, а именно:
Приложения
Примеры простых производящих функций
На последнем шаге приведения производящей функции к замкнутому виду требуется разложить полученные слагаемые в ряд. Для этого можно воспользоваться таблицей основных производящих функций [4].
Все суммы выполняются по переменной от до . Элементы последовательности нумеруются от .
| Последовательность | Производящая функция в виде ряда | Производящая функция в замкнутом виде |
| ( нулей в начале) | ||
| (повторяется через ) | ||
См. также
- Производящая функция Дирихле
Примечания
- ↑ О разложении рациональной функции в ряд
- ↑ Расширенные биномиальные коэффициенты
- ↑ Геометрическое распределение
- ↑ Таблица производящих функций
Источники информации
- Вайнштейн Ф., Разбиение чисел. Журнал “Квант” № 11, 1988 год
- Производящие функции
- Wikipedia — Generating function
- Нахождение количества разбиений числа на слагаемые. Пентагональная теорема Эйлера
- Graham, Knuth, and Patashnik: Concrete Mathematics
Обычная производящая функция — это функция вида
. Разберем на примере, как ее использовать.
Представим, что нам нужно найти, сколькими способами можно составить сумму
. При этом можно использовать по одному элементу из каждого из следующих двух наборов:
и
.
Рассмотрим два многочлена:
— это количество способов составить сумму
с помощью одного элемента из каждого набора.
Например, коэффициент
во втором многочлене равен
. Значит, существует один способ составить сумму из четырех, используя только один элемент из набора.
Теперь рассмотрим произведение многочленов:
В полиномиальном произведении
— количество способов составить сумму из
, когда берется по одному числу из каждого набора.
Разложим произведение:
Коэффициент
равен нулю при
, так как мы не можем получить сумму больше
. Если взять самые большие числа из каждого набора, то получится число
.
То же самое относится и к
. Берем самые маленькие числа из наборов и получаем
.
Когда
, коэффициент равен трем. Это означает, что есть три способа получить число
. Если c помощью формулы дистрибутивности мы развернем произведение полностью, то увидим, что три члена
получаются из произведений:
Производящая функция придает смысл коэффициенту
, но не придает смысла
. Она кодирует числа объектов с помощью формальных степенных рядов — многочленов с бесконечно большим количеством членов.
В разобранном примере можно было просто подсчитать количество способов получения числа 10 путем проверки. Но производящие функции полезны, когда многочлены выражены в более компактной форме — например, с помощью суммы геометрического ряда.
Содержание:
- Примеры с решением
- Биномиальный закон
- Геометрический закон
- Закон Пуассона
Мы видели, что дискретные случайные величины, рассмотренные в предыдущих параграфах, принимали только целые значения 
Определение. Производящей функцией дискретной целочисленной случайной величины 

Поскольку все коэффициенты этого ряда не превосходят 1, то сравнение с геометрической прогрессией показывает, что этот ряд сходится, по крайней мере, для значений 

Теорема 4.4. Производящая функция суммы независимых случайных величин 
Доказательство. Имеем по определению
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Примеры с решением
Пример 4.8.
Найти производящую функцию для биномиального закона.
Решение:
Если вспомнить, что формула Бернулли получается из разложения бинома, то легко сообразить, что
Можно также вспомнить, что случайная величина 



Возможно вам будут полезны данные страницы:
Пример 4.9.
Найти производящую функцию для геометрического закона распределения.
Решение:
Имеем 



Пример 4.10.
Найти производящую функцию для распределения Пуассона.
Решение:
Для пуассоновского закона с параметром 
Поэтому
причем все ряды сходятся для любых значений аргумента 
В качестве следствия получим теорему.
Теорема 4.5. Сумма независимых случайных величин, распределенных по закону Пуассона, распределена по тому же закону.
Доказательство. Пусть 

а производящая функция суммы 
Отсюда видно, что сумма будет распределена по закону Пуассона с параметром 
Зная производящую функцию дискретной случайной величины 
Теорема 4.6. Для дискретной случайной величины 

Доказательство. Дифференцируя почленно ряд (4.22) два раза, имеем
Подставляя 
откуда легко получить формулы (4.25), (4.26).
Комбинируя полученные выражения для производящих функций биномиального, геометрического и пуассоновского законов (4.23), (4.24), (4.25) с формулами (4.26), (4.27), теперь нетрудно найти основные числовые характеристики этих законов.
Биномиальный закон
Из выражения (4.23) для производящей функции получим
Подставляя 

Используя формулы (4.26), (4.27), получим
откуда
Геометрический закон
Дифференцируя два раза производящую функцию, имеем
Отсюда
откуда 
Закон Пуассона
Имеем
поэтому 
Лекции:
- Комбинаторные задачи: пример решения
- Классическое определение вероятности
- Геометрическое определение вероятности
- Элементы комбинаторики
- Действии над событиями
- Количество сочетаний
- Число сочетаний: формула, расчет
- Сочетания с повторениями
- Комбинаторика формулы: основные элементы
- Элементы комбинаторики: примеры решения







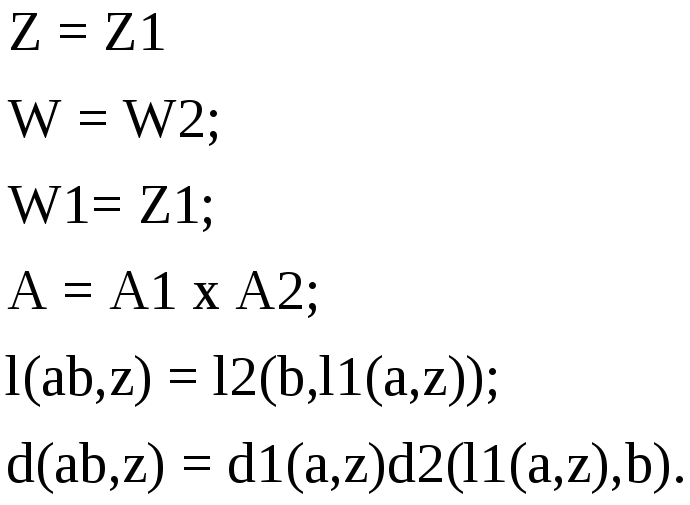
























![M[X]=P'(1)=Q(1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/6923a63f286d8200cf64cb7ea51857cf4b364278)
![M[X(X-1)]=sum {k(k-1)p_{k}}=P''(1)=2Q'(1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb5e1e74bcc3cd0ed5fb530c7da71ea6649ce6d)
![D[X]=P''(1)+P'(1)-P'^{2}(1)=2Q'(1)+Q(1)-Q^{2}(1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bfffe5693487c47103f352f67b836f9191eb585)



























