Как составить пропорцию чтобы узнать проценты

Один из способов решения задач на проценты – это использование пропорций. Как правильно составлять и решать подобные пропорции? Существует много практических задач, использующих понятие процентов. Часто для их решения используется понятие пропорции. В простых случаях можно решать вот таким образом: все мы знаем, что 50% это половина от числа, 25% – это его четвёртая часть, 20% – это пятая часть, 10% -это 10 часть , 5 % – 20 часть, 1% – 100 часть. Итак, найти один процент от 2000 это 2000/100=20. Найти 50 % от 60 это 60/2=30. А можно использовать универсальный способ – понятие пропорции. Предположим надо найти 13% от 180. Тогда составим: 180 – 100% Х – 13 % Мы должны числа писать под числами, проценты под процентами. Далее раскрывает пропорцию крест накрест. То с чем икс не в паре перемножаем, а с чем в паре по диагонали – делим. У нас получаем 180*13/100=23,4 система выбрала этот ответ лучшим Ксарф­акс [156K] 4 года назад  Пропорция с процентами составляется по следующему принципу: Исходное число (обозначим его буквой A) принимается за 100%. Первым членом пропорции будет цифровая запись числа A, ему будет соответствовать 100%. Остальными членами пропорции будут часть от этого числа (обозначим его буквой B) и проценты, соответствующие этой части (обозначим их буквой p). Вот как выглядет такая пропорция: A / B = 100% / p% Например: 1000 / 50 = 50% / 5%. Или можно записать по-другому: 1000 – 100%. 50 – 5%. При решении задач на проценты с помощью пропорции неизвестный её член (а здесь может быть 3 варианта) обычно обозначается за x. Решить пропорцию (то есть найти неизвестный член) можно благодаря её основному свойству: произведение крайних членов пропорции равно произведению средних (другими словами, нужно перемножить члены пропорции крест-накрест). Исходное число будет равно: A = 100% * B / p%. Часть от числа будет равна: B = A * p% / 100%. Проценты от числа можно найти по формуле: p% = 100% * B / A. Далее рассмотрим несколько простых примеров. Пример 1. Зарплата составляет 30000 рублей, а премия – 10% от зарплаты. Нужно определить размер премии. 30000 – 100%. x – 10%. Вспоминаем, что произведение крайних членов равно произведению средних: 30000 * 10 = 100 * x. x = (30000 * 10) / 100 = 3000. Значит, премия равна 3000 рублей. Пример 2. Сделано 20 выстрелов, 4 из них – мимо мишени. Нужно определить процент попадания. 20 – 100%. 4 – x%. Умножаем крест-накрест и приравниваем: 20 * x = 100* 4. x = (100 * 4) / 20 = 20. Здесь нужно учесть, что 20% – это процент выстрелов мимо мишени (так как рядом с неизвестным x были записаны именно промахи). Процент попадания в свою очередь равен 100% – 20% = 80%. Пример 3. За месяц было продано 30 ноутбуков, что составляет 20% от всего количества ноутбуков, имеющихся в продаже. Нужно найти, сколько всего ноутбуков было в магазине изначально. x – 100%. 30 – 20%. Умножаем крест-накрест: 20 * x = 100 * 30. x = (100 * 30) / 20 = 150. Таким образом, изначально в продаже было 150 ноутбуков. Zummy out off [226K] 3 года назад  Я как-то со школы запомнила принцип пропорции и способ ее решения называю «крест-накрест», не помню, кто это мне подсказал. Никогда не нахожу проценты по принципу умножения на сотую часть, мне не удобно, всегда использую свой «крест», единственное неудобство – нужно наглядно записывать это. Это не страшно – бумага всегда под рукой. Составляю пропорцию по условию, одно из значений неизвестное обозначаю Х. Затем решаю: перемножаю цифры, расположенные «на углах» слева и справа от Х, делю на число, расположенное на противоположном углу от Х. Пример: нужно найти 5% от числа 420. Пишу пропорцию. 420 – 100 % Х – 5 % Х = 5 • 420 : 100 = 21% Вот моя запись с крестом Ещё пример: сколько процентов от 200 составляет число 20. Составляю пропорцию. 200 – 100 % 20 – Х % Решение: X = 20 • 100 : 200 = 10% Алиса в Стран­е [363K] 3 года назад  Странно, конечно, для таких простых задач составлять какие-то дополнительные пропорции, они решаются в уме и очень быстро, но способ такой есть, давайте его рассмотрим, возможно, кому-то он пригодится. Допустим, нам надо найти сколько процентов составляет число 18 от числа 90, в принципе, мы и так сразу видим что 18 это одна пятая, то есть 20 процентов от числа 90, но давайте составим пропорцию, приняв за х искомое количество процентов, пропорция у нас будет такая: 90 – 100 % 18 – х %, откуда х = 100 х 18 / 90 = 20 процентов. Еще один пример для закрепления материала, найдем, сколько процентов составляет 24 от 250, пропорция: 24 – х 250 – 100 х = 24 х 100 /250 = 9,6 %. Go Green [537K] 3 года назад  Для определения процентного соотношения от числа нужно иметь представление об основных простых процентных соотношениях и о принципе вычисления любых из них. Для простоты давайте приведем примеры с числом 100. 1 % от ста – это одна сотая часть или один процент. 2% от ста – две сотых части от ста. 7% от ста – семь сотых части от ста и так далее. То есть сначала нам нужно узнать, сколько составляет один процент любого числа, разделив его на сто, а затем узнавать заданное процентное соотношение. Например, нам нужно найти, сколько будет равно 7 процентам от 200. Делим 200 на 100. Получится 2. Умножим 2 на 7, получится 14. Итого: 7% от 200 будет равняться числу 14. СТА 1106 [295K] 3 года назад  Всегда любила задачки на пропорции. Главное- правильно ее составить, а потом все просто, крест на крест и решение готово. Простейший пример. Найти на сколько процентов цех выполнил план по сборке за смену, если общий план 250 механизмов( штук), а всего за смену было собрано 262 ? Итак решаем. 250 штук – 100 % 262 штуки – х % Решение: 262 × 100:250= 104,8 %. Пример 2. Выяснить, сколько столовой нужно картофеля на год, если 20 тонн закрывают потребность лишь на 82%. Решение. Опять пропорция, где известно доля от потребности и в тоннах и процентах. Общая потребность , разумеется берется за 100. 20 тонн – 82 % Х тонн – 100 %. 20 × 100:82= 24,4 тонны. Бекки Шарп [71.2K] 3 года назад  Допустим по условию задачи нам известно сколько всего было единиц (1000 кг яблок) и надо узнать сколько единиц (кг сухого вещества) составляют 18%. Составляем пропорцию, в которой 1000 – это 100%, а неизвестной х – 18 %. То есть в пропорции у нас есть единицы и проценты. Соотносим соответственно кг к кг и проценты к процентам. это обязательное условие пропорции. Пропорция будет выглядеть так: Барха­тные лапки [382K] 3 года назад  Обычно в таких задачах задано общее число единиц, кг, км и нужно узнать сколько этих единиц составит определенное количество процентов. Или наоборот сколько процентов составляет количество единиц. То есть даны два известных, но мы помним что есть еще проценты, что общее количество чего-то это всегда 100%. Например нам нужно узнать сколько процентов составляет 38 рублей от 40 рублей. Составим пропорцию: 40/38=100/х, где 40 рублей это 100%, х – сколько рублей 38%. Из пропорции находим х = 95 %. Точно в цель [110K] 3 года назад  Посчитать пропорцию с процентами очень легко. В задачах на пропорции с процентами нам нужно посчитать проценты от числа. Для решения задачи нам нужно знать, что 50% – это половина от числа, 25% – одна четвертая от числа. То есть для того, чтобы найти пропорцию с процентами, нам нужно разделить число на 100 и умножить на процент. Например, мне нужно найти 20 процентов от числа 230. Сначала я 230 делю на 100, получается 2.3, а затем умножаю его на 20 – получаю 46. 50 процентов является половиной от числа, 25 является четвертой частью, 20 – пятой, 10 – 10, 5 является 20, а 1 процент – 100 часть. Один процент от 2000 найти не сложно. 2000 делим на 100 получим 20. Для того чтобы найти 50 процентов от 60 вам потребуется поделить на 2 = 30. Если нужно найти 13 процентов от 180 то 180 = 100 процентам , х = 14 получится 180 умножим на 13 делим на 100 и получаем 23,4. [поль­зоват­ель забло­киров­ан] [3.3K] 4 года назад  Всё очень просто. Всегда нужно начинать с того, что процент – это одна сотая часть. Ну, а далее – пропорция составляется исходя из этой посылки. Знаете ответ?

1. Как посчитать проценты, разделив число на 100

Так вы найдёте числовой эквивалент 1%. Дальше всё зависит от вашей цели. Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.

Пример 1

Вы заходите в супермаркет и видите акцию на кофе. Его обычная цена — 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.

Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.

Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.

Умножьте 4,58 на 7, и вы получите 32,06 рубля.

Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.

Пример 2

Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.

Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.

Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.

100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.

2. Как посчитать проценты, разделив число на 10

Этот способ похож на предыдущий, но считать с его помощью гораздо быстрее. Но только если речь идёт о процентах, кратных пяти.

Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.

Пример

Допустим, вы кладёте на депозит 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.

В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.

Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.

Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.

В любом случае такими крупными числами оперировать довольно просто.

3. Как посчитать проценты, составив пропорцию

Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:

сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.

Или можно записать её так: a : b = c : d.

Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.

Пример 1

Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.

Сначала вычисляем процентную долю оставшегося шоколада.

90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.

Х = 70 × 100 / 90 = 77,7%.

Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:

200 г : 100% = Х : 77,7%, где Х — нужное количество масла.

Х = 77,7 × 200 / 100 = 155,4.

Следовательно, в тесто нужно положить примерно 155 г масла.

Пример 2

Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.

Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.

Составьте пропорцию: 1 499 : 100 = Х : 87.

Х = 87 × 1 499 / 100.

Заплатите 1 304,13 рубля и носите блузку с удовольствием.

4. Как посчитать проценты с помощью соотношений

В некоторых случаях можно воспользоваться простыми дробями. Например, 10% — это 1/10 числа. И чтобы узнать, сколько это будет в цифрах, достаточно разделить целое на 10.

• 20% — 1/5, то есть нужно делить число на 5;
• 25% — 1/4;
• 50% — 1/2;
• 12,5% — 1/8;
• 75% — это 3/4. Значит, придётся разделить число на 4 и умножить на 3.

Пример

Вы нашли брюки за 2 400 рублей со скидкой 25%, но у вас в кошельке только 2 000 рублей. Чтобы узнать, хватит ли денег на обновку, проведите серию несложных вычислений:

100% — 25% = 75% — стоимость брюк в процентах от первоначальной цены после применения скидки.

2 400 / 4 × 3 = 1 800. Именно столько рублей стоят брюки.

5. Как посчитать проценты с помощью калькулятора

Если без калькулятора вам жизнь не мила, все вычисления можно делать с его помощью. А можно поступить ещё проще.

• Чтобы посчитать проценты от суммы, введите число, равное 100%, знак умножения, затем нужный процент и знак %. Для примера с кофе вычисления будут выглядеть так: 458 × 7%.
• Чтобы узнать сумму за вычетом процентов, введите число, равное 100%, минус, размер процентной доли и знак %: 458 – 7%.
• Аналогично можно складывать, как в примере с депозитом: 530 000 + 5%.

6. Как посчитать проценты с помощью онлайн-сервисов

Не все проценты можно посчитать в уме и даже на калькуляторе. Если речь идёт о доходности вклада, переплатах по ипотеке или налогах, требуются сложные формулы. Они учтены в некоторых онлайн-сервисах.

Planetcalc

На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.

Planetcalc→

Калькулятор — справочный портал

Ещё один сервис с калькуляторами на любой вкус.

Калькулятор — справочный портал→

Allcalc

Каталог онлайн-калькуляторов, 60 из которых предназначены для подсчёта финансов. Можно вычислить налоги и пени, размер субсидии на ЖКУ и многое другое.

Allcalc→

Читайте также 📑

• ТЕСТ:​ ​​Умеете ли вы считать в уме?
• Математические игры — отличная разминка для мозга
• 11 книг, которые прокачают математическое мышление
• Как выучить таблицу умножения легко и быстро

Задачи на проценты: стандартный расчет с помощью пропорций

12 ноября 2013

Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.

Итак, первая задача:

Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?

На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:

Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?

Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:

37 500 — 100%
X — 95%

Нужно составить пропорцию и найти x. Получаем:

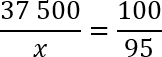
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:

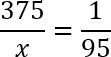
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:

x = 375 · 95

Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:

x = 35 625

Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.

Задача на проценты №2

Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?

Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:

45 000 — 100%
x — 80%

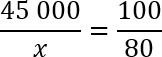
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:

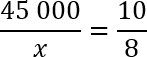
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:

45 000 · 8 = x · 10

Это простейшее линейное уравнение. Выразим из него переменную x:

x = 45 000 · 8 : 10

Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:

x = 4500 · 8

Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:

x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000

А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!

Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:

45 000 − 36 000 = 9000

Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.

Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)

Смотрите также:

1. Процент: налоги и зарплата. Считаем с помощью коэффициентов
2. Задачи на проценты: считаем проценты с помощью пропорции
3. Тест к уроку «Что такое числовая дробь» (легкий)
4. Тест: простейшие показательные уравнения (1 вариант)
5. Изюм и виноград (смеси и сплавы)
6. ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром

Как посчитать пропорцию

Пропорция – это очень удобный математический инструмент, который нашёл широкое применение в различных сферах нашей жизни. Чтобы посчитать пропорцию воспользуйтесь нашим простым онлайн калькулятором:

Онлайн калькулятор

Заполните поля a, c и b, и получите результат X

Теория

В прошлом видеоуроке мы рассматривали решение задач на проценты с помощью пропорций. Тогда по условию задачи нам требовалось найти значение той или иной величины.

В этот раз исходное и конечное значения нам уже даны. Поэтому в задачах будет требоваться найти проценты. Точнее, на сколько процентов изменилась та или иная величина. Давайте попробуем.

Задача. Кроссовки стоили 3200 рублей. После повышения цены они стали стоить 4000 рублей. На сколько процентов была повышена цена на кроссовки?

Итак, решаем через пропорцию. Первый шаг — исходная цена была равна 3200 рублей. Следовательно, 3200 рублей — это 100%.

Кроме того, нам дана конечная цена — 4000 рублей. Это неизвестное количество процентов, поэтому обозначим его за x
. Получим следующую конструкцию:

3200 — 100%
4000 — x
%

Что ж, условие задачи записано. Составляем пропорцию:

Дробь слева прекрасно сокращается на 100: 3200: 100 = 32; 4000: 100 = 40. Кроме того, можно сократить на 4: 32: 4 = 8; 40: 4 = 10. Получим следующую пропорцию:

Воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних. Получаем:

8 · x
= 100 · 10;
8x
= 1000.

Это обычное линейное уравнение. Отсюда находим x
:

x
= 1000: 8 = 125

Итак, мы получили итоговый процент x
= 125. Но является ли число 125 решением задачи? Нет, ни в коем случае! Потому что в задачи требуется узнать, на сколько процентов была повышена цена на кроссовки.

На сколько процентов — это значит, что нам нужно найти изменение:

∆ = 125 − 100 = 25

Получили 25% — именно настолько была повышена исходная цена. Это и является ответом: 25.

Задача B2 на проценты №2

Переходим ко второй задаче.

Задача. Рубашка стоила 1800 рублей. После снижения цены она стала стоить 1530 рублей. На сколько процентов была снижена цена на рубашку?

Переводим условие на математический язык. Исходная цена 1800 рублей — это 100%. А итоговая цена 1530 рублей — она нам известна, но неизвестно, сколько процентов она составляет от исходной величины. Поэтому обозначим ее за x
. Получим следующую конструкцию:

1800 — 100%
1530 — x
%

На основе полученной записи составляем пропорцию:

Давайте для упрощения дальнейших вычислений разделим обе части данного уравнения на 100. Другими словами, у числителя левой и правой дроби мы зачеркнем два нуля. Получим:

Теперь снова воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних.

18 · x
= 1530 · 1;
18x
= 1530.

Осталось найти x
:

x
= 1530: 18 = (765 · 2) : (9 · 2) = 765: 9 = (720 + 45) : 9 = 720: 9 + 45: 9 = 80 + 5 = 85

Мы получили, что x
= 85. Но, как и в прошлой задаче, это число само по себе не является ответом. Давайте вернемся к нашему условию. Теперь мы знаем, что новая цена, полученная после снижения, составляет 85% от старой. И для того, чтобы найти изменения, нужно из старой цены, т.е. 100%, вычесть новую цену, т.е. 85%. Получим:

∆ = 100 − 85 = 15

Это число и будет ответом: Обратите внимание: именно 15, а ни в коем случае не 85. Вот и все! Задача решена.

Внимательные ученики наверняка спросят: почему в первой задаче мы при нахождении разности вычитали из конечного числа начальное, а во второй задаче поступили в точности до наоборот: из исходных 100% вычли конечные 85%?

Давайте проясним этот момент. Формально, в математике изменением величины всегда называется разность между конечным значением и начальным. Другими словами, во второй задаче у нас должно было получиться не 15, а −15.

Однако этот минус ни в коем случае не должен попасть в ответ, потому что он уже учтен в условии исходной задачи. Там прямо сказано о снижении цены. А снижение цены на 15% — это то же самое, что повышение цены на −15%. Именно поэтому в решении и ответе задачи достаточно написать просто 15 — без всяких минусов.

Все, надеюсь, с этим моментом мы разобрались. На этом наш сегодняшний урок закончен. До новых встреч!

Задача 1
. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?

Решение.
Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги:

3,3:
300 или х:
500.

Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание:
пропорция — это равенство двух отношений
):

х=(3,3·
500):
300;

х=5,5.
Ответ:
пачка 500
листов бумаги имеет толщину 5,5 см
.

Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде:

или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см.

Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6
классе.

Задача 2.
Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?

Решение.

Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы.

5:
100 или х:
98. Получаем пропорцию:

5:
100 = х:
98.

х=(5·
98):
100;

х=4,9
Ответ: в 5кг
арбуза содержится 4,9 кг воды
.

Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?

Решение.

Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти:

16,8:
21 или х:
35. Получаем пропорцию:

16,8:
21=х:
35.

Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8
и 35
) и делим на известный средний член (21
). Сократим дробь на 7
.

Умножаем числитель и знаменатель дроби на 10
, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5
(5 и 10) и на 3
(168 и 3).

Ответ:
35
литров нефти имеют массу 28 кг.

После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?

Решение.

Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это:

х:
100 или 9:
18. Составляем пропорцию:

х:
100 = 9:
18.

Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100
и 9
) и делим на известный крайний член (18
). Сокращаем дробь.

Ответ
: площадь всего поля 50 га.

Страница 1 из 1
1

Пропо́рция –
равенство двух отношений, т. е. равенство вида a: b = c: d

, или, в других обозначениях, равенство

Если a
: b
= c
: d
, то a
и d
называют крайними

, а b
и c
– средними
членами

пропорции.

От « пропорции» никуда не деться, без нее не обойтись во многих задачах. Выход только один – разобраться с этим отношением и пользоваться пропорцией как палочкой-выручалочкой.

Прежде чем приступать к рассмотрению задач на пропорцию, важно вспомнить основное правило пропорции:

В пропорции

произведение крайних членов равно произведению средних

Если какая-то величина в пропорции неизвестна, ее легко будет найти, опираясь на это правило.

Например,

То есть неизвестная величина пропорции – значении дроби, в знаменателе

которой – то число, которое стоит напротив неизвестной величины

, в числителе – произведение оставшихся членов пропорции

(независимо от того, где эта неизвестная величина стоит
).

Задача 1.

Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?

Решение:

Мы понимаем, что уменьшение веса семени во сколько-то раз, влечет за собой уменьшение веса получаемого масла во столько же раз. То есть величины связаны прямой зависимостью.

Заполним таблицу:

Неизвестная величина – значение дроби , в знаменателе которой – 21 – величина, стоящая напротив неизвестного в таблице, в числителе – произведение оставшихся членов таблицы-пропорции.

Поэтому получаем, что из 7 кг семени выйдет 1,7 кг масла.

Чтобы правильно

заполнять таблицу, важно помнить правило:

Одинаковые наименования нужно записывать друг под другом. Проценты записываем под процентами, килограммы под килограммами и т.д

Задача 2.

Перевести в радианы.

Решение:

Мы знаем, что . Заполним таблицу:

Задача 3.

На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 27?

Решение:

Хорошо видно, что незаштрихованный сектор соответствует углу в (например, потому, что стороны сектора образованы биссектрисами двух смежных прямых углов). А поскольку вся окружность составляет , то на закрашенный сектор приходится .

Составим таблицу:

Откуда площадь круга – есть .

Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?

Решение:

Все поле составляет 100%, и поскольку вспахано 82%, то осталось вспахать 100%-82%=18% поля.

Заполняем таблицу:

Откуда получаем, что все поле составляет (га).

А следующая задача – с засадой.

Задача 5.

Расстояние между двумя городами пассажирский поезд прошел со скоростью 80км/ч за 3 часа. За сколько часов товарный поезд пройдет то же расстояние со скоростью 60 км/ч
?

Если вы будете решать эту задачу аналогично предыдущей, то получите следующее:

время, которое потребуется товарному поезду, чтобы пройти то же расстояние, что и пассажирским, есть часа. То есть, получается, что идя с меньшей скоростью, он преодолевает (за одно и тоже время) расстояние быстрее, нежели поезд с большей скоростью.

В чем ошибка рассуждений?

До сих пор мы рассматривали задачи, где величины были прямопропорциональны друг другу

, то есть рост

одной величины во сколько-то раз, дает рост

связанной с ней второй величины во столько же раз (аналогично с уменьшением, конечно). А здесь у нас другая ситуация: скорость пассажирского поезда больше

скорости товарного во сколько-то раз, а вот время, требуемое на преодоление одного и того же расстояния, требуется пассажирскому поезду меньшее

во столько же раз, нежели товарному поезду. То есть величины друг другу обратно пропорциональны

.

Схему, которой мы пользовались до сих пор, надо чуть изменить в данном случае.

Решение:

Рассуждаем так:

Пассажирский поезд со скоростью 80 км/ч ехал 3 ч, следовательно, он проехал км. А значит товарный поезд это же расстояние преодолеет за ч.

То есть, если бы мы составляли пропорцию, нам следовало бы поменять местами ячейки правой колонки предварительно. Получили бы: ч.

Поэтому, пожалуйста, будьте внимательны при составлении пропорции. Разберитесь сначала, с какой зависимостью имеете дело – с прямой или обратной.

Пропорция в переводе с латинского языка (proportio) обозначает соотношение, выравненность частей, то есть равенство 2-х отношений. Знание вычислять пропорции зачастую бывает нужным в бытовых обстановках.

Инструкция

1.
Легкой пример, когда нужно применить познания о решении пропорций: как вычислить 13% от вашей заработной платы – те самые проценты, которые уходят в Пенсионный фонд.

2.
Напишите две строчки пропорции. В первой укажите всеобщую сумму зарплаты, которая представляет собой 100%, то есть, скажем, 15 000 (рублей) = 100%.

3.
Строчкой ниже обозначьте ту сумму, которую надобно вычислить, знаком «Х», тот, что равен 13%, то есть Х = 13%.

4.
Основное качество пропорции звучит так: произведение крайних членов пропорции равно произведению её средних членов. Это значит, что если вы помножите 15 000 на 13, то полученное число будет равняться значению Х, помноженному на 100. То есть перемножая члены пропорции крест накрест, вы получите идентичное значение.

5.
Дабы вычислить, чему равен в финальном результате Х, умножьте 15 000 на 13 и поделите на 100. У вас получится, что 13 процентов от вашей зарплаты составляет 1950 рублей, таким образом, на руки вы получаете 15 000 – 1950 = 13 050 рублей чистой зарплаты.

6.
Если вам надобно взять для пирога 100 граммов сахарной пудры, а вы знаете, что в одном граненом стакане помещается 140 граммов, составьте следующую пропорцию:100 = Х140 = 1

7.
Подсчитайте, чему равен Х.Х = 100 х 1 / 140 = 0,7То есть вам потребуется 0,7 стакана сахарной пудры.

8.
Бывает, что надобно вычислить целое, зная только процентную часть. Скажем, вы знаете, что 21 человек на предприятии, а это 5% от всеобщего числа работников, имеют среднее особое образование. Составьте пропорцию, дабы вычислить всеобщее число работников: Х (человек) = 100%, 21 = 5%. 21 х 100 / 5 = 420 человек.

9.
Таким образом, записав в две строки имеющиеся данные, значение неведомого члена надобно находить так: помножьте между собой те члены пропорции, которые оказываются рядом и сверху незнакомого и поделите полученное число на значение, которое находится по диагонали от неведомого.А=БС=ДА = Б х С / Д; Б = А х Д / С; С = А х Д / Б; Д = С х Б / А

В геометрии существует несколько видов диагоналей. Диагональю
именуется отрезок, тот, что соединяет две не соседние (не принадлежащие одной стороне либо одному ребру) вершины многоугольника либо многогранника. Различают так же диагонали граней, рассматриваемых как многоугольники и пространственные диагонали, соединяющие вершины различных граней многогранника. Существуют фигуры, у которых все диагонали равны между собой. На плоскости это верный пятиугольник и квадрат, в пространстве – положительный октаэдр.Зная длины сторон положительного многоугольника либо длины рёбер положительного многогранника дозволено вычислить длину всякий диагонали.

Инструкция

1.
В любом верном многоугольнике углы равны между собой и вычисляются по формуле?? = (N – 2) * 180?/N, где?? – всякий из углов положительного многоугольника, N – число вершин.Зная углы при вершинах многоугольника, его диагонали дозволено вычислить, применяя теорему косинусовBE = v(AB? + AE? – 2 * AB * AE * cos??)

2.
Если число вершин огромнее пяти, то для вычисления диагоналей, которые соединяют вершины, лежащие на различных сторонах дозволено воспользоваться той же теоремой косинусов для вычисления углов образующихся треугольников. Скажем, в шестиугольнике ABCDEF, для нахождения диагонали BE, нужно вычислить диагональ CE, после этого по той же теореме косинусов вычислить угол??, тогда?? = ?? – ??. Таким образом,BE = v(BC? + CE? – 2 * BC * CE * cos??).

Видео по теме

Обратите внимание!

Для вычисления пространственной диагонали многогранника, нужно возвести сечение, содержащее эту диагональ, вычислить углы при вершинах этого сечения, рассматривая сечение как плоский многоугольник. Тогда диагональ дозволено рассчитать по приведённой выше схеме.

Что представляет собой пропорция? С математической точки зрения, пропорция – это равенство 2-х отношений. Все части пропорции являются взаимозависимыми, а их итог непоколебим.

Вам понадобится

• – Учебник алгебры за 7 класс.

Инструкция

1.
Числа, которые находятся по краям равенства, именуются крайними. Соответственно, те, что находятся в середине – средними. Основным свойством пропорции является то, что крайние и средние части равенства дозволено перемножать между собой. Возьмите пропорцию 6:3=8:4. Перемножьте между собой крайние части, получится 6*4=24, произведение средних частей тоже будет равным 24. Отсель итог: произведение одних частей пропорции должно быть равно произведению других частей (крайние = средние).

2.
Возьмите это качество пропорции на вооружение, вычислите незнакомый член уравнения x:4=15:3. Для того, дабы обнаружить неведомую часть пропорции, воспользуйтесь правилом равнозначности крайних и средних частей. Запишите это уравнение так: x*3=4*15. Решив это уравнение, вы получите правильную пропорцию.

3.
Если пропорция состоит из огромных либо дробных чисел, ее дозволено упростить. Уменьшите оба члена отношения на идентичное число раз. Дабы не случилось нарушения пропорции, сделайте так: 40:10=60:15. Увеличьте оба члена отношения в три раза (120:30=60:15) либо уменьшите части второго отношения (40:10=12:3). Обе пропорции будут положительными.

4.
Увеличивайте либо сокращайте пропорции только в идентичное число раз. Получив упрощенные реформирование, вы освобождаете пропорцию от дробных членов и упрощаете уравнение. Возьмите пример: 200:25=56:х. Дабы не исполнять вычисление с огромными числами, поделите их на одно и то же число. Если за это число взять 25, уравнение примет дальнейший вид: 8:1=56:х. Неведомую часть этой пропорции дозволено определить в уме, не прибегая к трудным вычислениям.

5.
Части пропорций дозволено переставлять. Возьмите пропорцию 3:5=12:20. Переставьте крайние части (20:5=12:3), допустима и одновременная перегруппировка всех частей (20:12=5:3). Все пропорции будут правильными. Так из одной пропорции вы получите несколько, и все они будут положительными.

Обратите внимание!

Перегруппировка частей пропорций местами комфортна при решении задач.

Полезный совет

Основное качество всех пропорций: ab = bc.

В математике пропорцией называют равенство 2-х отношений. Для всех ее частей характерна взаимозависимость и постоянный итог. Довольно разглядеть один пример, дабы осознать тезис решения пропорций.

Инструкция

1.
Изучите свойства пропорций. Числа по краям равенства называют крайними, а находящиеся посередине – средними. Основное качество пропорции заключается в том, что средние и крайние части равенства могут быть перемножены между собой. Довольно взять пропорцию 8:4=6:3. Если перемножить крайние части между собой, получится 8*3=24, как и при умножении средних чисел. Это обозначает, что произведение крайних частей пропорции неизменно равно произведению ее средних частей.

2.
Возьмите на вооружение основное качество пропорции, дабы вычислить неведомый член в уравнении x:4=8:2. Для нахождения незнакомой части пропорции следует воспользоваться правилом равнозначности средних и крайних частей. Запишите уравнение в виде x*2=4*8, то есть x*2=32. Решите это уравнение (32/2), вы получите недостающий член пропорции (16).

3.
Упростите пропорцию, если она состоит из дробных либо крупных чисел. Для этого поделите либо умножьте оба ее члена на идентичное число. Скажем, комбинированные части пропорции 80:20=120:30 дозволено упростить, поделив ее члены на 10 (8:2=12:3). Вы получите эквивалентное равенство. То же самое будет, если вы увеличите все члены пропорции, скажем, на 2, таким образом 160:40=240:60.

4.
Испробуйте переставить части пропорций. К примеру, 6:10=24:40. Поменяйте местами крайние части (40:10=24:6) либо же единовременно сделайте перегруппировку всех частей (40:24=10:6). Все полученные пропорции будут эквивалентными. Так вы сумеете получить несколько равенств из одного.

5.
Решите пропорцию с процентами. Запишите ее, скажем, в виде: 25=100%, 5=x. Сейчас необходимо перемножить средние члены (5*100) и поделить на знаменитый крайний (25). В результате получается, что x=20%. Таким же образом дозволено перемножать знаменитые крайние члены и разделять их на имеющийся средний, получая желанный итог.

Один процент – это сотая часть от числа. Данное понятие используется, когда нужно обозначить отношение доли к целому. Кроме этого, в процентах можно сравнивать несколько величин, при этом обязательно указывая, относительного какого целого проценты вычисляются. Например, расходы выше доходов на 10 % или цена на железнодорожные билеты возросла на 15 % в сравнении с тарифами прошлого года. Число процентов выше 100 означает, что доля превышает целое, как часто бывает при статистических расчетах.

Процент как финансовое понятие – плата, заемщика кредитору за предоставление денег во временное пользование. В бизнесе встречается выражение «работать за проценты». В данном случае подразумевается, что размер вознаграждения зависит от прибыли или оборота (комиссионные). Обойтись без вычисления процентов невозможно в бухгалтерии, бизнесе, банковском деле. Чтобы упростить расчеты, разработан онлайн-калькулятор процентов.

Калькулятор позволяет вычислить:

• Процент от заданного значения.
• Процент из суммы (налог по фактической зарплате).
• Процент от разницы (НДС из ).
• И многое другое…

При решении задач на калькуляторе процентов нужно оперировать тремя значениями, одно из которых неизвестно (по заданным параметрам вычисляется переменная). Сценарий расчета следует выбирать, исходя из заданных условий.

Примеры расчетов

1. Вычисление процента от числа

Чтобы найти число, составляющее 25 % от 1 000 руб., нужно:

• 1 000 × 25 / 100 = 250 руб.
• Или 1 000 × 0,25 = 250 руб.

Для расчета на обычном калькуляторе, нужно 1 000 умножить на 25 и нажать кнопку %.

2. Определение целого числа (100 %)

Мы знаем, что 250 руб. составляет 25 % от какого-то числа. Как его вычислить?

Составим простую пропорцию:

• 250 руб. – 25 %
• Y руб. – 100 %
• Y = 250 × 100 / 25 = 1 000 руб.

3. Процент между двумя числами

Допустим, предполагалась прибыль 800 руб., а получили 1 040 руб. Каков процент превышения?

Пропорция будет такой:

• 800 руб. – 100 %
• 1 040 руб. – Y %
• Y = 1 040 × 100 / 800 = 130 %

Перевыполнения плана по прибыли – 30 %, то есть выполнение – 130 %.

4. Расчет не из 100 %

Например, в магазин, состоящий из трех отделов, приходят 100 % покупателей. В продуктовый отдел – 800 человек (67 %), в отдел бытовой химии – 55. Какой процент покупателей приходит в отдел бытовой химии?

Пропорция:

• 800 посетителей – 67 %
• 55 посетителей – Y %
• Y = 55 × 67 / 800 = 4,6 %

5. На сколько процентов одно число меньше другого

Цена товара упала с 2 000 до 1 200 руб. На сколько процентов подешевел товар или на сколько процентов 1 200 меньше 2 000?

• 2 000 – 100 %
• 1 200 – Y %
• Y = 1 200 × 100 / 2 000 = 60 % (60 % к цифре 1 200 от 2 000)
• 100 % − 60 % = 40 % (число 1 200 меньше 2 000 на 40 %)

6. На сколько процентов одно число больше другого

Зарплата выросла с 5 000 до 7 500 рублей. На сколько процентов увеличилась зарплата? На сколько процентов 7 500 больше 5 000?

• 5 000 руб. – 100 %
• 7 500 руб. – Y %
• Y = 7 500 × 100 / 5 000 = 150 % (в цифре 7 500 150 % от 5 000)
• 150 % − 100 % = 50 % (число 7 500 больше 5 000 на 50 %)

7. Увеличение числа на определенный процент

Цена товара S выше 1 000 руб. на 27 %. Какова цена товара?

• 1 000 руб. – 100 %
• S – 100 % + 27 %
• S = 1 000 × (100 + 27) / 100 = 1 270 руб.

Онлайн-калькулятор делает вычисления намного проще: вам нужно выбрать вид расчета, ввести число и процент (в случае вычисления процентного соотношения – второе число), указать точность расчета и дать команду о начале действий.