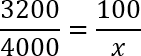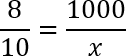|
Один из способов решения задач на проценты – это использование пропорций. Как правильно составлять и решать подобные пропорции? Существует много практических задач, использующих понятие процентов. Часто для их решения используется понятие пропорции. В простых случаях можно решать вот таким образом: все мы знаем, что 50% это половина от числа, 25% – это его четвёртая часть, 20% – это пятая часть, 10% -это 10 часть , 5 % – 20 часть, 1% – 100 часть. Итак, найти один процент от 2000 это 2000/100=20. Найти 50 % от 60 это 60/2=30. А можно использовать универсальный способ – понятие пропорции. Предположим надо найти 13% от 180. Тогда составим: 180 – 100% Х – 13 % Мы должны числа писать под числами, проценты под процентами. Далее раскрывает пропорцию крест накрест. То с чем икс не в паре перемножаем, а с чем в паре по диагонали – делим. У нас получаем 180*13/100=23,4 система выбрала этот ответ лучшим Ксарфакс 4 года назад Пропорция с процентами составляется по следующему принципу:
Вот как выглядет такая пропорция: A / B = 100% / p% Например: 1000 / 50 = 50% / 5%. Или можно записать по-другому: 1000 – 100%. 50 – 5%. При решении задач на проценты с помощью пропорции неизвестный её член (а здесь может быть 3 варианта) обычно обозначается за x. Решить пропорцию (то есть найти неизвестный член) можно благодаря её основному свойству: произведение крайних членов пропорции равно произведению средних (другими словами, нужно перемножить члены пропорции крест-накрест).
Далее рассмотрим несколько простых примеров. Пример 1. Зарплата составляет 30000 рублей, а премия – 10% от зарплаты. Нужно определить размер премии. 30000 – 100%. x – 10%. Вспоминаем, что произведение крайних членов равно произведению средних: 30000 * 10 = 100 * x. x = (30000 * 10) / 100 = 3000. Значит, премия равна 3000 рублей. Пример 2. Сделано 20 выстрелов, 4 из них – мимо мишени. Нужно определить процент попадания. 20 – 100%. 4 – x%. Умножаем крест-накрест и приравниваем: 20 * x = 100* 4. x = (100 * 4) / 20 = 20. Здесь нужно учесть, что 20% – это процент выстрелов мимо мишени (так как рядом с неизвестным x были записаны именно промахи). Процент попадания в свою очередь равен 100% – 20% = 80%. Пример 3. За месяц было продано 30 ноутбуков, что составляет 20% от всего количества ноутбуков, имеющихся в продаже. Нужно найти, сколько всего ноутбуков было в магазине изначально. x – 100%. 30 – 20%. Умножаем крест-накрест: 20 * x = 100 * 30. x = (100 * 30) / 20 = 150. Таким образом, изначально в продаже было 150 ноутбуков. Zummy out off 3 года назад Я как-то со школы запомнила принцип пропорции и способ ее решения называю «крест-накрест», не помню, кто это мне подсказал. Никогда не нахожу проценты по принципу умножения на сотую часть, мне не удобно, всегда использую свой «крест», единственное неудобство – нужно наглядно записывать это. Это не страшно – бумага всегда под рукой. Составляю пропорцию по условию, одно из значений неизвестное обозначаю Х. Затем решаю: перемножаю цифры, расположенные «на углах» слева и справа от Х, делю на число, расположенное на противоположном углу от Х. Пример: нужно найти 5% от числа 420. Пишу пропорцию. 420 – 100 % Х – 5 % Х = 5 • 420 : 100 = 21% Вот моя запись с крестом Ещё пример: сколько процентов от 200 составляет число 20. Составляю пропорцию. 200 – 100 % 20 – Х % Решение: X = 20 • 100 : 200 = 10% Алиса в Стране 3 года назад Странно, конечно, для таких простых задач составлять какие-то дополнительные пропорции, они решаются в уме и очень быстро, но способ такой есть, давайте его рассмотрим, возможно, кому-то он пригодится. Допустим, нам надо найти сколько процентов составляет число 18 от числа 90, в принципе, мы и так сразу видим что 18 это одна пятая, то есть 20 процентов от числа 90, но давайте составим пропорцию, приняв за х искомое количество процентов, пропорция у нас будет такая: 90 – 100 % 18 – х %, откуда х = 100 х 18 / 90 = 20 процентов. Еще один пример для закрепления материала, найдем, сколько процентов составляет 24 от 250, пропорция: 24 – х 250 – 100 х = 24 х 100 /250 = 9,6 %. Go Green 3 года назад Для определения процентного соотношения от числа нужно иметь представление об основных простых процентных соотношениях и о принципе вычисления любых из них. Для простоты давайте приведем примеры с числом 100. 1 % от ста – это одна сотая часть или один процент. 2% от ста – две сотых части от ста. 7% от ста – семь сотых части от ста и так далее. То есть сначала нам нужно узнать, сколько составляет один процент любого числа, разделив его на сто, а затем узнавать заданное процентное соотношение. Например, нам нужно найти, сколько будет равно 7 процентам от 200. Делим 200 на 100. Получится 2. Умножим 2 на 7, получится 14. Итого: 7% от 200 будет равняться числу 14. СТА 1106 3 года назад Всегда любила задачки на пропорции. Главное- правильно ее составить, а потом все просто, крест на крест и решение готово. Простейший пример. Найти на сколько процентов цех выполнил план по сборке за смену, если общий план 250 механизмов( штук), а всего за смену было собрано 262 ? Итак решаем. 250 штук – 100 % 262 штуки – х % Решение: 262 × 100:250= 104,8 %. Пример 2. Выяснить, сколько столовой нужно картофеля на год, если 20 тонн закрывают потребность лишь на 82%. Решение. Опять пропорция, где известно доля от потребности и в тоннах и процентах. Общая потребность , разумеется берется за 100. 20 тонн – 82 % Х тонн – 100 %. 20 × 100:82= 24,4 тонны. Бекки Шарп 3 года назад Допустим по условию задачи нам известно сколько всего было единиц (1000 кг яблок) и надо узнать сколько единиц (кг сухого вещества) составляют 18%. Составляем пропорцию, в которой 1000 – это 100%, а неизвестной х – 18 %. То есть в пропорции у нас есть единицы и проценты. Соотносим соответственно кг к кг и проценты к процентам. это обязательное условие пропорции. Пропорция будет выглядеть так: Бархатные лапки 3 года назад Обычно в таких задачах задано общее число единиц, кг, км и нужно узнать сколько этих единиц составит определенное количество процентов. Или наоборот сколько процентов составляет количество единиц. То есть даны два известных, но мы помним что есть еще проценты, что общее количество чего-то это всегда 100%. Например нам нужно узнать сколько процентов составляет 38 рублей от 40 рублей. Составим пропорцию: 40/38=100/х, где 40 рублей это 100%, х – сколько рублей 38%. Из пропорции находим х = 95 %. Точно в цель 3 года назад Посчитать пропорцию с процентами очень легко. В задачах на пропорции с процентами нам нужно посчитать проценты от числа. Для решения задачи нам нужно знать, что 50% – это половина от числа, 25% – одна четвертая от числа. То есть для того, чтобы найти пропорцию с процентами, нам нужно разделить число на 100 и умножить на процент. Например, мне нужно найти 20 процентов от числа 230. Сначала я 230 делю на 100, получается 2.3, а затем умножаю его на 20 – получаю 46. 50 процентов является половиной от числа, 25 является четвертой частью, 20 – пятой, 10 – 10, 5 является 20, а 1 процент – 100 часть. Один процент от 2000 найти не сложно. 2000 делим на 100 получим 20. Для того чтобы найти 50 процентов от 60 вам потребуется поделить на 2 = 30. Если нужно найти 13 процентов от 180 то 180 = 100 процентам , х = 14 получится 180 умножим на 13 делим на 100 и получаем 23,4. [пользователь заблокирован] 4 года назад Всё очень просто. Всегда нужно начинать с того, что процент – это одна сотая часть. Ну, а далее – пропорция составляется исходя из этой посылки. Знаете ответ? |
Задачи на проценты: считаем проценты с помощью пропорции
11 ноября 2013
В прошлом видеоуроке мы рассматривали решение задач на проценты с помощью пропорций. Тогда по условию задачи нам требовалось найти значение той или иной величины.
В этот раз исходное и конечное значения нам уже даны. Поэтому в задачах будет требоваться найти проценты. Точнее, на сколько процентов изменилась та или иная величина. Давайте попробуем.
Задача. Кроссовки стоили 3200 рублей. После повышения цены они стали стоить 4000 рублей. На сколько процентов была повышена цена на кроссовки?
Итак, решаем через пропорцию. Первый шаг — исходная цена была равна 3200 рублей. Следовательно, 3200 рублей — это 100%.
Кроме того, нам дана конечная цена — 4000 рублей. Это неизвестное количество процентов, поэтому обозначим его за x. Получим следующую конструкцию:
3200 — 100%
4000 — x%
Что ж, условие задачи записано. Составляем пропорцию:
Дробь слева прекрасно сокращается на 100: 3200 : 100 = 32; 4000 : 100 = 40. Кроме того, можно сократить на 4: 32 : 4 = 8; 40 : 4 = 10. Получим следующую пропорцию:
Воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних. Получаем:
8 · x = 100 · 10;
8x = 1000.
Это обычное линейное уравнение. Отсюда находим x:
x = 1000 : 8 = 125
Итак, мы получили итоговый процент x = 125. Но является ли число 125 решением задачи? Нет, ни в коем случае! Потому что в задачи требуется узнать, на сколько процентов была повышена цена на кроссовки.
На сколько процентов — это значит, что нам нужно найти изменение:
∆ = 125 − 100 = 25
Получили 25% — именно настолько была повышена исходная цена. Это и является ответом: 25.
Задача B2 на проценты №2
Переходим ко второй задаче.
Задача. Рубашка стоила 1800 рублей. После снижения цены она стала стоить 1530 рублей. На сколько процентов была снижена цена на рубашку?
Переводим условие на математический язык. Исходная цена 1800 рублей — это 100%. А итоговая цена 1530 рублей — она нам известна, но неизвестно, сколько процентов она составляет от исходной величины. Поэтому обозначим ее за x. Получим следующую конструкцию:
1800 — 100%
1530 — x%
На основе полученной записи составляем пропорцию:
Давайте для упрощения дальнейших вычислений разделим обе части данного уравнения на 100. Другими словами, у числителя левой и правой дроби мы зачеркнем два нуля. Получим:
Теперь снова воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних.
18 · x = 1530 · 1;
18x = 1530.
Осталось найти x:
x = 1530 : 18 = (765 · 2) : (9 · 2) = 765 : 9 = (720 + 45) : 9 = 720 : 9 + 45 : 9 = 80 + 5 = 85
Как видите, мы не стали считать полученное частное уголком, а просто несколько раз сократили нашу дробь. При этом нам потребовалось разложить на множители числитель и
Мы получили, что x = 85. Но, как и в прошлой задаче, это число само по себе не является ответом. Давайте вернемся к нашему условию. Теперь мы знаем, что новая цена, полученная после снижения, составляет 85% от старой. И для того, чтобы найти изменения, нужно из старой цены, т.е. 100%, вычесть новую цену, т.е. 85%. Получим:
∆ = 100 − 85 = 15
Это число и будет ответом: Обратите внимание: именно 15, а ни в коем случае не 85. Вот и все! Задача решена.
Внимательные ученики наверняка спросят: почему в первой задаче мы при нахождении разности вычитали из конечного числа начальное, а во второй задаче поступили в точности до наоборот: из исходных 100% вычли конечные 85%?
Давайте проясним этот момент. Формально, в математике изменением величины всегда называется разность между конечным значением и начальным. Другими словами, во второй задаче у нас должно было получиться не 15, а −15.
Однако этот минус ни в коем случае не должен попасть в ответ, потому что он уже учтен в условии исходной задачи. Там прямо сказано о снижении цены. А снижение цены на 15% — это то же самое, что повышение цены на −15%. Именно поэтому в решении и ответе задачи достаточно написать просто 15 — без всяких минусов.
Все, надеюсь, с этим моментом мы разобрались. На этом наш сегодняшний урок закончен. До новых встреч!
Смотрите также:
- Задачи на проценты: стандартный расчет с помощью пропорций
- Процент: неизвестно начальное значение (метод пропорции)
- Тест к уроку «Что такое числовая дробь» (легкий)
- Сводный тест по задачам B15 (1 вариант)
- Деление многочленов уголком
- Задача B4: строительные бригады
Не зря говорят, что всё гениальное просто. Не перестаю в этом постоянно убеждаться. Вот и данная статья наглядный тому пример. Речь пойдет о том, как легко и просто можно посчитать процент от какого-либо числа. Но сначала я бы хотел поделиться с вами двумя своими тематическими видеороликами, которые вам точно понравятся, раз вы здесь 😉
В первом видео я показываю наглядный графический метод умножения чисел, которому учат школьников в Японии.
А на видео ниже я демонстрирую самый быстрый способ рисования прерывистых линий.
Ну а теперь перейду непосредственно к теме сегодняшней публикации.
Задача: нужно найти 70% от числа 90.
Наверное, большинство из вас первым делом начнут рисовать в уме или на бумаге следующую пропорцию.
Если вы не понимаете запись выше, то либо вы не учились в школе либо ученик начальной школы. Ну правда есть ещё вариант. Возможно вы китаец или японец, которого обучали как-то по другому 😉
После составления вышеобозначенной пропорции вы легко найдете искомое.
Но, возможно, многие из вас удивятся, что для подобных задач можно применить гораздо более простой метод без составления пропорции.
В случае если речь идет о двузначных числах с нулём на конце (такие как в примере выше), то для решения достаточно просто перемножить между собой первые числа.
Это настолько просто, что многие из вас сейчас начнут писать комментарии вида: “В школе надо было учиться!”, “Это очевидно!” и так далее. Но я то знаю, что это лукавство 😉 И что при очередном примере вида “найти 40% от 90”, мозг сам потянется составлять пропорцию 😄
Так что внимательно всмотритесь в фото выше и запомните. Увидели подобный пример – просто перемножьте первые числа и точка 🙂
Кстати, вы знали, что большинство людей всю жизнь неправильно открывают пакет с кабельными стяжками??? А НАДО ВОТ ТАК! (жмём сюда).
Если информация пригодилась или натолкнула на размышления, то жмите “палец вверх” 👍 😉 А вот тут ещё много интересного
Процент — это величина, равная одной сотой доле и используемая для выражения части чего-либо к целому. Для обозначения процентной величины используют знак «%».
Как определить нужную долю от суммы
Процент от любого числа можно высчитать несколькими способами.
Способ 1
В первом случае необходимо разделить исходное число на 100, затем умножить полученный результат на процент, который нужно найти, т.е.:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
((A;/;100);times;B,;)
Где А — это число, от которого необходимо извлечь процент; B — процент, который нужно найти в числовом выражении.
Пример
К примеру, цена товара равна 154 рублям. У покупателя есть карта на скидку 5% в данный магазин. Найдем сумму скидки в рублях:
(154 / 100) × 5 = 7,7 = 7 руб. 70 коп.
Таким образом, покупатель сможет приобрести товар на 7 руб. и 70 коп. дешевле, т.е.:
154 − 7,7 = 146,3 = 146 руб. 30 коп.
Способ 2
По данному методу процентную долю находят посредством умножения исходной величины на коэффициент 0,B. Формула имеет вид:
A × 0,B,
Где А — это число, от которого необходимо извлечь процент; B — процент, который нужно найти в числовом выражении.
Пример
Стоимость набранного товара в сумме составила 862 рубля. В магазине проходила акция, по которой продавец предоставил покупателю скидку в 15%. Для нахождения итоговой стоимости вычислим величину скидки в рублях:
862 × 0,15 = 129,3 = 129 руб. 30 коп.
Теперь найдем сумму, которую заплатил покупатель:
862 − 129,3 = 732,7 = 732 руб. 70 коп.
Способ 3
Третий способ предполагает следующий алгоритм: исходное (базовое) число А умножается на процент В, который нужно извлечь. Полученный в итоге результат делится на 100. В виде формулы этот метод можно выразить так:
(А × В) / 100
Пример
Общая стоимость покупки составила 1250 рублей. Продукты питания составляют 75% от итоговой суммы, а 25 % — это стоимость бытовой химии и прочих товаров. На какую сумму были приобретены продукты питания?
Чтобы ответить на этот вопрос, произведем следующие вычисления:
1250 × 75 / 100 = 937,5
Стоимость всех купленных продуктов питания составила 937 руб. 50 коп.
Как найти процентное соотношение чисел
Чтобы определить, какой процент одно число (А) составляет от другого (В), используют формулу вида:
А / В × 100
Пример
Контрольная работа по математике состоит из 10 заданий. К середине урока ученик выполнил 6 заданий. На сколько процентов в данный момент завершена контрольная работа?
Для решения задачи выполним следующие расчеты:
6 / 10 × 100 = 60
Ответ: контрольная работа к середине урока выполнена на 60%.
Умножение и деление процентов на число
Перед тем, как выполнить умножение или деление процента на число, нужно привести величину, выраженную в процентном значении, в дробь.
Пример № 1
300 × 5% = 300 × (5 / 100) = 300 × 0,05 = 15.
Пример № 2
35 / 50% = 35 / (50 / 100) = 35 / 0,5 = 35 / (5/10) = 35 × (10/5) = 350/5 = 70.
Составление пропорций
Задачи на проценты могут решаться с помощью пропорций. Составление соотношений с процентами производится в следующей последовательности:
- Базовое число A принимается за 100%. Число А в цифровом обозначении будет первым членом пропорции, оно соответствует 100%.
- Другие члены пропорции — это часть исходного числа (обозначение B) и соответствующие этой части (p).
Пропорция будет иметь такой вид:
(A;/;B;=;100%;/;p%)
Пример:
500 — 100%
250 — 50%
Пропорция будет выглядеть так: 500 / 250 = 100% / 50%.
В задачах на проценты неизвестный член пропорции обозначают буквой х. Для его определения применяют основное свойство пропорций: при умножении крайних членов между собой получится число, равное произведению средних членов. Следовательно, чтобы найти х, необходимо крест-накрест перемножить члены соотношения. При этом можно вывести следующие формулы:
- A = 100 % × B / p %;
- B = A × p % / 100 %;
- p % = 100 % × B / A.
Пример
Зарплата преподавателя равна 25 000 рублей, премия составляет 10% от заработной платы. Определите размер премиальной выплаты.
Составим пропорцию:
25 000 — 100%
х — 10%.
По основному свойству пропорций:
25 000 × 10 = 100 × x
x = (25 000 × 10) / 100 = 2 500
Ответ: премия равна 2 500 рублей.
Соотношение чисел с использованием дробей
Отношение чисел, помимо процентного выражения, может быть представлено в виде дробей.
Отношение двух чисел представляет собой частное этих чисел. Эта величина отражает, во сколько раз одно число больше другого. Кроме того, отношение чисел показывает, какую часть одно число составляет от другого.
Пример
В 7 классе 35 учеников, 15 из них — мальчики, 20 — девочки. Какую часть от общего количества семиклассников составляют мальчики, какую часть — девочки?
Решим задачу с помощью отношений:
- 15/35 = 3/7 — доля мальчиков в 7 классе.
- 20/35 = 4/7 — доля девочек в 7 классе.
Как посчитать процент от числа
- Главная
- /
- Математика
- /
- Арифметика
- /
- Как посчитать процент от числа
Чтобы найти процент от числа или определить сколько процентов число составляет от другого числа, надо воспользоваться пропорцией или нашим онлайн калькулятором:
Онлайн калькулятор
Сколько будет % от числа ?
Ответ:
0
Для того чтобы найти процент от числа, нужно просто это число умножить на число процентов и разделить на 100%.
Сколько процентов число составляет от числа ?
Ответ:
0
%
Чтобы определить сколько процентов число составляет от другого числа, необходимо первое число умножить на 100% и разделить на второе.
Число это % от какого числа?
Ответ:
0
Для того чтобы выяснить от какого числа другое число (X) составляет определённое количество процентов, надо число X умножить на 100% и разделить на количество интересующих вас процентов.
Теория
Сколько будет P% от числа Y?
Формула
X = (Y*P)/100
Пример
К примеру, определим сколько будет 12% от 600?
X = (600*12)/100
Ответ: X = 72
Сколько процентов число X составляет от числа Y?
Формула
P = (X*100)/Y
Пример
К примеру, определим сколько процентов число 72 составляет от 600?
P = (72*100)/600
Ответ: P = 12%
Число X это P% от какого числа?
Формула
Y = (100*X)/P
Пример
К примеру, определим: число 72 это 12% от какого числа?
Y = (100*72)/12
Ответ: Y = 600