Как составить пропорцию с дробями - Сайт, где вы сможете решить свои вопросы

Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.

Что такое пропорция?

Пропорцией называют равенство двух отношений. Например, отношение равно отношению

Данная пропорция читается следующим образом:

Десять так относится к пяти, как два относится к одному

Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции выполнить деление в обеих дробях, то получится число 2 в обеих частях:

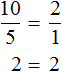
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:

10 : 5

Преобразуем данное отношение в дробь

Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:

2 : 1

Преобразуем данное отношение в дробь:

Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».

В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.

Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.

Поэтому отношение не пропорционально отношению .

Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.

Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.

Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:

Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2

2 = 2

Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.

В нашей пропорции крайние члены это 4 и 4, а средние члены это 2 и 8

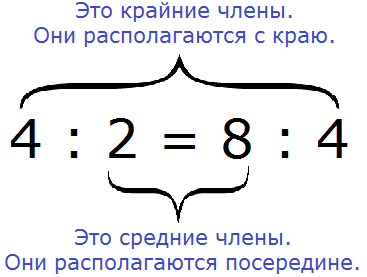
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:

4 : 2 = 8 : 4

Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:

2615

С помощью переменных пропорцию можно записать так:

Данное выражение можно прочесть следующим образом:

a так относится к b, как c относится к d

Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.

Основное свойство пропорции

Основное свойство пропорции выглядит следующим образом:

Произведение крайних членов пропорции равно произведению её средних членов.

Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.

Например, проверим правильно ли составлена пропорция . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:

2621

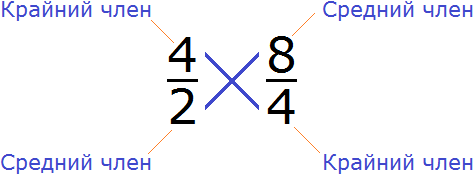
4 × 4 = 16 — произведение крайних членов пропорции равно 16.

2 × 8 = 16 — произведение средних членов пропорции так же равно 16.

4 × 4 = 2 × 8

16 = 16

4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция составлена правильно.

Пример 2. Проверить правильно ли составлена пропорция

Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:

2632

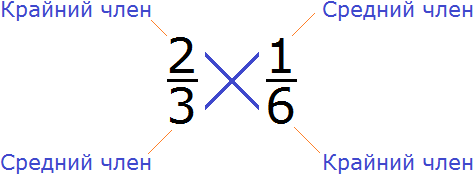
2 × 6 = 12 — произведение крайних членов пропорции равно 12

3 × 1 = 3 — произведение средних членов пропорции равно 3

2 × 6 ≠ 3 × 1

12 ≠ 3

2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция составлена неправильно.

Поэтому в пропорции разумнее заменить знак равенства (=) на знак не равно (≠)

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Рассмотрим решение пропорций на конкретных примерах.

Решить уравнения с пропорцией:

1) 25 : x = 10 : 18

Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции, произведение крайних членов разделим на известный средний член:

$[x = frac{{mathop {25}limits^5 cdot mathop {18}limits^9 }}{{mathop {10}limits_{mathop 2limits_1 } }}]$

25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.

Ответ: 45.

$[2)frac{y}{{21}} = frac{9}{{14}}]$

Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:

$[y = frac{{mathop {21}limits^3 cdot 9}}{{mathop {14}limits_2 }}]$

$[y = frac{{27}}{2}]$

Ответ: 13,5.

При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.

Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:

$[z = frac{{4,5 cdot 2,4}}{{0,6}}]$

В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:

$[z = frac{{4,5 cdot 10 cdot 2,4 cdot 10}}{{0,6 cdot 100}}]$

Сокращаем 24 и 6 на 6, 10 и 45 — на 5:

$[z = frac{{mathop {45}limits^9 cdot mathop {24}limits^4 }}{{mathop 6limits_1 cdot mathop {10}limits_2 }}]$

Еще раз сокращаем 4 и 2 на 2:

$[z = frac{{9 cdot mathop 4limits^2 }}{{mathop 2limits_1 }}]$

Ответ: 18.

Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.

$[4)k:2frac{3}{{23}} = 3frac{2}{7}:frac{1}{4}]$

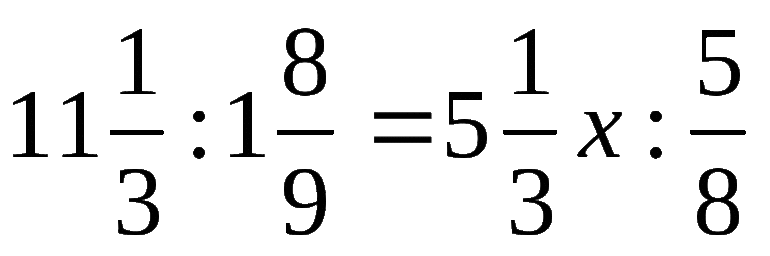
Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:

$[k = 2frac{3}{{23}} cdot 3frac{2}{7}:frac{1}{4}]$

Смешанные числа переводим в неправильные дроби:

$[k = frac{{49}}{{23}} cdot frac{{23}}{7} cdot 4]$

$[k = frac{{mathop {49}limits^7 cdot mathop {23}limits^1 cdot 4}}{{mathop {23}limits_1 cdot mathop 7limits_1 }}]$

Ответ: 28.

При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.

$[5)frac{{2x - 3}}{{15}} = frac{6}{5}]$

Произведение крайних членов пропорции равно произведению средних членов:

Здесь удобно упростить уравнение, разделив обе части на 5:

Ответ: 10,5.

$[6)frac{{2x - 3,2}}{{1,2}} = frac{{5x - 6}}{{0,5}}]$

Произведение крайних членов пропорции равно произведению ее средних членов:

Для упрощения вычислений удобно умножить каждую часть уравнения на 10:

$[1,2(5x - 6) = 0,5(2x - 3,2)___left| { cdot 10} right.]$

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

Ответ: 1,12.

Источник

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа.

Что поможет в решении:

если а не равно нулю, то у уравнения единственный корень: х = −b : а;
если а равно нулю, а b не равно нулю — у уравнения нет корней;
если а и b равны нулю, то корень уравнения — любое число.

Квадратное уравнение выглядит так:

ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

подобрать число, которое можно разделить на каждый из знаменателей без остатка;
умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

если значение переменной обращает знаменатель в 0, значит это неверное значение;
делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

Область допустимых значений: х ≠ −2.
Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Как решать пропорции – правила, методы и примеры вычислений

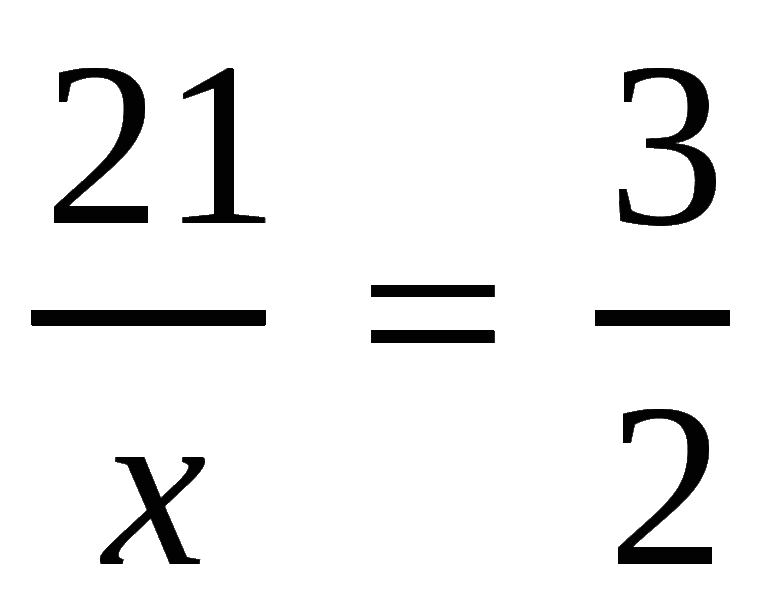
Общие сведения

Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.

Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.

Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.

Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.

Сферы применения

Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.

В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.

Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.

Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.

В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.

Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.

Основные свойства

Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:

Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].
Перемножение «крест-накрест»: x * z = y * v.
Перестановка: x / v = y / z и v / x = z / y.
Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.
Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.

Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).

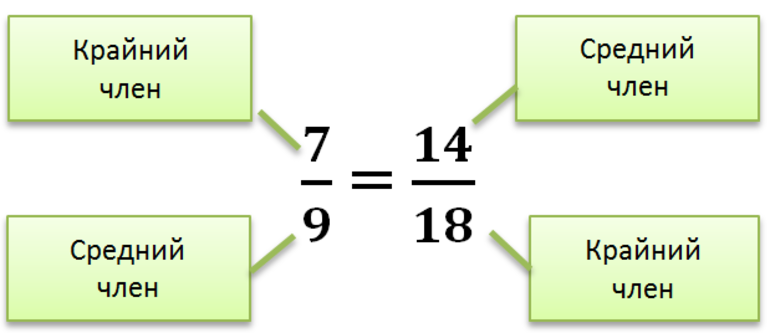
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.

Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.

Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.

Методика исследования

Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.

Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.

В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:

Записать функцию.
Рассмотреть составные части.
Если простой тип, перейти к 5 пункту.
Сложная — разложить на простые элементы, а затем перейти к 5 пункту.
Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.
Определить тип линейности, построив график.

По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.

К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.

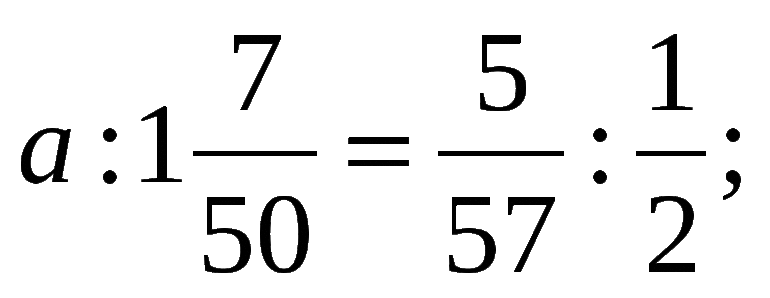
Универсальный алгоритм

Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:

Записать соотношение пропорции.
Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
Применить свойство умножения «крест-накрест».
Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
Решить уравнение.

Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.

Уравнения с пропорцией

Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:

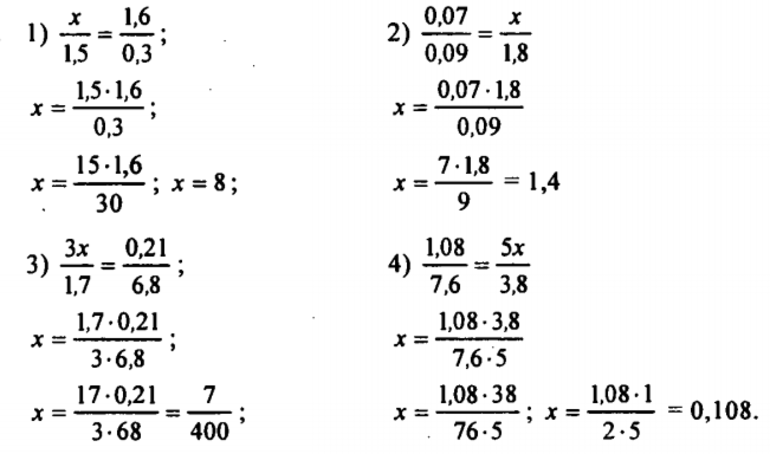
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.

Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:

Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.
При D равном 0 (один): р = (-b) / 2a.
Если D 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.

Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.

Решение пропорций

Рассмотрим решение пропорций на конкретных примерах.

Решить уравнения с пропорцией:

1) 25 : x = 10 : 18

Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции , произведение крайних членов разделим на известный средний член:

25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.

Сокращаем 24 и 6 на 6, 10 и 45 — на 5:

Еще раз сокращаем 4 и 2 на 2:

Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.

При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.

Произведение крайних членов пропорции равно произведению средних членов:

Здесь удобно упростить уравнение, разделив обе части на 5:

Произведение крайних членов пропорции равно произведению ее средних членов:

Для упрощения вычислений удобно умножить каждую часть уравнения на 10:

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

[spoiler title=”источники:”]

http://nauka.club/matematika/proportsii.html

Решение пропорций

[/spoiler]

Источник

Запомните!

Пропорция — это равенство двух отношений.

Рассмотрим два равных отношения:

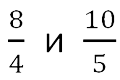
Соединив их знаком равенства, мы получим пропорцию.

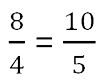
В пропорции различают крайние и средние члены.

8 и
5 называют крайними членами.
4 и 10 — средние члены.

Основное свойство пропорции

Если пропорция составлена верно, то есть отношения, составляющие эту пропорцию действительно равны,
то для пропорции верно следующее:

Запомните!

Произведение крайних членов пропорции равно произведению средних.

Правило выше и называется основным свойством пропорции.

Чтобы правильно применять правило, мы предлагаем вам запомнить правило (креста) «X».

Рассмотрим его на примере пропорции.

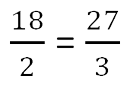
Убедимся, что пропорция составлена верно.

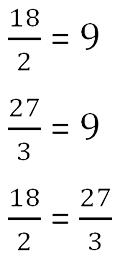
Теперь запишем пропорцию и нарисуем карандашом поверх знака равенства крест.

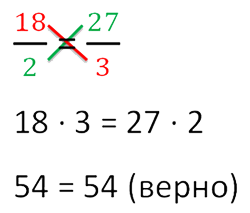
Нарисовав крест, гораздо легче составить нужное произведение (выполнить основное свойство пропорции).

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

2 января 2020 в 11:01

Sergei Mixailov
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Sergei Mixailov
Профиль
Благодарили: 0

Сообщений: 1

Можно ли менять местами неизвестный множитель буквы например в пропорции например в пропорции крайний член A D= C B средний

0
Спасибо thanks
Ответить

5 января 2020 в 14:18
Ответ для Sergei Mixailov

Эмма Аддамс
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Эмма Аддамс
Профиль
Благодарили: 0

Сообщений: 2

Если дана пропорция = , то верно следующее: = и
= . Таким образом, мы можем менять местами крайние и средние члены пропорции.

А вот здесь видео-уроки по математике:

https://www.youtube.com/channel/UChuPWiMp13sUQ6G6oPTjzag?disable_polymer=true

0
Спасибо thanks
Ответить

17 ноября 2016 в 21:51

Саша Икс
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Саша Икс
Профиль
Благодарили: 0

Сообщений: 1

Всем привет! Задача не сложная, но что то не до конца понимаю, поэтму ищу у Вас помощи. Задача такая:
Мужу с женой пришёл счёт за оплату электричество 2500 рублей. Они договорились вместе оплатить этот счёт, но каждый вносит равную долю по отношению к своей зарплате. Сколько внесёт в счёт за электричество муж и сколько жена, при условии, что зарплата мужа 15000 рублей, а зарплата жены 12000 рублей.

0
Спасибо thanks
Ответить

21 ноября 2016 в 13:21
Ответ для Саша Икс

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Необходимо определить долю, которую каждый из них приносит в общий бюджет. Т.е. 12000+15000 = 27000(общий бюджет). 12000/27000 = 0,44; 15000/27000=0,56. Т.е. Жена должна оплатить 44%, а муж 56% от счета. Находим проценты и считаем:
2500 · 0,44 = 1100 — должна внести жена
2500 · 0,56 = 1400 — должен внести муж

1
Спасибо thanks
Ответить

27 октября 2016 в 20:26

Анастасия Чакиева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Анастасия Чакиева
Профиль
Благодарили: 0

Сообщений: 1

Помогите пожалуйста ребёнок болел, а теперь нужно срочно сдавать доклад поматематике на темуосновное свойство пропорций

0
Спасибо thanks
Ответить

28 октября 2016 в 8:39
Ответ для Анастасия Чакиева

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Думаю для доклада, этого будет маловато, но как основа вполне подойдёт.

0
Спасибо thanks
Ответить

5 ноября 2016 в 21:48
Ответ для Анастасия Чакиева

София Деревянко
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
София Деревянко
Профиль
Благодарили: 0

Сообщений: 2

Я нашла на YuoTube ролик, в котором очень понятно разясняют https://www.youtube.com/watch?v=AWO4ISLFAaw, удачи

0
Спасибо thanks
Ответить

4 февраля 2016 в 16:30

Павел Жердев
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Павел Жердев
Профиль
Благодарили: 0

Сообщений: 1

Подскажите пожалуйста при составлении пропорции, как понять в отношениях какую величину нужно делить.Например в 20л.керосина весят 10кг, а 40л. 20кг.Что должно в отношении быть в числители, а что в знаменатели и почему?

0
Спасибо thanks
Ответить

19 сентября 2016 в 11:47
Ответ для Павел Жердев

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

В этой теме есть примеры на решение задач с пропорциями.
В конкретном случае:
20л — весят 10кг, а 20л -весят 40 кг.
Находим соотвествующие параметры. А именно. л и л, кг и кг. Проверяем логику. Она не нарушена. Значит в числитель ставим л, а в знаменатель кг. 20/10=40/20. Если сократим обе части, то увидим: 2=2, а значит пропорция составлена верно.

0
Спасибо thanks
Ответить

26 января 2016 в 6:15

Егор Король
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Егор Король
Профиль
Благодарили: 0

Сообщений: 1

Найдите отношения: 8 целых 2/13 к 15/13 желательно с решением
6 целых 5/6 к 8,2 тоже с решением
1,35 к 5 целых 5/8 Помогите очень прошу!!!

0
Спасибо thanks
Ответить

3 февраля 2016 в 21:41
Ответ для Егор Король

Сергей Аколоцев
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Сергей Аколоцев
Профиль
Благодарили: 0

Сообщений: 3

8*13+2=106/13 больше 15/13

6*6+5=41/6 и 82/10сокращаем, приводим к общему знаменателю 30, получаем 205/30 меньше 246/30

1целая 35/100 сокращаем получается 1 целая 7/10 или 17/10
5целых 5/8 получается 45/8
опять же приводим к общему знаменателю 40 получаем 68/40 меньше 225/40

0
Спасибо thanks
Ответить

15 января 2016 в 7:37

Артем Зурлов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Артем Зурлов
Профиль
Благодарили: 0

Сообщений: 1

Мне не понятно пропорция и отношение объясните пожалуста кратно

0
Спасибо thanks
Ответить

21 января 2016 в 20:51
Ответ для Артем Зурлов

Ангелина Дмитриева
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Ангелина Дмитриева
Профиль
Благодарили: 0

Сообщений: 2

Отношение — это просто частное двух чисел. Например 3:4, 6:13 и т. д. В записи отношения важна именно связь между двумя числами, а не результат, полученный при вычислении частного, что отличает отношение от деления.
Равенство двух отношений называют пропорцией.

12: 16 = 18: 24 (например)

cool

0
Спасибо thanks
Ответить

19 сентября 2016 в 10:48
Ответ для Артем Зурлов

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Вот здесь подробно описаны пропорции.

0
Спасибо thanks
Ответить

24 сентября 2015 в 13:12

Андрей Валах
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Андрей Валах
Профиль
Благодарили: 0

Сообщений: 1

Выберете из отношений из которых можно составить пропорцию состовте прпорцию 14* 21,8*14,15*10,27**18,18*24,36*54,20*35,6*8 *это разделить

0
Спасибо thanks
Ответить

12 сентября 2016 в 11:37
Ответ для Андрей Валах

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

На сайте имеется возможность ставить знак “: “.

Чтобы составить пропорции, предлагаю сократить обыкновенные дроби и увидеть, что может стать пропорцией.

=; =; =; =; =; =; =; =.
Отсюда видно, что пропорцию составляют: 1) и 6); 2) и 7); 3) и 4); 5) и 8).

0
Спасибо thanks
Ответить

16 сентября 2015 в 20:43

Альфия Абдалимова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Альфия Абдалимова
Профиль
Благодарили: 0

Сообщений: 1

0
Спасибо thanks
Ответить

8 сентября 2016 в 16:40
Ответ для Альфия Абдалимова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Воспользуемся свойством пропорции: произведение крайних членов пропорции равно произведению средних членов (правило креста).
1,8 · (6x + 1) = 2,5 · 7,2
1,8 · 6x + 1,8 = 18
10,8x=18 ?1,8
10,8x=16,2
x=1,5

0
Спасибо thanks
Ответить

6 сентября 2015 в 20:45

Кристина Папина
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Кристина Папина
Профиль
Благодарили: 0

Сообщений: 1

я взела у 1 друга 100 рублей и пошла в магазин по дороге всретила 2 друга и взяла у его взаймы 50 рублей пошла в магази и купила там 2 шоколадки по 10 рублей штука, у меня осталось 30 рублей их я оддала 1 другу и в сумме у меня получилось 70 рублей должна первому другу 50 руб. 2 другу и 20 рублей купила шоколадку и полус=чилось 140 рублей где 10 рублей?

0
Спасибо thanks
Ответить

2 сентября 2016 в 15:12
Ответ для Кристина Папина

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Считаем финальную сумму долга с твоей стороны: 100 (заняла у первого друга) ? 30 (вернула первому другу) + 50 (заняла у второго друга) = 120;
Считаем потраченные деньги: 100 (потеряные) + 20 (потрачено на шоколад) = 120.
120=120 — ничего не потеряно. Попытка запутать здесь, ведёт к нарушению логики.

0
Спасибо thanks
Ответить

19 мая 2015 в 4:26

Даша Казанцева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Даша Казанцева
Профиль
Благодарили: 0

Сообщений: 1

Правило нахождение элементов пропорции

0
Спасибо thanks
Ответить

19 мая 2015 в 20:30
Ответ для Даша Казанцева

Леся Деркачева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Леся Деркачева
Профиль
Благодарили: 0

Сообщений: 1

Произведение крайник членов равно произведению средних членов!

0
Спасибо thanks
Ответить

Источник

Калькулятор пропорций онлайн

Калькулятор рассчитывает неизвестный член пропорции. Можно также проверить пропорцию на верность.

Правила ввода

Вводить можно целые числа, десятичные дроби, правильные и неправильные дроби -5, 5, 0.25, -1.25, 10/8, -1/2 и.т.д.

Если вам необходимо ввести смешанное число то предварительно его нужно преобразовать в неправильную дробь. Т.е. 3 целые 1/3 нужно будет записать как 10/3

Поле которое необходимо рассчитать можно оставить пустым или ввести любую букву латинского(английского) алфавита.

В расчётное поле можно также вводить значения с переменными вида: 5x, 1.2x, 5/x, x/5, 3x/2, 2/3x. Т.е. если вам надо посчитать (2/3)*х то нужно записать как 2x/3. Если надо посчитать (1/2)*(1/x) то нужно будет ввести 1/2x.

Решить пропорцию это значит найти неизвестный член пропорции.

Пропорцию можно записать двумя способами:

a / b = c / d

a : b = c : d

Прочитать формулу выше можно как a относится к b, как c относится к d.

a, b, c, d – называются членами пропорции

a, d – называются крайними членами пропорции

b, c – называются средними членами пропорции

Главное свойство пропорции

Произведение крайних членов пропорции равно произведению средних членов пропорции.

a / b = c / d

a × d = b × c

Крайний член пропорции равен произведению средних членов пропорции, делённому на другой крайний член

a = bc/d

d = bc/a

Средний член пропорции равен произведению крайних членов пропорции, делённому на другой средний член

b = ad/c

c = ad/b

Примеры решения задач на пропорции

1) Решите пропорцию 3:x=2:5
Из основного свойства пропорции получается
2x=15,
x=15/2=7.5

2) Решите пропорцию x:9=10:3
Из основного свойства пропорции получается
3x=90,
x=90/3=30

3) Решите пропорцию 2x:8=28:16
Из основного свойства пропорции получается
2x·16=8·28,
32x=224,
x=224/32=7

Источник

Что такое пропорция?

Основное свойство пропорции

Решение уравнений с дробями

Понятие дроби

Основные свойства дробей

Понятие уравнения

Понятие дробного уравнения

Как решать уравнения с дробями

1. Метод пропорции

2. Метод избавления от дробей

Что еще важно учитывать при решении

Универсальный алгоритм решения

Примеры решения дробных уравнений

Как решать пропорции – правила, методы и примеры вычислений

Общие сведения

Сферы применения

Основные свойства

Методика исследования

Универсальный алгоритм

Уравнения с пропорцией

Решение пропорций

Основное свойство пропорции

Ваши комментарии

Калькулятор пропорций онлайн

Главное свойство пропорции

Примеры решения задач на пропорции

Вам также может понравиться

Прожгла куртку сигаретой как исправить

Как найти минусы в бизнесе

Как найти свой утерянный крестик

Добавить комментарий Отменить ответ