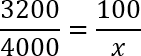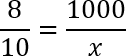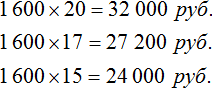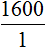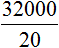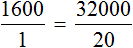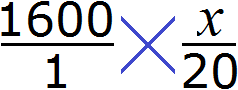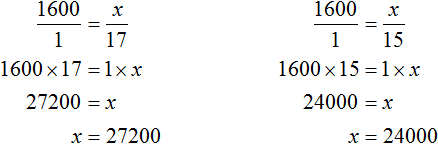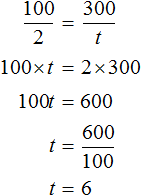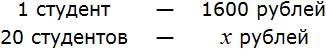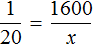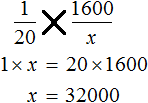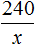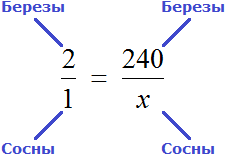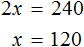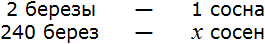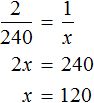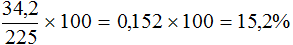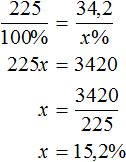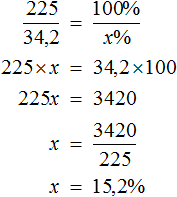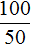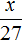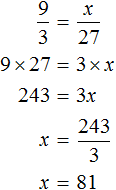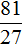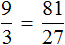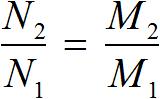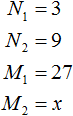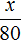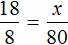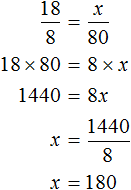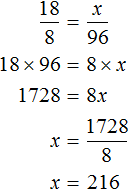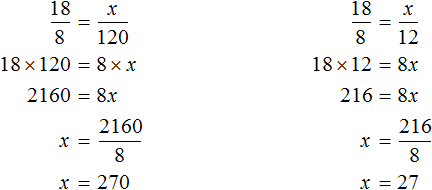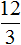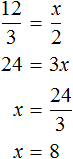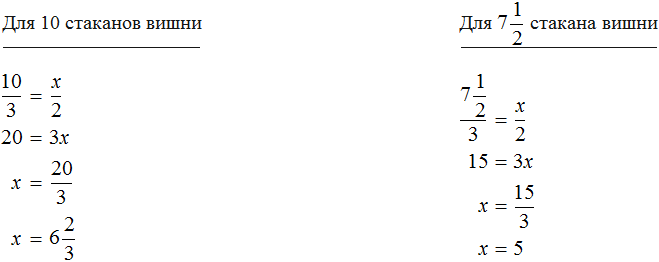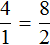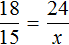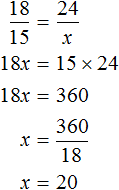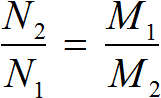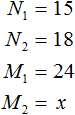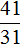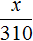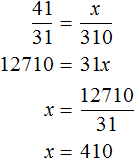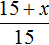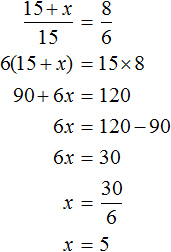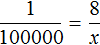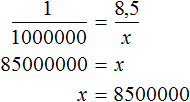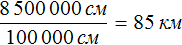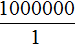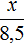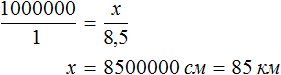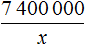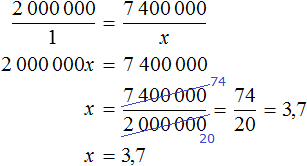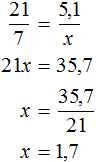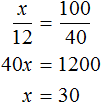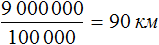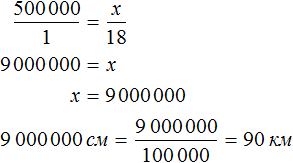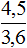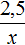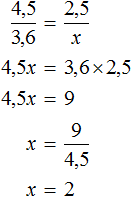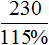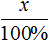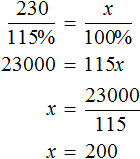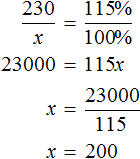Как составить пропорцию с двумя неизвестными в процентах

Один из способов решения задач на проценты – это использование пропорций. Как правильно составлять и решать подобные пропорции? Существует много практических задач, использующих понятие процентов. Часто для их решения используется понятие пропорции. В простых случаях можно решать вот таким образом: все мы знаем, что 50% это половина от числа, 25% – это его четвёртая часть, 20% – это пятая часть, 10% -это 10 часть , 5 % – 20 часть, 1% – 100 часть. Итак, найти один процент от 2000 это 2000/100=20. Найти 50 % от 60 это 60/2=30. А можно использовать универсальный способ – понятие пропорции. Предположим надо найти 13% от 180. Тогда составим: 180 – 100% Х – 13 % Мы должны числа писать под числами, проценты под процентами. Далее раскрывает пропорцию крест накрест. То с чем икс не в паре перемножаем, а с чем в паре по диагонали – делим. У нас получаем 180*13/100=23,4 система выбрала этот ответ лучшим Ксарф­акс [156K] 4 года назад  Пропорция с процентами составляется по следующему принципу: Исходное число (обозначим его буквой A) принимается за 100%. Первым членом пропорции будет цифровая запись числа A, ему будет соответствовать 100%. Остальными членами пропорции будут часть от этого числа (обозначим его буквой B) и проценты, соответствующие этой части (обозначим их буквой p). Вот как выглядет такая пропорция: A / B = 100% / p% Например: 1000 / 50 = 50% / 5%. Или можно записать по-другому: 1000 – 100%. 50 – 5%. При решении задач на проценты с помощью пропорции неизвестный её член (а здесь может быть 3 варианта) обычно обозначается за x. Решить пропорцию (то есть найти неизвестный член) можно благодаря её основному свойству: произведение крайних членов пропорции равно произведению средних (другими словами, нужно перемножить члены пропорции крест-накрест). Исходное число будет равно: A = 100% * B / p%. Часть от числа будет равна: B = A * p% / 100%. Проценты от числа можно найти по формуле: p% = 100% * B / A. Далее рассмотрим несколько простых примеров. Пример 1. Зарплата составляет 30000 рублей, а премия – 10% от зарплаты. Нужно определить размер премии. 30000 – 100%. x – 10%. Вспоминаем, что произведение крайних членов равно произведению средних: 30000 * 10 = 100 * x. x = (30000 * 10) / 100 = 3000. Значит, премия равна 3000 рублей. Пример 2. Сделано 20 выстрелов, 4 из них – мимо мишени. Нужно определить процент попадания. 20 – 100%. 4 – x%. Умножаем крест-накрест и приравниваем: 20 * x = 100* 4. x = (100 * 4) / 20 = 20. Здесь нужно учесть, что 20% – это процент выстрелов мимо мишени (так как рядом с неизвестным x были записаны именно промахи). Процент попадания в свою очередь равен 100% – 20% = 80%. Пример 3. За месяц было продано 30 ноутбуков, что составляет 20% от всего количества ноутбуков, имеющихся в продаже. Нужно найти, сколько всего ноутбуков было в магазине изначально. x – 100%. 30 – 20%. Умножаем крест-накрест: 20 * x = 100 * 30. x = (100 * 30) / 20 = 150. Таким образом, изначально в продаже было 150 ноутбуков. Zummy out off [226K] 3 года назад  Я как-то со школы запомнила принцип пропорции и способ ее решения называю «крест-накрест», не помню, кто это мне подсказал. Никогда не нахожу проценты по принципу умножения на сотую часть, мне не удобно, всегда использую свой «крест», единственное неудобство – нужно наглядно записывать это. Это не страшно – бумага всегда под рукой. Составляю пропорцию по условию, одно из значений неизвестное обозначаю Х. Затем решаю: перемножаю цифры, расположенные «на углах» слева и справа от Х, делю на число, расположенное на противоположном углу от Х. Пример: нужно найти 5% от числа 420. Пишу пропорцию. 420 – 100 % Х – 5 % Х = 5 • 420 : 100 = 21% Вот моя запись с крестом Ещё пример: сколько процентов от 200 составляет число 20. Составляю пропорцию. 200 – 100 % 20 – Х % Решение: X = 20 • 100 : 200 = 10% Алиса в Стран­е [363K] 3 года назад  Странно, конечно, для таких простых задач составлять какие-то дополнительные пропорции, они решаются в уме и очень быстро, но способ такой есть, давайте его рассмотрим, возможно, кому-то он пригодится. Допустим, нам надо найти сколько процентов составляет число 18 от числа 90, в принципе, мы и так сразу видим что 18 это одна пятая, то есть 20 процентов от числа 90, но давайте составим пропорцию, приняв за х искомое количество процентов, пропорция у нас будет такая: 90 – 100 % 18 – х %, откуда х = 100 х 18 / 90 = 20 процентов. Еще один пример для закрепления материала, найдем, сколько процентов составляет 24 от 250, пропорция: 24 – х 250 – 100 х = 24 х 100 /250 = 9,6 %. Go Green [537K] 3 года назад  Для определения процентного соотношения от числа нужно иметь представление об основных простых процентных соотношениях и о принципе вычисления любых из них. Для простоты давайте приведем примеры с числом 100. 1 % от ста – это одна сотая часть или один процент. 2% от ста – две сотых части от ста. 7% от ста – семь сотых части от ста и так далее. То есть сначала нам нужно узнать, сколько составляет один процент любого числа, разделив его на сто, а затем узнавать заданное процентное соотношение. Например, нам нужно найти, сколько будет равно 7 процентам от 200. Делим 200 на 100. Получится 2. Умножим 2 на 7, получится 14. Итого: 7% от 200 будет равняться числу 14. СТА 1106 [295K] 3 года назад  Всегда любила задачки на пропорции. Главное- правильно ее составить, а потом все просто, крест на крест и решение готово. Простейший пример. Найти на сколько процентов цех выполнил план по сборке за смену, если общий план 250 механизмов( штук), а всего за смену было собрано 262 ? Итак решаем. 250 штук – 100 % 262 штуки – х % Решение: 262 × 100:250= 104,8 %. Пример 2. Выяснить, сколько столовой нужно картофеля на год, если 20 тонн закрывают потребность лишь на 82%. Решение. Опять пропорция, где известно доля от потребности и в тоннах и процентах. Общая потребность , разумеется берется за 100. 20 тонн – 82 % Х тонн – 100 %. 20 × 100:82= 24,4 тонны. Бекки Шарп [71.2K] 3 года назад  Допустим по условию задачи нам известно сколько всего было единиц (1000 кг яблок) и надо узнать сколько единиц (кг сухого вещества) составляют 18%. Составляем пропорцию, в которой 1000 – это 100%, а неизвестной х – 18 %. То есть в пропорции у нас есть единицы и проценты. Соотносим соответственно кг к кг и проценты к процентам. это обязательное условие пропорции. Пропорция будет выглядеть так: Барха­тные лапки [382K] 3 года назад  Обычно в таких задачах задано общее число единиц, кг, км и нужно узнать сколько этих единиц составит определенное количество процентов. Или наоборот сколько процентов составляет количество единиц. То есть даны два известных, но мы помним что есть еще проценты, что общее количество чего-то это всегда 100%. Например нам нужно узнать сколько процентов составляет 38 рублей от 40 рублей. Составим пропорцию: 40/38=100/х, где 40 рублей это 100%, х – сколько рублей 38%. Из пропорции находим х = 95 %. Точно в цель [110K] 3 года назад  Посчитать пропорцию с процентами очень легко. В задачах на пропорции с процентами нам нужно посчитать проценты от числа. Для решения задачи нам нужно знать, что 50% – это половина от числа, 25% – одна четвертая от числа. То есть для того, чтобы найти пропорцию с процентами, нам нужно разделить число на 100 и умножить на процент. Например, мне нужно найти 20 процентов от числа 230. Сначала я 230 делю на 100, получается 2.3, а затем умножаю его на 20 – получаю 46. 50 процентов является половиной от числа, 25 является четвертой частью, 20 – пятой, 10 – 10, 5 является 20, а 1 процент – 100 часть. Один процент от 2000 найти не сложно. 2000 делим на 100 получим 20. Для того чтобы найти 50 процентов от 60 вам потребуется поделить на 2 = 30. Если нужно найти 13 процентов от 180 то 180 = 100 процентам , х = 14 получится 180 умножим на 13 делим на 100 и получаем 23,4. [поль­зоват­ель забло­киров­ан] [3.3K] 4 года назад  Всё очень просто. Всегда нужно начинать с того, что процент – это одна сотая часть. Ну, а далее – пропорция составляется исходя из этой посылки. Знаете ответ?

Задачи на проценты: считаем проценты с помощью пропорции

11 ноября 2013

В прошлом видеоуроке мы рассматривали решение задач на проценты с помощью пропорций. Тогда по условию задачи нам требовалось найти значение той или иной величины.

В этот раз исходное и конечное значения нам уже даны. Поэтому в задачах будет требоваться найти проценты. Точнее, на сколько процентов изменилась та или иная величина. Давайте попробуем.

Задача. Кроссовки стоили 3200 рублей. После повышения цены они стали стоить 4000 рублей. На сколько процентов была повышена цена на кроссовки?

Итак, решаем через пропорцию. Первый шаг — исходная цена была равна 3200 рублей. Следовательно, 3200 рублей — это 100%.

Кроме того, нам дана конечная цена — 4000 рублей. Это неизвестное количество процентов, поэтому обозначим его за x. Получим следующую конструкцию:

3200 — 100%
4000 — x%

Что ж, условие задачи записано. Составляем пропорцию:

Дробь слева прекрасно сокращается на 100: 3200 : 100 = 32; 4000 : 100 = 40. Кроме того, можно сократить на 4: 32 : 4 = 8; 40 : 4 = 10. Получим следующую пропорцию:

Воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних. Получаем:

8 · x = 100 · 10;
8x = 1000.

Это обычное линейное уравнение. Отсюда находим x:

x = 1000 : 8 = 125

Итак, мы получили итоговый процент x = 125. Но является ли число 125 решением задачи? Нет, ни в коем случае! Потому что в задачи требуется узнать, на сколько процентов была повышена цена на кроссовки.

На сколько процентов — это значит, что нам нужно найти изменение:

∆ = 125 − 100 = 25

Получили 25% — именно настолько была повышена исходная цена. Это и является ответом: 25.

Задача B2 на проценты №2

Переходим ко второй задаче.

Задача. Рубашка стоила 1800 рублей. После снижения цены она стала стоить 1530 рублей. На сколько процентов была снижена цена на рубашку?

Переводим условие на математический язык. Исходная цена 1800 рублей — это 100%. А итоговая цена 1530 рублей — она нам известна, но неизвестно, сколько процентов она составляет от исходной величины. Поэтому обозначим ее за x. Получим следующую конструкцию:

1800 — 100%
1530 — x%

На основе полученной записи составляем пропорцию:

Давайте для упрощения дальнейших вычислений разделим обе части данного уравнения на 100. Другими словами, у числителя левой и правой дроби мы зачеркнем два нуля. Получим:

Теперь снова воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних.

18 · x = 1530 · 1;
18x = 1530.

Осталось найти x:

x = 1530 : 18 = (765 · 2) : (9 · 2) = 765 : 9 = (720 + 45) : 9 = 720 : 9 + 45 : 9 = 80 + 5 = 85

Как видите, мы не стали считать полученное частное уголком, а просто несколько раз сократили нашу дробь. При этом нам потребовалось разложить на множители числитель и

Мы получили, что x = 85. Но, как и в прошлой задаче, это число само по себе не является ответом. Давайте вернемся к нашему условию. Теперь мы знаем, что новая цена, полученная после снижения, составляет 85% от старой. И для того, чтобы найти изменения, нужно из старой цены, т.е. 100%, вычесть новую цену, т.е. 85%. Получим:

∆ = 100 − 85 = 15

Это число и будет ответом: Обратите внимание: именно 15, а ни в коем случае не 85. Вот и все! Задача решена.

Внимательные ученики наверняка спросят: почему в первой задаче мы при нахождении разности вычитали из конечного числа начальное, а во второй задаче поступили в точности до наоборот: из исходных 100% вычли конечные 85%?

Давайте проясним этот момент. Формально, в математике изменением величины всегда называется разность между конечным значением и начальным. Другими словами, во второй задаче у нас должно было получиться не 15, а −15.

Однако этот минус ни в коем случае не должен попасть в ответ, потому что он уже учтен в условии исходной задачи. Там прямо сказано о снижении цены. А снижение цены на 15% — это то же самое, что повышение цены на −15%. Именно поэтому в решении и ответе задачи достаточно написать просто 15 — без всяких минусов.

Все, надеюсь, с этим моментом мы разобрались. На этом наш сегодняшний урок закончен. До новых встреч!

Смотрите также:

1. Задачи на проценты: стандартный расчет с помощью пропорций
2. Процент: неизвестно начальное значение (метод пропорции)
3. Тест к уроку «Что такое числовая дробь» (легкий)
4. Сводный тест по задачам B15 (1 вариант)
5. Деление многочленов уголком
6. Задача B4: строительные бригады

Решение уравнений с двумя неизвестными

В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.

Определение

Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:

a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.

Ниже приведены несколько примеров:

Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.

Решение задач

Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.

Для наглядности объяснений подберем корни для выражения: y-x = 6.

При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).

Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.

У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9

Приведем исходное равенство к следующему виду:

В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.

При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.

Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.

Оба равенства равносильны.

Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.

Оба уравнения также равносильны.

Система уравнений с двумя неизвестными

Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.

Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.

Решить подобные системы уравнений можно, применяя следующие методы.

Метод подстановки

1. Выражаем неизвестное из любого равенства через вторую переменную.
2. Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
3. Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.

Метод сложения

1. Приводим к равенству модули чисел при каком-либо неизвестном.
2. Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
3. Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.

Графический метод

1. Выражаем в каждом равенстве одну переменную через другую.
2. Строим графики двух имеющихся уравнений в одной координатной плоскости.
3. Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
4. Делаем проверку, подставив полученные значения в исходную систему равенств.

При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.

В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.

Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!

Видео

Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.

Решение задач с помощью пропорции

Решение задачи с помощью пропорции сводится к тому, чтобы сделать неизвестное значение x членом этой пропорции. Затем используя основное свойство пропорции получить линейное уравнение и решить его.

Как решить задачу с помощью пропорции

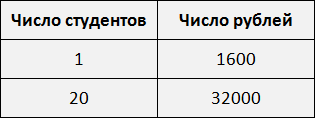
Рассмотрим простейший пример. Трем группам нужно выплатить стипендию по 1600 рублей каждому. В первой группе 20 студентов. Значит первой группе будет выплачено 1600 × 20, то есть 32 тыс. рублей.

Во второй группе 17 человек. Значит второй группе будет выплачено 1600 × 17, то есть 27,200 тыс. руб.

Ну и выплатим стипендию третьей группе. В ней 15 человек. На них нужно затратить 1600 × 15, то есть 24 тыс. руб.

В результате имеем следующее решение:

Для подобных задач решение можно записывать с помощью пропорции.

Пропорция по определению есть равенство двух отношений. К примеру, равенство 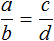является пропорцией. Эту пропорцию можно прочесть следующим образом:

a так относится к b, как c относится d

Аналогично можно соотнести стипендию и студентов, так чтобы каждому досталось по 1600 рублей.

Итак, запишем первое отношение, а именно отношение тысячи шестисот рублей на одного человека:

Мы выяснили, что для выплаты 20 студентам по 1600 рублей, нам потребуется 32 тыс. рублей. Значит второе отношение будет отношением тридцати двух тысяч к двадцати студентам:

Теперь соединим полученные отношения знаком равенства:

Мы получили пропорцию. Её можно прочесть следующим образом:

Тысяча шестьсот рублей так относятся к одному студенту, как тридцать две тысячи рублей относятся к двадцати студентам.

То есть по 1600 рублей каждому. Если выполнить деление в обеих частях равенства 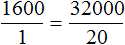, то обнаружим, что одному студенту, как и двадцати студентам достанется по 1600 рублей.

Теперь представим, что сумма денег, необходимых для выплаты стипендии двадцати студентам, была бы неизвестной. Скажем, если бы вопрос стоял так: в группе 20 студентов и каждому нужно выплатить по 1600 рублей. Сколько всего рублей требуется для выплаты стипендии?

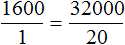
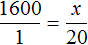
В таком случае пропорция приняла бы вид . То есть сумма денег, необходимая для выплаты стипендии, стала неизвестным членом пропорции. Эту пропорцию можно прочесть так:

Тысяча шестьсот рублей так относятся к одному студенту, как неизвестное число рублей относится к двадцати студентам

Теперь воспользуемся основным свойством пропорции. Оно гласит, что произведение крайних членов пропорции равно произведению средних:

Перемножив члены пропорции «крест-накрест», получим равенство 1600 × 20 = 1 × x . Вычислив обе части равенства, получим 32000 = x или x = 32000 . Иными словами, мы найдём значение неизвестной величины, которое искали.

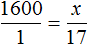
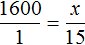
Аналогично можно было определить общую сумму и для остального количества студентов — для 17 и 15. Эти пропорции выглядели как и . Воспользовавшись основным свойством пропорции, можно найти значение x

Задача 2. Расстояние равное 100 км автобус проехал за 2 часа. Сколько времени потребуется автобусу, чтобы проехать 300 км, если будет ехать с той же скоростью?

Можно сначала определить расстояние, которое автобус проезжает за один час. Затем определить сколько раз это расстояние содержится в 300 километрах:

100 : 2 = 50 км на каждый час движения

300 км : 50 = 6 часов

Либо можно составить пропорцию «сто километров так относятся к двум часам, как триста километров к неизвестному числу часов»:

Отношение одноименных величин

Если крайние или средние члены пропорции поменять местами, то пропорция не нарушится.

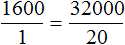
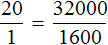
Так, в пропорции можно поменять местами крайние члены. Тогда получится пропорция .

Пропорция также не нарушится, если её перевернуть, то есть использовать обратные отношения в обеих частях.

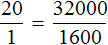
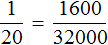
Перевернем пропорцию . Тогда получим пропорцию . Взаимосвязь при этом не нарушается. Отношение между студентами равно отношению между суммами денег, предназначенных для этих студентов. Такую пропорцию часто составляют в школе, когда для решения задачи составляются таблицы

Этот способ записи очень удобен, поскольку позволяет перевести условие задачи в более понятный вид. Решим задачу в которой требовалось определить сколько рублей нужно для выплаты стипендии двадцати студентам.

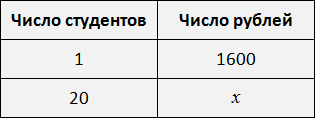
Условие задачи запишем следующим образом:

Составим таблицу на основе этого условия:

Составим пропорцию, используя данные таблицы:

Используя основное свойство пропорции, получим линейное уравнение и найдем его корень:

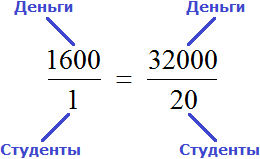
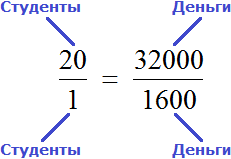
Изначально, мы имели дело с пропорцией 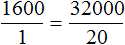, которая составлена из отношений величин разной природы. В числителях отношений располагались суммы денег, а в знаменателях количество студентов:

Поменяв местами крайние члены, мы получили пропорцию 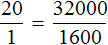. Эта пропорция составлена из отношений величин одной природы. В первом отношении содержатся количества студентов, а во втором — суммы денег:

Если отношение составлено из величин одной природы, то мы будем называть его отношением одноименных величин. Например, отношения между фруктами, деньгами, физическими величинами, явлениями, действиями.

Отношение может быть составлено, как из одноименных величин, так и из величин разной природы. Примерами последних являются отношение расстояния ко времени, отношения стоимости товара к его количеству, отношение общей суммы стипендии к количеству студентов.

Пример 2. В школьном саду посажены сосны и березы, причём на каждую сосну приходится 2 березы. Сколько посадили сосен в саду, если берез посадили 240?

Определим сколько сосен было посажено в саду. Для этого составим пропорцию. В условии сказано, что на каждую сосну приходится 2 березы. Напишем отношение, показывающее что на одну сосну приходится две березы:

Теперь напишем второе отношение, показывающее что на x сосен приходится 240 берез

Соединим эти отношения знаком равенства, получим следующую пропорцию:

«2 березы так относятся к одной сосне,
как 240 берез относятся к x соснам»

Используя основное свойство пропорции, находим значение x

Либо пропорцию можно составить, предварительно записав условие, как в прошлом примере:

Получится та же пропорция, но в этот раз она будет составлена из отношений одноименных величин:

Значит в саду посадили 120 сосен.

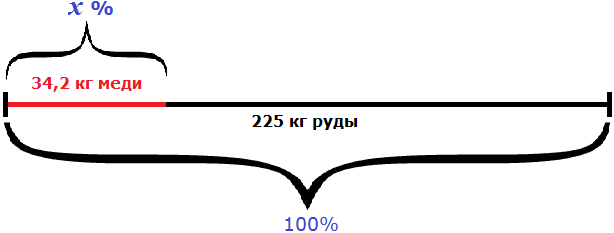
Пример 3. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?

Можно разделить 34,2 на 225 и полученный результат выразить в процентах:

Либо составить пропорцию 225 килограммам руды так приходятся на 100%, как 34,2 кг меди приходятся на неизвестное число процентов:

Либо составить пропорцию в которой отношения составлены из одноименных величин:

Задачи на прямую пропорциональность

Понимание отношений одноименных величин приводит к пониманию решения задач на прямую и обратную пропорциональность. Начнем с задач на прямую пропорциональность.

Для начала вспомним, что такое прямая пропорциональность. Это взаимосвязь между двумя величинами при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.

Если расстояние в 50 км автобус прошел за 1 час, то для прохождения расстояния в 100 км (при той же скорости) автобусу потребуется 2 часа. Во сколько раз увеличилось расстояние, во столько же раз увеличилось время движения. Как показать это с помощью пропорции?

Одно из предназначений отношения заключается в том, чтобы показать во сколько раз первая величина больше второй. А значит и мы c помощью пропорции можем показать, что расстояние и время увеличились в два раза. Для этого воспользуемся отношением одноименных величин.

Покажем, что расстояние увеличилось в два раза:

Аналогично покажем, что время увеличилось во столько же раз

Соединим эти отношения знаком равенства, получим пропорцию:

«100 километров так относятся к 50 километрам, как 2 часа относятся к 1 часу»

Если выполнить деление в обеих частях равенства 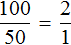, то обнаружим что расстояние и время были увеличены в одинаковое число раз.

Задача 2. За 3 ч на мельнице смололи 27 т пшеничной муки. Сколько тонн пшеничной муки можно смолоть за 9 ч, если темп работы не изменится?

Решение

Время работы мельницы и масса перемолотой муки — прямо пропорциональные величины. При увеличении времени работы в несколько раз, количество перемолотой муки увеличится во столько же раз. Покажем это с помощью пропорции.

В задаче дано 3 ч. Эти 3 ч увеличились до 9 ч. Запишем отношение 9 ч к 3 ч. Это отношение будет показывать во сколько раз увеличилось время работы мельницы:

Теперь запишем второе отношение. Это будет отношение x тонн пшеничной муки к 27 тоннам. Данное отношение будет показывать, что количество перемолотой муки увеличилось во столько же раз, сколько и время работы мельницы

Соединим эти отношения знаком равенства, получим пропорцию .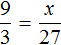

Воспользуемся основным свойством пропорции и найдем x

Значит за 9 ч можно смолоть 81 т пшеничной муки.

Вообще, если взять две прямо пропорциональные величины и увеличить их в одинаковое число раз, то отношение нового значения к старому значению первой величины будет равно отношению нового значения к старому значению второй величины.

Так и в предыдущей задаче старые значения были 3 ч и 27 т. Эти значения были увеличены в одинаковое число раз (в три раза). Новыми значениями стали 9 ч и 81 т. Тогда отношение нового значения времени работы мельницы к старому значению равно отношению нового значения массы перемолотой муки к старому значению

Если выполнить деление в обеих частях равенства, то обнаружим, что время работы мельницы и количество смолотой муки увеличилось в одинаковое число раз:

Пропорцию, которую составляют к задачам на прямую пропорциональность, можно описать с помощью выражения:

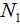
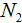
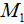
Применительно к нашей задаче значения переменных будут следующими:

Где впоследствии стало равно 81.

Задача 2. Для 8 коров в зимнее время доярка ежедневно заготовляет 80 кг сена, 96 кг корнеплодов, 120 кг силоса и 12 кг концентратов. Определить ежедневный расход этих кормов для 18 коров.

Решение

Количество коров и масса каждого из кормов — прямо пропорциональные величины. При увеличении количества коров в несколько раз, масса каждого из кормов увеличится во столько же раз.

Составим несколько пропорций, вычисляющих массу каждого из кормов для 18 коров.

Начнем с сена. Ежедневно для 8 коров его заготовляют 80 кг. Тогда для 18 коров будет заготовлено x кг сена.

Запишем отношение, показывающее во сколько раз увеличилось количество коров:

Теперь запишем отношение, показывающее во сколько раз увеличилась масса сена:

Соединим эти отношения знаком равенства, получим пропорцию:

Отсюда находим x

Значит для 18 коров нужно заготовить 180 кг сена. Аналогично определяем массу корнеплодов, силоса и концентратов.

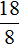
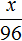
Для 8 коров ежедневно заготовляют 96 кг корнеплодов. Тогда для 18 коров будет заготовлено x кг корнеплодов. Составим пропорцию из отношений и , затем вычислим значение x

Определим сколько силоса и концентратов нужно заготовить для 18 коров:

Значит для 18 коров ежедневно нужно заготавливать 180 кг сена, 216 кг корнеплодов, 270 кг силоса и 27 кг концентратов.

Задача 3. Хозяйка варит вишнёвое варенье, причём на 3 стакана вишни кладёт 2 стакана сахара. Сколько сахара нужно положить на 12 стаканов вишни? на 10 стаканов вишни? на стакана вишни?

Решение

Количество стаканов вишни и количество стаканов сахарного песка — прямо пропорциональные величины. При увеличении количества стаканов вишни в несколько раз, количество стаканов сахара увеличится во столько же раз.

Запишем отношение, показывающее во сколько раз увеличилось количество стаканов вишни:

Теперь запишем отношение, показывающее во сколько раз увеличилось количество стаканов сахара:

Соединим эти отношения знаком равенства, получим пропорцию и найдем значение x

Значит на 12 стаканов вишни нужно положить 8 стаканов сахара.

Определим количество стаканов сахара для 10 стаканов вишни и стакана вишни

Задачи на обратную пропорциональность

Для решения задач на обратную пропорциональность опять же можно использовать пропорцию, составленную из отношений одноименных величин.

В отличие от прямой пропорциональности, где величины увеличиваются или уменьшаются в одну и ту же сторону, в обратной пропорциональности величины изменяются обратно друг другу.

Если одна величина увеличивается в несколько раз, то другая уменьшается во столько же раз. И наоборот, если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз.

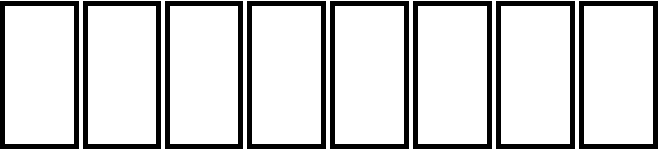
Допустим, что нужно покрасить забор, состоящий из 8 листов

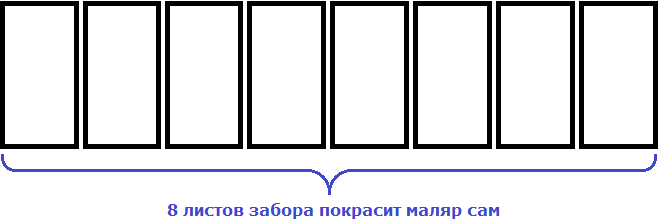
Один маляр будет красить все 8 листов сам

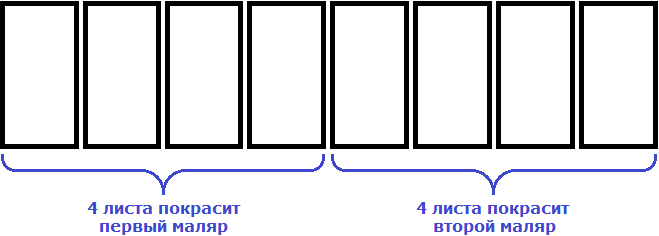
Если маляров будет 2, то каждый покрасит по 4 листа.

Это конечно же при условии, что маляры будут честными между собой и справедливо разделят эту работу поровну на двоих.

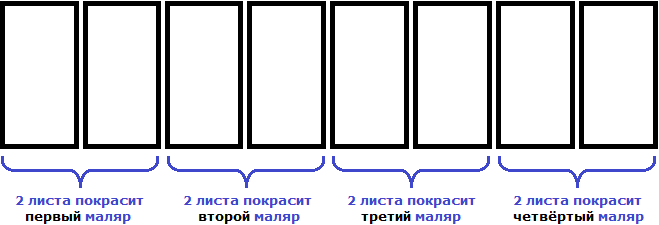
Если маляров будет 4, то каждый покрасит по 2 листа

Замечаем, что при увеличении количества маляров в несколько раз, количество листов которые приходятся на одного маляра уменьшаются во столько же раз.

Итак, мы увеличили количество маляров с 1 до 4. Другими словами, увеличили количество маляров в четыре раза. Запишем это с помощью отношения:

В результате количество листов забора, которые приходятся на одного маляра уменьшилось в четыре раза. Запишем это с помощью отношения:

Соединим эти отношения знаком равенства, получим пропорцию

«4 маляра так относятся к 1 маляру, как 8 листов относятся к 2 листам»

Задача 2. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?

Решение

Количество рабочих и количество дней, затраченных на работу — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней, необходимых для выполнения этой работы, уменьшится во столько же раз.

Запишем отношение 18 рабочих к 15 рабочим. Это отношение будет показывать во сколько раз увеличилось количество рабочих

Теперь запишем второе отношение, показывающее во сколько раз уменьшилось количество дней. Поскольку количество дней уменьшится с 24 дней до x дней, то второе отношение будет отношением старого количества дней (24 дня) к новому количеству дней (x дней)

Соединим полученные отношения знаком равенства, получим пропорцию:

Отсюда находим x

Значит 18 рабочих выполнят необходимую работу за 20 дней.

Вообще, если взять две обратно пропорциональные величины и увеличить одну из них в определенное число раз, то другая уменьшится во столько же раз. Тогда отношение нового значения к старому значению первой величины будет равно отношению старого значения к новому значению второй величины.

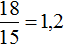
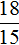
Так и в предыдущей задаче старые значения были 15 рабочих и 24 дня. Количество рабочих было увеличено с 15 до 18 (т.е. было увеличено в раза). В результате количество дней, необходимых для выполнения работы, уменьшилось во столько же раз. Новыми значениями стали 18 рабочих и 20 дней. Тогда отношение нового количества рабочих к старому количеству равно отношению старого количества дней к новому количеству

Для составления пропорции к задачам на обратную пропорциональность можно пользоваться формулой:

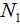
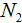
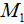
Применительно к нашей задаче значения переменных будут следующими:

Где впоследствии стало равно 20.

Задача 2. Скорость парохода относится к скорости течения реки, как 36 : 5. Пароход двигался вниз по течению 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?

Решение

Собственная скорость парохода составляет 36 км/ч. Скорость течения реки реки 5 км/ч. Поскольку пароход двигался по течению руки, то скорость его движения составила 36 + 5 = 41 км/ч. Время пути составила 5 ч 10 мин. Для удобства выразим время в минутах:

5 ч 10 мин = 300 мин + 10 мин = 310 мин

Поскольку на обратном пути пароход двигался против течения реки, то его скорость составила 36 − 5 = 31 км/ч.

Скорость парохода и время его движения — обратно пропорциональные величины. При уменьшении скорости в несколько раз, время его движения увеличится во столько же раз.

Запишем отношение, показывающее во сколько раз уменьшилась скорость движения:

Теперь запишем второе отношение, показывающее во сколько раз увеличилось время движения. Поскольку новое время x будет больше старого времени, в числителе отношения запишем время x , а в знаменателе старое время, равное трёхсот десяти минутам

Соединим полученные отношения знаком равенства, получим пропорцию 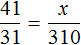. Отсюда найдём значение x

410 минут это 6 часов и 50 минут. Значит пароходу потребуется 6 часов и 50 минут, чтобы вернуться обратно.

Задача 3. На ремонте дороги работало 15 человек, и они должны были закончить работу за 12 дней. На пятый день утром подошли еще несколько рабочих, и оставшаяся работа была выполнена за 6 дней. Сколько рабочих прибыло дополнительно?

Решение

Вычтем из 12 дней 4 отработанных дня. Так мы определим сколько ещё дней осталось работать пятнадцати рабочим

12 дней − 4 дня = 8 дней

На пятый день дополнительно прибыло x рабочих. Тогда всего рабочих стало 15 + x .

Количество рабочих и количество дней, необходимых для выполнения работы — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней уменьшится во столько же раз.

Запишем отношение, показывающее во сколько раз увеличилось количество рабочих:

Теперь запишем во сколько раз уменьшилось количество дней, необходимых для выполнения работы:

Соединим эти отношения знаком равенства, получим пропорцию 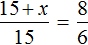. Отсюда можно вычислить значение x

Значит 5 рабочих прибыло дополнительно.

Масштаб

Масштабом называют отношение длины отрезка на изображении к длине соответствующего отрезка на местности.

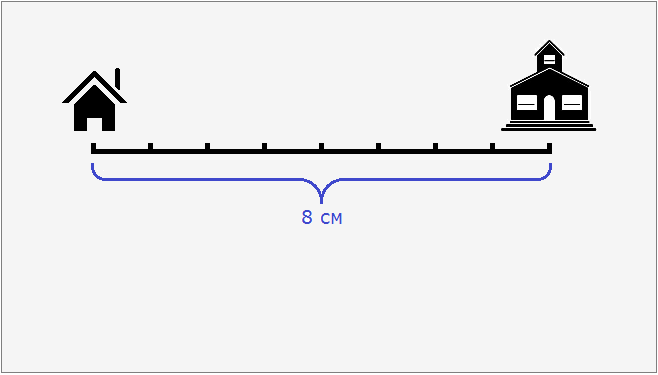
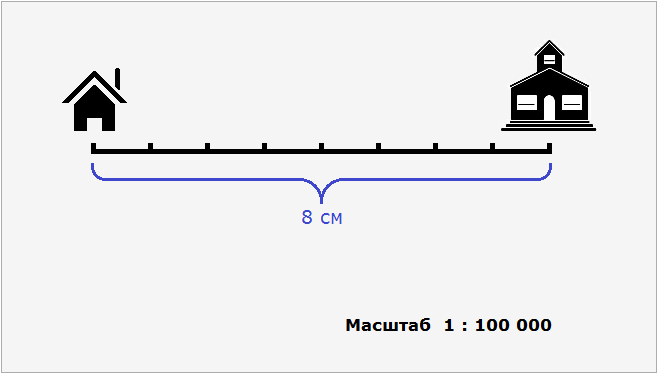
Допустим, что расстояние от дома до школы составляет 8 км. Попробуем нарисовать план местности, где будут указаны дом, школа и расстояние между ними. Но изобразить на бумаге расстояние, равное 8 км мы не можем, поскольку оно довольно велико. Но зато мы можем уменьшить это расстояние в несколько раз так, чтобы оно уместилось на бумаге.

Пусть километры на местности на нашем плане будут выражаться в сантиметрах. Переведем 8 километров в сантиметры, получим 800 000 сантиметров.

Уменьшим 800 000 см в сто тысяч раз:

800 000 см : 100 000 см = 8 см

8 см это расстояние от дома до школы, уменьшенное в сто тысяч раз. Теперь без труда можно нарисовать на бумаге дом и школу, расстояние между которыми будет 8 см.

Эти 8 см относятся к реальным 800 000 см. Так и запишем с помощью отношения:

Одно из свойств отношения гласит, что отношение не меняется если его члены умножить или разделить на одно и то же число.

В целях упрощения отношения 8 : 800 000 оба его члена можно разделить на 8. Тогда получим отношение 1 : 100 000. Это отношение и назовём масштабом. Данное отношение показывает, что один сантиметр на плане относится (или соответствует) ста тысячам сантиметров на местности.

Поэтому на нашем рисунке необходимо указать, что план составлен в масштабе 1 : 100 000

1 см на плане относится к 100 000 см на местности;
2 см на плане относится к 200000 см на местности;
3 см на плане относится к 300000 на местности и т.д.

К любой карте или плану указывается в каком масштабе они сделаны. Этот масштаб позволяет определять реальное расстояние между объектами.

Так, наш план составлен в масштабе 1 : 100 000. На этом плане расстояние между домом и школой составляет 8 см. Чтобы вычислить реальное расстояние между домом и школой, нужно 8 см увеличить в 100 000 раз. Иными словами, умножить 8 см на 100 000

8 см × 100 000 = 800 000 см

Получаем 800 000 см или 8 км, если перевести сантиметры в километры.

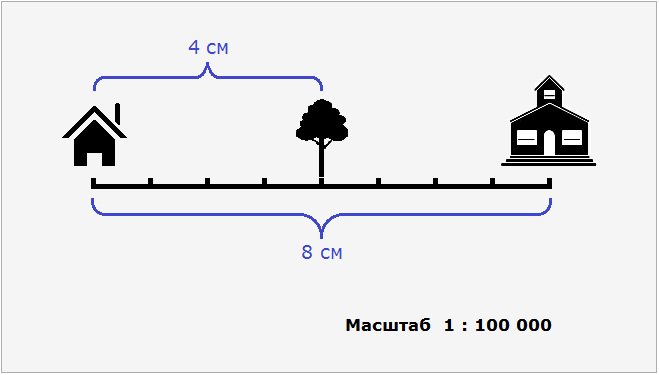
Допустим, что между домом и школой располагается дерево. На плане расстояние между школой и этим деревом составляет 4 см.

Тогда реальное расстояние между домом и деревом будет 4 см × 100 000 = 400 000 см или 4 км.

Расстояние на местности можно определять с помощью пропорции. В нашем примере расстояние между домом и школой будет вычисляться с помощью следующей пропорции:

Эту пропорцию можно прочитать так:

1 см на плане так относится к 100000 см на местности, как 8 см на плане относятся к x см на местности.

Из этой пропорции узнаём, что значение x равно 800000 см.

Пример 2. На карте расстояние между двумя городами составляет 8,5 см. Определить реальное расстояние между городами, если карта составлена в масштабе 1 : 1 000 000.

Решение

Масштаб 1 : 1 000 000 указывает, что 1 см на карте соответствует 1 000 000 см на местности. Тогда 8,5 см будут соответствовать x см на местности. Составим пропорцию 1 к 1000000 как 8,5 к x

В 1 км содержится 100000 см. Тогда в 8 500 000 см будет

Либо можно рассуждать так. Расстояние на карте и расстояние на местности — прямо пропорциональные величины. При увеличении расстояния на карте в несколько раз, расстояние на местности увеличится во столько же раз. Тогда пропорция примет следующий вид. Первое отношение будет показывать во сколько раз расстояние на местности больше расстояния на карте:

Второе отношение покажет, что расстояние на местности во столько же раз больше, чем 8,5 см на карте:

Отсюда x равен 8 500 000 см или 85 км.

Задача 3. Длина реки Невы 74 км. Чему равняется ее длина на карте, масштаб которой 1 : 2 000 000

Решение

Масштаб 1 : 2000000 говорит о том, что 1 см на карте соответствует 2 000 000 см на местности.

А 74 км на это 74 × 100 000 = 7 400 000 см на местности. Уменьшив 7 400 000 в 2 000 000, мы определим длину реки Невы на карте

7 400 000 : 2 000 000 = 3,7 см

Значит на карте, масштаб которой 1 : 2 000 000 длина реки Невы составляет 3,7 см.

Запишем решение с помощью пропорции. Первое отношение будет показывать сколько раз длина на карте меньше длины на местности:

Второе отношение будет показывать, что 74 км (7 400 000 см) уменьшились во столько же раз:

Отсюда находим x равный 3,7 см

Задачи для самостоятельного решения

Решение

Пусть x кг масла можно получить из 7 кг хлопкового семени. Масса хлопкового семени и масса получаемого масла — прямо пропорциональные величины. Тогда уменьшение хлопкового семени с 21 кг до 7 кг, приведет к уменьшению получаемого масла во столько же раз.

Ответ: из 7 кг хлопкового семени получится 1,7 кг масла.

Решение

Длина участка на котором производится замена рельсов равна 8 × 360 = 2880 м.

Пусть x двенадцатиметровых рельсов требуется для замены. Увеличение длины одного рельса с 8 м до 12 м приведет к уменьшению количества рельсов с 360 до x штук. Иными словами, длина рельса и их количество связаны обратно пропорциональной зависимостью

Ответ: для замены старых рельсов потребуется 240 новых.

Решение

Если 60% учащихся пошли в кино, а остальные 12 человек на выставку, то на 40% учащихся и будут приходиться 12 человек, пошедших на выставку. Тогда можно составить пропорцию в которой 12 учащихся так относятся к 40%, как все x учащихся относятся к 100%

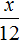
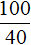
Либо можно составить пропорцию, состоящей из отношений одноименных величин. Количество учащихся и процентная доля изменяются прямо пропорционально. Тогда можно записать, что во сколько раз увеличилось количество участников во столько же раз увеличилась процентная доля (с 40% до 100%)

Ответ: в классе 30 учащихся.

Решение

Масштаб 1 : 500000 говорит о том, что 1 см на карте соответствует 500 000 см на местности.

Тогда увеличив 18 см в 500 000, мы получим действительное расстояние между городами

18 см × 500 000 = 9 000 000 см

Переведем 9 000 000 см в километры. В одном километре 100 000 см. Тогда в 9 000 000 см будет

Запишем решение с помощью пропорции:

Ответ: расстояние между городами 90 км.

Решение

Скорость и время — обратно пропорциональные величины. При увеличении скорости в несколько раз, время движения уменьшится во столько же раз.

Запишем отношение, показывающее по сколько раз увеличилась скорость движения пешехода:

Запишем отношение, показывающее что время движения уменьшилось во столько же раз:

Соединим эти отношения знаком равенства, получим пропорцию и найдём значение x

Ответ: пешеход затратит 2 часа если будет двигаться со скорость 4,5 км/ч.

Решение

Выражение «перевыполнили план на 15%» означает, что к имеющемуся 100% плану выполнили еще 15% того же плана. Итого выполнено 115% плана. На эти 115% приходятся 230 выпущенных станков

А по плану завод должен был выпустить x станков. Эти x станков приходятся на 100% изначального плана

Составим пропорцию из имеющихся отношений и найдём значение x

Либо можно воспользоваться отношениями одноименных величин. Количество выпущенных станков и процентная доля, на которые эти станки приходятся, связаны прямо пропорциональной зависимостью. При увеличении количества станков в несколько раз, процентная доля увеличивается во столько же раз. Тогда можно записать, что 230 станков во столько раз больше, чем x станков, во сколько раз больше 115%, чем 100%

Ответ: по плану завод должен был выпустить 200 станков.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

11 thoughts on “Решение задач с помощью пропорции”

Огромное спасибо за урок! Мне мама пыталась объяснить пропорции, а я не понимала) А теперь все просто благодаря вам!

Боже мой, почему мне так сложно? 🙁

Сразу не получится. Нужно время

Отличный урок! Пожалуйста, не забрасывайте этот проект, популяризировать математику необходимо. Уверен, многие люди, как и я, готовы поддержать Вас рублём, если вы дадите такую возможность. Большое спасибо за уже проделанную Вами работу, людей необходимо просвещать, особенно в наше время.

В разделе « решение задач с помощью пропорции» в задаче 2 есть фраза «сто километров так относятся к одному часу, как триста километров к неизвестному числу часов»:» и составлена пропорция 100/2= 300/x. Во
фразе опечатка, 100 километров при составлении пропорции относится к 2 часам а не к одному.

«составленнаю из отношений одноименных величин.» -> составленную

Калькулятор пропорций онлайн

Вводить можно целые числа, десятичные дроби, правильные и неправильные дроби -5, 5, 0.25, -1.25, 10/8, -1/2 и.т.д.

Если вам необходимо ввести смешанное число то предварительно его нужно преобразовать в неправильную дробь. Т.е. 3 целые 1/3 нужно будет записать как 10/3

Поле которое необходимо рассчитать можно оставить пустым или ввести любую букву латинского(английского) алфавита.

В расчётное поле можно также вводить значения с переменными вида: 5x, 1.2x, 5/x, x/5, 3x/2, 2/3x. Т.е. если вам надо посчитать (2/3)*х то нужно записать как 2x/3. Если надо посчитать (1/2)*(1/x) то нужно будет ввести 1/2x.

Метод решения задач с процентами

Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции

Данные задачи на проценты можно записать в виде следующих соотношений:

все – 100% часть – часть в %

которые можно записать в виде пропорции

все	=	100%
часть	часть в %

Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.

Примеры решения задач на проценты

30 соответствует 100% x соответствует 15%

решим полученное уравнение

Ответ: 15% от 30 равно 4.5.

20 соответствует 100% 35 соответствует x

решим полученное уравнение

Ответ: 35 составляет 175% от 20.

x соответствует 100% 20 соответствует 5%

решим полученное уравнение

Ответ: 400.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Как решать задачи с процентами

О чем эта статья:

Основные определения

Когда мы описываем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы называть сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

0,18 = 0,18 · 100% = 18%.

А вот, как перевести проценты в десятичную дробь — обратным действием:

Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. Блогер записал 500 видео для тиктока, но его продюсер сказал, что 20% из них — отстой. Сколько роликов придется перезаписать блогеру?

Как решаем: нужно найти 20% от общего количества снятых роликов (500).

Ответ: из общего количества снятых роликов продюсер забраковал 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

40 : 0,16 = 40 · 100 : 16 = 250

Ответ: 250 задач собрано в этом учебнике.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В секретном чатике 25 человек. 10 из них — девочки. Сколько процентов девочек в чате?

Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%

Ответ: в чатике 40% девочек.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

А можно воспользоваться формулой:

a = b · (1 + с : 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?

Как решаем: можно найти 12% от 110:

Прибавить к исходному числу:

110 + 13,2 = 123,2 рубля.

Или можно воспользоваться формулой, тогда:

110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.

Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

А можно воспользоваться формулой:

a = b · (1 − с : 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?

Как решаем: можно найти 25% от 100:

Вычесть из исходного числа 100 − 25 = 75 человек.

Или можно воспользоваться формулой, тогда:

100 · (1 − 25 : 100) = 75/p>

Ответ: 75 выпускников в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а · (1 + у · х : 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?

Как решаем: подставим в формулу данные из условий задачи.

70 000 · (1 + 12 · 8 : 100) = 137 200

Ответ: 137 200 рублей вернет Мария через год.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

S = а · (1 + х : 100) y ,

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?

Как решаем: просто подставим в формулу данные из условий задачи:

10000 · (1 + 10 : 100)3 = 13 310

Ответ: 13 310 рублей снимет Антон через год.

Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!

Способы нахождения процента

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем:

Переведем 15% в рубли:

250 : 100 = 2,5 — это 1% от стоимости шоколада,

значит 2,5 * 15 = 37,5 — это 15%.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

0,6х – 0,25 * 0,6x = 0,45x

После двух понижений изменение цены составит:

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Текстовые задачи на уравнения и системы.

Здесь Вы сможете потренироваться в решении текстовых задач ЕГЭ по математике, для которых, как правило, требуется составить и решить уравнение или систему уравнений, реже – неравенство или сиcтему неравенств. В демонстрационном варианте профильного уровня ЕГЭ 2022 года эти задачи могут встретиться под номером 8.

Рекомендую начинать решение таких задач с краткой записи их условия. И ни в коем случае не спешите смотреть ответы и решения раньше, чем успеете сами подумать о них. Возможны разные способы решения, и не факт, что Ваш способ намного хуже моего.

Задачи с участием водного транспорта.

Такие задачи очень часто сводятся к решению квадратного уравнения. Повторите его.

Задача 1

Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

Cкорость яхты в неподвижной воде обозначим символом v.
Плот движется со скоростью течения реки (2 км/ч), поэтому легко вычислить, за сколько времени плот прошел 24 км: 24/2 = 12 часов.
Яхта отправилась на час позже, значит она была в пути 12 – 1 = 11 часов. За это время она проследовала из пункта A в пункт В по течению реки со скоростью v + 2 км/ч, затратив на это 120/(v + 2) часов, и обратно – против течения со скоростью v – 2 км/ч, затратив на возвращение 120/(v – 2) часов.
Приравнивая сумму времен на путь туда и обратно общему времени в пути, составляем уравнение и решаем его.

Отрицательный корень уравнения в качестве скорости яхты не имеет смысла, поэтому v = 22 км/ч.

Ответ: 22

Задача 2

Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.

Обозначим символом v км/ч собственную скорость лодки. Тогда скорость лодки по течению реки составляет v + 1 км/ч, на обратном пути v – 1 км/ч.
Расстояние между пунктами нам известно. Определим время в пути по течению реки 30/(v + 1) часов и время в пути против течения 30/(v – 1) часов. Сложив эти времена, можем узнать общее время движения лодки.
С другой стороны, нам известны начальный и конечный моменты всей поезки, можем определить её длительность. Всего поездка длилась 18 – 10 = 8 часов. Из них 2 часа 30 минут = 2,5 часа лодка была на стоянке в пункте В, значит всего в движении 8 – 2,5 = 5,5 часов.
Приравнивая эти времена, составляем уравнение и решаем его. Так как в уравнении присутствуют дроби, то число 5,5 тоже удобнее записать в виде обыкновенной дроби 11/2.

Отрицательный корень уравнения в качестве скорости лодки не имеет смысла, поэтому v = 11 км/ч.

Ответ: 11

Задача 3

Пристани A и B расположены на озере, расстояние между ними равно 390 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.

Обозначим символом v км/ч скорость баржи в направлении от А к В. Тогда скорость баржи в обратном направлении равна v + 3 км/ч. От А к В баржа двигалась 390/v часов, обратно двигалась 390/(v + 3) часов и еще 9 часов стояла, всего на обратный путь ушло 390/(v + 3) + 9 часов. По условию время в пути туда равно времени на обратный путь, поэтому можем приравнять времена, составить и решить уравнение.

Отрицательный корень уравнения в качестве скорости баржи не имеет смысла, поэтому v = 10 км/ч.

Ответ: 10

Замечание: На озере нет скорости течения воды в одном направлении.

В следующей задаче появляется дополнительное “действующее лицо” – время года, поэтому становится удобнее решать не уравнением, а системой уравнений.

Задача 4

Весной катер идёт против течения реки в 1 2 /₃ раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 1 /₂ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Обозначим символом v собственную скорость катера (км/ч), символом x – скорость течения реки весной (км/ч). Тогда скорость течения реки летом составляет (x – 1) км/ч. Имеем
весной: катер идёт против течения со скоростью (v – x), по течению со скоростью (v + x). По условию первая скорость в 1 2 /₃ раза меньше, т.е.
(v + x)/(v – x) = 1 2 /₃ ;
летом: катер идёт против течения со скоростью (v – (x – 1)), по течению со скоростью (v + (x – 1)). По условию первая скорость в 1 1 /₂ раза меньше, т.е.
(v + (x – 1))/(v – (x – 1)) = 1 1 /₂ .
Объединяем уравнения в систему и решаем её:

Ответ: 5

Смешав 45%-ный и 97%-ный растворы кислоты и добавив 10 кг чистой воды, получили 62%-ный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ного раствора той же кислоты, то получили бы 72%-ный раствор кислоты. Сколько килограммов 45%-ного раствора использовали для получения смеси?

Задачи на проценты с уравнениями и без них.

Следующую задачу можно отнести к задачам на сплавы и растворы, а можно считать такой же обычной задачей на проценты, как простые текстовые задачи на проценты. В этот раздел, как я полагаю, она отнесена не за математическую трудность, а за “трудность” понятий “виноград” и “изюм”. Не так ли?

Задача 5

Виноград содержит 90% влаги, а изюм – 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?

Для получения изюма виноград сушат, т.е. удаляют из него влагу. Влага нам не нужна, нужно остальное!
Способ I.
Этого остального в изюме 100% – 5% = 95%, т.е. 20·0,95 = 19 кг. (95% = 0,95. Часть от числа находим умножением.)
В винограде остального было столько же, 19 кг. (Оно не исчезало и не прирастало при сушке.) По условию задачи остальное в винограде составляло 100% – 90% = 10%. Таким образом 10% = 0,1 составляют 19 кг. Число по его части находим делением: 19/0,1 = 190 кг.
Для получения 20 килограммов изюма потребуется 190 килограммов винограда.
Способ II.
Обозначим вес винограда за x кг. Определим количество не влаги (остального) в винограде: x – x·0,9. Определим количество не влаги (остального) в изюме: 20 – 20·0,05. Это равные количества, поэтому можно составить уравнение
x – x·0,9 = 20 – 20·0,05.
Решаем уравнение: x·(1 – 0,9) = 20 – 1; x·0,1 = 19; x = 19/0,1 = 190.

Ответ: 190

И еще одна простая задача на проценты, подобная тем, которые мы решали в разделе “Простые текстовые задачи”.

Задача 6

В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2010 году – на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?

В 2008 году проживало 100% или 40000 человек, в 2009 году – на 8% больше, т.е. 108%, или 40000·1,08 = 43200 человек.
В 2009 году проживало 100% или 43200 человек, в 2010 году – на 9% больше, т.е. 109%, или 43200·1,09 = 47088 человек.

Ответ: 47088

А теперь сравните следующую и предыдущую задачи. Похожи?

Задача 7

В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

При открытии торгов в понедельник акции стоили 100% или А рублей, до начала торгов во вторник – на х% больше, т.е. (100 + х)% или А·(100 + х)/100 рублей.
При открытии торгов во вторник акции стоили 100% или А·(100 + х)/100 рублей, по окончании торгов во вторник – на х% меньше, т.е. (100 – х)% или (А·(100 + х)/100)·(100 – х)/100 рублей.
С другой стороны,
при открытии торгов в понедельник акции стоили 100% или А рублей, по окончании торгов во вторник – на 4% меньше, т.е. 96% или А·0,96 рублей.
Составляем уравнение для стоимости акций на конец дня вторника:
(А·(100 + х)/100)·(100 – х)/100 = А·0,96.
Обе части уравнения разделим на А и умножим на 100 2 , получим:
(100 + х)·(100 – х) = 9600.
Таким образом, в уравнении величина А “сократилась”, т.е. она не была дана в условии потому, что не влияет на результат решения. Нам А понадобилась только для того, чтобы рассуждать аналогично предыдущей простой задаче.
Итак, решаем уравнение:
100 2 – х 2 = 9600;
х 2 = 10000 – 9600 = 400;
х = 20 (%).

Ответ: 20

Задача 8

Митя, Антон, Гоша и Борис учредили компанию с уставным капиталом 200000 рублей. Митя внес 14% уставного капитала, Антон – 42000 рублей, Гоша – 0,12 уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1000000 рублей причитается Борису? Ответ дайте в рублях.

Определим какая часть уставного капитала внесена каждым учредителем. Митя – 14% = 0,14. Антон – 42000/200000 = 0,21. Гоша – 0,12. Борис – 1 − (0,14 + 0,21 + 0,12) = 0,53.
Прибыль делится пропорционально внесенному капиталу. Следовательно, если Борис внес 0,53 части от 200000, то он должен получить также 0,53 части от 1000000. Часть от числа находим умножением 1000000×0,53 = 530000 (рублей).

Ответ: 530000

Задачи на системы линейных уравнений.

Задача 9

Имеется два сплава. Первый содержит 5% никеля, второй – 20% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Обозначим за х кг массу первого сплава, за y кг массу второго. Соединив сплавы вместе, получили х + y = 225 кг третьего сплава.
При получении третьего сплава также объединили весь никель. В первом сплаве его было х·0,05 кг, во втором было y·0,20 кг, в третьем стало х·0,05 + y·0,20, что по условию задачи составляет 15% от 225 кг, т.е. 225·0,15 кг = 33,75 кг. Таким образом, х·0,05 + y·0,20 = 33,75.Получили два уравнения объединяем их в систему и решаем её.

Определили массы обоих сплавов х = 75 кг и y = 150 кг. В ответе требуется записать их разность (на сколько масса первого меньше массы второго), т.е. 150 – 75 = 75 (кг).

Ответ: 75

Одна из главных трудностей при алгебраическом решении текстовых задач состоит в выборе неизвестной величины или величин, которые будут обозначены буквами. Я советую начинать либо с того, что спрашивается в вопросе задачи, либо с того, что содержится в основной формуле, которая описывает процесс. Например, решение задачи на движение основано на применении правила “расстояние = скорость × время”. Значит либо расстояние = x, либо время = t, либо скорость = v, смотря что дано, а что неизвестно. При этом, можно получить алгебраические уравнения разного вида. Ведь и “скорость = расстояние : время” и “время = расстояние : скорость”. Собственно это варианты одной и той же физической формулы. И от того, в каком варианте вы её раньше вспомните, будет зависеть, как вы введёте обозначения и какие получите уравнения. Здесь не может быть правильного или неправильного начала решения задачи, начните как-нибудь, важно, чтобы было правильным окончание. Однако, решение может оказаться оптимальным и неоптимальным. Вы можете получить слишком громоздкие и сложные уравнения. В этом случае стоит попробовать вернуться к началу задачи и ввести другое обозначение.

Системы уравнений имеет смысл составлять тогда, когда в задаче идет речь о двух или нескольких объектах, на которые одновременно действуют два или несколько факторов, накладывается два или несколько совместимых условий и т.п. Таких ситуаций много в быту, в технике и, особенно много, в экономике. Те из вас, кто собирается продолжать образование, еще не раз столкнутся с системами из разного количества уравнений с разным количеством неизвестных. На экзамене, как правило, вы будете составлять и решать системы из двух уравнений с двумя неизвестными.

Задачи на объезд, обгон и встречное движение.

Когда мы решаем на уроке математики задачи на движение, мы редко вспоминаем о том, что все формулы относятся к описанию движения материальной точки. Происходит это потому, что движущийся объект, как правило, очень мал по сравнению с расстоянием, которое он проходит. Например, поезд, который следует из Москвы в Тюмень всего лишь точка на карте России. Но поезд, который едет по железной дороге в то время, когда мы стоим на переезде и ждем его, вовсе не точка. Его проезд вдоль закрытого шлагбаума занимает порой значительное время. Можно ли в этом случае применять те же формулы? Давайте заглянем в учебник физики, раздел механика. Ответ: можно, если не требуется учитывать вращение или деформирование движущегося объекта. Как применять? Записать их для некоторой точки этого объекта, чаще всего, для центра тяжести. Однако это необязательно, можно выбрать любую точку, которая неподвижна относительно самого объекта.

Итак, чтобы решать задачи на поступательное движение с протяженным объектом, ставим на нём точку в удобном месте, затем чертим схему, на которой отмечаем положение этой точки в заданные моменты времени. И не забываем перейти к одинаковым единицам измерения.

В следующих задачах с поездами, точку я ставила в самом начале – “на носу” поезда. Схему рисовала на нижней линии, а выше рисунки, которые её поясняют.

Задача 10

Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.

Решение

1) Время дано в секундах, длину проезда нужно найти в метрах, поэтому выразим скорость в м/c. Умножим на 1000, чтобы перейти от километров к метрам, и дважды разделим на 60, чтобы перевести часы в минуты, а минуты в секунды: 80 км/ч = 80·1000/60/60 = 800/36 м/с.
2) Ставим красную точку “на носу” поезда. Чертим схему, на которой отмечаем положение этой точки, когда поезд только начал движение мимо столба, и положение этой точки через 36 секунд, когда поезд проехал мимо столба.

3) По схеме видно, что точка прошла расстояние AB. Известно время (36 с), известна скорость (800/36 м/с), можем найти это расстояние.
AB = (800/36)·36 = 800 (м).
4) Из рисунка видно, что это расстояние совпадает с длиной поезда.

Ответ: 800

Замечание: иногда лучше не производить до конца деление в промежуточных выкладках, потому что в конце дробь может легко сократиться, как это получилось здесь с числом 36.

Задача 11

Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.

Решение

1) Время дано в минутах, длину проезда нужно найти в метрах, поэтому выразим скорость в м/мин: 60 км/ч = 60·1000/60 м/мин = 1000 м/мин.
2) Ставим красную точку “на носу” поезда. Чертим схему, на которой отмечаем положение этой точки, когда поезд начал движение мимо лесополосы, и положение этой точки через минуту, когда поезд только что проехал её полностью.

3) По схеме видно, что точка прошла расстояние AС. Известно время (1 мин), известна скорость (1000 м/мин), можем найти это расстояние: AC = 1000·1 = 1000 (м).
4) Из рисунка видно, что это расстояние состоит из двух частей – отрезок AВ равен длине поезда и отрезок ВС равен длине лесополосы.
Находим AВ = AC − BC = 1000 − 400 = 600 (м).

Ответ: 600

Задача 12

По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.

Решение

1) Время дано в минутах, ответ нужно дать в метрах, поэтому выражаем обе скорости в м/мин: 90 км/ч = 90·1000/60 = 1500 м/мин; 30 км/ч = 30·1000/60 = 500 м/мин.
2) Ставим красную точку “на носу” пассажирского поезда, и фиолетовую точку “на носу” товарного поезда. Чертим схему, на которой отмечаем положение обеих точек в момент, когда пассажирский поезд догнал товарный, и их положение через минуту, когда пассажирский поезд закончил обгон товарного.

3) По схеме видно, что красная точка прошла расстояние AD за 1 минуту со скоростью 1500 м/мин, следовательно AD = 1500·1 = 1500 (м). Аналогично, фиолетовая точка прошла расстояние BС за 1 минуту со скоростью 500 м/мин, следовательно BC = 500·1 = 500 (м).
4) Из рисунка видно, что AD = AB + ВС + CD, где отрезок AВ равен длине пассажирского поезда, отрезок СD равен длине товарного поезда.
Находим длину пассажирского поезда AВ = AD − BC − CD = 1500 − 500 − 600 = 400 (м).

Ответ: 400

Задача 13

По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

Ответ: 300

Для тех из вас, кто знает, что такое относительная скорость, и не боится элементов физики в математических задачах, напоминаю, что существует приём, позволяющий заметно упростить решение задач на объезд, обгон и встречное движение. Нужно один объект “остановить”, а скорость другого увеличить на величину скорости первого, если они движутся навстречу друг другу, или, соответственно, уменьшить, если оба движутся в одном направлении. Ниже приведено решение задач 12 и 13 этим способом.

Решение способом II для задачи 12.
Рассмотрим движение пассажирского поезда относительно товарного. Тогда товарный поезд “стоит”, а пассажирский едет со скоростью 90 – 30 = 60 км/ч = 1000 м/мин. С этой скоростью за 1 минуту он проезжает расстояние 1000 м, равное длине товарного поезда плюс его собственная длина. (См. картинку к задаче 11 про лесополосу, в качестве которой теперь выступает “стоящий” товарный поезд.) Следовательно, его собственная длина = 1000 – 600 = 400 м.

Ответ: 400.

Решение способом II для задачи 13.
Рассмотрим движение скорого поезда относительно пассажирского. Тогда пассажирский поезд “стоит”, а скорый едет со скоростью 65 + 35 = 100 км/ч = 100×1000/3600 = 1000/36 м/c. С этой скоростью за 36 секунд он проезжает расстояние 1000 м, равное длине пассажирского поезда плюс его собственная длина. (См. картинку к задаче 11 про лесополосу, в качестве которой теперь выступает “стоящий” пассажирский поезд.) Следовательно, его собственная длина = 1000 – 700 = 300 м.

Ответ: 300.

Какой способ лучше – судить вам. Но сначала попробуйте самостоятельно решить следующую задачу.

Задача 14

По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй – длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Скорость движения первого сухогруза в метрах в минуту (м/мин) обозначим символом v₁, второго – символом v₂. Тогда за 12 минут первый сухогруз прошел расстояние v₁·t = v₁·12 (м), второй сухогруз прошел расстояние v₂·t = v₂·12 (м).
Ставим красную точку на носу первого сухогруза, зеленую – на носу второго. Рисуем схему: точки A, C – положение судов в начальный момент времени, D, F – в конечный. Точками B и Е обозначаем положение кормы сухогруза, идущего впереди.

На схеме AF = AB + BC + CD + DE + EF, где отрезки
АВ – отставание носа второго сухогруза от кормы первого в начале наблюдения, AB = 400 м;
ВС – длина первого сухогруза (расстояние от носа до кормы), ВС = 120 м;
СD – расстояние, пройденное первым сухогрузом за время наблюдения, СD = v₁·12 м;
DE – отставание носа первого сухогруза от кормы второго через 12 минут, DE = 600 м;
EF – длина второго сухогруза (расстояние от носа до кормы), EF = 80 м;
AF – расстояние, пройденное вторым сухогрузом за время наблюдения, AF = v₂·12 м.
Подставляем длины отрезков в равенство и проводим вычисления:
v₂·12 = 400 + 120 + v₁·12 + 600 + 80;
v₂·12 = v₁·12 + 1200; (v₂ − v₁)·12 = 1200; v₂ − v₁ = 1200/12 = 100 (м/мин).
Таким образом, скорость первого сухогруза меньше скорости второго на 100 метров в минуту. Чтобы дать ответ в километрах в час, нужно умножить на 60 (минут в часе) и разделить на 1000 (метров в километре): 100·60/1000 = 6 км/ч.

Найдём разность скоростей сухогрузов в метрах в минуту. Эта величина является относительной скоростью, с которой более быстрый корабль движется относительно “остановленного” медленного. Разберёмся, какое расстояние он прошел за описанные в условии задачи 12 минут:
1) нос движущегося сухогруза догнал корму “остановленного” – 400 м;
2) нос движущегося сухогруза прошел вдоль “остановленного” – 120 м;
3) сухогруз переместился на расстояние равное своей длине так, что его корма расположилась у носа “остановленного”, – 80 м;
4) движущийся сухогруз прошел ещё 600 м.
Итого движущийся с относительной скоростью сухогруз прошёл за 12 минут расстояние равное 400 + 120 + 80 + 600 = 1200 (м). Следовательно, относительная скорость составила 1200/12 = 100 (м/мин). Поскольку это и есть искомая разность скоростей, то для ответа на вопрос задачи осталось только перейти к километрам в час: 100×60/1000 = 6 (км/ч).

Ответ: 6

Замечание: Точек на схеме (даже не цветных) вполне достаточно, чтобы разобраться в задаче. Если трудно, то дайте точкам осмысленные имена. Например, Н₁ – нос первого, К₂ – корма второго. Если всё еще трудно, рисуйте поезда, корабли и самолёты символическими прямоугольниками.

Задачи на среднюю скорость.

Чтобы найти среднее арифметическое нескольких чисел, нужно их сложить и разделить сумму на количество слагаемых. Например, среднее арифметическое чисел 1, 12, 30, 45 равно 22. Но всегда ли на практике нас интересует именно среднее арифметическое? Если 19 учеников сдали экзамен на 5-ку и только один на 2-ку, можно ли считать, что класс в целом успевает посредственно и заслужил среднюю оценку (5 + 2)/2 = 3,5? Не справедливее ли было учесть “вес” 5-ки и 2-ки? В данном случае это можно сделать, сложив все оценки всех учеников и разделив сумму на число учеников в классе: (19×5 + 1×2)/20 = 4,85. Вполне достойный результат.

Итак, средняя величина и среднее арифметическое чисел, характеризующих эту величину, не одно и то же.

Например, если автомобиль двигался 3 часа со скоростью 100 км/ч и 1 час со скоростью 10 км/ч, то за 4 часа он проехал расстояние S = 100×3 + 10×1 = 310 (км). Значит его средняя скорость составляла 310/4 = 77,5 км/ч. А если автомобиль двигался 3 часа со скоростью 10 км/ч и 1 час со скоростью 100 км/ч, то за 4 часа он проехал расстояние S = 10×3 + 100×1 = 130 (км), и его средняя скорость составляла 130/4 = 32,5 км/ч.

Для сравнения вычислим среднее арифметическое значение: (110 + 10)/2 = 55 (км/ч). В первом случае автомобиль большую часть времени ехал быстро, поэтому его средняя скорость больше среднего арифметического значения, а во втором – большую часть времени медленно, поэтому средняя скорость меньше среднего арифметического.

Рассмотрим еще два случая.
Пусть автомобиль двигался 2 часа со скоростью 100 км/ч и 2 часа со скоростью 10 км/ч, тогда за 4 часа он проехал расстояние S = 100×2 + 10×2 = 220 (км). Значит его средняя скорость составляла 220/4 = 55 км/ч, что совпадает со средним арифметическим значением. Так получилось потому, что вклад быстрого и медленного движения был одинаковым по времени.
И, наконец, пусть автомобиль двигался первые 110 км со скоростью 100 км/ч, а следующие 110 км со скоростью 10 км/ч, в итоге на первую половину пути он потратил 110/100 = 1,1 часа, а на вторую – 110/10 = 11 часов. Тогда весь путь 220 км он проехал за 1,1 + 11 = 12,1 часа со средней скоростью 220/12,1 = 18,18182 км/ч, что снова сильно отличается от среднего арифметического значения. Так получилось потому, что вклад быстрого и медленного движения был разным по времени, хотя и одинаковым по длине пройденных участков.

Задача 15

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Всего в пути автомобиль был 2 + 1 + 2 = 5 часов. Проехал расстояние 50·2 + 100·1 + 75·2 = 350 километров. Средняя скорость 350/5 = 70 км/ч.

Ответ: 70

Задача 16

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км – со скоростью 90 км/ч, а затем 170 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Всего автомобиль проделал путь длиной 190 + 180 + 170 = 540 км. Первый участок проехал за 190/50 = 3,8 часа, второй – за 180/90 = 2 часа, третий – за 170/100 = 1,7 часа. Всего был в пути 3,8 + 2 + 1,7 = 7,5 часа. Средняя скорость 540/7,5 = 72 км/ч.

Ответ: 72

Задача 17

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Ответ: 88

Задачи на производительность.

Производительность труда – эффективность труда в процессе производства. Измеряется количеством продукции, произведенной в единицу времени, или количеством времени, затраченного на производство единицы продукции.
Производительность оборудования – объём продукции (работы), производимой в единицу времени данным оборудованием. Измеряется в тоннах, штуках, метрах и т.п. на единицу времени.

В любом случае к задачам на производительность, надо относиться так же, как к задачам на движение с заданной (или искомой) скоростью, так как

Задача 18

Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Способ I.
Весь заказ обозначим символом Z, время, которое рабочие работали вместе, обозначим символом t. Каждый из двух рабочих работает со скоростью Z/15. За 3 часа первый рабочий выполнил (Z/15)·3 заказа, еще за t часов оба рабочих выполнили (Z/15)·t·2 заказа. Таким образом, был выполнени весь заказ, т.е. (Z/15)·3 + (Z/15)·t·2 = Z.
Умножаем обе части уравнения на 15 и делим на Z. Получим
3 + t·2 = 15; t·2 = 12; t = 6.
Таким образом, на выполнение всего завказа потребовалось 3 + t = 3 + 6 = 9 часов.

Способ II.
Каждый из двух рабочих за час выполняет 1/15 часть заказа. За 3 часа первый рабочий выполнил 3·(1/15) = 3/15 = 1/5 часть заказа. Оставшиеся 1 – 1/5 = 4/5 части заказа рабочие делали вместе со скоростью 2·(1/15) = 2/15 части в час, следовательно выполнили эту работу за время (4/5)/(2/15) = (4·15)/(5·2) = 6 часов. Таким образом, весь заказ был выполнен за 3 + 6 = 9 часов.

Ответ: 9

Замечание: Способ II, на мой взгляд, лучше. Но, если вы за то время, которое занимались алгеброй, забыли арифметику, вводите дополнительную неизвестную величину – весь объем продукции или работы. После составления уравнения эта величина должна сократиться.

Задача 19

Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов теста, а Ваня – на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?

Пусть тест содержит х вопросов. Петя ответил за х/8 часов. Ваня ответил за х/9 часов. Петя закончил свой тест позже Вани на х/8 – х/9 часов или на (х/8 – х/9)·60 минут, что по условию задачи составило 20 минут:
(х/8 – х/9)·60 = 20;
х·(1/8 – 1/9)·3 = 1;
х·(3/8 – 1/3) = 1; х·(9 – 8)/24 = 1; х = 24.

Ответ: 24

Задача 20

Первый насос наполняет бак за 20 минут, второй – за 30 минут, а третий – за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?

В вопросе задачи время в минутах, поэтому везде перейдем к минутам. 1 час = 60 мин.
Способ I.
Объём бака обозначим символом V литров, тогда первый насос работает со скоростью V/20 л/мин, второй – со скоростью V/30 л/мин и третий – со скоростью V/60 л/мин. Работая одновременно, они наполняют бак со скоростью V/20 + V/30 + V/60 = V·(1/20 + 1/30 + 1/60) = V·(3 + 2 + 1)/60 = V·0,1 (л/мин). Значит весь бак будет наполнен за V/(V·0,1) = 10 минут.
Способ II.
Первый насос наполняет за минуту 1/20 часть бака, второй – 1/30 часть и третий – 1/60 часть. Работая одновременно, они наполняют за минуту 1/20 + 1/30 + 1/60 = 6/60 = 1/10 часть бака. Значит весь бак будет наполнен за 10 минут.

Ответ: 10

Задача 21

Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?

Пусть вторая труба наполняет резервуар за t минут, тогда за одну минуту она наполняет 1/t часть резервуара. Первая труба наполняет резервуар дольше, за t + 6 минут, а за минуту она наполняет 1/(t+6) часть резервуара. Обе трубы вместе за минуту наполняют 1/t + 1/(t+6) часть резервуара. С другой стороны, они вместе наполняют резервуар за 4 минуты, значит за минуту – 1/4 часть. Составим и решим уравнение:
1/t + 1/(t+6) = 1/4; 4(t+6) + 4t = t(t+6); 8t + 24 = t 2 + 6t;
t 2 − 2t − 24 = 0. Корни уравнения t₁ = 6; t₂ = −4. Отрицательный корень не имеет смысла, следовательно t = 6.

Ответ: 6

Если у Вас возникли трудности с решением этих задач, то уверены ли Вы, что разобрались с более простыми текстовыми задачами в заданиях с меньшими номерами демонстрационного варианта?

Вернуться к списку заданий первой части профильного уровня ЕГЭ по математике.

Нашли опечатку или ошибку? Пожалуйста, сообщите о ней.
E-mail: mathematichka@yandex.ru

Внимание, © mathematichka.
Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/kak-reshat-zadachi-s-procentami

http://mathematichka.ru/ege/problems/problem_B13.html

[/spoiler]

Метод решения задач с процентами

Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции

Данные задачи на проценты можно записать в виде следующих соотношений:

все      –      100%
часть      –      часть в %

которые можно записать в виде пропорции

Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.

Примеры решения задач на проценты

Пример 1.

Найти число B составляющее 15% от числа 30.

Решение:

30       соответствует       100%
x       соответствует       15%

Запишим пропорцию

решим полученное уравнение

Ответ: 15% от 30 равно 4.5.

Пример 2.

Найти сколько процентов составляет число 35 от числа 20.

Решение:

20       соответствует       100%
35       соответствует       x

Запишим пропорцию

решим полученное уравнение

Ответ: 35 составляет 175% от 20.

Пример 3.

Найти число, 5% которого равны 20.

Решение:

x       соответствует       100%
20       соответствует       5%

Запишим пропорцию

решим полученное уравнение

Ответ: 400.

При изучении процентов вам также будут полезны: