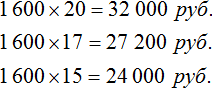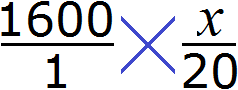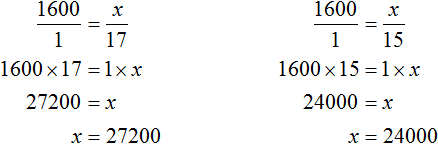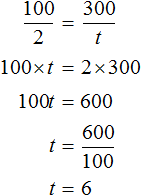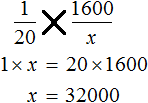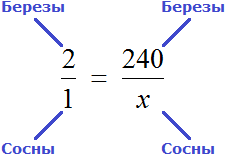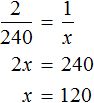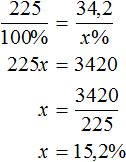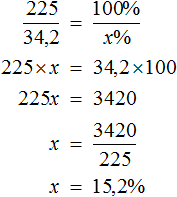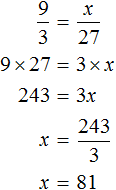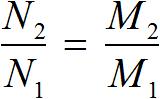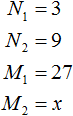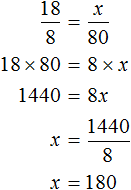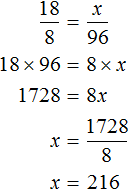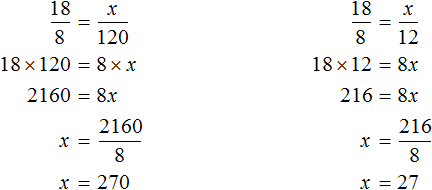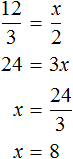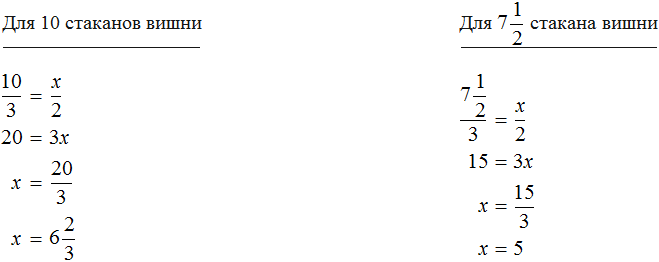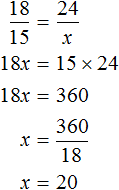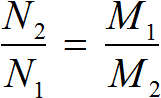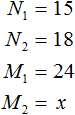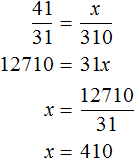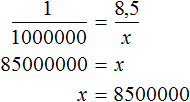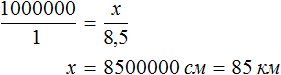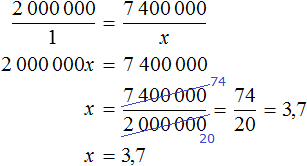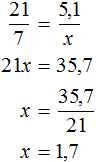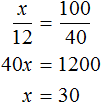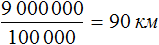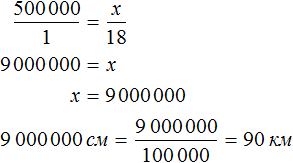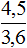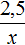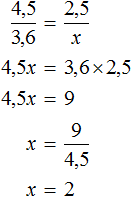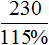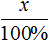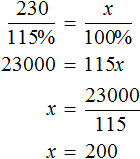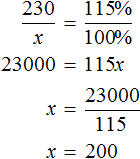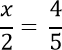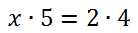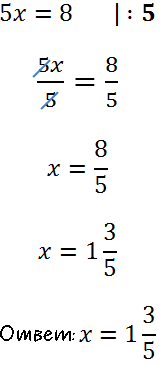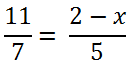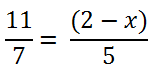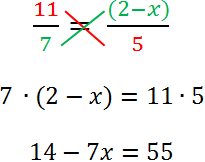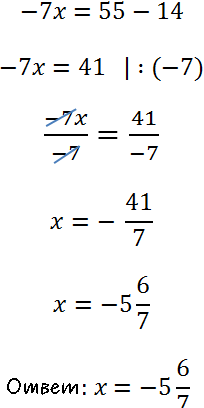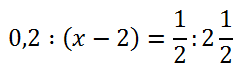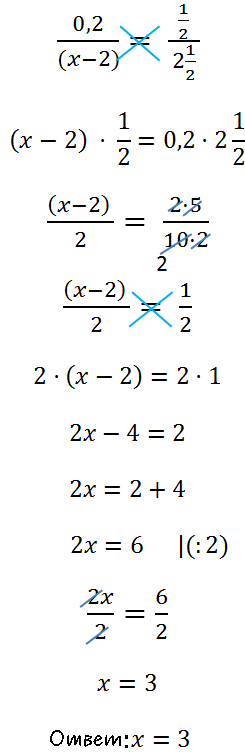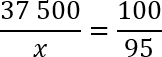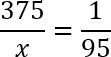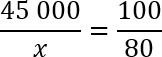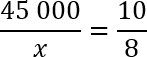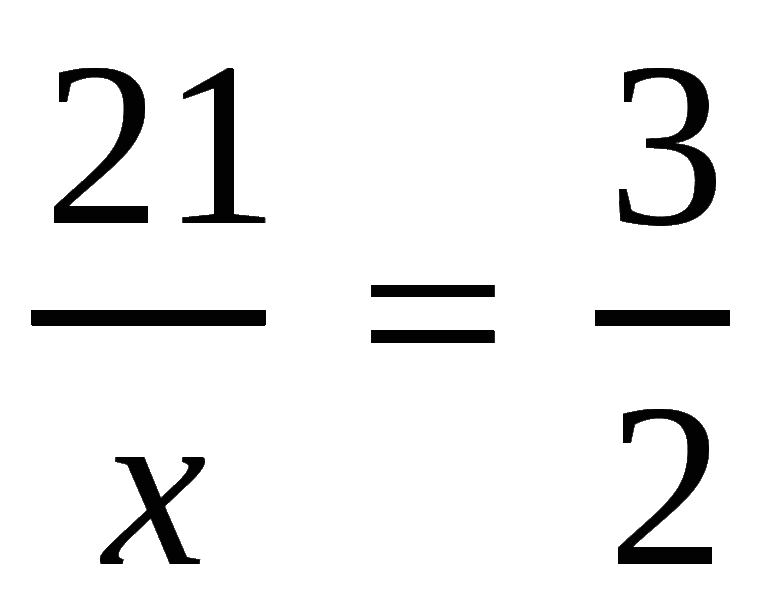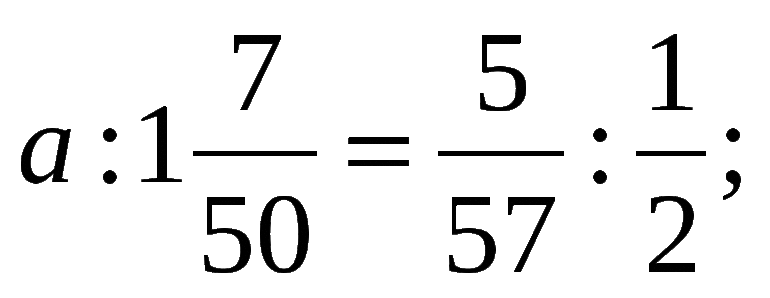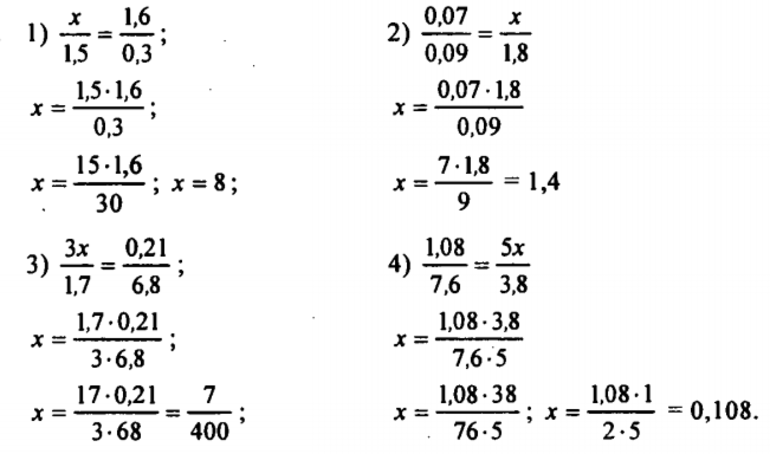Решение задачи с помощью пропорции сводится к тому, чтобы сделать неизвестное значение x членом этой пропорции. Затем используя основное свойство пропорции получить линейное уравнение и решить его.
Как решить задачу с помощью пропорции
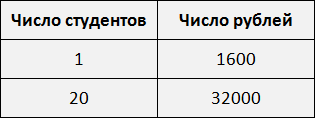
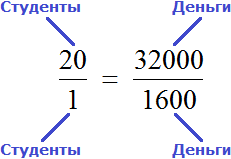
Рассмотрим простейший пример. Трем группам нужно выплатить стипендию по 1600 рублей каждому. В первой группе 20 студентов. Значит первой группе будет выплачено 1600 × 20, то есть 32 тыс. рублей.
Во второй группе 17 человек. Значит второй группе будет выплачено 1600 × 17, то есть 27,200 тыс. руб.
Ну и выплатим стипендию третьей группе. В ней 15 человек. На них нужно затратить 1600 × 15, то есть 24 тыс. руб.
В результате имеем следующее решение:
Для подобных задач решение можно записывать с помощью пропорции.
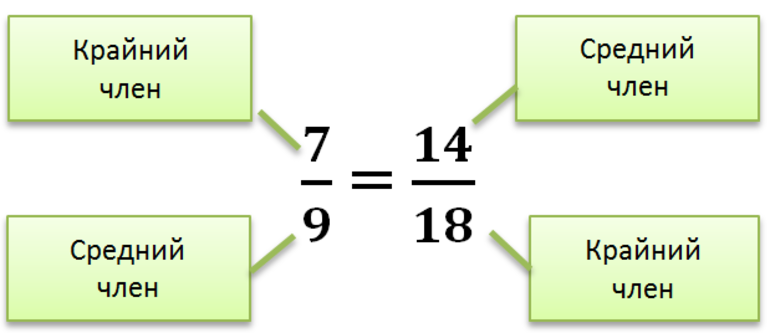
Пропорция по определению есть равенство двух отношений. К примеру, равенство является пропорцией. Эту пропорцию можно прочесть следующим образом:
a так относится к b, как c относится d
Аналогично можно соотнести стипендию и студентов, так чтобы каждому досталось по 1600 рублей.
Итак, запишем первое отношение, а именно отношение тысячи шестисот рублей на одного человека:
Мы выяснили, что для выплаты 20 студентам по 1600 рублей, нам потребуется 32 тыс. рублей. Значит второе отношение будет отношением тридцати двух тысяч к двадцати студентам:
Теперь соединим полученные отношения знаком равенства:
Мы получили пропорцию. Её можно прочесть следующим образом:
Тысяча шестьсот рублей так относятся к одному студенту, как тридцать две тысячи рублей относятся к двадцати студентам.
То есть по 1600 рублей каждому. Если выполнить деление в обеих частях равенства , то обнаружим, что одному студенту, как и двадцати студентам достанется по 1600 рублей.
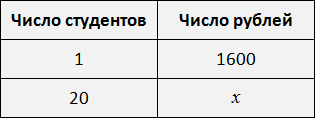
Теперь представим, что сумма денег, необходимых для выплаты стипендии двадцати студентам, была бы неизвестной. Скажем, если бы вопрос стоял так: в группе 20 студентов и каждому нужно выплатить по 1600 рублей. Сколько всего рублей требуется для выплаты стипендии?
В таком случае пропорция приняла бы вид
. То есть сумма денег, необходимая для выплаты стипендии, стала неизвестным членом пропорции. Эту пропорцию можно прочесть так:
Тысяча шестьсот рублей так относятся к одному студенту, как неизвестное число рублей относится к двадцати студентам
Теперь воспользуемся основным свойством пропорции. Оно гласит, что произведение крайних членов пропорции равно произведению средних:
Перемножив члены пропорции «крест-накрест», получим равенство 1600 × 20 = 1 × x. Вычислив обе части равенства, получим 32000 = x или x = 32000. Иными словами, мы найдём значение неизвестной величины, которое искали.
Аналогично можно было определить общую сумму и для остального количества студентов — для 17 и 15. Эти пропорции выглядели как и
. Воспользовавшись основным свойством пропорции, можно найти значение x
Задача 2. Расстояние равное 100 км автобус проехал за 2 часа. Сколько времени потребуется автобусу, чтобы проехать 300 км, если будет ехать с той же скоростью?
Можно сначала определить расстояние, которое автобус проезжает за один час. Затем определить сколько раз это расстояние содержится в 300 километрах:
100 : 2 = 50 км на каждый час движения
300 км : 50 = 6 часов
Либо можно составить пропорцию «сто километров так относятся к двум часам, как триста километров к неизвестному числу часов»:
Отношение одноименных величин
Если крайние или средние члены пропорции поменять местами, то пропорция не нарушится.
Так, в пропорции можно поменять местами крайние члены. Тогда получится пропорция
.
Пропорция также не нарушится, если её перевернуть, то есть использовать обратные отношения в обеих частях.
Перевернем пропорцию . Тогда получим пропорцию
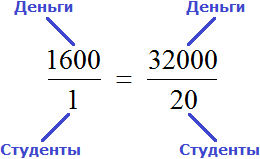
. Взаимосвязь при этом не нарушается. Отношение между студентами равно отношению между суммами денег, предназначенных для этих студентов. Такую пропорцию часто составляют в школе, когда для решения задачи составляются таблицы
Этот способ записи очень удобен, поскольку позволяет перевести условие задачи в более понятный вид. Решим задачу в которой требовалось определить сколько рублей нужно для выплаты стипендии двадцати студентам.
Условие задачи запишем следующим образом:
Составим таблицу на основе этого условия:
Составим пропорцию, используя данные таблицы:
Используя основное свойство пропорции, получим линейное уравнение и найдем его корень:
Изначально, мы имели дело с пропорцией , которая составлена из отношений величин разной природы. В числителях отношений располагались суммы денег, а в знаменателях количество студентов:
Поменяв местами крайние члены, мы получили пропорцию . Эта пропорция составлена из отношений величин одной природы. В первом отношении содержатся количества студентов, а во втором — суммы денег:
Если отношение составлено из величин одной природы, то мы будем называть его отношением одноименных величин. Например, отношения между фруктами, деньгами, физическими величинами, явлениями, действиями.
Отношение может быть составлено, как из одноименных величин, так и из величин разной природы. Примерами последних являются отношение расстояния ко времени, отношения стоимости товара к его количеству, отношение общей суммы стипендии к количеству студентов.
Пример 2. В школьном саду посажены сосны и березы, причём на каждую сосну приходится 2 березы. Сколько посадили сосен в саду, если берез посадили 240?
Определим сколько сосен было посажено в саду. Для этого составим пропорцию. В условии сказано, что на каждую сосну приходится 2 березы. Напишем отношение, показывающее что на одну сосну приходится две березы:
Теперь напишем второе отношение, показывающее что на x сосен приходится 240 берез
Соединим эти отношения знаком равенства, получим следующую пропорцию:
«2 березы так относятся к одной сосне,
как 240 берез относятся к x соснам»
Используя основное свойство пропорции, находим значение x
Либо пропорцию можно составить, предварительно записав условие, как в прошлом примере:
Получится та же пропорция, но в этот раз она будет составлена из отношений одноименных величин:
Значит в саду посадили 120 сосен.
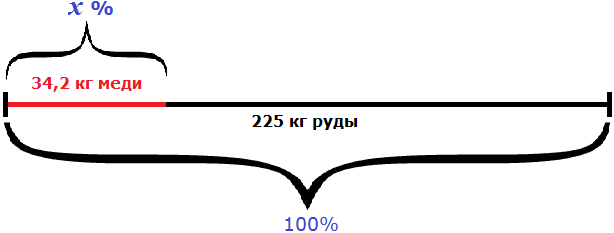
Пример 3. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?
Можно разделить 34,2 на 225 и полученный результат выразить в процентах:
Либо составить пропорцию 225 килограммам руды так приходятся на 100%, как 34,2 кг меди приходятся на неизвестное число процентов:
Либо составить пропорцию в которой отношения составлены из одноименных величин:
Задачи на прямую пропорциональность
Понимание отношений одноименных величин приводит к пониманию решения задач на прямую и обратную пропорциональность. Начнем с задач на прямую пропорциональность.
Для начала вспомним, что такое прямая пропорциональность. Это взаимосвязь между двумя величинами при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
Если расстояние в 50 км автобус прошел за 1 час, то для прохождения расстояния в 100 км (при той же скорости) автобусу потребуется 2 часа. Во сколько раз увеличилось расстояние, во столько же раз увеличилось время движения. Как показать это с помощью пропорции?
Одно из предназначений отношения заключается в том, чтобы показать во сколько раз первая величина больше второй. А значит и мы c помощью пропорции можем показать, что расстояние и время увеличились в два раза. Для этого воспользуемся отношением одноименных величин.
Покажем, что расстояние увеличилось в два раза:
Аналогично покажем, что время увеличилось во столько же раз
Соединим эти отношения знаком равенства, получим пропорцию:
«100 километров так относятся к 50 километрам, как 2 часа относятся к 1 часу»
Если выполнить деление в обеих частях равенства , то обнаружим что расстояние и время были увеличены в одинаковое число раз.
2 = 2
Задача 2. За 3 ч на мельнице смололи 27 т пшеничной муки. Сколько тонн пшеничной муки можно смолоть за 9 ч, если темп работы не изменится?
Решение
Время работы мельницы и масса перемолотой муки — прямо пропорциональные величины. При увеличении времени работы в несколько раз, количество перемолотой муки увеличится во столько же раз. Покажем это с помощью пропорции.
В задаче дано 3 ч. Эти 3 ч увеличились до 9 ч. Запишем отношение 9 ч к 3 ч. Это отношение будет показывать во сколько раз увеличилось время работы мельницы:
Теперь запишем второе отношение. Это будет отношение x тонн пшеничной муки к 27 тоннам. Данное отношение будет показывать, что количество перемолотой муки увеличилось во столько же раз, сколько и время работы мельницы
Соединим эти отношения знаком равенства, получим пропорцию .
Воспользуемся основным свойством пропорции и найдем x
Значит за 9 ч можно смолоть 81 т пшеничной муки.
Вообще, если взять две прямо пропорциональные величины и увеличить их в одинаковое число раз, то отношение нового значения к старому значению первой величины будет равно отношению нового значения к старому значению второй величины.
Так и в предыдущей задаче старые значения были 3 ч и 27 т. Эти значения были увеличены в одинаковое число раз (в три раза). Новыми значениями стали 9 ч и 81 т. Тогда отношение нового значения времени работы мельницы к старому значению равно отношению нового значения массы перемолотой муки к старому значению
Если выполнить деление в обеих частях равенства, то обнаружим, что время работы мельницы и количество смолотой муки увеличилось в одинаковое число раз:
3 = 3
Пропорцию, которую составляют к задачам на прямую пропорциональность, можно описать с помощью выражения:
Применительно к нашей задаче значения переменных
будут следующими:
Где впоследствии стало равно 81.
Задача 2. Для 8 коров в зимнее время доярка ежедневно заготовляет 80 кг сена, 96 кг корнеплодов, 120 кг силоса и 12 кг концентратов. Определить ежедневный расход этих кормов для 18 коров.
Решение
Количество коров и масса каждого из кормов — прямо пропорциональные величины. При увеличении количества коров в несколько раз, масса каждого из кормов увеличится во столько же раз.
Составим несколько пропорций, вычисляющих массу каждого из кормов для 18 коров.
Начнем с сена. Ежедневно для 8 коров его заготовляют 80 кг. Тогда для 18 коров будет заготовлено x кг сена.
Запишем отношение, показывающее во сколько раз увеличилось количество коров:
Теперь запишем отношение, показывающее во сколько раз увеличилась масса сена:
Соединим эти отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит для 18 коров нужно заготовить 180 кг сена. Аналогично определяем массу корнеплодов, силоса и концентратов.
Для 8 коров ежедневно заготовляют 96 кг корнеплодов. Тогда для 18 коров будет заготовлено x кг корнеплодов. Составим пропорцию из отношений и
, затем вычислим значение x
Определим сколько силоса и концентратов нужно заготовить для 18 коров:
Значит для 18 коров ежедневно нужно заготавливать 180 кг сена, 216 кг корнеплодов, 270 кг силоса и 27 кг концентратов.
Задача 3. Хозяйка варит вишнёвое варенье, причём на 3 стакана вишни кладёт 2 стакана сахара. Сколько сахара нужно положить на 12 стаканов вишни? на 10 стаканов вишни? на стакана вишни?
Решение
Количество стаканов вишни и количество стаканов сахарного песка — прямо пропорциональные величины. При увеличении количества стаканов вишни в несколько раз, количество стаканов сахара увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество стаканов вишни:
Теперь запишем отношение, показывающее во сколько раз увеличилось количество стаканов сахара:
Соединим эти отношения знаком равенства, получим пропорцию и найдем значение x
Значит на 12 стаканов вишни нужно положить 8 стаканов сахара.
Определим количество стаканов сахара для 10 стаканов вишни и стакана вишни
Задачи на обратную пропорциональность
Для решения задач на обратную пропорциональность опять же можно использовать пропорцию, составленную из отношений одноименных величин.
В отличие от прямой пропорциональности, где величины увеличиваются или уменьшаются в одну и ту же сторону, в обратной пропорциональности величины изменяются обратно друг другу.
Если одна величина увеличивается в несколько раз, то другая уменьшается во столько же раз. И наоборот, если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз.
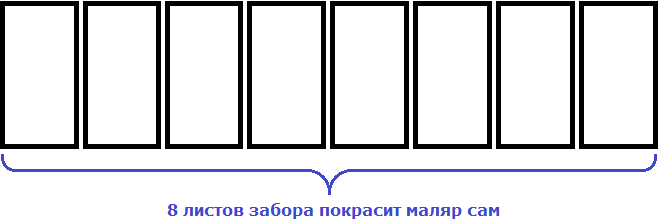
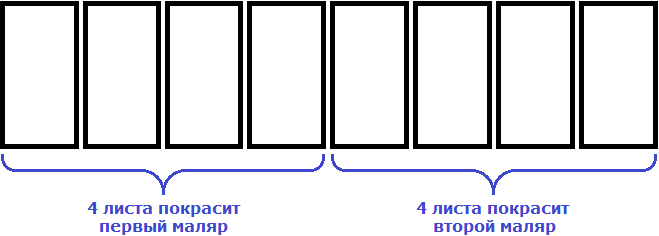
Допустим, что нужно покрасить забор, состоящий из 8 листов
Один маляр будет красить все 8 листов сам
Если маляров будет 2, то каждый покрасит по 4 листа.
Это конечно же при условии, что маляры будут честными между собой и справедливо разделят эту работу поровну на двоих.
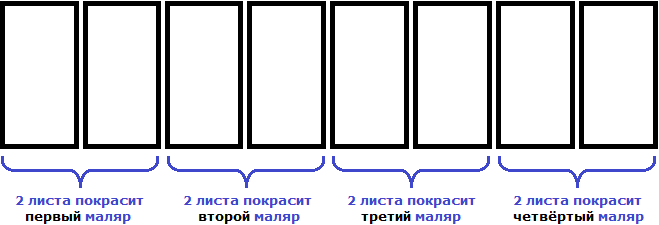
Если маляров будет 4, то каждый покрасит по 2 листа
Замечаем, что при увеличении количества маляров в несколько раз, количество листов которые приходятся на одного маляра уменьшаются во столько же раз.
Итак, мы увеличили количество маляров с 1 до 4. Другими словами, увеличили количество маляров в четыре раза. Запишем это с помощью отношения:
В результате количество листов забора, которые приходятся на одного маляра уменьшилось в четыре раза. Запишем это с помощью отношения:
Соединим эти отношения знаком равенства, получим пропорцию
«4 маляра так относятся к 1 маляру, как 8 листов относятся к 2 листам»
Задача 2. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?
Решение
Количество рабочих и количество дней, затраченных на работу — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней, необходимых для выполнения этой работы, уменьшится во столько же раз.
Запишем отношение 18 рабочих к 15 рабочим. Это отношение будет показывать во сколько раз увеличилось количество рабочих
Теперь запишем второе отношение, показывающее во сколько раз уменьшилось количество дней. Поскольку количество дней уменьшится с 24 дней до x дней, то второе отношение будет отношением старого количества дней (24 дня) к новому количеству дней (x дней)
Соединим полученные отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит 18 рабочих выполнят необходимую работу за 20 дней.
Вообще, если взять две обратно пропорциональные величины и увеличить одну из них в определенное число раз, то другая уменьшится во столько же раз. Тогда отношение нового значения к старому значению первой величины будет равно отношению старого значения к новому значению второй величины.
Так и в предыдущей задаче старые значения были 15 рабочих и 24 дня. Количество рабочих было увеличено с 15 до 18 (т.е. было увеличено в раза). В результате количество дней, необходимых для выполнения работы, уменьшилось во столько же раз. Новыми значениями стали 18 рабочих и 20 дней. Тогда отношение нового количества рабочих к старому количеству
равно отношению старого количества дней к новому количеству
Для составления пропорции к задачам на обратную пропорциональность можно пользоваться формулой:
Применительно к нашей задаче значения переменных
будут следующими:
Где впоследствии стало равно 20.
Задача 2. Скорость парохода относится к скорости течения реки, как 36 : 5. Пароход двигался вниз по течению 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?
Решение
Собственная скорость парохода составляет 36 км/ч. Скорость течения реки реки 5 км/ч. Поскольку пароход двигался по течению руки, то скорость его движения составила 36 + 5 = 41 км/ч. Время пути составила 5 ч 10 мин. Для удобства выразим время в минутах:
5 ч 10 мин = 300 мин + 10 мин = 310 мин
Поскольку на обратном пути пароход двигался против течения реки, то его скорость составила 36 − 5 = 31 км/ч.
Скорость парохода и время его движения — обратно пропорциональные величины. При уменьшении скорости в несколько раз, время его движения увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз уменьшилась скорость движения:
Теперь запишем второе отношение, показывающее во сколько раз увеличилось время движения. Поскольку новое время x будет больше старого времени, в числителе отношения запишем время x, а в знаменателе старое время, равное трёхсот десяти минутам
Соединим полученные отношения знаком равенства, получим пропорцию . Отсюда найдём значение x
410 минут это 6 часов и 50 минут. Значит пароходу потребуется 6 часов и 50 минут, чтобы вернуться обратно.
Задача 3. На ремонте дороги работало 15 человек, и они должны были закончить работу за 12 дней. На пятый день утром подошли еще несколько рабочих, и оставшаяся работа была выполнена за 6 дней. Сколько рабочих прибыло дополнительно?
Решение
Вычтем из 12 дней 4 отработанных дня. Так мы определим сколько ещё дней осталось работать пятнадцати рабочим
12 дней − 4 дня = 8 дней
На пятый день дополнительно прибыло x рабочих. Тогда всего рабочих стало 15 + x.
Количество рабочих и количество дней, необходимых для выполнения работы — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней уменьшится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество рабочих:
Теперь запишем во сколько раз уменьшилось количество дней, необходимых для выполнения работы:
Соединим эти отношения знаком равенства, получим пропорцию . Отсюда можно вычислить значение x
Значит 5 рабочих прибыло дополнительно.
Масштаб
Масштабом называют отношение длины отрезка на изображении к длине соответствующего отрезка на местности.
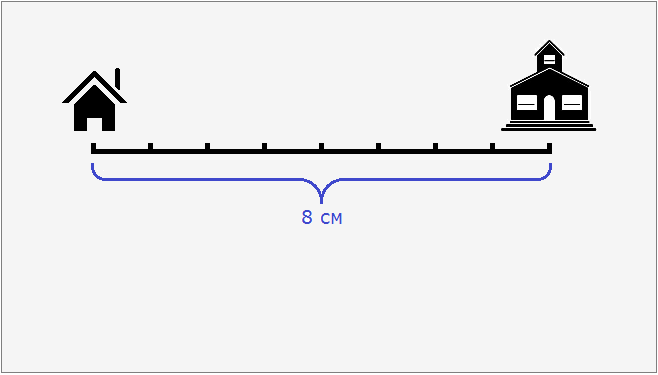
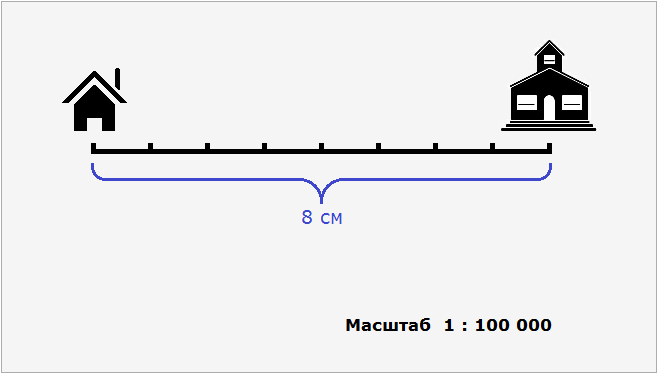
Допустим, что расстояние от дома до школы составляет 8 км. Попробуем нарисовать план местности, где будут указаны дом, школа и расстояние между ними. Но изобразить на бумаге расстояние, равное 8 км мы не можем, поскольку оно довольно велико. Но зато мы можем уменьшить это расстояние в несколько раз так, чтобы оно уместилось на бумаге.
Пусть километры на местности на нашем плане будут выражаться в сантиметрах. Переведем 8 километров в сантиметры, получим 800 000 сантиметров.
Уменьшим 800 000 см в сто тысяч раз:
800 000 см : 100 000 см = 8 см
8 см это расстояние от дома до школы, уменьшенное в сто тысяч раз. Теперь без труда можно нарисовать на бумаге дом и школу, расстояние между которыми будет 8 см.
Эти 8 см относятся к реальным 800 000 см. Так и запишем с помощью отношения:
8 : 800 000
Одно из свойств отношения гласит, что отношение не меняется если его члены умножить или разделить на одно и то же число.
В целях упрощения отношения 8 : 800 000 оба его члена можно разделить на 8. Тогда получим отношение 1 : 100 000. Это отношение и назовём масштабом. Данное отношение показывает, что один сантиметр на плане относится (или соответствует) ста тысячам сантиметров на местности.
Поэтому на нашем рисунке необходимо указать, что план составлен в масштабе 1 : 100 000
Примеры:
1 см на плане относится к 100 000 см на местности;
2 см на плане относится к 200000 см на местности;
3 см на плане относится к 300000 на местности и т.д.
К любой карте или плану указывается в каком масштабе они сделаны. Этот масштаб позволяет определять реальное расстояние между объектами.
Так, наш план составлен в масштабе 1 : 100 000. На этом плане расстояние между домом и школой составляет 8 см. Чтобы вычислить реальное расстояние между домом и школой, нужно 8 см увеличить в 100 000 раз. Иными словами, умножить 8 см на 100 000
8 см × 100 000 = 800 000 см
Получаем 800 000 см или 8 км, если перевести сантиметры в километры.
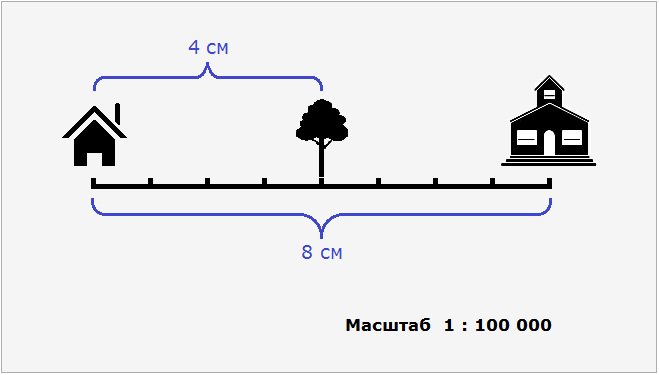
Допустим, что между домом и школой располагается дерево. На плане расстояние между школой и этим деревом составляет 4 см.
Тогда реальное расстояние между домом и деревом будет 4 см × 100 000 = 400 000 см или 4 км.
Расстояние на местности можно определять с помощью пропорции. В нашем примере расстояние между домом и школой будет вычисляться с помощью следующей пропорции:
Эту пропорцию можно прочитать так:
1 см на плане так относится к 100000 см на местности, как 8 см на плане относятся к x см на местности.
Из этой пропорции узнаём, что значение x равно 800000 см.
Пример 2. На карте расстояние между двумя городами составляет 8,5 см. Определить реальное расстояние между городами, если карта составлена в масштабе 1 : 1 000 000.
Решение
Масштаб 1 : 1 000 000 указывает, что 1 см на карте соответствует 1 000 000 см на местности. Тогда 8,5 см будут соответствовать x см на местности. Составим пропорцию 1 к 1000000 как 8,5 к x
В 1 км содержится 100000 см. Тогда в 8 500 000 см будет
Либо можно рассуждать так. Расстояние на карте и расстояние на местности — прямо пропорциональные величины. При увеличении расстояния на карте в несколько раз, расстояние на местности увеличится во столько же раз. Тогда пропорция примет следующий вид. Первое отношение будет показывать во сколько раз расстояние на местности больше расстояния на карте:
Второе отношение покажет, что расстояние на местности во столько же раз больше, чем 8,5 см на карте:
Отсюда x равен 8 500 000 см или 85 км.
Задача 3. Длина реки Невы 74 км. Чему равняется ее длина на карте, масштаб которой 1 : 2 000 000
Решение
Масштаб 1 : 2000000 говорит о том, что 1 см на карте соответствует 2 000 000 см на местности.
А 74 км на это 74 × 100 000 = 7 400 000 см на местности. Уменьшив 7 400 000 в 2 000 000, мы определим длину реки Невы на карте
7 400 000 : 2 000 000 = 3,7 см
Значит на карте, масштаб которой 1 : 2 000 000 длина реки Невы составляет 3,7 см.
Запишем решение с помощью пропорции. Первое отношение будет показывать сколько раз длина на карте меньше длины на местности:
Второе отношение будет показывать, что 74 км (7 400 000 см) уменьшились во столько же раз:
Отсюда находим x равный 3,7 см
Задачи для самостоятельного решения
Задача 1. Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
Решение
Пусть x кг масла можно получить из 7 кг хлопкового семени. Масса хлопкового семени и масса получаемого масла — прямо пропорциональные величины. Тогда уменьшение хлопкового семени с 21 кг до 7 кг, приведет к уменьшению получаемого масла во столько же раз.
Ответ: из 7 кг хлопкового семени получится 1,7 кг масла.
Задача 2. На некотором участке железнодорожного пути старые рельсы длиной в 8 м заменили новыми длиной в 12 м. Сколько потребуется новых двенадцатиметровых рельсов, если сняли 360 старых рельсов?
Решение
Длина участка на котором производится замена рельсов равна 8 × 360 = 2880 м.
Пусть x двенадцатиметровых рельсов требуется для замены. Увеличение длины одного рельса с 8 м до 12 м приведет к уменьшению количества рельсов с 360 до x штук. Иными словами, длина рельса и их количество связаны обратно пропорциональной зависимостью
Ответ: для замены старых рельсов потребуется 240 новых.
Задача 3. 60% учеников класса пошли в кино, а остальные 12 человек – на выставку. Сколько учащихся в классе?
Решение
Если 60% учащихся пошли в кино, а остальные 12 человек на выставку, то на 40% учащихся и будут приходиться 12 человек, пошедших на выставку. Тогда можно составить пропорцию в которой 12 учащихся так относятся к 40%, как все x учащихся относятся к 100%
Либо можно составить пропорцию, состоящей из отношений одноименных величин. Количество учащихся и процентная доля изменяются прямо пропорционально. Тогда можно записать, что во сколько раз увеличилось количество участников 
Ответ: в классе 30 учащихся.
Задача 4. Расстояние на карте между городами 18 см. Какое действительное расстояние между городами, если масштаб карты 1 : 500 000?
Решение
Масштаб 1 : 500000 говорит о том, что 1 см на карте соответствует 500 000 см на местности.
Тогда увеличив 18 см в 500 000, мы получим действительное расстояние между городами
18 см × 500 000 = 9 000 000 см
Переведем 9 000 000 см в километры. В одном километре 100 000 см. Тогда в 9 000 000 см будет
Запишем решение с помощью пропорции:
Ответ: расстояние между городами 90 км.
Задача 5. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч
Решение
Скорость и время — обратно пропорциональные величины. При увеличении скорости в несколько раз, время движения уменьшится во столько же раз.
Запишем отношение, показывающее по сколько раз увеличилась скорость движения пешехода:
Запишем отношение, показывающее что время движения уменьшилось во столько же раз:
Соединим эти отношения знаком равенства, получим пропорцию и найдём значение x
Ответ: пешеход затратит 2 часа если будет двигаться со скорость 4,5 км/ч.
Задача 6. Перевыполнив план на 15%, завод выпустил за месяц 230 станков. Сколько станков должен был выпустить за месяц завод по плану?
Решение
Выражение «перевыполнили план на 15%» означает, что к имеющемуся 100% плану выполнили еще 15% того же плана. Итого выполнено 115% плана. На эти 115% приходятся 230 выпущенных станков
А по плану завод должен был выпустить x станков. Эти x станков приходятся на 100% изначального плана
Составим пропорцию из имеющихся отношений и найдём значение x
Либо можно воспользоваться отношениями одноименных величин. Количество выпущенных станков и процентная доля, на которые эти станки приходятся, связаны прямо пропорциональной зависимостью. При увеличении количества станков в несколько раз, процентная доля увеличивается во столько же раз. Тогда можно записать, что 230 станков во столько раз больше, чем x станков, во сколько раз больше 115%, чем 100%
Ответ: по плану завод должен был выпустить 200 станков.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию.
Например, рассмотрим такое уравнение.
Для решения уравнения с пропорцией используют правило пропорции или,
как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке
«Пропорции».
В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Запомните!
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции,
то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции.
Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию
в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и
решим уравнение до конца.
В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Важно!
Если в члене пропорции присутствуют знаки «+» или «−»,
обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда
будете использовать правило пропорции.
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции
для дальнейшего решения.
Теперь раскроем скобки с помощью
правила раскрытия
скобок.
Из урока «Решение линейных уравнений» используем
правило переноса и
правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать
правило знаков.
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
Другие примеры решения уравнений с пропорцией
-
=
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число
-
=
3x · 6,8 = 0,21 · 1,7
20,4 x=
·
20
x =
=204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =
x =
x =
x =
x =
Ответ: x =
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Задачи на проценты: стандартный расчет с помощью пропорций
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X — 95%
Нужно составить пропорцию и найти x . Получаем:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x — 80%
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x · 10
Это простейшее линейное уравнение. Выразим из него переменную x :
x = 45 000 · 8 : 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Как решать пропорции – правила, методы и примеры вычислений
Общие сведения
Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.
Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.
Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.
Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.
Сферы применения
Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.
В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.
Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.
Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.
В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.
Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.
Основные свойства
Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:
- Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].
- Перемножение «крест-накрест»: x * z = y * v.
- Перестановка: x / v = y / z и v / x = z / y.
- Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.
- Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.
Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.
Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.
В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
- Записать функцию.
- Рассмотреть составные части.
- Если простой тип, перейти к 5 пункту.
- Сложная — разложить на простые элементы, а затем перейти к 5 пункту.
- Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.
- Определить тип линейности, построив график.
По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.
К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:
- Записать соотношение пропорции.
- Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
- Применить свойство умножения «крест-накрест».
- Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
- Решить уравнение.
Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:
- Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.
- При D равном 0 (один): р = (-b) / 2a.
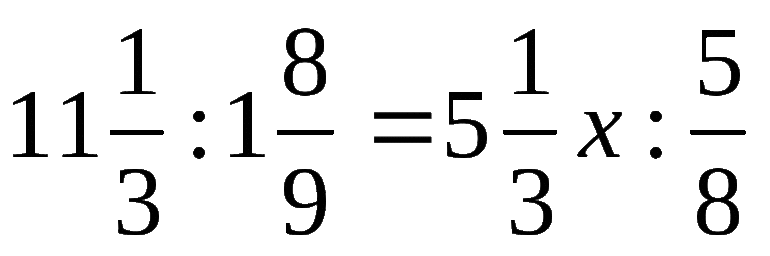
- Если D 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
[spoiler title=”источники:”]
http://nauka.club/matematika/proportsii.html
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami
[/spoiler]
Математика
6 класс
Урок № 7
Прямая и обратная пропорциональность. Решение задач
Перечень рассматриваемых вопросов:
- Понятия прямой и обратной пропорциональной зависимости.
- Краткая запись условия задачи.
- Составление и решение пропорций по условию задачи.
- Решение задач на прямую и обратную пропорциональную зависимость.
Тезаурус
Равенство двух отношений называют пропорцией.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Прямая пропорциональность.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Обратная пропорциональность.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.
Столбцы таблицы соответствуют наименованиям зависимых величин.
Строки таблицы соответствуют значениям величин при первом и втором измерении.
Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.
Задача.
Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?
Решение.
При постоянном пути скорость и время движения обратно пропорциональны.
Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.
Сделаем краткую запись условия.
Задача.
Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?
Решение.
При постоянной скорости путь прямо пропорционален времени движения.
Пусть х м проедет велогонщик за 45 с.
Сделаем краткую запись условия.
Задача.
Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?
Решение:
Решение.

Задача.
Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?
Решение.
Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.
Разбор заданий тренировочного модуля
№ 1. Подстановка элементов в пропуски в тексте.
Подставьте нужные элементы в пропуски.
Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?
Решение:
При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.
Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.
Составим пропорцию:
_________
х=_______
х=_______(ч).
Правильный ответ.
Решение:
При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.
Пусть х часов – пешеход идёт со скоростью 6 км/ч.
№ 2. Подстановка элементов в пропуски в таблице.
Заполните таблицу.
Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.
Варианты ответов:
135 км;
180 км;
225 км;
270 км.
Решение.
При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.
Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.
Ответ:

Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным.
Пропорция – это равенство двух отношений.
Отношение – это частное двух чисел. Отношение показывает, во сколько раз одно число больше другого или какую часть одно число составляет от другого.
Основное свойство пропорции: в верной пропорции произведение крайних членов равно произведению средних.
Задачи на пропорции из учебников
Основная сложность в задачах такого типа – составить пропорцию и определить, прямо или обратно пропорциональны величины.
В шестом классе условие задач на пропорции записывают таблицей, а пропорциональность обозначают стрелкам в одном либо противоположных направлениях.
Решите с помощью пропорции задачи:
1) Для изготовления 8 одинаковых приборов необходимо 18 кг металла. Сколько таких приборов можно изготовить из 27 кг металла?
Пусть из 27 кг металла возможно изготовить x приборов.
К-во приборов Масса металла
↓ 8 18 кг ↓
х 27 кг
$frac8x=frac{18}{27}$
18x = 8 * 27
$x=frac{8ast27}{18}$
$x=frac{4ast3}1$
x = 12
Значит, 12 приборов можно изготовить из 27 кг металла
Ответ: 12 приборов.
2) За 5 ч турист прошел 24 км. Какое расстояние он пройдет за 8 ч с той же скоростью?
Пусть x км пройдет турист за 8 ч.
Время Путь
↓ 5 ч 24 км ↓
8 ч х км
$frac58=frac{24}x$
5x = 8 * 24
$x=frac{8ast24}5$
$x=frac{192}5$
$x=38frac25=38,4$
Значит, 38,4 км пройдет турист за 8 ч с той же скоростью
Ответ: 38,4 км.
3) Из 140 кг свежих вишен получают 21 кг сушеных. Сколько килограммов сушеных вишен получится из 160 кг свежих? Сколько килограммов свежих вишен необходимо взять, чтобы получить 31,5 кг сушеных?
Пусть из 160 кг свежих вишен возможно получить x кг сухих вишен.
Масса свеж. Масса сух
↓ 140 кг 21 кг ↓
160 кг х кг
$frac{21}x=frac{140}{160}$
140x = 160 * 21
$x=frac{160ast21}{140}$
$x=frac{8ast3}1$
x = 24
Значит, 24 кг сушеных вишен получится из 160 кг свежихПусть из x кг свежих вишен необходимо взять, чтобы получить 31,5 кг сухих вишен.
$frac{21}{31,5}=frac{140}x$
21x = 31,5 * 140
$x=frac{31,5ast140}{21}$
$x=frac{1,5ast140}1$
x = 210
Значит, 210 кг свежих вишен необходимо взять, чтобы получить 31,5 кг сухих вишен
Ответ: 24 кг; 210 кг.
4) Объем бруска, изготовленного из древесины вишни, равен 800 см3, а его масса − 528 г. Какова масса бруска, изготовленного из этого же материала, если его объем равен 1500 см3?
Пусть x г масса бруска, если его объем равен 1500 см3.
$frac{800}{1500}=frac{528}x$
800x = 1500 * 528
$x=frac{1500ast528}{800}$
$x=frac{15ast66}1$
x = 990
Значит, 990 г масса бруска, если его объем равен 1500 см3.
Ответ: 990 г .
5) Из 45 т железной руды выплавляют 25 т железа. Сколько требуется тонн руды, чтобы выплавить 10 т железа?
Пусть x т руды требуется, чтобы выплавить 10 т железа.
$frac{45}x=frac{25}{10}$
25x = 45 * 10
$x=frac{45ast10}{25}$
$x=frac{9ast2}1$
x = 18
Значит, 18 т руды требуется, чтобы выплавить 10 т железа.
Ответ: 18 т руды.
6) Площадь поля 480 га. Пшеницей засеяли 24% площади поля. Сколько гектаров земли засеяли пшеницей?
Пусть x га земли засеяли пшеницей.
$frac{480}x=frac{100}{24}$
100x = 480 * 24
$x=frac{480ast24}{100}$
$x=frac{96ast6}5$
$x=frac{576}5=115frac15=115,2$
Значит, 115,2 га земли засеяли пшеницей.
Ответ: 115,2 га земли.
7) За первый час автомобиль проехал 70 км, что составило 14% всего пути. Сколько километров составляет весь путь?
Пусть x км составляет весь путь.
$frac{70}x=frac{14}{100}$
14x = 70 * 100
$x=frac{70ast100}{14}$
$x=frac{5ast100}1$
x = 500
Значит, 500 км составляет весь путь.
Ответ: 500 км.
8) Сплав содержит 12% цинка. Сколько килограммов цинка содержится в 80 кг сплава?
8) Пусть x кг цинка содержится в 80 кг сплава.
$frac{80}x=frac{100}{12}$
100x = 80 * 12
$x=frac{80ast12}{100}$
$x=frac{4ast12}5$
$x=frac{48}5=frac{96}{10}=9,6$
Значит, 9,6 кг цинка содержится в 80 кг сплава
Ответ: 9,6 кг цинка.
9) На пошив 14 одинаковых костюмов израсходовали 49 м ткани. Сколько таких костюмов можно сшить из 84 м ткани?
Пусть x костюмов можно сшить из 84 м ткани.
$frac{14}x=frac{49}{84}$
4x = 14 * 84
$x=frac{14ast84}{49}$
$x=frac{2ast12}1$
x = 24
Значит, 24 костюма можно сшить из 84 м ткани.
Ответ: 24 костюма.
10) За 7 ч в бассейн налилось 224 л воды. За какое время в него нальется 288 л воды?
Пусть за x часов в бассейн нальется 288 л воды.
$frac7x=frac{224}{288}$
224x = 7 * 288
$x=frac{7ast288}{224}$
$x=frac{1ast72}8$
x = 9
Значит, 9 часов в бассейн будет наливаться 288 л воды.
Ответ: 9 часов.
11) Из 150 кг картофеля получают 27 кг крахмала. Сколько килограммов крахмала получат из 420 кг картофеля? Сколько килограммов картофеля необходимо, чтобы получить 30,6 кг крахмала?
Пусть x кг крахмала получат из 420 кг картофеля.
$frac{27}x=frac{150}{420}$
150x = 27 * 420
$x=frac{27ast420}{150}$
$x=frac{27ast14}5$
$x=frac{378}5$
$x=frac{756}{10}=75,6$
Значит, 75,6 кг крахмала получат из 420 кг картофеля.
Ответ: 75,6 кг крахмала.Пусть x кг картофеля необходимо, чтобы получить 30,6 кг крахмала.
$frac{27}{30,6}=frac{150}x$
27x = 30,6 * 150
$x=frac{30,6ast150}{27}$
$x=frac{3,4ast50}1$
x = 170
Значит, 170 кг картофеля необходимо, чтобы получить 30,6 кг крахмала.
Ответ: 170 кг картофеля.
12) В саду растет 320 деревьев, из которых 40% составляют яблони. Сколько яблонь растет в саду?
Пусть x яблонь растет в саду.
К-во деревьев Проценты
320 д 100 %
х д 40 %
$frac{320}x=frac{100}{40}$
100x = 320 * 40
$x=frac{320ast40}{100}$
$x=frac{32ast4}1$
x = 128
Значит, 128 яблонь растет в саду
Ответ: 128 яблонь.
13) Масса соли составляет 24% массы раствора. Сколько килограммов раствора необходимо взять, чтобы он содержал 96 кг соли?
Пусть x килограммов раствора необходимо взять, чтобы он содержал 96 кг соли.
$frac{100}{24}=frac x{96}$
24x = 100 * 96
$x=frac{100ast96}{24}$
$x=frac{100ast4}1$
x = 400
Значит, 400 килограммов раствора необходимо взять, чтобы он содержал 96 кг соли.
Ответ: 400 кг.
14) На изготовление 3,5 кг ржаного хлеба требуется 2,5 кг муки. Сколько хлеба можно испечь из 17,5 т ржаной муки?
Пусть х кг хлеба можно испечь из 17,5 т муки.
17,5 т = 17500 кг
Масса хлеба Масса муки
↓ 3,5 кг 2,5 кг ↓
х кг 17500 кг
3,5 кг − 2,5 кг
x кг − 17500 кг
$frac{3,5}{2,5}=frac х{17500}$
$х=frac{3,5ast17500}{2,5}$ умножим по 1 числу в числ. и знам. на 10
$х=frac{35ast17500}{25}$
x = 24500
Значит, 24500 кг = 24,5 т хлеба можно испечь из 17,5 т ржаной муки.
Ответ: 24,5 т
В задачах выше зависимость между величинами была прямо пропорциональная, но бывают задачи и с обратно пропорциональной зависимостью.
1) Самолет со скоростью 200 км/ч преодолевает расстояние от Москвы до Тюмени за 2 часа, за сколько он преодолеет это же расстояние со скоростью 150 км/ч?
Пусть за х часов самолет преодолеет то же расстояние со скоростью 150 км/ч
Скорость Время
↑ 200 км/ч 2 ч ↓
150 км/ч х ч
Зависимость обратно пропорциональная, исходя из этого составляем пропорцию:
$frac{200}{150}=frac х2$
150 х = 200 * 2
$х=frac{200ast2}{150}$
$х=2frac23$
Значит, за $2frac23$ часа он преодолеет это же расстояние со скоростью 150 км/ч.
Ответ: за $2frac23$ часа.
2) Три трактора вспахали поле за 7 часов. Сколько нужно тракторов, чтобы вспахать такое же поле за 5 часов?
Пусть нужно х тракторов, чтобы вспахать поле за 5 часов.
К-во тракторов Время
↓3 7 ч ↑
х 5 ч
$frac3х=frac57$
5 х = 3 * 7
х = 4,2
Так как количество тракторов не может быть дробным числом, округлим до большей величины.
х ≈ 5
Значит, 5 тракторов нужно, чтобы вспахать такое же поле за 5 часов.
Ответ: 5 тракторов.
3) Для покрытия пола требуется 45 м линолеума шириной 2,2 м. Сколько потребуется линолеума шириной 1,5 м для покрытия пола той же площади?
Пусть х м линолеума шириной 1,5 м потребуется для покрытия пола той же площади.
Длина лин. Ширина лин.
↓ 45 м 2,2 м ↑
x м 1,5 м
$frac{45}х=frac{1,5}{2,2}$
$frac{45}х=frac{15}{22}$
15 х = 22 * 45
$х=frac{22ast45}{15}$
x = 66
Значит, 66 м линолеума шириной 1,5 м потребуется для покрытия пола той же площади..
Ответ: 66 метров.
Нестандартные задачи на пропорции
Задача 1. Поп нанял работника Балду на год, обещал ему 120 рублей и красный кафтан. Однако, проработав 7 месяцев, Балда стал просить у попа расчет и получил за работу 50 рублей и красный кафтан. Сколько стоит кафтан у Балды?
Эту задачу можно решить, не прибегая к уравнению и пропорции, однако можно и пропорцией.
Решение
Пусть x – цена кафтана. Тогда за 12 месяцев Балда мог получить 120 руб. и кафтан, т.е. 120 + x. Но за 7 месяцев он получил 50 + x. Запишем в привычном для шестиклассника виде:
| 12 120 + х |
↓ 7 50 + х ↓Записываем пропорцию
$frac{12}7=frac{120+х}{50+х}$
Применяя основное свойство пропорции, получаем уравнение:
7 * (120 + х) = 12 * (50 + х)
840 + 7 х = 600 + 12 х
12 х – 7 х = 840 – 600
5 х = 240
х = 48Ответ: 48 рублей стоил кафтан у Балды.
Гораздо сложнее ученикам даются задачи на пропорциональную зависимость трёх и более величин. Причем настолько, что когда в 7 классе в учебнике геометрии (например, в учебнике Погорелова) встречается задача, где в условии говорится, что углы треугольника пропорциональны числам 2, 3, 4 (т.е. относятся как 2:3:4), некоторые ученики приходят в замешательство и утверждают, что не понимают условие.
В последнее время задачи на пропорциональное деление стали встречаться в некоторых сборниках по занимательной, нестандартной и олимпиадной математике. Рассмотрим задачу такого плана.
Задача 2 на деление в данном отношении. Три предпринимателя – Давыдов, Петров и Максимов вложили в совместную организацию предприятия по производству мебели деньги. Первый вложил 60 тыс. руб., второй – 90 тыс. руб., а третий – 150 тыс. руб. Они получили прибыль в размере 117 тыс. руб. Сколько денег из прибыли получит каждый из предпринимателей при условии распределения ее пропорционально их вкладам?
Решение.
Найдём, каким числам пропорциональны вклады предпринимателей. Все числа запишем в тыс. руб.
60 : 90 : 150, т.е. 2 : 3 : 5.
Исходя из этого, можно записать, что 2x + 3x + 5x = 117, где 2x – часть прибыли, которую должен получить Давыдов, 3x – часть прибыли, которую должен получить Петров, 5x – часть прибыли, которую должен получить Максимов, исходя из пропорциональности вкладов. Отсюда x = 11,7 тыс. руб., т.е. Давыдов получит 23,4 тыс. руб., Петров – 35,1 тыс. руб., а Максимов – 58,5 тыс. руб.
Задачу можно решить и немного иначе:
1) 60 + 90 + 150 = 300 тыс. руб.
2) 117 : 300 x 60 = 23,4 тыс. руб.
3) 117 : 300 x 90 = 35,1 тыс. руб.
4) 117 : 300 x 150 = 58,5 тыс. руб.
Ответ: 23, 4 тыс. руб., 35,1 тыс., руб., 58,5 тыс. руб.
Классика нестандартных задач на пропорциональность трёх и более величин:
Задача 3. Три курицы за 3 дня снесли три яйца. Сколько яиц снесут 12 кур за 12 дней?
И сразу аналогичная, коих может быть бесконечное множество, а решаются они одинаково:
Задача 4. Пять землекопов за 5 часов выкапывают 5 метров канавы. Сколько потребуется землекопов, чтобы за 100 часов выкопать 100 м канавы?
Напрашивается ответ 12 в задаче про куриц и 100 в задаче с канавой, но это не верно. В задаче про куриц правильный ответ 48, а в задаче про землекопов правильный ответ – 5.
Если дней в 4 раза больше, а кур также в 4 раза больше, то яиц они снесут 3 х 4 х 4 = 48.
Что касается задачи про землекопов, то решение еще проще. Так как за 5 часов землекопы выкапывают 5 метров канавы, то за 1 час – 1 метр канавы. И значит, за 100 часов 100 м канавы выкопают те же 5 землекопов.
Задача 5. 2 робота за 3 часа собирают 1 компьютер. Сколько компьютеров соберут 10 роботов за 12 часов?
Иногда условия таких задач выписывают примерно также как обычную пропорцию и делают стрелочки. Например:
Роботы Часы Компьютеры
| 2 | 3 | 1
↓10 ↓12 ↓ х
Решение.
Если 2 робота за 3 часа собирают 1 компьютер, то сколько компьютеров соберут те же два робота за 12 часов?
12 : 3 = в 4 (раза) – больше будет времени у 2х роботов на сборку компьютеров
Если у двух роботов будет времени в 4 раза больше, то и соберут они в 4 раза больше компьютеров, т.е.
1 * 4 = 4 (компьютера) – собирают 2 робота за 12 часов.Если роботов будет 10, то сколько компьютеров они соберут за 12 часов?
10 : 2 = в 5 (раз) – больше роботов
Так как роботов будет в 5 раз больше, то и соберут они за 12 часов в 5 раз больше компьютеров.
4 * 5 = 20 (компьютера) – соберут 10 роботов за 12 часов.Ответ: 20 компьютеров.
Задача 6. 3 маляра за 5 дней могут покрасить 60 окон. Сколько окон покрасят 5 маляров за 4 дня?
Решение.
60 : 3 = 20 (окон) – может покрасить 1 маляр за 5 дней,
20 : 5 = 4 (окна) – маляр покрасит за 1 день
4 * 4 = 16 (окон) – он покрасит за 4 дня.
А если таких маляров будет 5, то окон будет покрашено
5 : 16 = 80 (окон) – покрасят 5 маляров за 4 дня
Ответ: 80 окон.
Лишь только тогда, когда ученик приобретает опыт в решении таких задач поэтапно, можно показать ему решение подобной задачи пропорцией.
3 маляра за 5 дней выполнят работу, которую можно измерить как 3 х 5 человеко-дней. Можно пояснить, что человеко-дни – единица, с помощью которой учитывается рабочее время на производстве. И по условию эта работа выражается в 60-ти окнах. В задаче требуется узнать, чему равна работа, которая измеряется как 4 х 5 человеко-дней.
Значит, можно составить пропорцию:
К-во окон К-во человеко-дней
60 окон 3*5 человеко-дней
х окон 4*5 человеко-дней$frac{60}х=frac{3ast5}{4ast5}$
$х=frac{4ast5ast60}{3ast5}=80$ (окон) – покрасят 5 маляров за 4 дня
Ответ: 80 окон.
Однако надо быть внимательным. В некоторых задачах имеет место быть и обратно пропорциональная зависимость. Если, например, количество рабочих увеличивается, то количество дней, за которые им надо выполнить заданную работу, уменьшается.
Задача 7. 3 маляра за 5 дней могут покрасить 60 окон. За сколько дней 5 маляров смогут покрасить 80 окон?
Решение.
За 1 день один маляр покрасит 4 окна, а 5 маляров за 1 день – 20 окон. А 80 окон 5 маляров смогут покрасить за 4 дня (80 : 20 = 4).
Через пропорцию:
Кол-во маляров Скорость покраски
3 м. 60/5 окон/день
5 м. 80/х окон/день$5astfrac{60}5=3astfrac{80}х$
…
х = 4
В заключение обзора сложных задач на пропорцию и методов их решения рассмотрим задачу, с четырьмя величинами. Такие задачи сегодня могут встречаться на олимпиадах. Но было время, когда они входили в курс школьной математики (учебник Киселева).
Задача 8. На 5 одинаковых керосинок, горевших 24 дня по 6 часов ежедневно, израсходовано 120 л керосина. На сколько дней хватит 216 л керосина, если 9 таких же керосинок будут гореть по 8 часов в день?
Решение.
С тем, чтобы не запутаться в условии, выпишем все данные в виде таблички. В учебнике Киселева таблицы отсутствуют, а условие записано двумя строчками. Последуем его примеру:
5 керосинок 24 дня по 6 часов – 120 л
9 керосинок x дней по 8 часов – 216 лДалее, если следовать логике решений задач, приведённых на этой странице, а также логике Киселева, решим задачу поэтапно. Сначала решим такую задачу: На сколько дней хватит 216 л керосина, если те же 5 керосинок будут гореть по 6 часов в день? То есть:
120 л – на 24 дня
216 л – на y дней$у=frac{216ast24}{120}=43,2$ (дня)
То есть 216 л керосина хватит на 43,2 дня, если будет работать 5 керосинок.
Теперь найдём, на сколько дней хватит 216 л керосина, если керосинок будет не 5, а 9. То есть, если 5 керосинок могут работать 43,2 дня, то 9 керосинок меньше в 1,8 раза (9 : 5 = 1,8). То есть 9 керосинок, работая по 6 часов в день при запасе в 216 литров, проработают 24 дня.
Осталось найти, на сколько дней хватит 216 л керосина, если 9 таких же керосинок будут гореть по 8 часов в день. То есть:
24 дня – по 6 часов в день
х дней – по 8 часов в деньТаким образом,
$х=frac{24ast6}8=18$ (дней)
Все выполненные действия можно записать одной дробью и сократить ее:
$х=frac{24ast216ast5ast6}{120ast9ast8}=18$ (дней)
Ответ: 18 дней.
Надеемся, что способы решения задач на пропорцию, изложенные в этой статье, помогут пятиклассникам и шестиклассникам, стремящимся изучить школьный материал, в том числе и тот, который выходит за рамки программы обычной школы, но который может быть полезен при подготовке к олимпиадам.