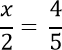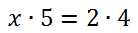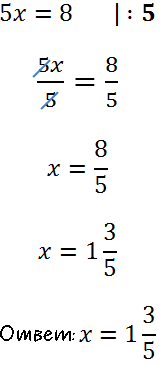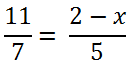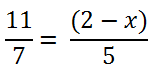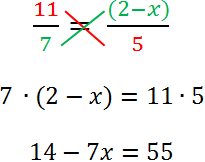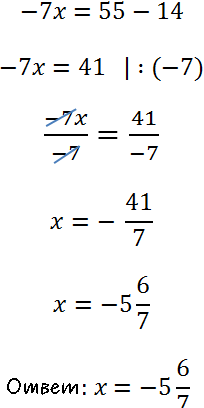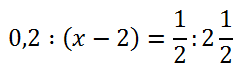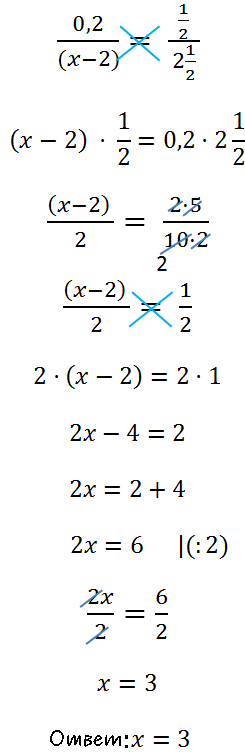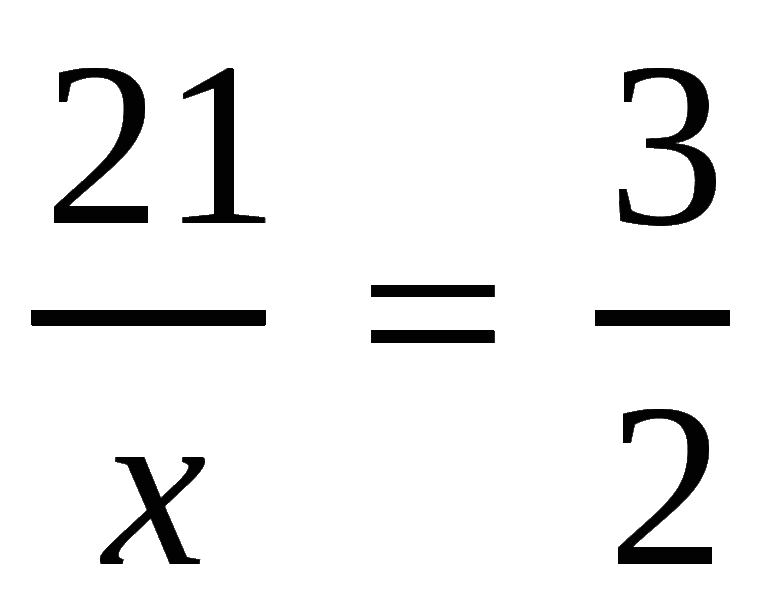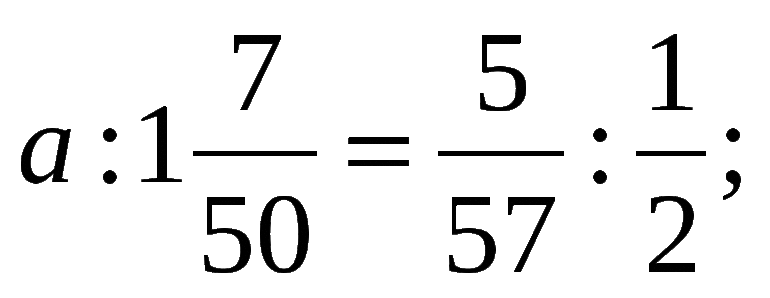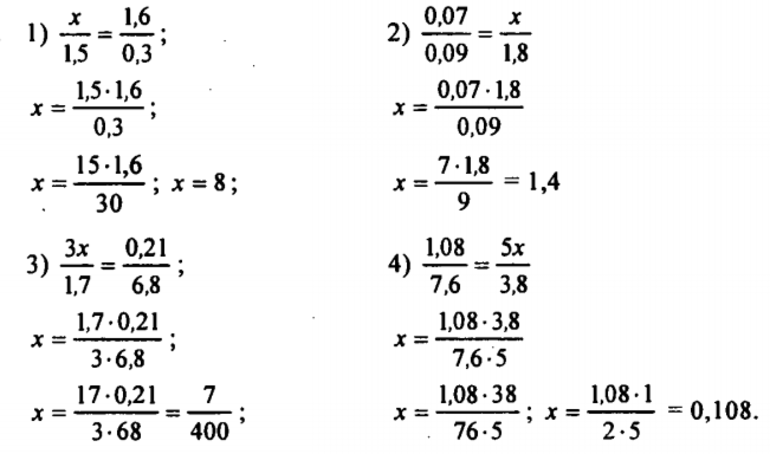Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию.
Например, рассмотрим такое уравнение.
Для решения уравнения с пропорцией используют правило пропорции или,
как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке
«Пропорции».
В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Запомните!
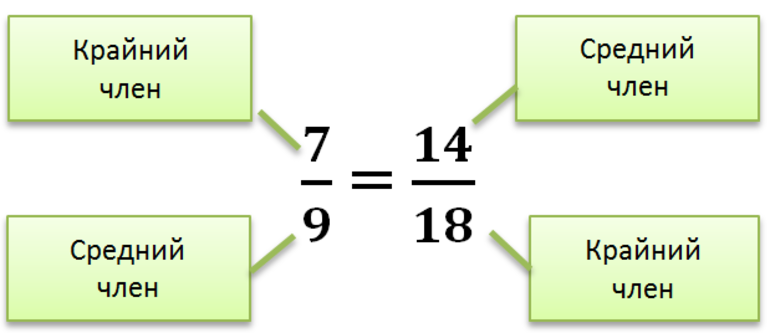
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции,
то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции.
Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию
в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и
решим уравнение до конца.
В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Важно!
Если в члене пропорции присутствуют знаки «+» или «−»,
обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда
будете использовать правило пропорции.
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции
для дальнейшего решения.
Теперь раскроем скобки с помощью
правила раскрытия
скобок.
Из урока «Решение линейных уравнений» используем
правило переноса и
правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать
правило знаков.
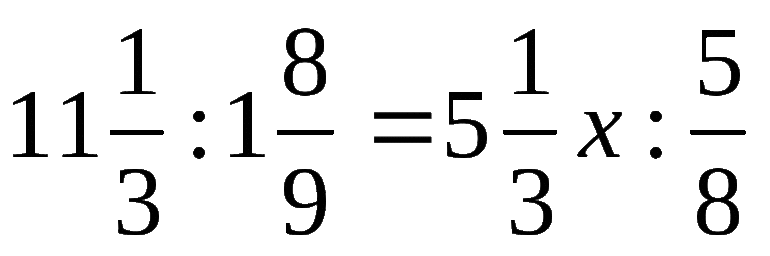
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
Другие примеры решения уравнений с пропорцией
-
=
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число
-
=
3x · 6,8 = 0,21 · 1,7
20,4 x=
·
20
x =
=204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =
x =
x =
x =
x =
Ответ: x =
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 |
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Что такое пропорция
О чем эта статья:
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
- a : b = c : d
a и d — крайние члены пропорции, b и с — средние члены пропорции.
Читается это выражение так: a так относится к b, как c относится к d
Например:
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
- Запишем эту непростую ситуацию в виде отношения 8 кусочков к 4 голодным друзьям: 8 : 4
- Далее преобразовываем это отношение в дробь: 8/4
- Выполняем деление: 8/4 = 2
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
- Запишем в виде отношения: 4 : 2
- Преобразовываем получившееся отношение в дробь: 4/2
- Выполняем деление: 4/2 = 2
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d
a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
- Чтобы проверить, верно ли составлена пропорция, перемножаем ее крайние члены: 6 * 4 = 24.
- Далее перемножаем средние члены пропорции: 2 * 12 = 24
- Произведение крайних членов пропорции равно 24, произведение средних членов пропорции также равно 24.
- 6 * 4 = 2 * 12
24 = 24
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
- Перемножаем крайние члены пропорции: 10 * 4 = 40.
- Перемножаем средние члены: 16 * 2 = 32.
- Произведение крайних членов пропорции равно 40. Произведение средних членов пропорции равно 32.
- 10 * 4 ≠ 16 * 2
40 ≠ 32
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Примеры решения задач с пропорцией
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
- По основному свойству пропорции перемножаем множители:
15 * 4 = 3x - Получаем уравнение: 60 = 3x
- 60/3 = x
x = 20.
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
- Записываем чиcла в виде дробей: 18/9 = 24/x
Где x — четвертый член пропорции. - По основному свойству пропорции, перемножаем средние члены: 9 * 24 = 216
- Выводим уравнение 18x = 216
- Находим x:
x = 216 : 18
x = 12 - Проверяем: 9 * 24 = 216, 18 * 12 = 216.
Пропорция составлена верно.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
- Записываем числа в виде обратной пропорции: 18/9 = x/8
- Перемножаем множители по основному свойству пропорции: 18 * 8 = 9x
- Находим х:
144 = 9x
144 : 9 = 16
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4
- По основному свойству пропорции перемножаем множители:
20 * 4 = 2y - Получаем уравнение: 80 = 2y
- Находим у:
80/2 = y
x = 40. - Проверяем пропорцию: 20 * 4 = 80, 40 * 2 = 80.
Решение пропорций
Рассмотрим решение пропорций на конкретных примерах.
Решить уравнения с пропорцией:
1) 25 : x = 10 : 18
Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции , произведение крайних членов разделим на известный средний член:
25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.
Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:
При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.
Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:
В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:
Сокращаем 24 и 6 на 6, 10 и 45 — на 5:
Еще раз сокращаем 4 и 2 на 2:
Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.
Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:
При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.
Произведение крайних членов пропорции равно произведению средних членов:
Здесь удобно упростить уравнение, разделив обе части на 5:
Произведение крайних членов пропорции равно произведению ее средних членов:
Для упрощения вычислений удобно умножить каждую часть уравнения на 10:
Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Как решать пропорции – правила, методы и примеры вычислений
Общие сведения
Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.
Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.
Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.
Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.
Сферы применения
Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.
В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.
Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.
Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.
В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.
Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.
Основные свойства
Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:
- Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].
- Перемножение «крест-накрест»: x * z = y * v.
- Перестановка: x / v = y / z и v / x = z / y.
- Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.
- Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.
Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.
Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.
В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
- Записать функцию.
- Рассмотреть составные части.
- Если простой тип, перейти к 5 пункту.
- Сложная — разложить на простые элементы, а затем перейти к 5 пункту.
- Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.
- Определить тип линейности, построив график.
По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.
К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:
- Записать соотношение пропорции.
- Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
- Применить свойство умножения «крест-накрест».
- Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
- Решить уравнение.
Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:
- Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.
- При D равном 0 (один): р = (-b) / 2a.
- Если D 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.
[spoiler title=”источники:”]
http://nauka.club/matematika/proportsii.html
[/spoiler]
Теория
a/b = c/X или, другими словами, a относится к b так же как c относится к X – это геометрическая пропорция, которая позволяет выяснить как одно число относится к другому, если известно, как третье относится к четвёртому. Например, с помощью геометрической пропорции можно посчитать процент от числа.
Пример
Мы положили в банк 4000 рублей под 5% годовых и хотим выяснить сколько в рублях составят эти пять процентов. Мы понимаем, что 4000 – это 100%, а сколько 5% –?
Геометрическая пропорция в данном случаи будет выглядеть так: 100/5=4000/X
X = (4000*5)/100 = 200
Ответ: 5% от 4000 рублей составляет 200 рублей
Видео
Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.

В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.
К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.

Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:
- Записать соотношение пропорции.
- Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
- Применить свойство умножения «крест-накрест».
- Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
- Решить уравнение.
Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
- Чтобы проверить, верно ли составлена пропорция, перемножаем ее крайние члены: 6 * 4 = 24.
- Далее перемножаем средние члены пропорции: 2 * 12 = 24
- Произведение крайних членов пропорции равно 24, произведение средних членов пропорции также равно 24.
- 6 * 4 = 2 * 12 24 = 24
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
- Перемножаем крайние члены пропорции: 10 * 4 = 40.
- Перемножаем средние члены: 16 * 2 = 32.
- Произведение крайних членов пропорции равно 40. Произведение средних членов пропорции равно 32.
- 10 * 4 ≠ 16 * 2 40 ≠ 32
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:

Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:
Решение уравнений кубического и биквадратного видов сводятся к разложению на множители. В результате этого происходит понижение степени до двойки. Кроме того, эффективным методом нахождения корней считается введение замены переменной.
Как сокращать пропорции?
Итак, для решения дробно-рациональных уравнений помните три правила:
- Сокращать можно только множители. Слагаемые — нельзя. …
- Основное свойство пропорции: произведение крайних элементов равно произведению средних;
- Уравнения можно умножать и делить только на числа k, отличные от нуля. Случай k = 0 надо проверять отдельно.
Пример решения
Решение уравнений в виде пропорции осуществляется по такому же принципу. При этом рекомендуется использовать любые свойства. Необходимо проходить процесс обучения постепенно. Начинать нужно с простых примеров, а затем практиковаться на сложных заданиях. Первый тип был рассмотрен выше на примере sin (p).
Итак, необходимо решить уравнение [(t — 5) / (t — 2)] = [(t — 5) / (t — 1)]. Для начала следует определить тип функций каждого из элементов. Просмотрев список нелинейных выражений, можно сделать вывод о том, что все члены пропорции являются линейными. Далее нужно решить равенства с неизвестными, находящихся в знаменателях: t1 = 2 и t2 = 1. Корни не являются решениями уравнения.
Затем следует воспользоваться третьим пунктом алгоритма: (t — 5)(t — 1) = (t — 2)(t — 5). Если раскрыть скобки, то должно получиться такое равенство: t 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.
Теги
Примеры решений пропорций
Ниже даны примеры пропорций, которые можно решить с помощью онлайн калькулятора.
$$frac{2}{x} = frac{8}{12}$$ (найти x)
$$dfrac{-frac{3}{5}}{-frac{2x}{3}} = dfrac{-frac{6}{7}}{frac{4}{9}}$$ (найти x)
$$dfrac{frac{1}{5}}{frac{5}{12}} = dfrac{-frac{4}{15}}{-frac{2}{3x}}$$ (найти x)
$$dfrac{-frac{4}{7x}}{2frac{1}{2}} = dfrac{-1frac{6}{11}}{frac{9}{5}}$$ (решить пропорцию)
$$dfrac{4,73}{-5frac{3}{7}} = dfrac{3x}{frac{2}{8}}$$ (решить пропорцию)
Решение сложных пропорций
Решить составные сложные пропорции можно с помощью другого инструмента – универсального математического калькулятора.
$$frac{5frac{1}{3}}{frac{72}{300}}=frac{4}{2x+frac{3}{25}}$$ (решить пропорцию)
$$frac{9,35+4frac{2}{15}}{6frac{32}{122}}=frac{6left(x+2,5right)}{2-1frac{2}{7}}$$ (решить пропорцию)
$$frac{7x+11-2x}{12,3-frac{2}{9}}=frac{8frac{3}{7}left(1,5+6frac{4}{5}-frac{3}{8}right)}{-2frac{5}{16}}$$ (решить пропорцию)
Что такое пропорция?
Пропорция – равенство отношений двух (и более) пар чисел a : b = c : d или $$dfrac{a}{b} = dfrac{c}{d}$$
Основное свойство пропорции – произведение крайних членов пропорции равно произведению её средних членов: $$a * d = b * c$$