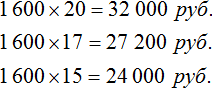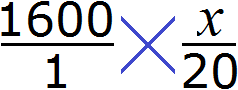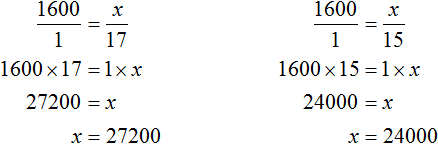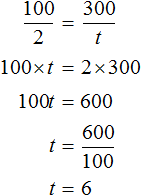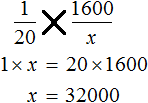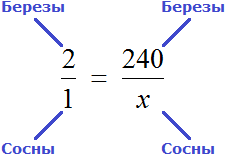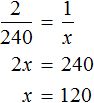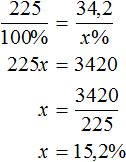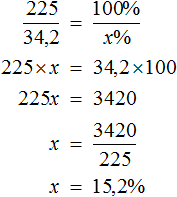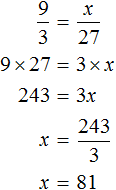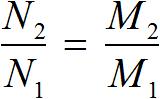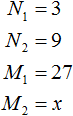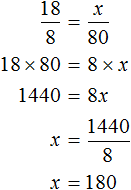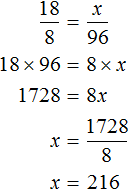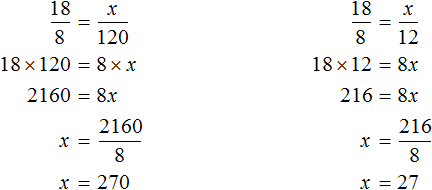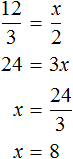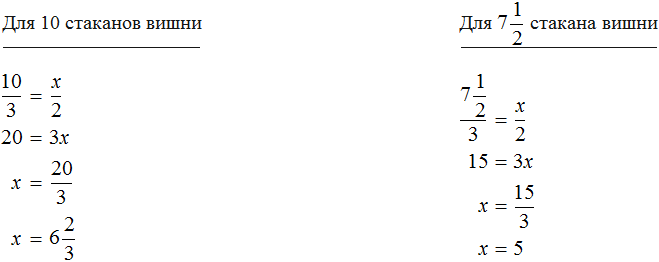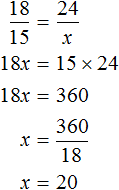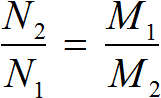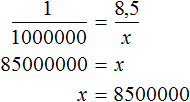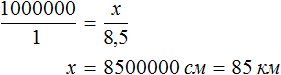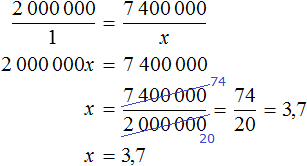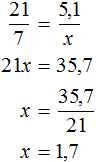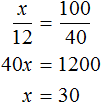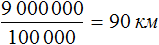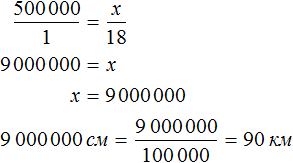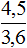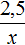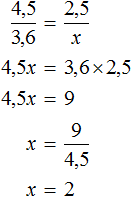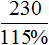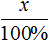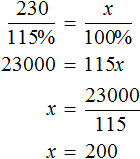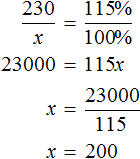Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 |
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Составить пропорцию. В этой статье хочу поговорить с вами о пропорции. Понимать, что такое пропорция, уметь составлять её – это очень важно, она действительно спасает. Это вроде бы маленькая и незначительная «буковка» в большом алфавите математики, но без неё математика обречена быть хромой и неполноценной.
Для начала напомню, что такое пропорция. Это равенство вида:
что тоже самое (это разная форма записи).
Пример:
Говорят – один относится к двум также, как четыре относится к восьми. То есть это равенство двух отношений (в данном примере отношения числовые).
Основное правило пропорции:
a:b=c:d
произведение крайних членов равно произведению средних
то есть
a∙d=b∙c
*Если какая-либо величина в пропорции неизвестна, ее всегда можно найти.
Если рассматривать форму записи вида:
то можно использовать следующее правило, его называют «правило креста»: записывается равенство произведений элементов (чисел или выражений) стоящих по диагонали
a∙d=b∙c
Как видите результат тот же.
Если три элемента пропорции известны, то
мы всегда можем найти четвёртый.
Именно в этом суть пользы и необходимость
пропорции при решении задач.
Давайте рассмотрим все варианты, где неизвестная величина х находится в «любом месте» пропорции, где a, b, c – числа:
Величина стоящая по диагонали от х записывается в знаменатель дроби, а известные величины стоящие по диагонали записываются в числитель, как произведение. Его запоминать не обязательно, вы и так всё верно вычислите, если усвоили основное правило пропорции.
Теперь главный вопрос, связанный с названием статьи. Когда пропорция спасает и где используется? Например:
1. Прежде всего это задачи на проценты. Мы рассматривали их в статьях ”
”
и ”
“.
2. Многие формулы заданы в виде пропорций:
> теорема синусов
> отношение элементов в треугольнике
> теорема тангенсов
> теорема Фалеса и другие.
3. В задачах по геометрии в условии часто задаётся отношение сторон (других элементов) или площадей, например 1:2, 2:3 и прочие.
4. Перевод единиц измерения, причём пропорция используется для перевода единиц как в одной мере, так и для перевода из одной меры в другую:
— часы в минуты (и наоборот).
— единицы объёма, площади.
— длины, например мили в километры (и наоборот).
— градусы в радианы (и наоборот).
здесь без составления пропорции не обойтись.
Ключевой момент в том, что нужно правильно установить соответствие, рассмотрим простые примеры:
Необходимо определить число, которое составляет 35% от 700.
В задачах на проценты за 100% принимается та величина, с которой сравниваем. Неизвестное число обозначим как х. Установим соответствие:
Можно сказать, что семисот тридцати пяти соответствует 100 процентов.
Иксу соответствует 35 процентов. Значит,
700 – 100%
х – 35 %
Решаем
Ответ: 245
Переведём 50 минут в часы.
Мы знаем, что одному часу соответствует 60 минут. Обозначим соответсвие –
x часов это 50 минут. Значит
1 – 60
х – 50
Решаем:
То есть 50 минут это пять шестых часа.
Ответ: 5/6
Николай Петрович проехал 3 километра. Сколько это будет в милях (учесть, что 1 миля это 1,6 км)?
Известно, что 1 миля это 1,6 километра. Число миль, которые проехал Николай Петрович примем за х. Можем установить соответствие:
Одной миле соответствует 1,6 километра.
Икс миль это три километра.
1 – 1,6
х – 3
Ответ: 1,875 миль
Вы знаете, что для перевода градусов в радианы (и обратно) существуют формулы. Я их не записываю, так как запоминать их считаю излишним, и так вам в памяти приходится держать много информации. Вы всегда сможете перевести градусы в радианы (и обратно), если воспользуетесь пропорцией.
Переведём 65 градусов в радианную меру.
Главное это запомнить, что 180 градусов это Пи радиан.
Обозначим искомую величину как х. Устанавливаем соответствие.
Ста восьмидесяти градусам соответствует Пи радиан.
Шестидесяти пяти градусам соответствует х радиан.
изучить статью
по этой теме на блоге. Материал в ней изложен несколько по иному, но принцип тот же. На этом закончу. Обязательно будет ещё что-нибудь интересненькое, не пропустите!
Если вспомнить само определение математики, то в нём есть такие слова: математика изучает количественные ОТНОШЕНИЯ (ОТНОШЕНИЯ
–
здесь ключевое слово). Как видите в самом определении математики заложена пропорция. Вообщем, математика без пропорции это не математика!!!
Всего доброго!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Но не все так сложо и непонятно, как кажется на первый взгляд. Для чего вообще все это нужно? Вот самый распространенный пример.
Допустим, у нас на сайте есть загрузка изображений, и мы хотим, чтобы после загрузки у нас создавалась миниатюрная копия, превьюшка какртинки. Часто это надо для анонса новостей, например. А скрипт требует, чтобы вы задали хотя бы примерные размеры миниатюрного изображения – его ширину и высоту.
Допустим также, что вы уже наметили его ширину, но как быть с высотой? Как высчитать ее та, чтобы картинка казалась более-менее пропорциональной по отношению к исходной.
Формула расчета
Все делается в два этапа:
- 1 – Делим исходную ширину на требуемую ширину;
- 2 – Получаем требуемую высоту, поделив исходную высоту на результат деления двух ширин (п.1).
Пример. Возьмем уже всем известные размеры изображений: 1024×768 и 800×600
. Представим, что мы не знаем высоту второй картинки. По формуле получается следующее: 768/(1024/800) = 600
. Это и есть требуемая нам высота.
Если же мы знаем высоту, а нам нужно получить ширину, то необходимо проделать все, как в первой формуле, только наоборот.
Чтобы получить требуемую ширину, нужно:
- 1 – Делим исходную высоту на требуемую высоту;
- 2 – Получаем требуемую ширину, поделив исходную ширину на результат деления двух высот (п.1).
То есть, 1024/(768/600) = 800
.
Пример 1
Вы заходите в супермаркет и видите акцию на . Его обычная цена – 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.
Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.
Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.
Умножьте 4,58 на 7, и вы получите 32,06 рубля.
Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.
Пример 2
Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.
Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.
Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.
100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.
2. Как посчитать проценты, разделив число на 10
Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.
Пример
Допустим, вы кладёте на 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.
В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.
Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.
Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.
В любом случае такими крупными числами оперировать довольно просто.
3. Как посчитать проценты, составив пропорцию
Составлять пропорции – одно из наиболее полезных умений, которому вас научили в . С его помощью можно посчитать любые проценты. Выглядит пропорция так:
сумма, составляющая 100% : 100% = часть суммы: доля в процентном соотношении.
Или можно записать её так: a: b = c: d.
Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.
Пример 1
Для примера вычислений используем рецепт . Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.
Сначала вычисляем процентную долю оставшегося шоколада.
90 г: 100% = 70 г: Х, где Х – масса оставшегося шоколада.
Х = 70 × 100 / 90 = 77,7%.
Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:
200 г: 100% = Х: 77,7%, где Х – нужное количество масла.
Х = 77,7 × 200 / 100 = 155,4.
Следовательно, в тесто нужно положить примерно 155 г масла.
Пример 2
Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.
Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.
Составьте пропорцию: 1 499: 100 = Х: 87.
Х = 87 × 1 499 / 100.
Заплатите 1 304,13 рубля и носите блузку с удовольствием.
4. Как посчитать проценты с помощью соотношений
В некоторых случаях можно воспользоваться простыми дробями. Например, 10% – это 1/10 числа. И чтобы узнать, сколько это будет в цифрах, достаточно разделить целое на 10.
- 20% – 1/5, то есть нужно делить число на 5;
- 25% – 1/4;
- 50% – 1/2;
- 12,5% – 1/8;
- 75% – это 3/4. Значит, придётся разделить число на 4 и умножить на 3.
Пример
Вы нашли брюки за 2 300 рублей со скидкой 25%, но у вас в кошельке только 2 000 рублей. Чтобы узнать, хватит ли денег на обновку, проведите серию несложных вычислений:
100% – 25% = 75% – стоимость брюк в процентах от первоначальной цены после применения скидки.
2 400 / 4 × 3 = 1 800. Именно столько рублей стоят брюки.
5. Как посчитать проценты с помощью калькулятора
Если без калькулятора вам жизнь не мила, все вычисления можно делать с его помощью. А можно поступить ещё проще.
- Чтобы посчитать проценты от суммы, введите число, равное 100%, знак умножения, затем нужный процент и знак %. Для примера с кофе вычисления будут выглядеть так: 458 × 7%.
- Чтобы узнать сумму за вычетом процентов, введите число, равное 100%, минус, размер процентной доли и знак %: 458 – 7%.
- Аналогично можно складывать, как в примере с депозитом: 530 000 + 5%.
6. Как посчитать проценты с помощью онлайн-сервисов
На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.
Умение вычисления процента от числа, когда нужно узнать пеню за просрочку, размер переплаты по кредиту или прибыль компании, если известен ее оборот и наценка.
- Как найти число по его проценту?
Правило. Чтобы найти число по его указанному проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на 100.
Таким вычислением сначала определим, сколько единиц этого числа содержится в 1%, а потом — в целом числе (в 100%).
Например:
Число, 23% которого составляют 52, находится так:
52: 23 * 100 = 226.1
Значит, если число 226,1 равно 100%, то число 52 равно 23% от этого числа.
Число, 125% которого составляют 240, находим так:
240: 125 * 100 = 192.
При определении числа по его проценту следует помнить, что:
— если процент меньше 100%, то число, полученное в результате вычислений, больше заданного числа (если 23% < 100%, то 226,1 > 52);
— если процент больше 100%, то число, полученное в результате вычислений, меньше заданного числа (если 125% > 100%, то 192 < 240).
Следовательно, при вычислении числа по его проценту для самоконтроля нужно проверить:
— заданный в условии процент больше или меньше 100%;
— результат вычисления больше или меньше заданного числа.
- Как узнать процент от суммы в общем случае?
После этого есть два варианта:
- Если нужно узнать, сколько процентов составляет другая сумма от первоначальной, нужно просто разделить ее на размер 1%, полученный ранее.
- Если же нужен размер суммы, которая составляет, скажем, 27,5% от первоначальной, нужно размер 1% умножить на требуемое количество процентов.
- Как высчитать процент от суммы с помощью пропорции?
Для этого придется использовать знания о методе пропорций, который проходят в рамках школьного курса математики. Это будет выглядеть так:
ПустьА — основная сумма, равная 100%, и В — сумма, соотношение которой с А в процентах нам нужно узнать. Записываем пропорцию:
(Х в данном случае — число процентов).
По правилам расчета пропорций мы получаем следующую формулу:
Х = 100 * В / А
Если же нужно узнать, сколько будет составлять сумма В при уже известном числе процентов от суммы А, формула будет выглядеть по-другому:
В = 100 * Х / А
Теперь остается подставить в формулу известные числа — и можно производить расчет.
- Как рассчитать процент от суммы с помощью известных соотношений?
Наконец, можно воспользоваться и более простым способом. Для этого достаточно помнить, что 1% в виде десятичной дроби — это 0,01. Соответственно, 20% — это 0,2; 48% — 0,48; 37,5% — это 0,375 и т.д. Достаточно умножить исходную сумму на соответствующее число — и результат будет означать размер процентов.
Кроме того, иногда можно воспользоваться и простыми дробями. Например, 10% — это 0,1, то есть 1/10 следовательно, узнать, сколько составят 10%, просто: нужно всего лишь разделить исходную сумму на 10.
Другими примерами таких соотношений будут:
- 12,5% — 1/8, то есть нужно делить на 8;
- 20% — 1/5, то есть нужно разделить на 5;
- 25% — 1/4, то есть делим на 4;
- 50% — 1/2, то есть нужно разделить пополам;
- 75% — 3/4, то есть нужно разделить на 4 и умножить на 3.
Правда, не все простые дроби удобны для расчета процентов. К примеру, 1/3 близка по размерам к 33%, но не равна точно: 1/3 — это 33,(3)% (то есть дробь с бесконечными тройками после запятой).
- Как вычесть процент от суммы без помощи калькулятора?
Если же требуется от уже известной суммы отнять неизвестное число, составляющее какое-то количество процентов, можно воспользоваться следующими методами:
- Вычислить неизвестное число с помощью одного из приведенных выше способов, после чего отнять его от исходного.
- Сразу рассчитать остающуюся сумму. Для этого от 100% отнимаем то число процентов, которое нужно вычесть, и полученный результат переводим из процентов в число любым из описанных выше способов.
Второй пример удобнее, поэтому проиллюстрируем его. Допустим, надо узнать, сколько останется, если от 4779 отнять 16%. Расчет будет таким:
- Отнимаем от 100 (общее количество процентов) 16. Получаем 84.
- Считаем, сколько составит 84% от 4779. Получаем 4014,36.
- Как высчитать (отнять) из суммы процент с калькулятором в руках?
Все вышеприведенные вычисления проще делать, используя калькулятор. Он может быть как в виде отдельного устройства, так и в виде специальной программы на компьютере, смартфоне или обычном мобильнике (даже самые старые из ныне используемых устройств обычно имеют эту функцию). С их помощью вопрос, как высчитать процент из суммы,
решается очень просто:
- Набирается исходная сумма.
- Нажимается знак «-».
- Вводится число процентов, которое требуется вычесть.
- Нажимается знак «%».
- Нажимается знак «=».
В итоге на экране высвечивается искомое число.
- Как отнять от суммы процент с помощью онлайн-калькулятора?
Наконец, сейчас в сети достаточно сайтов, где реализована функция онлайн-калькулятора. В этом случае даже не требуется знания того, как посчитать процент от суммы
: все операции пользователя сводятся к вводу в окошки нужных цифр (или передвижению ползунков для их получения), после чего результат сразу высвечивается на экране.
Особенно эта функция удобна тем, кто рассчитывает не просто абстрактный процент, а конкретный размер налогового вычета или сумму госпошлины. Дело в том, что в этом случае вычисления сложнее: требуется не только найти проценты, но и прибавить к ним постоянную часть суммы. Онлайн-калькулятор позволяет избежать подобных добавочных вычислений. Главное — выбрать сайт, пользующийся данными, которые соответствуют действующему закону.
Онлайн-калькулятор процентов:
calculator.ru — позволяет выполнять разнообразные расчеты при работе с процентами;
mirurokov.ru — калькуляятор процентов;
Источник информации:
- nsovetnik.ru — статьяя о том, как высчитать процент от суммы;
Один процент – это сотая часть от числа. Данное понятие используется, когда нужно обозначить отношение доли к целому. Кроме этого, в процентах можно сравнивать несколько величин, при этом обязательно указывая, относительного какого целого проценты вычисляются. Например, расходы выше доходов на 10 % или цена на железнодорожные билеты возросла на 15 % в сравнении с тарифами прошлого года. Число процентов выше 100 означает, что доля превышает целое, как часто бывает при статистических расчетах.
Процент как финансовое понятие – плата, заемщика кредитору за предоставление денег во временное пользование. В бизнесе встречается выражение «работать за проценты». В данном случае подразумевается, что размер вознаграждения зависит от прибыли или оборота (комиссионные). Обойтись без вычисления процентов невозможно в бухгалтерии, бизнесе, банковском деле. Чтобы упростить расчеты, разработан онлайн-калькулятор процентов.
Калькулятор позволяет вычислить:
- Процент от заданного значения.
- Процент из суммы (налог по фактической зарплате).
- Процент от разницы (НДС из ).
- И многое другое…
При решении задач на калькуляторе процентов нужно оперировать тремя значениями, одно из которых неизвестно (по заданным параметрам вычисляется переменная). Сценарий расчета следует выбирать, исходя из заданных условий.
Примеры расчетов
1. Вычисление процента от числа
Чтобы найти число, составляющее 25 % от 1 000 руб., нужно:
- 1 000 × 25 / 100 = 250 руб.
- Или 1 000 × 0,25 = 250 руб.
Для расчета на обычном калькуляторе, нужно 1 000 умножить на 25 и нажать кнопку %.
2. Определение целого числа (100 %)
Мы знаем, что 250 руб. составляет 25 % от какого-то числа. Как его вычислить?
Составим простую пропорцию:
- 250 руб. – 25 %
- Y руб. – 100 %
- Y = 250 × 100 / 25 = 1 000 руб.
3. Процент между двумя числами
Допустим, предполагалась прибыль 800 руб., а получили 1 040 руб. Каков процент превышения?
Пропорция будет такой:
- 800 руб. – 100 %
- 1 040 руб. – Y %
- Y = 1 040 × 100 / 800 = 130 %
Перевыполнения плана по прибыли – 30 %, то есть выполнение – 130 %.
4. Расчет не из 100 %
Например, в магазин, состоящий из трех отделов, приходят 100 % покупателей. В продуктовый отдел – 800 человек (67 %), в отдел бытовой химии – 55. Какой процент покупателей приходит в отдел бытовой химии?
Пропорция:
- 800 посетителей – 67 %
- 55 посетителей – Y %
- Y = 55 × 67 / 800 = 4,6 %
5. На сколько процентов одно число меньше другого
Цена товара упала с 2 000 до 1 200 руб. На сколько процентов подешевел товар или на сколько процентов 1 200 меньше 2 000?
- 2 000 – 100 %
- 1 200 – Y %
- Y = 1 200 × 100 / 2 000 = 60 % (60 % к цифре 1 200 от 2 000)
- 100 % − 60 % = 40 % (число 1 200 меньше 2 000 на 40 %)
6. На сколько процентов одно число больше другого
Зарплата выросла с 5 000 до 7 500 рублей. На сколько процентов увеличилась зарплата? На сколько процентов 7 500 больше 5 000?
- 5 000 руб. – 100 %
- 7 500 руб. – Y %
- Y = 7 500 × 100 / 5 000 = 150 % (в цифре 7 500 150 % от 5 000)
- 150 % − 100 % = 50 % (число 7 500 больше 5 000 на 50 %)
7. Увеличение числа на определенный процент
Цена товара S выше 1 000 руб. на 27 %. Какова цена товара?
- 1 000 руб. – 100 %
- S – 100 % + 27 %
- S = 1 000 × (100 + 27) / 100 = 1 270 руб.
Онлайн-калькулятор делает вычисления намного проще: вам нужно выбрать вид расчета, ввести число и процент (в случае вычисления процентного соотношения – второе число), указать точность расчета и дать команду о начале действий.
Для решения большинства задач в математике средней школы необходимо знание по составлению пропорций. Это несложное умение поможет не только выполнять сложные упражнения из учебника, но и углубиться в саму суть математической науки. Как составить пропорцию? Сейчас разберем.
Самым простым примером является задача, где известны три параметра, а четвертый необходимо найти. Пропорции бывают, конечно, разные, но часто требуется найти по процентам какое-нибудь число. Например, всего у мальчика было десять яблок. Четвертую часть он подарил своей маме. Сколько осталось яблок у мальчика? Это самый простой пример, который позволит составить пропорцию. Главное это сделать. Изначально было десять яблок. Пусть это 100%. Это мы обозначили все его яблоки. Он отдал одну четвертую часть. 1/4=25/100. Значит, у него осталось: 100% (было изначально) – 25% (он отдал) = 75%. Эта цифра показывает процентное отношение количества оставшихся фруктов к количеству имевшихся сначала. Теперь у нас есть три числа, по которым уже можно решить пропорцию. 10 яблок – 100%, х яблок – 75%, где х – искомое количество фруктов. Как составить пропорцию? Необходимо понимать, что это такое. Математически это выглядит так. Знак равно поставлен для вашего понимания.
10 яблок = 100%;
x яблок = 75%.
Оказывается, что 10/x = 100%/75. Это и есть основное свойство пропорций. Ведь чем больше x, тем больше процентов составляет это число от исходного. Решаем эту пропорцию и получаем, что x=7,5 яблок. Почему мальчик решил отдать нецелое количество, нам неизвестно. Теперь вы знаете, как составить пропорцию. Главное, найти два соотношения, в одном из которых есть искомое неизвестное.
Решение пропорции часто сводится к простому умножению, а потом к делению. В школах детям не объясняют, почему это именно так. Хотя важно понимать, что пропорциональные отношения есть математическая классика, сама суть науки. Для решения пропорций необходимо уметь обращаться с дробями. Например, часто приходится переводить проценты в обыкновенные дроби. То есть запись 95% не подойдет. А если сразу написать 95/100, то можно провести солидные сокращения, не начиная основного подсчета. Сразу стоит сказать, что если ваша пропорция получилась с двумя неизвестными, то ее не решить. Никакой профессор вам здесь не поможет. А ваша задача, скорее всего, имеет более сложный алгоритм правильных действий.
Рассмотрим еще один пример, где нет процентов. Автомобилист купил 5 литров бензина за 150 рублей. Он подумал о том, сколько он бы заплатил за 30 литров топлива. Для решения этой задачи обозначим за x искомое количество денег. Можете самостоятельно решить эту задачу и потом проверить ответ. Если вы еще не поняли, как составить пропорцию, то смотрите. 5 литров бензина – это 150 рублей. Как и в первом примере, запишем 5л – 150р. Теперь найдем третье число. Конечно, это 30 литров. Согласитесь, что пара 30 л – х рублей уместна в данной ситуации. Перейдем на математический язык.
5 литров – 150 рублей;
30 литров – х рублей;
5/30 = 150 / x.
Решаем эту пропорцию:
5x = 30*150;
x = 900 рублей.
Вот и решили. В своей задаче не забудьте проверить на адекватность ответ. Бывает, что при неправильном решении автомобили достигают нереальных скоростей в 5000 километров в час и так далее. Теперь вы знаете, как составить пропорцию. Также вы сможете ее решить. Как видите, в этом нет ничего сложного.
Решение задачи с помощью пропорции сводится к тому, чтобы сделать неизвестное значение x членом этой пропорции. Затем используя основное свойство пропорции получить линейное уравнение и решить его.
Как решить задачу с помощью пропорции
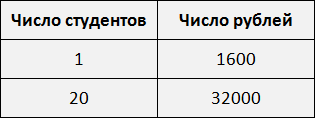
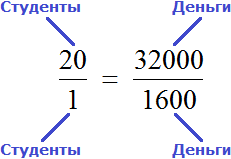
Рассмотрим простейший пример. Трем группам нужно выплатить стипендию по 1600 рублей каждому. В первой группе 20 студентов. Значит первой группе будет выплачено 1600 × 20, то есть 32 тыс. рублей.
Во второй группе 17 человек. Значит второй группе будет выплачено 1600 × 17, то есть 27,200 тыс. руб.
Ну и выплатим стипендию третьей группе. В ней 15 человек. На них нужно затратить 1600 × 15, то есть 24 тыс. руб.
В результате имеем следующее решение:
Для подобных задач решение можно записывать с помощью пропорции.
Пропорция по определению есть равенство двух отношений. К примеру, равенство является пропорцией. Эту пропорцию можно прочесть следующим образом:
a так относится к b, как c относится d
Аналогично можно соотнести стипендию и студентов, так чтобы каждому досталось по 1600 рублей.
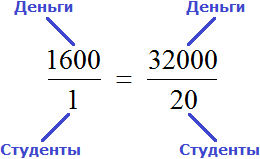
Итак, запишем первое отношение, а именно отношение тысячи шестисот рублей на одного человека:
Мы выяснили, что для выплаты 20 студентам по 1600 рублей, нам потребуется 32 тыс. рублей. Значит второе отношение будет отношением тридцати двух тысяч к двадцати студентам:
Теперь соединим полученные отношения знаком равенства:
Мы получили пропорцию. Её можно прочесть следующим образом:
Тысяча шестьсот рублей так относятся к одному студенту, как тридцать две тысячи рублей относятся к двадцати студентам.
То есть по 1600 рублей каждому. Если выполнить деление в обеих частях равенства , то обнаружим, что одному студенту, как и двадцати студентам достанется по 1600 рублей.
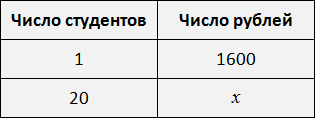
Теперь представим, что сумма денег, необходимых для выплаты стипендии двадцати студентам, была бы неизвестной. Скажем, если бы вопрос стоял так: в группе 20 студентов и каждому нужно выплатить по 1600 рублей. Сколько всего рублей требуется для выплаты стипендии?
В таком случае пропорция приняла бы вид
. То есть сумма денег, необходимая для выплаты стипендии, стала неизвестным членом пропорции. Эту пропорцию можно прочесть так:
Тысяча шестьсот рублей так относятся к одному студенту, как неизвестное число рублей относится к двадцати студентам
Теперь воспользуемся основным свойством пропорции. Оно гласит, что произведение крайних членов пропорции равно произведению средних:
Перемножив члены пропорции «крест-накрест», получим равенство 1600 × 20 = 1 × x. Вычислив обе части равенства, получим 32000 = x или x = 32000. Иными словами, мы найдём значение неизвестной величины, которое искали.
Аналогично можно было определить общую сумму и для остального количества студентов — для 17 и 15. Эти пропорции выглядели как и
. Воспользовавшись основным свойством пропорции, можно найти значение x
Задача 2. Расстояние равное 100 км автобус проехал за 2 часа. Сколько времени потребуется автобусу, чтобы проехать 300 км, если будет ехать с той же скоростью?
Можно сначала определить расстояние, которое автобус проезжает за один час. Затем определить сколько раз это расстояние содержится в 300 километрах:
100 : 2 = 50 км на каждый час движения
300 км : 50 = 6 часов
Либо можно составить пропорцию «сто километров так относятся к двум часам, как триста километров к неизвестному числу часов»:
Отношение одноименных величин
Если крайние или средние члены пропорции поменять местами, то пропорция не нарушится.
Так, в пропорции можно поменять местами крайние члены. Тогда получится пропорция
.
Пропорция также не нарушится, если её перевернуть, то есть использовать обратные отношения в обеих частях.
Перевернем пропорцию . Тогда получим пропорцию
. Взаимосвязь при этом не нарушается. Отношение между студентами равно отношению между суммами денег, предназначенных для этих студентов. Такую пропорцию часто составляют в школе, когда для решения задачи составляются таблицы
Этот способ записи очень удобен, поскольку позволяет перевести условие задачи в более понятный вид. Решим задачу в которой требовалось определить сколько рублей нужно для выплаты стипендии двадцати студентам.
Условие задачи запишем следующим образом:
Составим таблицу на основе этого условия:
Составим пропорцию, используя данные таблицы:
Используя основное свойство пропорции, получим линейное уравнение и найдем его корень:
Изначально, мы имели дело с пропорцией , которая составлена из отношений величин разной природы. В числителях отношений располагались суммы денег, а в знаменателях количество студентов:
Поменяв местами крайние члены, мы получили пропорцию . Эта пропорция составлена из отношений величин одной природы. В первом отношении содержатся количества студентов, а во втором — суммы денег:
Если отношение составлено из величин одной природы, то мы будем называть его отношением одноименных величин. Например, отношения между фруктами, деньгами, физическими величинами, явлениями, действиями.
Отношение может быть составлено, как из одноименных величин, так и из величин разной природы. Примерами последних являются отношение расстояния ко времени, отношения стоимости товара к его количеству, отношение общей суммы стипендии к количеству студентов.
Пример 2. В школьном саду посажены сосны и березы, причём на каждую сосну приходится 2 березы. Сколько посадили сосен в саду, если берез посадили 240?
Определим сколько сосен было посажено в саду. Для этого составим пропорцию. В условии сказано, что на каждую сосну приходится 2 березы. Напишем отношение, показывающее что на одну сосну приходится две березы:
Теперь напишем второе отношение, показывающее что на x сосен приходится 240 берез
Соединим эти отношения знаком равенства, получим следующую пропорцию:
«2 березы так относятся к одной сосне,
как 240 берез относятся к x соснам»
Используя основное свойство пропорции, находим значение x
Либо пропорцию можно составить, предварительно записав условие, как в прошлом примере:
Получится та же пропорция, но в этот раз она будет составлена из отношений одноименных величин:
Значит в саду посадили 120 сосен.
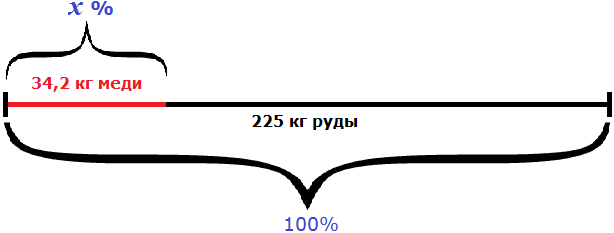
Пример 3. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?
Можно разделить 34,2 на 225 и полученный результат выразить в процентах:
Либо составить пропорцию 225 килограммам руды так приходятся на 100%, как 34,2 кг меди приходятся на неизвестное число процентов:
Либо составить пропорцию в которой отношения составлены из одноименных величин:
Задачи на прямую пропорциональность
Понимание отношений одноименных величин приводит к пониманию решения задач на прямую и обратную пропорциональность. Начнем с задач на прямую пропорциональность.
Для начала вспомним, что такое прямая пропорциональность. Это взаимосвязь между двумя величинами при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
Если расстояние в 50 км автобус прошел за 1 час, то для прохождения расстояния в 100 км (при той же скорости) автобусу потребуется 2 часа. Во сколько раз увеличилось расстояние, во столько же раз увеличилось время движения. Как показать это с помощью пропорции?
Одно из предназначений отношения заключается в том, чтобы показать во сколько раз первая величина больше второй. А значит и мы c помощью пропорции можем показать, что расстояние и время увеличились в два раза. Для этого воспользуемся отношением одноименных величин.
Покажем, что расстояние увеличилось в два раза:
Аналогично покажем, что время увеличилось во столько же раз
Соединим эти отношения знаком равенства, получим пропорцию:
«100 километров так относятся к 50 километрам, как 2 часа относятся к 1 часу»
Если выполнить деление в обеих частях равенства , то обнаружим что расстояние и время были увеличены в одинаковое число раз.
2 = 2
Задача 2. За 3 ч на мельнице смололи 27 т пшеничной муки. Сколько тонн пшеничной муки можно смолоть за 9 ч, если темп работы не изменится?
Решение
Время работы мельницы и масса перемолотой муки — прямо пропорциональные величины. При увеличении времени работы в несколько раз, количество перемолотой муки увеличится во столько же раз. Покажем это с помощью пропорции.
В задаче дано 3 ч. Эти 3 ч увеличились до 9 ч. Запишем отношение 9 ч к 3 ч. Это отношение будет показывать во сколько раз увеличилось время работы мельницы:
Теперь запишем второе отношение. Это будет отношение x тонн пшеничной муки к 27 тоннам. Данное отношение будет показывать, что количество перемолотой муки увеличилось во столько же раз, сколько и время работы мельницы
Соединим эти отношения знаком равенства, получим пропорцию .
Воспользуемся основным свойством пропорции и найдем x
Значит за 9 ч можно смолоть 81 т пшеничной муки.
Вообще, если взять две прямо пропорциональные величины и увеличить их в одинаковое число раз, то отношение нового значения к старому значению первой величины будет равно отношению нового значения к старому значению второй величины.
Так и в предыдущей задаче старые значения были 3 ч и 27 т. Эти значения были увеличены в одинаковое число раз (в три раза). Новыми значениями стали 9 ч и 81 т. Тогда отношение нового значения времени работы мельницы к старому значению равно отношению нового значения массы перемолотой муки к старому значению
Если выполнить деление в обеих частях равенства, то обнаружим, что время работы мельницы и количество смолотой муки увеличилось в одинаковое число раз:
3 = 3
Пропорцию, которую составляют к задачам на прямую пропорциональность, можно описать с помощью выражения:
Применительно к нашей задаче значения переменных
будут следующими:
Где впоследствии стало равно 81.
Задача 2. Для 8 коров в зимнее время доярка ежедневно заготовляет 80 кг сена, 96 кг корнеплодов, 120 кг силоса и 12 кг концентратов. Определить ежедневный расход этих кормов для 18 коров.
Решение
Количество коров и масса каждого из кормов — прямо пропорциональные величины. При увеличении количества коров в несколько раз, масса каждого из кормов увеличится во столько же раз.
Составим несколько пропорций, вычисляющих массу каждого из кормов для 18 коров.
Начнем с сена. Ежедневно для 8 коров его заготовляют 80 кг. Тогда для 18 коров будет заготовлено x кг сена.
Запишем отношение, показывающее во сколько раз увеличилось количество коров:
Теперь запишем отношение, показывающее во сколько раз увеличилась масса сена:
Соединим эти отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит для 18 коров нужно заготовить 180 кг сена. Аналогично определяем массу корнеплодов, силоса и концентратов.
Для 8 коров ежедневно заготовляют 96 кг корнеплодов. Тогда для 18 коров будет заготовлено x кг корнеплодов. Составим пропорцию из отношений и
, затем вычислим значение x
Определим сколько силоса и концентратов нужно заготовить для 18 коров:
Значит для 18 коров ежедневно нужно заготавливать 180 кг сена, 216 кг корнеплодов, 270 кг силоса и 27 кг концентратов.
Задача 3. Хозяйка варит вишнёвое варенье, причём на 3 стакана вишни кладёт 2 стакана сахара. Сколько сахара нужно положить на 12 стаканов вишни? на 10 стаканов вишни? на стакана вишни?
Решение
Количество стаканов вишни и количество стаканов сахарного песка — прямо пропорциональные величины. При увеличении количества стаканов вишни в несколько раз, количество стаканов сахара увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество стаканов вишни:
Теперь запишем отношение, показывающее во сколько раз увеличилось количество стаканов сахара:
Соединим эти отношения знаком равенства, получим пропорцию и найдем значение x
Значит на 12 стаканов вишни нужно положить 8 стаканов сахара.
Определим количество стаканов сахара для 10 стаканов вишни и стакана вишни
Задачи на обратную пропорциональность
Для решения задач на обратную пропорциональность опять же можно использовать пропорцию, составленную из отношений одноименных величин.
В отличие от прямой пропорциональности, где величины увеличиваются или уменьшаются в одну и ту же сторону, в обратной пропорциональности величины изменяются обратно друг другу.
Если одна величина увеличивается в несколько раз, то другая уменьшается во столько же раз. И наоборот, если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз.
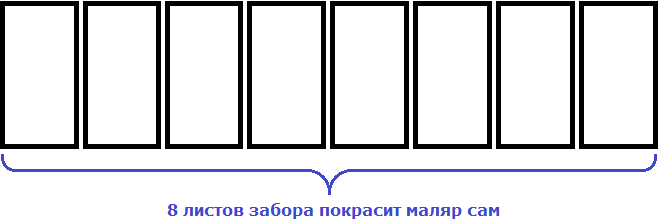
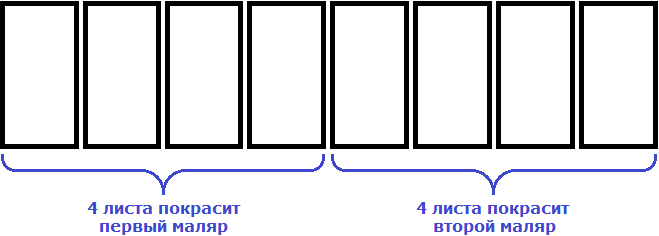
Допустим, что нужно покрасить забор, состоящий из 8 листов
Один маляр будет красить все 8 листов сам
Если маляров будет 2, то каждый покрасит по 4 листа.
Это конечно же при условии, что маляры будут честными между собой и справедливо разделят эту работу поровну на двоих.
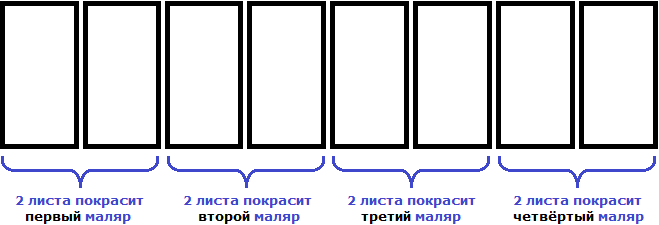
Если маляров будет 4, то каждый покрасит по 2 листа
Замечаем, что при увеличении количества маляров в несколько раз, количество листов которые приходятся на одного маляра уменьшаются во столько же раз.
Итак, мы увеличили количество маляров с 1 до 4. Другими словами, увеличили количество маляров в четыре раза. Запишем это с помощью отношения:
В результате количество листов забора, которые приходятся на одного маляра уменьшилось в четыре раза. Запишем это с помощью отношения:
Соединим эти отношения знаком равенства, получим пропорцию
«4 маляра так относятся к 1 маляру, как 8 листов относятся к 2 листам»
Задача 2. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?
Решение
Количество рабочих и количество дней, затраченных на работу — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней, необходимых для выполнения этой работы, уменьшится во столько же раз.
Запишем отношение 18 рабочих к 15 рабочим. Это отношение будет показывать во сколько раз увеличилось количество рабочих
Теперь запишем второе отношение, показывающее во сколько раз уменьшилось количество дней. Поскольку количество дней уменьшится с 24 дней до x дней, то второе отношение будет отношением старого количества дней (24 дня) к новому количеству дней (x дней)
Соединим полученные отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит 18 рабочих выполнят необходимую работу за 20 дней.
Вообще, если взять две обратно пропорциональные величины и увеличить одну из них в определенное число раз, то другая уменьшится во столько же раз. Тогда отношение нового значения к старому значению первой величины будет равно отношению старого значения к новому значению второй величины.
Так и в предыдущей задаче старые значения были 15 рабочих и 24 дня. Количество рабочих было увеличено с 15 до 18 (т.е. было увеличено в раза). В результате количество дней, необходимых для выполнения работы, уменьшилось во столько же раз. Новыми значениями стали 18 рабочих и 20 дней. Тогда отношение нового количества рабочих к старому количеству
равно отношению старого количества дней к новому количеству
Для составления пропорции к задачам на обратную пропорциональность можно пользоваться формулой:
Применительно к нашей задаче значения переменных
будут следующими:
Где впоследствии стало равно 20.
Задача 2. Скорость парохода относится к скорости течения реки, как 36 : 5. Пароход двигался вниз по течению 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?
Решение
Собственная скорость парохода составляет 36 км/ч. Скорость течения реки реки 5 км/ч. Поскольку пароход двигался по течению руки, то скорость его движения составила 36 + 5 = 41 км/ч. Время пути составила 5 ч 10 мин. Для удобства выразим время в минутах:
5 ч 10 мин = 300 мин + 10 мин = 310 мин
Поскольку на обратном пути пароход двигался против течения реки, то его скорость составила 36 − 5 = 31 км/ч.
Скорость парохода и время его движения — обратно пропорциональные величины. При уменьшении скорости в несколько раз, время его движения увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз уменьшилась скорость движения:
Теперь запишем второе отношение, показывающее во сколько раз увеличилось время движения. Поскольку новое время x будет больше старого времени, в числителе отношения запишем время x, а в знаменателе старое время, равное трёхсот десяти минутам
Соединим полученные отношения знаком равенства, получим пропорцию . Отсюда найдём значение x
410 минут это 6 часов и 50 минут. Значит пароходу потребуется 6 часов и 50 минут, чтобы вернуться обратно.
Задача 3. На ремонте дороги работало 15 человек, и они должны были закончить работу за 12 дней. На пятый день утром подошли еще несколько рабочих, и оставшаяся работа была выполнена за 6 дней. Сколько рабочих прибыло дополнительно?
Решение
Вычтем из 12 дней 4 отработанных дня. Так мы определим сколько ещё дней осталось работать пятнадцати рабочим
12 дней − 4 дня = 8 дней
На пятый день дополнительно прибыло x рабочих. Тогда всего рабочих стало 15 + x.
Количество рабочих и количество дней, необходимых для выполнения работы — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней уменьшится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество рабочих:
Теперь запишем во сколько раз уменьшилось количество дней, необходимых для выполнения работы:
Соединим эти отношения знаком равенства, получим пропорцию . Отсюда можно вычислить значение x
Значит 5 рабочих прибыло дополнительно.
Масштаб
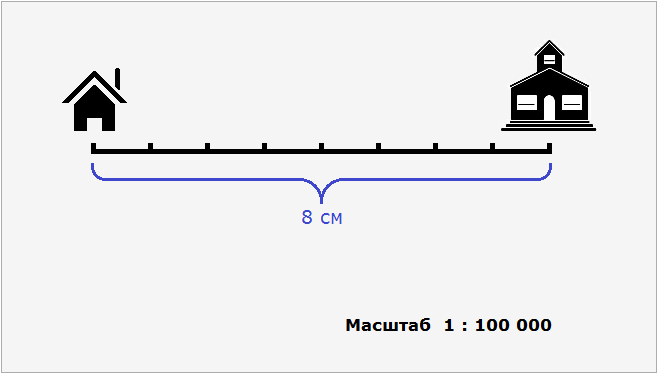
Масштабом называют отношение длины отрезка на изображении к длине соответствующего отрезка на местности.
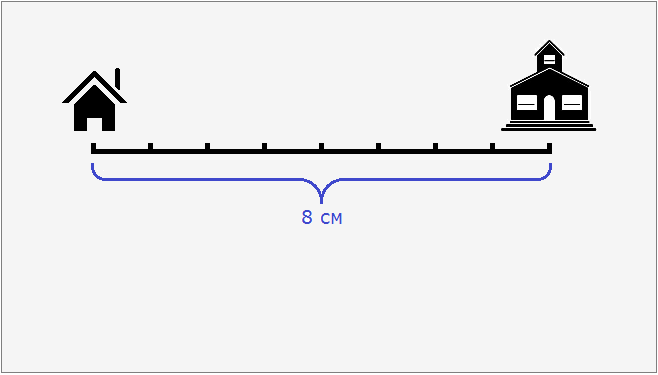
Допустим, что расстояние от дома до школы составляет 8 км. Попробуем нарисовать план местности, где будут указаны дом, школа и расстояние между ними. Но изобразить на бумаге расстояние, равное 8 км мы не можем, поскольку оно довольно велико. Но зато мы можем уменьшить это расстояние в несколько раз так, чтобы оно уместилось на бумаге.
Пусть километры на местности на нашем плане будут выражаться в сантиметрах. Переведем 8 километров в сантиметры, получим 800 000 сантиметров.
Уменьшим 800 000 см в сто тысяч раз:
800 000 см : 100 000 см = 8 см
8 см это расстояние от дома до школы, уменьшенное в сто тысяч раз. Теперь без труда можно нарисовать на бумаге дом и школу, расстояние между которыми будет 8 см.
Эти 8 см относятся к реальным 800 000 см. Так и запишем с помощью отношения:
8 : 800 000
Одно из свойств отношения гласит, что отношение не меняется если его члены умножить или разделить на одно и то же число.
В целях упрощения отношения 8 : 800 000 оба его члена можно разделить на 8. Тогда получим отношение 1 : 100 000. Это отношение и назовём масштабом. Данное отношение показывает, что один сантиметр на плане относится (или соответствует) ста тысячам сантиметров на местности.
Поэтому на нашем рисунке необходимо указать, что план составлен в масштабе 1 : 100 000
Примеры:
1 см на плане относится к 100 000 см на местности;
2 см на плане относится к 200000 см на местности;
3 см на плане относится к 300000 на местности и т.д.
К любой карте или плану указывается в каком масштабе они сделаны. Этот масштаб позволяет определять реальное расстояние между объектами.
Так, наш план составлен в масштабе 1 : 100 000. На этом плане расстояние между домом и школой составляет 8 см. Чтобы вычислить реальное расстояние между домом и школой, нужно 8 см увеличить в 100 000 раз. Иными словами, умножить 8 см на 100 000
8 см × 100 000 = 800 000 см
Получаем 800 000 см или 8 км, если перевести сантиметры в километры.
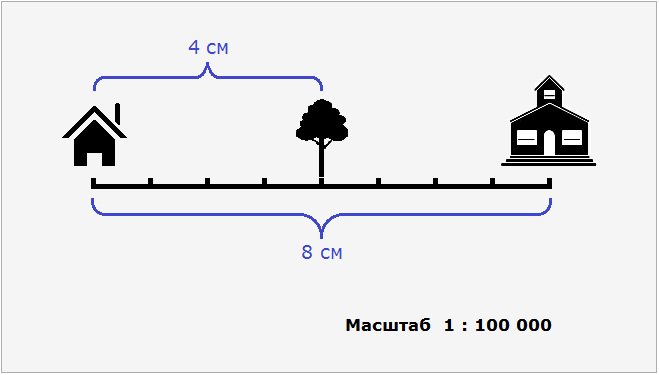
Допустим, что между домом и школой располагается дерево. На плане расстояние между школой и этим деревом составляет 4 см.
Тогда реальное расстояние между домом и деревом будет 4 см × 100 000 = 400 000 см или 4 км.
Расстояние на местности можно определять с помощью пропорции. В нашем примере расстояние между домом и школой будет вычисляться с помощью следующей пропорции:
Эту пропорцию можно прочитать так:
1 см на плане так относится к 100000 см на местности, как 8 см на плане относятся к x см на местности.
Из этой пропорции узнаём, что значение x равно 800000 см.
Пример 2. На карте расстояние между двумя городами составляет 8,5 см. Определить реальное расстояние между городами, если карта составлена в масштабе 1 : 1 000 000.
Решение
Масштаб 1 : 1 000 000 указывает, что 1 см на карте соответствует 1 000 000 см на местности. Тогда 8,5 см будут соответствовать x см на местности. Составим пропорцию 1 к 1000000 как 8,5 к x
В 1 км содержится 100000 см. Тогда в 8 500 000 см будет
Либо можно рассуждать так. Расстояние на карте и расстояние на местности — прямо пропорциональные величины. При увеличении расстояния на карте в несколько раз, расстояние на местности увеличится во столько же раз. Тогда пропорция примет следующий вид. Первое отношение будет показывать во сколько раз расстояние на местности больше расстояния на карте:
Второе отношение покажет, что расстояние на местности во столько же раз больше, чем 8,5 см на карте:
Отсюда x равен 8 500 000 см или 85 км.
Задача 3. Длина реки Невы 74 км. Чему равняется ее длина на карте, масштаб которой 1 : 2 000 000
Решение
Масштаб 1 : 2000000 говорит о том, что 1 см на карте соответствует 2 000 000 см на местности.
А 74 км на это 74 × 100 000 = 7 400 000 см на местности. Уменьшив 7 400 000 в 2 000 000, мы определим длину реки Невы на карте
7 400 000 : 2 000 000 = 3,7 см
Значит на карте, масштаб которой 1 : 2 000 000 длина реки Невы составляет 3,7 см.
Запишем решение с помощью пропорции. Первое отношение будет показывать сколько раз длина на карте меньше длины на местности:
Второе отношение будет показывать, что 74 км (7 400 000 см) уменьшились во столько же раз:
Отсюда находим x равный 3,7 см
Задачи для самостоятельного решения
Задача 1. Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
Решение
Пусть x кг масла можно получить из 7 кг хлопкового семени. Масса хлопкового семени и масса получаемого масла — прямо пропорциональные величины. Тогда уменьшение хлопкового семени с 21 кг до 7 кг, приведет к уменьшению получаемого масла во столько же раз.
Ответ: из 7 кг хлопкового семени получится 1,7 кг масла.
Задача 2. На некотором участке железнодорожного пути старые рельсы длиной в 8 м заменили новыми длиной в 12 м. Сколько потребуется новых двенадцатиметровых рельсов, если сняли 360 старых рельсов?
Решение
Длина участка на котором производится замена рельсов равна 8 × 360 = 2880 м.
Пусть x двенадцатиметровых рельсов требуется для замены. Увеличение длины одного рельса с 8 м до 12 м приведет к уменьшению количества рельсов с 360 до x штук. Иными словами, длина рельса и их количество связаны обратно пропорциональной зависимостью
Ответ: для замены старых рельсов потребуется 240 новых.
Задача 3. 60% учеников класса пошли в кино, а остальные 12 человек – на выставку. Сколько учащихся в классе?
Решение
Если 60% учащихся пошли в кино, а остальные 12 человек на выставку, то на 40% учащихся и будут приходиться 12 человек, пошедших на выставку. Тогда можно составить пропорцию в которой 12 учащихся так относятся к 40%, как все x учащихся относятся к 100%
Либо можно составить пропорцию, состоящей из отношений одноименных величин. Количество учащихся и процентная доля изменяются прямо пропорционально. Тогда можно записать, что во сколько раз увеличилось количество участников 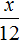
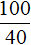
Ответ: в классе 30 учащихся.
Задача 4. Расстояние на карте между городами 18 см. Какое действительное расстояние между городами, если масштаб карты 1 : 500 000?
Решение
Масштаб 1 : 500000 говорит о том, что 1 см на карте соответствует 500 000 см на местности.
Тогда увеличив 18 см в 500 000, мы получим действительное расстояние между городами
18 см × 500 000 = 9 000 000 см
Переведем 9 000 000 см в километры. В одном километре 100 000 см. Тогда в 9 000 000 см будет
Запишем решение с помощью пропорции:
Ответ: расстояние между городами 90 км.
Задача 5. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч
Решение
Скорость и время — обратно пропорциональные величины. При увеличении скорости в несколько раз, время движения уменьшится во столько же раз.
Запишем отношение, показывающее по сколько раз увеличилась скорость движения пешехода:
Запишем отношение, показывающее что время движения уменьшилось во столько же раз:
Соединим эти отношения знаком равенства, получим пропорцию и найдём значение x
Ответ: пешеход затратит 2 часа если будет двигаться со скорость 4,5 км/ч.
Задача 6. Перевыполнив план на 15%, завод выпустил за месяц 230 станков. Сколько станков должен был выпустить за месяц завод по плану?
Решение
Выражение «перевыполнили план на 15%» означает, что к имеющемуся 100% плану выполнили еще 15% того же плана. Итого выполнено 115% плана. На эти 115% приходятся 230 выпущенных станков
А по плану завод должен был выпустить x станков. Эти x станков приходятся на 100% изначального плана
Составим пропорцию из имеющихся отношений и найдём значение x
Либо можно воспользоваться отношениями одноименных величин. Количество выпущенных станков и процентная доля, на которые эти станки приходятся, связаны прямо пропорциональной зависимостью. При увеличении количества станков в несколько раз, процентная доля увеличивается во столько же раз. Тогда можно записать, что 230 станков во столько раз больше, чем x станков, во сколько раз больше 115%, чем 100%
Ответ: по плану завод должен был выпустить 200 станков.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Математика
6 класс
Урок № 5
Пропорции
Перечень рассматриваемых вопросов:
- Понятие пропорции.
- Основное свойство пропорции.
- Как правильно составить пропорцию.
- Как найти неизвестный член пропорции.
Тезаурус
Равенство двух отношений называют пропорцией.
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.
Рассмотрим 3 способа нахождения неизвестного члена пропорции.
1 способ.
2 способ.
Способ 3.
Задача.
Решение:
Ответ:
1) можно;
2) можно;
3) нельзя;
4) нельзя.
Разбор решения заданий тренировочного модуля
№1. Тип задания: сортировка элементов по категориям.
№2. Тип задания: Подстановка элементов в пропуски в тексте.
Найдите неизвестный член пропорции.
Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.
Ответ: 3.