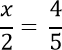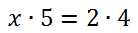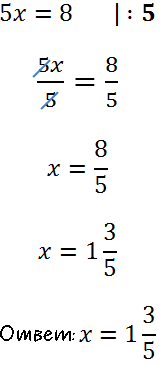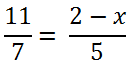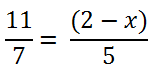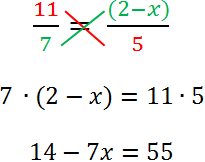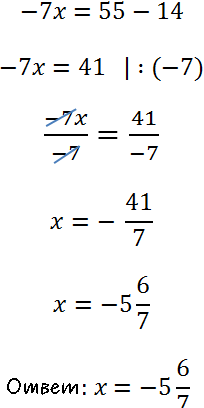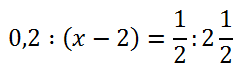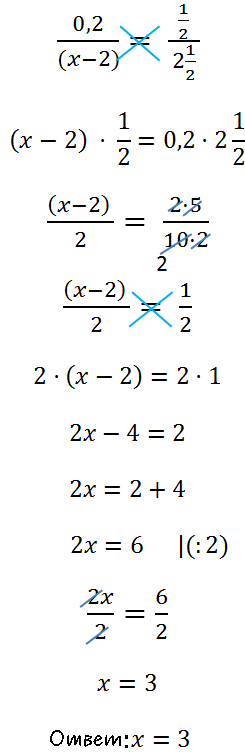Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 |
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Составить пропорцию. В этой статье хочу поговорить с вами о пропорции. Понимать, что такое пропорция, уметь составлять её – это очень важно, она действительно спасает. Это вроде бы маленькая и незначительная «буковка» в большом алфавите математики, но без неё математика обречена быть хромой и неполноценной.
Для начала напомню, что такое пропорция. Это равенство вида:
что тоже самое (это разная форма записи).
Пример:
Говорят – один относится к двум также, как четыре относится к восьми. То есть это равенство двух отношений (в данном примере отношения числовые).
Основное правило пропорции:
a:b=c:d
произведение крайних членов равно произведению средних
то есть
a∙d=b∙c
*Если какая-либо величина в пропорции неизвестна, ее всегда можно найти.
Если рассматривать форму записи вида:
то можно использовать следующее правило, его называют «правило креста»: записывается равенство произведений элементов (чисел или выражений) стоящих по диагонали
a∙d=b∙c
Как видите результат тот же.
Если три элемента пропорции известны, то
мы всегда можем найти четвёртый.
Именно в этом суть пользы и необходимость
пропорции при решении задач.
Давайте рассмотрим все варианты, где неизвестная величина х находится в «любом месте» пропорции, где a, b, c – числа:
Величина стоящая по диагонали от х записывается в знаменатель дроби, а известные величины стоящие по диагонали записываются в числитель, как произведение. Его запоминать не обязательно, вы и так всё верно вычислите, если усвоили основное правило пропорции.
Теперь главный вопрос, связанный с названием статьи. Когда пропорция спасает и где используется? Например:
1. Прежде всего это задачи на проценты. Мы рассматривали их в статьях ”
”
и ”
“.
2. Многие формулы заданы в виде пропорций:
> теорема синусов
> отношение элементов в треугольнике
> теорема тангенсов
> теорема Фалеса и другие.
3. В задачах по геометрии в условии часто задаётся отношение сторон (других элементов) или площадей, например 1:2, 2:3 и прочие.
4. Перевод единиц измерения, причём пропорция используется для перевода единиц как в одной мере, так и для перевода из одной меры в другую:
— часы в минуты (и наоборот).
— единицы объёма, площади.
— длины, например мили в километры (и наоборот).
— градусы в радианы (и наоборот).
здесь без составления пропорции не обойтись.
Ключевой момент в том, что нужно правильно установить соответствие, рассмотрим простые примеры:
Необходимо определить число, которое составляет 35% от 700.
В задачах на проценты за 100% принимается та величина, с которой сравниваем. Неизвестное число обозначим как х. Установим соответствие:
Можно сказать, что семисот тридцати пяти соответствует 100 процентов.
Иксу соответствует 35 процентов. Значит,
700 – 100%
х – 35 %
Решаем
Ответ: 245
Переведём 50 минут в часы.
Мы знаем, что одному часу соответствует 60 минут. Обозначим соответсвие –
x часов это 50 минут. Значит
1 – 60
х – 50
Решаем:
То есть 50 минут это пять шестых часа.
Ответ: 5/6
Николай Петрович проехал 3 километра. Сколько это будет в милях (учесть, что 1 миля это 1,6 км)?
Известно, что 1 миля это 1,6 километра. Число миль, которые проехал Николай Петрович примем за х. Можем установить соответствие:
Одной миле соответствует 1,6 километра.
Икс миль это три километра.
1 – 1,6
х – 3
Ответ: 1,875 миль
Вы знаете, что для перевода градусов в радианы (и обратно) существуют формулы. Я их не записываю, так как запоминать их считаю излишним, и так вам в памяти приходится держать много информации. Вы всегда сможете перевести градусы в радианы (и обратно), если воспользуетесь пропорцией.
Переведём 65 градусов в радианную меру.
Главное это запомнить, что 180 градусов это Пи радиан.
Обозначим искомую величину как х. Устанавливаем соответствие.
Ста восьмидесяти градусам соответствует Пи радиан.
Шестидесяти пяти градусам соответствует х радиан.
изучить статью
по этой теме на блоге. Материал в ней изложен несколько по иному, но принцип тот же. На этом закончу. Обязательно будет ещё что-нибудь интересненькое, не пропустите!
Если вспомнить само определение математики, то в нём есть такие слова: математика изучает количественные ОТНОШЕНИЯ (ОТНОШЕНИЯ
–
здесь ключевое слово). Как видите в самом определении математики заложена пропорция. Вообщем, математика без пропорции это не математика!!!
Всего доброго!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Но не все так сложо и непонятно, как кажется на первый взгляд. Для чего вообще все это нужно? Вот самый распространенный пример.
Допустим, у нас на сайте есть загрузка изображений, и мы хотим, чтобы после загрузки у нас создавалась миниатюрная копия, превьюшка какртинки. Часто это надо для анонса новостей, например. А скрипт требует, чтобы вы задали хотя бы примерные размеры миниатюрного изображения – его ширину и высоту.
Допустим также, что вы уже наметили его ширину, но как быть с высотой? Как высчитать ее та, чтобы картинка казалась более-менее пропорциональной по отношению к исходной.
Формула расчета
Все делается в два этапа:
- 1 – Делим исходную ширину на требуемую ширину;
- 2 – Получаем требуемую высоту, поделив исходную высоту на результат деления двух ширин (п.1).
Пример. Возьмем уже всем известные размеры изображений: 1024×768 и 800×600
. Представим, что мы не знаем высоту второй картинки. По формуле получается следующее: 768/(1024/800) = 600
. Это и есть требуемая нам высота.
Если же мы знаем высоту, а нам нужно получить ширину, то необходимо проделать все, как в первой формуле, только наоборот.
Чтобы получить требуемую ширину, нужно:
- 1 – Делим исходную высоту на требуемую высоту;
- 2 – Получаем требуемую ширину, поделив исходную ширину на результат деления двух высот (п.1).
То есть, 1024/(768/600) = 800
.
Пример 1
Вы заходите в супермаркет и видите акцию на . Его обычная цена – 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.
Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.
Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.
Умножьте 4,58 на 7, и вы получите 32,06 рубля.
Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.
Пример 2
Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.
Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.
Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.
100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.
2. Как посчитать проценты, разделив число на 10
Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.
Пример
Допустим, вы кладёте на 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.
В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.
Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.
Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.
В любом случае такими крупными числами оперировать довольно просто.
3. Как посчитать проценты, составив пропорцию
Составлять пропорции – одно из наиболее полезных умений, которому вас научили в . С его помощью можно посчитать любые проценты. Выглядит пропорция так:
сумма, составляющая 100% : 100% = часть суммы: доля в процентном соотношении.
Или можно записать её так: a: b = c: d.
Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.
Пример 1
Для примера вычислений используем рецепт . Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.
Сначала вычисляем процентную долю оставшегося шоколада.
90 г: 100% = 70 г: Х, где Х – масса оставшегося шоколада.
Х = 70 × 100 / 90 = 77,7%.
Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:
200 г: 100% = Х: 77,7%, где Х – нужное количество масла.
Х = 77,7 × 200 / 100 = 155,4.
Следовательно, в тесто нужно положить примерно 155 г масла.
Пример 2
Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.
Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.
Составьте пропорцию: 1 499: 100 = Х: 87.
Х = 87 × 1 499 / 100.
Заплатите 1 304,13 рубля и носите блузку с удовольствием.
4. Как посчитать проценты с помощью соотношений
В некоторых случаях можно воспользоваться простыми дробями. Например, 10% – это 1/10 числа. И чтобы узнать, сколько это будет в цифрах, достаточно разделить целое на 10.
- 20% – 1/5, то есть нужно делить число на 5;
- 25% – 1/4;
- 50% – 1/2;
- 12,5% – 1/8;
- 75% – это 3/4. Значит, придётся разделить число на 4 и умножить на 3.
Пример
Вы нашли брюки за 2 300 рублей со скидкой 25%, но у вас в кошельке только 2 000 рублей. Чтобы узнать, хватит ли денег на обновку, проведите серию несложных вычислений:
100% – 25% = 75% – стоимость брюк в процентах от первоначальной цены после применения скидки.
2 400 / 4 × 3 = 1 800. Именно столько рублей стоят брюки.
5. Как посчитать проценты с помощью калькулятора
Если без калькулятора вам жизнь не мила, все вычисления можно делать с его помощью. А можно поступить ещё проще.
- Чтобы посчитать проценты от суммы, введите число, равное 100%, знак умножения, затем нужный процент и знак %. Для примера с кофе вычисления будут выглядеть так: 458 × 7%.
- Чтобы узнать сумму за вычетом процентов, введите число, равное 100%, минус, размер процентной доли и знак %: 458 – 7%.
- Аналогично можно складывать, как в примере с депозитом: 530 000 + 5%.
6. Как посчитать проценты с помощью онлайн-сервисов
На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.
Умение вычисления процента от числа, когда нужно узнать пеню за просрочку, размер переплаты по кредиту или прибыль компании, если известен ее оборот и наценка.
- Как найти число по его проценту?
Правило. Чтобы найти число по его указанному проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на 100.
Таким вычислением сначала определим, сколько единиц этого числа содержится в 1%, а потом — в целом числе (в 100%).
Например:
Число, 23% которого составляют 52, находится так:
52: 23 * 100 = 226.1
Значит, если число 226,1 равно 100%, то число 52 равно 23% от этого числа.
Число, 125% которого составляют 240, находим так:
240: 125 * 100 = 192.
При определении числа по его проценту следует помнить, что:
— если процент меньше 100%, то число, полученное в результате вычислений, больше заданного числа (если 23% < 100%, то 226,1 > 52);
— если процент больше 100%, то число, полученное в результате вычислений, меньше заданного числа (если 125% > 100%, то 192 < 240).
Следовательно, при вычислении числа по его проценту для самоконтроля нужно проверить:
— заданный в условии процент больше или меньше 100%;
— результат вычисления больше или меньше заданного числа.
- Как узнать процент от суммы в общем случае?
После этого есть два варианта:
- Если нужно узнать, сколько процентов составляет другая сумма от первоначальной, нужно просто разделить ее на размер 1%, полученный ранее.
- Если же нужен размер суммы, которая составляет, скажем, 27,5% от первоначальной, нужно размер 1% умножить на требуемое количество процентов.
- Как высчитать процент от суммы с помощью пропорции?
Для этого придется использовать знания о методе пропорций, который проходят в рамках школьного курса математики. Это будет выглядеть так:
ПустьА — основная сумма, равная 100%, и В — сумма, соотношение которой с А в процентах нам нужно узнать. Записываем пропорцию:
(Х в данном случае — число процентов).
По правилам расчета пропорций мы получаем следующую формулу:
Х = 100 * В / А
Если же нужно узнать, сколько будет составлять сумма В при уже известном числе процентов от суммы А, формула будет выглядеть по-другому:
В = 100 * Х / А
Теперь остается подставить в формулу известные числа — и можно производить расчет.
- Как рассчитать процент от суммы с помощью известных соотношений?
Наконец, можно воспользоваться и более простым способом. Для этого достаточно помнить, что 1% в виде десятичной дроби — это 0,01. Соответственно, 20% — это 0,2; 48% — 0,48; 37,5% — это 0,375 и т.д. Достаточно умножить исходную сумму на соответствующее число — и результат будет означать размер процентов.
Кроме того, иногда можно воспользоваться и простыми дробями. Например, 10% — это 0,1, то есть 1/10 следовательно, узнать, сколько составят 10%, просто: нужно всего лишь разделить исходную сумму на 10.
Другими примерами таких соотношений будут:
- 12,5% — 1/8, то есть нужно делить на 8;
- 20% — 1/5, то есть нужно разделить на 5;
- 25% — 1/4, то есть делим на 4;
- 50% — 1/2, то есть нужно разделить пополам;
- 75% — 3/4, то есть нужно разделить на 4 и умножить на 3.
Правда, не все простые дроби удобны для расчета процентов. К примеру, 1/3 близка по размерам к 33%, но не равна точно: 1/3 — это 33,(3)% (то есть дробь с бесконечными тройками после запятой).
- Как вычесть процент от суммы без помощи калькулятора?
Если же требуется от уже известной суммы отнять неизвестное число, составляющее какое-то количество процентов, можно воспользоваться следующими методами:
- Вычислить неизвестное число с помощью одного из приведенных выше способов, после чего отнять его от исходного.
- Сразу рассчитать остающуюся сумму. Для этого от 100% отнимаем то число процентов, которое нужно вычесть, и полученный результат переводим из процентов в число любым из описанных выше способов.
Второй пример удобнее, поэтому проиллюстрируем его. Допустим, надо узнать, сколько останется, если от 4779 отнять 16%. Расчет будет таким:
- Отнимаем от 100 (общее количество процентов) 16. Получаем 84.
- Считаем, сколько составит 84% от 4779. Получаем 4014,36.
- Как высчитать (отнять) из суммы процент с калькулятором в руках?
Все вышеприведенные вычисления проще делать, используя калькулятор. Он может быть как в виде отдельного устройства, так и в виде специальной программы на компьютере, смартфоне или обычном мобильнике (даже самые старые из ныне используемых устройств обычно имеют эту функцию). С их помощью вопрос, как высчитать процент из суммы,
решается очень просто:
- Набирается исходная сумма.
- Нажимается знак «-».
- Вводится число процентов, которое требуется вычесть.
- Нажимается знак «%».
- Нажимается знак «=».
В итоге на экране высвечивается искомое число.
- Как отнять от суммы процент с помощью онлайн-калькулятора?
Наконец, сейчас в сети достаточно сайтов, где реализована функция онлайн-калькулятора. В этом случае даже не требуется знания того, как посчитать процент от суммы
: все операции пользователя сводятся к вводу в окошки нужных цифр (или передвижению ползунков для их получения), после чего результат сразу высвечивается на экране.
Особенно эта функция удобна тем, кто рассчитывает не просто абстрактный процент, а конкретный размер налогового вычета или сумму госпошлины. Дело в том, что в этом случае вычисления сложнее: требуется не только найти проценты, но и прибавить к ним постоянную часть суммы. Онлайн-калькулятор позволяет избежать подобных добавочных вычислений. Главное — выбрать сайт, пользующийся данными, которые соответствуют действующему закону.
Онлайн-калькулятор процентов:
calculator.ru — позволяет выполнять разнообразные расчеты при работе с процентами;
mirurokov.ru — калькуляятор процентов;
Источник информации:
- nsovetnik.ru — статьяя о том, как высчитать процент от суммы;
Один процент – это сотая часть от числа. Данное понятие используется, когда нужно обозначить отношение доли к целому. Кроме этого, в процентах можно сравнивать несколько величин, при этом обязательно указывая, относительного какого целого проценты вычисляются. Например, расходы выше доходов на 10 % или цена на железнодорожные билеты возросла на 15 % в сравнении с тарифами прошлого года. Число процентов выше 100 означает, что доля превышает целое, как часто бывает при статистических расчетах.
Процент как финансовое понятие – плата, заемщика кредитору за предоставление денег во временное пользование. В бизнесе встречается выражение «работать за проценты». В данном случае подразумевается, что размер вознаграждения зависит от прибыли или оборота (комиссионные). Обойтись без вычисления процентов невозможно в бухгалтерии, бизнесе, банковском деле. Чтобы упростить расчеты, разработан онлайн-калькулятор процентов.
Калькулятор позволяет вычислить:
- Процент от заданного значения.
- Процент из суммы (налог по фактической зарплате).
- Процент от разницы (НДС из ).
- И многое другое…
При решении задач на калькуляторе процентов нужно оперировать тремя значениями, одно из которых неизвестно (по заданным параметрам вычисляется переменная). Сценарий расчета следует выбирать, исходя из заданных условий.
Примеры расчетов
1. Вычисление процента от числа
Чтобы найти число, составляющее 25 % от 1 000 руб., нужно:
- 1 000 × 25 / 100 = 250 руб.
- Или 1 000 × 0,25 = 250 руб.
Для расчета на обычном калькуляторе, нужно 1 000 умножить на 25 и нажать кнопку %.
2. Определение целого числа (100 %)
Мы знаем, что 250 руб. составляет 25 % от какого-то числа. Как его вычислить?
Составим простую пропорцию:
- 250 руб. – 25 %
- Y руб. – 100 %
- Y = 250 × 100 / 25 = 1 000 руб.
3. Процент между двумя числами
Допустим, предполагалась прибыль 800 руб., а получили 1 040 руб. Каков процент превышения?
Пропорция будет такой:
- 800 руб. – 100 %
- 1 040 руб. – Y %
- Y = 1 040 × 100 / 800 = 130 %
Перевыполнения плана по прибыли – 30 %, то есть выполнение – 130 %.
4. Расчет не из 100 %
Например, в магазин, состоящий из трех отделов, приходят 100 % покупателей. В продуктовый отдел – 800 человек (67 %), в отдел бытовой химии – 55. Какой процент покупателей приходит в отдел бытовой химии?
Пропорция:
- 800 посетителей – 67 %
- 55 посетителей – Y %
- Y = 55 × 67 / 800 = 4,6 %
5. На сколько процентов одно число меньше другого
Цена товара упала с 2 000 до 1 200 руб. На сколько процентов подешевел товар или на сколько процентов 1 200 меньше 2 000?
- 2 000 – 100 %
- 1 200 – Y %
- Y = 1 200 × 100 / 2 000 = 60 % (60 % к цифре 1 200 от 2 000)
- 100 % − 60 % = 40 % (число 1 200 меньше 2 000 на 40 %)
6. На сколько процентов одно число больше другого
Зарплата выросла с 5 000 до 7 500 рублей. На сколько процентов увеличилась зарплата? На сколько процентов 7 500 больше 5 000?
- 5 000 руб. – 100 %
- 7 500 руб. – Y %
- Y = 7 500 × 100 / 5 000 = 150 % (в цифре 7 500 150 % от 5 000)
- 150 % − 100 % = 50 % (число 7 500 больше 5 000 на 50 %)
7. Увеличение числа на определенный процент
Цена товара S выше 1 000 руб. на 27 %. Какова цена товара?
- 1 000 руб. – 100 %
- S – 100 % + 27 %
- S = 1 000 × (100 + 27) / 100 = 1 270 руб.
Онлайн-калькулятор делает вычисления намного проще: вам нужно выбрать вид расчета, ввести число и процент (в случае вычисления процентного соотношения – второе число), указать точность расчета и дать команду о начале действий.
|
Один из способов решения задач на проценты – это использование пропорций. Как правильно составлять и решать подобные пропорции? Существует много практических задач, использующих понятие процентов. Часто для их решения используется понятие пропорции. В простых случаях можно решать вот таким образом: все мы знаем, что 50% это половина от числа, 25% – это его четвёртая часть, 20% – это пятая часть, 10% -это 10 часть , 5 % – 20 часть, 1% – 100 часть. Итак, найти один процент от 2000 это 2000/100=20. Найти 50 % от 60 это 60/2=30. А можно использовать универсальный способ – понятие пропорции. Предположим надо найти 13% от 180. Тогда составим: 180 – 100% Х – 13 % Мы должны числа писать под числами, проценты под процентами. Далее раскрывает пропорцию крест накрест. То с чем икс не в паре перемножаем, а с чем в паре по диагонали – делим. У нас получаем 180*13/100=23,4 система выбрала этот ответ лучшим Ксарфакс 4 года назад Пропорция с процентами составляется по следующему принципу:
Вот как выглядет такая пропорция: A / B = 100% / p% Например: 1000 / 50 = 50% / 5%. Или можно записать по-другому: 1000 – 100%. 50 – 5%. При решении задач на проценты с помощью пропорции неизвестный её член (а здесь может быть 3 варианта) обычно обозначается за x. Решить пропорцию (то есть найти неизвестный член) можно благодаря её основному свойству: произведение крайних членов пропорции равно произведению средних (другими словами, нужно перемножить члены пропорции крест-накрест).
Далее рассмотрим несколько простых примеров. Пример 1. Зарплата составляет 30000 рублей, а премия – 10% от зарплаты. Нужно определить размер премии. 30000 – 100%. x – 10%. Вспоминаем, что произведение крайних членов равно произведению средних: 30000 * 10 = 100 * x. x = (30000 * 10) / 100 = 3000. Значит, премия равна 3000 рублей. Пример 2. Сделано 20 выстрелов, 4 из них – мимо мишени. Нужно определить процент попадания. 20 – 100%. 4 – x%. Умножаем крест-накрест и приравниваем: 20 * x = 100* 4. x = (100 * 4) / 20 = 20. Здесь нужно учесть, что 20% – это процент выстрелов мимо мишени (так как рядом с неизвестным x были записаны именно промахи). Процент попадания в свою очередь равен 100% – 20% = 80%. Пример 3. За месяц было продано 30 ноутбуков, что составляет 20% от всего количества ноутбуков, имеющихся в продаже. Нужно найти, сколько всего ноутбуков было в магазине изначально. x – 100%. 30 – 20%. Умножаем крест-накрест: 20 * x = 100 * 30. x = (100 * 30) / 20 = 150. Таким образом, изначально в продаже было 150 ноутбуков. Zummy out off 3 года назад Я как-то со школы запомнила принцип пропорции и способ ее решения называю «крест-накрест», не помню, кто это мне подсказал. Никогда не нахожу проценты по принципу умножения на сотую часть, мне не удобно, всегда использую свой «крест», единственное неудобство – нужно наглядно записывать это. Это не страшно – бумага всегда под рукой. Составляю пропорцию по условию, одно из значений неизвестное обозначаю Х. Затем решаю: перемножаю цифры, расположенные «на углах» слева и справа от Х, делю на число, расположенное на противоположном углу от Х. Пример: нужно найти 5% от числа 420. Пишу пропорцию. 420 – 100 % Х – 5 % Х = 5 • 420 : 100 = 21% Вот моя запись с крестом Ещё пример: сколько процентов от 200 составляет число 20. Составляю пропорцию. 200 – 100 % 20 – Х % Решение: X = 20 • 100 : 200 = 10% Алиса в Стране 3 года назад Странно, конечно, для таких простых задач составлять какие-то дополнительные пропорции, они решаются в уме и очень быстро, но способ такой есть, давайте его рассмотрим, возможно, кому-то он пригодится. Допустим, нам надо найти сколько процентов составляет число 18 от числа 90, в принципе, мы и так сразу видим что 18 это одна пятая, то есть 20 процентов от числа 90, но давайте составим пропорцию, приняв за х искомое количество процентов, пропорция у нас будет такая: 90 – 100 % 18 – х %, откуда х = 100 х 18 / 90 = 20 процентов. Еще один пример для закрепления материала, найдем, сколько процентов составляет 24 от 250, пропорция: 24 – х 250 – 100 х = 24 х 100 /250 = 9,6 %. Go Green 3 года назад Для определения процентного соотношения от числа нужно иметь представление об основных простых процентных соотношениях и о принципе вычисления любых из них. Для простоты давайте приведем примеры с числом 100. 1 % от ста – это одна сотая часть или один процент. 2% от ста – две сотых части от ста. 7% от ста – семь сотых части от ста и так далее. То есть сначала нам нужно узнать, сколько составляет один процент любого числа, разделив его на сто, а затем узнавать заданное процентное соотношение. Например, нам нужно найти, сколько будет равно 7 процентам от 200. Делим 200 на 100. Получится 2. Умножим 2 на 7, получится 14. Итого: 7% от 200 будет равняться числу 14. СТА 1106 3 года назад Всегда любила задачки на пропорции. Главное- правильно ее составить, а потом все просто, крест на крест и решение готово. Простейший пример. Найти на сколько процентов цех выполнил план по сборке за смену, если общий план 250 механизмов( штук), а всего за смену было собрано 262 ? Итак решаем. 250 штук – 100 % 262 штуки – х % Решение: 262 × 100:250= 104,8 %. Пример 2. Выяснить, сколько столовой нужно картофеля на год, если 20 тонн закрывают потребность лишь на 82%. Решение. Опять пропорция, где известно доля от потребности и в тоннах и процентах. Общая потребность , разумеется берется за 100. 20 тонн – 82 % Х тонн – 100 %. 20 × 100:82= 24,4 тонны. Бекки Шарп 3 года назад Допустим по условию задачи нам известно сколько всего было единиц (1000 кг яблок) и надо узнать сколько единиц (кг сухого вещества) составляют 18%. Составляем пропорцию, в которой 1000 – это 100%, а неизвестной х – 18 %. То есть в пропорции у нас есть единицы и проценты. Соотносим соответственно кг к кг и проценты к процентам. это обязательное условие пропорции. Пропорция будет выглядеть так: Бархатные лапки 3 года назад Обычно в таких задачах задано общее число единиц, кг, км и нужно узнать сколько этих единиц составит определенное количество процентов. Или наоборот сколько процентов составляет количество единиц. То есть даны два известных, но мы помним что есть еще проценты, что общее количество чего-то это всегда 100%. Например нам нужно узнать сколько процентов составляет 38 рублей от 40 рублей. Составим пропорцию: 40/38=100/х, где 40 рублей это 100%, х – сколько рублей 38%. Из пропорции находим х = 95 %. Точно в цель 3 года назад Посчитать пропорцию с процентами очень легко. В задачах на пропорции с процентами нам нужно посчитать проценты от числа. Для решения задачи нам нужно знать, что 50% – это половина от числа, 25% – одна четвертая от числа. То есть для того, чтобы найти пропорцию с процентами, нам нужно разделить число на 100 и умножить на процент. Например, мне нужно найти 20 процентов от числа 230. Сначала я 230 делю на 100, получается 2.3, а затем умножаю его на 20 – получаю 46. 50 процентов является половиной от числа, 25 является четвертой частью, 20 – пятой, 10 – 10, 5 является 20, а 1 процент – 100 часть. Один процент от 2000 найти не сложно. 2000 делим на 100 получим 20. Для того чтобы найти 50 процентов от 60 вам потребуется поделить на 2 = 30. Если нужно найти 13 процентов от 180 то 180 = 100 процентам , х = 14 получится 180 умножим на 13 делим на 100 и получаем 23,4. [пользователь заблокирован] 4 года назад Всё очень просто. Всегда нужно начинать с того, что процент – это одна сотая часть. Ну, а далее – пропорция составляется исходя из этой посылки. Знаете ответ? |
Калькулятор пропорций онлайн
Калькулятор рассчитывает неизвестный член пропорции. Можно также проверить пропорцию на верность.
Правила ввода
Вводить можно целые числа, десятичные дроби, правильные и неправильные дроби -5, 5, 0.25, -1.25, 10/8, -1/2 и.т.д.
Если вам необходимо ввести смешанное число то предварительно его нужно преобразовать в неправильную дробь. Т.е. 3 целые 1/3 нужно будет записать как 10/3
Поле которое необходимо рассчитать можно оставить пустым или ввести любую букву латинского(английского) алфавита.
В расчётное поле можно также вводить значения с переменными вида: 5x, 1.2x, 5/x, x/5, 3x/2, 2/3x. Т.е. если вам надо посчитать (2/3)*х то нужно записать как 2x/3. Если надо посчитать (1/2)*(1/x) то нужно будет ввести 1/2x.
Решить пропорцию это значит найти неизвестный член пропорции.
Пропорцию можно записать двумя способами:
a / b = c / d
a : b = c : d
Прочитать формулу выше можно как a относится к b, как c относится к d.
a, b, c, d – называются членами пропорции
a, d – называются крайними членами пропорции
b, c – называются средними членами пропорции
Главное свойство пропорции
Произведение крайних членов пропорции равно произведению средних членов пропорции.
a / b = c / d
a × d = b × c
Крайний член пропорции равен произведению средних членов пропорции, делённому на другой крайний член
a = bc/d
d = bc/a
Средний член пропорции равен произведению крайних членов пропорции, делённому на другой средний член
b = ad/c
c = ad/b
Примеры решения задач на пропорции
1) Решите пропорцию 3:x=2:5
Из основного свойства пропорции получается
2x=15,
x=15/2=7.5
2) Решите пропорцию x:9=10:3
Из основного свойства пропорции получается
3x=90,
x=90/3=30
3) Решите пропорцию 2x:8=28:16
Из основного свойства пропорции получается
2x·16=8·28,
32x=224,
x=224/32=7
Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию.
Например, рассмотрим такое уравнение.
Для решения уравнения с пропорцией используют правило пропорции или,
как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке
«Пропорции».
В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Запомните!
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции,
то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции.
Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию
в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и
решим уравнение до конца.
В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Важно!
Если в члене пропорции присутствуют знаки «+» или «−»,
обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда
будете использовать правило пропорции.
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции
для дальнейшего решения.
Теперь раскроем скобки с помощью
правила раскрытия
скобок.
Из урока «Решение линейных уравнений» используем
правило переноса и
правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать
правило знаков.
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
Другие примеры решения уравнений с пропорцией
-
=
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число
-
=
3x · 6,8 = 0,21 · 1,7
20,4 x=
·
20
x =
=204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =
x =
x =
x =
x =
Ответ: x =
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий: