Как составить пропорцию сторон треугольника

Математика

В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

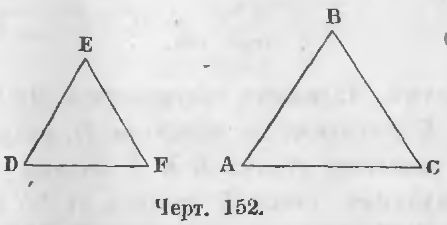
В треугольниках ABC и DEF (черт. 152), в которых

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

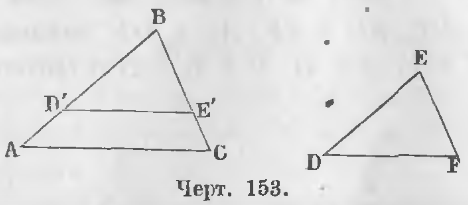
Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,

Если соответственные углы равны, то D’E || AC.

По теореме 86 имеют место равенства

AC/D’E’ = AB/BD’ = BC/BE’

Так как BD’ = ED, BE’ = EF, D’E’ = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆ BD’E’ = ∆ DEF, следовательно,

Так как имеет место пропорция

то сторона D’E’ || AC (теорема 87).

Поэтому ∠D’ = ∠A, ∠C = ∠E’.

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

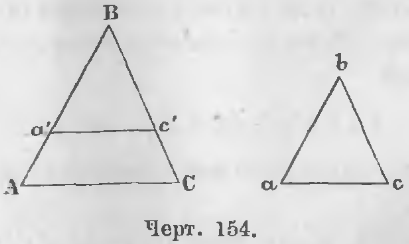
Требуется доказать, что у них углы равны, т. е.

Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:

AB/Ba’ = BC/Bc’ = AC/a’c’

Так как Ba’ = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc’ = AC/a’c’ (2)

Сопоставляя отношения (1) и (2), заключаем, что

следовательно, два треугольника a’Bc’ и abc равны, откуда

∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c

∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

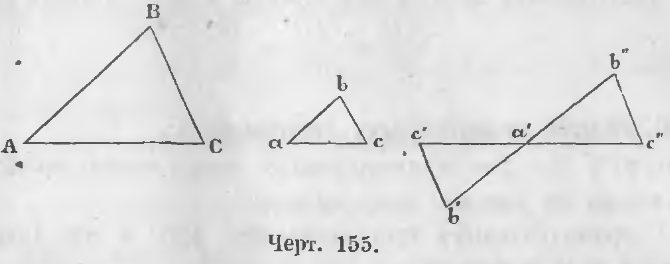
2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.

AB || a’b’, AC || a’c’, BC || b’c’.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b” = a’b’ и a’c” = a’c’.

Треугольники a’b”c” и a’b’c’ равны. Треугольник a’b”c” подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

a’b”c”, следовательно, ∆ ABC

a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’

Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

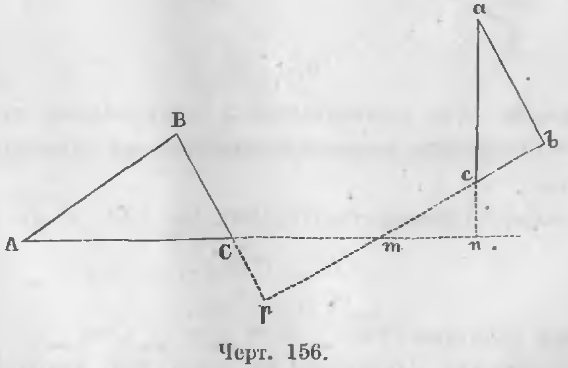
Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

∠pCm = ∠ACB, ∠mcn = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

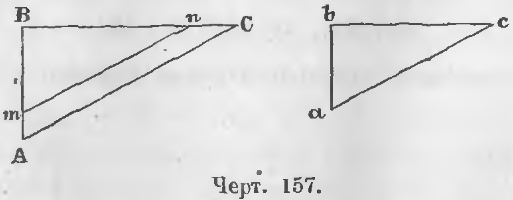
Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

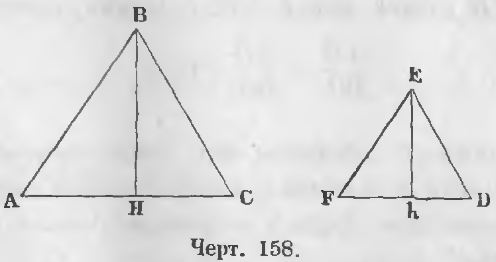
Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠ α = ∠ β

Требуется доказать, что AB/BC = AD/DC.

Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠ β как соответственные углы,
∠FAB = ∠ α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠ α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

Заменяя FB равным отрезком AB, получим пропорцию:

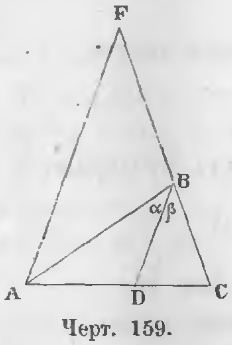
Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

Требуется доказать, что ∠ α = ∠β .

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

Так как ∠ α = ∠ FAB, ∠β = ∠ AFB, то и

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠ α = d, ∠ α + ∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α , которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

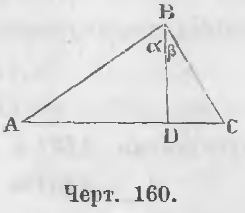
Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ ABC = ∠ADB как прямые, ∠A общий, следовательно,

Из подобия треугольников вытекает пропорция:

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠ β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB 2 = AD · AC
BC 2 = DC · AC

Складывая их, получим:

AB 2 + BC 2 = AD · AC + DC · AC или
AB 2 + BC 2 = AC (AD + DC) = AC · AC = AC 2 , т. е.
AC 2 = AB 2 + BC 2

a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC 2 = AB 2 + BC 2 .

Так как AB = BC, то AC 2 = 2AB 2 , откуда AC = AB √ 2 и AC/AB = √ 2 величина несоизмеримая.

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB 2 = BC 2 + AC 2 – 2AC · DC.

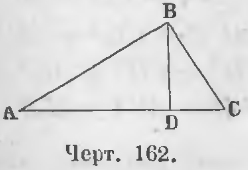
Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB 2 = BD 2 + AD 2 (a)
AD = AC – DC, AD 2 = (AC – DC) 2 = AC 2 + DC 2 – 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD 2 = BC 2 – DC 2

Вставляя величины BD 2 и AD 2 в равенство (a), получим:

AB 2 = BC 2 – DC 2 + AC 2 + DC 2 – 2AC · DC, откуда
AB 2 = BC 2 + AC 2 – 2AC · DC (ЧТД).

2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

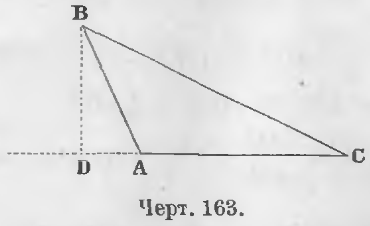
Доказательство. Из прямоугольного треугольника ABD имеем:

AB 2 = BD 2 + DA 2

Из прямоугольного треугольника BCD имеем:

BD 2 = BC 2 – CD 2

AB 2 = BC 2 – CD 2 + DA 2 .

DA = CD – AC
DA 2 = (CD – AC) 2 = CD 2 + AC 2 – 2CD · AC, то
AB 2 = BC 2 – CD 2 + CD 2 + AC 2 – 2CD · AC, откуда
AB 2 = BC 2 + AC 2 – 2CD · AC (ЧТД).

Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB 2 = AC 2 + BC 2 + 2AC · CD

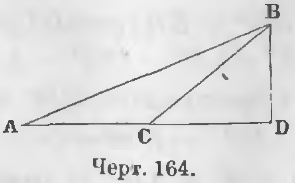
Доказательство. Из тупоугольного треугольника ABC имеем:

AB 2 = BD 2 + AD 2 (a)
AD = AC + CD, AD 2 = AC 2 + CD 2 + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD 2 = BC 2 – CD 2

Заменяя AD 2 и BD 2 в равенстве (a), получим:

AB 2 = BC 2 – CD 2 + AC 2 + CD 2 + 2AC · CD

AB 2 = BC 2 + AC 2 + 2AC · CD (ЧТД).

Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2

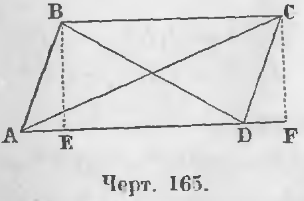
Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD 2 = AB 2 + AD 2 – 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC 2 = CD 2 + AD 2 + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD 2 + AC 2 = AB 2 + AD 2 + CD 2 + AD 2

Так как AD = BC, то

BD 2 + AC 2 = AB 2 + BC 2 + CD 2 + AD 2 (ЧТД).

Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB 2 + BC 2 = 2AD 2 + 2BD 2

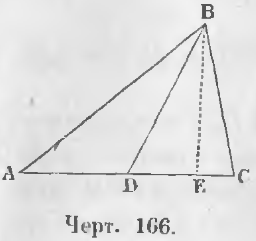
Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB 2 = BE 2 + AE 2
BC 2 = BE 2 + CE 2

Сложив их, находим:

AB 2 + BC 2 = 2BE 2 + AE 2 + CE 2 (a)

Так как AE = AD + DE = CD + DE, CE = CD – DE, то

AE 2 = (CD + DE) 2 = CD 2 + DE 2 + 2CD · DE
CE 2 = (CD – DE) 2 = CD 2 + DE 2 – 2CD · DE

AE 2 + CE 2 = 2CD 2 + 2DE 2 (b)

Заменяя в равенстве (a) сумму AE 2 + CE 2 из равенства (b), имеем:

AB 2 + BC 2 = 2BE 2 + 2CD 2 + 2DE 2 .

Из прямоугольного треугольника BDE видно, что

BE 2 = BD 2 – DE 2

AB 2 + BC 2 = 2BD 2 – 2DE 2 + 2CD 2 + 2DE 2

Подобные треугольники

Определение

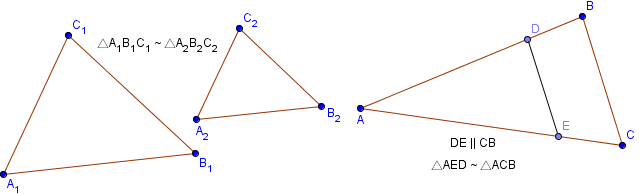
Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.

Математическое представление двух подобных треугольников A₁B₁C₁ и A₂B₂C₂ , показанных на рисунке, записывается следующим образом:

Два треугольника являются подобными если:

1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:
∠A₁ = ∠A₂, ∠B₁ = ∠B₂ и∠C₁ = ∠C₂

2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой:
$frac=frac=frac$

3. Отношения двух сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой и при этом
углы между этими сторонами равны:
$frac=frac$ и $angle A_1 = angle A_2$
или
$frac=frac$ и $angle B_1 = angle B_2$
или
$frac=frac$ и $angle C_1 = angle C_2$

Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:

Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.

Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:

1) три угла каждого треугольника (длины сторон треугольников знать не нужно).

Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника.
Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 – угол1 – угол2)

2) длины сторон каждого треугольника (углы знать не нужно);

3) длины двух сторон и угол между ними.

Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.

Практические задачи с подобными треугольниками

Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.

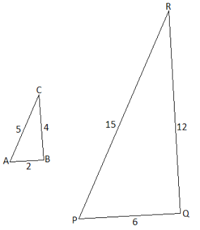
Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:

Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.

Решение:
∠A = ∠P и ∠B = ∠Q, ∠C = ∠R(так как ∠C = 180 – ∠A – ∠B и ∠R = 180 – ∠P – ∠Q)

Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно:
$frac=frac=frac$

Пример №3: Определите длину AB в данном треугольнике.

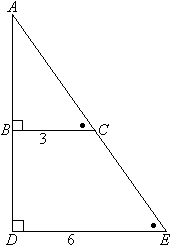
Решение:

∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными.

$frac = frac<3> <6>= frac = frac = frac = frac<1> <2>Rightarrow 2times AB = AB + 4 Rightarrow AB = 4$

Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.

Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.

AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC

Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.

Следовательно:
$frac = frac<7> <11>= frac = frac<15> Rightarrow CA = frac<15 times 11> <7>= 23.57$
x = AC – DC = 23.57 – 15 = 8.57

Практические примеры

Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1.

Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера.

Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.

Решение:

Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке.

Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно,

$frac = frac<3> <9>= frac = frac<8> Rightarrow AB = frac<8 times 9> <3>= 24 м$
x = AB – 8 = 24 – 8 = 16 м

Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта.

А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом:

Аналогично, $AC = sqrt = sqrt <24^2 + 9^2>= 25.63 м$
что является расстоянием, которое проходит продукция в данный момент при попадании на существующий уровень.

y = AC – AE = 25.63 – 8.54 = 17.09 м
это дополнительное расстояние, которое должна пройти продукция для достижения нового уровня.

Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем.

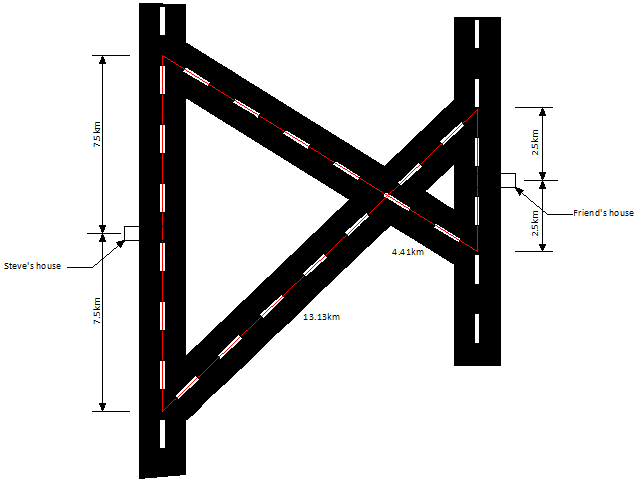
Решение:

Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке.

Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно:
$frac = frac = frac$

В условии задачи сказано, что:

AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км

Используя эту информацию, мы можем вычислить следующие расстояния:

Стив может добраться к дому своего друга по следующим маршрутам:

A -> B -> C -> E -> G, суммарное расстояние равно 7.5+13.23+4.38+2.5=27.61 км

F -> B -> C -> D -> G, суммарное расстояние равно 7.5+13.23+4.41+2.5=27.64 км

F -> A -> C -> E -> G, суммарное расстояние равно 7.5+13.13+4.38+2.5=27.51 км

F -> A -> C -> D -> G, суммарное расстояние равно 7.5+13.13+4.41+2.5=27.54 км

Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву.

Пример 7:
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.

Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания.

Решение:

Геометрическое представление задачи показано на рисунке.

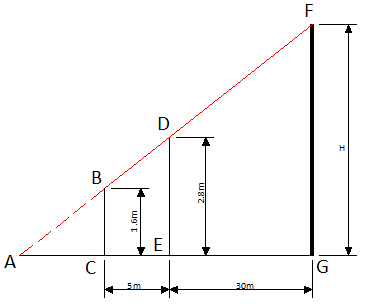
Сначала мы используем подобность треугольников ΔABC и ΔADE.

$frac = frac<1.6> <2.8>= frac = frac <5 + AC>Rightarrow 2.8 times AC = 1.6 times (5 + AC) = 8 + 1.6 times AC$

$(2.8 – 1.6) times AC = 8 Rightarrow AC = frac<8> <1.2>= 6.67$

Затем мы можем использовать подобность треугольников ΔACB и ΔAFG или ΔADE и ΔAFG. Давайте выберем первый вариант.

Подобные треугольники

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

[spoiler title=”источники:”]

http://www.math10.com/ru/geometria/podobnye-treugolniki.html

[/spoiler]

Подобные треугольники

3 октября 2022

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Подобные треугольники — ключевая тема геометрии 8 класса. Они будут преследовать нас до самого конца школы. И сегодня мы разберём всё, что нужно знать о них.

План такой:

1. Основное определение
2. Лемма о подобных треугольниках
3. Свойства подобных треугольников
4. Разбор задач

1. Основное определение

Определение. Треугольники называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Рассмотрим треугольники $ABC$ и $MNK$:

У них есть равные углы: $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. И пропорциональные стороны:

[frac{AB}{MN}=frac{BC}{NK}= frac{AC}{MK}= frac{color{red}{3}}{color{red}{2}}]

Следовательно, треугольники $ABC$ и $MNK$ подобны. Записывается это так:

[Delta ABCsim Delta MNK]

Число $k={color{red}{3}}/{color{red}{2}};$ называется коэффициентом подобия. К нему мы ещё вернёмся.

Пропорциональные стороны подобных треугольников (например, $AB$ и $MN$, либо $BC$ и $NK$) в некоторых учебниках называют сходственными. На практике этот термин применяется редко. Мы будем говорить просто «соответственные стороны».

Дальше идёт очень важное замечание.

1.1. Обозначение подобных треугольников

В геометрии один и тот же треугольник можно называть по-разному. Например, $Delta ABC$, $Delta BCA$ или $Delta CAB$ — это всё один и тот же треугольник. То же самое касается и углов.

Но в подобных треугольниках есть негласное правило:

При обозначении подобных треугольников порядок букв выбирают так, чтобы равные углы перечислялись в одной и той же последовательности.

Вернёмся к нашим треугольникам $ABC$ и $MNK$:

Поскольку $anglecolor{red}{A}=anglecolor{red}{M}$ и $anglecolor{blue}{B}=anglecolor{blue}{N}$, можно записать $Deltacolor{red}{A}color{blue}{B}Csim Deltacolor{red}{M}color{blue}{N}K$. Или $Delta Ccolor{red}{A}color{blue}{B}sim Delta Kcolor{red}{M}color{blue}{N}$. Но никак не $Deltacolor{red}{A}color{blue}{B}Csim Delta Kcolor{red}{M}color{blue}{N}$.

Да, это негласное правило. И если вы нарушите последовательность букв, это не ошибка. Никто не снизит вам за это баллы. А если снизит — добро пожаловать на апелляцию.

Правильная запись позволяет быстро и безошибочно выписывать пропорциональные стороны треугольников. Рассмотрим два подобных треугольника:

[Delta ABCsim Delta MNK]

Берём две первые буквы из каждого треугольника: ${AB}/{MN};$. Затем две последние буквы: ${BC}/{NK};$. Наконец, вычёркиваем «центральную» букву: ${AC}/{MK};$.

Приравниваем полученные три дроби:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Вот и всё! Даже рисунок не нужен! Этот приём настолько прост и эффективен, что его в обязательном порядке изучают на моих занятиях, курсах и вебинарах.

В будущем мы увидим, что подобные треугольники чаще всего ищут как раз для составления таких пропорций.

2. Лемма о подобных треугольниках

Подобные треугольники появляются всякий раз, когда прямая, параллельная стороне треугольника, пересекает его стороны.

Теорема 1. Прямая, пересекающая две стороны треугольника и параллельная третьей стороне, отсекает треугольник, подобный исходному.

Доказательство. Рассмотрим треугольник $ABC$. Пусть прямая $MNparallel AB$ отсекает треугольник $MNC$:

Докажем, что $Delta ABCsim Delta MNC$. Рассмотрим треугольники $ABC$ и $MNC$. У них есть общий угол $ACB$.

Углы $ABC$ и $MNC$ — соответственными при $MNparallel AB$ и секущей $BC$. Следовательно, они равны: $angle ABC=angle MNC$.

Аналогично равны углы $BAC$ и $NMC$. Следовательно, треугольники $ABC$ и $MNC$ имеют три соответственно равных угла.

Докажем теперь, что соответственные стороны пропорциональны. Т.е. докажем пропорцию

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Рассмотрим угол $ACB$. Параллельные прямые $AB$ и $MN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AC}{MC}=frac{BC}{NC}]

Это равенство — второе в искомом:

[frac{AB}{MN}= color{red}{frac{BC}{NC}=frac{AC}{MC}}]

Осталось доказать первое равенство. Дополнительное построение: прямая $KNparallel AC$:

Поскольку $AMparallel KN$ (по построению) и $AKparallel MN$ (по условию), четырёхугольник $AKNM$ — параллелограмм. Поэтому $AK=MN$.

Рассмотрим угол $ABC$. Параллельные прямые $AC$ и $KN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AB}{AK}=frac{BC}{NC}]

Учитывая, что $AK=MN$, получаем

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Итак, соответственные углы треугольников $ABC$ и $MNC$ равны, а их стороны пропорциональны. Следовательно, по определению подобных треугольников

[Delta ABCsim Delta MNC]

Что и требовалось доказать.

Эта лемма — не признак подобия. Это самостоятельная теорема, которая ускоряет решение многих задач.

Признаки подобия разобраны в отдельном уроке — см. «Признаки подобия треугольников».

Частный случай этой леммы — средняя линия. Она отсекает треугольник со сторонами в два раза меньше, чем у исходного:

Оформляется это так. Поскольку $AM=MC$ и $BN=NC$, то $MN$ — средняя линия треугольника $ABC$. Следовательно, прямые $AB$ и $MN$ параллельны, откуда

[Delta ABCsim Delta MNC]

3. Свойства подобных треугольников

Два важнейших свойства: связь периметров и связь площадей.

3.1. Периметры подобных треугольников

Теорема 2. Отношение периметров подобных треугольников равно коэффициенту подобия.

Доказательство. Рассмотрим подобные треугольники $ABC$ и $MNK$:

Запишем равенство из определения подобия. Поскольку $Delta ABCsimDelta MNK$, стороны этих треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

Здесь число $color{red}{k}$ — коэффициент подобия. Полученное тройное равенство можно переписать так:

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}; frac{AC}{MK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB&=color{red}{k}cdot MN \ BC &=color{red}{k}cdot NK \ AC &=color{red}{k}cdot MK \ end{align}]

Периметр треугольника $MNK$:

[{{P}_{Delta MNK}}=MN+NK+MK]

Периметр треугольника $ABC$:

[begin{align}{{P}_{Delta ABC}} &=AB+BC+CD= \ &=color{red}{k}cdot MN+color{red}{k}cdot NK+color{red}{k}cdot MK= \ &=color{red}{k}cdot left( MN+NK+MK right)= \ &=color{red}{k}cdot {{P}_{Delta MNK}} end{align}]

Итого получаем равенство

[{{P}_{Delta ABC}}=color{red}{k}cdot {{P}_{Delta MNK}}]

Обычно именно в таком виде это равенство и применяют. Но можно записать его и как отношение:

[frac{{{P}_{Delta ABC}}}{{{P}_{Delta MNK}}}=color{red}{k}]

В любом случае, мы получили отношение, которое и требовалось доказать.

3.2. Площади подобных треугольников

Теорема 3. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство. Первые шаги очень похожи на доказательство предыдущей теоремы. Вновь рассмотрим подобные треугольники $ABC$ и $MNK$:

Поскольку $Delta ABCsimDelta MNK$, углы $ABC$ и $MNK$ равны. Следовательно, равны синусы этих углов:

[begin{align}angle ABC &=angle MNK=color{blue}{alpha} \ sin angle ABC &=sin angle MNK=sin color{blue}{alpha} end{align}]

Кроме того, стороны подобных треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

В частности, из этого равенства следует, что

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB &= color{red}{k}cdot MN \ BC &= color{red}{k}cdot NK \ end{align}]

Площадь треугольника $MNK$:

[{{S}_{Delta MNK}}=frac{1}{2}cdot MNcdot NKcdot sin color{blue}{alpha} ]

Площадь треугольника $ABC$:

[begin{align}{{S}_{Delta ABC}} &=frac{1}{2}cdot ABcdot BCcdot sincolor{blue}{alpha} = \ &=frac{1}{2}cdotcolor{red}{k}cdot MNcdotcolor{red}{k}cdot NKcdot sincolor{blue}{alpha} = \ &={color{red}{k}^{2}}cdot frac{1}{2}cdot MNcdot NKcdot sin alpha = \ &={color{red}{k}^{2}}cdot {{S}_{Delta MNK}} end{align}]

Получаем равенство

[{{S}_{Delta ABC}}={color{red}{k}^{2}}cdot {{S}_{Delta MNK}}]

Перепишем в виде отношения:

[frac{{{S}_{Delta ABC}}}{{{S}_{Delta MNK}}}={color{red}{k}^{2}}]

Что и требовалось доказать.

Для доказательства теоремы мы использовали формулу площади треугольника:

[{{S}_{Delta }}=frac{1}{2}absin alpha ]

Тригонометрию проходят после подобия, поэтому мы опираемся на ещё не изученный материал.

Впрочем, ничто не мешает взять уже известную формулу:

[{{S}_{Delta }}=frac{1}{2}ah]

Здесь $a$ — сторона треугольника, $h$ — высота, проведённая к этой стороне. Дело в том, что высоты в подобных треугольниках тоже пропорциональны. И не только высоты. Назовём это Свойством 3.3.:)

3.3. Элементы подобных треугольников

Теорема 4. Отношение высот, биссектрис и медиан, проведённых к соответствующим сторонам подобных треугольников, равно коэффициенту подобия.

Проиллюстрируем это на высотах. Пусть треугольники $ABC$ и $MNK$ подобны:

В этом случае высоты $CDbot AB$ и $KLbot MN$ относятся как

[frac{CD}{KL}=frac{AB}{MN}= color{red}{k}]

Для доказательства этой теоремы нужно знать признаки подобия. Поэтому оставим его до следующего урока. А сейчас переходим к задачам.

4. Задачи на подобие

Здесь разобрано пять задач на подобие треугольников. Все они довольно простые. За сложными задачами добро пожаловать в задачник.:)

Задача 1. Готовые треугольники

Известно, что треугольники $ABC$ и $MNK$ подобны, причём $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. Кроме того, стороны $AB=6$, $BC=7$, $AC=10$ и $MN=9$. Найдите стороны $NK$ и $MK$.

Решение. Построим треугольники $ABC$ и $MNK$, отметим известные стороны:

Из условия $Delta ABCsim Delta MNK$ следует, что верно равенство

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Подставим в это равенство всё, что нам известно:

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}=frac{color{red}{10}}{MK}]

Опустим последнюю дробь и получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}]

Найдём сторону $NK$:

[NK=frac{color{red}{9}cdot color{red}{7}}{color{red}{6}}=10,5]

Аналогично, убирая среднюю дробь, получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{10}}{MK}]

Найдём сторону $MK$:

[NK=frac{color{red}{9}cdot color{red}{10}}{color{red}{6}}=15]

Ответ: $NK=10,5$, $MK=15$.

Задача 2. Прямая, параллельная стороне

Прямая, параллельная стороне $AC$ треугольника $ABC$, пересекает сторону $AB$ в точке $D$, а сторону $BC$ — в точке $E$. Найдите:

а) Отрезок $BD$, если $AB=16$, $AC=20$, $DE=15$.

б) Отрезок $AD$, если $AB=28$, $BC=63$, $BE=27$.

Решение. Для начала построим рисунок. Он будет общий для обоих пунктов.

Из условия следует, что прямая $DE$ пересекает стороны треугольника $ABC$:

Поскольку $DEparallel AC$, по лемме о подобных треугольниках прямая $DE$ отсекает от треугольника $ABC$ новый треугольник, подобный исходному:

[Delta ABCsim Delta DBE]

Из подобия треугольников $ABC$ и $DBE$ следует равенство

[frac{AB}{DB}=frac{BC}{BE}=frac{AC}{DE}]

Решаем пункт а). Подставляем в это равенство всё, что нам известно:

[frac{color{red}{16}}{DB}=frac{BC}{BE}=frac{color{red}{20}}{color{red}{15}}]

Вычёркиваем среднюю дробь и получаем пропорцию

[frac{color{red}{16}}{DB}=frac{color{red}{20}}{color{red}{15}}]

Отсюда легко найти $DB$ (или, что то же самое, $BD$):

[DB=frac{color{red}{16}cdotcolor{red}{15}}{color{red}{20}}=12]

Аналогично решаем пункт б). Подставляем в исходное равенство известные величины:

[frac{color{red}{28}}{DB}=frac{color{red}{63}}{color{red}{27}}=frac{AC}{DE}]

Первые две дроби образуют пропорцию, из которой вновь легко найти $DB$:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=12]

Осталось найти $AD$:

[begin{align}AD &=AB-BD= \ &=color{red}{28}-color{red}{12}=16 end{align}]

Ответ: а) $BD=12$; б) $AD=16$.

Важное замечание по работе с пропорциями. Ни в коем случае не нужно перемножать числа в числителе.

Напротив: нужно разложить их на множители и сократить!

Взгляните:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=frac{4cdotcolor{blue}{7}cdot 3cdotcolor{green}{9}}{color{blue}{7}cdotcolor{green}{9}}=12]

Так вы сэкономите время, избежите умножения столбиком и защитите себя от множества ошибок. Никогда не умножайте большие числа, если дальше их нужно будет сокращать.

Задача 3. Доказательство подобия

Точки $M$ и $K$ — середины сторон $CD$ и $AD$ квадрата $ABCD$ соответственно. Докажите, что треугольники $MDK$ и $BCD$ подобны.

Решение. Сделаем первоначальный рисунок по условию задачи:

Здесь нет прямых, параллельных сторонам треугольника, поэтому лемма о подобных треугольниках не поможет. Докажем подобие по определению.

Сначала разберёмся с углами. Поскольку $ABCD$ — квадрат, и $KD=MD$ — половина стороны квадрата, треугольники $MDK$ и $BCD$ — прямоугольные и равнобедренные.

Все острые углы треугольников $MDK$ и $BCD$ равны 45°. Можем записать это так:

[begin{align}angle BCD &=angle MDK={90}^circ \ angle CBD &=angle DMK={45}^circ \ angle CDB &=angle DKM={45}^circ \ end{align}]

Дополнительное построение: диагональ квадрата $color{red}{AC}$:

Рассмотрим треугольник $ACD$. Отрезок $KM$ — средняя линия, поэтому $KM={color{red}{AC}}/{2};$. С другой стороны, $AC=BD$ как диагонали квадрата. Поэтому верно равенство

[frac{KM}{BD}=frac{KM}{color{red}{AC}}=frac{1}{2}]

Но тогда выполняется следующее равенство:

[frac{MD}{BC}=frac{DK}{CD}=frac{MK}{BD}=frac{1}{2}]

А это вместе с равенством углов как раз и означает, что треугольники $MDK$ и $BCD$ подобны:

[Delta MDKsim Delta BCD]

Доказательство завершено.

Мы доказали подобие треугольников по определению. Если пользоваться признаками подобия, всё будет намного быстрее. Но пока мы не вправе пользоваться этими признаками.

Задача 4. Вписанный ромб

В треугольник $ABC$ вписан ромб $BDEK$ так, как показано на рисунке. Найдите сторону ромба, если $AB=10$, $BC=15$.

Решение. Пусть искомая сторона ромба равна $color{red}{x}$. Из условия задачи получим такой рисунок:

Зная, что $AB=10$ и $BC=15$, выразим $AK$ и $CD$:

[begin{align}AK &=10-color{red}{x} \ CD &=15-color{red}{x} \ end{align}]

Далее рассмотрим треугольник $ABC$. Поскольку $BDEK$ — ромб, то $KEparallel BC$. По лемме о подобных треугольниках имеем:

[Delta ABCsim Delta AKE]

В подобных треугольниках подобные стороны пропорциональны, поэтому

[frac{AB}{AK}=frac{BC}{KE}=frac{AC}{AE}]

Подставим в это равенство всё, что нам известно или выражено через $color{red}{x}$:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}=frac{AC}{AE}]

Последняя дробь оказалась бесполезной. Вычеркнем её и получим пропорцию:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}]

Применяем основное свойство пропорции и уравнение:

[begin{align}10cdotcolor{red}{x} &=15cdot left( 10- color{red}{x} right) \ 2cdotcolor{red}{x} &=3cdot left( 10- color{red}{x} right) \ &cdots\ color{red}{x} &=6 end{align}]

Это и есть искомая сторона ромба. Она равна $color{red}{x}=6$.

Ответ: $BD=6$.

Задача 5. Свойства биссектрисы

В треугольнике $ABC$ стороны $AB=8$, $BC=12$, угол $ABC={120}^circ $. Отрезок $BD$ — биссектриса. Найдите длину $BD$.

Решение. Из условия задачи можно сделать вот такой рисунок:

Поскольку $BD$ — биссектриса угла в треугольнике, точка $D$ делит сторону $AC$ на отрезки, пропорциональные сторонам $AB$ и $BC$. Это можно записать так:

[frac{AD}{CD}=frac{AB}{CB}=frac{color{red}{8}}{color{red}{12}}=frac{color{red}{2}}{color{red}{3}}]

Обозначим пропорциональные отрезки переменными. Пусть $AD=color{blue}{2x}$, $CD=color{blue}{3x}$.

Дополнительное построение: прямая $DMparallel AB$:

Рассмотрим угол $ACB$. Поскольку $DMparallel AB$, по теореме о пропорциональных отрезках получаем, что

[frac{BM}{CM}=frac{AD}{CD}=frac{color{red}{2}}{color{red}{3}}]

Вновь обозначим пропорциональные отрезки переменными. Пусть $BM=color{blue}{2y}$, $CM=color{blue}{3y}$. Но тогда

[BC=BM+MC=color{blue}{5y}=color{red}{12}]

Получаем, что $color{blue}{y}=color{red}{2,4}$. Отсюда легко найти длину $BM$:

[BM=color{blue}{2y}=2cdotcolor{red}{2,4}= color{red}{4,8}]

Далее заметим, что если угол $ABC$ равен 120°, то

[angle ABD=angle CBD={60}^circ ]

С другой стороны, прямые $AB$ и $MD$ параллельны по построению. Прямая $BD$ — секущая для этих параллельных прямых.

Следовательно, углы $ABD$ и $BDM$ — внутренние накрест лежащие, поэтому

[angle BDM=angle ABD={60}^circ ]

Рассмотрим треугольник $BDM$. В нём есть два угла по 60°. Следовательно, это равносторонний треугольник:

[BD=BM=color{red}{4,8}]

Мы нашли длину отрезка $BD$. Задача решена.

Ответ: $BD=4,8$.

Итак, с определением разобрались. В следующем уроке разберём признаки подобия.:)

Смотрите также:

1. Как применяется теорема косинусов и подобие треугольников для решения широкого класса задач в планиметрии.
2. Теорема менелая
3. Комбинаторика в задаче B6: легкий тест
4. Введение системы координат
5. Четырехугольная пирамида: как найти координаты вершин
6. Нестандартная задача B5 на площадь круга

О многоугольнике с тремя сторонами

Соотношение углов и сторон в треугольнике интуитивно можно понять, если хорошо представлять эту фигуру. Речь идет о плоском объекте, который состоит всего из трех отрезков. Они расположены таким образом, что начало первого совпадает с концом последнего, то есть они пересекаются. Каждый отрезок представляет собой независимую сторону фигуры. Точка пересечения является вершиной, а соответствующий ей угол является внутренним.

Таким образом, два ключевых элемента образуют рассматриваемую фигуру:

• вершина;
• сторона.

И вершин, и сторон в любом треугольнике по три, поэтому его принято обозначать большими латинскими буквами, например, ABC или MNK. Малые буквы резервируют для обозначения длин сторон, например, a, b, c.

На первый взгляд может показаться, что рассматриваемый объект является несложным, и в нем нечего изучать. Действительно, он является самым простым по построению многоугольником, однако, он обладает большим количеством свойств, количественное и качественное знание которых требуют понимания многих теорем.

Существование фигуры

Пусть имеется три отрезка, и необходимо понять, возможно ли из них построить треугольник. Это можно сделать с помощью одного простого правила, которое можно сформулировать следующим образом: любая сторона треугольника всегда меньше суммы длин двух других.

Знание этого правила является очень важным и эффективным инструментом при решении задач. Например, из отрезков с условными длинами 1, 2 и 4 построить треугольник невозможно, а из 2, 3, 4 это сделать можно.

Помимо соотношения длин сторон существует также еще одна теорема, которая гласит, что во всяком треугольнике сумма его внутренних углов всегда равна 180 °. Благодаря знанию этой теоремы можно все рассматриваемые фигуры разделить на три типа:

1. Остроугольные. В них все три угловые меры меньше 90 °. При этом возможны случаи взаимного их равенства, то есть каждый будет составлять 60 °. Такие треугольники называются равносторонними или правильными. Равны могут быть между собой также два угла, это будет уже равнобедренный треугольник, у которого боковые стороны имеют одинаковую длину.
2. Тупоугольные. Поскольку сумма составляет 180 °, то по определению в рассматриваемом многоугольнике не может быть больше одного тупого угла. Тупоугольные фигуры могут иметь либо произвольный тип, когда все их отрезки различаются, либо являться равнобедренными.
3. Прямоугольные. Это специальный тип треугольников, о котором известно многое, и который разграничивает два предыдущих типа. В них один угол равен 90 °, а два других являются острыми.

Полноты ради следует сказать о вырожденных фигурах. К ним относятся такие многоугольники, у которых тупой стремится к 180 °. Несложно представить, что в этом случае два других будут обращаться в ноль, а сумма противолежащих им сторон окажется равной длине отрезка, расположенного напротив тупого угла. На плоскости вырожденный треугольник представляет отрезок, его площадь стремится к нулю.

Важные линии

Несмотря на всю простоту построения треугольника, при решении задач могут понадобиться дополнительные отрезки. Внутри фигуры существует целая гамма типов этих отрезков, наиболее важными из них являются следующие:

1. Медиана — делящий на две равные по площади части исходный треугольник. Отрезок проводится из вершины к середине противоположной стороны.
2. Биссектриса. Ею называют отрезок, который на две половины делит угол при произвольной вершине.
3. Высота. Этот элемент проводится также из вершины, но по отношению к противоположной стороне он является перпендикуляром. Таким образом, высота делит исходную фигуру на два прямоугольных геометрических объекта, которые в общем случае между собой не равны.
4. Медиатриса — это серединный перпендикуляр, то есть он сочетает свойства медианы и высоты, однако, через вершину треугольника он может не проходить. Медиатрисами пользуются при построении описанной окружности.
5. Средняя линия — это отрезок, который посередине пересекает две стороны треугольника. Его длина всегда будет в два раза меньше стороны фигуры, которой он параллелен. Средняя линия приводит к созданию подобной исходной фигуры, которая в два раза меньше.

Для правильных, равнобедренных и прямоугольных треугольников некоторые из названных отрезков могут совпадать друг с другом, а также со сторонами фигуры. Например, в прямоугольном треугольнике две малые стороны (катеты) также являются высотами.

Соотношение отрезков и углов

Задачи на соотношение отрезков и угловых мер в рассматриваемой фигуре могут требовать либо качественный, либо количественный ответ. В первом случае следует провести определенное доказательство, опираясь на известные аксиомы и теоремы о сторонах треугольника и их следствия. Во втором же случае следует пользоваться формулами и выражениями, которые содержат тригонометрические функции. В действительности оба типа задач связаны между собой. Так, прежде чем использовать какую-либо формулу, следует доказать возможность ее применения в конкретной ситуации.

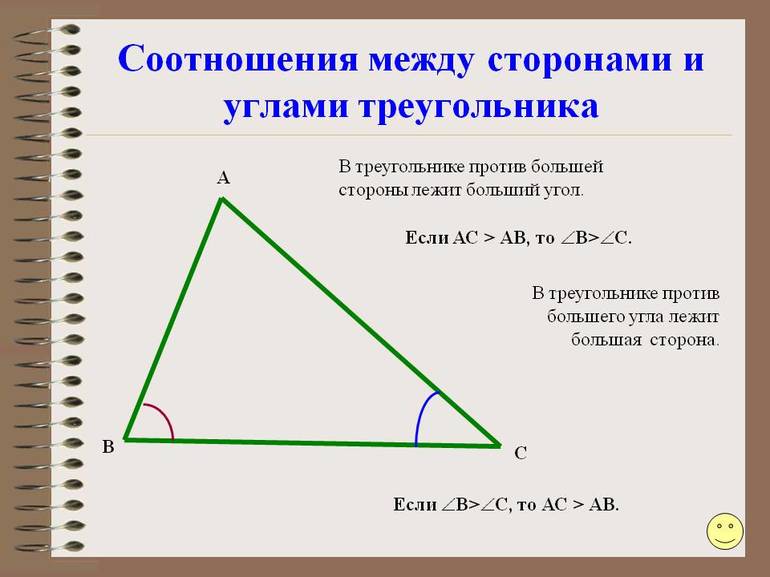
Большие и меньшие длины

Основная теорема о соотношении между элементами в рассматриваемом типе многоугольников гласит, что против большего угла лежит большая сторона. Ее доказательство провести несложно, если построить треугольник, например, тупоугольный. Из тупого провести отрезок к противоположной стороне таким образом, чтобы он образовывал новый равнобедренный треугольник внутри исходного. После этого следует воспользоваться тем свойством, что внешний угол треугольника всегда больше внутреннего.

Следуя условию равенства углов в построенном равнобедренном треугольнике, легко показать, что против тупого всегда находится самый длинный отрезок.

Обратно эта теорема также справедлива, то есть против большей стороны треугольника лежит больший угол. Ее справедливость понятна каждому школьнику на интуитивном уровне, а доказательство заключается в переборе возможных трех вариантов соотношения между отрезками (больше, меньше, равно) и в привлечении уже доказанной теоремы.

Рассмотренные теоремы приводят к двум важным следствиям:

1. Против равных сторон лежат равные углы, и наоборот. Следствие актуально для равносторонних и равнобедренных фигур.
2. Гипотенуза в треугольнике с прямым углом является самой длинной стороной, поскольку она лежит напротив самого большого угла.

Рассмотренные теоремы и их следствия активно используются при изучении подобных фигур. Поскольку напротив равных углов двух треугольников лежат соответствующие им длины отрезков, то последние будут попарно относиться друг к другу с определенным коэффициентом подобия.

Теоремы косинусов и синусов

Количественной характеристикой соотношения сторон и углов являются знаменитые формулы, содержащие зависимость длин отрезков и угловых мер. Первая из них называется теоремой косинусов. Соответствующая формула имеет вид:

c ² = a ² + b ² — 2*a*b*cos©.

Здесь величины a, b, c — это длины, C — угол напротив стороны c. Формула позволяет вычислить третью сторону по известным двум другим и углу между ними. Однако, возможности выражения шире, с его помощью можно посчитать всякий внутренний угол фигуры, если известны три ее стороны.

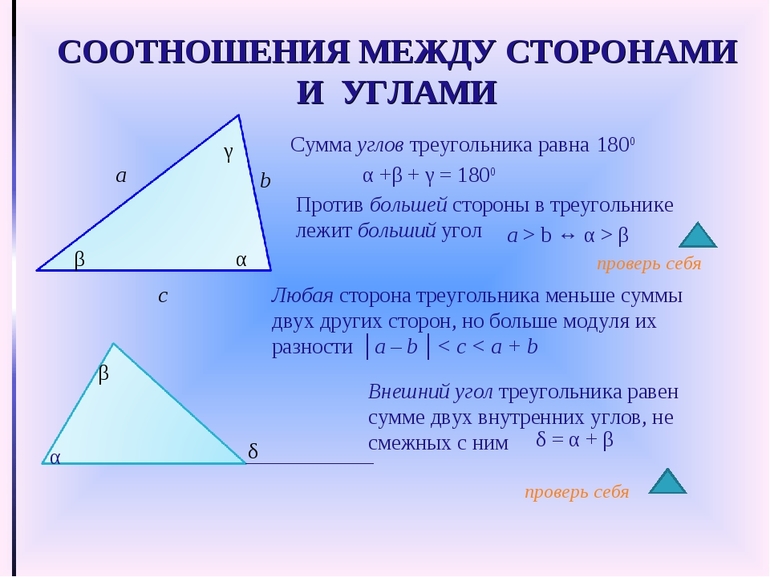
Следующая по счету, но не по важности теорема синусов. Ее математическое выражение записывается так:

a/sin (A) = b/sin (B) = c/sin©.

Эти равенства говорят о том, что отношение стороны к синусу противоположного ей угла является постоянной характеристикой конкретного треугольника. Зная связь двух углов и стороны или двух отрезков и одного угла можно рассчитать все остальные характеристики фигуры. Следует запомнить, что для любого рассматриваемого типа многоугольников однозначное вычисление всех его свойств требует знания минимум трех элементов (кроме трех углов).

Прямоугольный треугольник

Этот особый случай следует рассмотреть подробнее. Каждый школьник знает знаменитую теорему, позволяющую сравнить соответствие отрезков друг другу в этом типе фигуры. Она гласит, что сумма квадратов катетов соответствует квадрату гипотенузы, и называется пифагоровой теоремой, то есть можно записать:

c ² = a ² + b ² .

Работать с прямоугольными треугольниками удобно по одной простой причине: через их геометрические параметры вводятся в математику тригонометрические функции. Последние легко использовать при вычислении сторон и углов фигуры. Например, если фигура является не только прямоугольной, но и равнобедренной, то ее катеты равны, а углы напротив них составляют по 45 °. При этом любой из катетов всегда в 2 ^0,5 раза меньше гипотенузы:

sin (45 °) = a/c = ½ ^0,5.

Это соотношение можно получить также из теоремы Пифагора.

Другая ситуация, когда один из острых углов равен 30 °. Для лежащего напротив него катета a можно записать следующее выражение:

sin (30 °) = ½ = a/c.

Иными словами, лежащий против 30 ° катет составляет ровно половину длины гипотенузы.

Таким образом, в любом треугольнике существует прямая пропорциональность между длиной стороны и противолежащим ей углом. Для количественного решения задач по геометрии с этой фигурой следует пользоваться выражениями синусов, косинусов и теоремой Пифагора.

Соотношения в треугольнике

228. В этой главе мы будем главным образом понимать под обозначениями отрезков AB, AC и т. д. выражающие их числа.

Мы знаем (п. 226), что если даны геометрически два отрезка a и b, то мы можем построить средний пропорциональный между ними. Пусть теперь отрезки даны не геометрически, а числами, т. е. под a и b будем понимать числа, выражающие 2 данных отрезка. Тогда нахождение среднего пропорционального отрезка сведется к нахождению числа x из пропорции a/x = x/b, где a, b и x числа. Из этой пропорции имеем:

x² = ab
x = √ab

229. Пусть имеем прямоугольный треугольник ABC (чер. 224).

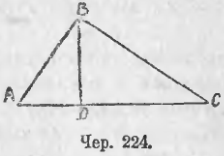
Опустим из вершины его прямого угла (∠B прямой) перпендикуляр BD на гипотенузу AC. Тогда из п. 225 мы знаем:

1) AC/AB = AB/AD и 2) AC/BC = BC/DC.

Отсюда мы получаем:

AB² = AC · AD и BC² = AC · DC.

Сложив по частям полученные равенства, получим:

AB² + BC² = AC · AD + AC · DC = AC(AD + DC).

т. е. квадрат числа, выражающего гипотенузу, равен сумме квадратов чисел, выражающих катеты прямоугольного треугольника.

Сокращенно говорят: Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Если мы дадим полученной формуле геометрическое толкование, то получим уже известную нам теорему Пифагора (п. 161):

квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах.

Из уравнения AB² + BC² = AC² иногда приходится находить катет прямоугольного треугольника, по гипотенузе и другому катету. Получим, напр.:

AB² = AC² – BC² и, следов.,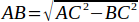

230. Найденное числовое соотношение между сторонами прямоугольного треугольника позволяет решать множество вычислительных задач. Решим некоторые из них:

1. Вычислить площадь равностороннего треугольника по данной его стороне.

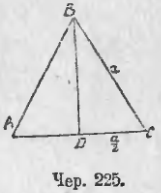
Пусть ∆ABC (чер. 225) равносторонний и каждая его сторона выражается числом a (AB = BC = AC = a). Для вычисления площади этого треугольника надо узнать сначала его высоту BD, которую мы назовем чрез h. Мы знаем, что в равностороннем треугольнике высота BD делит основание AC пополам, т. е. AD = DC = a/2. Поэтому из прямоугольного треугольника DBC имеем:

BD² = BC² – DC²,

или

h² = a² – a²/4 = 3a²/4 (выполняем вычитание).

Отсюда имеем:

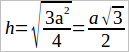(выносим множитель из под корня).

Следовательно, называя число, выражающее площадь нашего треугольника, чрез Q и зная, что площадь ∆ABC = (AC · BD)/2, находим:

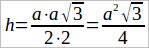
Мы можем смотреть на эту формулу, как на один из способов измерения площади равностороннего треугольника: надо измерить его сторону в линейных единицах, возвести найденное число в квадрат, умножить полученное число на √3 и разделить на 4 — получим выражение площади в квадратных (соответствующих) единицах.
2. Стороны треугольника равны 10, 17 и 21 лин. един. Вычислить его площадь.

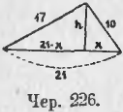
Опустим высоту h в нашем треугольнике (чер. 226) на большую сторону — она непременно пройдет внутри треугольника, так как в треугольнике тупой угол может быть расположен только против большей стороны. Тогда большая сторона, = 21, разделится на 2 отрезка, один из которых обозначим чрез x (см. чертеж) — тогда другой = 21 – x. Получим два прямоугольных треугольника, из которых имеем:

h² = 10² – x² и h² = 17² – (21 – x)²

Так как левые части этих уравнений одинаковы, то

10² – x² = 17² – (21 – x)²

Выполняя действия получим:

10² – x² = 289 – 441 + 42x – x²

Упрощая это уравнение, найдем:

42x = 252,

откуда

x = 6

Тогда из уравнения h² = 10² – x², получим:

h² = 10² – 6² = 64

и, следовательно,

h = √64 = 8

Тогда искомая площадь найдется:

Q = (21 · 8)/2 квад. един. = 84 квад. един.

3. Можно решить общую задачу:

как вычислить площадь треугольника по его сторонам?

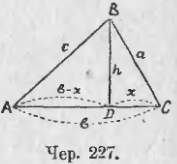
Пусть стороны треугольника ABC выражены числами BC = a, AC = b и AB = c (чер. 227). Положим, что AC есть большая сторона; тогда высота BD пойдет внутри ∆ABC. Назовем: BD = h, DC = x и тогда AD = b – x.

Из ∆BDC имеем: h² = a² – x².

Из ∆ABD имеем: h² = c² – (b – x)²,

откуда a² – x² = c² – (b – x)².

Решая это уравнение, последовательно получаем:

2bx = a² + b² – c² и x = (a² + b² – c²)/2b.

Далее, подставляя это выражение в уравнение h² = a² – x², найдем

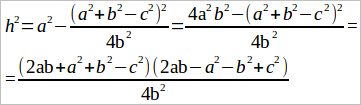
(Последнее написано на том основании, что числителя 4a²b² – (a² + b² – c²)² можно рассматривать, как равность квадратов, которую разлагаем на произведение суммы на разность).

Или

Эту формулу преобразовывают, вводя периметр треугольника, который обозначим чрез 2p, т. е.

a + b + c = 2p

Вычитая по 2c из обеих частей равенства, получим:

a + b + c – 2c = 2p – 2c или a + b – c = 2(p – c):

Также найдем:

c + a – b = 2(p – b) и c – a + b = 2(p – a).

Тогда получим:

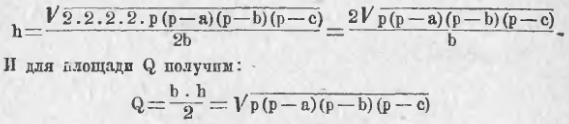
(p выражает полупериметр треугольника).
Этою формулою можно пользоваться для вычисления площади треугольника по трем его сторонам.

231. Упражнения.

1. Основание равнобедренного треугольника равно 10 дм., а его площадь = 60 кв. дм. Найти (вычислить) его периметр.
2. Параллельные стороны равнобочной трапеции равны 16 и 40 дм., а каждая из непараллельных сторон = 37 дм. Вычислить его площадь.
3. Стороны трапеции равны: параллельные 15 и 36 дм., а непараллельные 13 и 20 дм. Вычислить их площадь.
4. Сторона ромба и его меньшая диагональ одинаковы. Найти формулу для измерения площади такого ромба по его стороне.
5. Катеты прямоугольного треугольника равны соответственно 6 и 8 дм. Найти отрезок гипотенузы, заключенный между биссектором прямого угла треугольника и высотою, опущенною из вершины прямого угла.
6. Биссектор прямого угла прямоугольного треугольника делит гипотенузу на 2 отрезка, равные соответственно лин. един. Вычислить его площадь.
7. Найти сторону квадрата, равновеликого равнобедренному треугольнику, боковая сторона которого = 12 ½ лин. един., а высота относится к основанию, как 2 : 3.
8. Стороны параллелограмма равны a и b и один из его углов = 45°. Найти формулу для его площади.
9. Угол параллелограмма = 30°; выразить его площадь чрез его стороны (a и b).

232. В п. 229 мы нашли зависимость между сторонами прямоугольного треугольника. Можно найти подобную же зависимость для сторон (с присоединением еще одного отрезка) косоугольного треугольника.

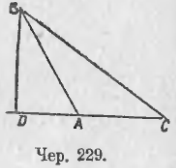
Пусть имеем сначала ∆ABC (чер. 228) такой, чтобы ∠A был острый. Постараемся найти выражение для квадрата стороны BC, лежащей против этого острого угла (подобно тому, как в п. 229 нашли выражение для квадрата гипотенузы).

Построив BD ⊥ AC, получим из прямоугольного треугольника BDC:

BC² = BD² + DC²

Заменим BD2, определяя его из ABD, откуда имеем:

BD² = AB² – AD²,

а отрезок DC заменим чрез AC – AD (очевидно, что DC = AC – AD). Тогда получим:

BC² = AB² – AD² + (AC – AD)² = AB² – AD² + AC² – 2AC · AD + AD²

Выполнив приведение подобных членов, найдем:

BC² = AB² + AC² – 2AC · AD.

Эта формула читается: квадрат стороны треугольника, лежащей против острого угла, равен сумме квадратов двух его других сторон, минус удвоенное произведение одной из этих сторон на ее отрезок от вершины острого угла до высоты.

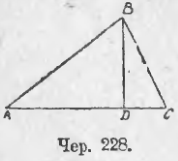
233. Пусть теперь ∠A и ∆ABC (чер. 229) тупой. Найдем выражение для квадрата стороны BC, лежащей против тупого угла.

Построив высоту BD — она теперь расположится несколько иначе: на 228 где ∠A острый, точки D и C располагаются по одну сторону от A, а здесь, где ∠A тупой, точки D и C расположатся по разные стороны от A. Тогда из прямоугольного ∆BDC получим:

BC² = BD² + DC²

Мы можем BD2 заменить, определяя его из прямоугольного ∆BDA:

BD² = AB² – AD²,

а отрезок DC = AC + AD, что очевидно. Заменяя, получим:

BC² = AB² – AD² + (AC + AD)² = AB² – AD² + AC² + 2AC · AD + AD²

Выполняя приведение подобных членов найдем:

BC² = AB² + AC² + 2AC · AD,

т. е. квадрат стороны треугольника, лежащей против тупого угла, равен сумме квадратов двух его других сторон, плюс удвоенное произведение одной из них на ее отрезок от вершины тупого угла до высоты.
Эта формула, а равно и формула п. 232, допускают геометрическое истолкование, которое легко найти.

234. Пользуясь свойствами пп. 229, 232, 233, мы можем, если нам даны стороны треугольника в числах, узнать, есть ли у этого треугольника прямой или тупой угол.

Прямой или тупой угол в треугольнике может быть расположен лишь против большей стороны, каков же угол против нее, легко узнать: этот угол острый, прямой или тупой, смотря по тому, будет ли квадрат большей стороны меньше, равен или больше суммы квадратов двух других сторон.

Узнать, имеется ли прямой или тупой угол в следующих треугольниках, определяемых своими сторонами:

1) 15 дм., 13 дм. и 14 дм.; 2) 20, 29 и 21; 3) 11, 8 и 13; 4) 7, 11 и 15.

235. Пусть имеем параллелограмм ABCD (чер. 230); построим его диагонали AC и BD и его высоты BK ⊥ AD и CL ⊥ AD.

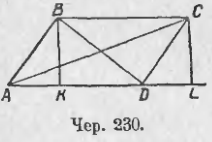
Тогда, если ∠A (∠BAD) острый, то ∠D (∠ADC) непременно тупой (ибо их сумма = 2d). Из ∆ABD, где ∠A считаем острым, имеем:

BD² = AB² + AD² – 2AD · AK,

а из ∆ACD, где ∠D тупой, имеем:

AC² = AD² + CD² + 2AD · DL.

Заменим в последней формуле отрезок AD равным ему отрезком BC и DL равным ему AK (DL = AK, ибо ∆ABK = ∆DCL, в чем легко убедиться). Тогда получим:

AC2 = BC2 + CD2 + 2AD · AK.

Сложив выражение для BD2 с последним выражением для AC², найдем:

BD² + AC² = AB² + AD² + BC² + CD²,

так как члены –2AD · AK и +2AD · AK взаимно уничтожаются. Полученное равенство можем прочитать:

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

236. Вычисление медианы и биссектора треугольника по его сторонам. Пусть в треугольнике ABC (чер. 231) построена медиана BM (т. е. AM = MC). Зная стороны ∆ABC: BC = a, AC = b и AB = c, вычислить медиану BM.

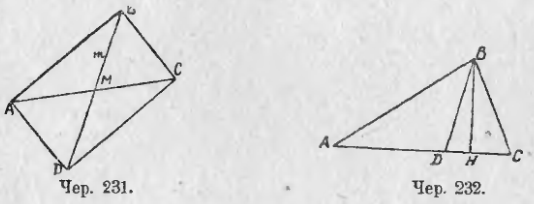
Продолжим BM и отложим отрезок MD = BM. Соединив D с A и D с C, получим параллелограмм ABCD (выяснить это легко, так как ∆AMD = ∆BMC и ∆AMB = ∆DMC).

Называя медиану BM чрез m, получим BD = 2m и тогда, пользуясь предыдущим п., имеем:

237. Вычисление радиуса, описанного около треугольника круга. Пусть около ∆ABC (чер. 233) описан круг O. Построим диаметр круга BD, хорду AD и высоту треугольника BH.

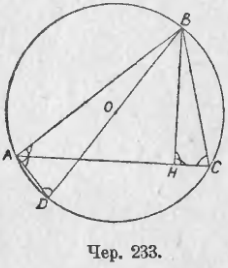
Тогда ∆ABD ~ ∆BCH (∠A = ∠H = d — угол A прямой, потому что он вписанный, опирающийся на диаметр BD и ∠D = ∠C, как вписанные, опирающиеся на одну дугу AB). Поэтому имеем:

BD/BC = AB/BH,

или, называя радиус OB чрез R, высоту BH чрез h и стороны AB и BC, как и раньше, соответственно чрез c и a:

2R/a = c/h,

откуда

R = ac/2h,

но площадь ∆ABC = Q = bh/2, откуда h = 2Q/b.

Следовательно, R = (abc) / (4Q).

Мы умеем (п. 230 зад. 3) вычислять площадь треугольника Q по его сторонам. Отсюда можем вычислить R по трем сторонам треугольника.

238. Вычисление радиуса вписанного в треугольник круга. Впишем в ∆ABC, стороны которого даны (чер. 234), круг O. Соединив его центр O с вершинами треугольника и с точками касания D, E и F сторон к кругу, найдем, что радиусы круга OD, OE и OF служат высотами треугольников BOC, COA и AOB.

Называя радиус вписанного круга чрез r, имеем:

Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8 класс. Задачи в основном на применение первого признака подобия треугольника. Они встречаются в 15 задании ОГЭ по математике. Не все задачи будем решать через первый признак подобия.

Задача №1. Применение средней линии треугольника.

Решение

Так как точки М и N являются серединами сторона АВ и ВС, то MN – средняя линия треугольника. Средняя линия треугольника – это отрезок соединяющий середины противоположных сторон. Всего в треугольнике может быть три средних линии.

Средняя линия треугольника параллельна одной из сторон треугольника и равна половине этой стороны.

Для решения предложенной задачи, достаточно взять одну сторону AC, которая параллельна МN. Остальные стороны треугольника даны для усложнения задачи.

Эту задачу можно решить через подобные треугольники MBN и ABC, но не будем усложнять то, что можно сделать легко.

Задача №2

Решение

Для решения этой задачи, вспомним первый признак подобия треугольников:

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Совет №1! Старайтесь рассматривать и доказывать, что треугольники подобны с маленького на большой.

Докажем, что треугольники MBN и ABC подобны.

Совет №2! После того как доказали, что треугольники подобны, запишите название этих треугольников так, чтобы вершины равных углов находились в записи на одинаковых местах.

Это нужно для того, чтобы безошибочно в более сложных задачах составить соотношение сходственных сторон в подобных треугольниках. Для этого расставим дуги следующим образом и по дугам составим соотношение сходственных сторон.

Теперь можно решить задачу:

Ответ 8

Задача №3

Решение

Эта задача на применение первого признака подобия треугольников. Можно рассмотреть треугольники ACH и CHB и доказать, что они подобны по двум углам. Но, можно воспользоваться пропорциональными отрезками в прямоугольном треугольнике.

Я немного перефразирую утверждения:

Квадрат высоты (СH) проведенный из вершины прямого угла к гипотенузе (AB) равен произведению отрезков гипотенузы (AH и HB), на которые поделила высота эту гипотенузу.

Ответ 8.

Задача №4 Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=8, AC = 32

Для катетов прямоугольного треугольника можно сказать так:

Квадрат катета прямоугольного треугольника равен произведению гипотенузы на отрезок гипотенузы заключенный между этим катетом и высотой

Ответ 16

Задача №5

Решение:

Рассмотрим треугольники KBM и ABC.

Ответ 42.

Задача №6

Решение

Треугольники CDE и СВА подобны по двум углам. Так как средняя линия треугольника равна половине стороны к которой она параллельна, то коэффициент подобия этих треугольников равен отношению сторон DE:AB=1:2.

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Ответ 28

Замечание. Если в задаче необходимо найти площадь четырехугольника (ABDE), то нужно и из площади большого треугольника (ABC) вычесть площадь маленького (CDE).

Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог