Как составить проверочную матрицу

Любой циклический
(n, k)
– код может быть задан в соответствии
с определением 2, порождающим многочленомg(x)
или проверочным многочленом.

Знание этих
многочленов позволяет построить
порождающую матрицу и матрицу проверок.
Для циклического (n,
k) – кода существует
простой способ нахожденияkлинейно независимых кодовых комбинаций,
образующих порождающую матрицу.
Этот способ состоит в следующем.
Записывается порождающий многочленg(x).
В соответствии с определением 2 комбинация,
соответствующая порождающему многочлену,
принадлежит циклическому (n,
k) – коду. В соответствии
с определением 1 циклические сдвиги
комбинации, соответствующейg(x),
также должны принадлежать этому же
коду. Алгебраически сдвиг соответствует
умножению кодовой комбинации нах.
Так как степеньg(x)равнаn–k,
то подобным образом мы можем получить
кодовые комбинации

Легко проверить,
что эти кодовые комбинации линейно
независимы, хотя бы потому, что степени
всех этих многочленов различны, поэтому
данный набор многочленов может быть
использован в качестве
:

.

Путем элементарных
преобразований эта матрица может быть
приведена к канонической форме.

Аналогичным образом
по проверочному многочлену
можно построить матрицу проверок

.

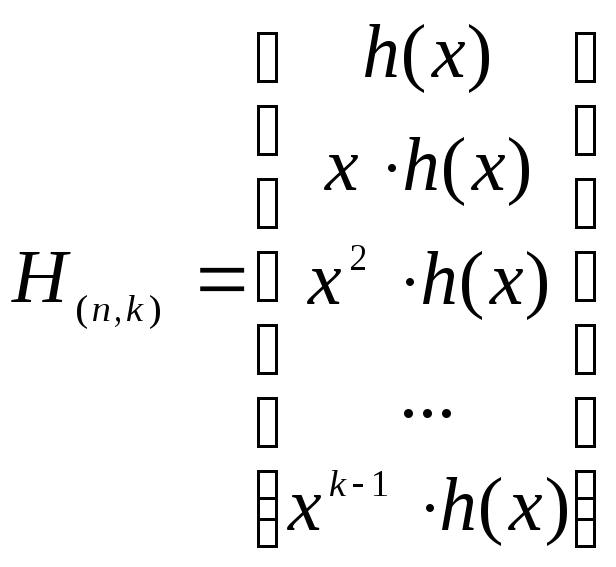Пример 6.4.Для
циклического (7,4) – кода с порождающим
многочленом(см. пример 6.3.) построить порождающую
матрицу.

Находим

Следовательно,
порождающая матрица для данного кода
имеет вид:

Полученные
результаты и рассуждения относительно
алгебраической структуры циклических
кодов, приведенные в разделе 6.2, позволяют
подметить одно важное свойство циклических
кодов, определенное их циклической
структурой.

Свойство 6.1.
Произведение кодовой комбинации
циклического кодана произвольный многочлендает
кодовую комбинацию этого же циклического
кода.

Действительно
,
а любое произведение такого вида равно
нулю, т.е. принадлежит кодовому
подпространству (раздел 6.2).

Более элементарное
доказательство:

.

Полученная сумма
есть сумма циклических сдвигов кодовых
комбинаций, что по свойству замкнутости
группового кода должно дать комбинацию
того же циклического кода.

При описании
циклических кодов следует учитывать
специфику действий над многочленами,
по сравнению с векторами и, в частности,
тот факт, что умножение многочленов не
совпадает со скалярным умножением
векторов, отображающих эти многочлены.
Однако в классе вычетов многочленов по
модулю
между этими понятиями существует весьма
тесная связь. Пусть имеется вектори соответствующий ему многочлен,
а также вектори соответствующий ему многочлен.
Будем считать многочленыиортогональными, если выполнено условие.

Коэффициент при
хв произведенииравен

.

Слагаемые, содержащие
,
появляются вследствие слагаемых в
произведении,
которые содержат.
Но так как,
т.е.,
то.
Равенство дляможно
представить в виде скалярного произведения:

.

В этом произведении
первый вектор соответствует а(х).
Второй вектор содержит коэффициентыb(х), расположенные
в обратном порядке и сдвинутые циклически
наj+1 элемент вправо.

Таким образом,
если произведение
равно нулю, то вектор, соответствующий
многочленуа(х), ортогонален вектору,
соответствующему многочлену b(х),
компоненты которого расположены в
обратном порядке, и кроме того каждому
циклическому сдвигу этого вектора.
Верно также и обратное утверждение.
Если векторортогонален векторуи каждому циклическому сдвигу этого
вектора, то

.

Учитывая эту
специфику необходимо при матричном
описании кода коэффициенты матрицы
проверок записывать в обратном порядке.
В этом случае будет выполнено условие

Пример 6.5.
Построить матрицу проверок для
циклического (7,4) – кода из предыдущего
примера.

Для построения
матрицы проверок найдем проверочный
многочлен

Отсюда

В силу того, что
условие равенства нулю произведения
многочленов и скалярного произведения
соответствующих им векторов не совпадают,
для выполнения равенства
при построении матрицыкомпоненты
векторов, соответствующихh(x),
xh(x)
и x²h(x)записываем в обратном порядке

.

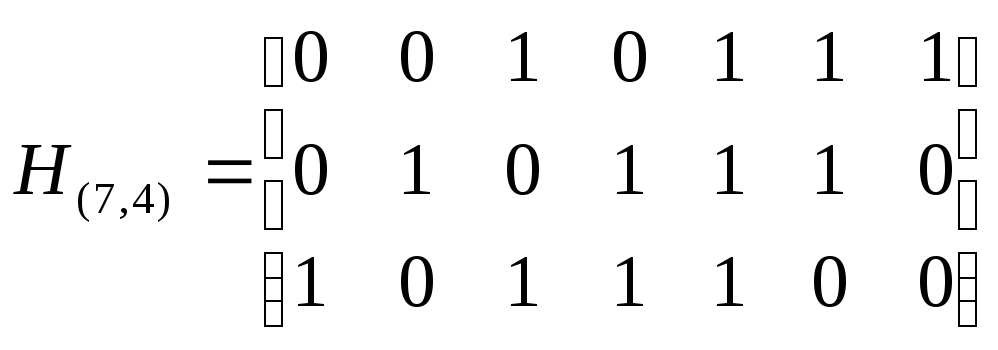В полученной
матрице проверок в качестве столбцов
записаны все 7 ненулевых последовательностей
длины 3. Следовательно, данный код
является кодом Хэмминга.

Вообще говоря,
циклические коды Хэмминга строятся на
основе порождающих многочленов степени
m, являющихся
сомножителями двучленов
и не являющихся сомножителями никаких
двучленов меньшей степени. Корни этих
многочленов имеют порядок 2^m-1,
т.е они являются примитивными элементами
поляGF(2^m).Это означает, что порождающий многочлен
кода Хэмминга порождает полеGF(2^m).

Условимся в любом
циклическом коде первые n–kэлементов кодовой комбинации, то есть
коэффициенты прииспользовать в качестве проверочных
элементов, а последниеkэлементов, то есть коэффициенты при,
– в качестве информационных (рис. 6.1).

a₀a,
….., a_n-1
= a₀x⁰+a₁x¹+
…. + a_n-1xⁿ⁺¹

x⁰
x¹
x²
x^n-k-1
x^n-k
x^n-2
x^n-1

a0

a1

a2

… … … … ..

an-k-1

an-k

… … … …

an-2

an-1

Избыточные
элементы
Информационные элементы

Рис
6.1

Структура кодовой
комбинации циклического кода

В этом случае в
канонической форме порождающей матрицы
единичная матрица располагается справа.
Такое расположение информационных и
проверочных элементов обусловлено
особенностями реализации кодирующих
и декодирующих устройств циклических
кодов.

Всякий циклический
(n, k)
– код приводится к этой форме следующим
образом.

Пусть
есть многочлен степениk-1,
соответствующий комбинации простогоk – элементного
кода, которую необходимо закодировать
циклическим (n, k)
– кодом. В комбинации циклического (n,
k) – кода этуk– элементную комбинацию необходимо
поместить на позиции информационных
элементов, для чего помножим многочленна.
В результате получаем многочлен,
степень которого равна n-1.
Так как по определению циклического
кода каждая кодовая комбинация должна
делиться на порождающий многочленg(x)степениn–k,
то проверим выполнение этого условия.
В общем случае в результате деления
получим частноеq_i(x)степениk-1 и остаток,
степень которого не превышаетn–k-1.
Результат деления представим в следующем
виде:

.

Рассмотрим многочлен
.
Коэффициенты приэтого многочлена являются коэффициентами
остатка,
а коэффициенты при степеняхэлементами первичной кодовой комбинации.

С другой стороны

,

то есть многочлен
делится наg(x).
Итак,и есть искомая кодовая комбинация
циклического (n, k)
– кода. Отсюда получаем правило построения
порождающей матрицы циклического (n,
k) – кода в канонической
форме:

,

где I_k– единичная матрица размерности,
соответствующая информационным элементам
кодовых комбинаций,;

– матрица размерности
,j-я– строка, которой
соответствует остатку от делениянаg(x).

Матрица проверок
строится на основании матрицыпо правилу

.

Пример 6.6.Построить порождающую матрицу и матрицу
проверок в канонической форме для
циклического (7,4) – кода с порождающим
многочленом.
Находим частное и остаток от делениянаg(x)и записываем результат деления в форме
равенства

I₃

R_4×3

О

R_4×3

I₄

кончательно получаем

.

Из рассмотренного
примера видно, что проверочная матрица
циклического (n, k)
– кода содержит в качестве столбцов
остатки от деленияна порождающий многочленg(x).Сравнение
столбцов найденной проверочной матрицы
с элементами поляGF(2³)показывает их полное совпадение с
ненулевыми элементамиGF(2³).Результаты рассмотренного примера
будут использованы для обоснования
эквивалентности различных столбцов
вычисления синдрома.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пусть  означает  информационных
бит, кодируемых в кодовое слово . В
этой главе мы следуем установленным соглашениям о представлении кодовых слов в виде векторов. Так, вектор из  информационных
бит на входе кодера обозначается так:

,

а
выходом кодера является вектор из  символов

.

Операцию
кодирования, выполняемую в линейном двоичном блоковом коде, можно представить
совокупностью из  уравнений
вида

                   
(8.1.2)

где
 или , а  представляют
произведение  и
. Линейные
уравнения (8.1.2)

можно
также представить в матричной форме

,                   
(8.1.3)

где  – порождающая
матрица кода, равная

                    (8.1.4)

Заметим,
что произвольное кодовое слово – это просто линейная комбинация векторов  из ,

                      (8.1.5)

Поскольку
линейный  код
с  кодовыми
словами является подпространством размерности , векторы  порождающей
матрицы  должны
быть линейно независимыми, т.е. они должны образовывать пространство
размерности .
Другими словами,  должны образовать базис для  кода.
Заметим, что ансамбль базовых векторов не единственный и,
следовательно,  не
уникальна. Мы также заметим, что, поскольку пространство имеет размерность , ранг матрицы  равен .

Любую порождающую матрицу
 кода
путём проведения операций над строками (и
перестановкой столбцов) можно свести к «систематической форме»:

,                    
(8.1.6)

где  –  единичная матрица,
а  –  матрица, которая
определяет  избыточных
или проверочных символов. Заметим, что порождающая матрица систематического
кода создает линейный блоковый код, в котором первые  бит любого кодового
слова идентичны информационным битам, а остающиеся  бит любого кодового слова являются
линейными комбинациями  информационных бит. Эти  избыточных бита называют паритетными
(проверочными) битами. Результирующий  код называется в этом случае систематическим кодом.

Если
 код
порождён матрицей, не имеющей систематической формы (8.1.6), он называется
несистематическим. Однако такая матрица эквивалентна матрице в систематической форме в том смысле, что одна может
быть получена из другой элементарными
операциями над строками и перемещением столбцов. Два  линейных кода, порожденных двумя эквивалентными
порождающими матрицами, называют эквивалентными
и один может быть получен из другого перестановкой элементов. Таким образом,
каждый линейный  код
эквивалентен линейному систематическому  коду.

Пример
8.1.1. Рассмотрим код (7, 4) с порождающей матрицей

.                    (8.1.7)

Типичное кодовое слово можно
выразить так:

,

где  представляют
четыре информационных бита, a  представляют три паритетных бита,
определённых так:

                                  

              (8.1.8)

                                                                    

Линейный
систематический  двоичный
блоковый кодер можно реализовать, используя -битовый регистр сдвига,  сумматоров , связанных с соответствующими
ячейками регистра сдвига и генерирующих проверочные символы, которые потом
временно располагаются во втором регистре сдвига длины . Затем  информационных
бита, а за ними  проверочных
бита последовательно покидают два регистра и подаются на модулятор. Это
кодирование иллюстрируется рис. 8.1.1 для кода (7, 4) из примера
(8.1.1).

Рис.
8.1.1. Линейный регистр сдвига для получения двоичного кода (7,4)

С любым линейным кодом  кодом связан дуальный код
размерностью .

Дуальный
код является линейным  кодом с  кодовыми векторами, которое
образуют нуль-пространство по отношению к  коду. Порождающая матрица для дуального кода,
обозначаемая ,
состоит из  линейно
независимых кодовых векторов, выбираемых в
нуль-пространстве. Любое кодовое слово  из  кода ортогонально любому кодовому
слову дуального кода. Следовательно, любое кодовое слово  кода ортогонально
любой строке матрицы , т.е.

,                    (8.1.9)

где  означает
вектор-столбец, состоящий из  нулей, а  – кодовое слово  кода.
Поскольку (8.1.9) справедливо для любого кодового слова  кода, то следует

,                     (8.1.10)

где  – теперь
 матрица
со всеми нулевыми элементами.

Теперь предположим,
что линейный  код
является систематическим, и его порождающая матрица дана в
систематической форме (8.1.6). Тогда, поскольку , следует, что

                    
(8.1.11)

Отрицательный знак в
(8.1.11) может быть опущен при работе с двоичными кодами, поскольку вычитание
по  идентично
сложению по .

Пример (8.1.2). Для систематического
кода (7, 4), генерируемого матрицей , определяемой
(8.1.7), имеем согласно (8.1.11) матрицу  в виде

                    
(8.1.12)

Теперь
уравнение  распадается
на три уравнения

                      (8.1.13)

Таким образом,
видим, что произведение  эквивалентно суммированию проверочных
символов с соответствующими линейными комбинациями информационных символов,
используемых для вычисления  Это значит, что (8.1.13) эквивалентно
(8.1.8).

Матрицу  можно использовать
в декодере для проверки того, удовлетворяет ли принимаемое кодовое
слово  условию
(8.1.13), т.е. .
Таким образом, декодер сверяет принятые проверочные символы с соответствующей линейной
комбинацией символов  и ,
которые формируют проверочные символы на передаче. Поэтому принято называть  проверочной матрицей,
связанной с  кодом.

Выскажем
соображение, касающееся связи минимального расстояния кода и его проверочной
матрицы .
Произведение  с  представляют
линейную комбинацию  столбцов . Поскольку , векторы-столбцы  линейно зависимы.
Допустим, что  означает
кодовое слово с минимальным весом линейного кода . Оно должно удовлетворять
условию .
Поскольку минимальный вес равен минимальному расстоянию, следует,
что  столбцов
 линейно
зависимы. Альтернативно, мы можем сказать, что не более, чем  столбцов  линейно независимы.
Поскольку ранг матрицы  не больше , имеем . Следовательно,
 имеет
верхнюю границу

                      
(8.1.14)

Задаваясь линейным двоичным кодом  с минимальным расстоянием , мы можем синтезировать
линейный двоичный код  путём добавления одного дополнительного проверочного символа к каждому
кодовому слову. Проверочный символ обычно
выбирается так, чтобы быть проверочным символом по всем символам кодового
слова. Таким образом, добавляемый проверочный символ равен 0, если исходное
кодовое слово имеет чётное число
единиц, и равен ,
если кодовое слово имеет нечетное число единиц. Следовательно, если минимальный вес и, следовательно,
минимальное расстояние кода нечётно,
добавляемый проверочный символ увеличит минимальное расстояние на . Мы называем код  расширенным
кодом. Его проверочная матрица

,                  
 (8.1.15)

где  -проверочная матрица исходного кода. Систематический  код может быть также укорочен размещением в начале информационного
блока нулевых символов. Это значит,
что линейный код ,
состоящий из  информационных
символов и  проверочных может быть укорочен до линейного кода , если установить первые  информационных символов (во всех
кодовых комбинациях) нулями. Эти  символов не передаются по каналу, а  проверочных символа рассчитываются обычным образом, как в исходном коде. Поскольку , замена первых  символов  нулями
эквивалентна сокращению числа строк матрицы  за счёт удаления первых  строк. Аналогично,
вследствие того, что

,

мы можем удалить первые  столбцов матрицы . Укороченный код  состоит из  кодовых слов.
Минимальное расстояние этих  кодовых слов по крайней мере не меньше, чем минимальное расстояние исходного  кода.

Порождающая и проверочная матрицы линейного кода

Поиск эффективных и простых в обработке корректирующих кодов осуществляется с использованием компьютерного моделирования и алгебраических методов. В теории кодирования n – разрядному двоичному слову ставится в соответствие многочлен степени n или вектор в  n – мерном пространстве с компонентами, принимающими значения 1 и 0 (например, слову 101101 – многочлен х⁵+х³+х²+1).  Преобразования кодовых слов рассматриваются как операции над многочленами или векторами.

 Любое кодовое слово V  линейного блокового кода (n, k) можно получить умножением вектора  U, представляющего информационное слово, на порождающую матрицу G размерности  k x n:  V =U G.

 Принятое слово можно проверить на отсутствие ошибок умножением его на транспонированную проверочную матрицу H^т . Если слово принято без ошибок, результат умножения нулевой:  V H^т=0. 

 Проверочная матрица (parity-check matrix) связана с порождающей матрицей соотношением G H^т=0.

Порождающая матрица выбирается неоднозначно. Для упрощения кодирования и декодирования удобно использовать порождающую матрицу, составленную из двух матриц: единичной матрицы размерности k x k  и дописываемой справа матрицы-дополнения, или контрольной подматрицы, размерности  k x (n-k). Такая матрица порождает систематический код: первые  k  символов слова совпадают с исходным информационным словом, а остальные символы являются проверочными.

Пример

Информация в лекции “32 Конфликты социально-психологического уровня” поможет Вам.

Помехоустойчивая кодовая комбинация V  = 1010101 получена умножением информационного слова U = 1010  на порождающую матрицу G.

Если в принятом слове (V) нет ошибки, при умножении этого слова на проверочную матрицу Н^Т код синдрома нулевой:  V Н^Т =0.

При ошибке в первом разряде слова  V₁  код синдрома V₁ Н^Т = 110.

Номер строки матрицы H^т с этим кодом синдрома совпадает с номером ошибочного разряда принятой кодовой комбинации (№1).

При ошибке во втором разряде слова V₂  результат проверки V₂ Н^Т = 101. Полученный синдром находится во второй строке матрицы H^т, следовательно ошибочен разряд №2 принятой кодовой комбинации.

Реализация матричных операций на интегральных микросхемах не представляет технических трудностей.

Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.4. Алгебраические системы на базе групп

Порождающая и проверочная матрицы

Откуда же берутся порождающие матрицы G? Порождающая матрица получается путем последовательного сдвига соответствующего порождающего многочлена g(x) по разрядам вправо. Последовательному сдвигу вправо отвечает умножение g(x) на xⁱ:

G = = .

Порождающая матрица G имеет размерность (k – 1) · m, поскольку для сдвига берутся степени xⁱ в пределах 0 < i < k – 1, а степень порождающего многочлена g(x) равна m. Мы знаем, что каждому порождающему многочлену соответствует проверочный многочлен h(x), который удобно записать в порядке убывания степеней:

g(x) = g₀ + g₁x + g₂x² + … +
g_mx^m, 

h(x) = h_kx^k + h_k–1 x^k–1 + … + h₀,

причем xⁿ + 1 = g(x)h(x), где, напомним,
n — общее число символов, k — число информационных, а m — число проверочных символов в кодовом слове. Если существует порождающая матрица G, то должна существовать и соответствующая ей проверочная матрица
H. Действительно, такую матрицу можно получить путем последовательного сдвига проверочного многочлена h(x) влево:

H = = .

Предположим, у нас есть конкретный порождающий многочлен g(x) = 1 + x² + x³. Проверочный многочлен h(x) находится простым делением многочлена x⁷ + 1 на заданный многочлен g(x); в результате имеем: h(x)= = x⁴ + x³ + x² + 1. В соответствии с вышеприведенными определениями, находим конкретный вид порождающей G и проверочной H матриц:

G = , H = ,

GH* = (HG*)* = 0.

Последнее равенство говорит о том, что матрицы G и H ортогональны относительно друг друга (звездочка означает операцию транспонирования матрицы).

Рассмотренные G и H матрицы называются ленточными, потому что нули и единицы вдоль обеих диагоналей этих матриц образуют своеобразные ленты. Но любая ленточная матрица может быть сведена к систематическому виду:

G’ = (E_{k · k} | G_{m · k}),    H’ = (H_{k · m} | E_{m · m}),

где E_{k · k} и E_{m · m} — единичные матрицы.

Существует, по крайней мере, два способа сведения ленточных матриц к систематическому виду. Первый наиболее надежный способ состоит в нахождении ряда остаточных многочленов. Если r_i(x) остаточный многочлен от деления x_i на порождающий многочлен g(x), то сумма элементов r_i (x) + x_i дает строки систематической матрицы G. Аналогичным способом находятся строки проверочной матрицы H. Второй способ заключается в том, чтобы найти соответствующие линейные комбинации строк или столбцов исходных матриц ленточного типа. Найдем G и H для предыдущего случая:

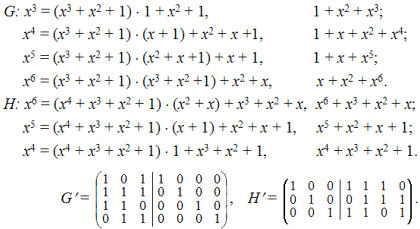
Эти две систематические матрицы можно было бы получить путем сложения векторов-столбцов исходных ленточных матриц (напоминаем, счет столбцов для G матрицы начинается с нуля, а для H матрицы — с шести).

G’ :   0′ = 1 + 2, 1′ = 1 + 5, 2′ = 3, 3′ = 0, 4′ = 1, 5′ = 4 + 1, 6′ = 6;

H’ :    0′ = 5, 1′ = 3, 2′ = 4, 3′ = 2, 4′ = 6, 5′ = 1, 6′ = 0.

Теперь поясним, как составить проверочные соотношения и определить коды ошибок si по известной проверочной матрице. С этой целью выпишем три равенства, отвечающих строкам матрицы H’ :

s₁ = h₆ + h₃ + h₂ + h₁ = 0,

s₂ = h₅ + h₂ + h₁ + h₀ = 0,

s₃ = h₄ + h₃ + h₂ + h₀ = 0.

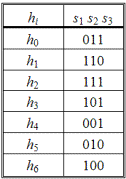
При ошибке в символе h₀ суммы s₂ и s₃ изменятся на 1, а при ошибке в h₁ не будут равны нулю суммы s₁ и s₂. Таким образом, можно составить все коды ошибок для всех символов (табл. 2.87).

Таблица 2.87

При одновременном появлении ошибок в двух символах, например в h₅ и h₆, коды ошибок будут складываться; в данном случае он становится таким же, как и при одиночной ошибке в символе h₁. Поэтому, характеризуя код с точки зрения помехозащищенности, мы должны сказать, что он обнаруживает и исправляет любые одиночные ошибки, а также обнаруживает, но не исправляет двойные ошибки.

Определение:

Линейный код (англ. Linear code) — код фиксированной длины (блоковый код), исправляющий ошибки, для которого любая линейная комбинация кодовых слов также является кодовым словом.

Линейные коды обычно делят на блоковые коды и свёрточные коды. Также можно рассматривать турбо-коды, как гибрид двух предыдущих.^[1]

По сравнению с другими кодами, линейные коды позволяют реализовывать более эффективные алгоритмы кодирования и декодирования информации (см. синдромы ошибок).

Формальное определение

Определение:

Линейный код длины и ранга является линейным подпространством размерности векторного пространства , где — конечное поле (поле Галуа) из элементов. Такой код с параметром называется -арным кодом (напр. если  — то это 5-арный код). Если или , то код представляет собой двоичный код, или тернарный соответственно.

Векторы в называют кодовыми словами. Размер кода — это количество кодовых слов, т.е. .

Весом кодового слова называют число его ненулевых элементов. Расстояние между двумя кодовыми словами определяется как расстояние Хэмминга. Расстояние линейного кода — это минимальный вес его ненулевых кодовых слов или равным образом минимальное расстояние между всеми парами различных кодовых слов.

Линейный код длины , ранга и с расстоянием называют -кодом (англ. [n,k,d] code). Параметр d в обозначении кода часто опускается, потому что через него не задается структура кода. В таком случае пишут просто -код. В литературе встречается обозначение как в квадратных, так и в круглых скобках.^[2][3]

Порождающая матрица

Определение:

Порождающая матрица — это матрица, столбцы которой задают базис линейного кода.

Так как линейный код является линейным подпространством , целиком код (может быть очень большим) может быть представлен как линейная оболочка набора из кодовых слов (т.е. базис). Этот базис часто объединяют в столбцы матрицы и называют такую матрицу порождающей матрицей кода .

В случае, если , где — это единичная матрица размера , а — это матрица размера говорят, что матрица находится в каноническом виде.

Имея матрицу можно получить из некоторого входного вектора кодовое слово линейного кода

,

где и — векторы-строки. Порождающая матрица линейного -кода имеет вид . Число избыточных бит тогда определяется как .

Проверочная матрица

Определение:

Проверочная матрица линейного кода — это порождающая матрица ортогонального дополнения . Другими словами, это матрица, которая описывает правила, которым должны удовлетворять части кодового слова.

Используется, чтобы определить, является ли некий вектор кодовым словом, а также в алгоритмах декодирования (напр. syndrome decoding).

Кодовое слово принадлежит коду тогда и только тогда, когда или, что то же самое, .

Проверочную матрицу можно получить из порождающей и наоборот: пусть дана порождающая матрица в каноническом виде , тогда проверочную матрицу можно получить по формуле

,

так как .

Кодирование и декодирование, примеры

Предположим, что имеется линия связи, по которой мы можем пересылать и принимать биты. В среднем какой-то известный процент переданных битов будет поврежден, ошибочен. Такая модель называется двоичным симметричным каналом.

Блок из символов сообщения будет кодироваться в кодовое слово , где ; эти кодовые слова образуют код.

Первая часть кодового слова состоит из информационных битов сообщения:

,

за которым следуют проверочных битов . Проверочные биты выбраны так, чтобы кодовые слова удовлетворяли уравнению

,

где — проверочная матрица.

Пример

Проверочная матрица

определяет код с и . Для этого кода

.

Сообщение кодируется в кодовое слово , которое начинается с самого сообщения:

,

а последующих три проверочных символа выбираются так, чтобы выполнялось уравнение .

Если сообщение , то , и проверочные биты легко определяются: , так что кодовое слово .

Минимальное расстояние и корректирующая способность

Линейность гарантирует, что расстояние Хэмминга между кодовым словом и любым другим кодовым словом не зависит от . Так как — тоже кодовое слово, а , то

Иными словами, чтобы найти минимальное расстояние между кодовыми словами линейного кода, необходимо рассмотреть ненулевые кодовые слова. Тогда ненулевое кодовое слово с минимальным весом будет иметь минимальное расстояние до нулевого кодового слова, таким образом показывая минимальное расстояние линейного кода.

Минимальное расстояние кода однозначно определяет количество ошибок, которое способен обнаружить () и исправить () данный код.

Синдромы и метод обнаружения ошибок в линейном коде

Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова соответствует наиболее вероятное переданное слово . Однако, данный метод требует применения огромных таблиц уже для кодовых слов сравнительно небольшой длины.

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора вычисляется синдром . Поскольку , где  — кодовое слово, а  — вектор ошибки, то . Затем с помощью таблицы по синдрому определяется вектор ошибки, с помощью которого определяется переданное кодовое слово. При этом таблица получается гораздо меньше, чем при использовании предыдущего метода.

Преимущества и недостатки линейных кодов

+ Благодаря линейности для запоминания или перечисления всех кодовых слов достаточно хранить в памяти кодера или декодера существенно меньшую их часть, а именно только те слова, которые образуют базис соответствующего линейного пространства. Это существенно упрощает реализацию устройств кодирования и декодирования и делает линейные коды весьма привлекательными с точки зрения практических приложений.

– Хотя линейные коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.

Примечания

Источники информации

• wikipedia.org — Линейный код
• wikipedia.org — Linear code
• Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с., стр. 12-33
• Ф.И. Соловьева — Введение в теорию кодирования
• В. А. Липницкий, Н. В. Чесалин — Линейные коды и кодовые последовательности: учеб.-метод. пособие для студентов мех.-мат. фак. БГУ. Минск: БГУ, 2008. — 41 с.