Как составить рабочую программу по математике по фгос

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Конструирование рабочей программы по математике в свете требований ФГОС ООО
  Кондратенко Лариса Николаевна, кандидат педагогических наук,
  доцент кафедры теории и методики общего образования
  МАОУ ДПО ИПК г. Новокузнецка

• 

  2 слайд

  Виды
  учебных программ
  Примерная (типовая) учебная программа

  Авторская программа

  Рабочая программа

• 

  3 слайд

  Примерная (типовая) учебная программа
  документ, рекомендуемый
  Минобрнауки России;
  детально раскрывает
  обязательные (федеральные)
  компоненты содержания
  обучения;
  требования к качеству
  усвоения учебного материала
  по конкретному предмету .

• 

  4 слайд

  Авторская
  учебная программа
  документ, созданный на основе
  ФГОС и примерной учебной программы ;
  имеющий авторскую концепцию построения
  содержания учебного курса, предмета, дисциплины
  (модуля);
  разрабатывается одним автором или группой авторов.

  Для авторской программы характерны оригинальные концепция и построение содержания.

  Внедрению авторской программы в практику работы ОУ предшествует её экспертиза и апробация.

• 

  5 слайд

  Различия авторской и рабочей программ
  авторская программа
  рабочая программа
  Разрабатывает учитель
  Разрабатывает автор или группа авторов
  Утверждается
  Проходит апробацию*
  * Апробация. Официальное одобрение, утверждение (лат. approbatio)
  =

• 

  6 слайд

  Различия авторской и рабочей программ
  НЕТ
  УЧЕБНИКА
  НЕТ
  УЧЕБНИКА

• 

  7 слайд

  Рабочая программа учебного предмета, курса
  (далее – рабочая программа) – учебная программа, разработанная педагогом на основе примерной (типовой) и (или) авторской учебной программы для конкретного ОУ и определенного класса (группы), имеющая изменения и дополнения в содержании, последовательности изучения тем, количестве часов, использовании организационных форм обучения и т. п.

  Рабочая
  программа
  по математике
  для 5 класса

• 

  8 слайд

  Специфика
  Рабочей программы
  конкретизирует соответствующий образовательный стандарт;
  описывает национально-региональный уровень;
  отражает специфику обучения в данном ОУ;
  учитывает возможности методического, информационного, технического обеспечения учебного процесса;
  учитывает уровень подготовки учащихся.

• 

  9 слайд

  Основа разработки
  Рабочей программы
  Основная образовательная программа образовательного учреждения

• 

  10 слайд

  Структура
  Рабочей программы
  Определяется требованиями стандарта основного общего образования п.18.2.2
  Пояснительная записка;
  Общая характеристика учебного предмета, курса;
  Описание места учебного предмета, курса в учебном плане;
  Требования к результатам освоения на личностном, метапредметном и предметном уровнях;
  Содержание учебного предмета, курса;
  Тематическое планирование определением основных видов учебной деятельности;
  Учебно-методическое и материально-техническое обеспечение образовательного процесса;
  Планируемые результаты изучения учебного предмета, курса.

• 

• 

  12 слайд

  Источники формирования содержания
  Рабочая программа по физике

• 

  13 слайд

  Структура рабочей программы
  Содержание учебного предмета
  Тематическое планирование
  Описание обеспечения учебного процесса
  Пояснительная записка
  цели и задачи обучения
  общая характеристика учебного предмета
  место в учебном плане
  результаты освоения учебного предмета
  личностные
  метапредметные
  предметные
  нормативные ссылки

• 

  14 слайд

  Пояснительная записка
  нормативные ссылки
  1. Международные нормативные акты
  2. Конституция Российской Федерации
  3. Законы Российской Федерации
  4. Образовательные стандарты
  5. Приказы Минобрнауки
  6. Региональные нормативные акты
  7. Программы
  8. Локальные нормативные акты

• 

  15 слайд

  Описание нормативных ссылок
  Федеральный государственный образовательный стандарт общего образования. — М. : Просвещение, 2011. — 48 с.
  Федеральный государственный образовательный стандарт общего образования // Российская Газета. — 19.12.2010.
  Федеральный государственный образовательный стандарт общего образования [Электронный ресурс]. — URL: www.минобрнауки.рф/документы/938

• 

  16 слайд

  Пояснительная записка
  место в учебном плане
  В соответствии с учебным планом школы № … на изучение биологии в основной школе отводится 245 часов: в 6 классе – 35 ч, в 7 – 9 классах — по 70 ч.

• 

  17 слайд

  Пояснительная записка
  результаты освоения учебного предмета
  личностные

• 

  18 слайд

  Пояснительная записка
  результаты освоения учебного предмета
  метапредметные

• 

  19 слайд

  предметные
  Пояснительная записка
  результаты освоения учебного предмета
  ЦЕЛИ

• 

  20 слайд

  Виды планов в учебном процессе
  БУП
  Учебный план
  школы № 1
  Учебный план
  гимназии № 2
  Учебный план
  лицея № n
  Календарно-тематическое планирование по …
  Календарно-тематическое планирование по …
  Календарно-тематическое планирование по …
  План урока № 1
  План урока № 2
  План урока № k

• 

  21 слайд

  Планы: назначение…
  Учебный план образовательной организации
  Планирование учебного процесса
  в целом
  Календарно-тематическое планирование
  Планирование учебного процесса
  по предмету
  План урока
  Планирование введения дидактических единиц

• 

  22 слайд

  Планы: назначение, содержание…
  Учебный план образовательной организации
  Перечень учебных предметов
  Число часов по предметам и годам
  Планирование учебного процесса
  в целом
  Календарно-тематическое планирование
  Учебный материал
  по урокам темы
  Планирование учебного процесса
  по предмету
  План урока
  Цели, содержание, методы, средства, организационные формы урока
  Планирование введения дидактических единиц

• 

  23 слайд

  Обеспечение учебного процесса
  Учебно-методическое обеспечение
  1
  — учебник
  — тетради
  — дидактические материалы
  — компакт-диск
  — методические материалы

• 

  24 слайд

  Обеспечение учебного процесса
  Материально-техническое обеспечение
  2
  Учебно-методический комплект
  Учебно-методический комплекс 1
  Учебно-методический комплекс 2
  Учебно-методический комплекс 3

• 

  25 слайд

  Описание в программе
  Учебно-методический комплект
  Дополнительная литература
  методическая
  учебная
  СО на печатной основе
  демонстрационные
  раздаточные
  Экранные и экранно-звуковые СО
  диапозитивы
  транспаранты
  фильмы
  Технические средства обучения
  проекторы
  компьютеры
  устройства затемнения
  Натуральные объекты
  Пример
  Пример
  Пример
  Пример
  Пример
  Пример

• 

  26 слайд

  Титульный лист
  наименование ОУ;
  гриф утверждения программы (с указанием даты и номера приказа руководителя ОУ);
  название учебного курса, предмета, дисциплины (модуля);
  Ф. И. О. педагога, разработавшего и реализующего учебный курс, предмет, дисциплину (модуль);
  класс (параллель), учащиеся которого изучают учебный курс, предмет, дисциплину (модуль);
  год составления программы.

• 

  27 слайд

  Рассмотрение и утверждение
  рабочей программы
  1. Сроки и порядок рассмотрения рабочих программ устанавливаются локальным актом ОУ.
  2. Порядок может быть, например, таковым:
  Программа рассматривается на заседании методического объединения учителей (результаты заносятся в протокол),
  При условии ее соответствия установленным требованиям, согласуется с заместителем директора по УВР
  Утверждается руководителем ОУ, после чего программа становится нормативным документом данного ОУ.

Краткое описание документа:

 Методический материал для учителя математики “Как составить рабочую программу по курсу математика  с учетом требований ФГОС.

Структура рабочей программы: Определяется требованиями стандарта основного общего образования п.18.2.2

1.Пояснительная записка; 2.Общая характеристикап учебного предмета, курса;3.Описание места учебного предмета, курса в учебном плане; 4.Требования к результатам освоения на личностном, метапредметном и предметном уровнях; 5.Содержание учебного предмета ,курса; 6.Тематическое планирование определением основных видов учебной деятельности; 7.Учебно-методическое и материально-техническое обеспечение образовательного процесса; 8.Планируемые результаты изучения учебного предмета,курса.          Материал взят с семенара КРИПиПРО.

 

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 261 879 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

ФГАОУ ВПО «Казанский (Приволжский) Федеральный университет»

Приволжский межрегиональный центр повышения квалификации и профессиональной переподготовки работников образования

Проект

«Проект рабочей программы

по математике с учетом требований ФГОС ООО»

Ф.И.О., должность участников рабочей группы

Костратова Валентина Сергеевна, учитель  математики МБОУ «Шапшинская средняя общеобразовательная школа Высокогорского муниципального района Республики Татарстан»,

Косова Наталья Владимировна, учитель математики МБОУ «Средняя общеобразовательная школа №11 с углубленным изучением отдельных предметов» Нижнекамского муниципального района Республики Татарстан.

Научный руководитель

Ахметшина Гульсия Хабриевна,

старший преподаватель отдела общего образования ПМ ЦПК и ППРО ИТ КФУ

Казань – 2015

Содержание

                                                                                                                                 Стр.

1. Постановка проблемы  ……………………………………………….         3

2. Цель и задачи проекта ……………………………………………….         3  

3.  Сроки  и место реализации проекта …………………………………       4

4. Раскрытие темы проекта ……………………………………………………………….      4

5. Этапы реализации проекта  …………………………………………        11

6.  План мероприятий по реализации проекта  ……………………….        12

7. Ресурсы……………………………………………………………………………………………      13

8.  Ожидаемые результаты реализации проекта  

     и методы диагностики…………………………………………………        14

9. Заключение………………………………………………………………        14

10.  Литература………………………………………………………………        15

Приложение 1.    Рабочая программа по математике

в 5 классе по УМК Виленкина  Н.Я., Жохова В.И. и др.  …………….        16

Постановка проблемы

С введением ФГОС изменяются структура и сущность результатов образовательной деятельности, содержание образовательных программ и технологии их реализации, методология, содержание и процедуры оценивания результатов освоения образовательных программ. Повышается значимость формирования условий реализации программ, в том числе создания образовательной инфраструктуры, изменяются требования к ним. Должна быть спроектирована система управления инновационными процессами, обеспечивающая достижение нового качества образования.

Федеральные государственные образовательные стандарты общего образования формулируют требования к подготовке учителя и руководителей общеобразовательного учреждения для реализации основной образовательной программы общего образования.

Новая парадигма образования, реализуемая ФГОС, – это переход от школы информационно-трансляционной к школе деятельностной, формирующей у обучающихся компетенции самостоятельной навигации по освоенным предметным знаниям при решении конкретных личностно значимых задач, в том числе и в ситуациях неопределенности.

Именно сегодня встает острая необходимость вооружить себя как учителя-предметника, не только теоретическими навыками введения ФГОС в основное звено, но и попробовать себя в качестве составителя рабочей программы по математике для продолжения введения стандартов начальной школы, т.е. для 5-6 классов.

Цель проекта: разработать проект рабочей  программы по математике в 5 классе по УМК Виленкин Н.Я. и др., с учетом требований ФГОС ООО

Задачи проекта:

1. Изучить  требования ФГОС  к разработке рабочей программы по математике.

2. Определить содержание каждого раздела рабочей программы по математике в 5 классе.  

3. Составить календарно-тематическое планирование раздела «Площади и объемы».

4. Разработать приложение к рабочей программе «Критерии оценки знаний умений и навыков учащихся по математике.

5. Апробировать рабочую программу по математике в 5 классе.

6. Разработать методические рекомендации по составлению рабочей программы  по математике.

Предмет проекта:  УМК Математика  Виленкина  Н.Я., Жохова В.И. и др.

 Целевая группа проекта: учителя математики.

Срок реализации проекта: сентябрь 2015 года – май 2017 года

Место реализации проекта: МБОУ «Шапшинская средняя общеобразовательная школа Высокогорского муниципального района Республики Татарстан»; МБОУ «Средняя общеобразовательная школа №11 с углубленным изучением отдельных предметов» Нижнекамского муниципального района Республики Татарстан.

Раскрытие темы проекта

В основе построения данной рабочей программы по математике лежит идея гуманизации математического образования, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание личности ученика, его интересам и способностям. В основе отбора методов и средств обучения лежит деятельностный подход.

 Образование в 5-6 классах школы является базой, фундаментом всего последующего обучения. В первую очередь, это касается сформированности «универсальных учебных действий», обеспечивающих «умение учиться».    Сегодня оно закладывает основу формирования учебной деятельности ребенка – систему учебных и познавательных мотивов, умение принимать, сохранять, реализовывать учебные цели, умение планировать, контролировать и оценивать учебные действия и их результат. Именно обучение в 5-6 классах должно обеспечить познавательную мотивацию и интересы учащихся, их готовность и способность к сотрудничеству и совместной деятельности учения с учителем и одноклассниками, сформировать основы нравственного поведения, определяющего отношения личности с обществом и окружающими людьми.

 Разработка данной рабочей программы позволяет обеспечить требуемый уровень подготовки школьников, предусматриваемый государственным стандартом математического образования, а также позволяет осуществлять при этом такую их подготовку, которая является достаточной для углубленного изучения математики.

         Цели обучения математике обусловлены общими целями образования, концепцией математического образования, статусом и ролью математики в науке, культуре и жизнедеятельности общества, ценностями математического образования, новыми образовательными идеями, среди которых важное место занимает развивающее обучение.

Основная цель обучения математике состоит в формировании всесторонне образованной и инициативной личности, владеющей системой математических знаний и умений, идейно-нравственных, культурных и этических принципов, норм поведения, которые складываются в ходе учебно-воспитательного процесса и готовят ученика к активной деятельности и непрерывному образованию в современном обществе.

 Исходя из общих положений концепции математического образования, курс математики 5-6 классов призван решать следующие задачи:

 – обеспечить прочное и сознательное овладение системой математических знаний и умений, необходимых для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;

 – обеспечить интеллектуальное развитие, сформировать качества мышления, характерные для математической деятельности и необходимые для полноценной жизни в обществе;

 – сформировать умение учиться;

 – сформировать представление об идеях и методах математики, о математике как форме описания и методе познания окружающего мира;

 – сформировать представление о математике как части общечеловеческой культуры, понимание значимости математики для общественного прогресса;

 – сформировать устойчивый интерес к математике;

 – выявить и развить математические и творческие способности.

 Рабочая программа по предмету «Математика» разработана на основе примерных программ основного общего образования, рекомендованных Министерством образования Российской Федерации.

Изучив большое количество литературы по данному вопросу, есть четкое структурное построение рабочей программы, но нет практической направленности данного вопроса. Во всей указанной литературы даются лишь рекомендации по составлению данных программ, где четко прописано, что составление рабочей программы – это дело самого учителя. Вои здесь и начинаются трудности у каждого учителя. На наш взгляд, уже сегодня в рамках школ, городов, предметных сообществ есть необходимость обсудить наработки каждого учителя, чтобы увидеть свою видимость данного вопроса.

Важнейшая задача программ отдельных учебных предметов, курсов, в частности математики — обеспечить достижение планируемых результатов освоения основной образовательной программы основного общего образования.

Базовым документом для создания примерных программ учебных предметов (также как и учебно-методических материалов и пособий) является Фундаментальное ядро содержания общего образования. Его основное назначение в системе нормативного сопровождения федерального государственного образовательного стандарта состоит в том, чтобы определить: систему ведущих идей, теорий, основных понятий, относящихся к областям знаний, представленным в рамках общего образования; состав ключевых задач, обеспечивающих формирование универсальных видов учебной деятельности, адекватных требованиям ФГОС к результатам образования.

Фундаментальное ядро содержания общего образования фактически определяет содержательные характеристики программ учебных предметов (и примерных, и рабочих), а также организацию образовательного процесса по отдельным учебным предметам.

Программа по математике разрабатывается на основе требований к результатам освоения основной образовательной программы с учётом приоритетных направлений программ, включённых в структуру основной образовательной программы.

Программы отдельных учебных предметов, курсов должны содержать (п. 18.2.2. ФГОС ООО):

– пояснительную записку, в которой конкретизируются общие цели основного общего образования с учётом специфики учебного предмета;

– общую характеристику учебного предмета, курса;

– описание места учебного предмета, курса в учебном плане;

– личностные, метапредметные и предметные результаты освоения конкретного учебного предмета, курса;

– содержание учебного предмета, курса;

– тематическое планирование с определением основных видов учебной деятельности;

– описание учебно-методического и материально-технического обеспечения образовательного процесса;

– планируемые результаты изучения учебного предмета, курса.

Это требование распространяется как на примерные, так и на рабочие программы отдельных учебных предметов.

Примерные программы отдельных учебных предметов должны показывать, как можно обеспечить достижение планируемых результатов (личностных, метапредметных, предметных) освоения основной образовательной программы основного общего образования с учётом необходимости формирования универсальных учебных действий.

Примерные программы описывают содержание учебного предмета, дают примерное распределение учебных часов по разделам и темам курса, годам обучения. Они выполняют две основные функции:

информационно-методическую (определяют общую стратегию обучения, воспитания и развития учащихся средствами данного учебного предмета, определяют цели изучения предмета, раскрывают через содержание учебного предмета обязательную часть основной образовательной программы основного общего образования);

организационно-планирующую (структурируют учебный материал по разделам, темам, годам обучения с определением основных видов учебной деятельности обучающихся, описывают количественные и качественные показатели результативности реализации программы, а также материально-техническое обеспечение образовательного процесса).

Характеристика разделов программы учебного предмета (презентация)

1. Пояснительная записка.

В данном разделе конкретизируются общие цели основного общего образования с учётом специфики учебного предмета, курса, подчёркивается новизна данной программы, её отличие от аналогичных программ, указывается, в рамках какой системы учебников или какой завершённой предметной линии учебников предполагается реализация данной программы.

В данном разделе уточняется и расширяется заявленная в концепции духовно-нравственного развития и воспитания личности гражданина России система базовых национальных ценностей: патриотизм, социальная солидарность, гражданственность, семья, труд и творчество, наука, традиционные российские религии, искусство и литература, природа, человечество.

Ценностные ориентиры должны раскрывать воспитательный потенциал образовательного процесса, связь программы учебного предмета с программой воспитания и социализации обучающихся, включая формирование экологической культуры, культуры здорового и безопасного образа жизни.

В пояснительной записке могут быть даны комментарии к каждому из разделов программы и краткие методические указания по изложению теоретического материала, выполнению лабораторных практических работ, а также пояснения, связанные с проектированием и возможной реализацией части, формируемой участниками образовательного процесса.

2. Общая характеристика учебного предмета.

Эта часть программы определяет место данного учебного предмета в решении общих целей и задач на ступени основного общего образования, устанавливает межпредметные связи (на какие учебные предметы опирается данный предмет, для каких предметов является базой; если эти связи сильны, то целесообразно отметить, как они могут быть реализованы).

Общая характеристика учебного предмета предполагает описание особенностей организации учебного процесса по предмету; предпочтительные формы организации учебного процесса и их сочетания; предпочтительные формы контроля и оценки, указывается возможность интеграции с внеурочной деятельностью (например, на основе метода проектов).

3. Место учебного предмета в учебном плане.

В данном разделе приводится распределение часов на изучение предмета по классам, определяется резерв свободного учебного времени в часах и процентах от общего количества, который может быть использован для реализации авторских подходов, разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий.

В этой части программы могут быть приведены рекомендации по наполнению плана внеурочной деятельности в аспекте решения общих с данным предметом задач.

4. Личностные, метапредметные и предметные результаты освоения учебного предмета.

В этом разделе конкретизируются планируемые результаты освоения обучающимися основной образовательной программы основного общего образования, включающими, в том числе, личностные, познавательные, регулятивные и коммуникативные универсальные учебные действия; показывается связь программы учебного предмета с программой развития универсальных учебных действий (программой формирования общеучебных умений и навыков) на ступени основного общего образования.

5. Содержание учебного предмета.

Данный раздел является основной частью программы. Он строится по разделам и темам в соответствии с тематическим планом.

При описании содержания тем учебной программы может быть рекомендована следующая последовательность изложения:

название темы;

необходимое количество часов для её изучения;

планируемые результаты (обобщённые требования к знаниям и умениям обучающихся по теме): обучающийся должен иметь представление, знать, уметь, иметь опыт;

содержание учебного материала (дидактические единицы);

темы практических и лабораторных работ.

6. Планируемые результаты.

7. Тематическое планирование с определением основных видов учебной деятельности.

В тематическом плане раскрывается последовательность изучения разделов и тем программы, показывается распределение учебных часов по разделам и темам из расчёта общего количества часов по учебному предмету. Тематический план составляется на весь срок обучения.

8. Учебно-методическое и материально-техническое обеспечение образовательного процесса.

В этом разделе указывается основная и дополнительная учебная литература, учебные и справочные пособия, учебно-методическая литература, перечень рекомендуемых технических средств обучения, демонстрационные печатные пособия, экранно-звуковые пособия, цифровые образовательные ресурсы, учебно-практическое и учебно-лабораторное оборудование и т. д. В библиографическом списке выделяются издания, предназначенные для учащихся, и литература для учителя. Литература оформляется в соответствии с ГОСТом.

Этапы реализации проекта

1. Подготовительный 

• Ознакомление с  нормативно-правовой базой по ФГОС;
• Изучение требований к разработке рабочих программ в условиях реализации ФГОС;
• Обучение на курсах повышения квалификации для  учителей  математики по теме: “Современные педагогические технологии в преподавании математики и методы оценки результатов обучения“

1. Основной 

• Разработка в соответствии с требованиями ФГОС ООО следующих разделов  Пояснительной записки к рабочей программе: «Цели изучения курса математики в 5 классе», «Общая характеристика учебного предмета», «Описание места учебного предмета в учебном плане»,  «Личностные, метапредметные и предметные результаты освоения математики в 5 классе», «Содержание учебного предмета», «Планируемые результаты», «Описание учебно-методического и материально-технического обеспечения  образовательного процесса»;
• Составление календарно-тематического планирования раздела «Площади и объемы» в соответствии с требованиями ФГОС ООО;

1. Внедрение

• Апробация рабочей программы по математике  в 5-х классах
• Обсудить результаты апробации  учебной рабочей программы на заседании методического объединения.

1. Оформление результатов 

• Методические рекомендации по составлению рабочей программы по математике в 5 классе в соответствии с требованиями ФГОС ООО.

Таблица 1

План мероприятий по реализации проекта

№	Наименование мероприятия	Место проведения	Срок проведения	Ответственный
1.	Курсы повышения квалификации для учителей математики по проблеме “Современные педагогические технологии в преподавании математики и методы оценки результатов обучения“	Приволжский межрегиональный центр повышения квалификации и профессиональной переподготовки работников образования	Сентябрь 2015г.	учителя математики
2.	Изучение нормативно-правовой базы по ФГОС ООО;	образовательные учреждения	Сентябрь 2015г.	учителя математики
3.	Разработка в соответствии с требованиями ФГОС ООО следующих разделов  Пояснительной записки к рабочей программе: «Цели изучения курса математики в 5 классе», «Общая характеристика учебного предмета», «Описание места учебного предмета в учебном плане»,  «Личностные, метапредметные и предметные результаты освоения математики в 5 классе», «Содержание учебного предмета», «Планируемые результаты», «Описание учебно-методического и материально-технического обеспечения  образовательного процесса»	образовательные учреждения	Сентябрь 2015г.	учителя математики
4.	Составление календарно-тематического планирования раздела «Площади и объемы» в соответствии с требованиями ФГОС ООО;	образовательные учреждения	Сентябрь 2015г.	учителя математики
5.	Апробация и внедрение рабочей программы по математике в 5 классах	образовательные учреждения	2015-2016 год	учителя математики
6.	Обсуждение результатов апробации рабочей программы на заседании методического объединения.	образовательные учреждения	Июнь- август2016г.	учителя математики
7.	Методические рекомендации по составлению рабочей программы по математике в соответствии с требованиями ФГОС ООО.	образовательные учреждения	Июнь- август2016г.	учителя математики

Таблица 2

Ресурсы

Условия	Необходимо	Имеется	Источники	Сроки
Нормативно-правовые: Закон РФ «Об образовании» ФГОС  по математике Учебный план ОУ	+ + +	+ + +	Интернет  Журнал «Вестник образования» Стандарты второго поколения (примерные программы ООО)	2015-2016 г.
Материально-технические: Кабинет математики	+	+	ОУ	2015-2016 г.
Кадровые: Преподаватели математики	+	+	ОУ
Научно-методические: Учебная и учебно-методическая литература по математике	+	+	ОУ	2015-2016 г.
Информационные: Программное обеспечение для организации проектной деятельности Выступление на районных семинарах, конференциях.	+ +	– +	ОУ	2015-2016 г.
Мотивационные: Повышение профессиональной квалификации преподавателей	+	+	КПФУ	2015-2016 г.
Организационные: Создание рабочей группы для разработки программы Утверждение программы	+ +	+ +	ОУ	2015-2016 г.
Финансовые:

Ожидаемые результаты реализации проекта:

1.Рабочая программа по математике в 5 классе, разработанная  в соответствии с требованиями ФГОС.  

2. Апробация рабочей программы по математике в 5 классах.

3. Методические рекомендации по составлению рабочей программы по математике в соответствии с требованиями ФГОС ООО.

Методы диагностики

Апробация рабочей программы  в 5 классах , работающих в условиях ФГОС ООО с использованием следующих методов диагностики:

• анкетирование;
• контрольно-методические срезы;
•  тестирование;
• наблюдение;
• беседы и другие.

Заключение

В ходе изучения теоретического материала и выполнении практической части работы нами разработана  рабочая  программа по математике в 5 классе в соответствии с требованиями ФГОС основного общего образования на основе примерной основной образовательной программы. Трудностей в ходе работы возникало не мало. В качестве положительного хочется выделить, что осмысление теоретического материала курса получило закрепление в виде практической работы, а именно данной проектной работы. В ходе работы мы прошли дистанционное обучение, очно слушали лекции опытных преподавателей: Г.Х. Ахметшиной, Софоновой Н.В, Багаутдиновой Е.П., Зеличёнок А.Б.  и др.

Трудности возникали в том, что УМК Виленкина Н.Я. и др. не в полной мере соответствует стандартам второго поколения, поэтому  и при работе по этим стандартам, если нет возможности ОУ  перейти к УМК Бунимовича Е.А., считаем  возможным применять разработанные им задачи в качестве дополнительных.

Литература

1. Федеральный государственный образовательный стандарт основного общего образования /М-во образования и науки РФ-М.: Просвещение, 2011.
2. Примерная основная образовательная программа образовательного учреждения: основная школа.
3. Программа  основного общего  образования по математике 5-9 классы.
4.  Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий. /под ред.А.Г. Асмолова.- М.:Просвещение, 2010./
5. Фундаментальное ядро содержания общего образования / Рос. акад. наук, Рос. акад. образования; под ред.В. В. Козлова, А. М. Кондакова. — 4е изд., дораб. — М. : Просвещение, 2011.
6. Концепция духовно-нравственного развития и воспитания личности гражданина России. Данилюк А. Я., Кондаков А. М., Тишков В. А.,М., Просвещение, 2009 г.
7.  Концепция государственных стандартов общего образования второго поколения – в части общих подходов и идеологии разработки  стандарта. – М «Просвещение» 2008 г. (под ред. Ф.М. Кондакова, Ф.Ф. Кузнецова.
8.  Журнал “Математика в школе”.
9. Приложение «Математика»  к газете «1 сентября»
10. Сайт «ФГОС»

Приложение

Рассмотрено  на заседании МО Руководитель  _______ протокол №          от «   »______2015г

Согласовано Заместитель директора по УР  _______________ «     »______2015г

Утверждено Директор школы ____________ Приказ №         от «   »______2015г

Рабочая программа по математике

в 5 классе

Костратова Валентина Сергеевна, учитель  математики МБОУ «Шапшинская средняя общеобразовательная школа Высокогорского муниципального района Республики Татарстан»,

Косова Наталья Владимировна, учитель математики МБОУ «Средняя общеобразовательная школа №11 с углубленным изучением отдельных предметов» Нижнекамского муниципального района Республики Татарстан.

2015 – 2016 учебный год

Пояснительная записка

Данная рабочая программа по математике разработана на основе:

1. Федерального закона от 29.12.2012 года № 273-ФЗ “Об образовании в Российской федерации”.

2. Федерального государственного образовательного стандарта основного общего образования,  утвержденного приказом Министерства образования и науки РФ от 17 декабря 2010 года № 1897;

3. Примерной программы по учебным предметам. Математика 5 – 9 классы. М.: Просвещение, 2011;

4. Примерной программы по математике для 5 класса по учебнику Н.Я. Виленкина, В.И.Жохова и др. / В.И.Жохов, М.: Мнемозина, 2010

5. Требований примерной образовательной программы образовательного учреждения.

Данная программа является рабочей программой по предмету «Математика» в 5 классе базового уровня.

Цели изучения:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
• систематическое развитие понятия числа;
• выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики; подготовка обучающихся к изучению систематических курсов алгебры и геометрии.

В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, получают начальные преставления об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство с геометрическими понятиями, приобретают навыки построения геометрических фигур и измерения геометрических величин.

Усвоенные знания и способы действий необходимы не только для дальнейшего успешного изучения математики и других школьных дисциплин, но и для решения многих практических задач во взрослой жизни.

Программа определяет ряд задач, решение которых направлено на достижение основных целей основного общего математического образования:

• Формировать элементы самостоятельной интеллектуальной деятельности на основе овладения математическими методами познания окружающего мира (умения устанавливать, описывать, моделировать и объяснять количественные и пространственные отношения);
• Развивать основы логического, знаково-символического и алгоритмического мышления; пространственного воображения; математической речи; умения вести поиск информации и работать с ней;
• Развивать познавательные способности;
• Воспитывать стремление к расширению математических знаний;
• Способствовать интеллектуальному развитию, формировать качества личности, необходимые человеку для полноценной жизни в современном обществе, свойственные математической деятельности: ясности и точности мысли, интуиции, логического мышления, пространственных представлений, способности к преодолению трудностей;
• Воспитывать культуру личности, отношение к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Решение названных задач обеспечит осознание школьниками универсальности математических способов познания мира, усвоение математических знаний, связей математики с окружающей действительностью и с другими школьными предметами, а также личностную заинтересованность в расширении математических знаний.

Общий курс математики является курсом интегрированным: в нём объединён арифметический, геометрический и алгебраический материал.

Содержание обучения представлено в программе разделами: «Числа и вычисления», «Выражения и их преобразования», «Уравнения и неравенства», «Геометрические фигуры и их свойства. Измерение геометрических величин».

Программа предусматривает дальнейшую работу с величинами (длина, площадь, масса, вместимость, время) и их измерением, с единицами измерения однородных величин и соотношениями между ними.

Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит основным элементом для изучения смежных дисциплин.

В после школьной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. Все больше специальностей, требующих высокого уровня образования связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология и т.д.).

Программой предусмотрено целенаправленное формирование совокупности умений работать с информацией. Эти умения формируются как на уроках, так и во внеурочной деятельности — на факультативных и кружковых занятиях. Освоение содержания курса связано не только с поиском, обработкой, представлением новой информации, но и с созданием информационных объектов: стенгазет, книг, справочников. Новые информационные объекты создаются в основном в рамках проектной деятельности. Проектная деятельность позволяет закрепить, расширить и углубить полученные на уроках знания, создаёт условия для творческого развития детей, формирования позитивной самооценки, навыков совместной деятельности с взрослыми и сверстниками, умений сотрудничать друг с другом, совместно планировать свои действия и реализовывать планы, вести поиск и систематизировать нужную информацию.

Общая характеристика
курса математики в 5 классе

Математика играет важную роль в формировании у школьников умения учиться.

Обучение математике закладывает основы для формирования приёмов умственной деятельности: школьники учатся проводить анализ, сравнение, классификацию объектов, устанавливать причинно-следственные связи, закономерности, выстраивать логические цепочки рассуждений. Изучая математику, они усваивают определённые обобщённые знания и способы действий. Универсальные математические способы познания способствуют целостному восприятию мира, позволяют выстраивать модели его отдельных процессов и явлений, а также являются основой формирования универсальных учебных действий. Универсальные учебные действия обеспечивают усвоение предметных знаний и интеллектуальное развитие учащихся, формируют способность к самостоятельному поиску и усвоению новой информации, новых знаний и способов действий, что составляет основу умения учиться.

       В курсе математики 5 класса можно выделить следующие основные содержательные линии: арифметика; элементы алгебры; вероятность и статистика; наглядная геометрия. Наряду с этим в содержание включены две дополнительные методологические темы: множества и математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждой из этих тем разворачивается в содержательно-методическую линию, пронизывающую все основные содержательные линии. При этом первая линия — «Множества» — служит цели овладения учащимися некоторыми элементами универсального математического языка, вторая — «Математика в историческом развитии» — способствует созданию общекультурного, гуманитарного фона изучения курса.

        Содержание линии «Арифметика» служит фундаментом для дальнейшего изучения учащимися математики и смежных дисциплин, способствует развитию не только вычислительных навыков, но и логического мышления, формированию умения пользоваться алгоритмами, способствует развитию умений планировать и осуществлять деятельность, направленную на решение задач, а также приобретению практических навыков, необходимых в повседневной жизни.

       Содержание линии «Элементы алгебры» систематизирует знания о математическом языке, показывая применение букв для обозначения чисел и записи свойств арифметических действий, а также для нахождения неизвестных компонентов арифметических действий.

      Содержание линии «Наглядная геометрия» способствует формированию у учащихся первичных представлений о геометрических абстракциях реального мира, закладывает основы формирования правильной геометрической речи, развивает образное мышление и пространственные представления.

      Линия «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим прежде всего для формирования у учащихся функциональной грамотности — умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.

      При изучении статистики и вероятности обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.

Место курса «Математика» в учебном плане

      Базисный учебный (образовательный) план на изучение математики в 5 классе основной школы отводит 5 часов в неделю, всего 170 уроков. Учебное время может быть увеличено до 6 часов в неделю за счёт вариативной части Базисного плана.

Ценностные ориентиры содержания учебного предмета

      Математическое образование играет важную роль как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей культуры.

      Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виду таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.

       Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.

       Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач — основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.

       Обучение математике дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.

      Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.

      Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.

       История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.

Личностные, метапредметные и предметные
результаты освоения содержания курса

        Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования.

Личностные:

у учащихся будут сформированы:

1) ответственное отношение к учению;

2) готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;

3) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

4) начальные навыки адаптации в динамично изменяющемся мире;

5) экологическая культура: ценностное отношение к природному миру, готовность следовать нормам природоохранного, здоровье-сберегающего поведения;

6) формирование способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

7) умение контролировать процесс и результат учебной математической деятельности;

у учащихся могут быть сформированы:

1) первоначальные представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;

2) коммуникативная компетентность в общении и сотрудничестве со сверстниками в образовательной, учебно-исследовательской, творческой и других видах деятельности;

3) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

4) креативность мышления, инициативы, находчивости, активности при решении арифметических задач.

Метапредметные:

регулятивные

учащиеся научатся:

1) формулировать и удерживать учебную задачу;

2) выбирать действия в соответствии с поставленной задачей и условиями её реализации;

3) планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

4) предвидеть уровень усвоения знаний, его временных характеристик;

5) составлять план и последовательность действий;

6) осуществлять контроль по образцу и вносить необходимые коррективы;

7) адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;

8) сличать способ действия и его результат с заданным эталоном с целью обнаружения отклонений и отличий от эталона;

учащиеся получат возможность научиться:

1) определять последовательность промежуточных целей и соответствующих им действий с учётом конечного результата;

2) предвидеть возможности получения конкретного результата при решении задач;

3) осуществлять констатирующий и прогнозирующий контроль по результату и по способу действия;

4) выделять и формулировать то, что усвоено и что нужно усвоить, определять качество и уровень усвоения;

5) концентрировать волю для преодоления интеллектуальных затруднений и физических препятствий;

познавательные

учащиеся научатся:

1) самостоятельно выделять и формулировать познавательную цель;

2) использовать общие приёмы решения задач;

3) применять правила и пользоваться инструкциями и освоенными закономерностями;

4) осуществлять смысловое чтение;

5) создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения задач;

6) самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

7) понимать сущность алгоритмических предписаний и уметь действовать в соответствии с предложенным алгоритмом;

8) понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

9) находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;

учащиеся получат возможность научиться:

1) устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;

2) формировать учебную и общепользовательскую компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);

3) видеть математическую задачу в других дисциплинах, в окружающей жизни;

4) выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

5) планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

6) выбирать наиболее рациональные и эффективные способы решения задач;

7) интерпретировать информации (структурировать, переводить сплошной текст в таблицу, презентовать полученную информацию, в том числе с помощью ИКТ);

8) оценивать информацию (критическая оценка, оценка достоверности);

9) устанавливать причинно-следственные связи, выстраивать рассуждения, обобщения;

коммуникативные

учащиеся научатся:

1) организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников;

2) взаимодействовать и находить общие способы работы; работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;

3) прогнозировать возникновение конфликтов при наличии разных точек зрения;

4) разрешать конфликты на основе учёта интересов и позиций всех участников;

5) координировать и принимать различные позиции во взаимодействии;

6) аргументировать свою позицию и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности.

Предметные:

учащиеся научатся:

1) работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию;

2) владеть базовым понятийным аппаратом: иметь представление о числе, дроби, об основных геометрических объектах (точка, прямая, ломаная, угол, многоугольник, многогранник, круг, окружность);

3) выполнять арифметические преобразования, применять их для решения учебных математических задач;

4) пользоваться изученными математическими формулами;

5) самостоятельно приобретать и применять знания в различных ситуациях для решения несложных практических задач, в том числе с использованием при необходимости справочных материалов, калькулятора и компьютера;

6) пользоваться предметным указателем энциклопедий и справочников для нахождения информации;

7) знать основные способы представления и анализа статистических данных; уметь решать задачи с помощью перебора возможных вариантов;

учащиеся получат возможность научиться:

1) выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;

2) применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов;

3) самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем, а также самостоятельно интерпретировать результаты решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.

Предметное содержание программы направлено на последовательное формирование и отработку универсальных учебных действий, развитие логического и алгоритмического мышления, пространственного воображения и математической речи.

Знание и понимание математических отношений и взаимозависимостей между различными объектами (соотношение целого и части, пропорциональные зависимости величин, взаимное расположение объектов в пространстве и др.), их обобщение и распространение на расширенную область приложений выступают как средство познания закономерностей, происходящих в природе и в обществе. Это стимулирует развитие познавательного интереса школьников, стремление к постоянному расширению знаний, совершенствованию освоенных способов действий.

Изучение математики способствует развитию алгоритмического мышления. Программа предусматривает формирование умений действовать по предложенному алгоритму, самостоятельно составлять план действий и следовать ему при решении учебных и практических задач, осуществлять поиск нужной информации, дополнять ею решаемую задачу, делать прикидку и оценивать реальность предполагаемого результата.

В процессе освоения программного материала школьники знакомятся с языком математики, осваивают некоторые математические термины, учатся высказывать суждения с использованием математических терминов и понятий, задавать вопросы по ходу выполнения заданий, обосновывать правильность выполненных действий, характеризовать результаты своего учебного труда и свои достижения в изучении этого предмета.

Овладение математическим языком, усвоение алгоритмов выполнения действий, умения строить планы решения различных задач и прогнозировать результат являются основой для формирования умений рассуждать, обосновывать свою точку зрения, аргументированно подтверждать или опровергать истинность высказанного предположения. Освоение математического содержания создаёт условия для повышения логической культуры и совершенствования коммуникативной деятельности учащихся.

Содержание программы предоставляет значительные возможности для развития умений работать в паре или в группе. Формированию умений распределять роли и обязанности, сотрудничать и согласовывать свои действия с действиями одноклассников, оценивать собственные действия и действия отдельных учеников (пар, групп) в большой степени способствует содержание, связанное с поиском и сбором информации.

Программа ориентирована на формирование умений использовать полученные знания для самостоятельного поиска новых знаний, для решения задач, возникающих в процессе различных видов деятельности, в том числе и в ходе изучения других школьных дисциплин.

Математические знания и представления о числах, величинах,
геометрических фигурах лежат в основе формирования общей картины мира и познания законов его развития. Именно эти знания и представления необходимы для целостного восприятия объектов и явлений природы, многочисленных памятников культуры, сокровищ искусства.

Обучение школьников математике на основе данной программы способствует развитию и совершенствованию основных познавательных процессов (включая воображение и мышление, память и речь). Дети научатся не только самостоятельно решать поставленные задачи математическими способами, но и описывать на языке математики выполненные действия и их результаты, планировать, контролировать и оценивать способы действий и сами действия, делать выводы и обобщения, доказывать их правильность. Освоение курса обеспечивает развитие творческих способностей, формирует интерес к математическим знаниям и потребность в их расширении, способствует продвижению учащихся в познании окружающего мира.

Содержание тем учебного курса

Содержание курса имеет концентрическое строение, отражающее последовательное расширение области чисел. Такая структура позволяет соблюдать необходимую постепенность в нарастании сложности учебного материала, создаёт хорошие условия для углубления формируемых знаний, отработки умений и навыков, для увеличения степени самостоятельности (при освоении новых знаний, проведении обобщений, формулировании выводов), для постоянного совершенствования универсальных учебных действий.

Структура содержания определяет такую последовательность изучения учебного материала, которая обеспечивает не только формирование осознанных и прочных, во многих случаях доведённых до автоматизма навыков вычислений, но и доступное для младших школьников обобщение учебного материала, понимание общих принципов и законов, лежащих в основе изучаемых математических фактов, осознание связей между рассматриваемыми явлениями. Сближенное во времени изучение связанных между собой понятий, действий, задач даёт возможность сопоставлять, сравнивать, противопоставлять их в учебном процессе, выявлять сходства и различия в рассматриваемых фактах.

1. Натуральные числа и шкалы (15 ч). Натуральные числа и их сравнение. Геометрические фигуры: отрезок, прямая, луч, треугольник. Измерение и построение отрезков. Координатный луч.

Цель: систематизировать и обобщить сведения о натуральных числах, полученные в начальной школе; закрепить навыки построения и измерения отрезков.

Систематизация сведений о натуральных числах позволяет восстановить у обучающихся навыки чтения и записи многозначных чисел, сравнения натуральных чисел, а также навыки измерения и построения отрезков. Рассматриваются простейшие комбинаторные задачи. В ходе изучения темы вводятся понятия координатного луча, единичного отрезка и координаты точки. Здесь начинается формирование таких важных умений, как умения начертить координатный луч и отметить на нем заданные числа, назвать число, соответствующее данному делению на координатном луче.

2. Сложение и вычитание натуральных чисел (21 ч). Сложение и вычитание натуральных чисел, свойства сложения. Решение текстовых задач. Числовое выражение. Буквенное выражение и его числовое значение. Решение линейных уравнений.

Цель: закрепить и развить навыки сложения и вычитания натуральных чисел.

Начиная с этой темы основное внимание уделяется закреплению алгоритмов арифметических действий над многозначными числами, так как они не только имеют самостоятельное значение, но и являются базой для формирования умений проводить вычисления с десятичными дробями. В этой теме начинается алгебраическая подготовка: составление буквенных выражений по условию задач, решение уравнений на основе зависимости между компонентами действий (сложение и вычитание).

3. Умножение и деление натуральных чисел (27 ч). Умножение и деление натуральных чисел, свойства умножения. Квадрат и куб числа. Решение текстовых задач.

Цель: закрепить и развить навыки арифметических действий с натуральными числами.

В этой теме проводится целенаправленное развитие и закрепление навыков умножения и деления многозначных чисел. Вводятся понятия квадрата и куба числа. Продолжается работа по формированию навыков решения уравнений на основе зависимости между компонентами действий. Развиваются умения решать текстовые задачи, требующие понимания смысла отношений «больше на… (в…)», «меньше на… (в…)», а также задачи на известные обучающимся зависимости между величинами (скоростью, временем и расстоянием; ценой, количеством и стоимостью товара и др.). Задачи решаются арифметическим способом. При решении с помощью составления уравнений так называемых задач на части учащиеся впервые встречаются с уравнениями, в левую часть которых неизвестное входит дважды. Решению таких задач предшествуют преобразования соответствующих буквенных выражений.

4. Площади и объемы (13 ч). Вычисления по формулам. Прямоугольник. Площадь прямоугольника. Единицы площадей.

Цель: расширить представления обучающихся об измерении геометрических величин на примере вычисления площадей и объемов и систематизировать известные им сведения о единицах измерения.

При изучении темы учащиеся встречаются с формулами. Навыки вычисления по формулам отрабатываются при решении геометрических задач. Значительное внимание уделяется формированию знаний основных единиц измерения и умению перейти от одних единиц к другим в соответствии с условием задачи.

5.  Обыкновенные дроби (23 ч). Окружность и круг. Обыкновенная дробь. Основные задачи на дроби. Сравнение обыкновенных дробей. Сложение и вычитание дробей с одинаковыми знаменателями.

Цель: познакомить обучающихся с понятием дроби в объеме, достаточном для введения десятичных дробей.

В данной теме изучаются сведения о дробных числах, необходимые для введения десятичных дробей. Среди формируемых умений основное внимание должно быть привлечено к сравнению дробей с одинаковыми знаменателями, к выделению целой части числа. С пониманием смысла дроби связаны три основные задачи на дроби, осознанного решения которых важно добиться от обучающихся.

6. Десятичные дроби. Сложение и вычитание десятичных дробей (13 ч). Десятичная дробь. Сравнение, округление, слежение и вычитание десятичных дробей. Решение текстовых задач.

Цель: выработать умения читать, записывать, сравнивать, округлять десятичные дроби, выполнять сложение и вычитание десятичных дробей.

При введении десятичных дробей важно добиться у обучающихся четкого представления о десятичных разрядах рассматриваемых чисел, умений читать, записывать, сравнивать десятичные дроби. Подчеркивая сходство действий над десятичными дробями с действиями над натуральными числами, отмечается, что сложение десятичных дробей подчиняется переместительному и сочетательному законам. Определенное внимание уделяется решению текстовых задач на сложение и вычитание, данные в которых выражены десятичными дробями. При изучении операции округления числа вводится новое понятие — «приближенное значение числа», отрабатываются навыки округления десятичных дробей до заданного десятичного разряда.

7. Умножение и деление десятичных дробей (26 ч). Умножение и деление десятичных дробей. Среднее арифметическое нескольких чисел. Решение текстовых задач.

Цель: выработать умения умножать и делить десятичные дроби, выполнять задания на все действия с натуральными числами и десятичными дробями.

Основное внимание привлекается к алгоритмической стороне рассматриваемых вопросов. На несложных примерах отрабатывается правило постановки запятой в результате действия. Кроме того, продолжается решение текстовых задач с данными, выраженными десятичными дробями. Вводится понятие среднего арифметического нескольких чисел.

8. Инструменты для вычислений и измерений (17 ч). Начальные сведения о вычислениях на калькуляторе. Проценты. Основные задачи на проценты. Примеры таблиц и диаграмм. Угол, треугольник. Величина (градусная мера) угла. Единицы измерения углов. Измерение углов. Построение угла заданной величины.

Цель: сформировать умения решать простейшие задачи на проценты, выполнять измерение и построение углов.

У обучающихся важно выработать содержательное понимание смысла термина «процент». На этой основе они должны научиться решать три вида задач на проценты: находить несколько процентов от какой-либо величины; находить число, если известно несколько его процентов; находить, сколько процентов одно число составляет от другого. Продолжается работа по распознаванию и изображению и геометрических фигур. Важно уделить внимание формированию умений проводить измерения и строить углы. Китовые диаграммы дают представления обучающимся о наглядном изображении распределения отдельных составных частей какой-нибудь величины. В упражнениях следует широко использовать статистический материал, публикуемый в газетах и журналах. В классе, обеспеченном калькуляторами, можно научить школьников использовать калькулятор при выполнении отдельных арифметических действий.

9. Повторение. Решение задач (11 ч).

Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс математики 5 класса.

10. Резерв (4 ч)

Планируемые результаты

В результате изучения курса математики в 5 классе учащиеся должны

знать / понимать:

– существо понятия алгоритма;

– как используются математические формулы и уравнения при решении математических и практических задач;

– как потребности практики привели математическую науку к необходимости расширения понятия числа;

– каким образом геометрия возникла из практических задач землемерия;

уметь:

– выполнять действия сложения и вычитания, умножения и деления с рациональными числами, возводить рациональное число в квадрат, в куб;

– переходить от одной формы записи чисел к другой, предоставлять десятичную дробь в виде обыкновенной и обыкновенную в виде десятичной, проценты в виде дроби и дробь в виде процентов;

– находить значение числовых выражений;

-находить значение числовых выражений;

– округлять натуральные числа и десятичные дроби;

– пользоваться основными единицами длины, массы, времени, скорости, площади, объёма; выражать более крупные единицы через более мелкие и наоборот;

– решать текстовые задачи арифметическим способом и с помощью уравнений, включая задачи, связанные с дробями и процентами;

– извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить графики и диаграммы;

– решать комбинаторные задачи путем систематического перебора возможных вариантов.

Использовать приобретённые знания и умения в практической деятельности и повседневной жизни:

– для решения несложных практических задач, в том числе с использованием справочных материалов, калькулятора, компьютера;

– устной прикидки и оценки результатов вычислений; проверки результатов вычислений с использованием различных приемов;

– интерпретации результатов решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.

Календарно-тематическое планирование  по математике в 5 классе

№ п/п	Тема урока	Характеристика основных видов деятельности ученика (на уровне УУД)	Планируемые результаты	Информационно-методическое и материально-техническое оснащение	Дата
Предметные	Личностные	Метапредметные
План	Факт
1	Формулы	Выражать одни единицы измерения величины в других единицах(м в км, мин.в ч и т.п.) Округлять натуральные числа и десятичные дроби. Выполнять оценку и прикидку в ходе вычислений. .Моделировать несложные зависимости с помощью формул, выполнять вычисления по формулам. Использовать знания о зависимостях между величинами (скорость, время, расстояние; работа, производительность, время и т.п.) при решении текстовых задач.	Иметь представление о формулах. Уметь: находить значение величины, используя данную формулу, составлять формулу по условию задачи, выражать из формул одну переменную через другую	Проявляют устойчивый интерес к способам решения познавательных задач; осознают и принимают социальную роль ученика	(Р) – составляют план выполнения заданий; обнаруживают и формулируют проблему; (П) – выводы «если… то…». (К) – умеют принимать точку зрения другого	учебник, рабочая тетрадь, таблица с формулами, единицами измерения,  интерактивные тесты и анимированные задачи с диска «Мат-ка. Интерактивные приложения», презентация к уроку.
2	Формулы
3	Площадь. Формула площади прямоугольника	Выражать одни единицы измерения площади через другие. Изображать геометрические фигуры и их конфигурации от руки и с использованием чертежных инструментов. Приводить примеры аналогов геометрических фигур в окружающем мире. Измерять с помощью инструментов длины отрезков. Вычислять площади квадратов и прямоугольников по формуле. Решать задачи на нахождение площади прямоугольника. Выделять в условии задачи данные, необходимые для ее решения , строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи.	Знать формулы площади прямоугольника и квадрата. Уметь: вычислять площади прямоугольника, квадрата, прямоугольного треугольника	Проявляют устойчивый интерес к способам решения познавательных задач; дают положительную самооценку и оценку результатов УД; Объясняют себе свои наиболее заметные достижения	(Р) – работают по составленному плану, учатся моделировать разнообразные ситуации расположения объектов в пространстве и на плоскости. (П) – записывают выводы «если… то…». (К) – умеют высказывать свою точку зрения, оформлять свои мысли в устной и письменной речи	учебник, рабочая тетрадь, таблица с формулами и единицами измерения площадей,  комплект чертежных инструментов (классных и раздаточных), интерактивные тесты с диска «Мат-ка. Интерактивные приложения», презентация к уроку.
4	Площадь. Формула площади прямоугольника
5	Единицы измерения площадей	Выражать одни единицы измерения площади через другие. Изображать геометрические фигуры и их конфигурации от руки и с использованием чертежных инструментов Решать задачи на нахождение площади прямоугольника. Выделять в условии задачи данные, необходимые для ее решения , строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи.	Знать единицы измерения площадей. Уметь: выражать более крупные единицы площади через более мелкие и наоборот	Объясняют себе свои наиболее заметные достижения; Проявляют устойчивый интерес к способам решения познавательных задач; осознают социальную роль ученика	(Р) – составляют план выполнения заданий; обнаруживают и формулируют проблему; (П) – записывают выводы правил «если… то…». (К) – умеют принимать точку зрения другого	учебник, рабочая тетрадь, таблица с единицами измерения площади,,  интерактивные тесты и анимированные задачи с диска «Мат-ка. Интерактивные приложения», презентация к уроку.
6	Единицы измерения площадей
7	Решение задач по теме: «Площадь прямоугольника»
8	Прямоугольный параллелепипед	Изготавливать пространственные фигуры из разверток; распознавать развертки куба, параллелепипеда; рассматривать простейшие сечения пространственных фигур, получаемые путем предметного или компьютерного моделирования, определять их вид. Исследовать и описывать свойства куба и прямоугольного параллелепипеда, используя эксперимент, наблюдение, измерение. Моделировать куб, прямоугольный параллелепипед, используя бумагу, пластилин, проволоку и др. Использовать компьютерное моделирование для изучения свойств геометрических объектов. Находить в окружающем мире пространственные фигуры, имеющие форму прямоугольного параллелепипеда и куба. Изображать куб и прямоугольный параллелепипед от руки и с использованием чертежных инструментов.	Иметь представление о прямоугольном параллелепипеде. Знать его элементы. Уметь: изображать и находить площадь его поверхности	дают положительную самооценку и оценку результатов УД;	(Р) – определяют цель УД, осуществляют средства её достижения, конструируют модели геометрических тел. (П) – передают содержание в сжатом или развёрнутом виде. (К) – умеют слушать других; уважительно относиться к мнению других	учебник, рабочая тетрадь, развертки и модели куба и прямоугольного параллелепипеда (демонстрационные и раздаточные), комплект чертежных инструментов (классных и раздаточных), комплект для моделирования,  интерактивные практические задания  с диска «Мат-ка. Интерактивные приложения», презентация к уроку.
9	Объёмы. Объём прямоугольного параллелепипеда	Вычислять объемы куба и прямоугольного параллелепипеда, используя формулы объема куба и прямоугольного параллелепипеда. Выражать одни единицы измерения объема через другие.	Знать формулу объёма прямоугольного параллелепипеда. Уметь: вычислять объёмы прямоугольного параллелепипеда и куба, зная их измерения, и решать обратную задачу	Проявляют положит-ное отн-е к урокам математики, объясняют самому себе свои наиболее заметные достижения, оценивают свою познавательную деятельность	(Р) – понимают причины неуспеха, (П) – делают предположения об инф-ции, нужной для решения задач (К) – умеют критично относиться к  своему мнению	уучебник, рабочая тетрадь, таблица с единицами измерения объема,,  интерактивные тесты и анимированные задачи с диска «Мат-ка. Интерактивные приложения», презентация к уроку с сайта www.school-collection.edu.ru
10	Объёмы. Объём прямоугольного параллелепипеда
11	Решение задач по теме «Объёмы. Объём прямоугольного параллелепипеда»	Решать задачи на нахождение объема прямоугольного параллелепипеда и куба. Выделять в условии задачи данные, необходимые для ее решения , строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи.	дают положительную самооценку и оценку результатов УД; учатся использовать различные инструменты и технические средства для измерений величин	(Р) – составляют план выполнения заданий; обнаруживают и формулируют проблему; (П) – выводы «если… то…». (К) – умеют принимать точку зрения другого	учебник, рабочая тетрадь, таблица с формулами,  интерактивные тесты и анимированные задачи с диска «Мат-ка. Интерактивные приложения», презентация к уроку.
12	Решение задач по теме «Площади и объемы»	Решать задачи на нахождение площади прямоугольника и объема прямоугольного параллелепипеда и куба. Выделять в условии задачи данные, необходимые для ее решения , строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи. Обобщение и систематизация знаний и умений по теме «Площади и объемы»	При изучении темы у уч-ся формируются ключевые компетенции-способность самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем-умением мотивированно отказываться от образца, искать новые методы решения задач	Объясняют себе свои наиболее заметные достижения; Проявляют устойчивый интерес к способам решения познавательных задач; осознают социальную роль ученика. дают положительную самооценку и оценку результатов УД; учатся использовать различные инструменты и технические средства для измерений величин	(Р) – составляют план выполнения заданий; обнаруживают и формулируют проблему; (П) – записывают выводы правил «если… то…». (К) – умеют прини-мать точку зрения другого	учебник, рабочая тетрадь, таблица с формулами,  интерактивные тесты и анимированные задачи с диска «Мат-ка. Интерактивные приложения», тестирование on-line: http://www. kokch.kts.ru/cdo/
13	К/р №6: Площади и объёмы	Решение к/р №6. итоговый контроль и учет знаний, умений и навыков	Уметь находить значение величины по формуле, вычислять площадь и объём, решать практико-ориентир. задачи	Формирование ценностных отношений к результатам обучения. Объясняют себе свои наиболее заметные достижения	(Р) – понимают причины неуспеха, (П) – делают предположения об инф-ции, нужной для решения задач (К) – умеют критично относиться к  своему мнению	карточки с заданиями

Информационно-методическое и материально техническое обеспечение к рабочей программе

1.Библиотечный фонд:

1. ФГОС_ОО. Утвержден приказом Министерства образования и науки РФ от 17.12.2010 №1897.
2. Математика: Учеб. для 5 кл. общеобразоват. учреждений/ Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. -М.: Мнемозина
3. А.С. Чесноков, К.И. Нешков Дидактические материалы по математике 5 класс — М.: Просвещение.
4. Математика. 5 класс. Рабочая программа по учебнику Н.Я.Виленкина, В.И.Жохова и др. / Т.А.Лопатина, Г.С.Мещерякова., Учитель, 2011.
5. Примерные программы по учебным предметам. Математика 5-9 классы. –  М.: Просвещение, 2011.
6. Жохов В.И. Математический тренажер. 5 класс. – М.: Мнемозина, 2012.
7. Жохов В.И. Контрольные работы по математике.  Пособие. 5 класс. – М.: Мнемозина, 2011.
8. Попов М.А. Дидактические материалы по математике. 5 класс. К учебнику Н.Я.Виленкина и др. – Экзамен, 2012.
9. Математика. 5 класс: рабочая программа по учебнику Н.Я.Виленкина, В.И.Жохова и др. / О.С.Кузнецова, Л.Н. Абознова и др. – Волгоград: Учитель, 2012

2.Печатные пособия:

1. Таблицы по математике для 5 классов.

2. Портреты выдающихся математиков.

3.Информационные средства:

1. Диск «Уроки математики . Мультимедийное приложение к урокам математики (Презентации к каждому уроку)»+Методическое пособие

2.Диск «математика. Интерактивные дидактические материалы. 5 класс по учебнику Н.Я.Виленкина (тесты, логические задания, кроссворды, анимированные задачи)»+ методическое пособие

3.Инструментальная среда по математике.

4. Электронная база данных для создания тематических, разноуровневых тренировочных и проверочных материалов для организации контроля.

Предполагается использование следующих программно-педагогических средств, реализуемых с помощью компьютера:

• Математика: еженедельное учебно-методическое приложение к газете «Первое сентября». http://mat.lseptember.ru.

Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих интернет-ресурсов:

• Министерство образования и науки РФ: http://www.mon.gov.ru/
• Федеральное государственное учреждение «Государственный научно-исследовательский институт информационных технологий и телекоммуникаций»: http://www. informika.ru/
• Тестирование on-line: 5-11 классы: http://www.kokch.kts.ru/cdo/
• Путеводитель «В мире науки» для школьников:
  http://www.uic.ssu. samara.ru/~nauka/
• Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru/
• Сайт энциклопедий: http://www.encyclopedia.ru/
• Электронные образовательные ресурсы к учебникам в Единой коллекции www.school-collection.edu.ru
• http://www.openclass.ru/node/226794
• http://forum.schoolpress.ru/article/44
• http://1314.ru/
• http://www.informika.ru/projects/infotech/school-collection/
• http://www.ug.ru/article/64
• http://staviro.ru
• http://www.youtube.com/watch?v=LLSKZJA8g2E&feature=related
• http://www.youtube.com/watch?v=Cn24EHYkFPc&feature=related
• http://staviro.ru/

4.Экранно-звуковые пособия.

Видеофильмы по истории развития математики, математических идей и методов.

5.Технические средства обучения.

1.Мультимедийный компьютер.

2.Мультимедиапроектор.

3.Экран.

4.Интерактивная доска.

6.Учебно-практическое и учебно-лабораторное оборудование.

1.Магнитная доска с координатной сеткой.

2.Комплект чертежных инструментов (классных и раздаточных).

3.Комплекты планиметрических и стереометрических тел (классных и раздаточных).

4.Комплекты для моделирования (цветная бумага, картон, калька, клей, ножницы, пластилин)

Приложение к рабочей программе.

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.

1. Оценка письменных контрольных работ обучающихся по математике.

• Ответ оценивается отметкой «5», если:
• работа выполнена полностью;
• в логических рассуждениях и обосновании решения нет пробелов и ошибок;
• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
• Отметка «4» ставится в следующих случаях:
• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
• Отметка «3» ставится, если:
• допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
• Отметка «2» ставится, если:
• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

 2.       Оценка устных ответов обучающихся по математике

• Ответ оценивается отметкой «5», если ученик:
• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
• продемонстрировал знание теории ранее изученных сопутствующих тем,  сформированность  и устойчивость используемых при ответе умений и навыков;
• отвечал самостоятельно, без наводящих вопросов учителя;
• возможны одна – две  неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
• Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
• допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
• допущены ошибка или более двух недочетов  при освещении второстепенных вопросов или в выкладках,  легко исправленные после замечания учителя.
• Отметка «3» ставится в следующих случаях:
• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
• Отметка «2» ставится в следующих случаях:
• не раскрыто основное содержание учебного материала;
• обнаружено незнание учеником большей или наиболее важной части учебного материала;
• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

3.  Общая классификация ошибок.

• При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
• незнание наименований единиц измерения;
• неумение выделить в ответе главное;
• неумение применять знания, алгоритмы для решения задач;
• неумение делать выводы и обобщения;
• неумение читать и строить графики;
• неумение пользоваться первоисточниками, учебником и справочниками;
• потеря корня или сохранение постороннего корня;
• отбрасывание без объяснений одного из них;
• равнозначные им ошибки;
• вычислительные ошибки, если они не являются опиской;
• логические ошибки.

3.2. К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного – двух из этих признаков второстепенными;
• неточность графика;
• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
• нерациональные методы работы со справочной и другой литературой;
• неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

• нерациональные приемы вычислений и преобразований;
• небрежное выполнение записей, чертежей, схем, графиков.

Введение

С введением ФГОС изменяются структура и сущность результатов образовательной деятельности, содержание образовательных программ и технологии их реализации, методология, содержание и процедуры оценивания результатов освоения образовательных программ. Повышается значимость формирования условий реализации программ, в том числе создания образовательной инфраструктуры, изменяются требования к ним. Должна быть спроектирована система управления инновационными процессами, обеспечивающая достижение нового качества образования.

Федеральные государственные образовательные стандарты общего образования формулируют требования к подготовке учителя и руководителей общеобразовательного учреждения для реализации основной образовательной программы общего образования.

Новая парадигма образования, реализуемая ФГОС, – это переход от школы информационно-трансляционной к школе деятельностной, формирующей у обучающихся компетенции самостоятельной навигации по освоенным предметным знаниям при решении конкретных личностно значимых задач, в том числе и в ситуациях неопределенности.

Именно сегодня встает острая необходимость вооружить себя как учителя-предметника, не только теоретическими навыками введения ФГОС в основное звено, но и попробовать себя в качестве составителя рабочей программы по математике для продолжения введения стандартов начальной школы, т.е. для 5-6 классов.

В основе построения данной рабочей программы по математике лежит идея гуманизации математического образования, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание личности ученика, его интересам и способностям. В основе отбора методов и средств обучения лежит деятельностный подход.
Образование в 5-6 классах школы является базой, фундаментом всего последующего обучения. В первую очередь, это касается сформированности «универсальных учебных действий», обеспечивающих «умение учиться». Сегодня оно закладывает основу формирования учебной деятельности ребенка – систему учебных и познавательных мотивов, умение принимать, сохранять, реализовывать учебные цели, умение планировать, контролировать и оценивать учебные действия и их результат. Именно обучение в 5-6 классах должно обеспечить познавательную мотивацию и интересы учащихся, их готовность и способность к сотрудничеству и совместной деятельности учения с учителем и одноклассниками, сформировать основы нравственного поведения, определяющего отношения личности с обществом и окружающими людьми.
Разработка данной рабочей программы позволяет обеспечить требуемый уровень подготовки школьников, предусматриваемый государственным стандартом математического образования, а также позволяет осуществлять при этом такую их подготовку, которая является достаточной для углубленного изучения математики.
Цели обучения математике обусловлены общими целями образования, концепцией математического образования, статусом и ролью математики в науке, культуре и жизнедеятельности общества, ценностями математического образования, новыми образовательными идеями, среди которых важное место занимает развивающее обучение.

Изучив большое количество литературы по данному вопросу, есть четкое структурное построение рабочей программы, но нет практической направленности данного вопроса. Во всей указанной литературы даются лишь рекомендации по составлению данных программ, где четко прописано, что составление рабочей программы – это дело самого учителя. Вои здесь и начинаются трудности у каждого учителя. На мой взгляд уже сегодня в рамках школ, городов, предметных сообществ есть необходимость обсудить наработки каждого учителя, чтобы увидеть себя и свою видимость данного вопроса. Надо в Интернет – ресурсах сделать форумное обсуждение разработчиков – педагогов и чтобы данное направление привлекало к себе и научных работников, хочется услышать и их мнение на свою работу.

Основная часть

Важнейшая задача программ отдельных учебных предметов, курсов, в частности математики — обеспечить достижение планируемых результатов освоения основной образовательной программы основного общего образования.

Базовым документом для создания примерных программ учебных предметов (также как и учебно-методических материалов и пособий) является Фундаментальное ядро содержания общего образования. Его основное назначение в системе нормативного сопровождения федерального государственного образовательного стандарта состоит в том, чтобы определить: систему ведущих идей, теорий, основных понятий, относящихся к областям знаний, представленным в рамках общего образования; состав ключевых задач, обеспечивающих формирование универсальных видов учебной деятельности, адекватных требованиям ФГОС к результатам образования.

Фундаментальное ядро содержания общего образования фактически определяет содержательные характеристики программ учебных предметов (и примерных, и рабочих), а также организацию образовательного процесса по отдельным учебным предметам.

Программа по математике разрабатывается на основе требований к результатам освоения основной образовательной программы с учётом приоритетных направлений программ, включённых в структуру основной образовательной программы.

Программы отдельных учебных предметов, курсов должны содержать (п. 18.2.2. ФГОС ООО):

• пояснительную записку, в которой конкретизируются общие цели основного общего образования с учётом специфики учебного предмета;
• общую характеристику учебного предмета, курса;
• описание места учебного предмета, курса в учебном плане;
• личностные, метапредметные и предметные результаты освоения конкретного учебного предмета, курса;
• содержание учебного предмета, курса;
• тематическое планирование с определением основных видов учебной деятельности;
• описание учебно-методического и материально-технического обеспечения образовательного процесса;
• планируемые результаты изучения учебного предмета, курса.

Это требование распространяется как на примерные, так и на рабочие программы отдельных учебных предметов.

Примерные программы отдельных учебных предметов должны показывать, как можно обеспечить достижение планируемых результатов (личностных, метапредметных, предметных) освоения основной образовательной программы основного общего образования с учётом необходимости формирования универсальных учебных действий.

Примерные программы описывают содержание учебного предмета, дают примерное распределение учебных часов по разделам и темам курса, годам обучения. Они выполняют две основные функции:

• информационно-методическую (определяют общую стратегию обучения, воспитания и развития учащихся средствами данного учебного предмета, определяют цели изучения предмета, раскрывают через содержание учебного предмета обязательную часть основной образовательной программы основного общего образования);
• организационно-планирующую (структурируют учебный материал по разделам, темам, годам обучения с определением основных видов учебной деятельности обучающихся, описывают количественные и качественные показатели результативности реализации программы, а также материально-техническое обеспечение образовательного процесса).

Характеристика разделов программы учебного предмета (презентация)

1. Пояснительная записка.

В данном разделе конкретизируются общие цели основного общего образования с учётом специфики учебного предмета, курса, подчёркивается новизна данной программы, её отличие от аналогичных программ, указывается, в рамках какой системы учебников или какой завершённой предметной линии учебников предполагается реализация данной программы.

В данном разделе уточняется и расширяется заявленная в концепции духовно-нравственного развития и воспитания личности гражданина России система базовых национальных ценностей: патриотизм, социальная солидарность, гражданственность, семья, труд и творчество, наука, традиционные российские религии, искусство и литература, природа, человечество.

Ценностные ориентиры должны раскрывать воспитательный потенциал образовательного процесса, связь программы учебного предмета с программой воспитания и социализации обучающихся, включая формирование экологической культуры, культуры здорового и безопасного образа жизни.

В пояснительной записке могут быть даны комментарии к каждому из разделов программы и краткие методические указания по изложению теоретического материала, выполнению лабораторных практических работ, а также пояснения, связанные с проектированием и возможной реализацией части, формируемой участниками образовательного процесса.

2. Общая характеристика учебного предмета.

Эта часть программы определяет место данного учебного предмета в решении общих целей и задач на ступени основного общего образования, устанавливает межпредметные связи (на какие учебные предметы опирается данный предмет, для каких предметов является базой; если эти связи сильны, то целесообразно отметить, как они могут быть реализованы).

Общая характеристика учебного предмета предполагает описание особенностей организации учебного процесса по предмету; предпочтительные формы организации учебного процесса и их сочетания; предпочтительные формы контроля и оценки, указывается возможность интеграции с внеурочной деятельностью (например, на основе метода проектов).

3. Место учебного предмета в учебном плане.

В данном разделе приводится распределение часов на изучение предмета по классам, определяется резерв свободного учебного времени в часах и процентах от общего количества, который может быть использован для реализации авторских подходов, разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий.

В этой части программы могут быть приведены рекомендации по наполнению плана внеурочной деятельности в аспекте решения общих с данным предметом задач.

4. Личностные, метапредметные и предметные результаты освоения учебного предмета.

В этом разделе конкретизируются планируемые результаты освоения обучающимися основной образовательной программы основного общего образования, включающими, в том числе, личностные, познавательные, регулятивные и коммуникативные универсальные учебные действия; показывается связь программы учебного предмета с программой развития универсальных учебных действий (программой формирования общеучебных умений и навыков) на ступени основного общего образования.

5. Содержание учебного предмета.

Данный раздел является основной частью программы. Он строится по разделам и темам в соответствии с тематическим планом.

При описании содержания тем учебной программы может быть рекомендована следующая последовательность изложения:

• название темы;
• необходимое количество часов для её изучения;
• планируемые результаты (обобщённые требования к знаниям и умениям обучающихся по теме): обучающийся должен иметь представление, знать, уметь, иметь опыт;
• содержание учебного материала (дидактические единицы);
• темы практических и лабораторных работ.

6. Тематическое планирование с определением основных видов учебной деятельности.

• В тематическом плане раскрывается последовательность изучения разделов и тем программы, показывается распределение учебных часов по разделам и темам из расчёта общего количества часов по учебному предмету. Тематический план составляется на весь срок обучения.

7. Учебно-методическое и материально-техническое обеспечение образовательного процесса.

В этом разделе указывается основная и дополнительная учебная литература, учебные и справочные пособия, учебно-методическая литература, перечень рекомендуемых технических средств обучения, демонстрационные печатные пособия, экранно-звуковые пособия, цифровые образовательные ресурсы, учебно-практическое и учебно-лабораторное оборудование и т. д. В библиографическом списке выделяются издания, предназначенные для учащихся, и литература для учителя. Литература оформляется в соответствии с ГОСТом.

В соответствие с данными рекомендациями я попыталась составить рабочую программу по математике в 5-6 классах в соответсвии с требованиями ФГОС ООО (приложение 1).

Заключение

В ходе изучения теоретического материала и выполнении практической части работы я сделала попытку разработать рабочую программу по математике в соответствии с требованиями ФГОС основного общего образования на основе примерной основной образовательной программы. Трудностей в ходе работы возникало не мало: в летнее время обучения не с кем было пообщаться по данной тематике, высказать свое мнение и услышать чужое, нет практического навыка данной работы, нет возможности провести диагностику совей работы. В качестве положительного хочется выделить: учитывая опять же летнее время, отпуск есть возможность посвятить много времени самообразованию, само осмыслению теоретического материала курса, представленного опытными преподавателями университета «Просвещение». Думаю, что с нового учебного года я много времени в своей работе буду уделять новым стандартам образования.

Муниципальное образование Первомайский район

Муниципальное казенное общеобразовательное учреждение

«Новокраюшкинская основная общеобразовательная школа»

Согласовано: Утверждено:

Протокол педагогического

совета № 8 приказом директора № 30

от « 29 » августа 2017г от « 29 » августа 2017 г.

Рабочая программа

по математике для 5-6 классов,

по алгебре и геометрии для 7-9 классов.

Срок реализации 5 лет

Разработчики:

Ткачук М.М.,

учитель математики

1 квалификационной категории

С. Новокраюшкино

2017 г.

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа по математике для 5-9 классов составлена с использованием материалов: Федерального государственного образовательного стандарта основного общего образования, авторской программы по математике для основной школы и рабочей программы по математике к предметной линии учебников Н.Я.Виленкин, В.И.Жохов и др. , Ю.Н. Макарычев, Н.Г. Миндюк и др., Л. С. Атанасян, В. Ф. Бутузов и др.с учетом примерной основной образовательной программы основного общего образования.

Математика играет важную роль в формировании у школьников умения учиться. Обучение математике закладывает основы для формирования приёмов умственной деятельности: школьники учатся проводить анализ, сравнение, классификацию объектов, устанавливать причинно-следственные связи, закономерности, выстраивать логические цепочки рассуждений. Изучая математику, они усваивают определённые обобщённые знания и способы действий. Универсальные математические способы познания способствуют целостному восприятию мира, позволяют выстраивать модели его отдельных процессов и явлений, а также являются основой формирования универсальных учебных действий. Универсальные учебные действия обеспечивают усвоение предметных знаний и интеллектуальное развитие учащихся, формируют способность к самостоятельному поиску и усвоению новой информации, новых знаний и способов действий, что составляет основу умения учиться.

Методологической основой реализации рабочей программы, в соответствии с требованиями ФГОС, является системно-деятельностный подход, который предполагает:

• воспитание и развитие качеств личности, отвечающих требованиям информационного общества;

• формирование соответствующей целям общего образования социальной среды развития обучающихся в системе образования, переход к стратегии социального проектирования и конструирования на основе разработки содержания и технологий образования, определяющих пути и способы достижения желаемого уровня (результата) личностного и познавательного развития обучающихся;

• ориентацию на достижение основного результата образования – развитие на основе освоения универсальных учебных действий, познания и освоения мира личности обучающегося, его активной учебно-познавательной деятельности, формирование его готовности к саморазвитию и непрерывному образованию;

• признание решающей роли содержания образования, способов организации образовательной деятельности и учебного сотрудничества в достижении целей личностного и социального развития обучающихся;

учет индивидуальных возрастных, психологических и физиологических особенностей обучающихся, роли, значения видов деятельности и форм общения при построении образовательного процесса и определении образовательно-воспитательных целей и путей их достижения;

Содержание программы по математике в основной школе обусловлено общей нацеленностью образовательного процесса на достижение личностных, метапредметных и предметных целей обучения

Цели изучения:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

• систематическое развитие понятия числа;

• выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики; подготовка обучающихся к изучению систематических курсов алгебры и геометрии.

В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, получают начальные преставления об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство с геометрическими понятиями, приобретают навыки построения геометрических фигур и измерения геометрических величин.

Усвоенные знания и способы действий необходимы не только для дальнейшего успешного изучения математики и других школьных дисциплин, но и для решения многих практических задач во взрослой жизни.

Программа определяет ряд задач, решение которых направлено на достижение основных целей основного общего математического образования:

• Формировать элементы самостоятельной интеллектуальной деятельности на основе овладения математическими методами познания окружающего мира (умения устанавливать, описывать, моделировать и объяснять количественные и пространственные отношения);

• Развивать основы логического, знаково-символического и алгоритмического мышления; пространственного воображения; математической речи; умения вести поиск информации и работать с ней;

• Развивать познавательные способности;

• Воспитывать стремление к расширению математических знаний;

• Способствовать интеллектуальному развитию, формировать качества личности, необходимые человеку для полноценной жизни в современном обществе, свойственные математической деятельности: ясности и точности мысли, интуиции, логического мышления, пространственных представлений, способности к преодолению трудностей;

• Воспитывать культуру личности, отношение к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Решение названных задач обеспечит осознание школьниками универсальности математических способов познания мира, усвоение математических знаний, связей математики с окружающей действительностью и с другими школьными предметами, а также личностную заинтересованность в расширении математических знаний.

II. Общая характеристика учебного предмета

Содержание математического образования в 5-9 классах представлено в виде следующих содержательных разделов: «Арифметика», «Числовые и буквенные выражения. Уравнения», «Геометрические фигуры. Измерение геометрических величин», «Элементы статистики, вероятности. Комбинаторные задачи», «Математика в историческом развитии», «Алгебра», «Числовые множества», «Функции», «Элементы прикладной математики», «Алгебра в историческом развитии»

Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися математики и смежных дисциплин, способствует развитию вычислительной культуры и логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе связано с изучением рациональных чисел: натуральных чисел, обыкновенных и десятичных дробей, положительных и отрицательных чисел.

Содержание раздела «Числовые и буквенные выражения. Уравнения» формирует знания о математическом языке. Существенная роль при этом отводится овладению формальным аппаратом буквенного исчисления. Изучение материала способствует формированию у учащихся математического аппарата решения задач с помощью уравнений.

Содержание раздела «Геометрические фигуры. Измерения геометрических величин» формирует у учащихся понятия геометрических фигур на плоскости и в пространстве, закладывает основы формирования геометрической «речи», развивает пространственное воображение и логическое мышление.

Содержание раздела «Элементы статистики, вероятности. Комбинаторные задачи» – обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности, умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор вариантов, в том числе в простейших прикладных задачах.

Раздел «Математика в историческом развитии» предназначен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рассмотрении проблематики основного содержания математического образования.

Содержание раздела «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, овладение навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе.

Раздел «Числовые множества» нацелен на математическое развитие учащихся, формирование у них точно, сжато и ясно излагать мысли в устной и письменной речи.

Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.

Содержание раздела «Элементы прикладной математики» раскрывают прикладное и практическое значения математики в современном мире. Материал способствует формированию умения представлять и анализировать информацию.

Раздел «Алгебра в историческом развитии» предназначается для формирования представлений о математике как части человеческой культуры, для общего развития школьников, создания культурно- исторической среды обучения.

Цель содержания раздела «Геометрия» — развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности со строгостью является неотъемлемой частью геометрических знаний. Материал, относящийся к блокам «Координаты» и «Векторы», в значительной степени несет в себе межпредметные знания, которые находят применение как в различных математических дисциплинах, так и в смежных предметах.

Содержание курса геометрии в 7-9 классах представлено в виде следующих содержательных разделов: «Геометриче­ские фигуры», «Измерение геометрических величин», «Координаты», «Векторы», «Геометрия в историческом развитии».

Содержание раздела «Геометрические фигуры» служит базой для дальнейшего изучения учащимися геометрии. Изучение материала способствует формированию у уча­щихся знаний о геометрической фигуре как важнейшей ма­тематической модели для описания реального мира. Глав­ная цель данного раздела — развить у учащихся воображе­ние и логическое мышление путём систематического изучения свойств геометрических фигур и применения этих свойств при решении задач вычислительного и конструк­тивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядно­сти с формально-логическим подходом является неотъемле­мой частью геометрических знаний.

Содержание раздела «Измерение геометрических вели­чин» расширяет и углубляет представления учащихся об из­мерениях длин, углов и площадей фигур, способствует фор­мированию практических навыков, необходимых как при решении геометрических задач, так и в повседневной жизни.

Содержание разделов «Координаты», «Векторы» расши­ряет и углубляет представления учащихся о методе коорди­нат, развивает умение применять алгебраический аппарат при решении геометрических задач, а также задач смеж­ных дисциплин.

Раздел «Геометрия в историческом развитии», содержа­ние которого фрагментарно внедрено в изложение нового материала как сведения об авторах изучаемых фактов и тео­рем, истории их открытия, предназначен для формирова­ния представлений о геометрии как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения.

III. Место учебного предмета «Математика» в учебном плане

Федеральный базисный (образовательный) учебный план для образовательных учреждений Российской Федерации (ва­риант 1) предусматривает обязательное изучение математики на этапе основного общего образования в объ­ёме 850 ч. В том числе: в 5 классе — 170 ч, в 6 классе — 170 ч, в 7 классе — 170 ч, в 8 классе — 170 ч, в 9 классе — 170 ч.

IV. Личностные, метапредметные и предметные результаты изучения учебного предмета

в личностном направлении:

1) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

2) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

3) представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;

4) креативность мышления, инициатива, находчивость, активность при решении математических задач;

5) умение контролировать процесс и результат учебной математической деятельности;

6) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

7) воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;

8) ответственное отношение к учению, готовность и спо­собность обучающихся к саморазвитию и самообразова­нию на основе мотивации к обучению и познанию;

9) осознанный выбор и построение дальнейшей индивиду­альной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к тру­ду, развитие опыта участия в социально значимом труде;

10) умение контролировать процесс и результат учебной и математической деятельности;

11) критичность мышления, инициатива, находчивость, активность при решении геометрических задач;

в метапредметном направлении:

1) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;

2) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;

3) умение находить в различных источниках информацию, необходимую для решения математических проблем, и пред-ставлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;

4) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;

5) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

6) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;

7) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;

8) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

9) умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

10) умение самостоятельно определять цели своего обуче­ния, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познава­тельной деятельности;

11) умение соотносить свои действия с планируемыми ре­зультатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требова­ний, корректировать свои действия в соответствии с из­меняющейся ситуацией;

12) умение определять понятия, создавать обобщения, ус­танавливать аналогии, классифицировать, самостоя­тельно выбирать основания и критерии для классифи­кации;

13) устанавливать причинно-следственные связи, проводить доказательное рассуждение, умозаключение (индуктив­ное, дедуктивное и по аналогии) и делать выводы;

14) умение иллюстрировать изученные понятия и свойства фигур, опровергать неверные утверждения;

15) компетентность в области использования информаци­онно-коммуникационных технологий;

16) первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техни­ки, о средстве моделирования явлений и процессов;

17) умение видеть геометрическую задачу в контексте про­блемной ситуации в других дисциплинах, в окружаю­щей жизни;

18) умение находить в различных источниках информа­цию, необходимую для решения математических про­блем, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;

19) умение понимать и использовать математические сред­ства наглядности (чертежи, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;

20) умение выдвигать гипотезы при решении задачи и по­нимать необходимость их проверки;

в предметном направлении:

1) овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;

2) умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;

3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками  устных, письменных, инструментальных вычислений;

4) овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;

5) овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей;

6) овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;

7) овладение геометрическим языком, умение использовать его для описания предметов окружающего мира; развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;

8) усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне — о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;

9) умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;

10) умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера;

11) осознание значения геометрии для повседневной жизни человека;

12) представление о геометрии как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;

13) развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую ин­формацию), точно и грамотно выражать свои мысли с применением математической терминологии и симво­лики, проводить классификации, логические обоснова­ния;

14) владение базовым понятийным аппаратом по основным разделам содержания;

15) систематические знания о фигурах и их свойствах;

16) практически значимые геометрические умения и навы­ки, умение применять их к решению геометрических и негеометрических задач, а именно:

• изображать фигуры на плоскости;

• использовать геометрический язык для описания предметов окружающего мира;

• измерять длины отрезков, величины углов, вычис­лять площади фигур;

• распознавать и изображать равные, симметричные и подобные фигуры;

• выполнять построения геометрических фигур с по­мощью циркуля и линейки;

• читать и использовать информацию, представлен­ную на чертежах, схемах;

• проводить практические расчёты

V. СОДЕРЖАНИЕ КУРСА

Cодержание курсов математики 5–6 классов, алгебры и геометрии 7–9 классов.

Элементы теории множеств и математической логики

Согласно ФГОС основного общего образования в курс математики введен раздел «Логика», который не предполагает дополнительных часов на изучении и встраивается в различные темы курсов математики и информатики и предваряется ознакомлением с элементами теории множеств.

Множества и отношения между ними

Множество, характеристическое свойство множества, элемент множества, пустое, конечное, бесконечное множество. Подмножество. Отношение принадлежности, включения, равенства. Элементы множества, способы задания множеств, распознавание подмножеств и элементов подмножеств с использованием кругов Эйлера.

Операции над множествами

Пересечение и объединение множеств. Разность множеств, дополнение множества, Интерпретация операций над множествами с помощью кругов Эйлера.

Элементы логики

Определение. Утверждения. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример.

Высказывания

Истинность и ложность высказывания. Сложные и простые высказывания. Операции над высказываниями с использованием логических связок: и, или, не. Условные высказывания (импликации).

Содержание курса математики в 5–6 классах

Натуральные числа и нуль

Натуральный ряд чисел и его свойства

Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками на числовой прямой. Использование свойств натуральных чисел при решении задач.

Запись и чтение натуральных чисел

Различие между цифрой и числом. Позиционная запись натурального числа, поместное значение цифры, разряды и классы, соотношение между двумя соседними разрядными единицами, чтение и запись натуральных чисел.

Округление натуральных чисел

Необходимость округления. Правило округления натуральных чисел.

Сравнение натуральных чисел, сравнение с числом 0

Понятие о сравнении чисел, сравнение натуральных чисел друг с другом и с нулём, математическая запись сравнений, способы сравнения чисел.

Действия с натуральными числами

Сложение и вычитание, компоненты сложения и вычитания, связь между ними, нахождение суммы и разности, изменение суммы и разности при изменении компонентов сложения и вычитания.

Умножение и деление, компоненты умножения и деления, связь между ними, умножение и сложение в столбик, деление уголком, проверка результата с помощью прикидки и обратного действия.

Переместительный и сочетательный законы сложения и умножения, распределительный закон умножения относительно сложения, обоснование алгоритмов выполнения арифметических действий.

Степень с натуральным показателем

Запись числа в виде суммы разрядных слагаемых, порядок выполнения действий в выражениях, содержащих степень, вычисление значений выражений, содержащих степень.

Числовые выражения

Числовое выражение и его значение, порядок выполнения действий.

Деление с остатком

Деление с остатком на множестве натуральных чисел, свойства деления с остатком. Практические задачи на деление с остатком.

Свойства и признаки делимости

Свойство делимости суммы (разности) на число. Признаки делимости на 2, 3, 5, 9, 10. Признаки делимости на 4, 6, 8, 11. Доказательство признаков делимости. Решение практических задач с применением признаков делимости.

Разложение числа на простые множители

Простые и составные числа, решето Эратосфена.

Разложение натурального числа на множители, разложение на простые множители. Количество делителей числа, алгоритм разложения числа на простые множители, основная теорема арифметики.

Алгебраические выражения

Использование букв для обозначения чисел, вычисление значения алгебраического выражения, применение алгебраических выражений для записи свойств арифметических действий, преобразование алгебраических выражений.

Делители и кратные

Делитель и его свойства, общий делитель двух более чисел, наибольший общий делитель, взаимно простые числа, нахождение наибольшего общего делителя. Кратное и его свойства, общее кратное двух и более чисел, наименьшее общее кратное, способы нахождения наименьшего общего кратного.

Дроби

Обыкновенные дроби

Доля, часть, дробное число, дробь. Дробное число как результат деления. Правильные и неправильные дроби, смешанная дробь (смешанное число).

Запись натурального числа в виде дроби с заданным знаменателем, преобразование смешанной дроби в неправильную дробь и наоборот.

Приведение дробей к общему знаменателю. Сравнение обыкновенных дробей.

Сложение и вычитание обыкновенных дробей. Умножение и деление обыкновенных дробей.

Арифметические действия со смешанными дробями.

Арифметические действия с дробными числами.

Способы рационализации вычислений и их применение при выполнении действий.

Десятичные дроби

Целая и дробная части десятичной дроби. Преобразование десятичных дробей в обыкновенные. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Округление десятичных дробей. Умножение и деление десятичных дробей. Преобразование обыкновенных дробей в десятичные дроби. Конечные и бесконечные десятичные дроби.

Отношение двух чисел

Масштаб на плане и карте. Пропорции. Свойства пропорций, применение пропорций и отношений при решении задач.

Среднее арифметическое чисел

Среднее арифметическое двух чисел. Изображение среднего арифметического двух чисел на числовой прямой. Решение практических задач с применением среднего арифметического. Среднее арифметическое нескольких чисел.

Проценты

Понятие процента. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентах. Решение несложных практических задач с процентами.

Диаграммы

Столбчатые и круговые диаграммы. Извлечение информации из диаграмм. Изображение диаграмм по числовым данным.

Рациональные числа

Положительные и отрицательные числа

Изображение чисел на числовой (координатной) прямой. Сравнение чисел. Модуль числа, геометрическая интерпретация модуля числа. Действия с положительными и отрицательными числами. Множество целых чисел.

Понятие о рациональном числе. Первичное представление о множестве рациональных чисел. Действия с рациональными числами.

Решение текстовых задач

Единицы измерений: длины, площади, объёма, массы, времени, скорости. Зависимости между единицами измерения каждой величины. Зависимости между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость.

Задачи на все арифметические действия

Решение текстовых задач арифметическим способом. Использование таблиц, схем, чертежей, других средств представления данных при решении задачи.

Задачи на движение, работу и покупки

Решение несложных задач на движение в противоположных направлениях, в одном направлении, движение по реке по течению и против течения. Решение задач на совместную работу. Применение дробей при решении задач.

Задачи на части, доли, проценты

Решение задач на нахождение части числа и числа по его части. Решение задач на проценты и доли. Применение пропорций при решении задач.

Логические задачи

Решение несложных логических задач. Решение логических задач с помощью графов, таблиц.

Основные методы решения текстовых задач: арифметический, перебор вариантов.

Наглядная геометрия

Фигуры в окружающем мире. Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. Четырехугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Правильные многоугольники. Изображение основных геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Длина отрезка, ломаной. Единицы измерения длины. Построение отрезка заданной длины. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира.

Периметр многоугольника. Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Приближенное измерение площади фигур на клетчатой бумаге. Равновеликие фигуры.

Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примеры разверток многогранников, цилиндра и конуса.

Понятие объема; единицы объема. Объем прямоугольного параллелепипеда, куба.

Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.

Решение практических задач с применением простейших свойств фигур.

История математики

Появление цифр, букв, иероглифов в процессе счёта и распределения продуктов на Древнем Ближнем Востоке. Связь с Неолитической революцией.

Рождение шестидесятеричной системы счисления. Появление десятичной записи чисел.

Рождение и развитие арифметики натуральных чисел. НОК, НОД, простые числа. Решето Эратосфена.

Появление нуля и отрицательных чисел в математике древности. Роль Диофанта. Почему ?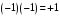

Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Л. Магницкий.

Содержание курса алгебра и геометрия в 7–9 классах Алгебра

Числа

Рациональные числа

Множество рациональных чисел. Сравнение рациональных чисел. Действия с рациональными числами. Представление рационального числа десятичной дробью.

Иррациональные числа

Понятие иррационального числа. Распознавание иррациональных чисел. Примеры доказательств в алгебре. Иррациональность числа 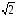. Применение в геометрии. Сравнение иррациональных чисел. Множество действительных чисел.

Тождественные преобразования

Числовые и буквенные выражения

Выражение с переменной. Значение выражения. Подстановка выражений вместо переменных.

Целые выражения

Степень с натуральным показателем и её свойства. Преобразования выражений, содержащих степени с натуральным показателем.

Одночлен, многочлен. Действия с одночленами и многочленами (сложение, вычитание, умножение). Формулы сокращённого умножения: разность квадратов, квадрат суммы и разности. Разложение многочлена на множители: вынесение общего множителя за скобки, группировка, применение формул сокращённого умножения. Квадратный трёхчлен, разложение квадратного трёхчлена на множители.

Дробно-рациональные выражения

Степень с целым показателем. Преобразование дробно-линейных выражений: сложение, умножение, деление. Алгебраическая дробь. Допустимые значения переменных в дробно-рациональных выражениях. Сокращение алгебраических дробей. Приведение алгебраических дробей к общему знаменателю. Действия с алгебраическими дробями: сложение, вычитание, умножение, деление, возведение в степень.

Преобразование выражений, содержащих знак модуля.

Квадратные корни

Арифметический квадратный корень. Преобразование выражений, содержащих квадратные корни: умножение, деление, вынесение множителя из-под знака корня, внесение множителя под знак корня.

Уравнения и неравенства

Равенства

Числовое равенство. Свойства числовых равенств. Равенство с переменной.

Уравнения

Понятие уравнения и корня уравнения. Представление о равносильности уравнений. Область определения уравнения (область допустимых значений переменной).

Линейное уравнение и его корни

Решение линейных уравнений. Линейное уравнение с параметром. Количество корней линейного уравнения. Решение линейных уравнений с параметром.

Квадратное уравнение и его корни

Квадратные уравнения. Неполные квадратные уравнения. Дискриминант квадратного уравнения. Формула корней квадратного уравнения. Теорема Виета. Теорема, обратная теореме Виета. Решение квадратных уравнений: использование формулы для нахождения корней, графический метод решения, разложение на множители, подбор корней с использованием теоремы Виета. Количество корней квадратного уравнения в зависимости от его дискриминанта. Биквадратные уравнения. Уравнения, сводимые к линейным и квадратным. Квадратные уравнения с параметром.

Дробно-рациональные уравнения

Решение простейших дробно-линейных уравнений. Решение дробно-рациональных уравнений.

Методы решения уравнений: методы равносильных преобразований, метод замены переменной, графический метод. Использование свойств функций при решении уравнений.

Простейшие иррациональные уравнения вида , .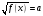

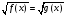
Уравнения вида 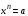.Уравнения в целых числах.

Системы уравнений

Уравнение с двумя переменными. Линейное уравнение с двумя переменными. Прямая как графическая интерпретация линейного уравнения с двумя переменными.

Понятие системы уравнений. Решение системы уравнений.

Методы решения систем линейных уравнений с двумя переменными: графический метод, метод сложения, метод подстановки.

Системы линейных уравнений с параметром.

Неравенства

Числовые неравенства. Свойства числовых неравенств. Проверка справедливости неравенств при заданных значениях переменных.

Неравенство с переменной. Строгие и нестрогие неравенства. Область определения неравенства (область допустимых значений переменной).

Решение линейных неравенств.

Квадратное неравенство и его решения. Решение квадратных неравенств: использование свойств и графика квадратичной функции, метод интервалов. Запись решения квадратного неравенства.

Решение целых и дробно-рациональных неравенств методом интервалов.

Системы неравенств

Системы неравенств с одной переменной. Решение систем неравенств с одной переменной: линейных, квадратных. Изображение решения системы неравенств на числовой прямой. Запись решения системы неравенств.

Функции

Понятие функции

Декартовы координаты на плоскости. Формирование представлений о метапредметном понятии «координаты». Способы задания функций: аналитический, графический, табличный. График функции. Примеры функций, получаемых в процессе исследования различных реальных процессов и решения задач. Значение функции в точке. Свойства функций: область определения, множество значений, нули, промежутки знакопостоянства, чётность/нечётность, промежутки возрастания и убывания, наибольшее и наименьшее значения. Исследование функции по её графику.

Представление об асимптотах.

Непрерывность функции. Кусочно заданные функции.

Линейная функция

Свойства и график линейной функции. Угловой коэффициент прямой. Расположение графика линейной функции в зависимости от её углового коэффициента и свободного члена. Нахождение коэффициентов линейной функции по заданным условиям: прохождение прямой через две точки с заданными координатами, прохождение прямой через данную точку и параллельной данной прямой.

Квадратичная функция

Свойства и график квадратичной функции (парабола). Построение графика квадратичной функции по точкам. Нахождение нулей квадратичной функции, множества значений, промежутков знакопостоянства, промежутков монотонности.

Обратная пропорциональность

Свойства функции . Гипербола.

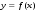
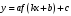
Графики функций. Преобразование графика функции для построения графиков функций вида .

Графики функций , , , .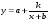

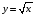
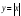
Последовательности и прогрессии

Числовая последовательность. Примеры числовых последовательностей. Бесконечные последовательности. Арифметическая прогрессия и её свойства. Геометрическая прогрессия. Формула общего члена и суммы n первых членов арифметической и геометрической прогрессий. Сходящаяся геометрическая прогрессия.

Решение текстовых задач

Задачи на все арифметические действия

Решение текстовых задач арифметическим способом. Использование таблиц, схем, чертежей, других средств представления данных при решении задачи.

Задачи на движение, работу и покупки

Анализ возможных ситуаций взаимного расположения объектов при их движении, соотношения объёмов выполняемых работ при совместной работе.

Задачи на части, доли, проценты

Решение задач на нахождение части числа и числа по его части. Решение задач на проценты и доли. Применение пропорций при решении задач.

Логические задачи

Решение логических задач. Решение логических задач с помощью графов, таблиц.

Основные методы решения текстовых задач: арифметический, алгебраический, перебор вариантов. Первичные представления о других методах решения задач (геометрические и графические методы).

Статистика и теория вероятностей

Статистика

Табличное и графическое представление данных, столбчатые и круговые диаграммы, графики, применение диаграмм и графиков для описания зависимостей реальных величин, извлечение информации из таблиц, диаграмм и графиков. Описательные статистические показатели числовых наборов: среднее арифметическое, медиана, наибольшее и наименьшее значения. Меры рассеивания: размах, дисперсия и стандартное отклонение.

Случайная изменчивость. Изменчивость при измерениях. Решающие правила. Закономерности в изменчивых величинах.

Случайные события

Случайные опыты (эксперименты), элементарные случайные события (исходы). Вероятности элементарных событий. События в случайных экспериментах и благоприятствующие элементарные события. Вероятности случайных событий. Опыты с равновозможными элементарными событиями. Классические вероятностные опыты с использованием монет, кубиков. Представление событий с помощью диаграмм Эйлера. Противоположные события, объединение и пересечение событий. Правило сложения вероятностей. Случайный выбор. Представление эксперимента в виде дерева. Независимые события. Умножение вероятностей независимых событий. Последовательные независимые испытания. Представление о независимых событиях в жизни.

Элементы комбинаторики

Правило умножения, перестановки, факториал числа. Сочетания и число сочетаний. Формула числа сочетаний. Треугольник Паскаля. Опыты с большим числом равновозможных элементарных событий. Вычисление вероятностей в опытах с применением комбинаторных формул. Испытания Бернулли. Успех и неудача. Вероятности событий в серии испытаний Бернулли.

Случайные величины

Знакомство со случайными величинами на примерах конечных дискретных случайных величин. Распределение вероятностей. Математическое ожидание. Свойства математического ожидания. Понятие о законе больших чисел. Измерение вероятностей. Применение закона больших чисел в социологии, страховании, в здравоохранении, обеспечении безопасности населения в чрезвычайных ситуациях.

Геометрия

Геометрические фигуры

Фигуры в геометрии и в окружающем мире

Геометрическая фигура. Формирование представлений о метапредметном понятии «фигура».

Точка, линия, отрезок, прямая, луч, ломаная, плоскость, угол, биссектриса угла и её свойства, виды углов, многоугольники, круг.

Осевая симметрия геометрических фигур. Центральная симметрия геометрических фигур.

Многоугольники

Многоугольник, его элементы и его свойства. Распознавание некоторых многоугольников. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

Треугольники. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренный треугольник, его свойства и признаки. Равносторонний треугольник. Прямоугольный, остроугольный, тупоугольный треугольники. Внешние углы треугольника. Неравенство треугольника.

Четырёхугольники. Параллелограмм, ромб, прямоугольник, квадрат, трапеция, равнобедренная трапеция. Свойства и признаки параллелограмма, ромба, прямоугольника, квадрата.

Окружность, круг

Их элементы и свойства; центральные и вписанные углы. Касательная и секущая к окружности, их свойства. Вписанные и описанные окружности для треугольников, четырёхугольников, правильных многоугольников.

Геометрические фигуры в пространстве (объёмные тела)

Многогранник и его элементы. Названия многогранников с разным положением и количеством граней. Первичные представления о пирамиде, параллелепипеде, призме, сфере, шаре, цилиндре, конусе, их элементах и простейших свойствах.

Отношения

Равенство фигур

Свойства равных треугольников. Признаки равенства треугольников.

Параллельно­сть прямых

Признаки и свойства параллельных прямых. Аксиома параллельности Евклида. Теорема Фалеса.

Перпендикулярные прямые

Прямой угол. Перпендикуляр к прямой. Наклонная, проекция. Серединный перпендикуляр к отрезку. Свойства и признаки перпендикулярности.

Подобие

Пропорциональные отрезки, подобие фигур. Подобные треугольники. Признаки подобия.

Взаимное расположение прямой и окружности, двух окружностей.

Измерения и вычисления

Величины

Понятие величины. Длина. Измерение длины. Единицы измерения длины. Величина угла. Градусная мера угла.

Понятие о площади плоской фигуры и её свойствах. Измерение площадей. Единицы измерения площади.

Представление об объёме и его свойствах. Измерение объёма. Единицы измерения объёмов.

Измерения и вычисления

Инструменты для измерений и построений; измерение и вычисление углов, длин (расстояний), площадей. Тригонометрические функции острого угла в прямоугольном треугольнике Тригонометрические функции тупого угла. Вычисление элементов треугольников с использованием тригонометрических соотношений. Формулы площади треугольника, параллелограмма и его частных видов, формулы длины ок­ружности и площади круга. Сравнение и вычисление площадей. Теорема Пифагора. Теорема синусов. Теорема косинусов.

Расстояния

Расстояние между точками. Расстояние от точки до прямой. Расстояние между фигурами.

Геометрические построения

Геометрические построения для иллюстрации свойств геометрических фигур.

Инструменты для построений: циркуль, линейка, угольник. Простейшие построения циркулем и линейкой: построение биссектрисы угла, перпендикуляра к прямой, угла, равного данному,

Построение треугольников по трём сторонам, двум сторонам и углу между ними, стороне и двум прилежащим к ней углам.

Деление отрезка в данном отношении.

Геометрические преобразования

Преобразования

Понятие преобразования. Представление о метапредметном понятии «преобразование». Подобие.

Движения

Осевая и центральная симметрия, поворот и параллельный перенос. Комбинации движений на плоскости и их свойства.

Векторы и координаты на плоскости

Векторы

Понятие вектора, действия над векторами, использование векторов в физике, разложение вектора на составляющие, скалярное произведение.

Координаты

Основные понятия, координаты вектора, расстояние между точками. Координаты середины отрезка. Уравнения фигур.

Применение векторов и координат для решения простейших геометрических задач.

История математики

Возникновение математики как науки, этапы её развития. Основные разделы математики. Выдающиеся математики и их вклад в развитие науки.

Бесконечность множества простых чисел. Числа и длины отрезков. Рациональные числа. Потребность в иррациональных числах. Школа Пифагора

Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рождение буквенной символики. П.Ферма, Ф. Виет, Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений степеней, больших четырёх. Н. Тарталья, Дж. Кардано, Н.Х. Абель, Э.Галуа.

Появление метода координат, позволяющего переводить геометрические объекты на язык алгебры. Появление графиков функций. Р. Декарт, П. Ферма. Примеры различных систем координат.

Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске. Сходимость геометрической прогрессии.

Истоки теории вероятностей: страховое дело, азартные игры. П. Ферма, Б.Паскаль, Я. Бернулли, А.Н.Колмогоров.

От земледелия к геометрии. Пифагор и его школа. Фалес, Архимед. Платон и Аристотель. Построение правильных многоугольников. Триссекция угла. Квадратура круга. Удвоение куба. История числа π. Золотое сечение. «Начала» Евклида. Л Эйлер, Н.И.Лобачевский. История пятого постулата.

Геометрия и искусство. Геометрические закономерности окружающего мира.

Астрономия и геометрия. Что и как узнали Анаксагор, Эратосфен и Аристарх о размерах Луны, Земли и Солнца. Расстояния от Земли до Луны и Солнца. Измерение расстояния от Земли до Марса.

Роль российских учёных в развитии математики: Л.Эйлер. Н.И.Лобачевский, П.Л.Чебышев, С. Ковалевская, А.Н.Колмогоров.

Математика в развитии России: Петр I, школа математических и навигацких наук, развитие российского флота, А.Н.Крылов. Космическая программа и М.В.Келдыш.

VI. Планируемые результаты:

В результате реализации Рабочей программы по математике для основной школы Выпускник научится в 5-6 классах Оперировать на базовом уровне¹ понятиями: множество, элемент множества, подмножество, принадлежность;

• задавать множества перечислением их элементов;

• находить пересечение, объединение, подмножество в простейших ситуациях

В повседневной жизни и при изучении других предметов:

• распознавать логически некорректные высказывания

Числа

• Оперировать на базовом уровне понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число;

• использовать свойства чисел и правила действий с рациональными числами при выполнении вычислений;

• использовать признаки делимости на 2, 5, 3, 9, 10 при выполнении вычислений и решении несложных задач;

• выполнять округление рациональных чисел в соответствии с правилами;

• сравнивать рациональные числа.

В повседневной жизни и при изучении других предметов:

• оценивать результаты вычислений при решении практических задач;

• выполнять сравнение чисел в реальных ситуациях;

• составлять числовые выражения при решении практических задач и задач из других учебных предметов

Статистика и теория вероятностей

• Представлять данные в виде таблиц, диаграмм,

• читать информацию, представленную в виде таблицы, диаграммы,.

Текстовые задачи

• Решать несложные сюжетные задачи разных типов на все арифметические действия;

• строить модель условия задачи (в виде таблицы, схемы, рисунка), в которой даны значения двух из трёх взаимосвязанных величин, с целью поиска решения задачи;

• осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию;

• составлять план решения задачи;

• выделять этапы решения задачи;

• интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;

• знать различие скоростей объекта в стоячей воде, против течения и по течению реки;

• решать задачи на нахождение части числа и числа по его части;

• решать задачи разных типов (на работу, на покупки, на движение), связывающих три величины, выделять эти величины и отношения между ними;

• находить процент от числа, число по проценту от него, находить процентное отношение двух чисел, находить процентное снижение или процентное повышение величины;

• решать несложные логические задачи методом рассуждений.

В повседневной жизни и при изучении других предметов:

• выдвигать гипотезы о возможных предельных значениях искомых величин в задаче (делать прикидку)

Наглядная геометрия

Геометрические фигуры

• Оперировать на базовом уровне понятиями: фигура, точка, отрезок, прямая, луч, ломаная, угол, многоугольник, треугольник и четырёхугольник, прямоугольник и квадрат, окружность и круг, прямоугольный параллелепипед, куб, шар. Изображать изучаемые фигуры от руки и с помощью линейки и циркуля.

В повседневной жизни и при изучении других предметов:

• решать практические задачи с применением простейших свойств фигур.

Измерения и вычисления

• выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;

• вычислять площади прямоугольников.

В повседневной жизни и при изучении других предметов:

• вычислять расстояния на местности в стандартных ситуациях, площади прямоугольников;

• выполнять простейшие построения и измерения на местности, необходимые в реальной жизни

История математики

• описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;

• знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей

Выпускник получит возможность научиться в 5-6 классах (для обеспечения возможности успешного продолжения образования на базовом и углублённом уровнях)

Элементы теории множеств и математической логики

• Оперировать² понятиями: множество, характеристики множества, элемент множества, пустое, конечное и бесконечное множество, подмножество, принадлежность,

• определять принадлежность элемента множеству, объединению и пересечению множеств;

задавать множество с помощью перечисления элементов, словесного описания

В повседневной жизни и при изучении других предметов:

• распознавать логически некорректные высказывания;

• строить цепочки умозаключений на основе использования правил логики

Числа

• Оперировать понятиями: натуральное число, множество натуральных чисел, целое число, множество целых чисел, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число, множество рациональных чисел, геометрическая интерпретация натуральных, целых, рациональных;

• понимать и объяснять смысл позиционной записи натурального числа;

• выполнять вычисления, в том числе с использованием приёмов рациональных вычислений, обосновывать алгоритмы выполнения действий;

• использовать признаки делимости на 2, 4, 8, 5, 3, 6, 9, 10, 11, суммы и произведения чисел при выполнении вычислений и решении задач, обосновывать признаки делимости;

• выполнять округление рациональных чисел с заданной точностью;

• упорядочивать числа, записанные в виде обыкновенных и десятичных дробей;

• находить НОД и НОК чисел и использовать их при решении задач.

• оперировать понятием модуль числа, геометрическая интерпретация модуля числа.

В повседневной жизни и при изучении других предметов:

• применять правила приближенных вычислений при решении практических задач и решении задач других учебных предметов;

• выполнять сравнение результатов вычислений при решении практических задач, в том числе приближенных вычислений;

• составлять числовые выражения и оценивать их значения при решении практических задач и задач из других учебных предметов;

Уравнения и неравенства Этого в содержании нет

• Оперировать понятиями: равенство, числовое равенство, уравнение, корень уравнения, решение уравнения, числовое неравенство

Статистика и теория вероятностей

• Оперировать понятиями: столбчатые и круговые диаграммы, таблицы данных, среднее арифметическое,

• извлекать, информацию, представленную в таблицах, на диаграммах;

• составлять таблицы, строить диаграммы на основе данных.

В повседневной жизни и при изучении других предметов:

• извлекать, интерпретировать и преобразовывать информацию, представленную в таблицах и на диаграммах, отражающую свойства и характеристики реальных процессов и явлений

Текстовые задачи

• Решать простые и сложные задачи разных типов, а также задачи повышенной трудности;

• использовать разные краткие записи как модели текстов сложных задач для построения поисковой схемы и решения задач;

• знать и применять оба способа поиска решения задач (от требования к условию и от условия к требованию);

• моделировать рассуждения при поиске решения задач с помощью граф-схемы;

• выделять этапы решения задачи и содержание каждого этапа;

• интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;

• анализировать всевозможные ситуации взаимного расположения двух объектов и изменение их характеристик при совместном движении (скорость, время, расстояние) при решении задач на движение двух объектов как в одном, так и в противоположных направлениях;

• исследовать всевозможные ситуации при решении задач на движение по реке, рассматривать разные системы отсчёта;

• решать разнообразные задачи «на части»,

• решать и обосновывать свое решение задач (выделять математическую основу) на нахождение части числа и числа по его части на основе конкретного смысла дроби;

• осознавать и объяснять идентичность задач разных типов, связывающих три величины (на работу, на покупки, на движение); выделять эти величины и отношения между ними, применять их при решении задач, конструировать собственные задачи указанных типов.

В повседневной жизни и при изучении других предметов:

• выделять при решении задач характеристики рассматриваемой в задаче ситуации, отличные от реальных (те, от которых абстрагировались), конструировать новые ситуации с учётом этих характеристик, в частности, при решении задач на концентрации, учитывать плотность вещества;

• решать и конструировать задачи на основе рассмотрения реальных ситуаций, в которых не требуется точный вычислительный результат;

• решать задачи на движение по реке, рассматривая разные системы отсчета

Наглядная геометрия

Геометрические фигуры

• Оперировать понятиями фигура, точка, отрезок, прямая, луч, ломаная, угол, многоугольник, треугольник и четырёхугольник, прямоугольник и квадрат, окружность и круг, прямоугольный параллелепипед, куб, призма, шар, пирамида, цилиндр, конус;

• извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах

• изображать изучаемые фигуры от руки и с помощью линейки, циркуля, компьютерных инструментов.

В повседневной жизни и при изучении других предметов:

• решать практические задачи с применением простейших свойств фигур

Измерения и вычисления

• выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;

• вычислять площади прямоугольников, квадратов, объёмы прямоугольных параллелепипедов, кубов.

В повседневной жизни и при изучении других предметов:

• вычислять расстояния на местности в стандартных ситуациях, площади участков прямоугольной формы, объёмы комнат;

• выполнять простейшие построения на местности, необходимые в реальной жизни;

• оценивать размеры реальных объектов окружающего мира

История математики

• Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей

Выпускник научится в 7-9 классах (для использования в повседневной жизни и обеспечения возможности успешного продолжения образования на базовом уровне)

Элементы теории множеств и математической логики

• Оперировать на базовом уровне³ понятиями: множество, элемент множества, подмножество, принадлежность;

• задавать множества перечислением их элементов;

• находить пересечение, объединение, подмножество в простейших ситуациях;

• оперировать на базовом уровне понятиями: определение, аксиома, теорема, доказательство;

• приводить примеры и контрпримеры для подтвержнения своих высказываний

В повседневной жизни и при изучении других предметов:

• использовать графическое представление множеств для описания реальных процессов и явлений, при решении задач других учебных предметов

Числа

• Оперировать на базовом уровне понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанная дробь, рациональное число, арифметический квадратный корень;

• использовать свойства чисел и правила действий при выполнении вычислений;

• использовать признаки делимости на 2, 5, 3, 9, 10 при выполнении вычислений и решении несложных задач;

• выполнять округление рациональных чисел в соответствии с правилами;

• оценивать значение квадратного корня из положительного целого числа;

• распознавать рациональные и иррациональные числа;

• сравнивать числа.

В повседневной жизни и при изучении других предметов:

• оценивать результаты вычислений при решении практических задач;

• выполнять сравнение чисел в реальных ситуациях;

• составлять числовые выражения при решении практических задач и задач из других учебных предметов

Тождественные преобразования

• Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем, степени с целым отрицательным показателем;

• выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые;

• использовать формулы сокращенного умножения (квадрат суммы, квадрат разности, разность квадратов) для упрощения вычислений значений выражений;

• выполнять несложные преобразования дробно-линейных выражений и выражений с квадратными корнями .

В повседневной жизни и при изучении других предметов:

• понимать смысл записи числа в стандартном виде;

• оперировать на базовом уровне понятием «стандартная запись числа»

Уравнения и неравенства

• Оперировать на базовом уровне понятиями: равенство, числовое равенство, уравнение, корень уравнения, решение уравнения, числовое неравенство, неравенство, решение неравенства;

• проверять справедливость числовых равенств и неравенств;

• решать линейные неравенства и несложные неравенства, сводящиеся к линейным;

• решать системы несложных линейных уравнений, неравенств;

• проверять, является ли данное число решением уравнения (неравенства);

• решать квадратные уравнения по формуле корней квадратного уравнения;

• изображать решения неравенств и их систем на числовой прямой.

В повседневной жизни и при изучении других предметов:

• составлять и решать линейные уравнения при решении задач, возникающих в других учебных предметах

Функции

• находить значение функции по заданному значению аргумента;

• находить значение аргумента по заданному значению функции в несложных ситуациях;

• определять положение точки по её координатам, координаты точки по её положению на координатной плоскости;

• по графику находить область определения, множество значений, нули функции, промежутки знакопостоянства, промежутки возрастания и убывания, наибольшее и наименьшее значения функции;

• строить график линейной функции;

• проверять, является ли данный график графиком заданной функции (линейной, квадратичной, обратной пропорциональности);

• определять приближённые значения координат точки пересечения графиков функций;

• оперировать на базовом уровне понятиями: последовательность, арифметическая прогрессия, геометрическая прогрессия;

• решать задачи на прогрессии, в которых ответ может быть получен непосредственным подсчётом без применения формул.

В повседневной жизни и при изучении других предметов:

• использовать графики реальных процессов и зависимостей для определения их свойств (наибольшие и наименьшие значения, промежутки возрастания и убывания, области положительных и отрицательных значений и т.п.);

• использовать свойства линейной функции и ее график при решении задач из других учебных предметов

Статистика и теория вероятностей поставить после текстовых задач, как с содержании.

• Иметь представление о статистических характеристиках, вероятности случайного события, комбинаторных задачах;

• решать простейшие комбинаторные задачи методом прямого и организованного перебора;

• представлять данные в виде таблиц, диаграмм, графиков;

• читать информацию, представленную в виде таблицы, диаграммы, графика;

• определять основные статистические характеристики числовых наборов;

• оценивать вероятность события в простейших случаях;

• иметь представление о роли закона больших чисел в массовых явлениях.

В повседневной жизни и при изучении других предметов:

• оценивать количество возможных вариантов методом перебора;

• иметь представление о роли практически достоверных и маловероятных событий;

• сравнивать основные статистические характеристики, полученные в процессе решения прикладной задачи, изучения реального явления;

• оценивать вероятность реальных событий и явлений в несложных ситуациях

Текстовые задачи

• Решать несложные сюжетные задачи разных типов на все арифметические действия;

• строить модель условия задачи (в виде таблицы, схемы, рисунка или уравнения), в которой даны значения двух из трёх взаимосвязанных величин, с целью поиска решения задачи;

• осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию;

• составлять план решения задачи;

• выделять этапы решения задачи;

• интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;

• знать различие скоростей объекта в стоячей воде, против течения и по течению реки;

• решать задачи на нахождение части числа и числа по его части;

• решать задачи разных типов (на работу, на покупки, на движение), связывающих три величины, выделять эти величины и отношения между ними;

• находить процент от числа, число по проценту от него, находить процентное снижение или процентное повышение величины;

• решать несложные логические задачи методом рассуждений.

В повседневной жизни и при изучении других предметов:

• выдвигать гипотезы о возможных предельных значениях искомых в задаче величин (делать прикидку)

Геометрические фигуры

• Оперировать на базовом уровне понятиями геометрических фигур;

• извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;

• применять для решения задач геометрические факты, если условия их применения заданы в явной форме;

• решать задачи на нахождение геометрических величин по образцам или алгоритмам.

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания

Отношения

• Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция.

В повседневной жизни и при изучении других предметов:

• использовать отношения для решения простейших задач, возникающих в реальной жизни

Измерения и вычисления

• Выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;

• применять формулы периметра, площади и объёма, площади поверхности отдельных многогранников при вычислениях, когда все данные имеются в условии;

• применять теорему Пифагора, базовые тригонометрические соотношения для вычисления длин, расстояний, площадей в простейших случаях.

В повседневной жизни и при изучении других предметов:

• вычислять расстояния на местности в стандартных ситуациях, площади в простейших случаях, применять формулы в простейших ситуациях в повседневной жизни

Геометрические построения

• Изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.

В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни

Геометрические преобразования

• Строить фигуру, симметричную данной фигуре относительно оси и точки.

В повседневной жизни и при изучении других предметов:

• распознавать движение объектов в окружающем мире;

• распознавать симметричные фигуры в окружающем мире

Векторы и координаты на плоскости

• Оперировать на базовом уровне понятиями вектор, сумма векторов, произведение вектора на число, координаты на плоскости;

• определять приближённо координаты точки по её изображению на координатной плоскости.

В повседневной жизни и при изучении других предметов:

• использовать векторы для решения простейших задач на определение скорости относительного движения

История математики

• Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;

• знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;

• понимать роль математики в развитии России

Методы математики

• Выбирать подходящий изученный метод для решении изученных типов математических задач;

• Приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.

VI1. Календарно-тематическое планирование по математике 5 класс (170 часов)

№ урока	Перечень разделов, тем	Кол-во часов	Количество и темы контрольных работ	Дата проведения
	Натуральные числа и шкалы	15	К.р. – 1
1	Обозначение натуральных чисел.	1
2	Обозначение натуральных чисел. Чтение и запись многозначных чисел.	1
3	Обозначение натуральных чисел. Упражнение в записи многозначных чисел.	1
4	Отрезок. Длина отрезка. Треугольник. Многоугольник.	1
5	Отрезок. Длина отрезка. Треугольник. Измерение и построение отрезков.	1
6	Повторение по теме «Отрезок. Длина отрезка. Треугольник.	1
7	Плоскость, прямая, луч.	1
8	Плоскость, прямая, луч. Решение задач на построение.	1
9	Шкалы и координаты. Координатный луч.	1
10	Шкалы и координаты. Решение задач на построение.	1
11	Шкалы и координаты. Повторение по теме «Координатный луч»	1
12	Меньше или больше.	1
13	Меньше или больше. Сравнение натуральных чисел.	1
14	Меньше или больше. Повторение по теме «Натуральные числа»	1
15	Контрольная работа по теме	1	«Натуральные числа и шкалы» В.И. Жохов стр.22-25
	Сложение и вычитание натуральных чисел	21	К. р. – 2
16	Сложение натуральных чисел и его свойства.	1
17	Сложение натуральных чисел и его свойства. Решение выражений на сложение.	1
18	Сложение натуральных чисел и его свойства.	1
19	Сложение натуральных чисел и его свойства. Решение текстовых задач.	1
20	Сложение натуральных чисел и его свойства.	1
21	Вычитание. Вычитание натуральных чисел.	1
22	Вычитание. Решение выражений на вычитание.	1
23	Вычитание. Свойства вычитания.	1
24	Вычитание. Повторение по теме «Сложение и вычитание натуральных чисел».	1
25	Контрольная работа по теме	1	Сложение и вычитание натуральных чисел В.И. Жохов стр. 26- 27
26	Числовые и буквенные выражения.	1
27	Числовые и буквенные выражения.	1
28	Числовые и буквенные выражения. Решение числовых и буквенных выражений.	1
29	Буквенная запись свойств сложения и вычитания.	1
30	Буквенная запись свойств сложения и вычитания.	1
31	Буквенная запись свойств сложения и вычитания.	1
32	Уравнения.	1
33	Уравнения. Решение линейных уравнений.	1
34	Уравнения. Решение линейных уравнений.	1
35	Уравнения. Повторение по теме «Числовые и буквенные выражения»	1
36	Контрольная работа по теме	1	Числовые и буквенные выражения. Уравнения. В. И. Жохов стр. 30-31
	Умножение и деление натуральных чисел	27	К.р. – 2
37	Умножение натуральных чисел и его свойства.	1
38	Умножение натуральных чисел и его свойства.	1
39	Умножение натуральных чисел и его свойства.	1
40	Умножение натуральных чисел и его свойства.	1
41	Умножение натуральных чисел и его свойства.	1
42	Деление.	1
43	Деление. Деление натуральных чисел.	1
44	Деление. Свойства деления натуральных чисел.	1
45	Деление. Решение числовых выражений.	1
46	Деление. Порядок действий в выражениях.	1
47	Деление. Решение выражений на деление.	1
48	Деление. Обобщение по теме «Деление натуральных чисел».	1
49	Деление с остатком.	1
50	Деление с остатком. Упражнение в делении натуральных чисел.	1
51	Деление с остатком.	1
52	Контрольная работа по теме	1	«Умножение и деление натуральных чисел». В.И. Жохов стр. 32-33
53	Упрощение выражений.	1
54	Упрощение выражений.	1
55	Упрощение выражений.	1
56	Упрощение выражений.	1
57	Упрощение выражений.	1
58	Порядок выполнения действий.	1
59	Порядок выполнения действий.	1
60	Порядок выполнения действий.	1
61	Квадрат и куб. Степень числа.	1
62	Квадрат и куб.	1
63	Контрольная работа по теме	1	«Порядок выполнения действий». В.И. Жохов стр. 34-35
	Площади и объемы.	12	К.р.-1
64	Формулы.	1
65	Формулы. Вычисления по формулам.	1
66	Площадь. Формула площади прямоугольника.	1
67	Площадь. Формула площади прямоугольника.	1
68	Единицы измерения площадей.	1
69	Единицы измерения площадей.	1
70	Единицы измерения площадей.	1
71	Прямоугольный параллелепипед.	1
72	Объемы. Объем прямоугольного параллелепипеда.	1
73	Объемы. Объем прямоугольного параллелепипеда.	1
74	Объемы. Объем прямоугольного параллелепипеда.	1
75	Контрольная работа по теме	1	«Площади и объемы» В.И. Жохов стр.36-39
	Обыкновенные дроби	23	К. р. -2
76	Окружность и круг.	1
77	Окружность и круг.	1
78	Доли. Обыкновенные дроби.	1
79	Доли. Обыкновенные дроби.	1
80	Доли. Обыкновенные дроби.	1
81	Доли. Обыкновенные дроби. Основные задачи на дроби.	1
82	Сравнение дробей.	1
83	Сравнение дробей.	1
84	Сравнение дробей.	1
85	Правильные и неправильные дроби.	1
86	Правильные и неправильные дроби.	1
87	Контрольная работа по теме	1	«Понятие обыкновенные дроби». В.И. Жохов стр. 40-43
88	Сложение и вычитание дробей с одинаковыми знаменателями.	1
89	Сложение и вычитание дробей с одинаковыми знаменателями.	1
90	Сложение и вычитание дробей с одинаковыми знаменателями.	1
91	Деление и дроби.	1
92	Деление и дроби.	1
93	Смешанные числа.	1
94	Смешанные числа.	1
95	Сложение и вычитание смешанных чисел.	1
96	Сложение и вычитание смешанных чисел.	1
97	Сложение и вычитание смешанных чисел.	1
98	Контрольная работа по теме	1	Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями. Сложение и вычитание смешанных чисел». В.И. Жохов стр. 44-47
	Десятичные дроби. Сложение и вычитание десятичных дробей.	13	К.р.- 1
99	Десятичная запись дробных чисел.	1
100	Десятичная запись дробных чисел.	1
101	Сравнение десятичных дробей.	1
102	Сравнение десятичных дробей.	1
103	Сравнение десятичных дробей.	1
104	Сложение и вычитание десятичных дробей.	1
105	Сложение и вычитание десятичных дробей.	1
106	Сложение и вычитание десятичных дробей.	1
107	Сложение и вычитание десятичных дробей.	1
108	Сложение и вычитание десятичных дробей. Решение текстовых задач.	1
109	Приближенные значения чисел. Округление чисел.	1
110	Приближенные значения чисел. Округление чисел.	1
111	Контрольная работа по теме	1	«Сложение и вычитание десятичных дробей». В.И. Жохов стр. 48-49
	Умножение и деление десятичных дробей	26	К.р. – 2
112	Умножение десятичных дробей на натуральные числа.	1
113	Умножение десятичных дробей на натуральные числа.	1
114	Умножение десятичных дробей на натуральные числа.	1
115	Деление десятичных дробей натуральные числа.	1
116	Деление десятичных дробей натуральные числа.	1
117	Деление десятичных дробей натуральные числа.	1
118	Деление десятичных дробей натуральные числа.	1
119	Деление десятичных дробей натуральные числа.	1
120	Контрольная работа по теме	1	«Умножение и деление десятичных дробей на натуральное число» В.И. Жохов стр. 50-51
121	Умножение десятичных дробей.	1
122	Умножение десятичных дробей.	1
123	Умножение десятичных дробей.	1
124	Умножение десятичных дробей.	1
125	Умножение десятичных дробей. Решение текстовых задач.	1
126	Деление десятичных дробей.	1
127	Деление десятичных дробей.	1
128	Деление десятичных дробей.	1
129	Деление десятичных дробей.	1
130	Деление десятичных дробей.	1
131	Деление десятичных дробей.	1
132	Деление десятичных дробей.	1
133	Среднее арифметическое.	1
134	Среднее арифметическое.	1
135	Среднее арифметическое.	1
136	Среднее арифметическое.	1
137	Контрольная работа по теме	1	«Умножение и деление десятичных дробей». В.И. Жохов стр. 52-53
	Инструменты для вычислений и измерений	17	К.р. – 2
138	Микрокалькулятор.	1
139	Микрокалькулятор.	1
140	Проценты.	1
141	Проценты.	1
142	Проценты. Основные задачи на проценты.	1
143	Проценты. Решение текстовых задач .	1
144	Проценты. Повторение по теме «Проценты»	1
145	Контрольная работа по теме	1	«Проценты». В.И. Жохов стр. 54-55
146	Угол. Прямой и развернутый угол. Чертежный треугольник. Величина (градусная мера) угла.	1
147	Угол. Прямой и развернутый угол. Чертежный треугольник.	1
148	Угол. Прямой и развернутый угол. Чертежный треугольник.	1
149	Измерение углов. Транспортир.	1
150	Измерение углов. Транспортир.	1
151	Измерение углов. Транспортир. Построение угла заданной величины.	1
152	Круговые диаграммы.	1
153	Круговые диаграммы. Примеры таблиц и диаграмм.	1
154	Контрольная работа по теме	1	«Углы. Измерение углов». В.И. Жохов стр.56-57
	Итоговое повторение	13
155	Повторение по теме «Натуральные числа и шкалы»	1
156	Повторение по теме «Сложение и вычитание натуральных чисел»	1
157	Повторение по теме «Порядок действий в выражениях»	1
158	Повторение по теме «Площади и объемы»	1
159	Повторение по теме « Обыкновенные дроби»	1
160	Повторение по теме « Свойства дробей»	1
161	Повторение по теме « Сложение и вычитание десятичных дробей»	1
162	Контрольная работа итоговая	1	В.И. Жохов стр. 58-61
163	Повторение по теме « Округление десятичных дробей»	1
164	Повторение по теме « Действия с десятичными дробями»	1
165	Повторение по теме « Умножение и деление десятичных дробей»	1
166	Повторение по теме «Решение выражений на упрощение»	1
167	Повторение по теме « Порядок действий в выражениях»	1
168	Повторение по теме «Построение углов»	1
169	Повторение по теме « Решение выражений»	1
170	Повторение по теме « Упрощение выражений»	1
	Итого	170	14

Календарно – тематическое планирование учебного материала по математике 6 класс ( 170 часов ) № урока Перечень разделов, тем Кол-во часов Количество и темы контрольных работ Дата проведения Делимость чисел . 20 К.р.-1 1 Делители и кратные. 1 2 Делители и кратные. Упражнение в нахождении делителей числа. 1 3 Делители и кратные. Решение задач на нахождение делителей и кратных числа. 1 4 Признаки делимости на 10, на 5 и на 2. 1 5 Признаки делимости на 10, на 5 и на 2. Нахождение делителей по признаку. 1 6 Признаки делимости на 10, на 5 и на 2. Решение задач на нахождение делителей по признаку. 1 7 Признаки делимости на 9 и на 3. 1 8 Признаки делимости на 9 и на 3. Применение признаков при решении задач. 1 9 Простые и составные числа. 1 10 Простые и составные числа. Нахождение простых и составных чисел. 1 11 Разложение на простые множители. 1 12 Разложение на простые множители. Упражнение в разложении на простые множители. 1 13 Наибольший общий делитель. Взаимно простые числа. 1 14 Наибольший общий делитель. Взаимно простые числа . Решение задач на нахождение НОД 1 15 Наибольший общий делитель. Взаимно простые числа. Решение задач на нахождение НОД 1 16 Наименьшее общее кратное. 1 17 Наименьшее общее кратное. Решение задач на нахождение НОК. 1 18 Наименьшее общее кратное. Нахождение НОД и НОК чисел. 1 19 Наименьшее общее кратное. Повторение «Делимость чисел». 1 20 Контрольная работа 1 « Делимость чисел» В.И. Жохов стр.4-7 Сложение и вычитание дробей с разными знаменателями. 22 К.р.-2 21 Основное свойство дроби. 1 22 Основное свойство дроби. Решение упражнений с помощью свойства. 1 23 Сокращение дробей. 1 24 Сокращение дробей. Решение упражнений на сокращение дробей. 1 25 Сокращение дробей. Решение упражнений на сокращение дробей. 1 26 Приведение дробей к общему знаменателю. 1 27 Приведение дробей к общему знаменателю. Решение выражений. 1 28 Приведение дробей к общему знаменателю. Решение выражений. 1 29 Сравнение, сложение и вычитание дробей с разными знаменателями. 1 30 Сравнение, сложение и вычитание дробей с разными знаменателями. Решение выражений на сложение. 1 31 Сравнение, сложение и вычитание дробей с разными знаменателями. Решение выражений на вычитание. 1 32 Сравнение, сложение и вычитание дробей с разными знаменателями. 1 33 Сравнение, сложение и вычитание дробей с разными знаменателями. Повторение сравнение дробей. 1 34 Сравнение, сложение и вычитание дробей с разными знаменателями. 1 35 Контрольная работа 1 «Сравнение, сложение и вычитание дробей с разными знаменателями». В.И. Жохов стр. 8-11 36 Сложение и вычитание смешанных чисел. 1 37 Сложение и вычитание смешанных чисел. 1 38 Сложение и вычитание смешанных чисел. Решение выражений на действия смешанных чисел. 1 39 Сложение и вычитание смешанных чисел. Упражнение в сложении и вычитании смешанных чисел. 1 40 Сложение и вычитание смешанных чисел. Упражнение в сложении и вычитании смешанных чисел. 1 41 Повторение по теме «Сложение и вычитание смешанных чисел». 1 42 Контрольная работа 1 « Сложение и вычитание смешанных чисел». В.И. Жохов стр. 12-15 Умножение и деление обыкновенных дробей. 32 К.р.-3 43 Умножение дробей. 1 44 Умножение дробей. Умножение смешанных чисел. 1 45 Умножение дробей. Решение упражнений на умножение дробей. 1 46 Умножение дробей. Решение упражнений на умножение дробей. 1 47 Повторение материала «Сложение и вычитание дробей с разными знаменателями» 1 48 Нахождение дроби от числа. 1 49 Нахождение дроби от числа. Решение задач на нахождение дроби от числа. 1 50 Нахождение дроби от числа. Упражнение на нахождение дроби от числа. 1 51 Нахождение дроби от числа. Решение выражений на нахождение дроби от числа. 1 52 Применение распределительного свойства умножения. 1 53 Применение распределительного свойства умножения. Решение задач на применение свойств умножения. 1 54 Применение распределительного свойства умножения. Решение упражнений на применение свойств. 1 55 Применение распределительного свойства умножения. Решение выражений , порядок действий. 1 56 Применение распределительного свойства умножения. Повторение по теме « Умножение дробей» 1 57 Контрольная работа 1 «Умножение дробей» В.И. Жохов стр.16-19 58 Взаимно обратные числа. 1 59 Взаимно обратные числа. Нахождение взаимно обратных чисел. 1 60 Деление. 1 61 Деление. Решение упражнений на деление. 1 62 Деление. Решение выражений на деление. 1 63 Деление. Решение уравнений на деление. 1 64 Деление. Повторение по теме «Взаимно обратные числа». 1 65 Контрольная работа 1 «Деление» В.И. Жохов стр. 20-22 66 Нахождение числа по его дроби. 1 67 Нахождение числа по его дроби. Решение задач на нахождение числа по его дроби. 1 68 Нахождение числа по его дроби. Решение задач на нахождение числа по его дроби. 1 69 Нахождение числа по его дроби. Упражнение в нахождении числа по его дроби. 1 70 Нахождение числа по его дроби. Задачи на нахождение числа по его дроби. 1 71 Дробные выражения. 1 72 Дробные выражения. Решение дробных выражений. 1 73 Дробные выражения. Решение дробных выражений. 1 74 Контрольная работа 1 « Дробные выражения» В.И. Жохов стр. 24-27 Отношения и пропорции. 19 К.р.-2 75 Отношения. 1 76 Отношения. Решение задач на нахождение отношений. 1 77 Отношения. Решение задач на нахождение отношений. 1 78 Отношения. Решение упражнений на составление отношений. 1 79 Отношения. Решение упражнений на составление отношений. 1 80 Пропорции. 1 81 Пропорции. Задачи на составление пропорции. 1 82 Повторение . Решение задач по теме «отношения и пропорции.» 1 83 Прямая и обратная пропорциональные зависимости. 1 84 Прямая и обратная пропорциональные зависимости. Решение задач на применение зависимостей. 1 85 Прямая и обратная пропорциональные зависимости. Решение задач на применение зависимостей. 1 86 Контрольная работа 1 « Отношения и пропорции» В.И. Жохов стр.28-31 87 Масштаб. 1 88 Масштаб. Решение задач на нахождение масштаба. 1 89 Длина окружности и площадь круга. 1 90 Длина окружности и площадь круга. Решение задач на нахождение длины окружности и площади круга. 1 91 Шар . 1 92 Шар. Решение задач на построение. 1 93 Контрольная работа 1 «Масштаб. Длина окружности и площадь круга» В.И. Жохов стр. 32-33 Положительные и отрицательные числа 13 К.р.-1 94 Координаты на прямой. 1 95 Координаты на прямой. Решение упражнений на построение точек на прямой. 1 96 Координаты на прямой. . Решение упражнений на построение точек на прямой. 1 97 Противоположные числа 1 98 Противоположные числа. Нахождение противоположных чисел. 1 99 Модуль числа. 1 100 Модуль числа. Решение упражнений на нахождение модуля числа. 1 101 Сравнение чисел. 1 102 Сравнение чисел. Решение задач на сравнение чисел. 1 103 Сравнение чисел. Решение задач на сравнение чисел 1 104 Изменение величин. 1 105 Изменение величин. Повторение по теме « Координаты на прямой». 1 106 Контрольная работа 1 «Координаты на прямой» В.И. Жохов стр.34-37 Сложение и вычитание положительных и отрицательных чисел. 11 К.р.-1 107 Сложение чисел с помощью координатной прямой. 1 108 Сложение чисел с помощью координатной прямой. Решение упражнений по сложению чисел. 1 109 Сложение отрицательных чисел. 1 110 Сложение отрицательных чисел. Решение выражений на сложение чисел . 1 111 Сложение чисел с разными знаками. 1 112 Сложение чисел с разными знаками. Решение выражений. 1 113 Сложение чисел с разными знаками. Решение выражений. 1 114 Вычитание. 1 115 Вычитание. Решение упражнений на вычитание. 1 116 Вычитание. Решение упражнений на вычитание. 1 117 Контрольная работа 1 « Сложение и вычитание положительных и отрицательных чисел» В.И. Жохов стр.38-41 Умножение и деление положительных и отрицательных чисел. 12 К.р.-1 118 Умножение. 1 119 Умножение. Решение упражнений на умножение. 1 120 Умножение. Решение упражнений на умножение. 1 121 Деление. 1 122 Деление. Решение упражнений на деление. 1 123 Деление. Решение упражнений на деление. 1 124 Рациональные числа. 1 125 Рациональные числа. 1 126 Контрольная работа 1 « Умножение и деление положительных и отрицательных чисел» В.И. Жохов стр. 42-45 127 Свойства действий с рациональными числами. 1 128 Свойства действий с рациональными числами. Применение свойств действий при решении выражений 1 129 Свойства действий с рациональными числами. Применение свойств действий при решении выражений 1 Решение уравнений. 15 К.р.- 2 130 Раскрытие скобок. 1 131 Раскрытие скобок. Решение выражений на раскрытие скобок. 1 132 Повторение по теме «Сложение и вычитание положительных и отрицательных чисел» . 1 133 Повторение по теме « Умножение и деление положительных и отрицательных чисел». 1 134 Коэффициент. 1 135 Коэффициент. Нахождение коэффициента. 1 136 Подобные слагаемые. 1 137 Подобные слагаемые. Упрощение выражений на приведение подобных слагаемых. 1 138 Подобные слагаемые. Упрощение выражений на приведение подобных слагаемых. 1 139 Контрольная работа 1 «Раскрытие скобок. Подобные слагаемые» В.И. Жохов стр. 46-49 140 Решение уравнений. 1 141 Решение уравнений. Упражнение в решении уравнений. 1 142 Решение уравнений. Нахождение корней уравнения. 1 143 Решение уравнений. Нахождение корней уравнения. 1 144 Контрольная работа 1 «Решение уравнений» В.И. Жохов стр. 50-53 Координаты на плоскости. 13 К.р.-2 145 Перпендикулярные прямые. 1 146 Перпендикулярные прямые. Решение задач на построение прямых . 1 147 Параллельные прямые. 1 148 Параллельные прямые. Решение задач на построение прямых . 1 149 Координатная плоскость. 1 150 Координатная плоскость. Построение точек на плоскости. 1 151 Координатная плоскость. Построение точек на плоскости. 1 152 Столбчатые диаграммы. 1 153 Столбчатые диаграммы. Построение диаграмм. 1 154 Графики. 1 155 Графики. Решение задач с помощью графика. 1 156 Графики. Решение задач с помощью графика. 1 157 Контрольная работа 1 « Координаты на плоскости». В.И. Жохов стр. 54-55 Повторение 13 158 Повторение по теме «Наибольший общий делитель» 1 159 Повторение по теме « Наименьшее общее кратное» 1 160 Повторение по теме «Сокращение дробей» 1 161 Повторение по теме « Приведение дробей к общему знаменателю» 1 162 Повторение по теме « Сравнение. Сложение и вычитание дробей с разными знаменателями» 1 163 Повторение по теме « Сложение и вычитание смешанных чисел» 1 164 Повторение по теме « Умножение дробей. 1 165 Итоговая контрольная работа 1 В.И. Жохов стр. 56-61 166 Повторение по теме « Деление. 1 167 Повторение по теме « Дробные выражения. 1 168 Повторение по теме « Пропорции. 1 169 Повторение по теме «Длина окружности и площадь круга. 1 170 Повторение по теме « Положительные и отрицательные числа. 1 Итого 170 15

Календарно – тематическое планирование учебного материала по алгебре 7 класс (102 часа)

№ урока	Перечень разделов, тем	Количество часов	Количество и темы контрольных работ	Дата проведения
	1.Выражения, тождества, уравнения.	22	К.р.-2
1	Выражения. Числовые выражения.	1
2	Выражения. Нахождение значения выражения .	1
3	Выражения. Выражения с переменными.	1
4	Выражения. Решение выражения с переменными.	1
5	Выражения. Сравнение значений с переменными.	1
6	Преобразования выражений.	1
7	Преобразования выражений.	1
8	Преобразования выражений. Тождества.	1
9	Преобразования выражений. Тождественные преобразования выражений.	1
10	Контрольная работа по теме № 1	1	Выражения. Преобразование выражений Н.Г. Миндюк стр.162
11	Уравнения с одной переменной.	1
12	Уравнения с одной переменной. Линейное уравнение.	1
13	Уравнения с одной переменной. Решение линейных уравнений.	1
14	Уравнения с одной переменной. Решение линейных уравнений.	1
15	Уравнения с одной переменной. Решение задач с помощью уравнений.	1
16	Уравнения с одной переменной. Решение задач с помощью уравнений.	1
17	Уравнения с одной переменной. Решение линейных уравнений.	1
18	Статистические характеристики.	1
19	Статистические характеристики. Среднее арифметическое, размах и мода.	1
20	Статистические характеристики. Медиана как статистическая характеристика.	1
21	Статистические характеристики. Решение задач на нахождение размаха, моды и медианы.	1
22	Контрольная работа по теме №2	1	Уравнения с одной переменной Н.Г. Миндюк стр.162-163
	2. Функции.	11	К.р. – 1
23	Функции и их графики.	1
24	Функции и их графики.	1
25	Функции и их графики. Вычисление значений функции по формуле.	1
26	Функции и их графики. Построение графиков функции.	1
27	Функции и их графики. Решение задач на построение графиков функции.	1
28	Линейная функция.	1
29	Линейная функция. Построение графиков линейной функции	1
30	Линейная функция. Прямая пропорциональность.	1
31	Линейная функция. Чтение графиков функции.	1
32	Линейная функция. Взаимное расположение графиков линейных функций.	1
33	Контрольная работа по теме №3	1	Функции Н.Г. Миндюк стр. 163-164
	3. Степень с натуральным показателем.	11	К.р. – 1
34	Степень и ее свойства.	1
35	Степень и ее свойства. Умножение и деление степеней.	1
36	Степень и ее свойства. Преобразование выражений со степенью.	1
37	Степень и ее свойства. Возведение в степень произведения и степени.	1
38	Степень и ее свойства. Решение задач на применение свойств степени.	1
39	Одночлены. Одночлен и его стандартный вид.	1
40	Одночлены. Умножение одночленов.	1
41	Одночлены. Возведение одночлена в степень.	1
42	Одночлены. Преобразование одночленов.	1
43	Одночлены. Функции у = х2 и у=х3 и их графики.	1
44	Контрольная работа по теме №4	1	Степень с натуральным показателем Н.Г. Миндюк стр. 164-165
	4. Многочлены.	17	К.р. – 2
45	Сумма и разность многочленов. Многочлен и его стандартный вид.	1
46	Сумма и разность многочленов. Преобразование многочленов.	1
47	Сумма и разность многочленов. Преобразование многочленов	1
48	Произведение одночлена на многочлен.	1
49	Произведение одночлена на многочлен. Решение выражений.	1
50	Произведение одночлена на многочлен. Вынесение общего множителя за скобки.	1
51	Произведение одночлена на многочлен. Решение выражений на вынесение множителя за скобки.	1
52	Произведение одночлена на многочлен. Решение выражений на вынесение множителя за скобки.	1
53	Произведение одночлена на многочлен. Повторение по теме «Многочлены»	1
54	Контрольная работа по теме №5	1	Сумма и разность многочленов. Произведение одночлена на многочлен Н.Г. Миндюк стр. 165-166
55	Произведение многочленов.	1
56	Произведение многочленов. Умножение многочлена на многочлен.	1
57	Произведение многочленов. Преобразование выражений на умножение многочленов.	1
58	Произведение многочленов. Разложение многочлена на множители способом группировки.	1
59	Произведение многочленов. Решение задач на разложение многочленов на множители.	1
60	Произведение многочленов. Доказательство тождеств.	1
61	Контрольная работа по теме №6	1	Произведение многочленов Н.Г. Миндюк стр.166
	5.Формулы сокращенного умножения.	19	К.р. – 2
62	Квадрат суммы и квадрат разности.	1
63	Квадрат суммы и квадрат разности. Возведение в квадрат суммы двух выражений.	1
64	Квадрат суммы и квадрат разности. Применение формул в преобразовании выражений	1
65	Квадрат суммы и квадрат разности. Разложение на множители с помощью формулы квадрата суммы и квадрата разности.	1
102		1
66	Квадрат суммы и квадрат разности. Преобразование выражений на разложение на множители.	1
67	Разность квадратов .Сумма и разность кубов.	1
68	Разность квадратов .Сумма и разность кубов. Решение выражений на умножение.	1
69	Разность квадратов .Сумма и разность кубов. Разложение разности квадратов на множители.	1
70	Разность квадратов .Сумма и разность кубов. Разложение выражений на множители.	1
71	Разность квадратов .Сумма и разность кубов. Преобразование выражений на разложение на множители.	1
72	Разность квадратов. Сумма и разность кубов. Преобразование выражений.	1
73	Контрольная работа по теме №7	1	Формулы сокращенного умножения Н.Г. Миндюк стр.167
74	Преобразование целых выражений.	1
75	Преобразование целых выражений. Применение формул сокращенного умножения при разложении.	1
76	Преобразование целых выражений. Преобразование целого выражения в многочлен.	1
77	Преобразование целых выражений. Применение различных способов для разложения на множители.	1
78	Преобразование целых выражений. Решение выражений.	1
79	Преобразование целых выражений. Обобщение по теме	1
80	Контрольная работа по теме №8	1	Преобразование целых выражений Н.Г. Миндюк стр. 167-168
	6.Системы линейных уравнений.	16	К.р. -1
81	Линейные уравнения с двумя переменными и их системы.	1
82	Линейные уравнения с двумя переменными и их системы.	1
83	Линейные уравнения с двумя переменными и их системы.	1
84	Линейные уравнения с двумя переменными и их системы. График линейного уравнения с двумя переменными.	1
85	Линейные уравнения с двумя переменными и их системы. Решение уравнений с помощью графика.	1
86	Решение систем линейных уравнений.	1
87	Решение систем линейных уравнений. Способ подстановки.	1
	подстановки.
88	Решение систем линейных уравнений.	1
89	Решение систем линейных уравнений. Способ сложения.	1
90	Решение систем линейных уравнений.	1
91	Решение систем линейных уравнений различными способами.	1
92	Решение систем линейных уравнений.	1
93	Решение систем линейных уравнений. Решение задач с помощью систем.	1
94	Решение систем линейных уравнений. Решение задач с помощью систем.	1
95	Повторение по теме «Решение систем линейных уравнений»	1
96	Контрольная работа по теме №9	1	Системы линейных уравнений Н.Г. Миндюк стр. 168-169
	Повторение	6	К.р. -1
97	Повторение по теме «Преобразование выражений.	1
159		1
160	Уравнения с одной переменной.	1
98	Повторение по теме «Решение уравнений с одной переменной.	1
99	Повторение по теме «Функции и их графики.	1
100	Итоговый зачет	1
101	Повторение по теме «Степень и ее свойства.	1
102	Итоговая контрольная работа №10	1	Методические рекомендации Н.Г. Миндюк стр. 169
	Итого	102	К.р.-.10

Календарно – тематическое планирование учебного материала по геометрии 7 класс ( 68 часов)

№ урока	Перечень разделов, тем	Количество часов	Количество и темы контрольных работ	Дата проведения
	1.Начальные геометрические сведения	10	К.р.-1
1	Прямая и отрезок	1
2	Луч и угол.	1
3	Сравнение отрезков и углов.	1
4	Измерение отрезков.	1
5	Измерение отрезков.	1
6	Измерение углов.	1
7	Перпендикулярные прямые.	1
8	Перпендикулярные прямые. Задачи на построение.	1
9	Решение задач по теме «Начальные геометрические сведения»	1
10	Контрольная работа №1	1	Начальные геометрические сведения Мет. рекоменд. Л.С. Атанасян стр.21
	2.Треугольники	17	К.р.-1
11	Первый признак равенства треугольников.	1
12	Первый признак равенства треугольников.	1
13	Первый признак равенства треугольников.	1
14	Медианы, биссектрисы и высоты треугольника.	1
15	Медианы, биссектрисы и высоты треугольника.	1
16	Медианы, биссектрисы и высоты треугольника.	1
17	Второй и третий признаки равенства треугольников.	1
18	Второй и третий признаки равенства треугольников.	1
19	Второй и третий признаки равенства треугольников.	1
20	Второй и третий признаки равенства треугольников.	1
21	Задачи на построение.	1
22	Задачи на построение.	1
23	Задачи на построение.	1
24	Решение задач по теме «Первый признак равенства треугольников»	1
25	Решение задач по теме « Второй признак равенства треугольников»	1
26	Решение задач по теме « Третий признак равенства треугольников.»	1
27	Контрольная работа № 2	1	Треугольники Мет. рекоменд. Л.С. Атанасян стр. 44
	3.Параллельные прямые	13
28	Признаки параллельности двух прямых.	1
29	Признаки параллельности двух прямых.	1
30	Признаки параллельности двух прямых.	1
31	Признаки параллельности двух прямых.	1
32	Аксиома параллельных прямых.	1
33	Аксиома параллельных прямых.	1
34	Аксиома параллельных прямых.	1
35	Аксиома параллельных прямых.	1
36	Аксиома параллельных прямых.	1
37	Решение задач по теме « Признаки параллельности двух прямых»	1
38	Решение задач по теме «Аксиома параллельных прямых»	1
39	Решение задач по теме «Параллельные прямые»	1
40	Контрольная работа №3	1	Параллельные прямые Мет. рекоменд. Л.С. Атанасян стр.61-62
	4.Соотношения между сторонами и углами треугольника.	18	К.р.-2
41	Сумма углов треугольника.	1
42	Сумма углов треугольника.	1
43	Соотношения между сторонами и углами треугольника.	1
44	Соотношения между сторонами и углами треугольника.	1
45	Соотношения между сторонами и углами треугольника.	1
46	Контрольная работа №4	1	Сумма углов треугольника Мет. рекоменд. Л.С. Атанасян стр. 73-74
47	Прямоугольные треугольники.	1
48	Прямоугольные треугольники.	1
49	Прямоугольные треугольники.	1
50	Прямоугольные треугольники.	1
51	Построение треугольника по трем элементам.	1
52	Построение треугольника по трем элементам.	1
53	Построение треугольника по трем элементам.	1
54	Построение треугольника по трем элементам.	1
55	Решение задач по теме « Прямоугольные треугольники»	1
56	Решение задач по теме « Прямоугольные треугольники»	1
57	Решение задач по теме «Построение треугольника»	1
58	Контрольная работа №5	1	Прямоугольные треугольники Мет. рекоменд. Л.С. Атанасян стр. 81
	Повторение. Решение задач.	10
59	Повторение по теме «Начальные геометрические сведения.»	1
60	Повторение по теме «Признаки равенства треугольников.»	1
61	Повторение по теме «Прямоугольный треугольник.»	1
62	Повторение по теме «Соотношения между сторонами и углами треугольника.»	1
63	Решение задач на применение признаков равенства треугольников.	1
64	Решение задач по теме «Прямоугольные треугольники»	1
65	Решение задач по теме «Соотношения между сторонами и углами треугольника.»	1
66	Решение задач на построение.	1
67	Повторение по теме «Параллельные прямые»	1
68	Решение задач.	1
	Итого	68	К.р.-5

Приложение к рабочей программе

Программно-нормативное, учебно-методическое

и техническое обеспечение образовательного процесса

5 класс

1. Учебник авт. Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд

23 –е изд. испр. М.: Просвещение – 2015г.

1. Контрольные работы по математике авт. В.И. Жохов

II. Литература для учителя.

1) Поурочные разработки авт. Л.П. Попова, /к учебному комплекту Н.Я. Виленкина и др. / М.: ВАКО -2012

2) Интернет портал PROШколу.ru  http://www.proshkolu.ru/club/maths/file2/322771/

3) http://school-collection.edu.ru/ – единая коллекция цифровых образовательных ресурсов.

4) Программа: Планирование учебного материала. Мат-ка. 5 – 6 классы / авт.-сост. В.И. Жохов. – М.: Мнемозина, 2009. – 31 с.

6 класс

1. Учебник авт. Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд

1. –е изд. стер. М.: Просвещение – 2015 г.

1. Контрольные и самостоятельные работы по математике авт. В.И. Жохов

II. Литература для учителя.

1) Поурочные разработки авт. В.В. Выговская, /к учебному комплекту Н.Я. Виленкина и др. / М.: ВАКО -2009 г

3) Интернет портал PROШколу.ru  http://www.proshkolu.ru/club/maths/file2/322771/

4) http://school-collection.edu.ru/ – единая коллекция цифровых образовательных ресурсов.

5) Программа: Планирование учебного материала. Мат-ка. 5 – 6 классы / авт.-сост. В.И. Жохов. – М.: Мнемозина, 2009. – 31 с

7 класс

1.Алгебра-7:учебник/автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова, Просвещение, 2016г.

2.Геометрия: учеб, для 7—9 кл. / [Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др.]. — М.: Просвещение, 2016г

3.Поурочные разработки по алгебре авт. А.Н. Рурукин, Г.В. Лупенко, И.А. Масленникова ( к учебникам Ю. Н. Макарычева, Ш. А. Алимова) М.: ВАКО – 2009г.

4.Поурочные разработки по геометрии авт. Н.Ф. Гаврилова 2-изд., перераб. и доп. – М.: ВАКО-2007г.

Приложение 1

КРИТЕРИИ И НОРМЫ ОЦЕНКИ ЗНАНИЙ ОБУЧАЮЩИХСЯ

1.Оценка письменных контрольных работ обучающихся по математике

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обоснованиях решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

 Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

• работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

 2. Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем,  сформированность  и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна – две  неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов  при освещении второстепенных вопросов или в выкладках,  легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

 Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя

• ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

3. Общая классификация ошибок

При оценке знаний, умений и навыков учащихся следует учитывать все ошибки и недочёты.

3.1. Ошибками считаются:

–                незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

–      незнание наименований единиц измерения;

–      неумение выделить в ответе главное;

–      неумение применять знания, алгоритмы для решения задач;

–      неумение делать выводы и обобщения;

–      неумение читать и строить графики;

–      неумение пользоваться первоисточниками, учебником и справочниками;

–      потеря корня или сохранение постороннего корня;

–      отбрасывание без объяснений одного из них;

–      равнозначные им ошибки;

–      вычислительные ошибки, если они не являются опиской;

–      логические ошибки.

            3.2. Недочетами являются:

–     нерациональные приемы вычислений и преобразований;

–    небрежное выполнение записей, чертежей, схем

1 Здесь и далее – распознавать конкретные примеры общих понятий по характерным признакам, выполнять действия в соответствии с определением и простейшими свойствами понятий, конкретизировать примерами общие понятия.

2 Здесь и далее – знать определение понятия, уметь пояснять его смысл, уметь использовать понятие и его свойства при проведении рассуждений, доказательств, решении задач.

3 Здесь и далее – распознавать конкретные примеры общих понятий по характерным признакам, выполнять действия в соответствии с определением и простейшими свойствами понятий, конкретизировать примерами общие понятия.