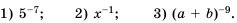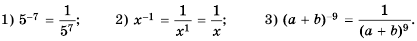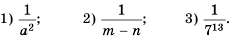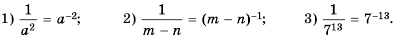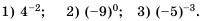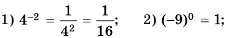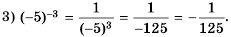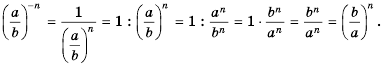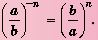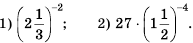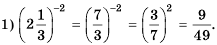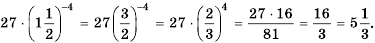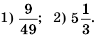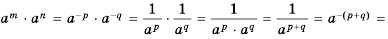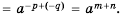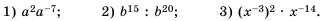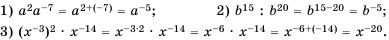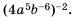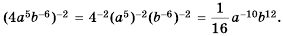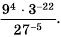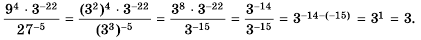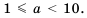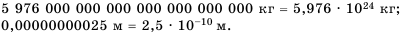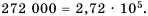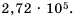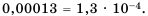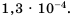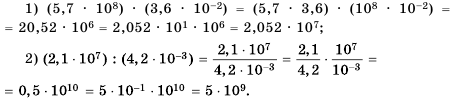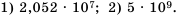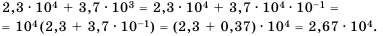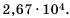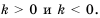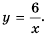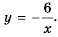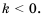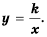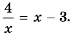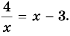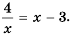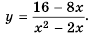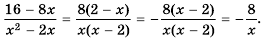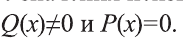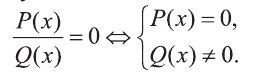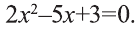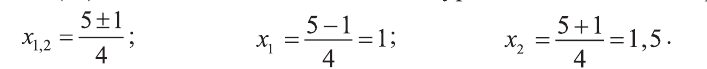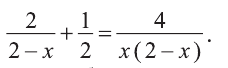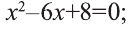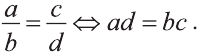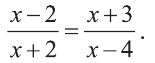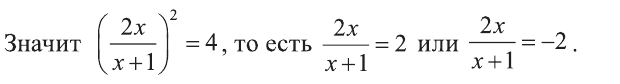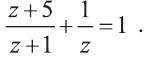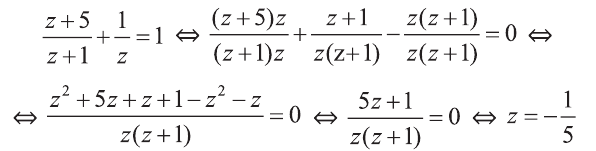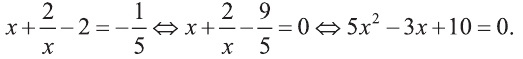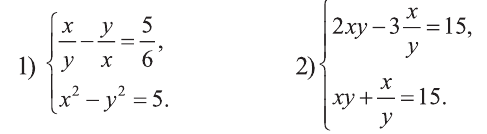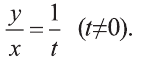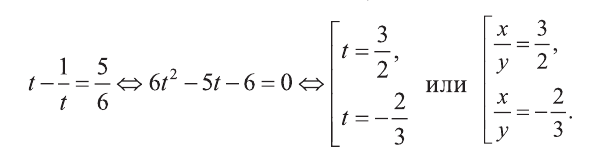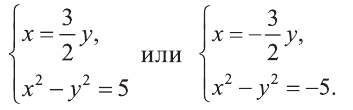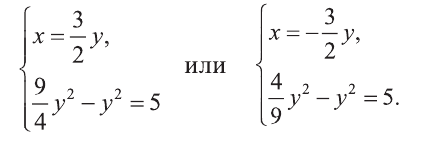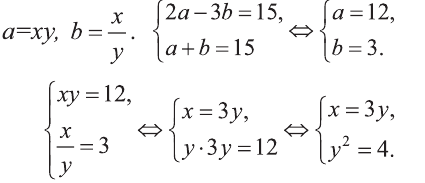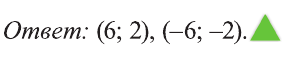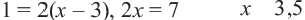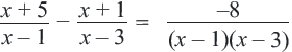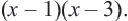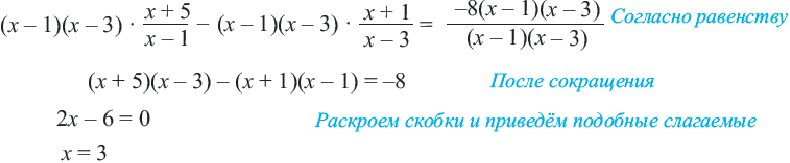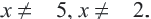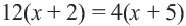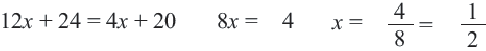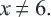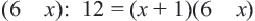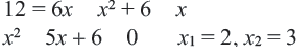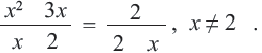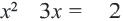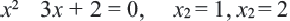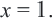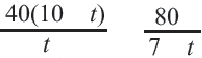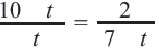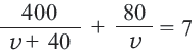Математика в наши дни проникает во все сферы
жизни. Овладение практически любой профессией
требует тех или иных знаний по математике. Особое
значение в этом смысле имеет умение
смоделировать математически определённые
реальные ситуации. Данное умение интегрирует в
себе разнообразные специальные умения,
адекватные отдельным элементам математических
знаний, их системам, а также различные
мыслительные приёмы, характеризующие культуру
мышления.
В школьной математике знакомство с
математическим моделированием основано, прежде
всего, на решении текстовых задач. Текстовая
задача несет в себе важные элементы
математического моделирования. Решая ее,
учащийся некие производственные, экономические,
житейские связи зашифровывает с помощью
математических символов, придавая им
абстрактную математическую форму. Решая
уравнения, учащийся расшифровывает результат,
согласуя его со здравым смыслом. Вот почему
решению текстовых задач, этому важнейшему
мостику между математикой и ее приложениями
должно уделяться особое внимание. При этом
представляется, что техника решения текстовых
задач может отрабатываться на любых задачах.
Было бы наивным думать, что задача на движение,
начинающаяся словами “Два автомобиля:”
непременно предназначена для будущих водителей,
а для школы со спортивным уклоном она должна
начинаться словами “Два лыжника:”.
Применение на практике различных задач на
составление уравнений позволяет создавать такие
учебные ситуации, которые требуют от учащегося
умения смоделировать математически
определённые физические, химические,
экономические процессы и явления, составить план
действия в решении реальной проблемы. Практика
последних лет говорит о необходимости
формирования умений решения задач на
составление уравнений различных типов ещё и в
связи с включением их в содержание ГИА и ЕГЭ.
Однако, анализ образовательной практики по
данному направлению говорит о том, что
значительная часть учащихся испытывает
серьёзные затруднения при решении задач на
составление уравнений. В большей степени это
связано с недостаточной сформированностью у
учащихся умения составлять план действий,
алгоритм решения конкретной задачи, культурой
моделирования явлений и процессов. Большинство
учащихся решают такие задачи лишь на
репродуктивном уровне.
Решению текстовых задач предшествует
достаточно долгое время, отводимое на отработку решения уравнений.
Начиная с 8 класса, как только выучены дробные
рациональные выражения, решения задач
по алгебре практически все сводятся к решению
дробных рациональных уравнений, которые, в свою
очередь, включают чаще всего решение
квадратных уравнений.
В 8 классе решение задач с помощью дробных
рациональных уравнений как показывает опыт
эффективнее решать табличным методом, так как он
является более наглядным, что важно для
подготовки к ГИА в 9 классе.
Все задачи, решаемые с помощью дробных
рациональных уравнений, можно разделить на
несколько групп:
- Задачи на движение по местности.
- Задачи на движение по воде.
- Задачи на работу.
- Задачи на нахождение дробей и т.д.
Начинать обучение следует с простых задач,
условия которых полностью соответствуют
названиям основных типов, и сводящихся к решению
дробных рациональных уравнений. Затем можно
приступать к решению более сложных задач.
Рекомендуется подобрать разноуровневые задачи
по каждому типу, что дает возможность работать со
школьниками разных математических способностей.
Мы стараемся научить детей строить таблицы с
данными величинами задачи, слева обозначаются
объекты (автомобили, лодки, пешеходы, самолеты и
т.д.), сверху в колонках – величины,
характеризующие данную задачу, и обязательно
единицы их измерения. И дети понимают, что из трех
величин, зная две, всегда можно записать третью.
Приведем пример оформления задачи:
Автобус-экспресс отправился от вокзала в
аэропорт, находящийся на расстоянии 120км от
вокзала. Пассажир, опоздавший на 10 минут на
автобус, решил добраться до аэропорта на такси.
Скорость такси на 10км/ч больше скорости автобуса.
С какой скорость ехал автобус, если он приехал в
аэропорт одновременно с такси?
Пусть 
км/ч –
скорость автобуса, тогда составим и заполним
таблицу:
Т.к. по условию задачи пассажир опоздал на
автобус на 10 минут =
часа,
то составим и решим уравнение:
, ОДЗ: 
>0 (т.к. скорость
положительна)
720(х+10) – 720х= х (х+10),
х2+10х-7200=0,
Далее решая квадратное уравнение, получаем:
х1=80,
х2=-90,
-90 – не входит в ОДЗ, значит, скорость автобуса
равна 80 км/ч.
Ответ: 80км/ч.
Основная часть класса уверенно заполняет
таблицу и составляет уравнение.
В зависимости от выделенного времени,
обучаемым может быть предложен широкий спектр
мероприятий – семинары, кружки, факультативы,
индивидуальные и групповые консультации и т.д., в
рамках которых обучаемые более глубоко
осваивают решение задач с помощью уравнений.
Практикум по решению задач табличным методом с
помощью дробных рациональных уравнений можно
провести во второй половине дня на групповой
консультации по математике, что целесообразно в
рамках школы полного дня.
Список предлагаемых задач:
Числитель обыкновенной дроби на 4 меньше ее
знаменателя. Если к числителю этой дроби
прибавить 19, а к знаменателю 28, то она увеличится
на 
. Найдите
эту дробь.
Теплоход, собственная скорость которого 18 км/ч,
прошел 50 км по течению реки и 8 км против течения,
затратив на весь путь 3 часа. Какова скорость
течения реки?
Два комбайна убрали поле за 4 дня. За сколько
дней мог убрать поле каждый комбайн, если одному
из них для выполнения этой работы потребовалось
бы на 6 дней меньше, чем другому?
Моторная лодка прошла против течения 8 км и
вернулась обратно, затратив на обратный путь на 30
мин меньше, чем при движении против течения.
Найдите скорость лодки в неподвижной воде, если
скорость течения равна 4 км/ч.
Расстояние 700 км экспресс проходит на 4 часа
быстрее товарного поезда, так как его скорость
больше скорости товарного поезда на 20 км/ч.
Определите скорость каждого из поездов, если
известно, что они движутся с постоянной
скоростью без остановок.
Мастеру на выполнение заказа потребуется на 5
дней меньше, чем его ученику, но при совместной
работе они выполнят заказ на 4 дня быстрее, чем
мастер, работающий в одиночку. За сколько дней
выполнит заказ мастер, работая в одиночку?
На участке пути длиной 300 км поезд увеличил
скорость на 10 км/ч, в результате чего прибыл на
конечную станцию на 1 час раньше, чем
планировалось по расписанию. С какой скоростью
должен был идти поезд по расписанию?
Прозаик хочет набрать на компьютере рукопись
объемом 450 страниц. Если он будет набирать на 5
страниц в день больше, чем запланировал, то
закончит работу на 3 дня раньше. Сколько страниц в
день планирует набирать прозаик?
Дорога между пунктами А и В состоит из подъема и
спуска, а ее длина равна 19 км. Пешеход прошел путь
из А в В за 5 часов. Время его движения на спуске
составило 4 часа. С какой скоростью пешеход шел на
спуске, если скорость его движения на подъеме
меньше скорости движения на спуске на 1 км/ч?
Велосипедист отправился с некоторой скоростью
из города А в город В, расстояние между которыми
равно 88 км. Возвращаясь из В в А, он ехал поначалу
с той же скоростью, но через 2 часа пути вынужден
был сделать остановку на 10 минут. После этого он
продолжил путь в А, увеличив скорость на 2 км/ч, и в
результате затратил на обратный путь столько же
времени, сколько на путь из А в В. Найдите
скорость велосипедиста на пути из А в В.
Количество решаемых задач может меняться в
зависимости от отводимого на это время.
Используемая литература:
- И.Л.Бродский, А.М.Видус, А.Б.Коротаев “Сборник
текстовых задач по математике для профильных
классов”. - В.И. Жохов, Ю.Н.Макарычев, Н.Г.Миндюк
“Дидактические материалы по алгебре 8 класс”. - Сборник задач для подготовки и проведения
письменного экзамена по алгебре за курс основной
школы под редакцией С.А.Шестакова. - Ш.А.Алимов, М.Ю.Колягин и др. “Алгебра 8 класс”.
- А.П.Ершова, В.В.Голобородько, А.С.Ершова
“Самостоятельные и контрольные работы по
алгебре и геометрии для 8 класса”.
Примеры
Об общем алгоритме решения задач с помощью уравнений, см. §31 данного справочника.
Пример 1. От посёлка до речки 60 км. Утром турист на скутере отправился на речку. Вечером он возвратился в посёлок, но при этом ехал со скоростью на 10 км/ч меньшей и потратил на дорогу на 18 мин больше. Сколько времени ехал турист от речки к посёлку?
Пусть t – время вечером, на дорогу от речки к посёлку.
Тогда время утром, на дорогу от посёлка к речке t- $frac{18}{60}$ = t-0,3 (ч)
Заполним таблицу:
Скорость, км/ч
Время, ч
Расстояние, км
Утром
$frac{60}{t-0,3}$
t-0,3
60
Вечером
$frac{60}{t}$
t
60
По условию разность скоростей равна 10:
$$ frac{60}{t-0,3} – frac{60}{t} = =10 |:10 $$
$$ frac{6}{t-0,3} – frac{6}{t} = 1 Rightarrow frac{6(t-(t-0,3) )}{t(t-0,3)} = 1 $$
$$1,8=t(t-0,3), t neq 0, t neq 0,3$$
$$ t^2-0,3t-1,8 = 0 $$
$$ D = 0,3^2-4 cdot (-1,8) = 0,09+7,2=7,29 = 2,7^2 $$
$$ t = frac{0,3 pm 2,7}{2} = left[ begin{array}{cc} t_1 = -1,1 \ t_2 = 1,5 end{array} right. $$
Выбираем положительный корень, t = 1,5 ч
Ответ: 1,5 ч
Пример 2. Катер прошёл по течению 120 км. На этот же путь против течения от тратит времени в 1,5 раза больше. Найдите скорость течения, если скорость катера в стоячей воде 20 км/ч.
Пусть u – скорость течения
Заполним таблицу:
Скорость, км/ч
Время, ч
Расстояние, км
По течению
20+u
$frac{120}{20+u}$
120
Против течения
20-u
$frac{120}{20-u}$
120
По условию время против течения в 1,5 раз больше:
$$ 1,5 cdot frac{120}{20+u} = frac{120}{20-u} |:120 $$
$$ frac{1,5}{20+u} = frac{1}{20-u}$$
$$ 1,5(20-u) = 20+u, u neq pm 20 $$
$$ 30-1,5u = 20+u $$
$$ 2,5u = 10 $$
$$ u = 4 $$
Ответ: 4 км/ч
Пример 3. В раствор, содержащий 50 г соли, добавили 150 г воды. В результате концентрация соли уменьшилась на 7,5%. Найдите первоначальную массу раствора.
Пусть x – масса воды в первоначальном растворе, в граммах.
Заполним таблицу:
Раствор после
50
x+150
x+200
По условию разность концентраций:
$$ frac{50}{x+50} – frac{50}{x+200} = 0,075 $$
$$ frac{50(x+200-x-50)}{(x+50)(x+200)} = 0,075 $$
$$ 50 cdot 150 = frac{75}{1000} (x+50)(x+200), x neq -50, x neq -200 $$
Сократим дробь:
$$ frac{50 cdot 150 cdot 1000}{75} = frac{50}{5} cdot frac{150}{15} cdot 1000 = 100000 $$
Получаем:
$$ (x+50)(x+200) = 100000 $$
$$ x^2+250x+10000 = 100000 $$
$$ x^2+250x-90000 = 0 $$
$$ D = 250^2-4 cdot (-90000) = 62500+360000 = 100(625+3600) = $$
$$ = 100 cdot 4225 = 650^2 $$
$$ x = frac{-250 pm 650}{2} = left[ begin{array}{cc} x_1 = -450 \ x_2 = 200 end{array} right. $$
Выбираем положительный корень x=200 г – начальное количество воды в растворе. Начальная масса всего раствора: 50+200 = 250 г.
Ответ: 250 г
Пример 4. Мастер и его ученик, работая вместе, выполняют норму на 8 ч. Если каждый работает самостоятельно, то мастер тратит на выполнение нормы на 12 ч меньше, чем ученик. Сколько часов тратит каждый из них на выполнении нормы?
Пусть N изделий – это норма, t – время, потраченное мастером.
Заполним таблицу:
Производительность, изделий/ч
Время, ч
Результат, изделий
Ученик
$frac{N}{t+12}$
t+12
N
Вместе
$frac{N}{t}+frac{N}{t+12}$
8
N
Из последней строки таблицы получаем:
$$ frac{N}{t}+frac{N}{t+12} = frac{N}{8} |:N $$
$$ frac{1}{t}+frac{1}{t+12} = frac{1}{8} $$
$$ frac{t+12+t}{t(t+12)} = frac{1}{8} $$
$$ 8(2t+12) = t(t+12), t neq 0, t neq -12$$
$$ 16t+96 = t^2+12t $$
$$ t^2-4t-96 = 0 Rightarrow (t-12)(t+8) = 0 Rightarrow left[ begin{array}{cc} t_1 = -8 \ t_2 = 12 end{array} right. $$
Выбираем положительный корень, t=12 ч – время, которое мастер потратит самостоятельно. Ученик потратит 12+12=24 ч.
Ответ: 12 ч и 24 ч
Пример 5*. Один фрилансер может выполнить проект на 12 дней быстрее, чем второй. Над новым проектом первый фрилансер сначала проработал самостоятельно 6 дней, а затем к нему присоединился второй. Через 3 дня совместной работы frac{3}{5} проекта было готово.
За сколько дней каждый из фрилансеров может выполнить проект самостоятельно? За сколько дней проект был фактически выполнен?
Пусть d – количество дней первого фрилансера при самостоятельной работе.
Заполним таблицу:
Производительность, проект/день
Время, дни
Результат, проект
Фрилансер 1
$frac{1}{d}$
d
1
Фрилансер 2
$frac{1}{d+12}$
d+12
1
Первые 6 дней
$frac{1}{d}$
6
$frac{6}{d}$
Совместные 3 дня
$frac{1}{d} + frac{1}{d+12}$
3
$frac{3}{5}-frac{6}{d}$
Из последней строки таблицы получаем:
$$ 3 Biggl(frac{1}{d} + frac{1}{d+12}Biggr) = frac{3}{5}-frac{6}{d} |:3 $$
$$ frac{1}{d} + frac{1}{d+12} = frac{1}{5}-frac{2}{d} $$
$$ frac{d+12+d}{d(d+12)} = frac{d-10}{5d} | times 5d(d+12), d neq 0, d neq -12 $$
$$ 5(2d+12) = (d-10)(d+12) Rightarrow 10d+60 = d^2+2d-120 $$
$$ d^2-8d-180 = 0 Rightarrow (d-18)(d+10) = 0 Rightarrow left[ begin{array}{cc} d_1 = -10 \ d_2 = 18 end{array} right. $$
Выбираем положительный корень, d=18 дней – время самостоятельной работы 1-го фрилансера. 2-й фрилансер будет самостоятельно работать 18+12 = 30 дней.
Найдём фактически потраченное время.
3/5 проекта было сделано за 9 дней. Осталось 2/5, которые выполнялись совместно:
$$ frac{2}{5}: Biggl( frac{1}{18}+ frac{1}{30} Biggr) = frac{2}{5}: frac{5+3}{90} = frac{2}{5} cdot frac{45}{4} = frac{9}{2} = 4,5 $$
Всего было потрачено 9+4,5 = 13,5 дней.
Ответ: 18 дней 1-й фрилансер; 30 дней 2-й фрилансер; 13,5 дней фактически.
Мы с вами уже научились решать рациональные уравнения.
Напомним, что рациональные уравнения
– это уравнения, у которых левая и правая части являются рациональными
выражениями. Рациональное уравнение, в котором левая или правая части
являются дробными выражениями, называют дробным.
Очень часто решение задач сводится к решению
дробных рациональных уравнений. Решим несколько задач, которые сводятся к
решению таких уравнений.
Задача 1. Числитель дроби на меньше её знаменателя.
Сумма дроби и обратной ей дроби в раза больше исходной
дроби. Найти исходную дробь.
Решение:
Обозначим за – знаменатель дроби. Тогда
– числитель этой дроби. Значит,
исходная дробь имеет вид . Так как по условию
задачи сумма дроби и обратной ей дроби
в
раза больше исходной
дроби, то можем составить уравнение:
Задача 2. Велосипедисту надо проехать 15 км. Он
выехал на 15 минут позже намеченного срока и, чтобы приехать вовремя, увеличил
скорость на 2 км/ч. С какой скоростью ехал велосипедист?
Решение:
Пусть (км/ч) – скорость
велосипедиста. Тогда расстояние в км велосипедист проедет
за часов. Если бы велосипедист
выехал вовремя, то его скорость была бы равна км/ч. И тогда расстояние
в км он проехал бы за
часов. По условию
задачи, велосипедист выехал на минут позже намеченного
срока, или, что тоже самое, на часа позже. Составим
уравнение:
Задача 3. Моторная лодка прошла вниз по реке 14 км, а
затем 9 км против течения, затратив на весь путь 5 часов. Найти скорость
течения реки, если скорость моторной лодки в стоячей воде равна 5 км/ч.
Решение:
Пусть (км/ч) – скорость
течения реки. Тогда расстояние в км/ч скорость моторной
лодки по течению реки и км/ч скорость моторной
лодки против течения. Известно, что моторная лодка прошла по течению реки км, а значит, затратила
на это расстояние часов. Затем против
течения лодка прошла км, затратив на это
расстояние часов. По условию
известно, что на весь путь моторная лодка затратила часов. Составим уравнение:
Задача 4. Вело эквилибрист, проектируя своё
оборудование для выступления в цирке, рассчитал, что если длину окружности
колеса его одноколёсного велосипеда увеличить на один метр, то на расстоянии
990 м оно сделает на 40 оборотов меньше. Найти длину окружности велосипедного
колеса эквилибриста.
Решение:
Пусть метров – длина
окружности колеса. Тогда на расстоянии в метров это колесо делает
оборотов.
И тогда на расстоянии метров такое колесо
сделает оборотов. По условию
задачи известно, что после увеличения длины окружности колеса, оно делает на
расстоянии метров на
оборотов меньше. Составим
уравнение:
Итоги:
Итак, сегодня на уроке мы с вами познакомились с задачами,
решение которых предполагает составление и решение дробных рациональных
уравнений, и научились решать такие задачи.
Решение задач с помощью дробных рациональных уравнений
Примеры
Пример 1. От посёлка до речки 60 км. Утром турист на скутере отправился на речку. Вечером он возвратился в посёлок, но при этом ехал со скоростью на 10 км/ч меньшей и потратил на дорогу на 18 мин больше. Сколько времени ехал турист от речки к посёлку?
Пусть t – время вечером, на дорогу от речки к посёлку.
Тогда время утром, на дорогу от посёлка к речке t- $frac<18><60>$ = t-0,3 (ч)
По условию разность скоростей равна 10:
$$1,8=t(t-0,3), t neq 0, t neq 0,3$$
$$ D = 0,3^2-4 cdot (-1,8) = 0,09+7,2=7,29 = 2,7^2 $$
$$ t = frac<0,3 pm 2,7> <2>= left[ begin t_1 = -1,1 \ t_2 = 1,5 end right. $$
Выбираем положительный корень, t = 1,5 ч
Пример 2. Катер прошёл по течению 120 км. На этот же путь против течения от тратит времени в 1,5 раза больше. Найдите скорость течения, если скорость катера в стоячей воде 20 км/ч.
Пусть u – скорость течения
По условию время против течения в 1,5 раз больше:
$$ 1,5(20-u) = 20+u, u neq pm 20 $$
Пример 3. В раствор, содержащий 50 г соли, добавили 150 г воды. В результате концентрация соли уменьшилась на 7,5%. Найдите первоначальную массу раствора.
Пусть x – масса воды в первоначальном растворе, в граммах.
По условию разность концентраций:
$$ 50 cdot 150 = frac<75> <1000>(x+50)(x+200), x neq -50, x neq -200 $$
$$ D = 250^2-4 cdot (-90000) = 62500+360000 = 100(625+3600) = $$
$$ = 100 cdot 4225 = 650^2 $$
$$ x = frac<-250 pm 650> <2>= left[ begin x_1 = -450 \ x_2 = 200 end right. $$
Выбираем положительный корень x=200 г – начальное количество воды в растворе. Начальная масса всего раствора: 50+200 = 250 г.
Пример 4. Мастер и его ученик, работая вместе, выполняют норму на 8 ч. Если каждый работает самостоятельно, то мастер тратит на выполнение нормы на 12 ч меньше, чем ученик. Сколько часов тратит каждый из них на выполнении нормы?
Пусть N изделий – это норма, t – время, потраченное мастером.
Из последней строки таблицы получаем:
$$ 8(2t+12) = t(t+12), t neq 0, t neq -12$$
$$ t^2-4t-96 = 0 Rightarrow (t-12)(t+8) = 0 Rightarrow left[ begin t_1 = -8 \ t_2 = 12 end right. $$
Выбираем положительный корень, t=12 ч – время, которое мастер потратит самостоятельно. Ученик потратит 12+12=24 ч.
Ответ: 12 ч и 24 ч
Пример 5*. Один фрилансер может выполнить проект на 12 дней быстрее, чем второй. Над новым проектом первый фрилансер сначала проработал самостоятельно 6 дней, а затем к нему присоединился второй. Через 3 дня совместной работы frac<3> <5>проекта было готово.
За сколько дней каждый из фрилансеров может выполнить проект самостоятельно? За сколько дней проект был фактически выполнен?
Пусть d – количество дней первого фрилансера при самостоятельной работе.
Решение задач с помощью дробных рациональных уравнений табличным методом
Разделы: Математика
Математика в наши дни проникает во все сферы жизни. Овладение практически любой профессией требует тех или иных знаний по математике. Особое значение в этом смысле имеет умение смоделировать математически определённые реальные ситуации. Данное умение интегрирует в себе разнообразные специальные умения, адекватные отдельным элементам математических знаний, их системам, а также различные мыслительные приёмы, характеризующие культуру мышления.
В школьной математике знакомство с математическим моделированием основано, прежде всего, на решении текстовых задач. Текстовая задача несет в себе важные элементы математического моделирования. Решая ее, учащийся некие производственные, экономические, житейские связи зашифровывает с помощью математических символов, придавая им абстрактную математическую форму. Решая уравнения, учащийся расшифровывает результат, согласуя его со здравым смыслом. Вот почему решению текстовых задач, этому важнейшему мостику между математикой и ее приложениями должно уделяться особое внимание. При этом представляется, что техника решения текстовых задач может отрабатываться на любых задачах. Было бы наивным думать, что задача на движение, начинающаяся словами “Два автомобиля:” непременно предназначена для будущих водителей, а для школы со спортивным уклоном она должна начинаться словами “Два лыжника:”.
Применение на практике различных задач на составление уравнений позволяет создавать такие учебные ситуации, которые требуют от учащегося умения смоделировать математически определённые физические, химические, экономические процессы и явления, составить план действия в решении реальной проблемы. Практика последних лет говорит о необходимости формирования умений решения задач на составление уравнений различных типов ещё и в связи с включением их в содержание ГИА и ЕГЭ.
Однако, анализ образовательной практики по данному направлению говорит о том, что значительная часть учащихся испытывает серьёзные затруднения при решении задач на составление уравнений. В большей степени это связано с недостаточной сформированностью у учащихся умения составлять план действий, алгоритм решения конкретной задачи, культурой моделирования явлений и процессов. Большинство учащихся решают такие задачи лишь на репродуктивном уровне.
Решению текстовых задач предшествует достаточно долгое время, отводимое на отработку решения уравнений. Начиная с 8 класса, как только выучены дробные рациональные выражения, решения задач по алгебре практически все сводятся к решению дробных рациональных уравнений, которые, в свою очередь, включают чаще всего решение квадратных уравнений.
В 8 классе решение задач с помощью дробных рациональных уравнений как показывает опыт эффективнее решать табличным методом, так как он является более наглядным, что важно для подготовки к ГИА в 9 классе.
Все задачи, решаемые с помощью дробных рациональных уравнений, можно разделить на несколько групп:
- Задачи на движение по местности.
- Задачи на движение по воде.
- Задачи на работу.
- Задачи на нахождение дробей и т.д.
Начинать обучение следует с простых задач, условия которых полностью соответствуют названиям основных типов, и сводящихся к решению дробных рациональных уравнений. Затем можно приступать к решению более сложных задач. Рекомендуется подобрать разноуровневые задачи по каждому типу, что дает возможность работать со школьниками разных математических способностей.
Мы стараемся научить детей строить таблицы с данными величинами задачи, слева обозначаются объекты (автомобили, лодки, пешеходы, самолеты и т.д.), сверху в колонках – величины, характеризующие данную задачу, и обязательно единицы их измерения. И дети понимают, что из трех величин, зная две, всегда можно записать третью.
Приведем пример оформления задачи:
Автобус-экспресс отправился от вокзала в аэропорт, находящийся на расстоянии 120км от вокзала. Пассажир, опоздавший на 10 минут на автобус, решил добраться до аэропорта на такси. Скорость такси на 10км/ч больше скорости автобуса. С какой скорость ехал автобус, если он приехал в аэропорт одновременно с такси?
Пусть 
км/ч – скорость автобуса, тогда составим и заполним таблицу:
| Скорость (км/ч) | Время (ч) | Путь (км) | |
| Автобус |  |
 |
 |
| Такси |  |
 |
 |
Т.к. по условию задачи пассажир опоздал на автобус на 10 минут =
часа, то составим и решим уравнение:
, ОДЗ: 
>0 (т.к. скорость положительна)
720(х+10) – 720х= х (х+10),
Далее решая квадратное уравнение, получаем:
-90 – не входит в ОДЗ, значит, скорость автобуса равна 80 км/ч.
Основная часть класса уверенно заполняет таблицу и составляет уравнение.
В зависимости от выделенного времени, обучаемым может быть предложен широкий спектр мероприятий – семинары, кружки, факультативы, индивидуальные и групповые консультации и т.д., в рамках которых обучаемые более глубоко осваивают решение задач с помощью уравнений.
Практикум по решению задач табличным методом с помощью дробных рациональных уравнений можно провести во второй половине дня на групповой консультации по математике, что целесообразно в рамках школы полного дня.
Список предлагаемых задач:
Числитель обыкновенной дроби на 4 меньше ее знаменателя. Если к числителю этой дроби прибавить 19, а к знаменателю 28, то она увеличится на 
. Найдите эту дробь.
Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 часа. Какова скорость течения реки?
Два комбайна убрали поле за 4 дня. За сколько дней мог убрать поле каждый комбайн, если одному из них для выполнения этой работы потребовалось бы на 6 дней меньше, чем другому?
Моторная лодка прошла против течения 8 км и вернулась обратно, затратив на обратный путь на 30 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
Расстояние 700 км экспресс проходит на 4 часа быстрее товарного поезда, так как его скорость больше скорости товарного поезда на 20 км/ч. Определите скорость каждого из поездов, если известно, что они движутся с постоянной скоростью без остановок.
Мастеру на выполнение заказа потребуется на 5 дней меньше, чем его ученику, но при совместной работе они выполнят заказ на 4 дня быстрее, чем мастер, работающий в одиночку. За сколько дней выполнит заказ мастер, работая в одиночку?
На участке пути длиной 300 км поезд увеличил скорость на 10 км/ч, в результате чего прибыл на конечную станцию на 1 час раньше, чем планировалось по расписанию. С какой скоростью должен был идти поезд по расписанию?
Прозаик хочет набрать на компьютере рукопись объемом 450 страниц. Если он будет набирать на 5 страниц в день больше, чем запланировал, то закончит работу на 3 дня раньше. Сколько страниц в день планирует набирать прозаик?
Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 19 км. Пешеход прошел путь из А в В за 5 часов. Время его движения на спуске составило 4 часа. С какой скоростью пешеход шел на спуске, если скорость его движения на подъеме меньше скорости движения на спуске на 1 км/ч?
Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 88 км. Возвращаясь из В в А, он ехал поначалу с той же скоростью, но через 2 часа пути вынужден был сделать остановку на 10 минут. После этого он продолжил путь в А, увеличив скорость на 2 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
Количество решаемых задач может меняться в зависимости от отводимого на это время.
Используемая литература:
Рациональные уравнения с примерами решения
Содержание:
Рациональные уравнения. Равносильные уравнения
два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.
Так, например, равносильными будут уравнения 
Уравнения 
– не равносильны, так как корнем первого уравнения является число 10, а корнем второго – число 9.
Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.
1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;
2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;
3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Левая и правая части каждого из них являются рациональными выражениями.
Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.
В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения – дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.
Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.
Применение условия равенства дроби нулю
Напомним, что 
когда 
Пример №202
Решите уравнение 
Решение:
С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду 
где 
и 
– целые рациональные выражения. Имеем:
Окончательно получим уравнение: 
Чтобы дробь 
равнялась нулю, нужно, чтобы числитель 
равнялся нулю, а знаменатель 
не равнялся нулю.
Тогда 
откуда 
При 
знаменатель 
Следовательно, 
– единственный корень уравнения.
Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:
Значит, решая дробное рациональное уравнение, можно:
1) с помощью тождественных преобразований привести уравнение к виду 
2) приравнять числитель 
к нулю и решить полученное целое уравнение;
3) исключить из его корней те, при которых знаменатель 
равен нулю, и записать ответ.
Использование основного свойства пропорции
Если 
то 
где 
Пример №203
Решите уравнение 
Решение:
Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то 
Имеем: 
то есть ОДЗ переменной 
содержит все числа, кроме 1 и 2.
Сложив выражения в правой части уравнения, приведем его к виду: 
получив пропорцию: 
По основному свойству пропорции имеем:
Решим это уравнение:
откуда 
Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.
Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:
Таким образом, для решения дробного рационального уравнения можно:
1) найти область допустимых значений (ОДЗ) переменной в уравнении;
2) привести уравнение к виду 
3) записать целое уравнение 
и решить его;
4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.
Метод умножения обеих частей уравнения на общий знаменатель дробей
Пример №204
Решите уравнение 
Решение:
Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:
Областью допустимых значений переменной будут те значения 
при которых 
то есть все значения 
кроме чисел 
А простейшим общим знаменателем будет выражение 
Умножим обе части уравнения на это выражение:
Получим: 
а после упрощения: 
то есть 
откуда 
или 
Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.
Следовательно, число 12 – единственный корень уравнения. Ответ. 12.
Решая дробное рациональное уравнение, можно:
3) умножить обе части уравнения на этот общий знаменатель;
4) решить полученное целое уравнение;
5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.
Пример №205
Являются ли равносильными уравнения
Решение:
Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.
Первое уравнение имеет единственный корень 
а второе – два корня 
(решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.
Степень с целым показателем
Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:
где 
– натуральное число, 
В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: 
кг. Как понимать смысл записи 
Рассмотрим степени числа 3 с показателями 
– это соответственно 
В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим: 
Число 
должно быть втрое меньше числа 
равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, 
Равенство 
справедливо для любого основания 
при условии, что 
Нулевая степень отличного от нуля числа а равна единице, то есть 
при 
Вернемся к строке со степенями числа 3, где слева от числа 
записано число 
Это число втрое меньше, чем 1, то есть равно 
Следовательно, 
Рассуждая аналогично получаем: 
и т. д.
Приходим к следующему определению степени с целым отрицательным показателем:
если 
натуральное число, то 
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/571941
http://www.evkova.org/ratsionalnyie-uravneniya
[/spoiler]
Содержание:
Рациональные уравнения. Равносильные уравнения
Напомним что:
два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.
Так, например, равносильными будут уравнения
Уравнения – не равносильны, так как корнем первого уравнения является число 10, а корнем второго – число 9.
Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.
1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;
2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;
3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Рассмотрим уравнения:
Левая и правая части каждого из них являются рациональными выражениями.
Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.
В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения – дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.
Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.
Применение условия равенства дроби нулю
Напомним, что когда
Пример №202
Решите уравнение
Решение:
С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и – целые рациональные выражения. Имеем:
Окончательно получим уравнение:
Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.
Тогда откуда При знаменатель Следовательно, – единственный корень уравнения.
Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:
Ответ. 3.
Значит, решая дробное рациональное уравнение, можно:
1) с помощью тождественных преобразований привести уравнение к виду
2) приравнять числитель к нулю и решить полученное целое уравнение;
3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.
Использование основного свойства пропорции
Если то где
Пример №203
Решите уравнение
х – 1 х – 2
Решение:
Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.
Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:
По основному свойству пропорции имеем:
Решим это уравнение:
откуда
Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.
Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:
Ответ. 4.
Таким образом, для решения дробного рационального уравнения можно:
1) найти область допустимых значений (ОДЗ) переменной в уравнении;
2) привести уравнение к виду
3) записать целое уравнение и решить его;
4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.
Метод умножения обеих частей уравнения на общий знаменатель дробей
Пример №204
Решите уравнение
Решение:
Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:
Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение
Умножим обе части уравнения на это выражение:
Получим: а после упрощения: то есть откуда или
Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.
Следовательно, число 12 – единственный корень уравнения. Ответ. 12.
Решая дробное рациональное уравнение, можно:
1) найти ОДЗ переменной в уравнении; & 2) найти простейший общий знаменатель дробей, входящий в уравнение;
3) умножить обе части уравнения на этот общий знаменатель;
4) решить полученное целое уравнение;
5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.
Пример №205
Являются ли равносильными уравнения
Решение:
Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.
Первое уравнение имеет единственный корень а второе – два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.
Ответ. Нет.
Степень с целым показателем
Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:
где – натуральное число,
В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи
Рассмотрим степени числа 3 с показателями – это соответственно
В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:
Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что
Нулевая степень отличного от нуля числа а равна единице, то есть при
Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.
Приходим к следующему определению степени с целым отрицательным показателем:
если натуральное число, то
Пример №206
Замените степень дробью:
Решение:
По определению:
Пример №207
Замените дробь степенью с целым отрицательным показателем:
Решение:
Пример №208
Вычислите: 
Решение:
Рассмотрим, как возвести дробь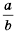 
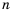
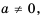
в целую отрицательную степень. Если 
– натуральное число и 
имеем:
Следовательно,
Если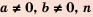 
– натуральное число, то 
Пример №209
Найдите значение выражения:
Решение:
2) Учитывая порядок выполнения арифметических действий, сначала возведем дробь в степень, а затем выполним умножение:
Ответ. 
Свойства степени с целым показателем
Свойства степени с натуральным показателем справедливы и для степени с ненулевым основанием и целым показателем. Следовательно,
Для любого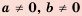 
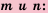
любых целых 
Эти свойства можно доказать на основании формулы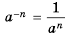 
и свойств степени с натуральным показателем.
Докажем, например, формулу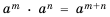 
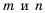
для случая, когда 
отрицательные целые числа.
Пусть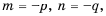 
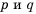
где 
натуральные числа. Имеем:
Следовательно,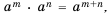 
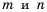
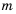
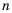
где 
– отрицательные целые числа. В случае, когда один из показателей 
или 
-целое отрицательное число, а второй – натуральное число или нуль, формула доказывается аналогично.
Пример №210
Выполните действие:
Решение:
Пример №211
Упростите выражение 
Решение:
Пример №212
Вычислите 
Решение:
Представим 9 и 27 в виде степени с основанием 3 и воспользуемся свойствами степени:
Ответ. 3.
Стандартный вид числа
В физике, химии, технике, астрономии часто имеют дело как с очень большими, так и с очень малыми значениями величин. Например, масса Земли равна 5 976 ООО ООО ООО ООО ООО ООО ООО кг, а диаметр молекулы водорода 0,00000000025 м.
Читать или записывать такие числа в виде десятичных дробей неудобно, неудобно и использовать десятичную их запись при вычислениях. В таких случаях имеет смысл записывать число в виде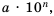 
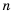
где 
– целое число, 
Например,
Говорят, что числа 5 976 000 000 000 000 000 000 000 и 0,00000000025 записаны в стандартном виде.
Стандартным видом числа называют его запись в виде произведении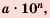 
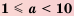
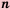
где 
и 
— целое число.
Если число записано в стандартном виде, то показатель степени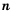 
называют порядком числа. Например, порядок числа, которым записана масса Земли в килограммах, равен 24, а порядок числа, которым записан диаметр молекулы водорода в метрах, равен -10.
В стандартном виде можно записать любое положительное число. Порядок числа дает представление об этом числе.
Если порядок числа 
равен 4, это значит, что 
то есть 
Если порядок числа 
равен -2, то 
то есть 
Большой положительный порядок числа показывает, что число очень большое. Большой по модулю отрицательный порядок числа показывает, что число очень маленькое.
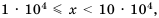
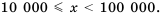
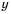
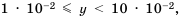
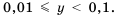
Следовательно, если говорят, что одно число на порядок больше второго, это означает, что оно в 10 раз больше второго, если на два порядка – в 100 раз больше и т. д.
Пример №213
Представьте число 272 000 в стандартном виде.
Решение:
В данном числе поставим занятую так, чтобы в целой части была одна цифра, отличная от нуля. В итоге будем иметь 2,72. Занятой отделили 5 цифр с конца числа, чем уменьшили данное число в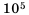 
раз. Следовательно, 
Ответ. 
Пример №214
Представьте число 0,00013 в стандартном виде.
Решение:
В данном числе перенесем запятую на 4 знака вправо, будем иметь 1,3. При этом число увеличили в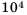 
раз (на 4 порядка). Следовательно, 
Ответ. 
Пример №215
Выполните действия и представьте результат в стандартном виде:
Решение:
Ответ. 
Пример №216
Найдите сумму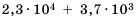 
и запишите результат в стандартном виде.
Решение:
Имеем два слагаемых разных порядков. 
Ответ. 
Функция Y=K/X ее график и свойства
Функция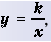 
ее график и свойства
Пример №217
Пешеход должен преодолеть путь в 16 км. Если он будет двигаться со скоростью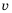 
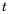
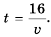
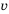
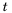
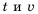
км/ч, то зависимость времени 
(в часах) для преодоления этого расстояния от скорости движения можно выразить формулой 
При увеличении значения 
в несколько раз значение 
во столько же раз уменьшится. В этом случае говорят, что переменные 
обратно пропорциональны.
Пример №218
Площадь прямоугольника равна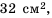 
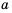
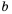
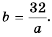
а одна из его сторон 
см. Тогда вторую сторону 
(в см) можно найти по формуле 
Здесь переменные 
также обратно пропорциональны.
В примерах 1 и 2 переменные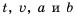 
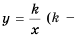
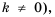
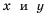
принимают только положительные значения. В дальнейшем будем рассматривать функции, которые задают формулой вида 
число, 
где переменные 
могут принимать как положительные, так и отрицательные значения. Каждую из таких функций называют обратной пропорциональностью.
Функцию вида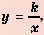 
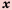
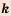
где 
— независимая неременная, 
– некоторое отличное от нуля число, называют обратной пропорциональностью.
Область определения функции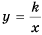 
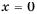
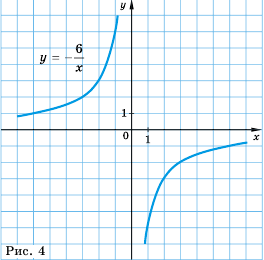
все числа за исключением нуля, так как при 
выражение 
не имеет смысла.
Построим график функции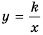 
отдельно для каждого из случаев 
Пример №219
Постройте график функции 
Решение:
Составим таблицу значений функции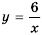 
для нескольких значений аргумента:
Отметим на координатной плоскости точки из составленной таблицы (рис. 2). 
Если бы мы на этой плоскости обозначили больше точек, удовлетворяющих формуле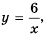 
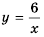
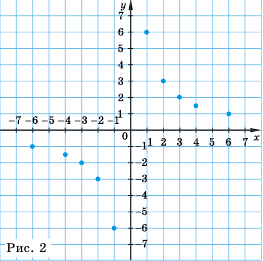
а потом соединили их плавной линией, то получили бы график функции 
(рис. 3).
График обратной пропорциональности называют гиперболой.
Гипербола состоит из двух ветвей. Для функции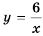 
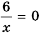
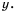
одна из них лежит в первой координатной четверти, а другая – в третьей. Гипербола не пересекает координатные оси: график не содержит точек, у которых 
(т. к. нуль не принадлежит области определения функции), и не содержит точек, у которых
(т. к. уравнение 
не имеет решений). Чем больше по модулю значение 
тем меньше по модулю значение 
и наоборот, чем меньше по модулю значение 
тем больше по модулю значение 
Это значит, что ветви гиперболы неограниченно приближаются к осям координат.
Так же выглядит график функции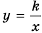 
при любом 
Пример №220
Постройте график функции 
Решение:
Рассуждая как и в предыдущем примере, построим график функции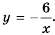 
Он изображен на рисунке 4.
Это также гипербола, одна из ветвей которой лежит во второй координатной четверти, а другая – в четвертой.
Так же выглядит график функции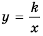 
при любом 
Обобщим свойства обратной пропорциональности 
1. Область определения функции состоит из всех чисел за исключением нуля.
2. Область значений функции состоит из всех чисел за исключением нуля.
3. График функции – гипербола, ветви которой при 
лежат в первой и третьей координатных четвертях, а при 
– во второй и четвертой.
4. Ветви гиперболы неограниченно приближаются к осям координат.
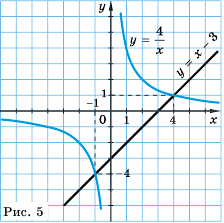
Пример №221
Постройте в одной системе координат графики функций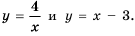 
Найдите их точки пересечения и, пользуясь построенным графиком, решите уравнение 
Решение:
График функции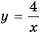 
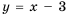
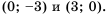
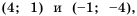
гипербола, ветви которой лежат в первой и третьей координатных четвертях, а график функции 
прямая, проходящая через точки 
Графики функций изображены на рисунке 5. Они пересекаются в точках 
абсциссы 4 и -1 которых являются решениями уравнения 
Действительно, при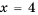 
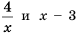
выражения 
принимают
равные значения: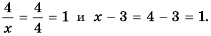 
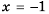
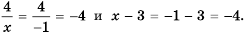
При 
аналогично: 
Следовательно, числа 4 и -1 – корни уравнения 
Ответ: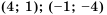 
– точки пересечения; 4, -1 – корни уравнения.
Предложенный в примере 5 метод решения уравнений называют графическим методом решения уравнений.
Если абсцисса точки пересечения графиков функций – целое число, надо выполнить проверку, т. к. часто корни уравнения этим методом можно найти только приблизительно.
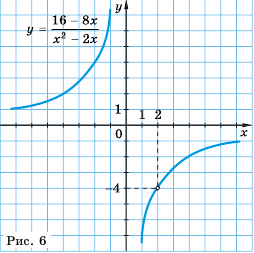
Пример №222
Постройте график функции 
Решение:
Область определения функции – все числа за исключением чисел 0 и 2, которые обращают знаменатель 
в нуль.
Упростим дробь: 
Значит при условии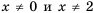 
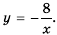
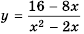
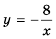
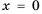
функция принимает вид 
Графиком функции 
является гипербола 
с «выколотой» точкой 
точек же с абсциссой 
у гиперболы нет (рис. 6).
————
Если все решения одного уравнения также являются решениями второго, то второе уравнение называется следствием первого уравнения.
Если множества решений двух уравнений совпадают, то эти уравнения называются равносильными.
Пример 1.
Равносильны ли уравнения?
Решение:
1) Оба уравнения имеют общий корень: х=1. Так как они не имеют других корней, то они являются равносильными.
2) Первое уравнение имеет корень, равный 0. Второе же уравнение такого корня не имеет. Значит, данные уравнения не равносильны.
Пусть Р(х) и Q(x) – многочлены переменной х.
Выражение вида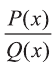 
называется рациональным.
Пусть А(х) и В(х) – рациональные выражения. Уравнение вида А(х)=В(х) называется рациональным.
Рассмотрим сначала простейшее рациональное уравнение вида
Известно, что дробь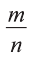 
равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен от нуля (на нуль делить нельзя!). Значит, для того, чтобы решить уравнение (1) , необходимо и достаточно найти все значения неизвестной х, для которых одновременно выполнены условия 
Для краткости, это мы будем записывать так: 
- Заказать решение задач по высшей математике
Пример:
Решите уравнение:
Решение:
Уравнение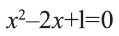 
имеет единственное решение х=1. При х=1 знаменатель отличен от нуля. Значит, данное уравнение тоже имеет единственное решение х=1.
2) Квадратное уравнение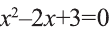 
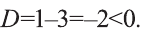
не имеет корней, так как 
Значит, данное уравнение тоже не имеет корней.
3) Для квадратного уравнения 
Значит, это уравнение имеет два корня:
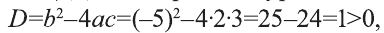
Однако число 1,5 обращает знаменатель выражения 
в нуль, а число 1 – нет. Значит, данное уравнение имеет единственное решение х=1.
4) Уравнение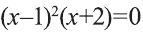 
имеет два корня 1 и-2. Однако число 1 обращает знаменатель (х-1) в нуль, а число -2 – нет. Значит, данное уравнение имеет единственное решение х=—2.
В случае, когда хотя бы одно из выражений А(х) и В(х) представимо в виде суммы нескольких рациональных выражений, рациональное уравнение А(х)=В(х) можно решить так:
- 1 шаг. Ищем общий знаменатель дробей, входящих в уравнение;
- 2 шаг. Обе части уравнения умножаем на этот общий знаменатель;
- 3 шаг. Ищем решения полученного уравнения;
- 4 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель в нуль.
Пример:
Решите уравнение 
Решение:
Умножаем обе части уравнения на общий знаменатель 2х(2-х). Упрощая полученное уравнение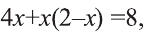 
, приводим его к следующему квадратному уравнению: 
Так как D=9-8=l>0, то данное квадратное уравнение имеет два корня:
х=2; х=4.
Проверка.
При х=2 знаменатель обращается в нуль: х(2-х) = 2(2-2) = 0. Значит, х=2
не является решением исходного уравнения.
При х=4 знаменатель отличен от нуля х(2-х) = 4(2-4) Ф 0. Значит, х=4
является решением исходного уравнения.
Если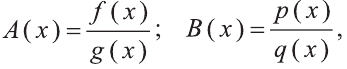 
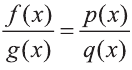
то при решении рационального уравнения вида 
полезно воспользоваться основным свойством пропорции: 
При этом получим следующий алгоритм решения:
- 1 шаг. Ищем решения уравнения f (х)q(х) = р(х)g(х)
- 2 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель q(x)g(x) в нуль.
Пример:
Решите уравнение 
Решение:
В некоторых случаях удачно выполненная замена позволяет привести заданное уравнение к более простому.
Пример:
Решите уравнение:
Решение:
1) Выполним замену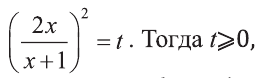 
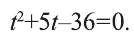
а уравнение получит вид 
Последнее имеет корни t=-9 и t=4, из которых второе положительно.
При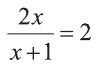 
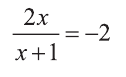
уравнение не имеет решение, а при 
уравнение имеет единственное решение х=-0,5.
Ответ: х=-0,5.
2) Очевидно, что х=0 удовлетворяет уравнению. Пусть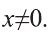 
. Разделив в каждой дроби уравнения числитель и знаменатель на х, получим уравнение
Тогда наше уравнение получит вид: 
Решим последнее уравнение:
Теперь найдем x.
В силу того, что дискриминант квадратного уравнения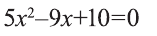
отрицателен, то последнее уравнение не имеет действительных решений. Ответ: х=0.
Системы рациональных уравнений
Решение систем, состоящих из рациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует не забывать, что знаменатели, участвующих рациональных выражений, не могут обращаться в нуль.
Пример:
Решите систему:
Решение:
1) Сделаем в первом уравнении замену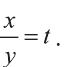 
Получим 
Отсюда или 
Решим полученные системы: 
Первая система имеет решения (3,2), (-3, -2), а вторая не имеет решений. Ответ: (3; 2), (-3; -2).
2). Обозначим 
——
Рациональные уравнения
Рациональные уравнения широко применяются в приборостроении, космических исследованиях, финансовых операциях и т.д.
Подобие фигур широко применяется в измерительных, конструкторских и дизайнерских работах.
Это интересно!
На рисунке изображена модель орбитального космического корабля, предназначенная для полёта в космос туристов. Корабль рассчитан на 6 пассажиров и 2 членов экипажа.
Для того, чтобы рассчитать оптимальные размеры корабля конструкторам и инженерам пришлось решить много рациональных уравнений.
Рациональные уравнения
Уравнение, содержащее в левой и правой части рациональные выражения называется рациональным уравнением. Во многих задачах приходится решать рациональные уравнения, содержащие переменную в знаменателе. В этом случае необходимо указывать область допустимых значений переменных (ОДЗ).
Пример:
В данном уравнении ОДЗ 
Учитывая, что 
умножим обе части уравнения на 
отсюда получим 
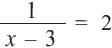
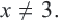
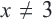
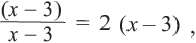
Подставим полученное значение в уравнение: 
Таким образом,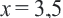 
является корнем уравнения. Данное уравнение не имеет других корней.
Пример:
Решим уравнение 
ОДЗ данного уравнения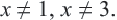 
Умножим обе части уравнения на общий
знаменатель 
Пример:
В уравнении,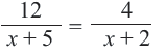 
ОДЗ 
Используя свойство пропорции можно написать: 
Пример:
Решим уравнение.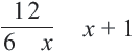 
Здесь ОДЗ, 
Умножим обе части уравнения на 
Отсюда 
Проверьте, являются ли оба этих числа корнями данного уравнения.
Пример:
Решим уравнение 
Запишем уравнение в виде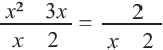 
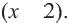
и умножим обе стороны на общий множитель 
Получим 
Отсюда 
При проверке, убеждаемся что,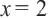 
не удовлетворяет уравнению, т.к. превращает знаменатель в «0». Таким образом, корнем данного уравнения является только 
Внимание! После решения рационального уравнения, содержащего переменную в знаменателе, нужно обязательно выполнить проверку корней.
Решение задач с помощью рациональных уравнений
Задачи на работу
Задача. Двое рабочих могут выполнить некоторую работу за 12 дней. За сколько дней каждый рабочий выполнит эту работу в отдельности, если одному из них для выполнения этой работы потребуется на 10 дней больше ,чем другому? Решение: Пусть, 2-ой рабочий может выполнить работу за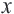 
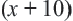
дней, тогда 1-ый рабочий выполнит её за 
дней
Первый рабочий за 1 день выполняет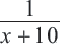 
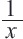
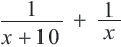
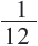
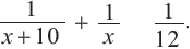
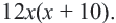
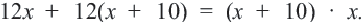
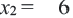
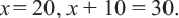
– ую часть работы, 2-ой – 
– ую. Вместе, за 1 день они выполнят 
часть работы. Зная, что вместе за 1 день они выполняют 
часть работы (согласно условию), составим уравнение 
Умножим обе части уравнения на 
Получим, 
После упрощения имеем 
Решением данного уравнения являются числа 
и 
(не удовлетворяет условию, т.к. 
). Итак 
Ответ: 2-ой рабочий выполняет работу за 20 дней, а 1-ый – за 30 дней.
Задачи на движение
Задача. Путь длиной 480 км проходит по асфальтовой и по просёлочной дороге. Автомобиль расстояние 80 км по просёлочной дороге, прошёл со скоростью на 40 км/час меньше, чем по асфальтовой дороге. Зная, что на весь путь он затратил 7 часов, найдите время, которое потратил автомобиль при движении по просёлочной дороге.
1-й способ:
Из 2-ой строки таблицы: 
Из 3-е1 строки таблицы: 
Отсюда получаем рациональное уравнение 
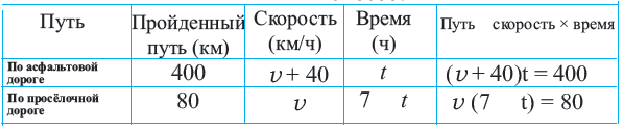
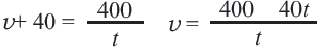
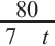
Разделим обе части уравнения на 40: 
Получим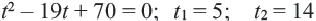 
(противоречит условию задачи)
Ответ: по просёлочной дороге 2 часа
2-ой способ: Автомобиль ехал по дороге, покрытой асфальтом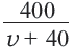 
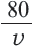
часов, а по проселочной дороге 
часов.
Зная, что на весь путь он потратил 7 часов, составим уравнение: 
Решив данное уравнение, получим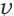 
= 40 км/ч. Тогда по просёлочной дороге он двигался 80 : 40 = 2 часа.
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Интеграл и его применение
- Параллельность в пространстве
- Перпендикулярность в пространстве
- Векторы и координаты в пространстве
- Множества
