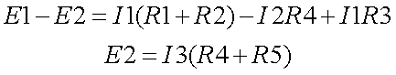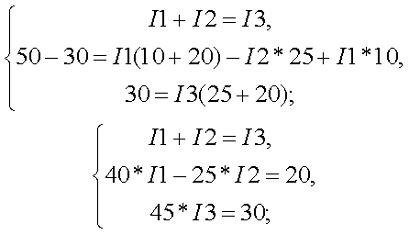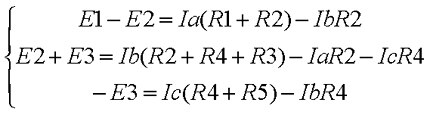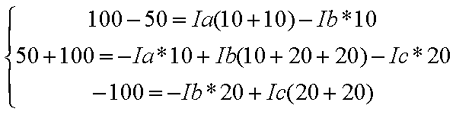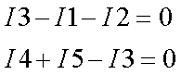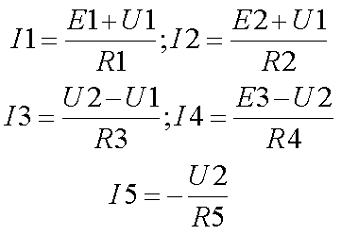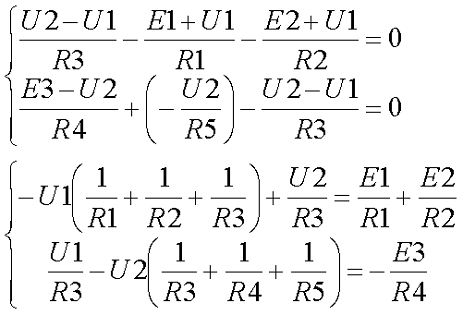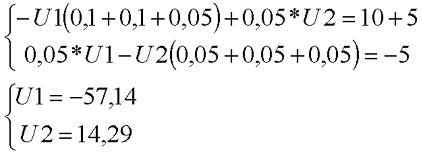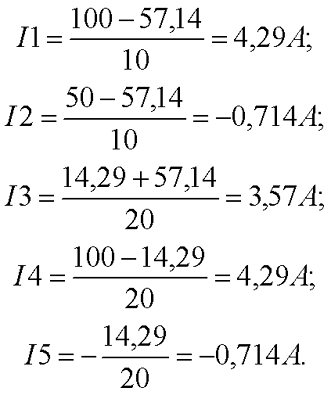Как составить расчетную схему электрической цепи

36

Лабораторная
работа 4 (Lr4)

РАЗВЕТВЛёННАЯ
ЦЕПЬ ПОСТОЯННОГО ТОКА

ЦЕЛЬ
РАБОТЫ

Теоретическое
и экспериментальное исследование
линейной разветвлённой цепи постоянного
тока.

ТЕОРЕТИЧЕСКИЕ
СВЕДЕНИЯ И РАСЧЁТНЫЕ ФОРМУЛЫ

Задача
анализа разветвленной электрической
цепи обычно сводится к нахождению токов
ветвей и напряжений на различных участках
цепи. Руководствуясь обобщенной схемой
замещения цепи (рис. 4.1) и табл. 4.1 вариантов
задания, необходимо вычертить в отчете
расчётную схему цепи.

При
этом ветви схемы цепи с незаданными
источниками тока
J_k
необходимо разомкнуть (т. е. исключить),
а участки цепи с незаданными идеальными
источниками напряжения E_k
заменить проводниками, оставив в ветвях
резисторы R_k.
В преобразованной схеме должны остаться
два источника нап­ряжения (ИН) и один
источник тока (ИТ). Если ЭДС E_k
или ток J_k
задан со знаком “минус”, то направление
их стрелок на схеме целесообразно
изменить на противоположное и в исходных
данных записать эти источники со знаком
“плюс”. Условные положительные
направления токов в ветвях и узловых
напряжений указаны на рис. 4.1.

2. Расчёт схемы цепи методом узловых

НАПРЯЖЕНИЙ

Для
расчёта сложных электрических цепей
используют метод узловых напряжений
(МУН) или метод контурных токов (МКТ).
Необходимое число уравнений для расчета
цепи этими методами определяют по
формулам:

N_МУН
= У

1; N_МКТ
= B

(У

1),

где
В
и У –
число ветвей (без учёта ветвей с
источниками тока) и узлов в схеме.

Выполним расчет
схемы цепи (рис. 4.2) (вариант N
= 36, см. табл. 4.1) методом узловых напряжений.
Исходные данные для расчета: J₁
= 2 А; E₁
= = 10 B;
E₅
= 20 B;
R₁
= 1 Ом; R₂
= 2 Ом; R₃
= 3 Ом; R₄
= 4 Ом; R₅
= 5 Ом; R₆
= 6 Ом.
Направление
тока J₁
изменено
на противоположное, т. к. в табл. 4.1
(вариант 36) ток задан со знаком “минус”
(J₁
= 2
А).

Т а б л и ц а 4.1

Топологический
анализ схемы показывает, что в ней 7
ветвей, 4 узла, 3 независимых контура и
6 неизвестных токов I₁,
… , I₆.
Число независимых уравнений

N_МУН
= У
– 1 = 4 
1 = 3.

Выбираем
базисный узел (узел 0), направляем к нему
узловые напряжения U₁₀,
U₂₀
и U₃₀
(см. рис.
4.2) и составим систему уравнений:

где
G₁₁
= G₁
+ G₂
+ G₆
= 1/R₁
+ 1/R₂
+ 1/R₆
= = 1/1 + 1/2 +
1/6 = 1,667 См;

G₂₂
= G₁
+ G₃
+ G₄
= 1/R₁
+ 1/R₃
+ 1/R₄
= 1/1 + 1/3 + 1/4
= 1,583 См;

G₃₃
= G₂
+ G₃
+ G₅
= 1/R₂
+ 1/R₃
+ 1/R₅
= 1/2 + 1/3 + 1/5
= 1,033 См 
узловые проводимости; G₁₂
= G₂₁
= G₁
= 1 См; G₂₃
= G₃₂
= G₃
= 0,333 См;
G₁₃
= G₃₁
= G₂
= 1/2 =
0,5 См –
межузловые проводимости; J₁
+ G₁E₁
= =
2
+ 110
= 8 A;
G₁E₁=
110
= 10
A;
G₅E₅
=
1/520
= 4 A
– узловые токи.

Подставив
числовые значения в сис­тему уравнений,
имеем:

Воспользовавшись
калькулятором Elcalc
(рис. 4.3),
записываем
узловые напряжения в табл. 4.2.

Токи
ветвей определим по обоб­щенному
закону Ома (с учетом выб­ран­­ных
условно положительных нап­ра­влений
токов в ветвях (см. рис. 4.2)):

I₁
=
(E₁
– U₁₂)/R₁
= (E₁
– (U₁₀
–
U₂₀))/R₁
= (10 – (6,028 + 1,16))/1 = 2,812
А;

I₂
=
U₃₁/R₂
= (U₃₀

U₁₀)/R₂
= (6,416 – 6,028)/2 = 0,194 А;

I₃
=
U₂₃/R₃
=
(U₂₀

U₃₀)/R₃
= (1,16
– 6,416)/3 = 2,525
А;

I₄
=
U₂₀/R₄
=
1,16/4 = 0,29 А;

I₅
=
(E₅

U₃₀)/R₅
= (20 
6,416)/5 = 2,717
А;

I₆
=
U₁₀/R₆
= 6,028/6
= 1,005
А.

Вычисленные
значения токов заносим в табл. 4.2.

Моделируем
схему цепи варианта 36 на рабочем поле
программы MS10
(рис. 4.4). Запускаем программу на исполнение
и заносим показания приборов в табл.
4.2. Убеждаемся, что расчетные и
экспериментальные данные практически
совпадают.

Т а б л и ц а 4.2

Соседние файлы в папке лабы по тоэ

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Тема. Расчет простых
электрических цепей

Решение любой задачи по расчету
электрической цепи следует начинать с выбора метода, которым будут произведены
вычисления. Как правило, одна и таже задача может быть решена несколькими
методами. Результат в любом случае будет одинаковым, а сложность вычислений
может существенно отличаться. Для корректного выбора метода расчета следует
сначала определиться к какому классу относится данная электрическая цепь: к
простым электрическим цепям или к сложным.

К простым относят
электрические цепи, которые содержат либо один источник электрической энергии,
либо несколько находящихся в одной ветви электрической цепи. Ниже изображены
две схемы простых электрических цепей. Первая схема содержит один источник
напряжения, в таком случае электрическая цепь однозначно относится к простым
цепям. Вторая содержит уже два источника, но они находятся в одной ветви,
следовательно это также простая электрическая цепь.
 
Расчет простых
электрических цепей обычно производят в такой последовательности:

1. Сначала упрощают схему последовательно преобразовав все
пассивные элементы схемы в один эквивалентный резистор. Для этого необходимо
выделять участки схемы, на которых резисторы соединены последовательно или
параллельно, и по известным формулам заменять их эквивалентными резисторами (сопротивлениями).
Цепь постепенно упрощают и приводят к наличию в цепи одного эквивалентного
резистора.

2. Далее подобную процедуру проводят с активными элементами
электрической цепи (если их количество более одного источника). По аналогии с
предыдущим пунктом упрощаем схему до тех пор, пока не получим в схеме один
эквивалентный источник напряжения.

3. В итоге мы приводим любую
простую электрическую схему к следующему виду:  Теперь
есть возможность применить закон Ома – соотношение  и фактически определить
значение тока протекающего через источник электрической энергии.

соотношение (1.22) и фактически
определить значение тока протекающего через источник электрической энергии.

Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Расчёт электрических цепей с помощью законов Кирхгофа

Существует несколько методов расчёта электрических цепей, которые различаются между собой параметрами, которые необходимо найти, а так же количеством необходимых расчётов.

Вначале я расскажу, как произвести расчёт цепи в общем виде, но в результате размеры вычислений будут неоправданно большими. Данный метод расчёта основан на законах Ома и Кирхгофа и используется при расчётах небольших цепей с малым количеством контуров. Для этого составляют систему уравнений из (q — 1) уравнений для узлов цепи и n уравнений для независимых контуров. Независимые контуры характеризуются тем, что при составлении уравнений для каждого нового контура входит хотя бы одна новая ветвь, не вошедшая в предыдущий контур. Таким образом, количество уравнений в системе уравнений по данному методу расчёта цепи будет определяться следующим выражением

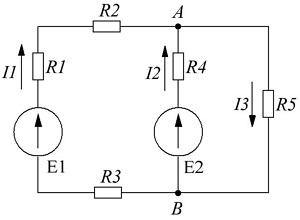
В качестве примера рассчитаем электрическую цепь, приведённую на рисунке ниже

Пример электрической цепи для расчёта по законам Ома и Кирхгофа.

В качестве примера возьмём следующие параметры схемы: E1 = 50 B, E2 = 30 B, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.

1. Составим уравнение по первому закону Кирхгофа. Так как узла у нас два, то выберем узел А и составим для него уравнение. Я выбрал условно, что токи I1 и I2 втекают в узел, а I3 – вытекает, тогда уравнение будет иметь вид

   

2. Составим недостающие уравнения по второму закону Кирхгофа. В схеме у нас два независимых контура: E1R1R2R4E2R3  и E2R4R5, поэтому выбирая произвольное направление контуров составим недостающие два уравнения. Я выбрал обход по ходу часовой стрелке, поэтому уравнения имеют вид

   

Таким образом, получившаяся система уравнений будет иметь следующий вид

Решив данную систему, получим следующие результаты: I1 ≈ 0,564 А, I2 ≈ 0,103 А, I2 ≈ 0,667 А.

В результате решения системы уравнений по данному методу может оказаться, что токи получились отрицательными. Это значит, что действительное направление токов противоположно по направлению выбранному.

Метод контурных токов

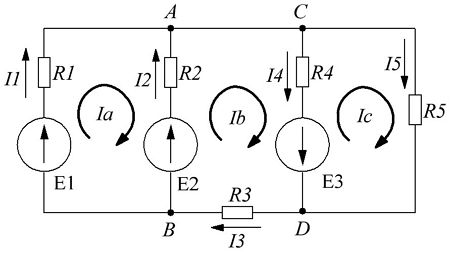
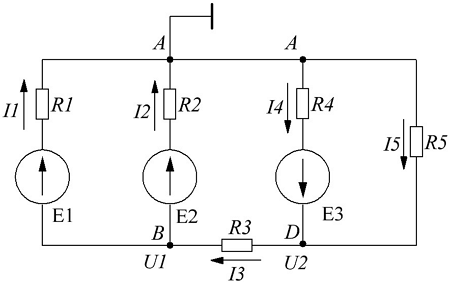
Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже

Расчет цепи методом контурных токов.

Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.

В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях

Остальные же токи можно найти как разность двух контурных токов

В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.

Метод узловых напряжений

Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает

где q – количество узлов в электрической цепи.

Принцип расчёта электрической цепи заключается в следующем:

1. Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю;
2. Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление;
3. После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома.

В качестве примера возьмём предыдущую цепь и составим систему уравнений

Схема для решения уравнений методом узловых потенциалов.

В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа

Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома

В результате получившаяся система будет иметь следующий вид

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы уравнений мы пришли к следующим результатам: потенциал в узле В – U1 = -57,14 В, а в узле D – U2 = 14,29 В. Теперь нетрудно посчитать, что токи в ветвях будут равны

Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.