Расчетная схема
Расчетная
Схема Сопромат
Расчетная
схема –
это упрощенная, идеализированная схема,
которая отражает наиболее существенные
особенности объекта, определяющие его
поведение поднагрузкой.
Расчет
реальной конструкции начинается с
выбора расчетной
схемы.
Выбор расчетной схемы начинается со
схематизации свойств материала и
характера деформирования твердого
тела, затем выполняется схематизация
геометрической формы реального объекта.
ФОРМЫ
ЭЛЕМЕНТОВ КОНСТРУКЦИИ НА РАСЧЕТНОЙ
СХЕМЕ
Формы
элементов конструкций, используемых в
расчетных схемах, можно свести к четырем
категориям: стержню, оболочке, пластине
и массивному телу.
Стержень
на расчетной схеме
Стержень –
тело, у которого один размер (длина)
значительно превышает два других
размера.
Представим
себе некоторую плоскую фигуру,
перемещающуюся в пространстве так, что
центр тяжести этой фигуры все время
остается на некоторой линии (прямой или
кривой), а сама фигура остается
перпендикулярной к этой линии. Описанная
такой фигурой форма дает нам очертание
стержня. Линия, вдоль которой перемещается
фигура, называется осью стержня, а сама
фигура – его поперечным сечением.
Оболочка
и пластина на расчетной схеме
Оболочка –
это тело, ограниченное двумя криволинейными
поверхностями, у которого один размер
(толщина) много меньше двух других
размеров.Пластина –
это тело, ограниченное двумя параллельными
плоскостями.
Массивное
тело на расчетной схеме
Массивное
тело –
тело, у которого все три размера имеют
один порядок.
В
курсе сопромата в
основном изучается напряженно-деформированное
состояние призматических стержней с
прямолинейной осью. Оболочки
и массивные тела, как правило, не могут
быть рассчитаны методами сопромата.
Метод
сечений. Силовые факторы в методе сечений
Метод
Сечений. Силовые Факторы В Методе Сечений
Сопромат
Метод
сечений позволяет
определить внутренние
силы,
которые возникают встержне,
находящемся в равновесии под
действием внешней
нагрузки.
Рассмотрим
идеально упругий призматический стержень
прямоугольного поперечного сечения
(рис. 1.2, а).
Выделим
внутри стержня какие-либо две частицы
K и L, расположенные на бесконечно малом
расстоянии друг от друга. Для большей
наглядности предположим, что между
этими частицами имеется некоторая
пружинка, удерживающая их на определенном
расстоянии друг от друга. Пусть натяжение
пружинки равно нулю.
Приложим
теперь к стержню растягивающую силу (рис.
1.2, б).
Пусть в результате деформации стержня,
частица K перейдет
в положение ,
а частица L
– в
положение .
Соединяющая эти частицы пружинка при
этом растянется. После снятия внешней
нагрузки частицы вернутся в первоначальное
положение K и Lблагодаря
усилию, которое возникло в пружинке.
Сила, которая возникла между частицами
(в пружинке) в результате деформации
идеально упругого стержня, называются
силой упругости или
внутренней силой. Она может быть
найдена методом
сечений.
ЭТАПЫ
МЕТОДА СЕЧЕНИЙ
Метод
сечений состоит
из четырех последовательных
этапов: разрезать,
отбросить, заменить, уравновесить.
Разрежем стержень,
находящийся в равновесии под действием
некоторой системы сил (рис.
1.3, а) на две части плоскостью,
перпендикулярной к его оси z.
Отбросим одну
из частей стержня и рассмотрим оставленную
часть.
Поскольку
мы как бы разрезали бесчисленное
множество пружинок, соединявших
бесконечно близкие частицы тела,
разделенного теперь на две части, в
каждой точке поперечного сечения стержня
необходимо приложить силы упругости,
которые при деформации тела возникли
между этими частицами. Иными
словами,заменим действие
отброшенной части внутренними
силами (рис.
1.3, б).
ВНУТРЕННИЕ
СИЛЫ В МЕТОДЕ СЕЧЕНИЙ
Полученную
бесконечную систему сил по правилам
теоретической механики можно привести
к центру тяжести поперечного сечения.
В результате получим главный вектор R
и главный момент M (рис. 1.3, в).
Разложим
главный вектор и главный момент на
составляющие по осям x, y (главные
центральные оси) и z.
Получим
6 внутренних
силовых факторов,
возникающих в поперечном сечении стержня
при его деформировании: три силы (рис.
1.3, г) и три момента (рис.
1.3, д).
Сила
N – продольная сила
– поперечные
силамы,
момент
относительно оси z () –
крутящий момент
моменты
относительно осей x, y ()
– изгибающие моменты.
Запишем
для оставленной части тела уравнения
равновесия (уравновесим):
.
Из
уравнений определяются внутренние
усилия, возникающие в рассматриваемом
поперечном сечении стержня.
ВЫЧИСЛЕНИЕ
ПРОДОЛЬНОЙ И ПОПЕРЕЧНЫХ СИЛ, КРУТЯЩЕГО
И ИЗГИБАЮЩИХ МОМЕНТОВ
продольная
сила N
равна сумме проекций всех сил (активных
и реактивных), действующих на любую из
частей рассеченного стержня, на ось z;
поперечные
силы равны
сумме проекций всех сил, действующих
на любую из частей стержня, на оси x и y,
соответственно;
крутящий
момент равен
сумме моментов всех сил, действующих
на любую из частей стержня, относительно
продольной оси z;
изгибающие
моменты равны
сумме моментов всех сил, действующих
на любую из частей стержня, относительно
осей x и y, соответственно.
Напряжение
в точке тела
Напряжение
В Точке Тела Сопромат
Напряженное
состояние в точке тела
является ключевым понятием всопромате.
Необходимость введения понятия напряжения
в точке для
суждения об интенсивности внутренних
сил в некоторой точке сечения стержня
вызвана неравномерным распределением
внутренних сил по длине и поперечному
сечению в общем случае нагружения.
Напряжение в
точке тела K (обозначено буквой p) –
это интенсивность
внутренней силы ,
возникающей на бесконечно малой
площадке в
окрестности данной точки (рис. 1.4, а).
В
количественном выражении .
|
|
Понятие
о напряжении
в точке твердого тела в
некотором смысле напоминает понятие о
давлении, действующем, например, внутри
жидкости. Однако давление в точке
жидкости одинаково во всех направлениях.
Если проведем через точку K тела другое
сечение, иной будет внутренняя сила.
Следовательно, иным будет и напряжение,
хотя оно возникает в той же самой точке
K.
Напряжение
в точке тела в
разных направлениях (на разных площадках,
проходящих через данную точку тела)
может быть различным (в частности, оно
может возникать только в одном
направлении).
Понятие
о напряжении в точке деформируемого
твердого тела ввел в 1822 г. французский
ученый Огюстен Луи Коши.
Основную
роль в расчетах прочности играет не
полное напряжение p, а его проекции на
оси координат x, y и z: нормальное
напряжение ( –
сигма), направленное по перпендикуляру
к площадке (параллельно оси z), и касательные
напряжения ( –
тау), лежащие в плоскости сечения и
направленные, соответственно, вдоль
осей x и y (рис. 1.4, б). Первый индекс
у касательных
напряжений характеризует
нормаль к площадке z, на которой они
возникают.
Между
полным (), нормальным
() и касательными
напряжениями ( и
)
существует зависимость:
.
Касательные
напряжения служат мерой тенденции одной
части сечения смещаться (или скользить)
относительно другой его части.
Единицы
нормальных и касательных напряжений в
СИ – паскаль (Па). Один паскаль – это
напряжение, при котором на площадке в
один квадратный метр возникает внутренняя
сила, равная одному ньютону (то есть
равная, приблизительно, весу одного
яблока). Как мы увидим в дальнейшем, эта
единица напряжения мизерно мала. В
сопромате чаще используются другие
единицы:
1
МПа = 106 Па; 1 кН/см2 = 107 Па.
В
технической системе единиц напряжения
измеряются в килограммах
силы на миллиметр (сантиметр) в квадрате
(кгс/мм2 или кгс/см2) . Следует запомнить,
что 1 кН/см2 » 1 кгс/мм2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчетная схема
Расчетная схема – это упрощенная, идеализированная схема, которая отражает наиболее существенные особенности объекта, определяющие его поведение под нагрузкой.
Расчет реальной конструкции начинается с выбора расчетной схемы. Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела, затем выполняется схематизация геометрической формы реального объекта.
Формы элементов конструкции на расчетной схеме
Формы элементов конструкций, используемых в расчетных схемах, можно свести к четырем категориям: стержню, оболочке, пластине и массивному телу.
Стержень на расчетной схеме
Стержень – тело, у которого один размер (длина) значительно превышает два других размера.
Представим себе некоторую плоскую фигуру, перемещающуюся в пространстве так, что центр тяжести этой фигуры все время остается на некоторой линии (прямой или кривой), а сама фигура остается перпендикулярной к этой линии. Описанная такой фигурой форма дает нам очертание стержня. Линия, вдоль которой перемещается фигура, называется осью стержня, а сама фигура – его поперечным сечением.
Оболочка и пластина на расчетной схеме
Оболочка – это тело, ограниченное двумя криволинейными поверхностями, у которого один размер (толщина) много меньше двух других размеров. Пластина – это тело, ограниченное двумя параллельными плоскостями.
Массивное тело на расчетной схеме
Массивное тело – тело, у которого все три размера имеют один порядок.
В курсе сопромата в основном изучается напряженно-деформированное состояние призматических стержней с прямолинейной осью. Оболочки и массивные тела, как правило, не могут быть рассчитаны методами сопромата.
Содержание:
- Понятие о расчетной схеме
- Схематизация по материалу
- Схематизация по нагрузке
- Закон Гука используется при решении большинства задач сопротивления материалов
Понятие о расчетной схеме
Необходимость довести решение каждой практической задачи до некоторого числового результата заставляет в сопротивлении материалов прибегать к упрощающим гипотезам – т. е. предположениям, которые оправдываются в дальнейшем путем сопоставления расчетных данных с экспериментом.
- Таким образом, приступая к расчету конструкции, следует прежде всего установить, что в данном случае является существенным и что не существенно.
Необходимо, как говорят, произвести схематизацию объекта конструкции (рис. 1.1), т. е. отбросить все те факторы, которые не могут сколько-нибудь заметным образом повлиять на работу системы в целом.
Такого рода упрощения задачи совершенно необходимы, так как решение с полным учетом всех свойств реального объекта является принципиально невозможным в силу их очевидной неисчерпаемости.
Реальный объект, освобожденный от несущественных признаков, носит название расчетной схемы.
Схематически процесс получения расчетной схемы показан на рис. 1.1. Остановимся подробнее на отдельных этапах процесса превращения реальной конструкции в расчетную схему.
Схематизация по материалу
Будем считать, что материал рассчитываемой конструкции однороден, т.е. его свойства не зависят от величины выделенного из тела объема.
Вводится понятие сплошности среды, как среды, непрерывно заполняющей отведенный ей объем. Вследствие чего к сплошной среде может быть применен анализ бесконечно малых.
Эти положения позволяют не принимать во внимание дискретную, атомистическую структуру вещества. Они применяются даже при расчете конструкций из такого неоднородного материала, как бетон.
Материал изотропен, т.е. обладает во всех направлениях одинаковыми свойствами. Это предпосылка используется при решении большинства задач сопротивления материалов, хотя для некоторых материалов (дерево, железобетон, медь, пластмассы и др.) она весьма условна.
Материалы, свойства которых в разных направлениях различны, называются анизотропными.
Материал конструкции обладает свойством идеальной упругости, т.е. способностью полностью восстанавливать первоначальные форму и размеры тела после снятия внешней нагрузки.
Эта предпосылка справедлива лишь при напряжениях, не превышающих для данного материала определенной, постоянной величины, называемой пределом упругости.
Предпосылка об идеальной упругости материала используется при решении большинства задач сопротивления материалов.
Схематизация по геометрии отдельных элементов конструкции.
Возможно вам будут полезны данные страницы:
Основное внимание в сопротивлении материалов уделяется изучению брусьев, являющихся наиболее распространенным элементом многих конструкций.
Брусом называется элемент, длина которого значительно больше его поперечных размеров.
Осью бруса называется линия, соединяющая центры тяжести его поперечных сечений.
Плоская фигура, имеющая свой центр тяжести на оси и нормальная к ней, называется его поперечным сечением.
Брус с прямолинейной осью часто называют стержнем (рис. 1.2, а).
Элемент конструкции, длина и ширина которого во много раз превышают его толщину, называется оболочкой (рис. 1.2, б).
Геометрическое место точек, равноудаленных от наружной и внутренней поверхностей оболочки, называется срединной поверхностью.
Оболочка, срединная поверхность которой представляет собой плоскость, называется пластинкой (рис. 1.2, в).
Элемент конструкции, размеры которого во всех направлениях мало отличаются друг от друга (например, сплошная опора моста), называется массивным телом (рис. 1.2, г ).
Методы расчета пластинок, оболочек и массивов рассматриваются в курсе «Прикладная теория упругости».
Для прикрепления сооружения к основанию служат опоры, обеспечивающие неподвижность опорных точек конструкции. Обычно в сопротивлении материалов рассматривают три основных типа опор: шарнирно подвижная опора, шарнирно неподвижная опора и жесткое защемление.
На рис. 1.3, а изображена простейшая схема устройства шарнирно подвижной опоры, а на рис. 1.3, б – ее условное изображение. Подвижная опора допускает вращение вокруг оси, проходящей через центр шарнира 


Шарнирно неподвижная опора (рис. 1.3, в) обеспечивает вращение верхнего балансира 


Шарнирно неподвижная опора (рис. 1.3, в) обеспечивает вращение верхнего балансира 


Жесткое защемление (рис. 1.3, д, е, з) не допускает каких либо линейных перемещений и поворота. В защемлении возникают две составляющие


Схематизация по нагрузке
Распределенные нагрузки могут быть поверхностными (давление ветра, воды на стенку) или объемными (сила тяжести, силы инерции). Если давление 


Сосредоточенная сила 


Если давление 



На расчетной схеме вместо бруса изображается его ось.
Нагрузки, распределенные по линии и сосредоточенные в точках, реально не существуют. Их можно получить лишь в результате схематизации реальных нагрузок, распределенных по объему (объемных сил) или по поверхности.
Нагрузки различаются не только по способу их приложения (распределенные и сосредоточенные), но также по длительности действия (постоянные и временные) и характеру воздействия на конструкцию (статические и динамические).
Постоянные нагрузки (например, собственный вес конструкции) действуют на протяжении всего периода эксплуатации конструкции.
Временные нагрузки (например, вес поезда) действуют в течение ограниченного промежутка времени.
Статическими называются нагрузки, которые изменяют свою величину или точку приложения (или направление) с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.
Если ускорения значительны и нагрузка изменяется во времени с большой скоростью, то мы имеем дело с динамической нагрузкой. Действие таких нагрузок сопровождается возникновением колебаний сооружений. При этом, согласно второму закону Ньютона, возникают силы инерции, пропорциональные массам и ускорениям, которыми при расчете пренебречь нельзя.
Временная нагрузка может сохранять более или менее постоянную величину в течение всего периода ее действия, а может непрерывно изменяться по некоторому закону; в последнем случае она называется переменной нагрузкой.
Если переменная нагрузка изменяется по циклическому (повторяющемуся) закону, то она называется циклической.
- В заключение отметим, что если для одного объекта может быть предложено несколько расчетных схем, то, с другой стороны, одной расчетной схеме может быть поставлено в соответствие много различных реальных объектов.
Последнее обстоятельство является весьма важным, так как исследуя некоторую схему, можно получить решение целого конкретных задач, сводящихся к данной схеме.
Принцип независимости действия сил гласит, что результат действия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу последовательно и в любом порядке.
Например, прогиб 


Он применим к деформируемым телам лишь тогда, когда перемещения точек приложения сил, являющиеся результатом деформации тела, во-первых малы по сравнению с размерами тела и во-вторых линейно зависят от действующих сил (закон Гука).
Закон Гука используется при решении большинства задач сопротивления материалов
- На основании принципа Сен-Венана в точках тела, достаточно удаленных от мест приложения нагрузок, величина внутренних сил весьма мало зависит от конкретного способа приложения этих нагрузок, а зависит только от ее статического эквивалента (рис. 1.6).
Этот принцип во многих случаях позволяет производить замену одной системы сил другой системой, статически эквивалентной, что позволяет часто значительно упростить расчет.
Под внутренними силами будем понимать изменение взаимодействия между частицами материала, вызванное внешней нагрузкой. 
Гипотеза плоских сечений предполагает, что сечение, плоское и перпендикулярное к продольной оси до деформации, остается таким же и после деформации (рис. 1.7).
Эта предпосылка впервые была введена Бернулли. Она играет исключительно важную роль в сопротивлении материалов и используется при
выводе большинства формул для расчета брусьев.
- Гипотеза об отсутствии начальных напряжений отрицает наличие в теле внутренних сил до приложения внешней нагрузки.
Это допущение полностью не выполняется ни для одного материала. Например, в стальных деталях имеются внутренние силы, вызванные неравномерным остыванием, в дереве – неравномерным высыханием, в бетоне – в процессе твердения и т.д. Однако, часто они достаточно малы, чтобы их учитывать.
По мере необходимости, при выводе формул, будем принимать и другие гипотезы и предположения, основанные на опыте.
Расчетная схема реальной конструкции показывает только те условия и факторы, которые необходимы для решения задачи, отбрасывая несущественные детали не влияющие на её решение.
Реальные конструкции, как правило, характеризуются большой сложностью конструктивных форм (мост, купол и т.п.).
Провести расчёт реальных конструкции с учётом всех конструктивных особенностей очень часто сложно и иногда даже невозможно.
Вместе с тем конструктивные особенности не всегда оказывают существенное влияние на работу сооружения.
Поэтому при расчёте реальной конструкции её всегда заменяют идеализированной упрощённой схемой – так называемой расчётной схемой, выбор которой является исключительно ответственным этапом расчёта.
От этого выбора зависит точность и трудоёмкость расчёта. Иногда даже небольшое уточнение её ведёт за собой существенное усложнение расчёта или наоборот.
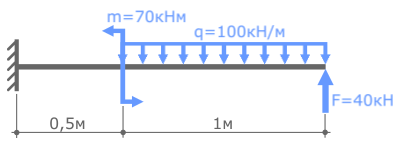
Пример расчетной схемы для решения задачи
Расчётная схема должна полностью отражать основной характер работы реальной конструкции, устраняя несущественные второстепенные факторы.
Другие видео
При схематизации реальных объектов основными элементами расчётных схем являются: брус, оболочка, конструкция крепления этих элементов (опоры), также делаются упрощения в системе сил, приложенных к элементу конструкции.
Примеры решения задач >
Внешние силы и нагрузки >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Сопротивление материалов
К
семинарским занятиям
4. Понятие расчетной схемы.

расчетной схемы
Расчетная
схема оси блока
Расчетная схема траверсы крюка
1. Основные положения
ОБЪЕКТЫ РАСЧЕТНЫЕ
СХЕМЫ

множество расчетных схем.
Условное
изображение конструкции или детали принимаемое для выполнения расчета,
называется расчетной схемой.
Расчетная
схема выбирается так, чтобы существенно упростить расчет, не искажая действительной
картины работы конструкции или детали
Расчетную
схему составляют в следующем порядке:
1.Разбивают
конструкцию на простые элементы;
2. Каждый простой элемент конструкции
заменяют соответствующим расчетным элементом (брусом, пластиной, 060лочкой, массивным
телом);
3. Выбирают схему опорных частей
элемента или конструкции (подвижный и неПОДВИЖНЫЙ шарнир, жесткая заделка и
другие);
4.Выбирают
вариант соединения элементов конструкции между собой и с опорными частями
(жесткий или шарнирный) .
Основные положения
Упрощенное представление нагруженного реального тела без учета
несущественных факторов называется расчетной схемой Основные объекты, которые
подвергаются схематизации при построении расчетной схемы:
Рассмотрим в отдельности каждый
из объектов. 6
Схематизация тела
(к построению расчетной схемы)
Схематизация тела,

–
Понятие расчетной схемы
Расчетные формы и их классификация
Брусом
называется расчетный элемент, длина которого значительно больше размеров его
поперечного сечения.
Брусья классифицируются по форме поперечного сечения и форме оси. По
форме поперечного сечения различают брусья постоянного сечения и переменного
сечения. По форме оси — прямолинейные и криволинейные брусья.
Примерами прямых брусьев являются балки и стержни мостовых и козловых
кранов, валы редукторов и коробок передач, оси транспортных средств.
Примерами
кривых брусьев служат грузоподъёмные крюки, звенья сварных цепей, струбцины,
коленчатые валы, станины станков.
Расчетные формы и их классификация
Оболочкой
называется элемент произвольной формы, длина и ширина которого во много раз
превышает его толщину.
Оболочки
МОГУТ иметь цилиндрическую, коническую или сферическую форму.
Оболочка, срединная поверхность которой представляет собой
плоскость, называется пластинкой.
Встречаются
пластинки прямоугольные и круглые.
Соединение расчетных форм между собой
Конструкция, составленная из
нескольких шарнирно соединенных брусьев, в которые действуют только
растягивающие или сжимающие усилия, называется ф8рмой.
Соединение расчетных форм между собой
Плоская или пространственная, геометрически неизменяемая конструкция,
составленная из нескольких брусьев (стоек и ригелей) во всех или нескольких
узлах жестко соединенных между собой и в которых действует изгибающий момент,
называется рамой.
|
|
Вертикальный, неподвижный элемент рамы, выполненный в виде сплошного или
решетчатого бруса, называется стойкой.
Горизонтальный или наклонный брус (сплошной или решетчатый), связывающий
между собой стойки рам называется ригелем. Ригель служит опорой для плит,
прогонов, навесных элементов
Схематизация нагрузок
(к построению расчетной схемы)
Схематизация нагрузок
Внешние силы
— [сила / длина], кН / м
2
[Е] = [сила] н, кн, мн,

схема
Расчетная схема

– расчетная схема на кручение
Схематизация опор
(к построению расчетной схемы)
Перемещения
В механике различают 2 вида
перемещений:
линейное и угловое.
Линейное перемещение связано с распределенной или
сосредоточенной силой, угловое — с моментом.
Перемещения могут быть действительными (реальными) или
возможными
По числу возможных перемещений и
схематизируют опоры.
Схематизация
опор
Условное
изображение опор (Для плоскости
1 ,
Жесткая заделка.
реакции !

– 2 реакции !

реакции
по нитям !
З, Шарнирно-подвижная опора 
23
Определение реакций
Расчеты в механике выполняются для равновесных систем относительно
внешних сил: активные и реактивные силы должны уравновешивать друг друга.
Математически это выражается в выполнении уравнений равновесия (уравнений
статики
В
пространстве — это 6 уравнений статики.
На плоскости 3 уравнения:
Из этих уравнений определяют реакции
точки
Если уравнений недостаточно для определения реакций системастатически неопределима.
Степень статической неопределимости к (число реакций)О (число уравнений
статики) к = 0 — система статически определима.
число реакций < З — механизм! Не рассматриваем! 24
Пример: ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ

: ЕУ = 0
Схематизация материала
(к построению расчетной схемы)
Основные
Схематизация материала. Большинство гипотез, используемых при построении
расчетной схемы, относятся к схематизации материала.
Сплошность – не принимается во внимание молекулярное строение
тела. Эта гипотеза позволяет использовать математический аппарат непрерывных
функций.
Однородность
материала одинаковые свойства во всех точках тела независимо от его размеров.
Массив
различных горных пород – неоднороден 27
Изотропность одинаковые физикомеханические свойства по всем направлениям
(сталь, чугун, пластмасса, гранит).
Материалы,
обладающие по разным направлениям различными свойствами, называются
анизотропными (Древесина, текстолит),
Упругость способность тела восстанавливать свою первоначальную форму и
размеры после снятия нагрузки.
1,0сновные
Математически идеальная упругость выражается в линейной зависимости между
перемещением д и силой F, его вызывающей:

г),
К — коэффициент пропорциональности, зависит от физических свойств
материала и геометрии системы.
Системы, для которых выполняется закон Гука, называются
линейными системами.
В
заключение данного раздела заметим, что выбор расчетной схемы представляет
ответственную часть инженерного расчета, который состоит из трех этапов:
1. Идеализация объекта.
2. Анализ расчетной схемы. ! ! !
З.
Обратный переход от расчетной схемы к реальному объекту и выдача практических
рекомендаций. 29
Одному реальному объекту может соответствовать несколько
расчетных схем.
Сопротивление материалов занимается
только расчетными схемами !
зо