Как составить расписание самолетов

Хочу поговорить об этом, как человек, который имел к этому самое прямое отношение. Хорошо созданное расписание позволяет работать предприятию с прибылью, при этом обеспечивая регулярность, а не в турборежиме закрывая всё новые дыры в графике. Сколько же нужно самолётов и как обеспечить это расписание – поговорим сегодня.

На самом деле вопрос, как говорится, со звёздочкой. Потому что в ФАП-246 (Федеральные авиационные правила, утв. Пр. МТ РФ №246 «Об утверждении требований к эксплуатантам) (пишу сокращённо, там намного длиннее название) указано следующее:

«15. … Эксплуатант для выполнения регулярных коммерческих воздушных перевозок пассажиров по расписанию регулярных перевозок воздушным транспортом пассажиров владеет воздушными судами, включенными в сертификат эксплуатанта, в количестве , определяемом графиком оборота воздушных судов, с учетом необходимого резерва, но не менее восьми воздушных судов с количеством пассажирских мест 55 и более или не менее трех воздушных судов с количеством пассажирских мест 55 и более в случае, если воздушные суда зарегистрированы в Государственном реестре гражданских воздушных судов Российской Федерации и с даты их производства до даты подачи заявления в уполномоченный орган о внесении воздушного(ых) судна(ов) в эксплуатационную спецификацию сертификата эксплуатанта прошло не более пяти лет, или не менее трех воздушных судов с количеством пассажирских мест до 55…»

Таким образом авиакомпания должна иметь график оборота воздушных судов, который определяется расписанием. При составлении расписания должны быть поэтапно решены следующие задачи:

– Количество и типы воздушных судов, их спецификации, компоновки;

– Аэропорты по программе полётов, их характеристики, инфраструктура;

– Наличие резерва для выполнения регулярных рейсов;

– Наличие согласованных слотов (ОКР) в аэропортах назначения;

– Достаточное количество лётных экипажей, с учётом резервирования, санитарных норм;

– Выделенные периоды для выполнения технического обслуживания воздушных судов.

Это основное. Но можно пройтись по пунктам подробнее.

Характеристики парка и их значение для расписания.

Пример, у Аэрофлота есть в парке самолёты Сухой Суперджет, А-320, А-321, Боинг-737-800. Чем руководствуется авиакомпания при составлении расписания. Ну во-первых у авиакомпании есть определенная история о количестве налёта часов на одну более-менее серьезную ошибку или поломку, которая требует вывода самолёта из резерва. Поэтому Сухие летают всегда, имея резерв на земле. У других авиакомпаний налёт на среднесписочное воздушное судно этого же типа выше, проблемы с запчастями есть, но не так, когда в Трансаэро у одного самолёта Ту-214 сгорела ВСУ, ждали два месяца от изготовителя, в конце концов производитель снял с рабочего прототипа идентичную, чтобы самолёт авиакомпании не простаивал. По этой причине Сухие всегда имеют резерв на земле. Изредка Сухие заменяют А-320, но это тоже бывает не часто – А-320 эксплуатируются чаще, реже выпадает свободный борт, в некоторые аэропорты А-320 не сядет (ну так было со старым аэропортом Саратова). А-320 и Боинг-737-800 взаимозаменяемые, имеют одинаковую вместимость, но для расписания имеются некоторые более важные факторы. В Боинге сделали больший бизнес-класс, что более важно для курортных и деловых направлений. В А-320 можно грузить в контейнерах, что позволяет ускорить оборот, поэтому Питер чаще выполняется на А-320. Боинг летит дальше, в А-320 войдет в багажники больше. Все эти факторы имеют значение. По этой причине в Женеву или Сочи зимой чаще ставят Боинг-737 – он позволяет проще грузить лыжи, ну и бизнес больше. А вот в Германию лучше А-320 – бизнес заполняется не очень, зато много багажа и груза, чтобы ускорить оборот, можно грузить в контейнерах.

Иногда, в расписании система Revenue отслеживает определенные аномальности при продаже перевозок. Например, где-то стали больше брать бизнес, где-то вообще стали брать больше или меньше. От системы поступит предложение об изменении типа воздушного судна. Самолёт могут предварительно поменять, если будет такая техническая возможность. С заменой типа, наверное, сталкивались все.

С учётом особенностей обслуживания самолёта разрабатывается ТГО (технологический график обслуживания). Хорошо разработанный ТГО включает не только основные операции, но и промежуточные. Например, не просто «Погрузка багажа», а отдельно «Открытие багажника», «Подгон транспортёра», «Открытие сеток», «Выгрузка багажа», «Проверка багажника на предмет наличия повреждений», «Фотофиксация», «Отгон транспортера», «Закрытие багажника». Продолжительность оборотного ТГО от 25 минут до полутора часов.

Именно ТГО позволяет рассчитать точное время, необходимое для обслуживания самолёта между прибытием и отправлением, что позволяет составить график оборота воздушных судов.

Аэропорты и их инфраструктура

Это второй важнейший фактор. Аэропорт для планирования программы полётов должен обладать возможностью для приёмки и обслуживания Вашего воздушного судна. В первую очередь это характеристики полосы и рулежных дорожек. В характеристики полосы входит длина и число PCN (предельное давление на покрытие), которые определяют её возможность приёмки рейсов на том или ином типе. Рулёжные дорожки тоже не всегда могут пропустить указанный тип, так как в случае узкой рулёжной дорожки некоторые элементы конструкции ВС могут оказаться за её пределами. Такое было в аэропорту Владивостока, когда функционировал старый терминал – основная рулёжная дорожка (РД-6) не пропускала самолёты А-330 и Ил-96 к терминалу, их приходилось обслуживать на двух специально оборудованных стоянках рядом с полосой.

Кроме этого могут быть ограничения терминала по стойкам регистрации (в конкретный момент времени может не быть свободных стоек регистрации), выходам на посадку (у нас в большинстве региональных аэропортов до сих пор один или два выхода). Аэропорт может не иметь оборудования для работы с пакетированной загрузкой (погрузчик контейнеров, контейнерные тележки и столы). В аэропорту может не оказаться средств механизации для обслуживания данного типа – например, буксировочного водила. В необходимое для обслуживания рейса может не оказаться свободных стоянок для обслуживания данного типа. (Часто бывает такое, что в региональном аэропорту имеется две стоянки для обслуживания широкофюзеляжных самолётов, которые в необходимое время заняты).

Третий момент – регламент работы. Далеко не все аэропорты работают круглосуточно и ежедневно. Многие аэропорты имеют регламент работы. Вне этого регламента в аэропорту отсутствуют сотрудники и он не может обслуживать рейсы. Максимум – будет диспетчер, СПАСОП и ЭРТОС, чтобы принять борт на запасной, но коммерческого обслуживания не будет. Особенно этим грешат аэропорты севера и востока. В круглосуточных аэропортах сотрудники работают в сменном графике из четырёх смен по схеме «день-ночь-отсыпной-выходной».

Наличие резерва

Это самый сложный пункт. Резерв, как его понимают многие, это стоящий на земле борт, который может обслужить рейс в случае поломки планового. Но это слишком просто и невыгодно. За стоящий борт нужно платить всё равно, чтобы поддерживать его лётную годность и лизинг. Да и не решит это проблему, если выйдут из строя два самолёта. Для ответа на данный вопрос следует ответить на произвольный отказ в расписании – чем будет производиться замена в том или ином случае. Вариантов в таком случае несколько:

– Подождать, пока произойдёт устранение неисправности. За это время разместить пассажиров в гостиницах, накормить и напоить. Всё согласно ФАП-82.

– Дождаться прибытия в базовый борт следующего борта, у которого есть «окошко» в графике оборота. По этой причине их необходимо обязательно делать. Как и в каком количестве – чтобы найти ответ на вышеуказанный вопрос.

– В случае внебазового аэропорта или отсутствия свободных окошек в базовом – попробовать заказать рейс у другого перевозчика, либо временно арендовать борт. В последнее время крайне редко – высокая конкуренция, да и сильно загружены парки, чтобы иметь возможность резервирования другого перевозчика.

– Ну и если пассажиров немного – пересадить их на рейсы другого перевозчика по FIM .

Кроме поломок следует рассматривать вероятность плохих погодных условий, которая легко нарушит график оборота, необходимость облива, происшествия на территории аэропорта, введения ограничений на выполнение полётов в воздушно пространстве. Их много. Да те же ошибки наземного персонала, которые повлекли задержку рейса.

Согласованные слоты.

Процедура оговорена в приказе МТ РФ №310. Аэропорт может не всегда подтвердить необходимый слот, так как может иметь ограничения по пропускной способности, стойкам регистрации, выходам на посадку, стоянкам. Об инфраструктурных ограничениях говорил выше.

Лётные экипажи.

Самолёт может выполнять рейсы без остановки, но люди – нет. У экипажей есть месячная и годовая санитарные нормы полётного времени и ограничения по рабочему времени. Кроме того есть ограничения по полётам в ночное время, постоянные проверки, комиссии. Отпуска и больничные тоже имеют место быть. Необходимо, чтобы график оборота самолётов соответствовал нормам работы летных экипажей. А если полёты с эстафетами, то решены вопросы с засылкой, доставкой, проживанием.

Техническое обслуживание воздушных судов.

На него тоже нужно выделять время. Чеки выполняются по часам налёта, поэтому нетрудно посчитать, когда и где будет производиться следующий чек. Но в момент выполнения чека самолёт не сможет выполнять рейсы. Поэтому это тоже необходимо учитывать. При этом нужно учитывать и тяжелые формы обслуживания, а также чеки силовой установки.

Таким образом расписание создаётся. Хорошее расписание позволяет (во, первых наверное его соблюсти хотя бы) наиболее эффективно эксплуатировать парк самолётов, при этом обеспечивая регулярность выполнения рейсов.

——————————————————————————-

Копия данной статьи расположена на платформе Livejournal по адресу:

https://travelfoxes.livejournal.com/155853.html

Автором данной публикации является владелец данного канала. Статья не содержит конкретных данных по какому-либо рейсу и перевозчику, не содержит конфиденциальную и коммерческую информацию. Статьи могут содержать фактические неточности в силу того, что являются воспоминаниями, а не источником официальной информации. В силу специфики канала – автор не может публиковать собственные фотоматериалы из контролируемой зоны аэропорта, поэтому фотоматериалы используются из сети Интернет, находящиеся в открытом доступе, которые могут помочь понять особенности объекта статьи. В силу особенностей политики Яндекс.Дзен, фотоматериалы на канале Яндекс.Дзен представляются в ограниченном объёме.

Как и любой другой вид транспорта, авиация движется и функционирует по установленному  расписанию, упорядоченно и слаженно. За этим скрывается гигантская работа по созданию расписания и  его обеспечению, ведь расписание рейсов – это одна из главнейших составляющих привлекательности услуг авиаперевозчика, так как при выборе рейса пассажир во многом ориентируется исключительно на время вылета и прибытия при выборе маршрута своего путешествия. Расписание – это основной документ, если можно так выразиться, по которому работает авиакомпания. Все производственные процессы отталкиваются от очередного сезонного расписания регулярных рейсов.   Так что же это такое, расписание?

Прежде всего, нужно понять, из каких компонентов оно состоит. Если говорить просто, то это время вылета воздушного судна, время прибытия и его полётное время. Время вылета и прилёта называются, соответственно, вылетной слот и слот на прибытие (их именуют просто «слоты»). В переводе с английского slot  обозначает паз или желобок. Образно говоря, рейс как бы «вставляется» в графики аэропортов. О взгляде на расписание со стороны аэропортов я расскажу в следующих постах.

В общем, расписание полётов авиакомпании и составляют вот такие наборы рейсов со своими слотами и полётными временами.

В авиации общепринято разделение календарного года на два сезона лётной навигации – зиму и лето. Это закреплено международными соглашениями под эгидой ИАТА – Международной Ассоциации воздушного транспорта. Лето начинается в последнее воскресенье марта, заканчивается в последнюю  субботу октября, зима, соответственно, начинается в последнее воскресенье  октября и заканчивается в последнюю субботу марта, при этом присваивается индекс  текущего года, например, Зима2012, Лето2012, а нумерация начинается с летнего периода.  На данный момент все летают в разгар Лета2012,следом будет Зима2012 )). Как правило, авиакомпании в зависимости от сезона корректируют свою программу полётов (летом увеличивают, зимой сокращают) и именно по этой причине меняется и расписание. То, что было летом, совершенно не обязательно будет выполняться в зимний период. Вот такая вот цикличность и сезонность.

В зависимости от сезона компании формируют свое расписание регулярных полётов. Для этого принимается во внимание статистика прошлых лет, опыт выполнения тех или иных рейсов, желание ввести новые направления, конкурентная обстановка, и на основании всего этого «рисуется» расписание. За основу может браться текущее расписание, аналогичное прошлому сезону либо создается совершенно новое. Надо заметить, что подготовка к новому сезону начинается очень и очень загодя. Например, для сезона «Лето» проект расписания готовится уже октябре-ноябре, то есть за 6-7 месяцев. Причин для этого множество, основной среди которых является коммерческая загрузка – чем раньше рейс откроется в продаже, тем выше шанс его загрузить по максимуму.

Как правило, у авиакомпании всегда есть понимание, что и в каком объёме она будет выполнять в конкретном будущем сезоне, где-то на 2-3 года вперед. Есть наработанные рейсы, расписание которых изменяется очень нечасто и которые являются основными для авиакомпании. Такие рейсы называются историческими рейсами, а слоты под них  – соответственно, историческими слотами. Такие слоты имеют приоритетное право при согласовании их аэропортами и являются своего рода «бронированием» расписания на сезон. Причем историческое расписание подтверждается по принципу «аналогичного сезона», то есть после окончания, допустим, зимнего расписания  у авиакомпании есть право исторического слота на следующий зимний сезон, а не наступивший летний ). В международных соглашениях и российском авиационном законодательстве закреплены чёткие сроки согласования и подтверждения такого расписания, и если по каким-то причинам авиакомпания «промухала» эти сроки, с историческими слотами можно распрощаться ).

На этом, пожалуй, закончу первую часть рассказа. Мыслей много, объем достаточно большой, поэтому буду выкладывать порциями, чтобы не получалось огромных простыней ).

В следующих частях я опишу сам процесс формирования расписания, принципы его распределения по авиапарку, согласование слотов в аэропортах и многое другое. Keep, как говорится, online ). 

1. Технология формирования, согласования и издания расписания движения воздушных судов

Составление
расписания движения самолетов проходит
следующие последовательные стадии:

• Формирование
  авиаперевозчиками проекта расписания
  собственных рейсов;

• Формирование
  и согласование проектов внутреннего
  расписания движения ВС авиаперевозчиков
  РФ;

• Издание
  внутреннего расписания движения ВС
  авиаперевозчиков РФ.

В
масштабах всей страны практически не
возможно составить расписание,
удовлетворяющее всем требованиям
заинтересованных авиапредприятий.
Конечным критерием оптимальности
расписания является экономическая
эффективность эксплуатации воздушных
линий.

Базой
для составления расписания является
наличие пассажиропотоков и потенциального
спроса на авиаперевозки между парами
городов. Величина отправок является
одним из показателей, позволяющим
принять решение по назначению рейсов.
Проект расписания согласовывается со
службами управления, связанными с
организацией технического обслуживания,
обеспечением летной работы, планированием
и т.д.

Проект
расписания составляется на основе плана
движения самолетов. Этот документ
фиксирует сеть авиалиний в виде перечня
планируемых авиарейсов с указанием по
каждому рейсу следующих параметров:
маршрута, чистоты, периода навигации,
типа самолета, принадлежности самолета
и а/п базирования, времени полета по
кратчайшему маршруту, вида движения
и.т.д. На основе указанных параметров
рассчитывается число авиарейсов, налет
часов самолетами авиапредприятия,
расход ГСМ.

План
движения является основой при
предварительном расчете потребного
количества самолетов и экипажей для
выполнения налета часов.

При
составлении проекте расписания
учитывается старое расписание, которое
корректируется с учетом имеющихся
возможностей и ограничений.

Проект
расписания должен быть в обязательном
порядке предварительно согласован с
заинтересованными службами авиапредприятия
и органами Министерства связи.

К
расписанию движения ВС предъявляются
определенные требования, обеспечивающие
высокую безопасность полетов. Каждый
рейс закрепляется во времени и пространстве
таким образом, чтобы осуществлялась
увязка по безопасности между рейсами
всех авиапредприятий. Высокая безопасность
полетов обеспечивается соблюдением
нормативов пропускной способности
аэропортов и контролирующих также
пересечение трасс.

При
разработке проекта расписания
авиапредприятия обеспечивают соблюдение
всех установленных на планируемый сезон
ограничений авиатранспортной сети и
увязывают свои коммерческие интересы
с ресурсами, которыми они располагают
(самолетный парк, экипажи, топливо). Для
этого учитывается большое количество
исходных данных. Необходимо иметь:

1. Информацию
   об исправности самолетного парка по
   месяцам, где необходимо указать:

   • Отход
     самолетов в ремонт, на планово-техническое
     обслуживание и сроки окончания ремонта;

   • Количество
     выдаваемых самолетов под расписание
     по месяцам.

2. Данные
   о поступлении новых самолетов с указанием
   точной даты.

3. Статистические
   данные по отправкам пассажиров между
   парами городов.

4. Проект
   международного расписания, заявки на
   чартерную программу.

5. Наличие
   экипажей.

Также
необходимо учитывать ограничения по:

• Использованию
  самолетного парка и экипажа;

• Точкам
  схождения и пересечения трасс;

• Аэропортам:

а)
периоды ремонта аэродромов;

б)
возможность приема аэропортом самолетов
данного типа;

• Удовлетворению
  заявок различных организаций;

Ограничения
по использованию самолетного парка
заключаются в обеспечении заданного
объема работы минимальным числом
самолетов при налете на один самолет
не менее нормативного времени.

Общее
число самолетов, обеспечивающих
нормальное функционирование расписание
с учетом резерва парка, ремонта и
регламентного обслуживания, равно:

N
_парк
= N _расп
+N _рез
+N _рем
+N _регл

Минимизация
числа самолетов позволяет увеличить
налет на один самолет, повысить
регулярность за счет резерва, а также
выполнить дополнительный объем работ.

Аэропорты
по времени работы могут быть круглосуточными
и некруглосуточными, что ограничивает
возможности прокладки рейса. Другой
ограничивающий фактор – ремонт ВПП.
Ряд аэродромов закрыт для приема и
вылета из-за ограничения по шумам
вследствие близкого расположения
населенных пунктов. Таким образом,
имеются интервалы времени Т; Т+ t, в
пределах которых рейсы не могут
осуществляться.

Рейсы,
обслуживающие заявку Министерства
связи и других организаций являются
приоритетными и прокладываются в первую
очередь. Их изменение во времени являются
минимальными.

Предварительная
прокладка рейсов осуществляется
графически, путем составления графика
оборота самолетов (ГО).

Размещение
рейсов производиться по возможности в
коммерчески – выгодное время,
обеспечивающие наибольшую занятость
кресел. Для каждой воздушной линии
характерен свой интервал коммерческого
времени. Так, для одних линий, например,
Санкт-Петербург – Москва, ночной вылет
не пользуется спросом, для других
Санкт-Петербург – Сочи – безразличен.

Размещение
рейсов производиться так, чтобы не
только формально вылет или прилет не
попадал в запретную зону, но и находился
в достаточном удалении от границ
интервала.

Формирование
авиаперевозчика проекта расписания
собственных рейсов.

Сроки
выполнения этапа по сезонам:

«ЛЕТО»
– 15 мая – 15 июня;

«ЗИМА»
-15 октября – 15 ноября.

Формирование
проекта расписания осуществляется
авиаперевозчиком по собственной
технологии, учитывающей его организационную
структуру, объемы информации, обрабатываемой
на этом этапе планирования, степени
автоматизации расчетов и других
специфических факторов.

В
целях повышения достоверности расчетов
за счет использования актуальной
информации и снижения трудоемкости
работ по агрегированию данных и вводу
их в собственные компьютерные системы,
Центр расписания тарифов по запросу
авиаперевозчика обеспечивает поставку
на бумажном или магнитном носителе
нормативно-справочной и текущей
информации, приведенной в таблице 2.

Для
разработки проекта расписания
осуществляется авиаперевозчиком по
собственной технологии, учитывающей
его организационную структуру, объемы
информации, обрабатываемой на этом
этапе планирования, степени автоматизации
расчетов и других специфических факторов.

Для
разработки проекта расписания на
планируемый сезон, как правило,
используется информация о рейсах
расписания аналогичного сезона
предыдущего года. Это базовая информация
приводиться в России (РУ ФАВТ).

Рейсы,
обслуживающие воздушные линии, на
которые авиаперевозчики не имеют
лицензий, должны быть исключены из
проекта расписания.

Каждому
участку рейса в проекте расписания в
соответствии с разделом должен быть
назначен номер маршрута ОВД и определен
эшелон полета.

Авиаперевозчик
согласовывает с аэропортами временные
интервалы.

При
возникновении конфликтных ситуаций с
аэропортом по выделению временного
интервала, авиаперевозчик обращается
в ФАВТ России, который на основе информации
ЦРТ по результатам контроля соблюдения
нормативов пропускной способности
аэропорта принимает соответствующее
решение.

На
основании фактического расстояния
полета между аэропортами отправления
и назначения по выбранному авиаперевозчиком
маршруту рассчитывается время полета.
авиаперевозчик вправе, исходя из
коммерческих, технических и организационных
соображений, выделенных в аэропортах
временных интервалов, устанавливать
продолжительность полета по расписанию,
отличающуюся от расчетной по выбранному
маршруту полета.

При
разработке проекта расписания
авиаперевозчик обеспечивает соблюдение
всех, установленных на планируемый
сезон, ограничений автотранспортной
сети и увязывает в расписании свои
коммерческие интересы с располагаемыми
ресурсами (самолетный парк, экипажи,
топливо и др.).

Разработанный
авиаперевозчиком проект расписания на
бумажном или магнитном носителе с
сопроводительными документами,
подписанными руководством, представляется
в ЦРТ. Проект расписания должен быть
согласован с РУ ФАВТ, если в него включены
внутрирегиональные воздушные линии.

Рейсы,
включенные в проект расписания, могут
представляться в ЦРТ:

• на
  бумажном или магнитном носителе. В этом
  случае обязательно должна быть ссылка
  на согласование с аэропортами временных
  интервалов (например, слоты по аэропортам,
  включенным в проект расписания,
  согласованы);

Формирование
и согласование проекта расписания.

Сроки
выполнения этапа по сезонам:

«ЛЕТО»
– 15 мая – 15 августа;

«ЗИМА»
-15 ноября – 15 января.

Проект
расписания формируется Центром расписания
и тарифов на основе проектов расписания
авиаперевозчиков.

При
объединении проектов расписания
авиаперевозчиков осуществляются
контроль параметров рейсов по следующим
направлениям:

–
Контроль выполнения требований по
описанию параметров рейса и форме
сообщений.

–
Контроль соблюдения параметров и условий
лицензий.

–
Контроль согласования с аэропортами
временных интервалов.

–
Контроль назначения каждому участку
рейса маршрута ОВД и эшелона полета и
контроль соответствия назначенного
маршрута ОВД действующей информации
«Каталога зарегистрированных маршрутов
обслуживания воздушного движения
(ОВД)».

–
Контроль ограничений работы аэропортов.

–
Контроль продолжительности полета
между парой аэропортов по указанному
маршруту. Формируется предупреждение
о возможной ошибки в проекте расписания,
если продолжительность полета, указанная
в проекте, отличается от расчетной на:

20%
– при продолжительности полета от 30 до
180 минут;

10%
– при продолжительности полета от 185
минут и выше.

–
Контроль соблюдения нормативов пропускной
способности элементов воздушного
пространства.

Центр
расписания и тарифов в пределах своих
полномочий, установленных данным
Положением, принимает меры к устранению
нарушений, обнаруженных по результатам
контроля.

Неустраненные
нарушения выносятся на согласование
представителей ФАВТ России, ГЦ ППВД,
авиаперевозчиков, аэропортов и ЦРТ.

В
согласовании участвуют представители
авиаперевозчиков, рейсы которых нарушают
нормативы пропускной способности
элементов воздушного пространства и
аэропортов, у которых имеются конфликты
с авиаперевозчиками по выделению
временных интервалов.

ЦРТ
готовит предложения по устранению
нарушений, организует и проводит
согласование на своей базе.

Решения,
принятые на согласование представителями
ФАВТ России и ГЦ ППВД, являются
обязательными для исполнения.

ЦРТ
вносит согласованные и принятые решения
в компьютерную базу данных. Информация
о расписании на бумажных или магнитных
носителях направляются авиаперевозчикам,
агентствам воздушных сообщений и в
аэропорты.

На
основе расписания, маршрутов ОВД и
нормативно-справочной информации, ЦРТ
формирует повторяющиеся планы полетов
и направляет их в ГЦ ППВД для доведения
до органов УВД.

Издание
внутреннего расписания движения
самолетов.

Сроки
выполнения этапа по сезонам:

«ЛЕТО»
– 15 августа- 15 сентября;

«ЗИМА»
– 15 января – 15 февраля.

По
завершению составления расписания, ЦРТ
формирует макет –оригинал книги
«Внутреннее расписание движения ВС
авиаперевозчиков РФ», который передается
в типографию для издания.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Наверняка каждому доводилось летать в полупустом самолете или встречаться с переносом рейса, возможно вы задумывались об оптимальности затрат и эффективности такого рейса. Сколько потенциальной прибыли недополучает авиакомпания? Действительно, рейсы бывают малоприбыльными, а иногда даже убыточными. Могут ли быть такого рода решения объяснимы с точки зрения оптимального поведения авиаперевозчика? Например, в текущей ситуации с отменой рейсов из-за COVID-19: как распределяется парк самолетов по другим направлениям, что обеспечивает локальную норму прибыли? Давайте попробуем построить динамическую модель, которая будет реагировать на внешние изменения и стремиться прийти к состоянию равновесия. В данной статье возьмем лишь небольшой набор параметров, попробуем спрогнозировать спрос, отправлять самолеты меньшей вместимости, снижать частоту рейсов когда это невыгодно.

При первом рассмотрении, задача очень похожа на «задачу о рюкзаке». В самом деле, имеется

аэропортов

, каждый из аэропортов может вместить

самолетов. Сами самолеты относятся к разным типам

. Затраты на содержание самолета

-го типа в

-ом аэропорте обходятся в

, а прибыль

. Требуется найти такие

(

) при которых максимизируется общая прибыль

:

а общие затраты

на содержание самолетов в аэропортах минимизируются:

При ограничениях вместимости каждого аэропорта:

Теперь примем во внимание, что аэропорты соединены между собой авиалиниями

. Тогда, расстановку самолетов по аэропортам придется выполнять не только с учетом их типа, но еще и направления, по которому они будут совершать рейсы, т.е. изначально искомые

теперь становятся

. При этом сами направления могут комбинироваться в произвольные маршруты, по которым происходит перемещение самолетов.

Описание модели

Очевидно, что значение общей прибыли и убытков зависит от некоторой довольно сложной стратегии авиакомпании: выбранных типов самолетов, составленных маршрутов и расписаний для каждого из них. Но чтобы говорить о стратегиях более предметно, необходимо сделать множество уточнений.

Спрос на авиаперевозки

Одним из важнейших параметров для формирования оптимальной стратегии является спрос на авиаперевозки между отдельными городами, но собираемые данные не позволяют составить достоверное представление о нем. Тем не менее, даже в таких условиях неопределенности, по мере поступления новой информации должны предприниматься какие-то действия, направленные на увеличение прибыли и снижение убытков.

Сделать некоторые косвенные выводы о спросе на конкретное направление можно на основе данных по количеству перевезенных по нему пассажиров. Например, если по некоторому направлению самолет совершил 5 рейсов и в среднем был заполнен более, чем на 90%, то можно сделать вывод, что спрос по данному направлению довольно велик и принять решение об увеличении числа перевозок по данному направлению. С другой стороны, если после этих пяти рейсов на шестом произошло резкое снижение числа пассажиров, то этот фактор влияет в долгосрочной перспективе на «среднее» заполнение и может оказаться веской причиной для корректировок.

Самый простой способ принимать решения на основе таких случайных данных — это воспользоваться скользящими средними. Однако, проблема в том, что авиакомпания не может себе позволить опытным путем проверять свои гипотезы о спросе, т.е., если после какого-то рейса произошло резкое снижение загрузки самолета пассажирами, то это уже считается сигналом к действию. Например, в этом случае можно снизить частоту выполнения рейсов по данному направлению и увеличить его на другом со стабильно высокой заполняемостью. С другой стороны, знание о среднем значении заполняемости предыдущих 10 рейсов как раз и позволяет более-менее точно судить о том насколько стабильна заполняемость самолета по данному направлению. Если значение средней заполняемости начинает стабильно снижаться, то это может послужить сигналом к принятию более серьезных мер, например, замене самолета на самолет с меньшей вместимостью, более кардинальному изменению маршрута самолета или замене самолета и смене его маршрута одновременно.

Для того что бы создать модель, предположим, что значение истинного спроса по каждому направлению является случайной величиной

и может принимать значения из интервала

с одинаковой вероятностью. Теперь предположим, что по данному направлению курсирует самолет с максимальной вместимостью

, очевидно, что если

гораздо больше чем

, то вероятнее всего, самолет окажется заполнен практически полностью. Для того, чтобы был возможен процесс моделирования предположим, что значение

по каждому направлению может быть грубо оценено, например по величине городов, которые соединены данным направлением. Так же предположим, что для изучения поведения модели данное значение может быть изменено, но не может быть предсказано.

Расчет прибыли и убытков от каждого отдельного самолета

Затраты на обслуживание каждого самолета могут быть определены соотношением:

Это соотношение показывает, что затраты на содержание самолета типа

в аэропорте

зависят от времени его пребывания в этом аэропорте. Имеется некоторая фиксированная плата

, которая может взиматься за взлет и посадку. В дальнейшем эта фиксированная плата увеличивается пропорционально коэфициенту

. Данное соотношение не позволяет «замораживать» отдельные самолеты в каких-то аэропортах, т.е. отражает очень важную черту реальной действительности: “бездействие самолета = убытки“.

Поскольку речь зашла об отдельных самолетах, то для того что бы однозначно идентифицировать каждый их них, введем еще один индекс

где

. Тогда прибыль по каждому отдельному самолету может быть рассчитана по формуле:

Величина

определяет то, насколько заполнен самолет с индексом $x$ при естественном ограничении

, которое показывает, что заполненность самолета не может превышать его максимальную вместимость. Стоимость одного билета по направлению

на самолете

задается величиной

. Помимо этого, данная формула учитывает, что затраты на рейс так же зависят от типа самолета и времени, которое ему необходимо на совершение данного рейса:

— это коэффициент, определяющий затраты на единицу времени полета самолета типа

, а

— это время которое необходимо самолету данного типа на преодоление направления

.

Если обозначить маршрут самолета как

, то совокупная прибыль и затраты от всех входящих в него рейсов запишутся как

где

пробегает индексы всех входящих в маршрут направлений, а

— это время задержки самолета в каждом аэропорте маршрута. Тогда, общая прибыль и затраты от всех самолетов можно вычислить по формулам:

С другой стороны, при наличии всей информации по маршрутам всех самолетов, общая прибыль и затраты могут быть вычислены по формулам:

Стоимость управляющего действия

Выражения для вычисления прибыли и затрат уже могут быть пригодны для моделирования, но они не учитывают важный факт того, что после некоторого управляющего действия функционирование всей системы меняется, причем перестройка работы всей системы не может быть мгновенной. К тому же следует понимать, что само управляющее действие не может носить «волшебный» характер, т.е. мы не можем телепортировать самолеты, заставлять их лететь сутками напролет и т.д. Для синхронизации расписания одного самолета с расписаниями других можно либо задержать, либо отложить его вылет. Если момент применения управляющего действия застал самолет в воздухе, то мы все равно вынуждены дождаться его приземления.

В случаях, когда момент применения управляющего действия застает самолет в одном из аэропортов, появляется еще одно ограничение — невозможность заставить самолет совершить вылет сразу после посадки. Для каждого типа самолета должно существовать какое-то минимальное время пребывания в аэропорту

, необходимое для обязательного обслуживания самолета (дозаправка, уборка салона и т.д.)

Это означает, что момент применения управляющего действия все равно придется соотносить с моментом посадки самолета.

После применения управляющего действия самолеты снова летают по четкому, периодическому расписанию, т.е. время пребывания самолета в аэропорту, с помощью которого происходит корректировка расписания, может отличаться от всех последующих, равных между собой интервалов времени. Это значит, что затраты, связанные с управляющим действием, так же могут отличаться от всех последующих и требовать отдельных вычислений. Поскольку управляющее действие всегда соотносится с моментом приземления самолета, можно обозначить этот интервал времени как

и определить связанные с ним затраты по уже знакомой формуле

Формула для вычисления общих затрат для всех самолетов, так же не претерпит особых изменений.

Маршруты самолетов

К маршрутам самолетов выдвигается одно очень важное требование — цикличность. Это требование может показаться необоснованным, так как жесткая привязка самолетов к таким маршрутам может оказаться невыгодной. Однако, это требование не обязывает самолеты выполнять обход циклов целиком. Так же это требование не меняет того факта, что состояние системы по прежнему делится на два этапа — «до» и «после» применения управляющего действия. Это означает, что если в системе произошли какие-то изменения, например, изменился спрос по одному из направлений, задержался или вовсе сломался (исчез) один из самолетов, то совершается всего одно управляющее действие, т.е. все самолеты начинают выполнять свои маршруты циклически только после того как оно совершено. В принципе, если изменения маршрутов происходят очень часто, после каждого управляющего действия, то и никакой цикличности в маршрутах самолетов наблюдаться не будет. Но зато, если после какого-то оптимизирующего, управляющего действия изменений маршрутов больше не последует, то это будет означать, что сама система будет сохранять свое оптимальное и стационарное состояние.

Требование того чтобы все маршруты были цикличными можно обосновать еще и тем, что никакой информации о возникновении необходимости изменений маршрутов в будущем нет вообще, то есть может оказаться так, что самолет будет лететь произвольное количество времени по некоторому маршруту без единой корректировки. Если этот маршрут не является циклом, то на одной из итераций он прекратит свое движение. Это значит, что на каждой итерации придется отслеживать такие остановки для каждого самолета и принимать какие-то решения по их дальнейшему движению.

Помимо всего перечисленного, имеется еще одно важное требование к маршрутам и расписаниям — максимальное одновременное пребывание самолетов в каждом аэропорту не должно превышать их вместимости. Поэтому, после составления маршрута необходимо составить такое расписание, которое могло бы гарантировать, что ни в какой момент времени ни в одном аэропорту не окажется самолетов больше, чем тот способен принять. Если самолеты обладают очень длинными маршрутами, которые не являются циклами, то придется вычислять количество самолетов в каждом аэропорту этого маршрута, причем эти вычисления будут связаны с маршрутами и расписаниями других самолетов. С другой стороны, если самолеты выполняют обход цикличных маршрутов с известным периодом, то зная периодичность посещения каждого аэропорта можно очень легко, составить расписания, которые не буду приводить к превышению лимитов вместимости.

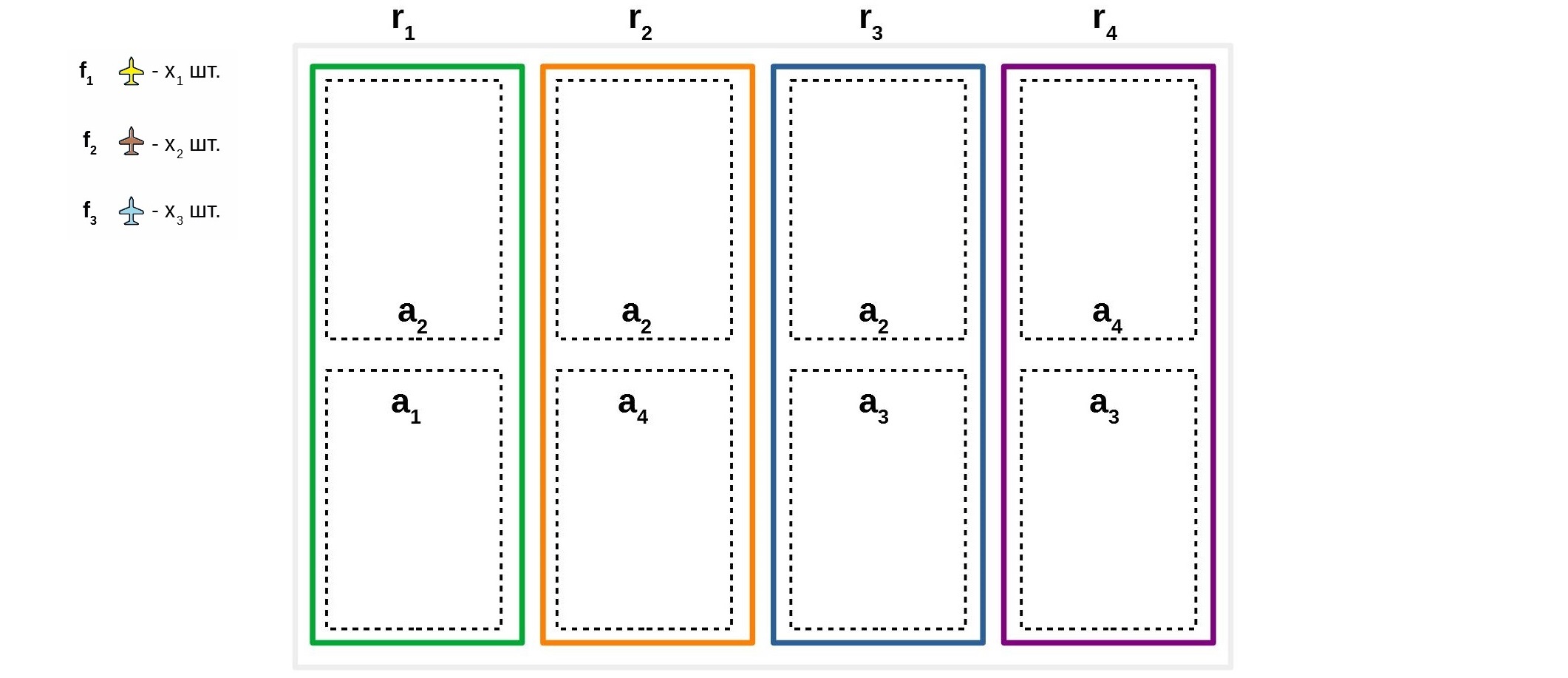
Поскольку появляется жесткое требование того что бы маршруты были циклами, становится очевидным, что все маршруты должны состоять из простых циклов ориентированного графа, который моделирует сеть. Что бы продемонстрировать это изобразим четыре аэропорта, которые соединены между собой следующим образом:

Данный граф состоит из шести простых циклов:

,

,

,

,

,

. Циклы, полученные циклическим смещением входящих в них вершин, считаются эквивалентными, например, эквивалентными будут циклы:

,

и

.

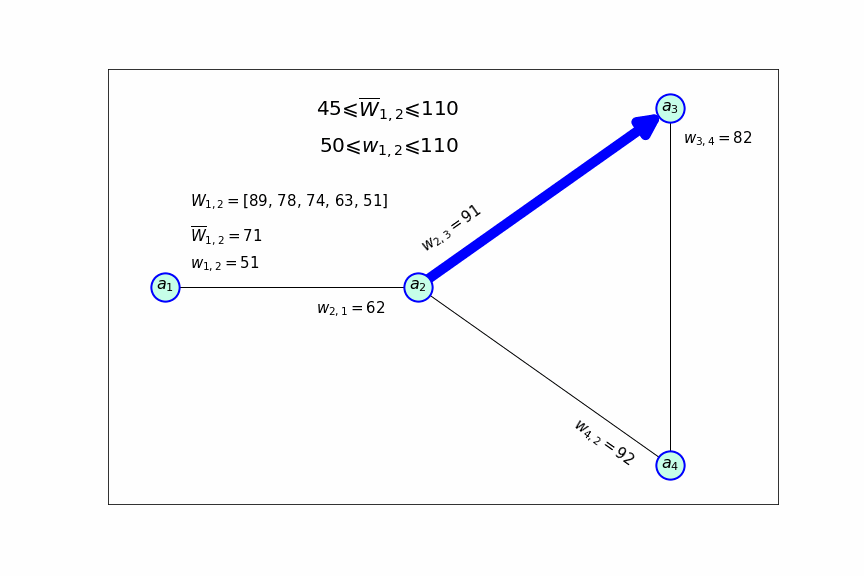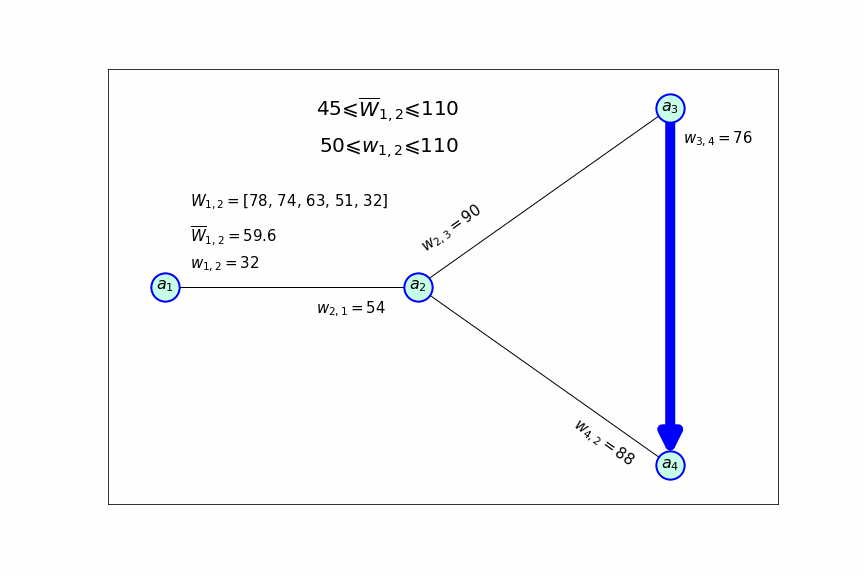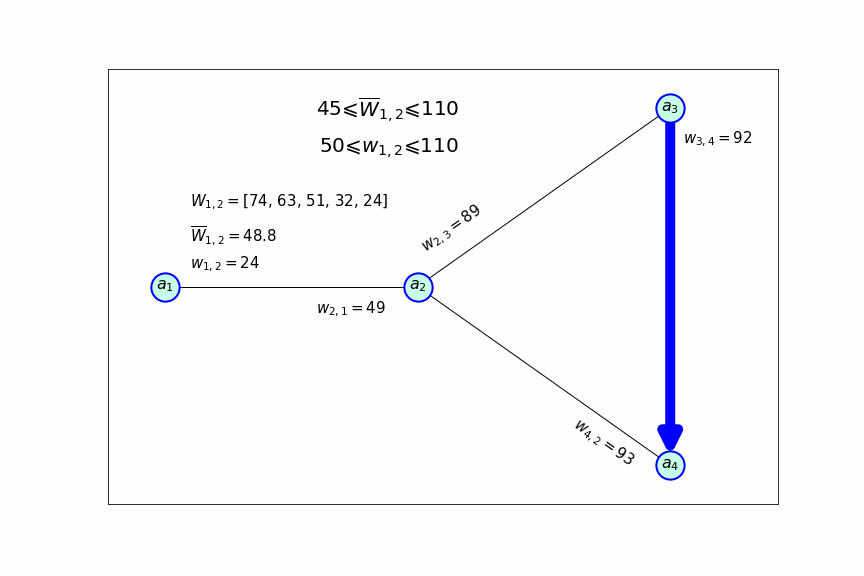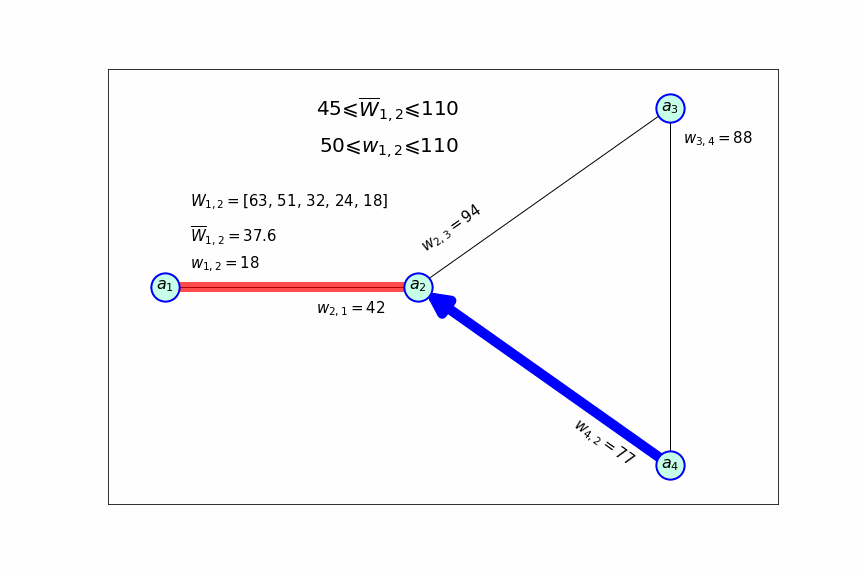
Однако, если известно, что некоторый самолет находится в конкретном аэропорту, то порядок следования вершин в его маршруте становится важен. Составление маршрута для конкретного самолета, находящегося в некотором аэропорту, выполняется путем объединения элементарных циклов, включения одних циклов в другие, или, если маршрут уже содержит внутренние циклы, исключения их.

Рассмотрим простой пример, допустим некоторый самолет расположен в аэропорту

, тогда он может летать по одному из двух простых циклов:

и

. Цикл

можно объединить с циклом

, в результате получится цикл

. Так же цикл

может быть включен в цикл

в результате чего получится

.

Теперь предположим, что самолет находящийся в аэропорту

, будет циклически курсировать по маршруту

, но в этом случае не удовлетворяется спрос по направлениям

,

и

это означает, что можно добавить в маршрут имеющегося самолета еще один простой цикл

и получится

или добавить еще один самолет, который будет циклически летать по маршруту

.

Здесь стоит внести некоторые уточнения в понятия «изменения» и «замены» маршрутов. Изменение маршрута предполагает его модификацию путем увеличения или снижения числа его внутренних элементарных циклов. А замена маршрута предполагает замену самих элементарных циклов.
Очевидно, что маршруты самолетов могут накладываться друг на друга, и желательно в тех участках сети, где имеется особо повышенный спрос.

Найти все простые циклы графа можно с помощью алгоритма Джонсона, сложность которого равна

, где

— количество вершин,

— количество ребер, а

— количество элементарных цепей. В дальнейшем следует изменять маршруты самолетов с проверкой того, чтобы объединение множеств ребер. из которых они состоят

, совпадало с множеством ребер всего графа

, т.е. если общее количество самолетов равно

, то должно выполняться равенство:

Условия соблюдения лимита вместимости аэропортов

Помимо того, что составленное расписание влияет на пропускную способность по каждому из направлений, оно так же влияет и на количество самолетов, которые могут одновременно оказаться в аэропорту. Для удобства представим, что некоторый аэропорт может принимать одновременно только два самолета, но этот аэропорт входит в маршруты трех самолетов. Очевидно, что для соблюдения лимита должны существовать некоторые строгие условия.

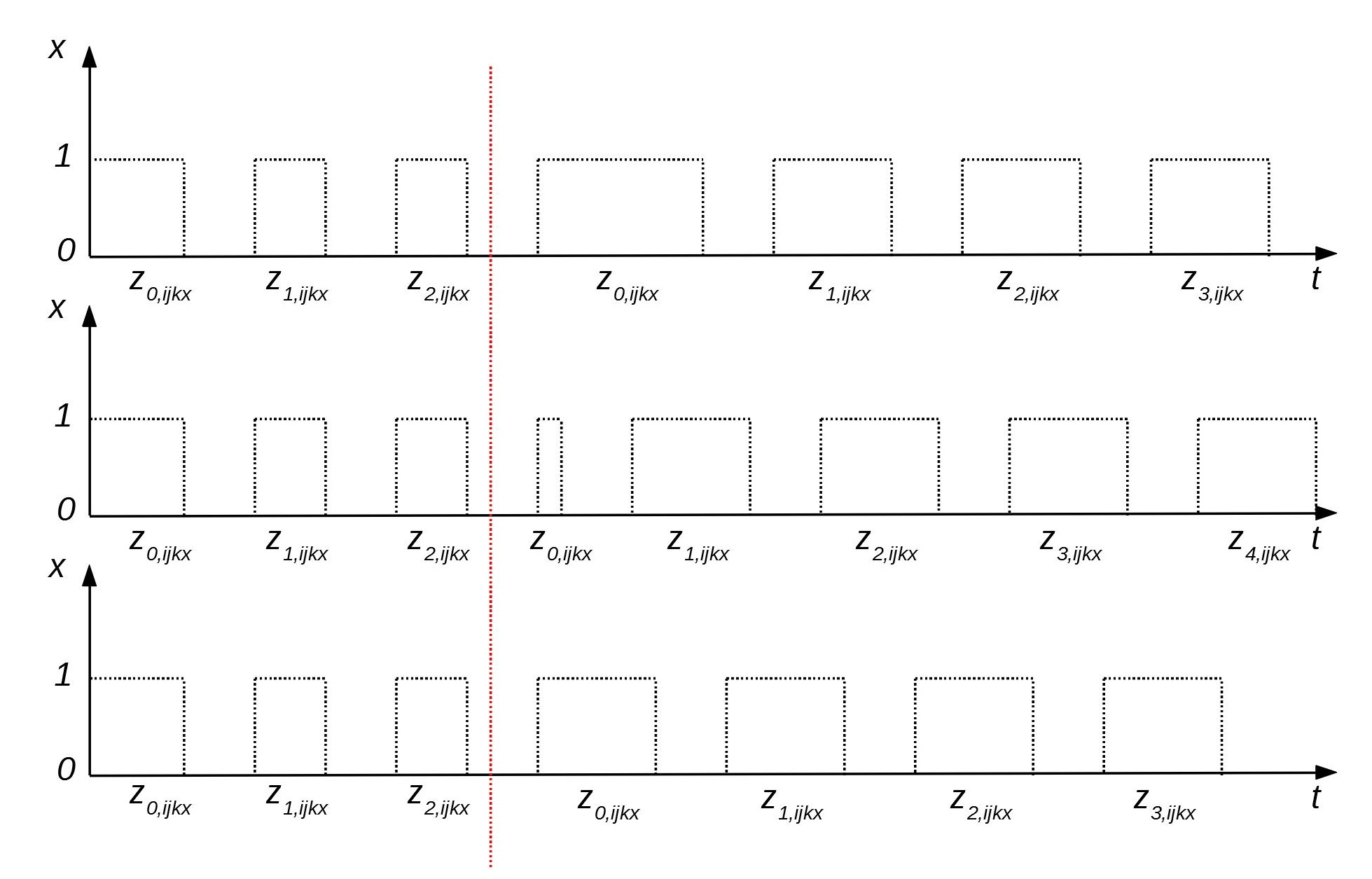
Сначала попытаемся определить общий подход, учитывающий то, что самолеты выполняют свои маршруты циклически с заданным периодом и то, что корректировка расписаний возможна только с помощью одного управляющего действия, связанного с изменением времени вылета самолета.

Красная пунктирная линия показывает тот момент, когда система приходит в оптимальное стационарное состояние. Все, что находится до этой линии, можно считать тем интервалом времени, когда выполняется управляющее действие. В данном случае показано как с помощью изменения интервалов времени

и

можно управлять периодами посещения двумя самолетами одного аэропорта. На рисунке видно, что самолеты проводят в аэропорту разное количество времени но при этом эти интервалы времени не пересекаются. Это возможно только в том случае, если их периоды равны или если наименьшее общее кратное этих периодов равно одному из периодов.

Например, если периоды посещения аэропорта двумя самолетами составляют 200 и 600 часов, то может быть выбрано такое их смещение относительно друг друга, при котором они никогда не будут посещать аэропорт одновременно. Но если их периоды равны 300 и 700 часов, то как бы они не были смещены относительно друг друга, рано или поздно, они прибудут в аэропорт одновременно.

Однако, так же очевидно, что управляющее действие может быть таким, что это условие выполнится, но интервалы все равно могут пересекаться, что означает выполнение следующих условий (буква

в индексе означает, что самолет прилетел в аэропорт;

— вылетел из аэропорта):

В случае если аэропорт имеет вместимость 2 самолета, но он входит в маршрут трех самолетов, то попарное выполнение данных условий сразу для всех трех самолетов означает, что лимит будет превышен.

С другой стороны, если два самолета имеют такие периоды которые не приводят к их одновременному пребыванию в аэропорту, то третий самолет может иметь произвольный период. Но в этом случае обязательно выполнение требования того, чтобы время его пребывания в аэропорту было строго меньше, чем интервал времени, когда два предыдущих самолета отсутствуют в аэропорту.

Это приводит к двум простым правилам соблюдения лимита вместимости аэропорта:

1. Если вместимость аэропорта равна , то периоды пребывания самолетов, должны быть разделены на множеств. Причем наименьшее общее кратное периодов в каждом из множеств должно быть равно одному из периодов этих множеств.
2. Условие пересечения интервалов не может выполняться для более чем периодов.

Строгое выполнение данных условий может быть обосновано только в одном случае, когда точно известно, что никаких управляющих действий в дальнейшем не предвидится. Но поскольку таких гарантий нет, то и данные условия могут быть несколько ослаблены. К тому же строгое выполнение данных условий может потребовать очень больших задержек самолетов, которые необходимы для смещения периодов, т.е. оказаться очень дорогостоящими. Поэтому, данные условия можно адаптировать так, чтобы превышение лимита вместимости наступало только через какой-то приемлемый промежуток времени, после которого можно производить очередную корректировку расписаний. Однако, гарантий того, что такое поэтапное корректирование будет всегда приводить к снижению стоимости корректировок тоже нет. Все это говорит о том, что данные правила могут послужить основой для более сложных правил, например, можно подстраивать расписания самолетов, маршрут которых поменялся, под расписания самолетов, маршруты которых остались неизменны, или вычислять стоимости комбинаций различных последовательных корректировок и выбирать лучшую из них.

Процесс моделирования и принятие оптимальных решений

Предположим, что в начальный момент времени самолеты расставлены в некотором случайном или заранее определенном порядке. Поскольку в начальный момент времени, нет никакой информации о количестве перевезенных пассажиров, то на начальном этапе происходит «разведка обстановки». На данном этапе, перед запуском процесса моделирования, необходимо каждому самолету назначить некоторый маршрут. Очевидно, что все эти маршруты должны покрывать всю сеть аэропортов и способствовать тому, чтобы все перемещения между аэропортами выполнялись оптимальным образом относительно загрузки.

Процесс оптимизации для некоторого самолета может быть начат как только значения загруженности станут известны по всем направлениям его маршрута. Только в этот момент появится возможность вычислить значения прибыли и затрат от данного самолета на этом маршруте, которые могут быть использованы для процесса оптимизации. Если возможно такое изменение маршрута и расписания, которые увеличат известную прибыль и снизят затраты, то они заменят предыдущие.

Замена маршрутов самолетов не может быть произведена до того, как все значения загруженности по каждому направлению не стали известны, потому что это не позволит судить о суммарной прибыли и затратах. Лишь после того как станут известны все значения загруженности по каждому направлению, можно приступать не только к изменениям маршрутов и расписаний отдельных самолетов, но и к изменениям в общее планирование перевозки.

Каждому направлению мы ставим в соответствие массив

определенной длины (например 5), в который заносятся значения загруженности пассажирами каждого самолета

, совершившего рейс по данному направлению. Данный массив будет представлять собой стек таких значений. Последнее значение в этом массиве — загруженность на предыдущем рейсе, будет позволять делать выводы о необходимости небольших тактических действий, а среднее значение по всему массиву будет служить индикатором появления необходимости серьезных стратегических корректировок.

Если последнее значение массива

выходит за пределы некоторого интервала

, определяющего целесообразность изменений, то принимаются соответствующие действия по снижению или увеличению частоты выполнения рейсов по данному направлению. В то же время, если после снижения или увеличения частоты выполнения рейсов по данному направлению значение

все равно продолжает снижаться или расти, то это может быть сигналом к тому, что нужны более кардинальные изменения, например, включение данного направления в маршруты нескольких самолетов или исключение данного направления из маршрутов всех самолетов.

Для примера, допустим, что некоторый самолет летает по циклическому маршруту

. Предположим, что при очередном вылете из аэропорта

количество пассажиров в самолете резко упало. В этом случае, по прилету в аэропорт

может быть принято решение изменить маршрут

на

. Такая замена полезна тем, что если падение спроса по направлению

не является случайностью, а устойчивым трендом, то по крайней мере, произойдет снижение частоты выполненных рейсов по данному направлению. Если же при очередном посещении данного направления количество перевозимых пассажиров оказалось таким же низким или стало еще меньше, то маршрут

может быть снова изменен на маршрут

, который снижает частоту посещения направления

еще сильнее. Если направление

продолжает стабильно снижаться, то можно вообще заменить маршрут

на

или любой другой маршрут, который не содержит направления

.

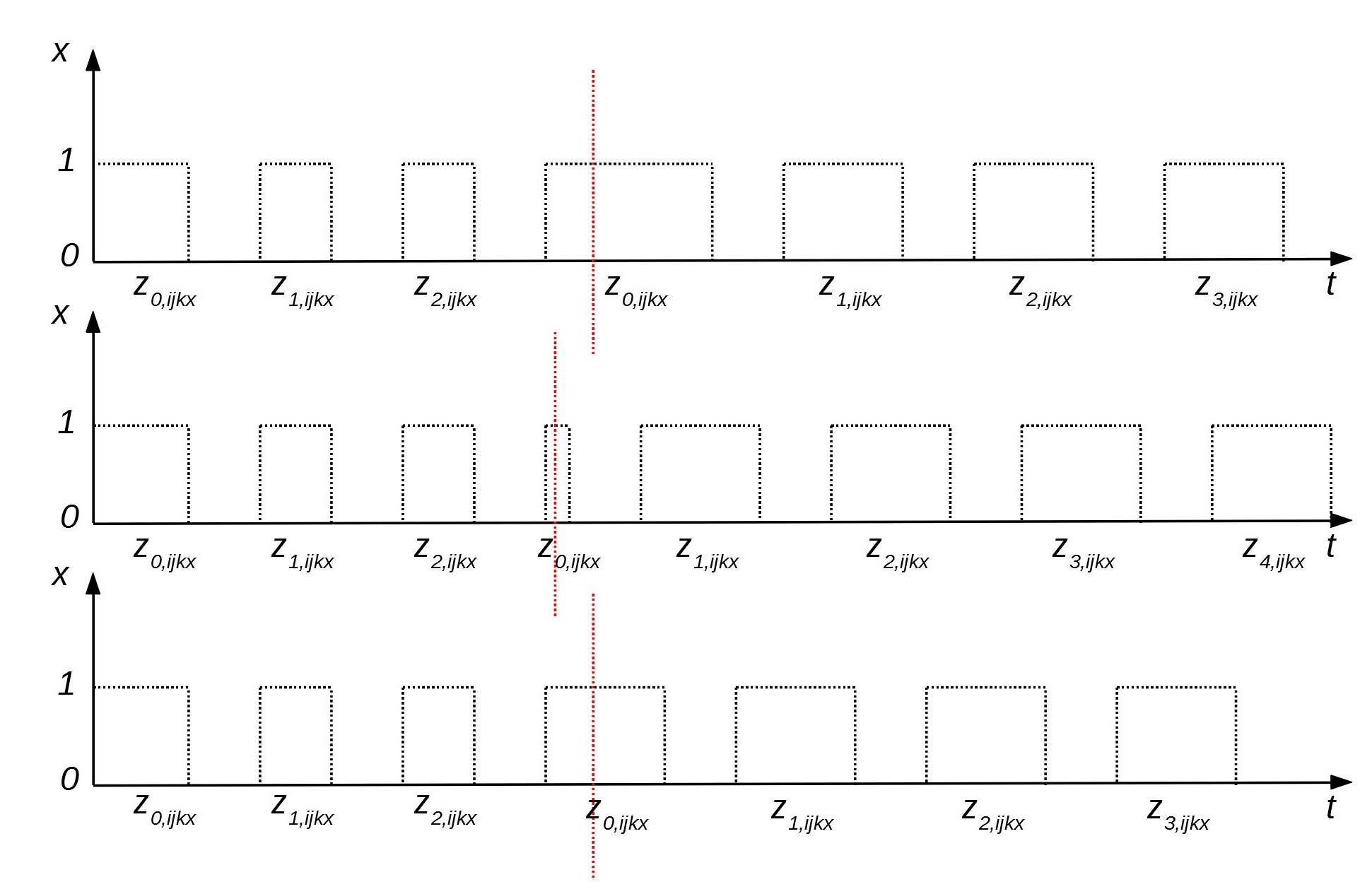
Все это можно продемонстрировать с помощью следующей схемы, которая показывает, как меняется частота посещения направления, прибыльность которого сильно снижается:

Индикатором для снижения частоты рейсов по направлению

служит значение

, каждый раз, когда оно становится меньше 50, принимается решение о том, что бы посещать это направление с меньшей частотой. После того как значение

становится ниже минимального значения допустимого интервала, данное направление вообще исключается из маршрута самолета.

Так же для каждого типа самолета можно определить свой допустимый интервал для среднего значения элементов массива

. Если данное значение входит в приемлемый интервал для определенного типа самолета, но не входит для самолета, который по нему уже летает, то производятся такие последовательные замены маршрутов, которые приводят к замене типов самолетов на более подходящие.

Может показаться, что с течением времени, как только все средние значения количества пассажиров по каждому направлению придут в равновесие, все самолеты сконцентрируются только в одном, самом выгодном маршруте. Это действительно было бы так, если бы вместительность каждого аэропорта была безграничной. Но в силу того, что каждый аэропорт имеет вместительность

, каким-то самолетам придется курсировать по менее выгодным маршрутам. Очевидно, что выполнять действия по оптимизации одного или нескольких самолетов имеет смысл только после изменений

или того как некоторое значение

переместится из одного интервала в другой. Все это можно изобразить в виде следующей схемы:

На данной схеме показано как изменяются маршруты для пяти самолетов четырех разных типов (с разной вместимостью). Изначально, некоторые самолеты выполняют не самые выгодные рейсы, но по мере того, как появляется больше информации о перевезенных пассажирах, их маршруты меняются, так что бы максимально соответствовать их вместимостям. В конечном итоге, достигается состояние равновесия, при котором каждый самолет приносит наибольшую прибыль, т.е. курсирует по своим маршрутам с максимально возможной частотой. Так же учитывается вместимость аэропортов, которая не позволяет маршрутам полностью накладываться друг на друга.

Возникает очень важный вопрос — как находить, оптимизирующие систему действия? Этот вопрос напрямую связан с глобальной оптимизацией, т.е. нужно подобрать такие комбинации маршрутов самолетов, их типов и расписаний, при которых общая прибыль будет максимальной, а затраты минимальны. Если бы речь шла только о самолетах и их маршрутах, то даже в таком случае область поиска решений была бы чрезвычайно велика, так как размер области зависит от числа простых циклов в сети аэропортов факториально, а от числа самолетов экспоненциально. С учетом того что, маршруты могут быть разной длины и содержать разное количество внутренних циклов, то самая оптимистичная оценка величины пространства решений будет выглядеть как

, где

— это количество простых циклов, а

— количество самолетов. С добавлением комбинаций типов самолетов и их расписаний пространство решений увеличивается факториально еще сильнее.

Естественно, поиск оптимальных действий возможен только с помощью метаэвристических алгоритмов, причем этот поиск будет выполняться после любого сильного изменения количества заполненных мест отдельного самолета, что может происходить довольно часто. Так же процесс оптимизации является двухэтапным: сначала выполняется поиск оптимальных маршрутов для каждого типа самолета, затем выполняется оптимизация их расписаний. В то же время, оптимизация расписаний может быть абсолютно детерминированным процессом, а благодаря знанию о количестве перевезенных пассажиров по отдельным простым циклам, изменение или замена маршрутов на более оптимальные может выполняться гораздо быстрее чем простым перебором. Но так же следует помнить о возможных локальных максимумах и минимумах, например, маршрут с наибольшей степенью загрузки, т.е. самый прибыльный может потребовать расписания с очень долгими задержками в аэропортах, т.е. резко увеличить затраты на его содержание.

Появляется следующий вопрос: «Какую метаэвристику выбрать: муравьиную, имитации отжига или эволюционную?» Муравьиный алгоритм хорош при поиске выгодных маршрутов, но на определенном этапе моделирования, потребность в этом поиске исчезает и появляется другая — изменение и замена маршрутов, причем не обязательно с наибольшей загрузкой пассажирами.
Эволюционный алгоритм, не гарантирует попадания в глобальный максимум и при этом очень усложняется правилами протекания процессов мутирования и скрещивания маршрутов.
Некоторые выгодные части маршрутов, могут быть разрушены мутацией при следующей итерации или не быть скрещены с выгодными частями других членов популяции. Однако, размерность задачи не настолько велика, что бы утверждать это, как факт, и предсказать, как именно поведет себя данный алгоритм в действительности очень сложно.

Самым простым и перспективным методом поиска оптимальных действий является алгоритм имитации отжига, он очень прост в реализации и настройке параметров. Так же данный алгоритм, позволяет применять различные эмпирические политики генерации более оптимальных маршрутов, например, наиболее выгодные простые циклы маршрута могут остывать быстрее, чем менее выгодные, т.е. претерпевать меньшие изменения, что будет способствовать наискорейшей сходимости.

Заключение

Конечно, рассмотренная задача — это только верхушка айсберга, а созданная модель — не более чем основа для дальнейших исследований в следующих частях цикла статей. Например, нужно учесть, что на рынке гражданских авиаперевозок существует множество авиакомпаний, т.е. им приходится конкурировать между собой. В модели спрос представлен абсолютно случайной величиной, но на самом деле он должен иметь какую-то зависимость от ценовой политики авиакомпаний. Так же нужно принять во внимание, что и работа аэропортов устроена гораздо сложнее, так как самолеты в них образуют нечто вроде очередей. Помимо этого, существуют множеств самых разных ограничений, которые регулируются различными соглашениями и законодательством.

В перспективе, точная модель может стать незаменимым централизованным инструментом для облегчения анализа и прогноза рынка гражданских авиаперевозок и позволит принимать наиболее оптимальные решения.