Рядом
распределения называется совокупность
значений признака вместе с соответствующими
им частотами или частостями. Ряд
распределения записывается в виде
таблицы, в которой в определенном порядке
перечислены возможные значения случайной
величины (признака) и соответствующие
им частоты (или) и частости. Иногда такие
ряды называют статистическими.
В
ряде распределения возможные значения
случайной величины могут быть представлены
или в виде дискретных значений или в
виде интервалов (разрядов). Они образуют
соответственно дискретный и интервальный
ряды (сгруппированный и интервальный
статистические ряды [10]).
Выбор
того или иного ряда определяется
выбранным методом для нахождения закона
распределения и его числовых характеристик
и применяемым критерием согласия.
Построение
ряда распределения представляет собой
первичную обработку статистических
данных. Он строится по частотам или
частостям (статистическим вероятностям)
на основе простого статистического
(табл.1) или вариационного рядов. В табл.
2 приведен пример построения дискретного
ряда. В такой ряд записываются те значения
параметра, которые получаются при
измерениях, и подсчитывается их количество
(частоты). По частотам могут быть вычислены
частости
.
Дискретный
ряд распределения используется при
применении графического метода и
критериев согласия Колмогорова и Мизеса
.
В других случаях, особенно при большом
числе исходных статистических данных,
удобнее использовать интервальный ряд
распределения.
Таблица 2
|
Параметры |
Подсчет |
Частоты |
Частости |
|
800 805 810 . . . 870 |
|| ||||! ||||!| ||||!|| |
2 5 6 . . . 7 |
0,010 0,025 0,030 . . . 0,035 |
|
Контроль |
200 |
1,000 |
При
построении интервального ряда наибольшую
трудность составляет выбор количества
интервалов, которое определяет ширину
интервала. Количество интервалов
оказывает влияние на форму эмпирической
кривой распределения, которая
представляется графически, на объем
вычислительных работ, на показатели
асимметрии и эксцесса, на выбор
теоретического закона распределения,
который описывает исследуемую совокупность
случайных величин, а также на результат
оценки согласия по критериям Колмогорова
и Пирсона [12]. Это объясняется тем, что
при большом числе интервалов эмпирическая
кривая может оказаться многовершинной,
иметь нехарактерные для нее случайные
колебания, так как при малой ширине
интервалов в него попадает мало данных.
Наоборот, при малом число интервалов
могут быть потеряны характерные
особенности распределения. Следовательно,
количество интервалов надо выбирать
таким, чтобы оно способствовало выявлению
основных черт распределения и сглаживанию
случайных колебаний. При этом все
интервалы могут иметь одинаковую
(равноширотные интервалы) или разную
ширину (разноширотные интервалы).
Интервалы разной ширины используются
в том случае, когда имеет место крайне
неравномерное распределение случайных
величин. Тогда в области наибольшей
плотности распределения берутся
интервалы более узкие, чем в области
малой плотности. Часто более широкие
интервалы приходится брать на краях
распределения, так как требуется, чтобы
количество частот в интервале было не
менее пяти. Но трудности в расчете
характеристик, которые при этом возникают,
приводят к тому, что обычно берутся
интервалы одинаковой ширины (равноширотные
интервалы). При выборе числа ин
тервалов необходимо
иметь в виду, что ширина интервала должна
быть не менее чем в два раза больше
погрешности измерения параметра.
В
работах [36, 37] показано, что группировка
данных в общем случае приводит к потере
информации. В [36] установлено, что для
каждого закона распределения существует
оптимальное число интервалов гистограммы,
при котором вид гистограммы оказывается
наиболее близким к действительному
виду кривой плотности распределения.
Но поскольку, приступая к обработке
опытных данных, мы, как правило, не знаем
закона распределения исследуемой
величины, то для выбора количества
интервалов приходится пользоваться
ниже- приведенными рекомендациями,
которые весьма различны.
Так, в [2] указывается,
что довольно часто число интервалов
берут равным 7, 9 или 11 в зависимости от
числа наблюдений и точности измерений.
В [9] рекомендуется число интервалов
принимать равным 12 с отклонением от
него на 2-3 единицы в ту или иную стороны,
т.е. от 9 до 15. В [10] указывается, что
количество интервалов берут произвольно,
обычно не меньше 5 и не более 15. В [11]
рекомендуется брать число интервалов
от 10 до 20 при количестве наблюдений
порядка 200-300. Таким образом, количество
интервалов выбирается в пределах от 5
до 20. Естественно, что чем больше данных
наблюдений, тем больше можно брать
интервалов. Оптимальное количество
интервалов выбирается по правилу
Старджесса
,
где
n
– количество наблюдений (объем выборки).
Но
в [5] указывается, что такое количество
интервалов берется только при объеме
выборки n100.
А при объеме выборки n>100
следует количество интервалов определять
по формуле
.
Можно пользоваться
для выборки количества интервалов
следующей таблицей, приведенной в [5]:
|
n |
25.. 40 |
40.. 60 |
60.. 100 |
100 |
100.. 160 |
100.. 250 |
250.. 400 |
400.. 630 |
630.. 1000 |
|
|
6 |
7 |
8 |
10 |
11 |
12 |
13 |
14 |
15 |
Однако
в стандартах требуется, чтобы количество
интервалов выбиралось в следующих
рекомендованных пределах
|
n |
50..100 |
200 |
400 |
1000 |
|
|
10..20 |
18..20 |
25..30 |
35..40 |
Следует отметить, что
это предварительный выбор количества
интервалов, который в дальнейшем иногда
подлежит уточнению при построении
эмпирической кривой распределения для
устранения зигзагообразности, провалов
и т.п.
После выбора количества
интервалов определяют ширину интервала
hпутем деления размаха варьированияR,
равного разности между наибольшим и
наименьшим значениями признака, на
количество интервалов
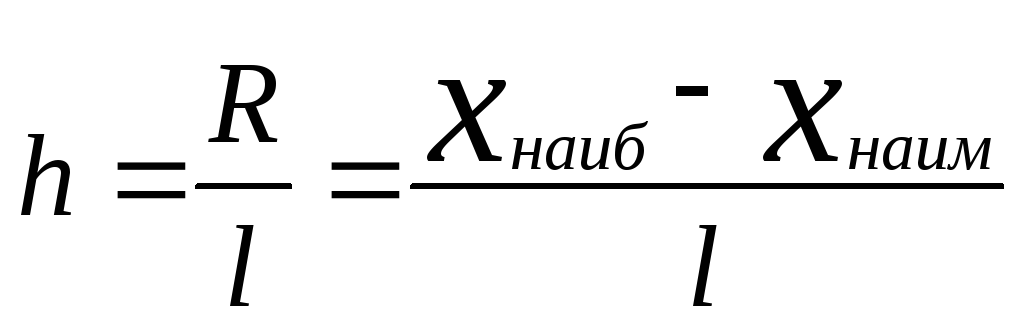
Полученное число
округляется до ближайшего из
предпочтительного ряда. Рекомендуется
выбирать значения hравными 1, 2, 3, 5, 7, 10, 15 или числу, кратному
5 [5]. Там же рекомендуется выбиратьhпримерно в два раза больше, чем цена
деления измерительного прибора, что не
всегда возможно, так как при этом
уменьшается количество интервалов. Но
в любом случае ширина интервала не
должна быть меньше цены деления
измерительного прибора [2]. Для ширины
интервала нужно всегда выбирать удобное
число и не записывать ее с “дикой”
точностью, благодаря большому числу
разрядов, например в калькуляторах,
применяемых при расчетах.
И еще
некоторые рекомендации для построения
интервального ряда распределения.
Границы интервалов не должны совпадать
с измеренными значениями [2]. Если это
получилось, то следует расширить размах
варьирования за счет некоторого смещения
его нижнего предела влево, а его верхнего
предела – вправо. Например, если ширина
интервала равна цене деления измерительного
прибора, то следует величину смещения
взять равной половине ширины интервала.
Тогда все данные будут располагаться
в серединах интервалов. Если при смещении
крайних границ не удается избежать
совпадения измеренных значений с
границами промежуточных интервалов,
то в таких случаях следует условиться
к какому из интервалов, левому или
правому, отнести эти значения. Довольно
часто рекомендуется значения, совпадающие
с границами интервалов, делить пополам,
т.е. половину таких значений относить
к левому интервалу, а половину – к правому.
Чтобы не иметь дело с дробями при нечетном
количестве значений, совпадающих с
границей интервалов, следует условиться,
к какому интервалу, левому или правому,
будет отнесено лишнее значение. Можно
в этом случае также все количество
значений умножить на два. Это не внесет
ошибки, так как вероятность попасть в
каждый из интервалов не изменится.
Следует заметить, что от способа
распределения значений, совпадающих с
промежуточными границами, по интервалам
несколько зависят результаты расчетов.
Рассмотрим
на примере наиболее часто используемый
способ построения интервального ряда
распределения по крайним значениям
признака. Обычно используется следующий
порядок построения.
1. По
табл.1 или вариационному ряду находим
наибольшее и наименьшее значения
параметра
,
.
2.
Определяем размах варьирования
.
3.
Выбираем число интервалов
.
В нашем случае удобно
выбрать
.
4.
Определяем ширину интервала
.
5.
Чтобы крайние границы размаха варьирования
не совпадали с измеренными значениями,
отступаем на половину ширины интервала
вправо
и влево соответственно
от верхнего и нижнего пределов
варьирования. Получаем новые границы.
При
этом границы первого интервала будут
795 и 805, второго – 805 и 815 и т.д. Теперь
интервалов стало
= 8. По правилу Старджесса
.
Как видно из табл.1,
нам не удалось избежать совпадения
измеренных значений с промежуточными
границами интервалов. Поэтому условимся
относить те значения, которые попадают
на границы интервалов, к левому интервалу.
Пример
построения интервального ряда
распределения приведен в табл. 3.
Таблица 3
|
Интервалы l |
Границы |
Подсчет |
Частоты |
Частости |
|
1 |
795-805 |
////!// |
7 |
0,035 |
|
2 |
805-815 |
////!////!//// |
14 |
0,070 |
|
3 |
815-825 |
34 |
0,170 |
|
|
4 |
825-835 |
47 |
0,235 |
|
|
5 |
835-845 |
44 |
0,220 |
|
|
6 |
845-855 |
33 |
0,165 |
|
|
7 |
855-865 |
14 |
0,070 |
|
|
8 |
865-875 |
7 |
0,035 |
|
|
Контроль |
|
200 |
1,000 |
В графе
“Подсчет отдельных значений”
приведены три способа подсчета количества
значений, попадающих в тот или иной
интервал. Эти значки в интервалах
ставятся при последовательной обработке
табл.1. Каждый значок (точка или линия в
любом положении) соответствует одному
значению из табл. 1.
Если
значения, совпадающие с границами
интервалов, делятся на два интервала,
то, чтобы не ошибиться, рекомендуется
эти значения при обработке табл. 1
последовательно записывать во
вспомогательную таблицу, одновременно
регистрируя их в соответствующем
интервале табл. 3.
Соседние файлы в папке ТОПИН.Лекции, задания
- #
11.05.201512.39 Mб581.rtf
- #
- #
- #
- #
- #
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) – результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | – |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Что такое группировка статистических данных, и как она связана с рядами распределения, было рассмотрено в первой части этой лекции, там же можно узнать, о том что такое дискретный и вариационный ряд распределения.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.
Как построить дискретный вариационный ряд распределения
Пример 1. Имеются данные о количестве детей в 20 обследованных семьях. Построить дискретный вариационный ряд распределения семей по числу детей.
0 1 2 3 1
2 1 2 1 0
4 3 2 1 1
1 0 1 0 2
Решение:
- Начнем с макета таблицы, в которую затем мы внесем данные. Так как ряды распределения имеют два элемента, то таблица состоять будет из двух колонок. Первая колонка это всегда варианта – то, что мы изучаем – ее название берем из задания (конец предложения с заданием в условиях) — по числу детей – значит наша варианта это число детей.
Вторая колонка это частота – как часто встречается наша варианта в исследуемом явление – название колонки так же берем из задания — распределения семей – значит наша частота это число семей с соответствующим количеством детей.
В итоге макет нашей таблицы будет выглядеть так:
| Варианта Число детей в семье — (х) |
Частота Количество семей (f) |
- Теперь из исходных данных выберем те значения, которые встречаются хотя бы один раз. В нашем случае это
0 2 4 1 и 3.
И расставим эти данные в первой колонке нашей таблицы в логическом порядке, в данном случае возрастающем от 0 до 4. Получаем
| Число детей в семье — (х) | Количество семей (f) |
| 0 1 2 3 4 |
И в заключение подсчитаем, сколько же раз встречается каждое значение варианты.
0 1 2 3 1
2 1 2 1 0
4 3 2 1 1
1 0 1 0 2
В результате получаем законченную табличку или требуемый ряд распределения семей по количеству детей.
| Число детей в семье — (х) | Количество семей (f) |
| 0 1 2 3 4 |
4 8 5 2 1 |
| Итого | 20 |
Задание. Имеются данные о тарифных разрядах 30 рабочих предприятия. Построить дискретный вариационный ряд распределения рабочих по тарифному разряду. 2 3 2 4 4 5 5 4 6 3
1 4 4 5 5 6 4 3 2 3
4 5 4 5 5 6 6 3 3 4
Как построить интервальный вариационный ряд распределения
Построим интервальный ряд распределения, и посмотрим чем же его построение отличается от дискретного ряда.
Пример 2. Имеются данные о величине полученной прибыли 16 предприятий, млн. руб. — 23 48 57 12 118 9 16 22 27 48 56 87 45 98 88 63. Построить интервальный вариационный ряд распределения предприятий по объему прибыли, выделив 3 группы с равными интервалами.
Общий принцип построения ряда, конечно же, сохраниться, те же две колонки, те же варианта и частота, но в здесь варианта будет располагаться в интервале и подсчет частот будет вестись иначе.
Решение:
- Начнем аналогично предыдущей задачи с построения макета таблицы, в которую затем мы внесем данные. Так как ряды распределения имеют два элемента, то таблица состоять будет из двух колонок. Первая колонка это всегда варианта – то, что мы изучаем – ее название берем из задания (конец предложения с заданием в условиях) — по объему прибыли – значит, наша варианта это объем полученной прибыли.
Вторая колонка это частота – как часто встречается наша варианта в исследуемом явление – название колонки так же берем из задания — распределения предприятий – значит наша частота это число предприятий с соответствующей прибылью, в данном случае попадающие в интервал.
В итоге макет нашей таблицы будет выглядеть так:
| Варианта Объем полученной прибыли, млн. руб. — (х) | Частота Число предприятий (f) |
- Построим интервалы. Следует сказать, что есть несколько способов построения интервала: визуальный способ без дополнительных расчетов на основе логического анализа данных, расчет по формуле, если по условию требуется построить равные интервалы. Для упрощения расчетов величины интервала чаще всего эта формула имеет следующий вид:
где i – величина или длинна интервала,
Хmax и Xmin – максимальное и минимальное значение признака,
n – требуемое число групп по условию задачи.
Рассчитаем величину интервала для нашего примера. Для этого среди исходных данных найдем самое большое и самое маленькое
23 48 57 12 118 9 16 22 27 48 56 87 45 98 88 63 – максимальное значение 118 млн. руб., и минимальное 9 млн. руб. Проведем расчет по формуле.
В расчете получили число 36,(3) три в периоде, в таких ситуациях величину интервала нужно округлить до большего, чтобы после подсчетов не потерялось максимальное данное, именно поэтому в расчете величина интервала 36,4 млн. руб.
- Теперь построим интервалы – наши варианты в данной задаче. Первый интервал начинают строить от минимального значения к нему добавляется величина интервала и получается верхняя граница первого интервала. Затем верхняя граница первого интервала становится нижней границей второго интервала, к ней добавляется величина интервала и получается второй интервал. И так далее столько раз сколько требуется построить интервалов по условию.
| Объем полученной прибыли, млн. руб. — (х) | Число предприятий (f) |
| 9,0 + 36,4 = 45,4 45,4 + 36,4 = 81,8 81,8 + 36,4 = 118,2 |
Обратим внимание если бы мы не округлили величину интервала до 36,4, а оставили бы ее 36,3, то последнее значение у нас бы получилось 117,9. Именно для того чтобы не было потери данных необходимо округлять величину интервала до большего значения.
- Проведем подсчет количества предприятий попавших в каждый конкретный интервал. При обработке данных необходимо помнить, что верхнее значение интервала в данном интервале не учитывается (не включается в этот интервал), а учитывается в следующем интервале (нижняя граница интервала включается в данный интервал, а верхняя не включается), за исключением последнего интервала.
При проведении обработки данных лучше всего отобранные данные обозначить условными значками или цветом, для упрощения обработки.
23 48 57 12 118 9 16 22
27 48 56 87 45 98 88 63
Первый интервал обозначим желтым цветом – и определим сколько данных попадает в интервал от 9 до 45,4, при этом данное 45,4 будет учитываться во втором интервале (при условии что оно есть в данных) – в итоге получаем 7 предприятий в первом интервале. И так дальше по всем интервалам.
| Объем полученной прибыли, млн. руб. — (х) | Число предприятий (f) |
| 9,0 — 45,4 45,4 — 81,8 81,8 — 118,2 |
7 5 4 |
| Итого | 16 |
- (дополнительное действие) Проведем подсчет общего объема прибыли полученного предприятиями по каждому интервалу и в целом. Для этого сложим данные отмеченные разными цветами и получим суммарное значение прибыли.
По первому интервалу — 23 + 12 + 9 + 16 + 22 + 27 + 45 = 154 млн. руб.
По второму интервалу — 48 + 57 + 48 + 56 + 63 = 272 млн. руб.
По третьему интервалу — 118 + 87 + 98 + 88 = 391 млн. руб.
| Объем полученной прибыли, млн. руб. — (х) | Число предприятий (f) | Общий объем прибыли, млн. руб. |
| 9,0 — 45,4 45,4 — 81,8 81,8 — 118,2 |
7 5 4 |
154 272 391 |
| Итого | 16 | 817 |
Задание. Имеются данные о величине вклада в банке 30 вкладчиков, тыс. руб. 150, 120, 300, 650, 1500, 900, 450, 500, 380, 440,
600, 80, 150, 180, 250, 350, 90, 470, 1100, 800,
500, 520, 480, 630, 650, 670, 220, 140, 680, 320
Построить интервальный вариационный ряд распределения вкладчиков, по размеру вклада выделив 4 группы с равными интервалами. По каждой группе подсчитать общий размер вкладов.
Может еще поучимся? Загляни сюда!
Для атрибутивных и вариационных рядов применяют различные способы построения.
1. Построение атрибутивных рядов распределения. Атрибутивные ряды распределения обычно представляются в форме таблицы, причем в подлежащем такой таблицы перечисляются варианты атрибутивного признака, по которому строится ряд распределения. Как правило, число таких вариантов конечно. Если вариантов слишком много, то можно объединить некоторые из них (сущностно подобные) в классы, которые и будут новыми вариантами атрибутивного признака. В сказуемом таблицы отражаются частоты или частости каждого варианта, либо накопленные частоты или накопленные частости. Ряды распределения могут строиться по накопленным частотам, которые показывают, какое количество единиц имеет величину варианта не больше данной. Если вместо абсолютных частот взять частости, то аналогично получают и накопленные частости.
2. Построение дискретных вариационных рядов производится в следующей последовательности:
1) располагают варианты изучаемого признака в ранжированном порядке;
2) производят разноску единиц совокупности по вариантам (группировкам). Для этого строят таблицу;
3) подсчитывают количество единиц в каждой группе, т.е. определяют частоту каждого варианта. Частоты можно заменять частостями или использовать накопленные частоты (частости).
3. Построение интервального вариационного ряда производится в следующей последовательности:
1) выбирают оптимальное число групп (интервалов признака), на которые следует разбить совокупность. Число групп выбирается так, чтобы отразить многообразие значений признака в совокупности. Число групп устанавливается по формуле: к= 1 + 3,32lg N = 1 ,44 × ln N+ 1 (формула Стерджесса), где к— число групп; N — численность совокупности;
2) устанавливают длину интервала (шаг), которую рассчитывают по формуле:
3) определяют границы всех интервалов. Нижняя граница первого интервала принимается за хmin, верхняя граница первого интервала находится по формуле: xmin + h.
В качестве нижней границы второго интервала принимается верхняя граница первого, а верхнюю границу второго интервала получают прибавлением к верхней границе шага h. Процедуру повторяют до тех пор, пока не будут определены границы последней группы;
4) разносят единицы совокупности по интервалам;
5) подсчитывают единицы совокупности в каждом интервале.
Если полученные указанными выше способами группировки не удовлетворяют требованиям анализа, то производят перегруппировку. Ряды распределения используются в статистике как средство систематизации и упорядочивания материалов наблюдения, как метод изучения структуры явлений, анализа самих распределений и вариативности группировочного признака.








