Как составить равносильную формулу

Логическая равносильность формул

Понятие равносильности формул

Определение 4.1. Формулы и алгебры высказываний называются равносильными (эквивалентными), если при любых значениях входящих в них пропозициональных переменных логические значения получающихся из формул и высказываний совпадают. Для указания равносильности формул используют обозначение . Определение равносильности формул можно записать символически для любых конкретных высказываний

Не следует думать, что в обе формулы и непременно входят одни и те же переменные. Некоторые из переменных могут фактически отсутствовать в любой из них. Проверим, например, равносильность формул и . Для этого составим таблицы истинности обеих формул и убедимся, что значения истинности получающихся из них высказываний одинаковы для любых одинаковых наборов значений пропозициональных переменных и

Проверьте самостоятельно справедливость равносильностей

Выписывание в предыдущем определении в формулах и одних и тех же пропозициональных переменных обусловлено стремлением сделать записи и рассуждения более краткими и лаконичными. Это замечание следует иметь в виду и далее.

Для лучшего усвоения понятия равносильности формул алгоритм проверки на равносильность двух формул и можно представить в виде условной схемы (приведена в тексте). Формулы и заданы своими таблицами значений:

Алгоритм проверки формул на равносильность

Проанализируйте работу данного алгоритма и сопоставьте ее с определением понятия равносильности формул.

---

Признак равносильности формул

Сущность признака состоит в выявлении тесной связи между понятием равносильности формул и понятием тавтологии.

Теорема 4.2 (признак равносильности формул). Две формулы и алгебры высказываний равносильны тогда и только тогда, когда формула является тавтологией:

Доказательство. Если , то по определению 4.1 для любых высказываний . Тогда (по определению 1.9 операции эквивалентности) , откуда на основании соотношения (1.5) заключаем, что для любых . Последнее означает по определению тавтологии, что . Обратными рассуждениями доказывается утверждение: если , то . Итак, теорема доказана.

Отметим, что равносильность формул — это не (логическая) операция над формулами, а отношение между формулами логики высказываний. Это означает, что если и — формулы, то выражение уже не является формулой алгебры высказываний; оно — утверждение о некотором взаимоотношении между формулами и , лишь сокращенная (символическая) запись утверждения (высказывания) “ равносильна ” об этих формулах. Это утверждение либо истинно, либо ложно, т.е. и либо находятся в отношении равносильности, либо нет. В приведенном далее следствии из теоремы 4.2 устанавливаются некоторые свойства этого отношения между формулами алгебры высказываний.

Следствие 4.3. Отношение равносильности между формулами алгебры высказываний:

а) рефлексивно: ;
б) симметрично: если , то ;
в) транзитивно: если и , то , т.е. отношение равносильности является отношением эквивалентности.

Доказательство. Рефлексивность следует непосредственно из тавтологии теоремы 3.3, о и теоремы 4.2.

Для доказательства симметричности отношения предположим, что , т.е. на основании признака равносильности (теорема 4.2) . Тогда по тавтологии теоремы 3.3, пункт п) заключаем: формула принимает всегда те же самые значения, что и формула , т.е. только истинные значения. Следовательно, или (по признаку равносильности) . Симметричность доказана.

Наконец, если и , т.е. и , то на основании определения конъюнкции заключаем, что: . Привлекая теперь тавтологию из теоремы 3.3, пункт р) и правило заключения для получения тавтологий (теорема 3.5), получаем , или (по теореме 4.2) . Следовательно, отношение транзитивно.

Таким образом, отношение есть отношение эквивалентности, что и требовалось доказать.

Как и всякое отношение эквивалентности, отношение = разбивает множество, на котором оно задано, на непересекающиеся классы эквивалентных элементов. В данном случае множество всех формул алгебры высказываний распадается на попарно непересекающиеся классы, в каждом из которых находятся равносильные между собой формулы. Один класс, например, образуют все тавтологии, другой — все тождественно ложные формулы; имеется и много других классов.

---

Примеры равносильных формул

В теореме 4.4 перечисляются некоторые основные равносильности. Они получаются из тавтологий, приведенных в теоремах 3.1–3.4, на основании признака равносильности формул.

Теорема 4.4. Справедливы следующие равносильности:

Сформулируем и докажем лемму о замене, которая служит основанием для равносильных преобразований и упрощения формул.

Лемма 4.5 (о замене). Если , то для любой формулы алгебры высказываний имеет место равносильность

Другими словами, если в формуле некоторую ее подформулу заменить на равносильную ей формулу, то полученная формула будет равносильна исходной.

Доказательство. Поскольку формулы и принимают всегда одинаковые значения при одинаковых значениях пропозициональных переменных , то формулы

и

принимают одинаковые значения при любых одинаковых наборах значений переменных и Следовательно,

то есть , что и требовалось доказать.

Например, на основании этой леммы и равносильности из теоремы 4.4 (пункт п), формула

равносильна формуле .

Общая формулировка леммы о замене может быть конкретизирована в соответствии с индуктивным определением формулы следующим образом. Пусть имеется формула . Если , то . Далее, пусть исходная формула имеет следующее строение: . Если , то . Если, кроме того, , то

, то есть .

Об этом свойстве говорят, что отношение равносильности формул стабильно относительно операции конъюнкции. (Предыдущее свойство означает стабильность относительно отрицания.) Аналогично, отношение равносильности стабильно и относительно остальных логических операций — дизъюнкции, импликации и эквивалентности. Это означает, что если и , то

---

Равносильные преобразования формул

Используя лемму о замене и приведенные в теореме 4.4 равносильности, можем от одной формулы переходить к равносильной ей формуле. Такой переход называется равносильным преобразованием исходной формулы. Равносильные преобразования формул применяются прежде всего для упрощения формул.

Пример 4.6. Упростим формулу , используя равносильности из теоремы 4.4:

Равносильные преобразования формул применяются также для приведения формул к специальному виду или к специальной форме (к так называемой совершенной нормальной форме), имеющей исключительно важное значение как в самой алгебре высказываний, так и в ее приложениях. Об этом речь пойдет в следующей лекции.

Замечание 4.7. Отметим, что если некоторая формула является тавтологией, то и всякая равносильная ей формула также является тавтологией:

и .

Сделанное замечание позволяет обнаружить еще одну сферу применения равносильных преобразований: доказательство тождественной истинности тех или иных формул. Для этого данную формулу нужно равносильными преобразованиями свести к формуле, очевидно, являющейся тавтологией.

---

Равносильности в логике и тождества в алгебре

Можно провести параллель между понятием логической равносильности формул в алгебре высказываний и известным понятием тождества школьной алгебры. Равносильность формул и — это не что иное, как их тождественное равенство с точки зрения школьной алгебры, с той лишь разницей, что тождественность рассматривается относительно различных базисных множеств: в школьной алгебре — относительно множества всех вещественных чисел, а в алгебре логики — относительно двухэлементного множества .

Ввиду конечности базисного множества алгебры логики проверить справедливость той или иной равносильности можно механическим перебором всех возможных наборов значений (пропозициональных) переменных, входящих в равносильность, и вычислением на них значений левой и правой частей равносильности. В школьной алгебре бесконечность базисного множества не позволяет доказать ни одно тождество методом перебора всех значений входящих в него переменных. Для этого разработан метод тождественных преобразований алгебраических выражений, опирающийся на основные свойства арифметических операций над вещественными числами. Этими свойствами являются перестановочность (коммутативность) и сочетательность (ассоциативность) сложения и умножения, распределительность (дистрибутивность) умножения относительно сложения и т. п. Правда, ввиду нестрогости введения понятия вещественного числа в школьном курсе математики сами эти свойства принимаются без доказательства.

Подобно тому как в школьной алгебре понятие тождества (тождественного равенства) приводит к понятию тождественного преобразования алгебраических выражений, так в алгебре логики понятие равносильности формул естественным образом приводит к понятию равносильного преобразования формул логики высказываний. Здесь важно уяснить, что равносильные преобразования формул основываются на лемме 4.5 о замене. Равносильные преобразования используют основные равносильности, приведенные в теореме 4.4.

Полезно сравнить свойства логических операций, выраженные в основных равносильностях, со свойствами арифметических операций, помня, что некоторые логические операции имеют претензии на аналогию с некоторыми арифметическими операциями. Так, конъюнкция нередко называется логическим умножением, а дизъюнкция — логическим сложением. Наиболее разительны отличия в следующих свойствах: идемпотентность конъюнкции и дизъюнкции (это означает, что невозможны степени и “умножения” на натуральные числа), дистрибутивность дизъюнкции относительно конъюнкции, законы поглощения. Таким образом, мы приходим к некой новой алгебре, необычной по сравнению со школьной алгеброй, основанной на вещественных числах. Это и есть алгебра логики или алгебра высказываний. Равносильные преобразования в ней, как и в школьной алгебре, предназначены для приведения логических выражений (формул) к определенному виду.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Определение 1.4.:Две формулыАиВ называются равносильными, если
они принимают одинаковые логические
значения при любом наборе значений
входящих в формулу элементарных
высказываний.

Равносильность обозначается знаком
«».
Для преобразования формул в равносильные
важную роль играют основные равносильности,
выражающие одни логические операции
через другие, равносильности, выражающие
основные законы алгебры логики.

Для любых формул А,В,Ссправедливы равносильности.

1. Основные равносильности

закон идемпотентности

1-истина

0-ложь

закон
противоречия

закон исключенного третьего

закон поглощения

формулы расщепления

закон склеивания

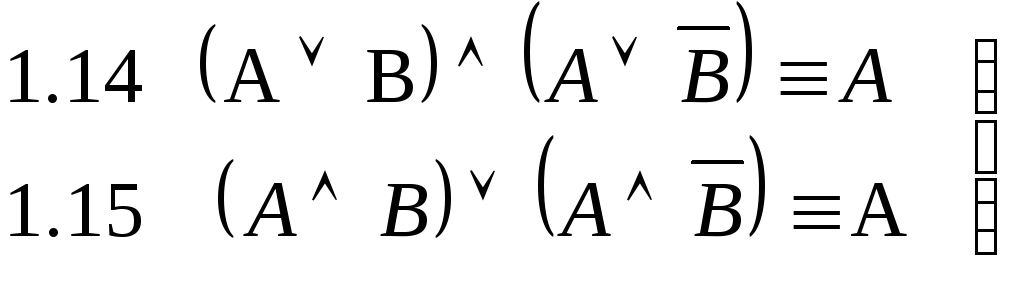
1. Равносильности, выражающие одни
   логические операции через другие.

закон де Моргана

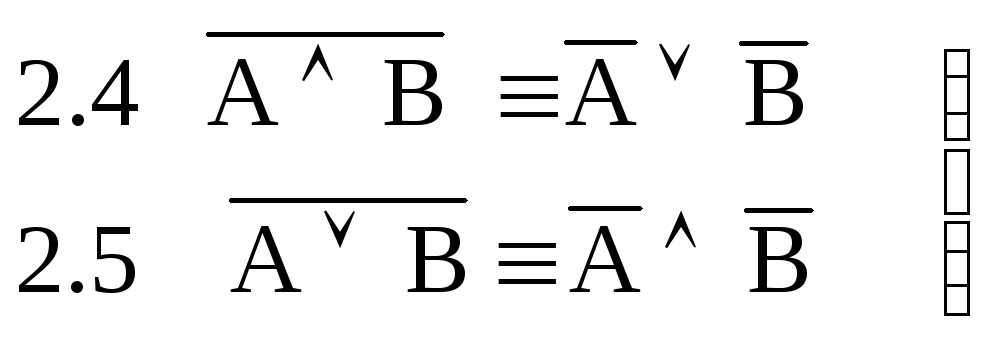
1. Равносильности, выражающие основные
   законы алгебры логики.

коммутативный закон

ассоциативный закон

дистрибутивный закон

Любая из равносильностей легко может
быть доказана с помощью таблицы
истинности. Докажем первый закон де
Моргана. Построим таблицу истинности
для левой и правой части закона.

А 1	В 1	1	0	0	0	0
1	0	0	1	0	1	1
0	0	0	1	1	0	1
0	0	0	1	1	1	1

Если результирующие столбцы совпали,
то формулы, стоящие в левой и правой
части закона, равносильны.

Отношение равносильности есть отношение
эквивалентности. Оно рефлексивно:
симметрично,
т.к. для любых двух формулАиВ:
еслитранзитивно : еслиТаким образом, эквивалентные формулы
можно рассматривать как разные формулы
записи одной и той же формулы. Используя
равносильностиI,II,IIIгрупп, можно формулу
заменить равносильной ей формулой.
Такие преобразования формул называются
равносильными. Равносильные преобразования
используются для доказательства
равносильностей; для приведения формул
к заданному виду, для упрощения формул.

Пример 14. Упростить формулу

При упрощении были использованы
равносильности:

II (1), I (9), I (2), III (1), I (10).

Пример 15. Закон поглощения
можно вывести при помощи равносильностей

I(3),III(5),I(4)

Вопросы и задания.

1. Среди следующих предложений выделите
те, которые являются высказываниями, и
установите, если это возможно, истинны
они или ложны.

1) Число 2 является делителем числа 7.

2) На улице идет дождь.

3) Меню в программе – это список возможных
вариантов.

4) Как пройти в библиотеку?

5) Математика – интересный предмет.

6) Москва – столица России.

7) «Да здравствуют музы!»

8) Студент МИКТ.

9) Алюминий тяжелее свинца.

2. Сформулируйте отрицание следующих
высказываний, укажите значение истинности
данных высказываний и их отрицаний.

1) Все простые числа нечетные.

2) 2>3.

3) Австралия – остров.

4) 12 есть составное число.

5) 2+2=4.

3. Определите значение истинности
следующих высказываний:

1) Липецк расположен на берегу реки
Воронеж и в нем проживает 100 тыс. человек.

2) 7 – простое число и 6 – составное число.

3) 7 – простое число или 6 – составное
число.

4) Если 12 делится на 3, то 12 – составное
число.

4. Даны два высказывания:

а: «число 5 является делителем 125»,

в: «число 5 – составное число».

В чем заключаются высказывания:

5. Определить, являются ли данная
последовательность формулой:

1)
;

2)
;

3)
;

4)
;

5)
.

6. Составить таблицы истинности для
следующих формул и указать, какие из
формул являются выполнимыми, какие –
тождественно истинными, какие –
тождественно ложными:

1)
;

2)
;

3)
;

4)
;

5)
;

6)
.

7. Какие из следующих формул являются
тавтологиями?

1)
;

2)
;

3)
.

8. Какие из рассмотренных логических
законов аналогичны законам алгебры
чисел, а какие нет?

9. Доказать следующие равносильности:

1)
;

2)
;

3)
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Равносильные формулы алгебры высказываний

Две формулы алгебры высказываний $A$ и $B$ называются равносильными или эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний.

Равносильность формул будем обозначать знаком $equiv$, а запись $Aequiv B$ означает, что формулы $A$ и $B$ равносильны.

Например, равносильны формулы:

$overline { overline { X } } equiv X$,

$Xvee Xequiv X$,

Тождественно истинная формула

Формула $A$ называется тождественно истинной { или тавтологией } , если она принимает значение 1 при всех значениях входящих в нее переменных.

Например, тожественно истинны формулы $Xvee overline { X } $, $Xrightarrow (Yrightarrow X)$

Тождественно ложная формула

Формула $A$ называется тождественно ложной { или противоречием } , если она принимает значение 0 при всех значениях входящих в нее высказываний.

Например, тождественно ложна формула $Xwedge overline { X } $

Выполнимая формула

Формула $A$ называется выполнимой, если она принимает значение 1 при всех значениях входящих в нее высказываний.

Например, выполнима формула $Xvee overline { X } $

Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно.

Группы равносильностей

Между понятиями равносильности и операцией $leftrightarrow$ существует следующая связь: если формулы $A$ и $B$ равносильны, то формула $Aleftrightarrow B$ – тавтология, и обратно, если формула $Aleftrightarrow B$ – тавтология, то формулы $A$ и $B$ равносильны.

Важнейшие равносильности алгебры высказываний можно разбить на следующие группы.

Равносильности алгебры Буля

Закон двойного отрицания: $overline { overline { X } } equiv X$

Коммутативность: $Xwedge Yequiv Ywedge X$; $Xvee Yequiv Yvee X$

Ассоциативность: $Xwedge (Ywedge Z)equiv (Xwedge Y)wedge Z$; $Xvee (Yvee Z)equiv (Xvee Y)vee Z$

Дистрибутивность $wedge$ относительно $vee$: $Xwedge (Yvee Z)equiv (Xwedge Y)vee (Xwedge Z)$; $(Xvee Y)wedge Zequiv (Xwedge Z)vee (Ywedge Z)$

Дистрибутивность $vee $ относительно $wedge $: $Xvee (Ywedge Z)equiv (Xvee Y)wedge (Xvee Z)$; $(Xwedge Y)vee Zequiv (Xvee Z)wedge (Yvee Z)$

Законы де Моргана: $overline { Xwedge Y } equiv overline { X } vee overline { Y } $; $overline { Xvee Y } equiv overline { X } wedge overline { Y } $

Законы поглощения: $Xwedge (Yvee X)equiv X$; $Xvee (Ywedge X)equiv X$

Законы идемпотентности: $Xwedge Xequiv X$; $Xvee Xequiv X$

Свойства констант: $Xwedge 1equiv X$; $Xvee 1equiv 1$; $Xwedge 0equiv 0$; $Xvee 0equiv X$

Закон противоречия: $Xwedge overline { X } equiv 0$

Закон исключения третьего: $Xvee overline { X } equiv 1$

Равносильности, выражающие одни логические операции через другие

$Xleftrightarrow Yequiv (Xrightarrow Y)wedge (Yrightarrow X)$

$Xleftrightarrow Yequiv (overline { X } vee Y)wedge (overline { Y } vee X)$

$Xleftrightarrow Yequiv (Xwedge Y)wedge (overline { Y } wedge overline { X } )$

$Xrightarrow Yequiv overline { X } vee Y$

$Xwedge Yequiv overline { overline { X } vee overline { Y } } $

$Xvee Yequiv overline { overline { X } wedge overline { Y } } $

$X | Yequiv overline { Xcdot Y } $

$X downarrow Yequiv overline { Xvee Y } $

$X rightarrow Yequiv overline { X } vee Y$

$X bigoplus Yequiv (X cdot bar { Y } )vee (bar { X } cdot Y)$

$X sim Yequiv overline { X bigoplus Y } equiv (XY)vee (bar { X } bar { Y } )$

Некоторые преобразования позволяют нам перейти от решаемого уравнения к равносильным, а также к уравнениям-следствиям, благодаря чему упрощается решение первоначального уравнения. В данном материале мы расскажем, что из себя представляют эти уравнения, сформулируем основные определения, проиллюстрируем их наглядными примерами и поясним, как именно осуществляется вычисление корней исходного уравнения по корням уравнения-следствия или равносильного уравнения.

Понятие равносильных уравнений

Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.

Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.

Уравнение f(x)=g(x) считается равносильным уравнению r(x)=s(x), если у них одинаковые корни или у них обоих нет корней.

Уравнения с одинаковыми корнями считаются равносильными. Также ими считаются два уравнения, одинаково не имеющие корней.

Если уравнение f(x)=g(x) имеет то же множество корней, что и уравнение p(x)=h(x), то они считаются равносильными по отношению друг к другу.

Когда мы говорим о совпадающем множестве корней, то имеем в виду, что если определенное число будет корнем одного уравнения, то оно подойдет в качестве решения и другому уравнению. Ни одно из уравнений, являющихся равносильными, не может иметь такого корня, который не подходит для другого.

Приведем несколько примеров таких уравнений.

Например, равносильными будут 4·x=8, 2·x=4 и x=2, поскольку каждое из них имеет только один корень – двойку. Также равносильными будут x·0=0 и 2+x=x+2, поскольку их корнями могут быть любые числа, то есть множества их решений совпадают. Также равносильными будут уравнения x=x+5 и x4=−1, каждое из которых не имеет ни одного решения.

Для наглядности рассмотрим несколько примеров неравносильных уравнений.

К примеру, таковыми будут x=2 и x2=4, поскольку их корни отличаются. То же относится и к уравнениям xx=1 и x2+5×2+5, потому что во втором решением может быть любое число, а во втором корнем не может быть 0.

Определения, данные выше, подойдут и для уравнений с несколькими переменными, однако в том случае, когда мы говорим о двух, трех и более корнях, более уместно выражение «решение уравнения». Таким образом, подытожим: равносильные уравнения – это те уравнения, у которых одни и те же решения или их совсем нет.

Возьмем примеры уравнений, которые содержат несколько переменных и являются равносильными друг другу. Так, x2+y2+z2=0 и 5·x2+x2·y4·z8=0 включают в себя по три переменных и имеют только одно решение, равное 0, во всех трех случаях. А пара уравнений x+y=5 и x·y=1 равносильной по отношению друг к другу не будет, поскольку, например, значения 5 и 3 подойдут для первого, но не будут решением второго: при подстановке их в первое уравнение мы получим верное равенство, а во второе – неверное.

Понятие уравнений-следствий

Процитируем несколько примеров определений уравнений-следствий, взятых из учебных пособий.

Следствием уравнения f(x)=g(x) будет уравнение p(x)=h(x) при условии, что каждый корень первого уравнения будет в то же время корнем второго.

Если первое уравнение имеет те же корни, что и второе, то второе будет уравнением-следствием первого.

Возьмем несколько примеров таких уравнений.

Так, x·2=32 будет следствием x−3=0, поскольку в первом есть только один корень, равный трем, и он же будет корнем второго уравнения, поэтому в контексте данного определения одно уравнение будет следствием другого. Еще один пример: уравнение (x−2)·(x−3)·(x−4) =0 будет следствием x-2·x-3·x-42x-4, потому что второе уравнение имеет два корня, равные 2 и 3, которые в то же время будут корнями первого.

Из данного выше определения можно сделать вывод, что следствием любого уравнения, не имеющего корней, будет также любое уравнение. Приведем здесь некоторые другие следствия из всех сформулированных в данной статье правил:

Как найти корни уравнения по корням уравнения-следствия или равносильного уравнения

Исходя из того, что мы написали в определениях, то в случае, когда мы знаем корни одного уравнения, то нам известны и корни равносильных ему, поскольку они будут совпадать.

Если мы знаем все корни уравнения-следствия, то можем определить корни второго уравнения, следствием которого оно является. Для этого нужно только отсеять посторонние корни. О том, как это делается, мы написали отдельную статью. Советуем вам ее прочитать.