Содержание:
- § 1 Равносоставленные фигуры
- § 2 Равновеликие фигуры
§ 1 Равносоставленные фигуры
В этом уроке познакомимся с равносоставленными и равновеликими фигурами.
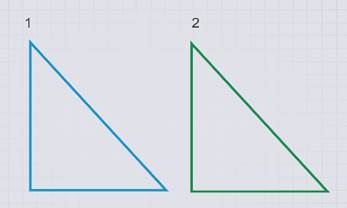
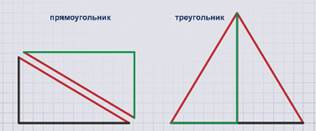
Возьмем два одинаковых прямоугольных треугольника.
Какие фигуры можно из них составить?
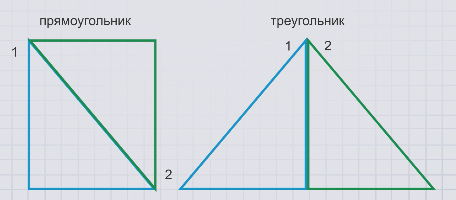
Можно составить прямоугольник, треугольник.
Для составления прямоугольника и треугольника использовали одинаковый набор фигур, поэтому полученные фигуры называют равносоставленными.
Дадим определение.
Равносоставленные фигуры – это те, которые можно составить (способом приложения) из одного и того же набора плоских фигур, при этом все фигуры набора должны участвовать в составлении. Из одного набора плоских фигур можно составить несколько новых фигур, и все они будут равносоставленными, если при составлении мы использовали все фигуры набора.
Так как равносоставленные фигуры состоят из одних и тех же фигур, можно заключить, что они имеют одинаковую площадь.
Докажем это.
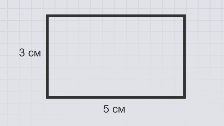
Начертим прямоугольник со сторонами 3 и 5 см.
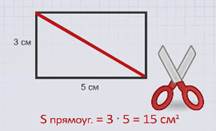
Площадь данного прямоугольника равна произведению 3 и 5.
3 умножить на 5, равно 15 см2.
§ 2 Равновеликие фигуры
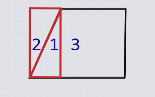
Вырежем прямоугольник.
Проведем в нем диагональ и разрежем по ней прямоугольник на два одинаковых треугольника.
Сложим из полученных фигур новую фигуру – треугольник.
Полученный треугольник и прямоугольник – равносоставленные фигуры, так как состоят из одного и того же набора плоских фигур.
Изначально у нас был прямоугольник, площадь которого не изменилась после того как мы разрезали его на два треугольника, из которых потом составили треугольник.
Т.е. можно сделать вывод, что данный прямоугольник и треугольник, составленный из частей прямоугольника, имеют одинаковую площадь.
Фигуры, имеющие одинаковую площадь, называются равновеликими.
Все равносоставленные фигуры являются равновеликими.
Выполним практическое задание.
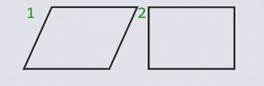
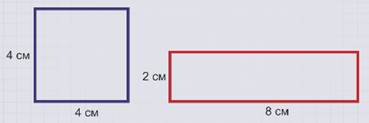
Даны две фигуры: четырехугольник и прямоугольник.
Докажите, что они равновеликие.
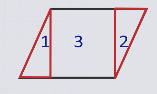
Разделим четырехугольник на части, из которых можно сложить данный прямоугольник: 2 треугольника и квадрат.
Переложим один треугольник так, чтобы получился прямоугольник.
Новый прямоугольник и данный прямоугольник при наложении совпадают.
Прямоугольник и четырехугольник состоят из одного и того же набора фигур, следовательно, четырехугольник и прямоугольник являются фигурами равносоставленными, а значит, равновеликими.
Найдем площадь квадрата со стороной 4 см и прямоугольника со сторонами 8 и 2 см.
Площадь квадрата равна произведению 4 и 4, равно 16 см2, площадь прямоугольника равна произведению 8 и 2, равно 16 см2.
Данные квадрат и прямоугольник – равновеликие фигуры, так как площади их равны.
Заметим, что не все равновеликие фигуры обязательно должны быть равносоставленными.
Выполним практическое задание на нахождение площади.
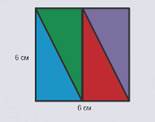
Возьмем квадрат со стороной 6 см. Разделим его на 4 одинаковых треугольника.
Чему равна площадь каждого треугольника?
Найдем сначала площадь квадрата: 6 ∙ 6 = 36 см2.
Квадрат составлен из 4 одинаковых треугольников.
Значит, площадь одного треугольника в 4 раза меньше площади квадрата.
36 : 4 = 9 см2.
Получили, что площадь каждого треугольника равна 9 см2.
В этом уроке вы познакомились с равносоставленными и равновеликими фигурами, а также решили несколько заданий по теме урока.
Список использованной литературы:
- Чекин А.Л. Математика: 3 кл.: Учебник: В 2 ч. / А.Л. Чекин; под ред. Р.Г. Чураковой. – М.: Академкнига/ Учебник, 2013.
- Чуракова Р.Г. Математика. Поурочное планирование методов и приемов индивидуального подхода к учащимся в условиях формирования УУД. 3 кл.: в 4 ч. Ч. 1 / Р.Г. Чуракова, Г.В. Янычева. — М.: Академкнига/Учебник, 2014. — 96 с.
- Чекин А.Л. Математика: 3 кл.: Методическое пособие /А.Л. Чекин; под. ред. Р.Г. Чураковой. – М.: Академкнига/ Учебник, 2012. – 224 с.
- Математика. 3 класс: поурочные планы по учебнику А.Л.Чекина. в 2 частях/ Авт.-сост. Н.В. Лободина. – Волгоград: Учитель, 2011.-269 с.
Муниципальное бюджетное общеобразовательное учреждение
гимназия №19 имени Н.З. Поповичевой г. Липецка
Исследовательский проект
«Равносоставленные фигуры и их свойства»
Автор:
Тарасов Дмитрий Владимирович
МБОУ гимназия № 19
имени Н. З. Поповичевой,
8 б класс.
Научный руководитель:
Васильева Марина Анатольевна,
учитель математики
МБОУ гимназии № 19
имени Н. З. Поповичевой.
г. Липецк
2018-2019 учебный год
Оглавление
|
Введение |
3 |
|
5 |
|
1.1. Теорема о фигуре, равносоставленной с одной и той же фигурой |
5 |
|
1.2. Основная теорема о равносоставленности |
5 |
|
2. Применение равносоставленности в геометрии |
6 |
|
2.1. Теорема о средней линии треугольника |
6 |
|
2.2. Теорема Пифагора |
6 |
|
2.3. Теорема о площади трапеции |
7 |
|
3. Примеры применения равносоставленности фигур при решении задач |
7 |
|
Заключение |
10 |
|
Библиографический список |
11 |
Введение
Проблема:
равносоставленность фигур очень мало обозначена в курсе геометрии.
Гипотеза:
равносоставленность фигур удобно применять при доказательстве и решении геометрических задач, теорем.
Цель работы:
показать, что равносоставленность фигур крайне востребована при решении геометрических задач на ОГЭ и ЕГЭ.
Задачи работы:
- разобрать понятие равносоставленныхных фигур и их свойства;
- доказать теоремы, не изучаемые в школьном курсе геометрии;
- создать подборку задач по данной теме, которые можно использовать при подготовке к ОГЭ по математике.
Аннотация
В начале изучения темы “Площади фигур” в 8 классе дано свойство площадей: « Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников». На это свойство в учебнике приведено всего 2-3 задачи. Однако эта тема имеет огромное практическое применение. Например: при покрытии пола паркетом в комнате каждая паркетина имеет форму прямоугольника и ими надо уложить весь пол в комнате. Еще! При укладке кафеля на стены ванной комнаты, мы не задумываясь, используем свойство равносоставленности фигур. Именно, поэтому я решил рассмотреть эту тему.
- Равносоставленность
Две фигуры называются равносоставленными, если они могут быть разрезаны на одинаковое число попарно равных фигур.
Из свойств площади следует, что равносоставленные фигуры равновелики (то есть имеют одинаковую пдощадь).
1.1. Теорема о фигуре, равносоставленной с одной и той же фигурой
Две фигуры, равносоставленные с одной и той же фигурой, равносоставлены.
Доказательство. Действительно, пусть фигуры Ф’ и Ф” равносоставлены с фигурой Ф. Рассмотрим линии, разбивающие фигуру Ф на части, из которых можно составить фигуру Ф’ и, кроме того, линии, разбивающие фигуру Ф на части, из которых можно составить фигуру Ф”. Те и другие линии разбивают фигуру Ф на более мелкие части, из которых можно составить как фигуру Ф’, так и Ф”. Таким образом, фигуры Ф’ и Ф” равносоставлены.
Ч.Т.Д.
1.2. Основная теорема о равносоставленности
Любые два равновеликих многоугольника равносоставлены
Доказательство.
Пусть М’ и М” – равновеликие многоугольники. Рассмотрим равносоставленные с ними треугольники Т’ и Т”, соответственно. Эти треугольники равновелики, а следовательно, равносоставлены. Значит, равносоставлены и исходные многоугольники М’ и М”.
Ч.Т.Д.
2. Применение равносоставленности в геометрии
2.1. Теорема о средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна её половине.
Так как



Также, отсюда следует, что угол A равен углу BMN( как соответственные элементы подобных треугольников), значит MN|| AC
2.2. Теорема Пифагора
На языке площадей теорему Пифагора можно переформулировать в следующем виде:
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.
Доказательство.
Расположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого. Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту S=1|2(a+b)h, где h=а+в, так как трапеция прямоугольная. C другой стороны, площадь трапеции равна сумме площадей полученных треугольников: S=S1+S2+S3 или S=2∙1/2ав+1/2с2. Треугольник с катетами с прямоугольный, так как сумма острых углов прямоугольного треугольника равна 90°., а угол с вершиной на высоте трапеции равен 180°-90°=90°. Приравнивая данные выражения, получаем: с2 = a2 + b2.
Ч.Т.Д.
2.3. Теорема о площади трапеции
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Доказательство.
- Через середину стороны CD (точка К) провели прямую, пересекающую сторону AD в точке L.
- Рассмотрим треугольники BCK и LDК: CK = DK (по построению), ∟ВCК = ∟LDK (как внутренние накрест лежащие при параллельных прямых ВС и LD и секущей CD ), ∟CKB = ∟DKL (как вертикальные), Δ BCK = ΔLDК (по стороне и двум прилежащим к ней углам), следовательно, BC = LD и SBCK = SLDК.
- SABCD = SABL =
3. Примеры применения равносоставленности фигур при решении задач
Задача 1. Найдите площадь фигуры.
1 способ
Ответ: 13см2
Задача 2.
В детском саду дети сделали родителям аппликации в подарок. Найдите площадь аппликации, если размер клетки 1см на 1см.
Задача 3.
Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых – до 35 т., вяза – 43 т., дуба – до 50 т., бука – до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке (масштаб 1 см. – 200 м.)
Задача 4.
В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.

Задача 5.
Требуется покрасить стену заводского здания. Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров. Масштаб 1 см – 5 м.

Заключение
В своей работе я доказал две теоремы о равносоставленности, которые не изучаются в школе, показал применение теорем о равносоставленности в школьном курсе математики. Доказал теорему Пифагора способом, не изучаемым в школьном курсе геометрии.
Считаю, что моя гипотеза о том, что равносоставленность фигур удобно применять при доказательстве и решении геометрических задач, теорем подтверждена полностью. Равносоставленность фигур крайне востребована на ОГЭ и ЕГЭ, поэтому мною собран банк задач на равносоставленность, который можно использовать при подготовке к ОГЭ.
Библиографический список
1. Атанасян Л.С, 8 класс. Геометрия. // Москва. Просвещение – 2013.
2. Болтянский В.Г. Равновеликие и равносоставленные фигуры. ГИТТЛ –Москва – 1956.
3. Савин А.П. Задачи на разрезание // Квант. – 1987. – № 7.
Ресурсы сети интернет.
- http://www.vasmirnov.ru/Lecture/Razrez/Razrez.htm
- http://www.mathedu.ru/lib/books/boltyanskiy_ravnovelikie_i_ravnosostavlennye_figury_1956/
- https://wiki.eduvdom.com/subjects/geometry/площадь_трапеции
- https://blog.tutoronline.ru/teorema-pifagora
- https://dic.academic.ru/dic.nsf/bse/125573/Равновеликие
- http://www.fipi.ru/
- http://yun.moluch.ru/archive/6/347/
Управление образования администрации
Павловского района
Муниципальное бюджетное
общеобразовательное учреждение
средняя школа №1 г. Павлово.
Научно-исследовательская работа на тему
«Равновеликие и равносоставленные фигуры».
Отделение: физико-математическое
Секция: математическая
Работу выполнил:
ученик 8 А класса
Бочкарев Максим (14 лет)
Научный руководитель:
учитель математики
Лефанова Н. А.
г. Павлово
2017 г.
Оглавление.
1.
Введение…………………………………………………………………
3-4
2.
Основная
часть………………………………………………………… 5-11
3.
Практическое применение
равносоставленности…………………… 12-14
4.
Заключение……………………………………………………………….
15
5. Список литературы……………………………………………………… 16
I.
Введение.
Рассмотрим две совершенно непохожие друг на друга фигуры. Казалось
бы они совершенно разные, т.е. с точки зрения обывателя неравны. Но если эти
фигуры вырезать из бумаги и разрезать одну из них на более мелкие фигуры, как
показано на рисунке, то из этих частей можно сложить вторую фигуру.

Данная головоломка «Танграм» появилась в Китае в конце восемнадцатого века
(рисунок). Головоломка “Танграм” – квадрат, разрезанный на 7 частей
из которых составляют различные силуэты. Первое ее изображение (1780
г.) обнаружено на ксилографии японского художника Утамаро, где две девушки
складывают фигурки “чи чао ту” – так называется танграм на его родине
(в переводе – умственная головоломка из семи частей”). Название танграм
возникло в Европе вероятнее всего от слова “тань” (на кантонском
диалекте – китаец) и часто встречающегося греческого корня “грамма”
(буква). Известно около семи тысяч различных комбинаций. Впрочем, авторы многих
книг по занимательной математике приписывают изобретение танграма якобы жившему
4 тысячи лет назад в Китае ученому Тангу. Суть этой игры не только и не столько
в собирании первоначальной фигуры — из разрезанных кусочков можно собирать
разнообразные силуэты людей, животных, предметов домашнего обихода, игрушек,
цифр, букв и т. д.
Какая же связь этой игры с
математикой? Во первых, в основе всей игры лежат геометрические фигуры, а во
вторых при разрезании одной фигуры и составлении из нее другой фигуры
используются свойства площадей данных фигур.
В 8 классе на уроках геометрии мы начали изучать площади
многоугольников. При доказательстве форму площади параллелограмм и треугольника
мы использовали способ перекраивания. Параллелограмм разрезанием и перекладыванием сводится
к прямоугольнику, треугольник – к параллелограмму. Меня заинтересовали
задачи, связанные с «разрезанием фигуры на части и
перекладыванием этих частей». Так я впервые познакомился с
понятиями «равновеликие фигуры и равносоставленные фигуры». Что же такое
равновеликие и равносоставленные фигуры? Могут ли равные фигуры быть неравными
и наоборот? Исследованием этих вопросов я занялся в своей работе.
При изучении теоремы Пифагора, я узнал, что теорему Пифагора
можно доказывать различными способами, один из которых и использует
равносоставленность и равновеликость.
Актуальность моего исследования состоит в том, что на основании
понятий равносоставленности и перекраивания можно находить площади разных
фигур, а также составлять головоломки.
Основная цель
моей работы – исследовать различные геометрические плоские фигуры и способы
нахождения площадей этих фигур путем «перекраивания», а также применение этих
способов для доказательства некоторых теорем геометрии.
Занимаясь данным исследованием, я попытался решить следующие
задачи:
1.
Изучить понятия
равносоставленность и равновеликость и теоремы связанные с этими понятиями;
2.
Рассмотреть способы
перекраивания многоугольников при определении их площадей
3.
Составить и решить
некоторые головоломки на составление различных равновеликих фигур.
4.
Найти практическое
применение геометрических понятий равносоставленности и равновеликости
При исследовании различных многоугольников, я выдвинул гипотезу,
что из любого многоугольника путем разрезания его определенным образом на
конечное число частей можно составить любой другой равновеликий ему
многоугольник.
А что же такое равновеликие и равносоставленные фигуры?
Равновеликие фигуры
— плоские фигуры одинаковой площади , а равносоставленные фигуры — фигуры,
которые можно разрезать на одинаковое число соответственно равных частей.
Эквивалентным понятию равносоставленности является понятие равнодополняемости,
которое лежит в основе «метода дополнения», то есть дополнения двух фигур
равными частями так, чтобы получившиеся после такого дополнения фигуры были
равны.
II.
Основная часть. Теоретические основы
равносоставленности и равновеликости.
1.
Метод разбиения.
Рассмотрим две фигуры (черт.1). Эти
фигуры равносоставлены, т.к. разрезав первую фигуру по пунктирным линиям, мы
составили из них вторую фигуру-квадрат. Мы можем доказать, что эти
равносоставленные фигуры равновелики.
На этом свойстве равносоставленности основан способ вычисления
площадей фигур, называемый способом разложения. Этот способ был известен еще
Евклиду 2000 лет назад. Для нахождения площади фигуры ее разбивают на конечное
число частей так, чтобы из них составить более простую фигуру, площадь которой
уже известна или легко находится. Из уроков геометрии мы знаем примеры
применения этого метода. (черт.2, 3,4)
Во всех данных ситуациях можно доказать, что все равносоставленные
фигуры равновелики. Возникает вопрос: всякие ли равновеликие фигуры
равносоставлены?
Ответом на этот вопрос занимались почти одновременно
сразу несколько математиков, не зная о работе друг друга. В 1790 г. впервые
эту проблему сформулировал венгерский ученый Фаркаш Бойяи, а в 1807 г. ее
решил Вильям Валлас, шотландский математик, в 1833 году немецкий офицер,
любитель математики Пауль Гервин , а в 1835 году, наконец, Бойяи, не зная о
существовании этих решений, дал свое. Потому до наших дней эта теорема дошла
под именем Бойя-Гервина.
Рассмотрим несколько утверждений:
1.
Если фигура P
равносоставлена с фигурой Q, а фигура Q с фигурой F, то фигура P
равносоставлена с фигурой F.
2.
Всякий треугольник
равносоставлен с некоторым прямоугольником. (Т.е. из любого треугольника,
разрезав его на конечное число многоугольников, можно составить прямоугольник
такой же как треугольник площади)
Черт. 5
3.
Два параллелограмма,
имеющие одинаковые площади и общую сторону, равносоставлены.
4.
Любой многоугольник
равносоставлен с некоторым прямоугольником.
5.
Два прямоугольника,
имеющие одинаковую площадь равносоставлены.
Доказательства
этих утверждений можно провести, применив способ «прекраивания» фигур.
А
на основании этих утверждений и доказывается теорема Бойя-Гервина: Любые два
равновеликих многоугольника равносоставлены.
Доказательство:
По утверждению (4) любой многоугольник равносоставлен с некоторым равновеликим
ему прямоугольником. Если , если каждый из многоугольников равносоставлен с
равновеликим ему прямоугольником, значит, полученные прямоугольники
равновеликие, и поэтому равносоставленные. Следовательно, согласно утверждению
(1), исходные многоугольники равносоставлены.
2.
Метод дополнения.
Метод
разбиения иногда проще заменить другим способом: способом дополнения. В нем
вместо разрезания фигуры на части, фигуру дополняют равными фигурами, так,
чтобы получившиеся фигуры были равными. Естественно, что равнодополняемые
фигуры имеют одинаковую площадь. А всякие ли два многоугольника, имеющие
одинаковую площадь, равнодополняемы? Утвердительный ответ на этот вопрос дает
также теорема Бойя-Гервина.
Рассмотрим
два многоугольника А и В одинаковой площади. Возьмем два равных квадрата таких,
чтобы в них можно было разместить эти многоугольники.
Черт. 6
Потом
вырежем из этих квадратов соответственно многоугольники А и и В, тогда от
квадратов останутся две равновеликие фигуры С и D.
Из равенства площадей фигур С и D
следует их равносоставленность по теореме Бойя-Гервина. Таким образом, фигуры
С и D можно разрезать на попарно равные части, а это доказывает
равнодополняемость многоугольников А и В
Рассмотрим
пример с черт.. 1 На том рисунке применяется способ разбиения. На следующем
рисунке (черт. 7), фигуры дополнены равными треугольниками, и поэтому также
равновелики.
Черт. 7
5.
Теорема
Пифагора.
Методы
разбиения и дополнения удобно использовать при доказательстве многих теорем
планиметрии. Например, для доказательства того, что параллелограмм и
прямоугольник, имеющие одинаковые основания и высоты, равновелики.
Черт.8
Идея перекраивания легла в основу доказательства и теоремы
Пифагора. Как известно, доказательств теоремы Пифагора существует существенно
много. В них, квадраты, построенные на катетах и на гипотенузе, разрезаются
так, что каждой части квадрата, построенного на гипотенузе, соответствует часть
одного из двух квадратов, построенного на катетах. Отличаются эти
доказательства только способами перекраивания. Но во всех случаях для понимания
доказательства достаточно одного взгляда на чертеж и все рассуждения можно
заменить одним словом «смотри», как это делалось в сочинениях древних индусских
математиков. Рассмотрим одно из таких доказательств. Это доказательство
Эпштейна. В доказательстве, в качестве составных частей, используются только
треугольники.
Черт.9
Но
имея современные методы геометрии и, зная основные теоремы геометрии я доказал,
что квадрат, построенный на гипотенузе составлен из треугольников, равных
треугольникам, из которых составлены квадраты катетов. Т.к. доказательство
равенства всех треугольников очень длинное, я приведу в работе только пример
доказательства некоторых треугольников.
Например,
рассмотрим треугольники, обозначенные номером 1.
Черт.10
1.
ОСН=
(т.к. они
вертикальные), а величина (т.к. СF-диагональ квадрата СОFВ) , следовательно,
МСА=45
.
2.
Прямую СD мы провели перпендикулярно прямой ЕF, поэтому
3.
,
Отсюда
следует, что СА=АЕ.
4.
+
=90
5.
6.
п.5 и 6
следует, что
7.
По стороне и двум прилежащим к ней
углам треугольники МСА и КРА равны.
Еще более удобное и наглядное доказательство теоремы Пифагора
предложил Бетхер. При доказательстве нужно переставить большие и маленькие
части квадратов, расположенные над стрелкой.
Черт. 11
6.
Терема Хадвигера – Глюра.
Исследуя равносоставленность и равнодополняемость, я узнал, что
эти понятия равносильны понятию равновеликость.
Основная сложность применения теорем равновеликости и
равносоставленности заключается в способах разрезания и дополнения. Как же
нужно разрезать, например, квадрат, чтобы из него получился треугольник или
выполнить разрезание квадратов при доказательстве теоремы Пифагора. Наверное,
нужны какие-то дополнительные условия для числа частей, на которые нужно
разрезать многоугольник и их расположения. Изучая литературу по этому вопросу,
я узнал, что в 1951 году швейцарские математики Хадвингер и Глюр установили,
что в теореме Бойя-Гервина нужно еще дополнительно потребовать, чтобы части,
на которые разрезается один из многоугольников и равные им части другого
равновеликого многоугольника имели соответственно параллельные стороны.
Черт.12
Такм образом, каждые два равновеликих многоугольника можно разбить
на части так, чтобы отвечающие друг другу части в виде треугольников или
многоугольников в разбиении обеих фигур были равны, и их соответствующие
стороны были параллельны (т.е. эти части получались одна из другой параллельным
переносом или центральной симметрией. Но исследование этого вопроса-это
возможно уже тема моей следующей работы.
III.
Практическое применение равносоставленности.
1.
Разбиение Дьюдени.
На какое минимальное число частей необходимо разбить
равносторонний треугольник, чтобы из них можно было составить квадрат?
Эта задача была предложена читателям газеты «Дейли мейл»
Генри Дьюдени в выпусках от 1 и 8 февраля 1905 года. Среди сотен полученных
ответов правильным был всего один: достаточно четырёх частей. Как же догадаться
до такого разбиения? Необходимо взять равновеликие треугольник и квадрат, а
затем составить из каждой фигуры регулярную полоску. Наложив одну полоску на
другую так, чтобы максимальное число середин сторон одной полосы попадало на
стороны другой полосы, получаем искомое разбиение. Это, в каком-то смысле,
общий способ нахождения разбиений равновеликих многоугольников. Легко заметить,
что все четыре части образуют нечто вроде цепочки. Если закрутить эту цепочку в
одном направлении, то получится треугольник, а если её закрутить в
противоположную сторону, то получится квадрат».
2.
Мозаики.
Идеи равносоставленности нашли свое воплощение во многих
областях жизни. Один из примеров применения приведен в начале моей работы. Это
головоломки «Танграм». Существует очень много задач-головоломок на разрезание и
составление различных фигур. Такие же задачи-головоломки приходится решать,
когда необходимо что-либо перекроить, т.е. из фигуры одной формы получить
равновеликую фигуру другой формы. Например, при составлении мозаики, когда
приходится разрезать одни многоугольники, чтобы составить из них какие либо
картины или панно.

3.
Детская труба-мозаика
Идеи мозаичных панно повторились в детской
игрушке «Мозаика», где в качестве элементов собраны части стеклышек, которые
собираются в различных комбинациях в виде круга.
4. Паркеты
Еще одним применением
идеи равносоставленности служат паркеты. В геометрии под паркетом понимают заполнение
плоскости одинаковыми фигурами (элементами паркета), которые не перекрывают
друг друга и не оставляют на плоскости пустого пространства (иногда паркетом
называют заполнение плоскости несколькими фигурами, например, правильными
многоугольниками). Обычный тетрадный лист в клеточку представляет собой
простейшую геометрическую мозаику. Элементом здесь является квадрат. Элементами
паркета могут быть также равносторонний треугольник, правильный шестиугольник,
произвольный параллелограмм, произвольный четырехугольник. Можно придумать
сотни, тысячи разных элементов паркетов.
5. Лоскутное шитье
Еще одно применение
равноставленности и равновеликости – народное творчество, а конкретно:
лоскутное шитье. Лоскутное шитье –
это искусство соединения небольших разноцветных кусочков ткани (лоскутов) в
единое целое путем сшивания. Основой таких изделий служат геометрические
фигуры; преимущественно квадраты и треугольники. Сщивая их по определенным
схемам, мастера лоскутного шитья получают изделия различных форм и размеров.

IV.
Заключение.
В своей работе я
исследовал вопросы равносоставленности различных геометрических фигур. Я
научился считать площади фигур, используя способы перекраивания. Основные
теоремы о равносоставленности позволяют сделать вывод, что любую фигуру можно
перекроить в другую равновеликую ей фигуру, а две равновеликие фигуры можно
составить из одних и тех же более мелких фигур. Также я изучил различные
способы доказательства теоремы Пифагора. Очень интересно с помощью различных
разрезаний составлять головоломки на составление фигур. Еще много вопросов
остались для меня нераскрытыми. Например, а как нужно разрезать многоугольник,
так, чтобы разрезов было как можно меньше, и из получившихся многоугольников
составить другой многоугольник.
Список
литературы и интернет-ресурсы.
1. В.Г.Болтянский. Равновеликие и
равносоставленные фигуры.-М.: Гостехиздат, 1956
2. Г. Линдгрен. Занимательные задачи на
разрезание.-М.: Мир,1977
3. Журнал «Квант»,1980, №6
4. В.Литцман. теорема Пифагора.
-М.:Государственное издательство физико-математической литературы, 1956
5. http://www.etudes.ru/ru/sketches/
6. http://mathlife.ru/parket
7. http://mosaic.su/nauka/geometricheskiy-parket/
Содержание
- – Какие фигуры называют Равносоставленными?
- – Что такое Равносоставленные фигуры примеры?
- – Как определить Равносоставленность?
- – Что такое равновеликий многоугольник?
- – Какие фигуры называются равномерными?
- – Что означает равные фигуры?
- – Что такое Равносоставленные фигуры 3 класс?
- – Как доказать что фигуры Равносоставленные?
- – Как понять равновеликие фигуры?
- – Какие Равносоставленными?
- – Какие многогранники называются равновеликими?
- – Что такое равновеликий куб?
- – Что такое равновеликий в математике?
- – Какие Параллелограммы называют равновеликими?
- – Как доказать что треугольники равновелики?
Равновеликие фигуры — плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры — фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей.
Какие фигуры называют Равносоставленными?
Равносоставленность Две фигуры называются равносоставленными, если они могут быть разрезаны на одинаковое число попарно равных фигур. Из свойств площади.
Что такое Равносоставленные фигуры примеры?
РАВНОВЕЛИКИЕ И РАВНОСОСТАВЛЕННЫЕ ФИГУРЫ — две фигуры в R2, имеющие равные площади и соответственно два многоугольника M1 и М 2 такие, что их можно разрезать на многоугольники так, что части, составляющие М 1, соответственно конгруэнтны частям, составляющим М 2.
Как определить Равносоставленность?
Равносоставленность — отношение между фигурами определённого типа (например, многогранниками). Означает, что одну фигуру можно разбить на более мелкие куски, из которых можно составить другую фигуру.
Что такое равновеликий многоугольник?
Определение равновеликих многоугольников
Равновеликие многоугольники – это многоугольники, площади которых равны.
Какие фигуры называются равномерными?
Две фигуры на плоскости (в пространстве) называются равными, если существует движение, взаимно однозначно переводящее одну фигуру в другую. Элементы данных фигур (вершины, стороны, центры и т. … * Равные фигуры имеют одинаковую площадь.
Что означает равные фигуры?
Фигуры называют равными, если совпадает их форма и размеры.
Или, два круга однозначно имеют одну и туже форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры.
Что такое Равносоставленные фигуры 3 класс?
Равносоставленные фигуры – это те, которые можно составить (способом приложения) из одного и того же набора плоских фигур, при этом все фигуры набора должны участвовать в составлении.
Как доказать что фигуры Равносоставленные?
Две фигуры называются равносоставленными, если они могут быть разложены на одинаковое число попарно равных фигур. Из свойств площади следует, что равносоставленные фигуры равновелики. В частности, равносоставленные многоугольники равновелики.
Как понять равновеликие фигуры?
РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры, имеющие равные площади, или пространственные фигуры (тела), имеющие равные объемы.
Какие Равносоставленными?
Многоугольники, имеющие равные площади, называют равновеликими. Если один из многоугольников можно разрезать на несколько частей, из которых можно сложить другой, то эти многоугольники называются равносоставленными.
Какие многогранники называются равновеликими?
Многогранники A и B называются равновеликими, ес- ли их объемы равны.
Что такое равновеликий куб?
Равновеликие многогранники имеют одинаковые объёмы. Объём куба тоже равен 216. Все рёбра у куба равны, его объём вычисляется так: V = a3, где а – ребро куба.
Что такое равновеликий в математике?
РАВНОВЕЛИКИЕ ФИГУРЫ – плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами.
Какие Параллелограммы называют равновеликими?
Два многоугольника, не равные между собою, но имеющие равные площади, называются равновеликими. … Рассмотрим один пример равновеликих многоугольников, важный для последующего. Построим два параллелограмма с одинаковыми основаниями и высотами.
Как доказать что треугольники равновелики?
Определение. Равновеликие треугольники — это треугольники, которые имеют одинаковую площадь. Равновеликие треугольники могут быть равными (так как равные треугольники имеют равные площади), но также могут иметь разные стороны и разные углы. Например, треугольники ABC и MKF — равновеликие, так как их площади равны.
Интересные материалы:
Можно ли с телефона отсканировать документ?
Можно ли снять деньги со счета телефона мтс?
Можно ли снять защитное стекло с телефона?
Можно ли со счета телефона оплатить покупку?
Можно ли спасти утопленный телефон?
Можно ли ставить телефон на зарядку в машине?
Можно ли сушить телефон в рисе?
Можно ли связаться со службой поддержки майл ру по телефону?
Можно ли у детей забирать телефон?
Можно ли участвовать в вебинаре с телефона?
Презентация на тему: ” Равносоставленные фигуры – это фигуры, которые можно разрезать на одинаковое число соответственно равных частей.” — Транскрипт:
1
2
Равносоставленные фигуры – это фигуры, которые можно разрезать на одинаковое число соответственно равных частей.
3
Фигуры из 2 равных треугольников Разбиение фигур Фигуры из 4 равных треугольников Фигуры из 3 треугольников
4
Фигуры из 4 равных квадратов Фигуры из 2 равных треугольников и 1 прямоугольника
5
Головоломка Пифагора Стомахион
6
Колумбово яйцо Головоломки художника Громова
7
8
Почти 4000 тысячи лет тому назад у немолодого императора Китая родился наследник Лао. Император призвал к себе трех мудрецов и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали “Ши-Чао-Тю” – квадрат, разрезанный на семь частей. математикхудожникфилософ
9
Возникла игра в Китае, примерно 4000 лет назад. Называется «ши чао тю», то есть семь хитроумных фигур. Название «танграм» – европейское. Вероятнее всего, от слова «тань» (что означает «китаец») и корня «грамма» (в переводе с греческого «линия»).
10
Танграм – геометрическая головоломка, состоящая из семи танов – геометрических фигур, полученных делением квадрата на семь частей – два больших треугольника, два маленьких треугольника, маленький квадрат и четырехугольник.
11
В каждую собираемую фигуру должны войти непременно все семь элементов. При составлении фигуры элементы не должны налегать друг на друга. Элементы фигур должны примыкать один к другому. Начинать нужно с того, чтобы найти место самого большого треугольника.
12
Вам понадобится: шаблон головоломки; цветной картон; ножницы.
13
Задание: собрать фигуру из танграма по образцу.
14
15
16
17