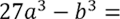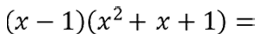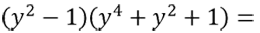Формула суммы кубов
Возьмём формулу куба суммы (см. §23 данного справочника):
$$ (a+b)^3 = a^3+3a^2 b+3ab^2+b^3 $$
и найдём из неё сумму двух кубов:
$$ a^3+b^3 = (a+b)^3-3a^2 b-3ab^2 = (a+b)^3-3ab(a+b) = $$
$$= (a+b)((a+b)^2-3ab) = (a+b)(a^2+2ab+b^2-3ab) =$$
$$ = (a+b)(a^2-ab+b^2 ) $$
Скобка $(a^2-ab+b^2 )$ называется неполным квадратом разности.
Полный квадрат разности – это $ (a^2-2ab+b^2 ) = (a-b)^2 $
Мы получили формулу для разложения суммы двух кубов на множители:
$$ a^3+b^3 = (a+b)(a^2-ab+b^2 ) $$
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
$$ a^3+b^3 = (a+b)(a^2-ab+b^2 )$$
Формула разности кубов
Возьмём формулу куба разности (см. §23 данного справочника):
$$ (a-b)^3 = a^3-3a^2 b+3ab^2-b^3 $$
и найдём из неё разность двух кубов:
$$ a^3-b^3 = (a-b)^3+3a^2 b-3ab^2 = (a-b)^3+3ab(a-b) = $$
$$ = (a-b)((a-b)^2+3ab) = (a-b)(a^2-2ab+b^2+3ab) = $$
$$ = (a-b)(a^2+ab+b^2 ) $$
Скобка $(a^2+ab+b^2 )$ называется неполным квадратом суммы.
Полный квадрат суммы – это $(a^2+2ab+b^2 ) = (a+b)^2$
Мы получили формулу для разложения разности двух кубов на множители:
$$ a^3-b^3 = (a-b)(a^2+ab+b^2 ) $$
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
$$ a^3-b^3 = (a-b)(a^2+ab+b^2 ) $$
Примеры
Пример 1. Разложите на множители:
а) $ x^3+y^3 = (x+y)(x^2-xy+y^2 )$
б) $ m^3-n^3 = (m-n)(m^2+mn+n^2 ) $
в) $ 8a^3+1 = (2a)^3+1^3 = (2a+1)(4a^2-2a+1) $
г) $125-64y^3 = 5^3-(4y)^3 = (5-4y)(25+20y+16y^2 )$
д) $ frac{1}{8} k^6-8 = ( frac{1}{2} k^2 )^3-2^3=(frac{1}{2} k^2-2)(frac{1}{4} k^4+k^2+4) $
е) $27+ frac{m^3}{125} = 3^3+(frac{m}{5})^3 = (3+frac{m}{5})(9-frac{3m}{5}+frac{m^2}{25})$
Пример 2. Докажите что выражения $19^3-11^3$ кратно 8
$$ frac{19^3-11^3}{8} = frac{(19-11)(19^2+19cdot11+11^2 )}{8} = frac{8(19^2+19cdot11+11^2 )}{8} = $$
$ = 19 ^2+19cdot11+11^2 $
Что и требовалось доказать.
Пример 3*. Дайте геометрическое объяснение формуле суммы кубов (аналогичная задача – см. Пример 5 §23 данного справочника).
Рассмотрим куб со стороной (a+b), в противоположные углы которого вписаны кубы со сторонами a и b.
Объемы кубов: $V_{a+b} = (a+b)^3, V_a = a^3, V_b = b^3$
Объём фигуры, закрашенной оранжевым: $V_{ор} = a(a+b)^2-V_a = a(a^2+2ab+b^2 )-a^3$ $= 2a^2 b+ab^2$
Объём фигуры, закрашенной синим: $V_{син} = b(a+b)^2-V_b = b(a^2+2ab+b^2 )-b^3$ $= a^2 b+2ab^2$
Общий объём:
$$ V_{a+b} = V_a+V_b+V_{ор}+V_{син} $$
$$ (a+b)^3 = a^3+b^3+2a^2 b+ab^2+a^2 b+2ab^2 $$
$$ a^3+b^3 = (a+b)^3-3a^2 b-3ab^2 = (a+b)^3-3ab(a+b) = $$
$$ = (a+b)((a+b)^2-3ab) = (a+b)(a^2+2ab+b^2-3ab) = $$
$$ = (a+b)(a^2-ab+b^2 )$$
Мы получили формулу суммы кубов.
В данной публикации мы рассмотрим одну из формул сокращенного умножения, а именно, разложение разности кубов на множители. Также разберем примеры решения задач для закрепления представленного материала.
-
Формула разности кубов
- Доказательство формулы
- Примеры задач
Формула разности кубов
Разность кубов чисел/выражений равняется произведению их разности на неполный квадрат их суммы.
a3 – b3 = (a – b)(a2 + ab + b2)
Полный квадрат суммы выглядит следующим образом: (a + b)2 = a2 + 2ab + b2. В нашем случае во второй скобке напротив второго слагаемого нет множителя 2, поэтому выражение является неполным.
Формула верна и в обратную сторону:
(a – b)(a2 + ab + b2) = a3 – b3
Примечание: a3 – b3 ≠ (a – b)3
Доказательство формулы
Достаточно просто умножить скобку (a – b) на (a2 + ab + b2), чтобы убедиться в том, что выражение верно, т.е. пойти от обратного:
(a – b)(a2 + ab + b2) = a3 + a2b + ab2 – a2b – ab2 – b3 = a3 – b3.
Примеры задач
Задание 1
Представьте в виде произведения множителей выражение: (7x)3 – 53.
Решение
(7x)3 – 53 = (7x – 5)((7x)2 + 7x ⋅ 5 + 52) = (7x – 5)(49x2 + 35x + 25)
Задание 2
Представьте выражение 512x3 – 27y3 в виде разности кубов и разложите его на множители.
Решение
512x3 – 27y3 = ((8x)3 – (3y)3) = (8x – 3y)((8x)2 + 8x ⋅ 3y + (3y)2) = (8x – 3y)(64x2 + 24xy + 9y2)
Разность кубов
Определение.
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы:
a3 – b3 = (a – b)·(a2 + ab + b2)
Вывод формулы разности кубов
Для доказательства справедливости формулы разности кубов достаточно перемножить выражения раскрыв скобки:
(a – b)·(a2 + ab + b2) =
= a3 + a2b + ab2 – ba2 – ab2 – b3 = a3 – b3
Применение формулы разности кубов
Формулу разности кубов удобно использовать:
- для разложения на множители
- для упрощения выражений
Примеры задач на применение формулы разности кубов
Пример 1.
Разложить на множители x3 – 27.
Решение:
x3 – 27 = x3 – 33 = (x – 3)·(x2 + 3x + 9)
Пример 2.
Разложить на множители 8x3 – 27y6.
Решение:
8x3 – 27y6 = (2x)3 – (3y2)3 =
= (2x – 3y2)·(4x2 + 6xy2 + 9y4)
Пример 3.
Упростить выражение
27x3 – 13x – 1
.
Решение:
Можно заметить, что для выражения в числителе можно применить формулу разности кубов
27x3 – 13x – 1 = (3x – 1)·(9x2 + 3x +1)3x – 1 = 9x2 + 3x +1
Что такое разность кубов и куб разности
Для возведения чисел и выражений в степень, а также для упрощения умножения используют формулы сокращенного умножения. Благодаря им вычисления проводятся компактнее и быстрее. К ним относят формулу разности кубов, которую важно не путать с кубом разности.
Разность кубов двух переменных равна произведению разности этих переменных на неполный квадрат их суммы.
(a^3-b^3=left(a-bright)left(a^2+ab+b^2right))
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Буквами a и b в формуле могут служить любые числа, переменные, одночлены и многочлены.
В этом определении квадрат суммы выражений называют неполным, поскольку он представляет собой сокращенный вариант формулы вида:
(left(a+bright)^2=a^2+2ab+b^2.)
Как видно, в формуле разности кубов во второй скобке не удвоенное произведение, а одинарное.
Куб разности двух переменных равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое, минус куб второго выражения.
({(a-b)}^3=a^3-3a^2b+3ab^2-b^3)
Вывод формулы разности кубов, как раскладывается
Формулу разности двух кубов можно вывести из куба разности .(a^3-b^3=left(a-bright)^3+3a^2b-3ab^2={(a-b)}^3+3ab(a-b)=(a-b)({(a-b)}^2+3ab)=(a-b)(a^2-2ab+b^2+3ab)=(a-b)(a^2+ab+b^2)
)Что и требовалось доказать.
Правила применения формул сокращенного умножения
Формулу разности кубов используют:
- для разложения многочленов на множители;
- для упрощения сложных выражений.
Основное свойство формул сокращенного умножения заключается в том, что они работают в обе стороны. Чтобы доказать это, достаточно пойти от обратного:
- раскрыть скобки;
- разложить многочлен на множители;
- сократить.
((a-b)(a^2+ab+b^2)=a^3+a^2b+ab^2-a^2b-ab^2-b^3=a^3-b^3)
Примеры задач с решением
Задача № 1
Упростить выражение (x^2-1)(x^4+x^2+1).
Решение:
Данное произведение многочленов является правой частью формулы разности кубов. На месте a стоит (x^2), а на месте b — 1. Тогда:
((x^2-1)(x^4+x^2+1)=x^8-1)
Ответ: (x^8-1)
Задача № 2
Представить в виде произведения множителей выражение ({(4y)}^3-5^3.)
Решение:
По формуле, ({(4y)}^3-5^3=(4y-5)(16y^2+20y+25).)
Ответ: ((4y-5)(16y^2+20y+25).)
В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители:
вынесение общего множителя за скобки
и
способ группировки.
В этом уроке мы рассмотрим еще один способ разложения многочлена на множители
с применением формул сокращённого умножения.
Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все
формулы сокращённого умножения себе на небольшую
шпаргалку.
Вспомним, как выглядит формула разности кубов.
a3 − b3 =
(a − b)(a2 + ab + b2)
Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать
специальный способ
для её запоминания.
Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону.
(a − b)(a2 + ab + b2)
= a3 − b3
Как разложить на множители разность кубов
Рассмотрим пример. Необходимо разложить на множители разность кубов.
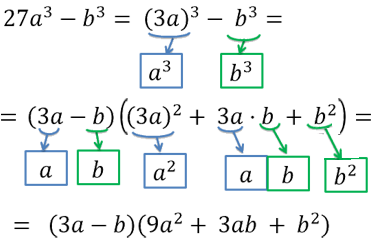
Обратим внимание, что «27а3» — это
«(3а)3», значит, для формулы разности кубов
вместо «a» мы используем «3a».
Используем формулу разности кубов. На месте «a3» у
нас стоит «27a3», а на месте
«b3», как и в формуле, стоит
«b3».
Применение разности кубов в обратную сторону
Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного
умножения.
Обратите внимание, что произведение многочленов
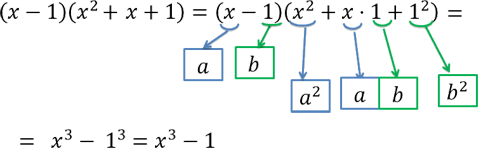
«(x − 1)(x2 + x + 1)» напоминает правую часть формулы разности кубов
«a3 − b3 = (a − b)(a2 + ab + b2)»,
только вместо «a» стоит «x»,
а на месте «b» стоит «1».
Используем для «(x − 1)(x2 + x + 1)» формулу разности кубов в обратную сторону.
Рассмотрим пример сложнее. Требуется упростить произведение многочленов.
Если сравнить «(y2 − 1)(y4 + y2 + 1)» с правой частью
формулы разности кубов
«a3 − b3 = (a − b)(a2 + ab + b2)», то
можно понять, что на месте «a» из первой скобки стоит «y2,
а на месте «b» стоит «1».
Важно!
Одночлены, которые стоят на месте «a» или «b» могут стоять в
степени.
Например, в рассматриваемом примере на месте «a» стоит «y2».
Это означает, что именно «y2» мы рассматриваем как «a».
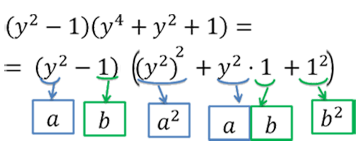
Представим скобку «(y4 + y2 + 1)» таким образом, чтобы
она соответствовала правой части формулы разности кубов.
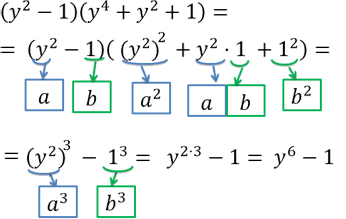
Используем формулу разности кубов и решим пример до конца.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий: