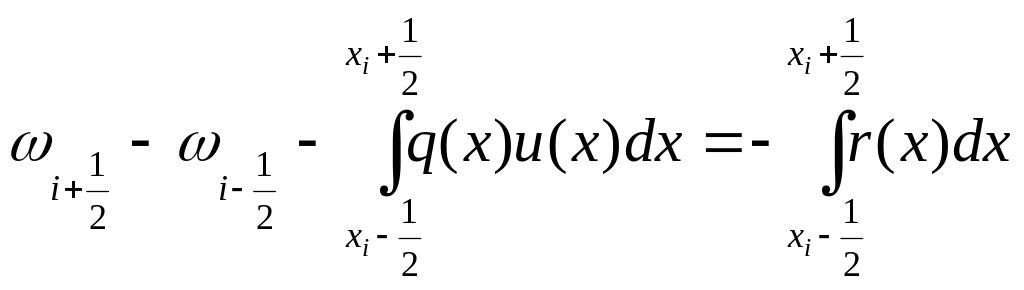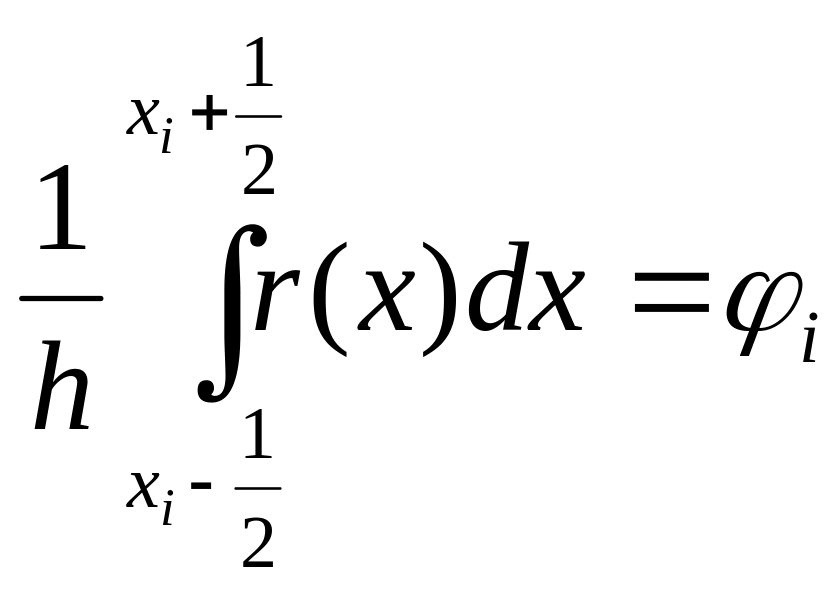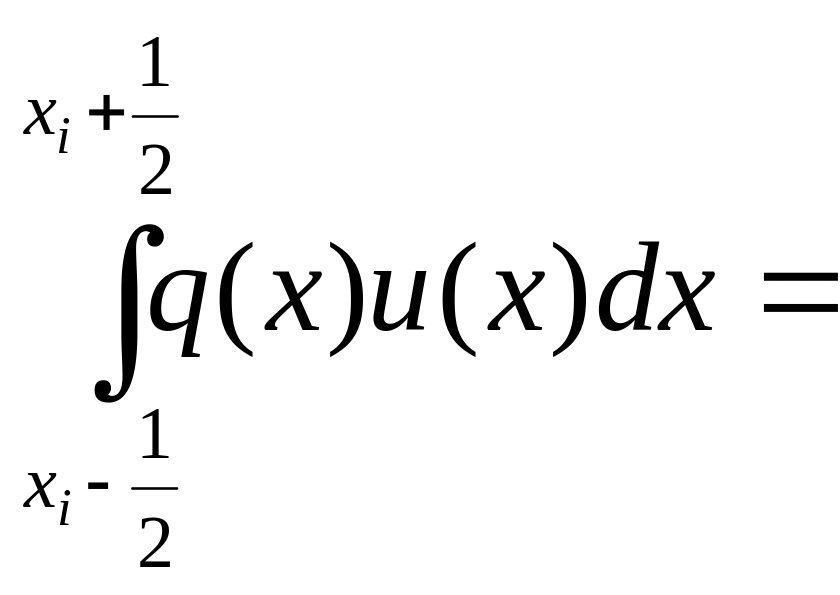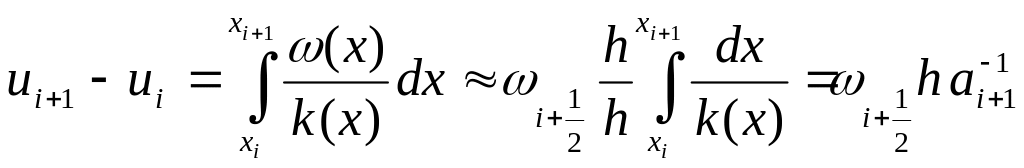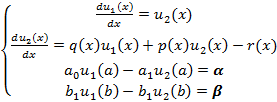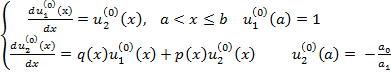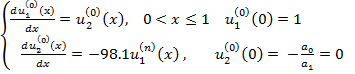Как составить разностную схему

Рассмотрим
ДУ

С
краевыми условиями
-краевая
задача 1 рода

-краевая
задача 2 рода

-краевая
задача 3 рода

Эти
краевые задачи имеют единственное
решение, когда
.
Тогда
.
При таких условиях краевая задача
корректно поставлена. Построим дискретную
модель:

В
зависимости от требований точности, от
порядка точности метода, от условия
устойчивости, выбираем
.

1.
-число
разбиений.
-число
точек сеточного аргумента(т.е.длины
массивов для сеточных функций в этой
задаче)
-число
внутренних точек, в которой ищется
решение. В результате построим равномерную
сетку аргумента.

2.Ддля
простоты точно заданы
.

3.Линейный
дифференциальный оператор заменяем
разностным. Для получения разностных
отношений в виде дискретных представим
решение в виде 2-ух разложений по формуле
Тейлора:

Из
такого разложения получаем:

В
итоге получим разностный оператор в
виде:

4.Разностная
схема это совокупность конечно разностных
уравнений и условий.

Приведем
эту разностную схему к удобному виду
для исследования устойчивости.

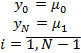
Пример.

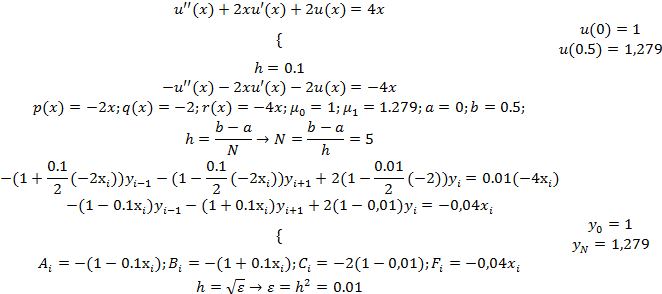
Где
-погрешность.

Билет
11.

Дана
линейная краевая задача первого
рода. Привести определение сходимости
трех точечной разностной схемы
приближенного решения этой задачи
. Доказать теорему сходимости.

Рассмотрим
ДУ:

Краевые
условия первого рода:

Запишем
разностное уравнение для погрешности

точное
решение разностной схемы,

– уравнение для погрешности

при
точном задании краевых условий на
границе:

Теорема:
Если разностная схема устойчива и
аппроксимирует исходную задачу с
порядком О(h²), то
существует
.
Т.е. разностная схема сходится с порядком
h².

Замечание:
Если задана погрешность ε, то по ней
и по тому что h≤2/p^*,
можно выбрать шаг h=(b-a)/N.
То. чтобы h
.

Алгоритм:

-выбрать
N и h

-задать
p,q,r

-построить
коэффициенты A_i,B_i,C_i,F_i

-осуществить
прогонку:

прямой
ход: α₁=0, β₁=μ₀,
i=1,…N

,

обратный
ход: y[N]=μ₁,
i=N-1,..0

Пример.

Построить
разностную схему второго порядка
точности для краевой задачи

//Заебись пример. E4

13. Провести построение разностной схемы методом баланса для линейной краевой задачи с краевыми условиями первого рода с оду.

Интегро-интерполяционный
метод (метод баланса)

Простейшая задача
: стержень без поперечного сечения, но
с массой. Распространение тепла идет
вдоль стержня в

момент времени. Возникает тепловой
поток

k(x)-
коэффициент теплопроводности,

u–
температура

q(x)-
коэффициент теплообмена с окружающей
средой

,

–
плотность источников тепла.

Проинтегрируем
на

– уравнение теплового
баланса.

– средняя величина

заменим u(x)
интерполяционным многочленом 0-ой
степени, т.е константой

Для потока рассмотрим
формулу :
.
Проинтегрируем эти выражения

,
где

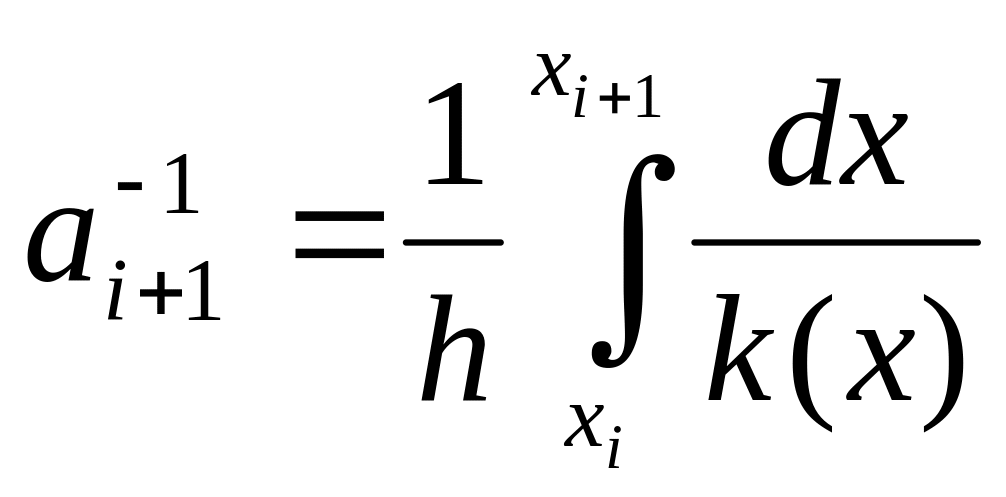
В итоге

, где

,

Для решения этой
разностной схемы используется метод
прогонки с коэффициентами

1. метод неопределенных
   коэффициентов

2. конечно-разностный
   метод

3. метод баланса

14. Пример. Методом
баланса построить консервативную
разностную схему с h=0.1
для
краевой задачи

.

Решение:

,

(в обозначениях
из теории)

15.

Привести постановку
линейной и нелинейной краевой задачи
для ОДУ 2 порядка. Провести построение
метода сведение к решению задачи Коши
(метод пристрелки).

Дана линейная
краевая задача:

(6)

Могут быть также
кр. Усл. 1-го и 2-го рода:1)
;
,
но случай с усл. 3-го рода – общий.

Для применения
метода пристрелки, сделаем замену
переменных:

В результате
получим систему вида:

(7)

Общее решение
системы ОДУ в (7) представим.

(x)

(2)

Для применения
метода Руне-Кутты, соответствующие
задачи Кошипредставим в виде задач для
системы ОДУ первого порядка:

Неоднородной:

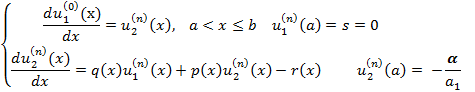
Для однородной
задачи r(x)=α=

получим:

(9)

Чтобы (2)было
решением (6) выберем с
из краевого условия для точки x=b
в (6). По
найденному

получим

(10)

Решение исходной
краевой задачи находим, подставляя

Пример: решить
методом пристрелки: y’’+98.1siny=0,
y’(0)=0,
y
(1)=
.

Делаем замену
.
Краевые условия запишем в виде:

.
Тогда нам нужно решить две задачи Коши:

неоднородная
задача:

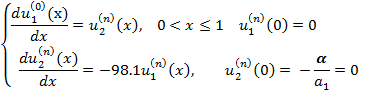
однородная:

Замечание: уравнения
однородны и в первом и во втором случаях,
разл. только нач. усл.

Решение будем
произв, например, методом Р.-К. 4-го порядка
точности:

Представив системы
в векторном виде

применяем формулы метода Р.-К.

,

После тог, как
алгоритм Р.-К. отработал мы получим
.
Тогда
.
И, наконец,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Разностные схемы решения уравнений параболического типа

Сначала рассмотрим проблему конструирования явных разностных схем. Основная идея состоит в том, что после замены дифференциального уравнения параболического типа его конечно-разностной аппроксимацией получаются формулы, явно выражающие значения решения для одного расчетного временного слоя через значения решения на предыдущем временном слое. Таким образом, если известно решение в начальный момент времени, можно шаг за шагом (послойно) найти решение для всех последующих моментов. Чтобы проиллюстрировать общий подход, рассмотрим типичную задачу теплопроводности.

Пример 8.3. Построить явную разностную схему для решения задачи теплопроводности в стержне, начальная температура которого равна нулю. Пусть температура левого конца фиксирована, а на правом конце происходит теплообмен с окружающей средой, так что тепловой поток пропорционален разности температур конца стержня и среды (определяется функцией ).

Решается третья начально-краевая задача:

(начальное условие)
(краевое условие на левой границе)
(краевое условие на правой границе).

Сравнивая с общей постановкой задачи, получаем ( — заданные числа)

Для аппроксимации производных в решаемом уравнении будем использовать (8.27),(8.26): . Отсюда

Эта формула при фиксированном значении выражает решение на (n+1)-м временном слое через решение на n-м слое. Ей соответствует четырехточечный шаблон, изображенный на рис. 8.5, в.

При записи в разностной форме начальное условие , запишется в следующем виде:

краевые условия на левом конце

краевые условия на правом конце определяются левой разностью по формуле (8.21): . Отсюда

Заметим, что соотношения (8.42),(8.43) точно аппроксимируют начальное и соответствующее краевое условие. Соотношения (8.41)–(8.44) образуют явную двухслойную разностную схему, имеющую первый порядок аппроксимации по и второй — по .

Замечания

1. Данная схема условно устойчива (устойчива при выполнении условия , т.е. при ). Тем самым накладываются серьезные ограничения на выбор шага по времени. Например, если шаг сетки по переменной выбрать равным , то шаг сетки по времени не должен быть больше, чем (это означает, что отрезок будет пройден за 200 шагов). Наилучшим с точки зрения минимизации ошибок является соотношение .

2. Разностная схема для уравнения строится аналогично и является устойчивой при , где .

Методика вычислений по явной схеме

1. Задать значения шагов сетки так, что , где — целые положительные числа, причем значение шага по времени выбрать из условия устойчивости . Вычислить . Положить .

2. Найти решение на (n+1)-м слое (рис. 8.7):

3. Если , вычисления завершить. Иначе положить и перейти к пункту 2.

Пример 8.4. Пользуясь явной схемой, используемой в примере 8.3, найти приближенное решение первой начально-краевой задачи вида:

(начальное условие)

(краевое условие на левой границе)

(краевое условие на правой границе).

Сравнивая с общей постановкой задачи (см. разд. 8.2), получаем

1. Зададим шаг по пространству: , следовательно, . Выберем шаг по времени из условия обеспечения устойчивости и минимизации ошибок , поэтому . Таким образом, получаем

Вычислим значения решения на нулевом слое:

Краевые условия на левой и правой границах записываются в виде:

2,3. Поскольку решение на следующих слоях при находится по формуле, следующей из (8.41):

и занесено в табл. 8.1.

Подчеркнем, что полученное решение на каждом из временных слоев является симметричным.

Теперь рассмотрим проблему конструирования неявных разностных схем. Для их получения все производные, входящие в дифференциальное уравнение, заменяются конечно-разностными аппроксимациями. Однако значения решения на (n+1)-м слое уже не выражаются в явном виде через значения на предыдущих слоях. В неявных схемах для нахождения решения на следующем временном слое необходимо решать систему линейных алгебраических уравнений.

Для иллюстрации общего подхода решим следующую задачу теплопроводности.

Пример 8.5. Построить неявную разностную схему решения задачи теплопроводности в стержне, начальная температура которого равна 1, а температура левого и правого концов равна нулю.

Данным физическим условиям соответствует первая начально-краевая задача:

(начальное условие)
(краевое условие на левой границе)
(краевое условие на правой границе).

Сравнивая с общей постановкой задачи, получаем — заданные числа.

Для аппроксимации производных в решаемом уравнении будем использовать формулу (8.27) и формулу (8.26), записанную на (n+1)-м временном слое:

Отсюда

Эта формула выражает решение на (n+1)-м временном слое через решение на n-м слое. Ей соответствует четырехточечный шаблон, изображенный на рис. 8.8,а.

При записи в разностной форме начальное условие , запишется в следующем виде:

краевые условия:

Соотношения (8.45)–(8.47) образуют неявную двухслойную разностную схему, имеющую первый порядок аппроксимации по и второй — по . Она является абсолютно устойчивой и сходящейся.

Методика вычислений по неявной схеме

1. Задать значения шагов сетки из условия обеспечения требуемой точности решения так, что , где — целые положительные числа. Вычислить . Положить .

2. Сформируем систему линейных алгебраических уравнений для некоторого временного слоя, записывая уравнение (8.45) при (рис. 8.9):

Согласно п.1, . Поэтому для нахождения решения на следующем временном слое требуется решить трехдиагональную систему линейных алгебраических уравнений с неизвестными

Методы решения таких систем рассматривались ранее.

3. Если у вычисления завершить. Иначе положить и перейти к пункту 2.

Методику вычислений по неявной схеме можно проследить на рис. 8.9, где выделен используемый четырехточечный шаблон. Заметим, что в неявной схеме объем вычислений на каждом шаге больше, чем в явных, но хорошую точность можно получить при гораздо большем шаге по времени.

Получим еще одну неявную схему. Для аппроксимации производной щ применим (8.27), а для аппроксимации и^ взвешенное среднее выражения (8.26), записанного для узлов на n-м и (n+1)-м временных слоях (см. рис. 8.8,б):

то есть , где . При получается обычное среднее, при одна из разностных производных берется с весом , а другая — с весом . В результате получаем разностную схему:

Перенесем в первых уравнениях все неизвестные в левую часть. Тогда получаем

Эта схема абсолютно устойчива и сходится. Для нахождения решения на следующем слое, как и ранее, требуется решать трехдиагональную систему линейных алгебраических уравнений. При схема называется схемой Кранка-Николсон. При из (8.48) следует явная схема (8.41), а при — неявная схема (8.45). Шеститочечный шаблон, соответствующий схеме (8.48), изображен на рис. 8.8,б. При схема имеет второй порядок аппроксимации по и по , а при — первый порядок аппроксимации по и второй — по .

Методику вычислений, совпадающую с уже описанной для схемы (8.45), продемонстрируем на примере.

1. Зададим . Тогда , то есть . Тогда начальные и краевые условия примут вид:

Положим . Вычислим .

2. Запишем систему (8.48) , принимая с учетом пункта 1:

Тогда получаем или в матричной форме В результате имеем

3. Далее, полагая , можно сделать следующий шаг по времени, решая новую систему алгебраических уравнений. Аналогичный процесс продолжается до достижения значения .

---

Разностные схемы решения уравнений гиперболического типа

Методы сеток для решения гиперболических уравнений имеют много общего с соответствующими методами для параболических уравнений. Однако они имеют и свои особенности, связанные с типом уравнения.

Сначала рассмотрим проблему конструирования явных разностных схем. Основная идея состоит в том, что после замены дифференциального уравнения гиперболического типа его конечно-разностной аппроксимацией получаются формулы, явно выражающие значения решения для одного расчетного временного слоя через значения решения на предыдущем временном слое. Таким образом, если известно решение в начальный момент времени, можно шаг за шагом (послойно) найти решение для всех последующих моментов. Чтобы проиллюстрировать общий подход, рассмотрим типичную краевую задачу для волнового уравнения.

Пример 8.6. Построить явную и неявную разностные схемы для решения задачи, в которой имеется струна длиной , натянутая между двумя точками оси , точкой и точкой . Концы струны закреплены, начальное смещение струны описывается функцией , а начальная скорость — функцией .

Решается первая начально-краевая задача:

(начальное условие)
(начальное условие)
(краевое условие на левой границе)
(краевое условие на правой границе).

Сравнивая с общей постановкой задачи, получаем — заданные числа.

Для аппроксимации производных в решаемом уравнении будем использовать (8.30) и (8.26):

Отсюда

Эта формула выражает решение на (n+1)-м временном слое через решение на n-м и (n-1)-м слоях. В отличие от схем для уравнения теплопроводности, в которых использовались только два временных слоя (n-й и (n+1)-й) , здесь требуется использовать три слоя: (n-1)-й, n-й и (n+1)-й. Ей соответствует пятиточечный шаблон, изображенный на рис. 8.10,а , называемый “крест”.

При записи в разностной форме начальное условие , запишется в следующем виде:

начальное условие , с применением (8.27) при в виде , или, используя предыдущее соотношение,

краевые условия представляются в форме:

Соотношения (8.49)–(8.52) образуют явную трехслойную разностную схему. Эта схема имеет первый порядок аппроксимации по и второй — по , так как соотношение (8.51) аппроксимирует дифференциальное начальное условие с первым порядком.

Замечания

1. Данная схема условно устойчива (устойчива при выполнении условия .

2. Разностная схема для уравнения строится аналогично и является устойчивой при , где .

3. Простейшая замена (8.51) имеет первый порядок аппроксимации. Поскольку разностная схема (8.49) аппроксимирует дифференциальное уравнение со вторым порядком, желательно, чтобы разностное начальное условие также имело второй порядок аппроксимации. Для этого запишем аналог формулы Тейлора (8.17) в направлении при

Если функция имеет ограниченную вторую производную, то в силу исходного дифференциального уравнения получаем . Из предыдущего соотношения получаем

или

где . В результате соответствующее начальное условие в разностной форме имеет вид .

Так как , то

Если в разностной схеме используется (8.51), схема имеет первый порядок аппроксимации по и второй — по , а если (8.53), то имеет второй порядок аппроксимации по и по .

Методика вычислений по явной схеме

1. Задать значения шагов сетки так, что , где — целые положительные числа, причем значение шага по времени выбрать из условия устойчивости . Вычислить

Приведенные выражения дают решение задачи для первых двух слоев сетки (рис. 8.8). Положить .

2. Найти решение на (n+1)-м слое (рис. 8.11):

3. Если , вычисления завершить. Иначе положить и перейти к пункту 2.

Теперь рассмотрим проблему конструирования неявных разностных схем. Для их получения все производные, входящие в дифференциальное уравнение, заменяются конечно-разностными аппроксимациями с использованием (n+1)-го слоя для аппроксимации . Однако значения решения на (n+1)-м слое уже не выражаются в явном виде через значения на предыдущих слоях. В связи с этим в неявных схемах для нахождения решения на следующем временном слое необходимо решать систему линейных алгебраических уравнений.

Для иллюстрации общего подхода получим неявную схему для волнового уравнения. При аппроксимации производных в уравнении будем использовать (8.30) и формулу (8.26), записанную на (n-1)-м, n-м и (n+1)-м слоях:

где — параметр, . Значения приближенного решения на нулевом и первом слоях вычисляются по формулам (8.50)–(8.52), как и в явной схеме. На остальных слоях схема представляет собой линейную систему алгебраических уравнений с трехдиагональной матрицей, в которой диагональные элементы преобладают. Решение этой системы существует, единственно и вычисляется методом прогонки.

Формула (8.54) выражает три неизвестных значения решения на (n+1)-м временном слое через решения на n-м и (n-1)-м слоях. В отличие от схем для уравнения теплопроводности, в которых использовались только два временных слоя (n-й и (n+1)-й) , здесь требуется использовать три слоя: (n-1)-й, n-й и (n+1)-й. Поэтому такая схема называется неявной трехслойной. Ей соответствует девятиточечный шаблон, изображенный на рис. 8.10,б. При схема (8.50)-(8.52),(8.54) переходит в явную схему “крест”.

При схема абсолютно устойчива, а при схема условно устойчива (устойчива при выполнении условия ) При схема имеет второй порядок аппроксимации по и по .

Пример 8.7. Пользуясь явной схемой, найти приближенное решение первой начально-краевой задачи:

(начальное условие)
(начальное условие)
(краевое условие на левой границе)
(краевое условие на правой границе).

Сравнивая с общей постановкой задачи, получаем

1. Зададим шаг по пространству, равным , шаг по времени выберем из условия устойчивости: . Положим . Тогда

По формулам (8.50), (8.52), (8.53), учитывая, что , получаем значения приближенного решения на нулевом и первом слоях:

2,3. Поскольку , решение на последующих слоях вычисляется по И формуле, следующей из (8.49):

В табл. 8.2 приведены результаты расчетов при , так как решение симметрично относительно при фиксированном .

Замечание. В практике применения численных методов существует полезный прием, позволяющий на основе результатов расчетов судить о том, с какой точностью они получены. С этой целью используется правило Рунге, изложенное выше применительно к уточнению результатов численного дифференцирования и интегрирования. Аналогичный подход можно использовать для оценки точности решения задач математической физики. Опишем идею его реализации:

а) находится численное решение с шагом по пространственной переменной и шагом по времени ;

б) расчет повторяется с шагами и с тем, чтобы образовывались слои, некоторые из которых совпадали бы со слоями, полученными ранее;

в) сравниваются оба численных решения в одинаковых узлах сетки (им соответствуют одни и те же значения пространственной координаты и времени). Если отклонение удовлетворяет заданным требованиям, то процесс завершается и в качестве приближенного решения задачи принимается полученное в п.б. Иначе шаги снова делятся пополам и процесс продолжается.

---

Разностные схемы решения уравнений эллиптического типа

Рассмотрим проблему решения краевых задач для уравнений эллиптического типа. Эти задачи являются стационарными, так как в них отсутствует временная переменная. В них требуется найти решение уравнения с частными производными в данной области пространства, если на границе области решение или его производная заданы. Разностные схемы получаются путем замены производных их конечно-разностными аппроксимациями. В результате приближенное решение эллиптических задач сводится к решению системы линейных алгебраических уравнений для значений искомой функции во внутренних узлах сетки.

Чтобы проиллюстрировать общий подход, рассмотрим задачу Дирихле для уравнения Лапласа.

Пример 8.8. Построить разностную схему для решения задачи Дирихле (где — заданная функция, — заданные числа):

В данном случае задача решается в области П прямоугольной формы, краевые условия заданы на сторонах прямоугольника. В плоскости построим сетку , где — величины шагов по и и — целые положительные числа.

Заменим дифференциальные операторы в уравнении Лапласа по формулам, следующим из (8.25) при замене переменной на переменную

Применяя краткую запись , получаем

или

Полагая , краевые условия можно записать в виде:

Для нахождения искомого решения требуется решить систему линейных алгебраических уравнений. Схема (8.55),(8.56) имеет второй порядок аппроксимации по и по , является абсолютно устойчивой и сходится. Ей соответствует пятиточечный шаблон, изображенный на рис. 8.12. При , т.е. одинаковых шагах в горизонтальном и вертикальном направлениях, получаем

Разрешив относительно , имеем

Это означает, что решение аппроксимируется средним значением по четырем соседним узлам. Как правило, для решения системы (8.58) применяются различные итерационные методы, например, метод простой итерации или метод Зейделя.

Рассмотрим частный случай поставленной задачи при Так как , то запишем систему (8.57) для четырех внутренних точек

Краевые условия (8.56) запишутся в форме

С учетом краевого условия система может быть записана в следующей матричной форме

В результате имеем .

Методика вычислений

1. Задать сетку , где — величины шагов по и и — целые положительные числа; — желаемую точность. Вычислить

Положить ; задать начальное приближение искомого решения во внутренних узлах: .

2. Вычислить одним из двух методов (рис. 8.13):

а) методом простых итераций:

б) методом Зейделя:

Шаг 1. Положить .

Шаг 2. Вычислить

Шаг 3. Если , процесс завершить. Иначе положить и перейти к шагу 2.

3. Если выполняется условие окончания , процесс завершить. Иначе положить и перейти к п.2.

Замечания

1. Метод Зейделя обеспечивает движение по узлам слева направо, начиная с первого слоя сетки по переменной . Использование значений с (k+1)-й итерации, как правило, улучшает сходимость.

2. Вместо метода Зейделя можно использовать более эффективные релаксационные методы:

где — параметр релаксации. Член характеризует “память” алгоритма о значении решения на предыдущей итерации. При итерационный метод называется методом верхней релаксации, при — методом нижней релаксации, при совпадает с методом Зейделя. Существует оптимальное значение параметра релаксации, зависящее от шагов сетки и способа получения , при котором достигается максимальная скорость сходимости метода.

3. При решении задачи Неймана или третьей краевой задачи производные, входящие в краевые условия, следует также заменить их конечно-разностными аппроксимациями.

4. Если область , в которой решается задача, имеет неправильную форму, можно покрыть ее сеткой (рис. 8.14) и найти решение в ближайших к границе точках, а затем рассчитать значения искомой функции на границе, например, с помощью линейной интерполяции.

5. В данной главе рассмотрены принципы конструирования разностных схем для простейших линейных начальных, краевых и начально-краевых задач. Для нелинейных задач, которые решаются при расчетно-теоретической проработке современных технических систем, применяют те же разностные схемы, что и для линейных задач.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Макеты страниц