Математика – довольно непростая наука, однако усвоить ее азы нужно каждому. Без этих навыков и знаний в современном мире никуда.
Элементарные математические приемы и задачи закладываются в память школьников еще в младших классах. А «упустив» более легкий материал, решить сложные задания становится не под силу. Долгие и серьезные уроки математики делают детей особо неусидчивыми, а значит подавать информацию нужно в игровой форме, например, с помощью ребусов. Такие задания не нужно заставлять решать из-под палки, детки сами охотно будут браться за их разгадывание.
Далее вы узнаете, чем же все-таки полезны математические ребусы для школьников, научитесь составлять и разгадывать разные ребусы и головоломки вместе со своими отпрысками.

Главное в статье
- Польза ребусов на математическую тему для развития ребенка
- Правила составления математических ребусов для детей
- Как придумать математический ребус?
- Особенности математических ребусов для начальной школы
- Математические ребусы для 1 класса с ответами
- Математические ребусы для 2 класса с ответами
- Математические ребусы для 3 класса с ответами
- Математические ребусы для 4 класса с ответами
- Математические ребусы для 5 класса с ответами
- Математические ребусы для 6 класса с ответами
- Математические ребусы с цифрами с ответами
- Математические загадки, ребусы, кроссворды
- Как решать математические ребусы с буквами?
- Решение математических ребусов с буквами
- Математические ребусы и головоломки
- Самые легкие математические ребусы
- Сложные математические ребусы
Польза ребусов на математическую тему для развития ребенка
Ребусы на математическую тему – это те же загадки и головоломки, в которых используются рисунки и графика. Они бывают разные по уровню сложности в зависимости от возрастной категории школьников.
- В тех случаях, когда ребенок разгадывает, а особенно, когда составляет ребусы для своих сверстников – очень хорошо развивается логическое мышление и тренируется интеллект.
- Есть ребусы, решение которых требует немалых усилий со стороны ребятни. Пытаясь найти разгадку, дети развивают у себя нестандартное мышление. В будущем это умение здорово пригодится, когда нужно будет принять решения и найти выход из жизненных проблем.
- И самое главное: процесс разгадывания математических ребусов здорово поднимает настроение, а также помогает лучше построить отношения со сверстниками.

Правила составления математических ребусов для детей
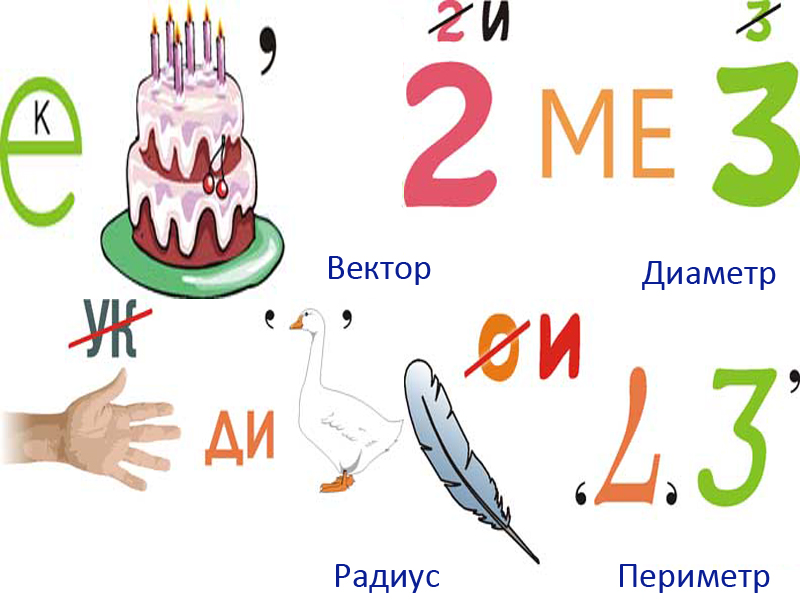
- Если вы видите перед словом или картинкой запятую, то нужно убрать первую букву с этого названия. То же самое нужно сделать, если запятая стоит в конце слова. Когда около картинки две запятых, то убирается две буквы соответственно. Например, на первой картинке изображен сок — нужно убрать первую букву «С», рука — уберите слог «ка», буква «ж» так и остается, нос — слово остается целиком, пять — уберите две первые буквы. Зашифрованное слово — «окружность».
- Если цифры, обозначающие последовательность букв в слове зачеркнуты, то их необходимо выбросить из него. Тоже самое касается и букв. На втором рисунке изображен цирк — уберите последнюю букву, из слова «акула» нужно убрать букву «А», готовый ответ: «циркуль».
- Когда рядом с картинкой стоят цифры, поменянные местами, то и в названии самого предмета нужно поменять местами буквы, которые стоят в последовательности с указанными цифрами.
- Если картинка изображена вверх тормашками, то отгадку нужно читать в обратном порядке: справа-налево.
- Для ребусов используется только именительный падеж в словах.
- Указатель в виде стрелки или математический знак «равно» обозначает, что нужно заменить буквы одну другой.
- В ребусах одно значение может быть расположено внутри другой картинки, за ней или под ней. Тогда применяйте слова: В, НА, НАД, ПОД, ЗА.
- Цифры, стоящие в ряд около изображения, обозначают, что нужно использовать из этого значения буквы в указанной последовательности цифр.
 Вот несколько примеров математических ребусов, соответствующих приведенным правилам:
Вот несколько примеров математических ребусов, соответствующих приведенным правилам:
Под третьим рисунком зашифровано слово «вектор», под четвертым — «степень», под пятым — «два», под шестым — «доказательство».

Как придумать математический ребус?
Следуя общим правилам составления ребусов, попробуйте придумать для начала несложные математические задачки, используя цифры и математические термины. А затем, немного освоив простые задания, переходите к более усложненным. Вот несколько образцов ребусов по математике с ответами, которые вдохновят вас и покажут, как их нужно составлять:
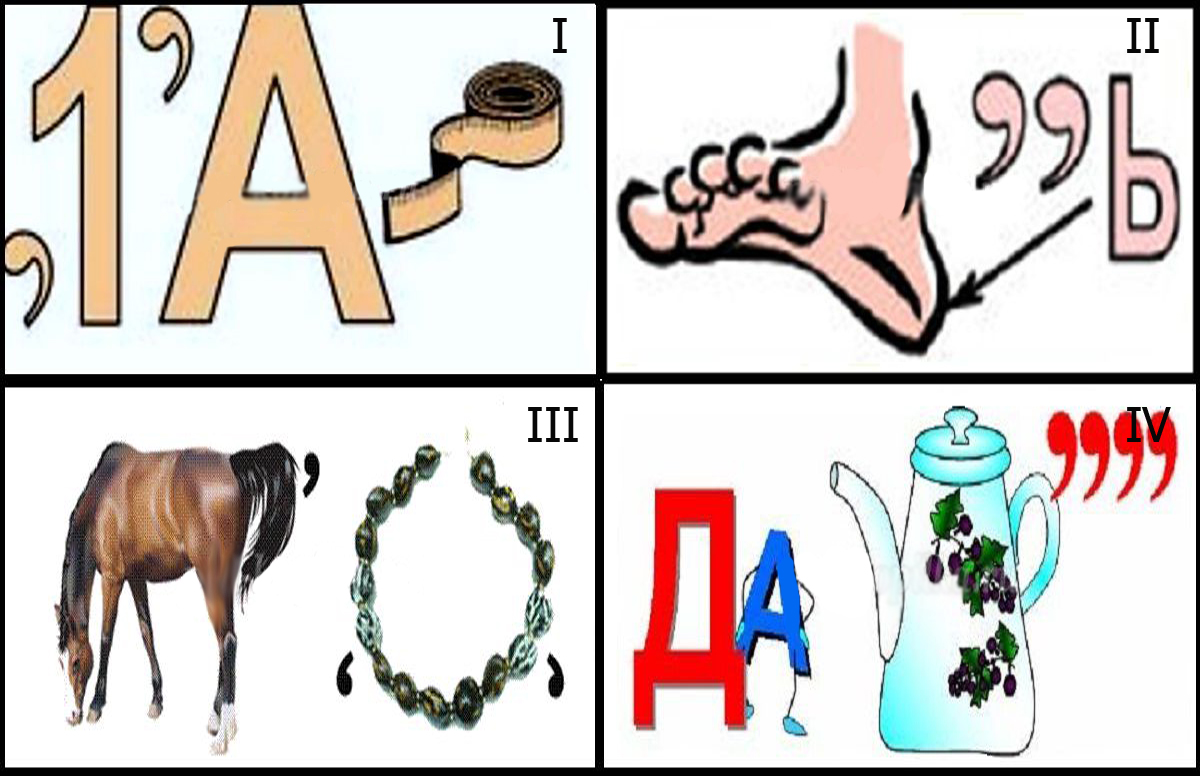
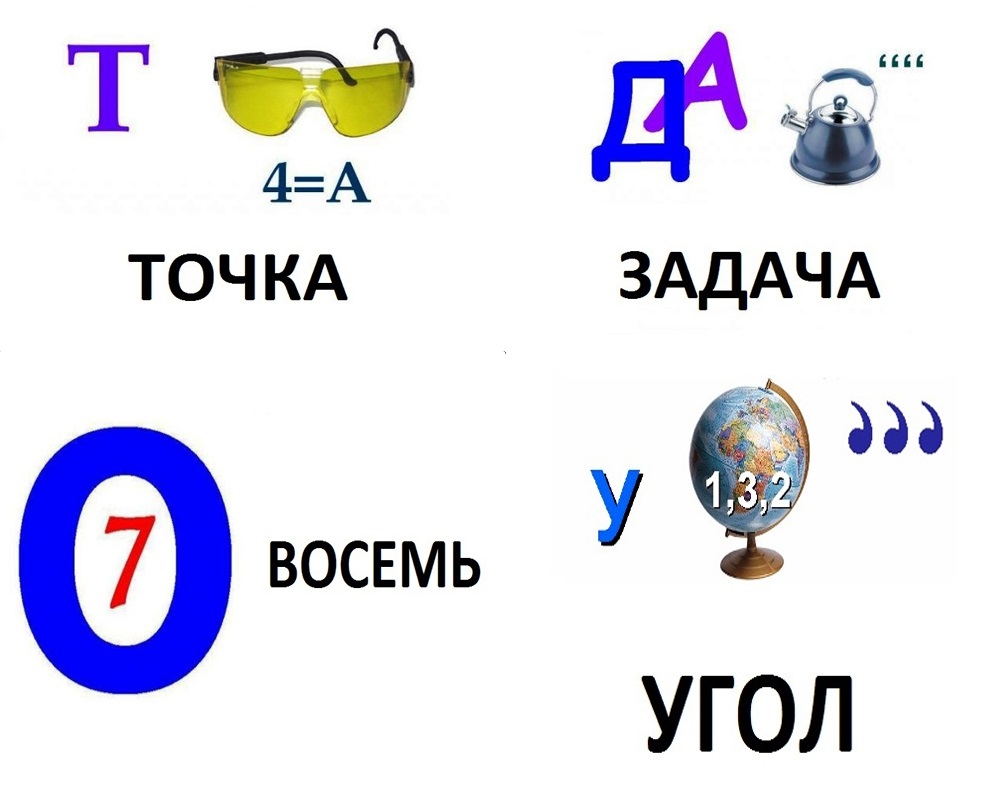
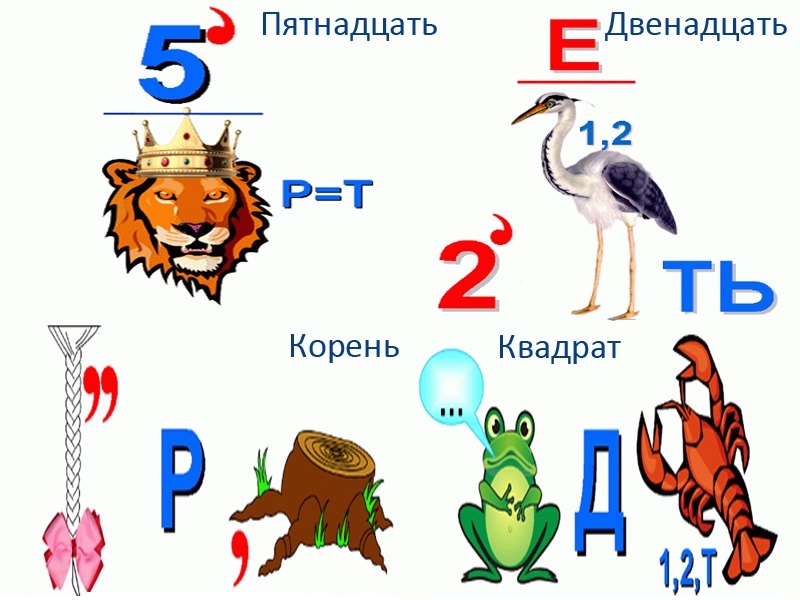
Ответы: первый ребус — «диаметр», второй — «пять», третий — «конус», четвертый — «задача».
Пятая картинка — «алгебра», шестая — «геометрия», седьмая — «линейка», восьмая — «уравнение».
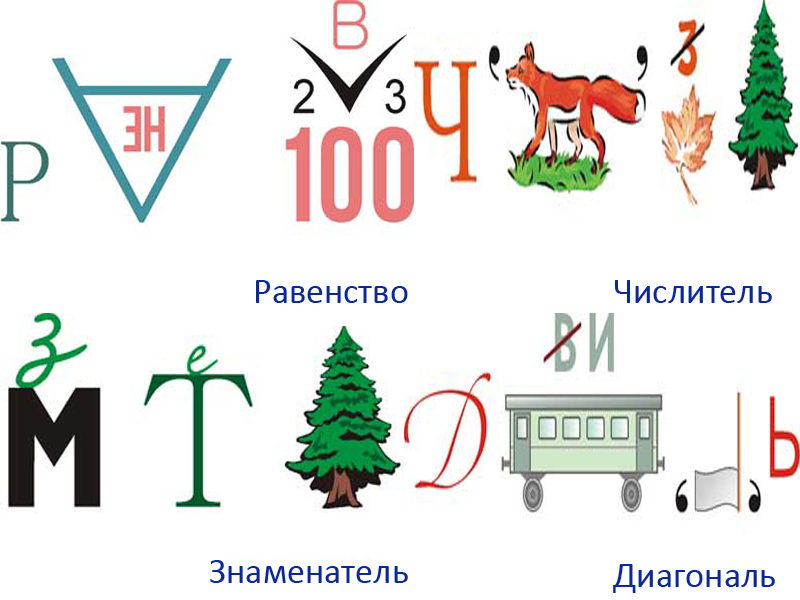
Девятая загадка — «диаметр», десятая — «циркуль», одиннадцатая — «транспортир», двенадцатая — «конус».

Особенности математических ребусов для начальной школы
Лучше всего приобщать ребенка к разгадыванию математических ребусов еще в детском саду, в выпускной группе. Это послужит отличной разминкой перед школой, освежит у малыша весь пройденный материал с педагогом.
Только нужно учитывать, что такие ребусы должны быть довольно легкими, и включать только те знания, которые ребенок уже усвоил и знает. Это может быть головоломка из двух-трех составляющих, ответ которой таит в себе простое математическое значение.
Эти же ребусы пригодятся для «разогрева» первоклашек. Поступление в школу – и так огромная эмоциональная нагрузка для ребенка, поэтому не стоит удручать обучение математике столь сложными ребусами. Подойдут следующие примеры:
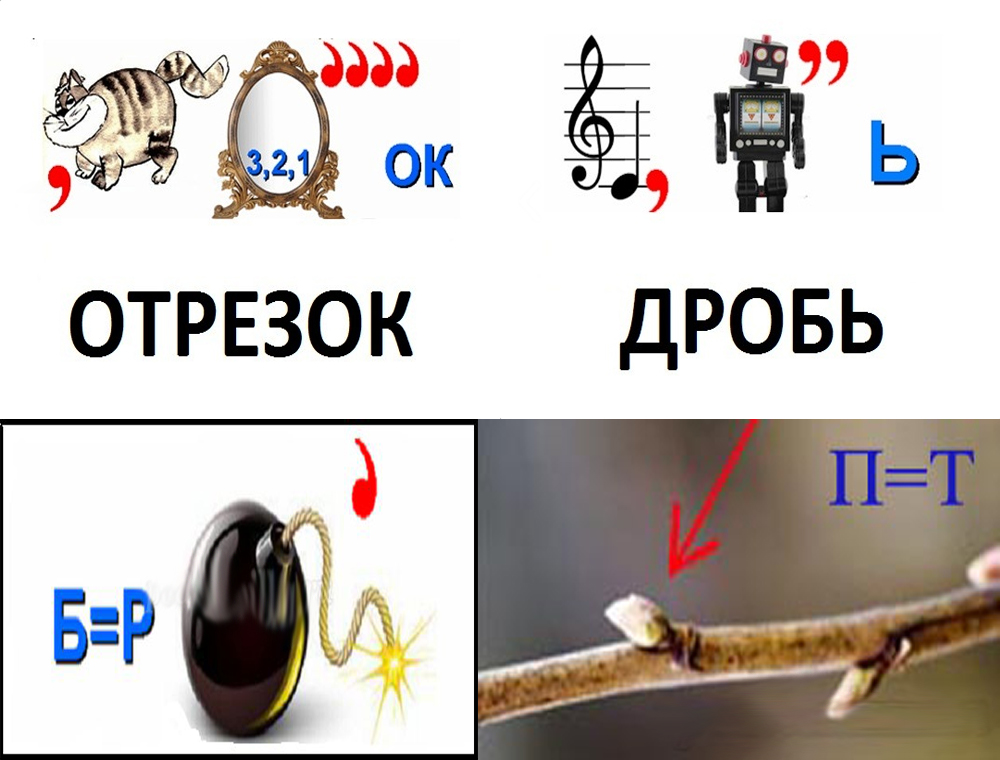
Первоклассники уже хорошо знают цифры и простые математические действия, которые можно включить в ребусы. Причем для таких ребусов характерно то, что математическое значение может присутствовать как в самой загадке, так и в ее значении. А может случиться такое, что ответ совершенно не будет связан с этой точной наукой. Предложите ребенку следующие математические ребусы:
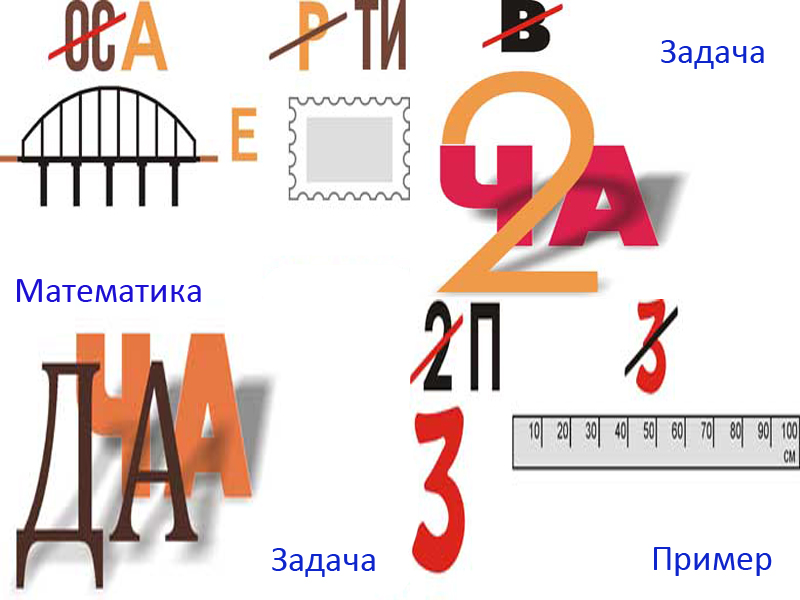

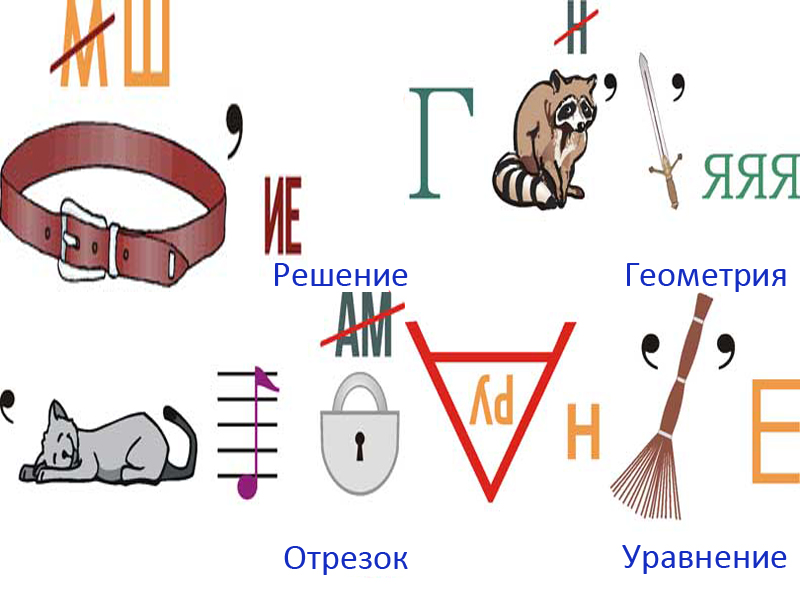
Математические ребусы для 2 класса с ответами
Для того, чтобы составить математический ребус второкласснику, нужно ориентироваться в его знаниях, то есть предлагаемая задача должна быть ему посильной. Вот что должен знать и уметь учащийся во втором классе:
- При решении заданий использовать в правильном порядке числа от 1 до 100, правильно озвучивая их.
- Решать примеры сложения и вычитания чисел, которые не превышают цифру 20.
- В ряде случаев применять математические действия умножения и деления.
- Четко знать правила использования скобок в примерах и решать их.
- Применять в своей лексике единицы измерения длины и объема.
- Вести сравнения больше-меньше цифр в пределах 100.
- Уметь устно прибавлять и отнимать числа в пределах 100.
- Решать несложные задачи с четырьмя основными арифметическими действиями, уметь увеличивать (уменьшать) число на (в) раз (единиц).
- С помощью линейки чертить и мерить длину отрезка.
- Распознавать плоские углы.
- Узнавать и озвучивать плоские геометрические фигуры.
- Уметь вычислять периметр многоугольников.



Математические ребусы для 3 класса с ответами
Чтобы разгадать посильные математические ребусы, третьеклассник на уроке математики должен:
- Считать и называть числа до тысячи.
- Выполняя основные четыре арифметические действия, называть каждую составляющую примера своим названием.
- Владеть таблицей умножения и оговаривать результат действия деления.
- Уметь решать примеры со скобками и без них.
- Знать единицы измерения величин и выражать их в разной интерпретации.
- Устно решать математические действия до значения 100.
- Делить многозначное число на однозначное, руководствуясь таблицей умножения.
- Проверять правильность расчета примеров.
- Выполнять задачи на одно-два действия.
- Придумывать задачи, обратные исходной.
- Уметь кратко записать задачу.
- Вычислять уравнения и неравенства.
- Чертить простые геометрические фигуры, согласно исходным данным задания, вычислять их периметр и площадь.
- Уметь пользоваться циркулем, чертя окружности заданных радиусов.

Математические ребусы для 4 класса с ответами
На уроках математики четвероклассник должен:
- Уметь решать задачи рациональным и нерациональным способом.
- Решать задачи, записывая ход их решения.
- Иметь представление вычисления объема и площади геометрических фигур, исходя из выученных формул.
- Чертить геометрические фигуры, обозначать их компоненты латинскими буквами.
- Строить и мерить углы транспортиром.
- Знать свойства равенства.
- Решать задания с количеством арифметических действий от одного до четырех.
- Знать свойства сторон, углов, радиусов геометрических фигур.
- Вычитать и прибавлять многозначные числа.
- Делить многозначное число на однозначное и многозначное.
- Иметь понятие натурального ряда.
- Умножать дробь на натуральное число.
- Правильно называть и писать дроби: числитель и знаменатель.
- Сравнивать дроби.
Математические ребусы для 5 класса с ответами
Программа по математике для пятиклассника схожа с предыдущим годом, только имеет более обширный характер. Недаром ведь в некоторых школах четвертый класс пропускается, а вся школьная программа за пропущенный год изучается в пятом классе.

Математические ребусы для 6 класса с ответами
- В шестом классе активно изучается геометрия, в частности ее теоремы.
- Ребенок знакомится с известными учеными в области математики и других точных наук.
- Школьник имеет дело с изучением геометрических фигур на плоскости, учится вычислять их объем и площадь по изученным формулам.
- По алгебре в ход идет решение уравнений с двумя неизвестными, неравенств.

Математические ребусы с цифрами с ответами
Цифры, изображенные в математических ребусах, могут быть двух видов:
- Те, название или часть названия которых используется для ответа.
- Те, которые стоят около изображения, и указывают на то, что из названия этого изображения нужно позаимствовать буквы, соответствующие последовательности стоящих цифр в ряду.


Математические загадки, ребусы, кроссворды
Хорошо тренируют умственную активность не только ребусы по математике, но еще и логические, арифметические загадки, кроссворды. Они развивают любознательность и сообразительность у детей. А игровая форма заданий помогает достигнуть высокой скорости мышления и догадки.
Для самых маленьких подойдут такие задачки:

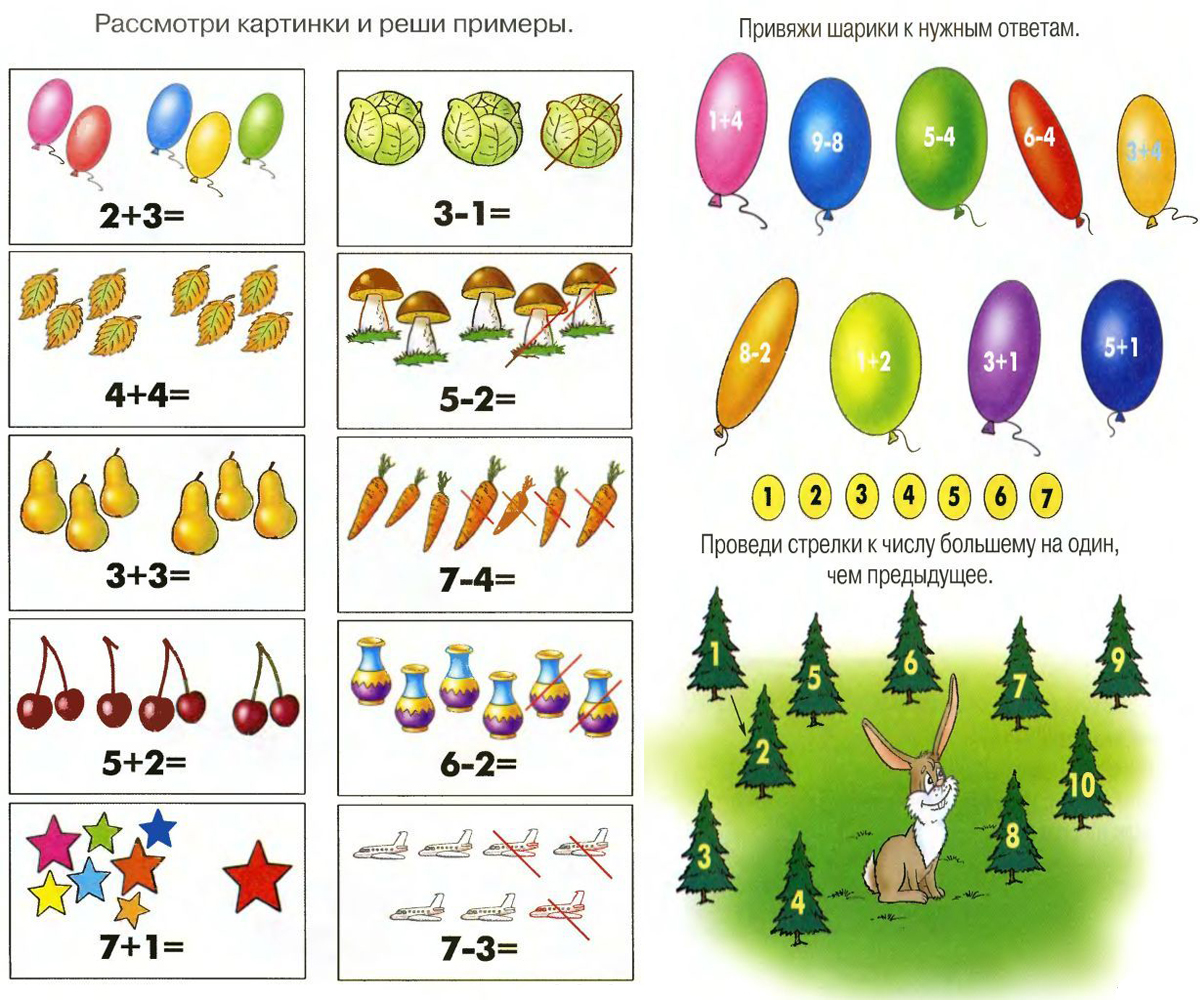 Решите еще такие кроссворды и задания:
Решите еще такие кроссворды и задания:
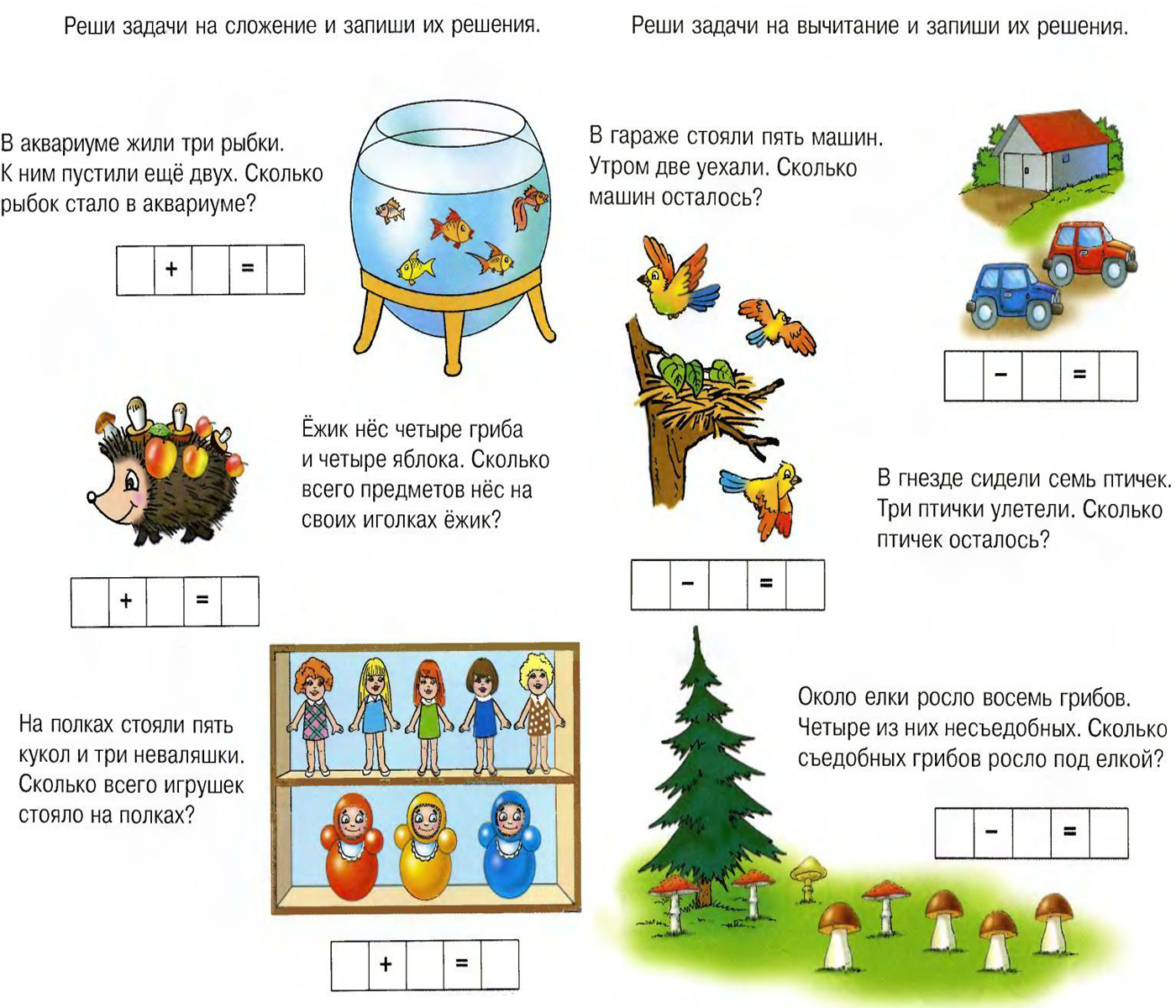
- Решите примеры, линиями соедините ответ и группу детишек, соответствующую ему (первое задание).
- Решите примеры на веслах, а затем линиями соедините каждое из них с лодками, имеющими правильный ответ (второе задание).
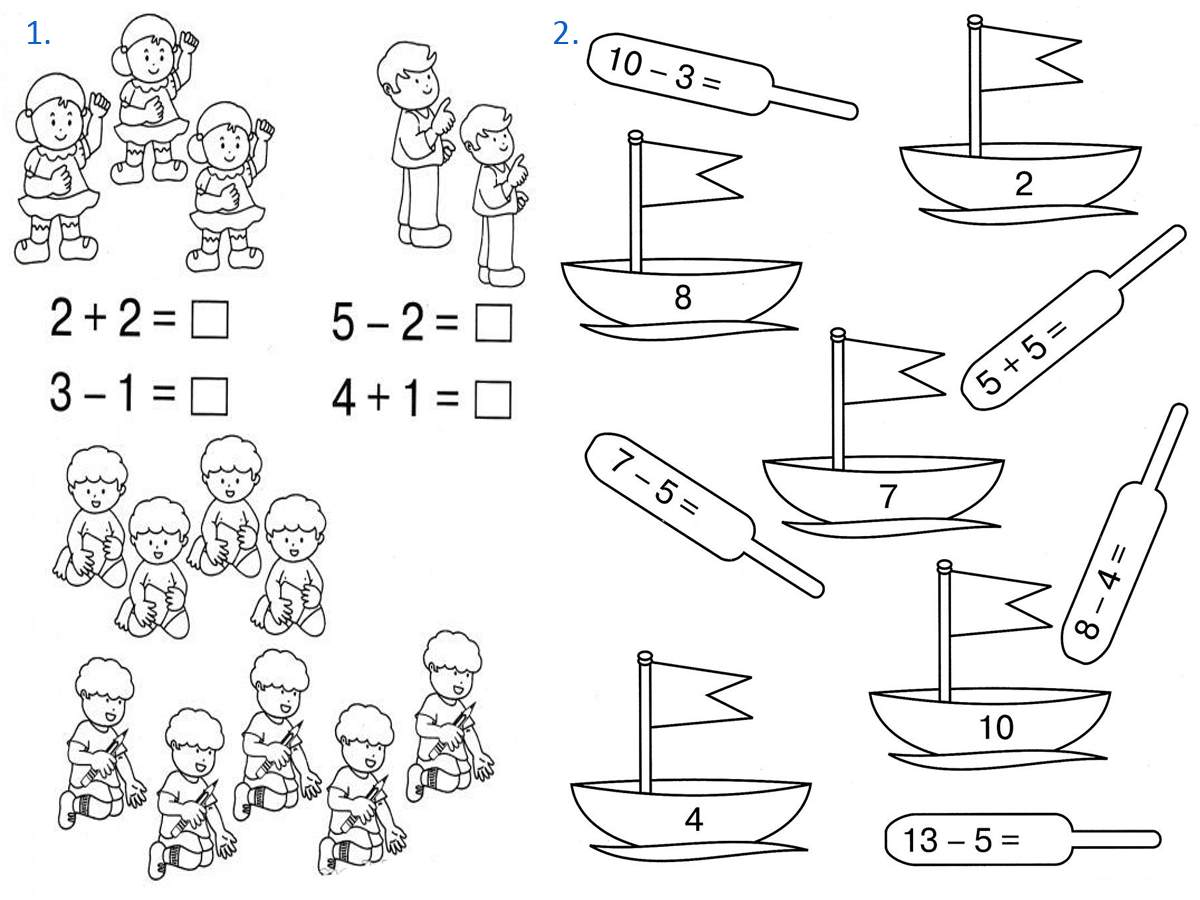
- Заполните пропущенные клеточки цифрами таким образом, чтобы по горизонтали и по вертикали всегда ответ получался 15 (третье задание).
- Заполните пропуски и решите примеры (четвертое задание).
 Разгадайте кроссворды:
Разгадайте кроссворды:
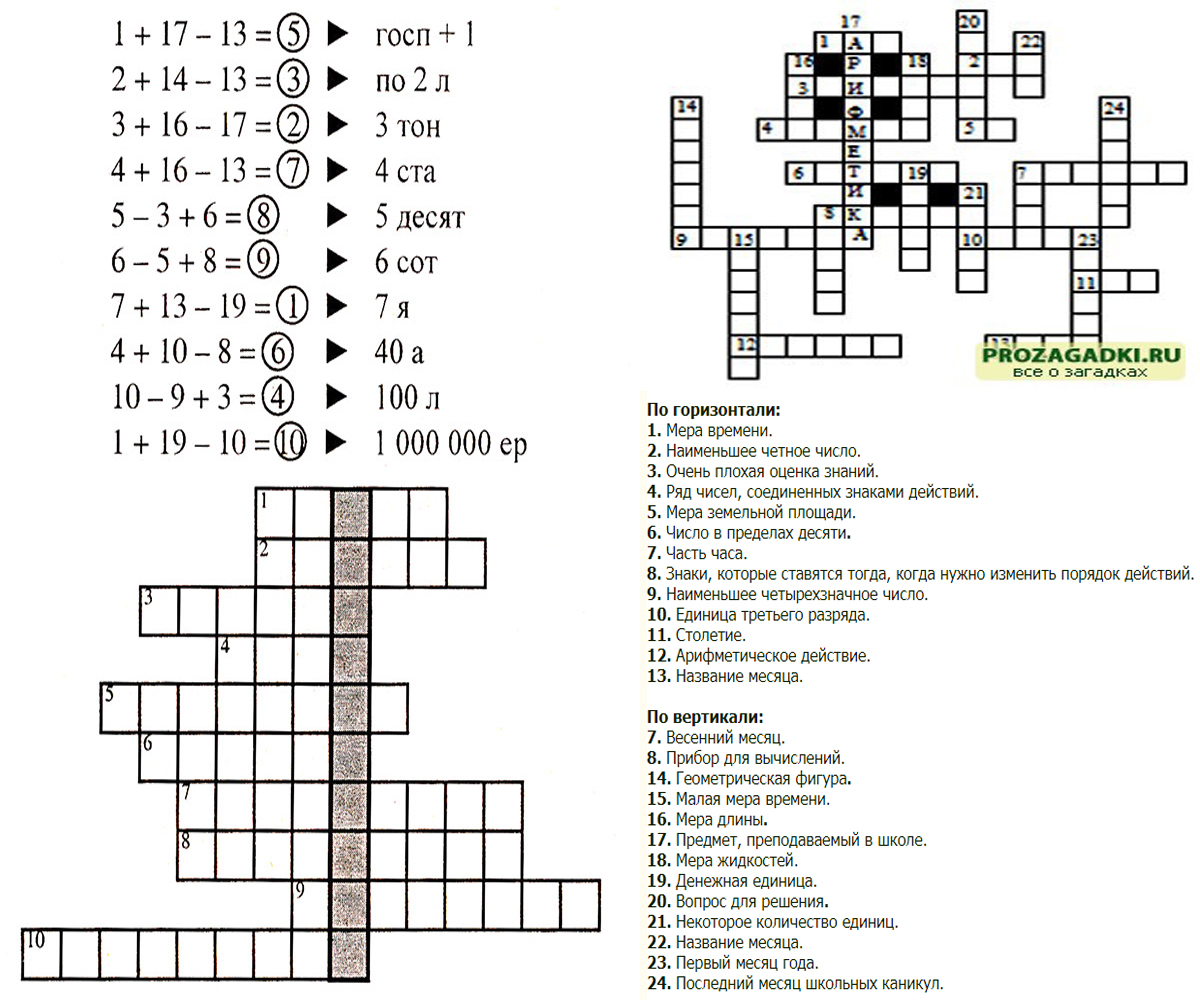
Вот более сложные ребусы:

Как решать математические ребусы с буквами?
Решение математических ребусов с буквами
Все слова состоят из букв, поэтому множество ребусов содержат в своей структуре буквы. Руководствуясь основными принципами решения ребусов, вы с легкостью осилите математические ребусы с буквами.
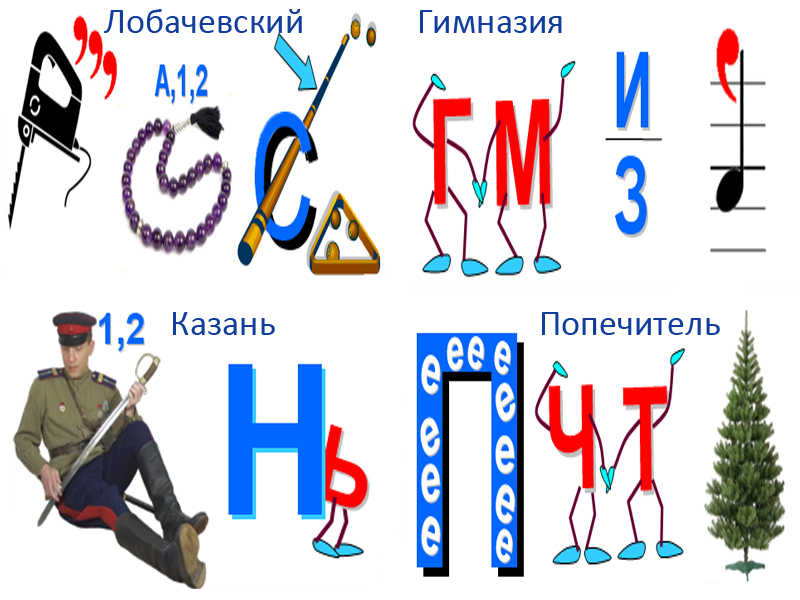

Математические ребусы и головоломки
Такие загадки и головоломки будут интересны не только школьникам, но и их родителям:

Самые легкие математические ребусы
Пусть школьник потренируется для начала на простых математических ребусах. К примеру, на таких:
 Сложные математические ребусы
Сложные математические ребусы
Попробуйте предоставить вашему сорванцу вот такие головоломки, которые позволят сконцентрировать смекалку и потренировать интеллект. Это задание предположительно для учеников пятых классов.
В нашей статье приведены примеры математических ребусов с ответами разных уровней сложности, зависящих от возраста школьника. Изучив основные правила разгадывания ребусов, попробуйте составить интересные задания своим деткам. Такого рода занятия помогут ребенку активизировать свои интеллектуальные способности, выработают усидчивость и концентрацию внимания, а также закрепят пройденный материал по математике. Это увлекательное занятие поможет сплотить родных (товарищей), и создать дружескую атмосферу в семье и школьном коллективе.
Содержание
- Правила составления математических ребусов для детей
- Как придумать математический ребус?
- Пример простого ребуса про цифры
- Как их решать?
- ВИДЫ РЕБУСОВ
- Математические ребусы – сложные и легкие
- Пустышки
- C картинками
- Чёт и нечет
- С буквами
- Математические ребусы квадрат
Правила составления математических ребусов для детей
- Если вы видите перед словом или картинкой запятую, то нужно убрать первую букву с этого названия. То же самое нужно сделать, если запятая стоит в конце слова. Когда около картинки две запятых, то убирается две буквы соответственно. Например, на первой картинке изображен сок — нужно убрать первую букву «С», рука — уберите слог «ка», буква «ж» так и остается, нос — слово остается целиком, пять — уберите две первые буквы. Зашифрованное слово — «окружность».
- Если цифры, обозначающие последовательность букв в слове зачеркнуты, то их необходимо выбросить из него. Тоже самое касается и букв. На втором рисунке изображен цирк — уберите последнюю букву, из слова «акула» нужно убрать букву «А», готовый ответ: «циркуль».
- Когда рядом с картинкой стоят цифры, поменянные местами, то и в названии самого предмета нужно поменять местами буквы, которые стоят в последовательности с указанными цифрами.
- Если картинка изображена вверх тормашками, то отгадку нужно читать в обратном порядке: справа-налево.
- Для ребусов используется только именительный падеж в словах.
- Указатель в виде стрелки или математический знак «равно» обозначает, что нужно заменить буквы одну другой.
- В ребусах одно значение может быть расположено внутри другой картинки, за ней или под ней. Тогда применяйте слова: В, НА, НАД, ПОД, ЗА.
- Цифры, стоящие в ряд около изображения, обозначают, что нужно использовать из этого значения буквы в указанной последовательности цифр.

Вот несколько примеров математических ребусов, соответствующих приведенным правилам:
Под третьим рисунком зашифровано слово «вектор», под четвертым — «степень», под пятым — «два», под шестым — «доказательство».

Как придумать математический ребус?
Следуя общим правилам составления ребусов, попробуйте придумать для начала несложные математические задачки, используя цифры и математические термины. А затем, немного освоив простые задания, переходите к более усложненным. Вот несколько образцов ребусов по математике с ответами, которые вдохновят вас и покажут, как их нужно составлять:
Ответы: первый ребус — «диаметр», второй — «пять», третий — «конус», четвертый — «задача».
Пример простого ребуса про цифры

Какое число зашифрован
Ответ: 2.
2.

В обычных ребусах слова изображают картинками, буквы часто заменяют взаимным расположением объектов, запятыми обозначают вычитаемые из слов буквы.
Чтобы научиться разгадывать ребусы с буквами и цифрами, достаточно понять основные правила и немного потренироваться.
Как их решать?
Математические ребусы не являются задачками, к которым мы привыкли в школе, хотя некоторые элементы подобных действий они все же могут содержать. Давайте вспомним, как выглядит традиционный ребус.
Берется какое-нибудь слово для зашифровки. Далее оно делится на части и зашифровывается каждая из частей. Разгадав каждую часть ребуса в отдельности, необходимо сложить слово.
Математические ребусы могут быть как лингвистического, так и числового характера. Например, в задачке путем математических действий можно вычислить необходимую цифру. Если же математические ребусы с числами для детей зашифрованы словами, тогда задача упрощается.
ВИДЫ РЕБУСОВ
- Литературные это когда в ребусе зашифровываются слова или предложения. Используются различные методы; картинки – ребусы, ребусы с запятыми, с цифрами, картинки перевертыши и т.д.
- Музыкальные это ребусы в которых используются картинки музыкальных нот. В таком ребусе картинка может означать либо само слово, либо нота является частью слова.
- Математические ребусы это ребусы из простых задач по математике на сложение, вычитание, умножение и другие. Все цифры или некоторые заменены картинками или другими символами. Задача заключается в том, чтобы восстановить вид примера математическими цифрами.
Математические ребусы – сложные и легкие
Математические ребусы и головоломки – прекрасный и увлекательный способ развития логического мышления и воображения. С помощью математических ребусов можно интуитивно понять закономерность поведения чисел в различных ситуациях, а значит – освоение математики как науки будет даваться ребенку непринужденно, что снизит количество сложностей при обучении в школе.
Внешний вид задачек такого рода напоминает столбики, сложенные из кирпичей, поэтому назову их «кирпичики».
Правила такие:
- каждый квадратик – это одна цифра;
- ни одно число не начинается на 0;
- сумма чисел каждого вертикального ряда равна результату соответствующей горизонтальной строки;
- действия производятся последовательно слева направо, то есть правила приоритета не работают.
Решим для примера вот такие «кирпичики»:

Для начала, используя правило [3], зеркально относительно диагонали отразим и дополним результаты столбцов и строк. Шестёрка из результата второго столбца скопируется во вторую строку, а тройка из результата первой строки скопируется в первый столбец.

Посмотрим на вторую строку. Первые два числа однозначные, значит их сумма не больше 18, а значит отнять можно только 16, иначе у нас получится отрицательное число. Значит, третье число во второй строке 16. Допустим, сумма двух первых чисел 17. Тогда 17-16=1. Один умножить на однозначное число и получается двузначное – так не бывает. Значит, сумма двух первых чисел строки не 17, а 18. Значит, это обе девятки, 9+9-16=2. А на какое однозначное число надо умножить двойку, чтобы получилось двузначное с шестёркой на конце? На 8! Итого, получили целиком вторую строку: 9+9-16×8=16. Не забываем, что порядок действий – слева направо, то есть как будто запись вот такая: [(9+9)-16]×8=16.

Теперь смотрим на второй столбец. 16-2-9=5. То есть третье и четвёртое числа во втором столбце дают в сумме 5. Теперь посмотрим на третью строку. Результат сложения двузначного числа, оканчивающегося семёркой и второго числа должен делиться на 5, а значит должен заканчиваться на 5 или 0. А значит, третье число во втором столбце должно быть или 3 или 8. Но оно ведь должно быть меньше пяти! Значит, это тройка. А тогда четвёртое число во втором столбце – это двойка.
Результат первой строки – это 30 или 35, так как в конце стоит умножение на 5. Значит, сумма первого столбца тоже 30 или 35.
В первом столбце третье число – это 17, или 27, или 37, или т.д. Допустим, 27. Тогда 27+9=36, а это уже больше, чем весь возможный результат столбца – 35. Значит, у нас не 27, а 17. Итого, получилась третья строка: 17+3:5×8=32.

Итак, результат первой строки 30 или 35. Пусть 35. Тогда сумма первых двух чисел равна 7, а третье число – единица. Значит, третий столбец начинается с единицы. Получается, что четвёртое число в третьем столбце должно равняться 32-1-16-5=10. Но оно однозначное! Мы допустили, что результат первой строки 35 и пришли к противоречию. Значит, не 35, а 30.
А раз 30, думаем над первой строкой. Третье число, как мы уже установили, не единица. Значит, двойка. Любого другого будет уже много. Получаем первую строку: 1+2x2x5=30. Ну и тут уже легко получается четвёртая строка: 3+2×9-12=33. И вот он результат:

Как вы заметили, самое нижнее правое число (сумма последней строки, она же сумма последнего столбца) получилось в самом конце решения головоломки. Его невозможно получить в результате промежуточных вычислений, а значит, что такие типы задач можно применять, если в квесте нужно загадать какое-то трёхзначное число. Например, шифр от сейфа. Хотя не, 1000 комбинаций и перебрать можно. Допустим, надо ввести код для отключения бомбы и ошибаться нельзя. Вот тогда три цифры – самый раз .
У нас есть 10 цифр, а в русском языке довольно много слов, состоящих из 10-ти разных неповторяющихся букв. Их можно использовать как ключевые слова в головоломках, которые некоторые называют «ребусы с ключевыми словами», а я называю «Рамки».
Каждая такая задачка состоит из 6-ти уравнений, связанных между собой знаками « + », « – », « × », « : », « = ». Цифры зашифрованы буквами, разным цифрам соответствуют разные буквы. Обычно используется 10 букв для 10-ти цифр, но можно составить пример и из меньшего количества цифр, тогда и букв будет меньше.

Это настоящая математическая задача, причём довольно сложная, поэтому подойдёт не для каждого квеста. Решается задача так.
Рассмотрим первый столбец ПЗ+УУ=ИГЕ. Сумма двух двузначных чисел не может быть больше 99+99=198, значит, И=1.
В равенстве ПЕП-ЗТ=ИНЗ (третий столбец) видно, что к трёхзначному числу ИНЗ, начинающемуся на 1, прибавили двузначное число ЗТ и получили снова трёхзначное ПЕП. П – не 1, так как 1 уже занято буквой И. Выходит, П=2, потому что больше оно быть не может (потому что 298 – максимально возможная сумма двухзначного и трёхзначного, начинающегося на 1).
В третьей строке ИГЕ+НО=ИНЗ при сложении Г десятков с Н десятками снова получается Н десятков. Это может быть только если Г=0 или Г=9. Но если бы Г было равно 9, то был бы перенос единицы в разряд сотен, а у нас было И и осталось И. Значит, Г=0.
Итак, Г=0, И=1, П=2. А поэтому в равенстве ПЗ+УУ=ИГЕ У может быть или 7, или 8, ведь нам надо к двум с чем-то десяткам прибавить двузначное число, и чтобы получилось больше сотни. Пусть, У=8. Тогда из УУ+У=ЗТ следует, что Т=6 и З=9. Но тогда в разности ПЕП-ЗТ=ИНЗ получаем П=5. Но ведь П=2! Значит, У≠8. Следовательно, У=7. Тогда из УУ+У=ЗТ получаем Т=4, З=9. Равенство ПЗ+УУ=ИГЕ при З=8 и У=7 даёт нам ещё одну букву: Е=5.
В сумме ИГЕ+НО=ИНЗ Е=5, З=8, а значит, О=3. В третьем столбце нам уже стали известны все буквы, кроме Н. Поэтому, значение её легко находится: Н=6. И, наконец, из равенства АxУ=НО получаем А=9.
В результате имеем: 0123456789=ГИПОТЕНУЗА. Слово разгадано, его можно как-то использовать дальше в виде ключевого слова или подсказки для решения следующих квестовых задач.
Ниже приведены примеры «математических ребусов».

Ответы: 1-гипотенуза, 2-справочник, 3-демократия, 4-крестовина, 5-струбцина, 6-хлопчатник, 7-деформация, 8-заповедник, 9-лесотундра, 10-метилоранж, 11-проявитель, 12-экспертиза, 13-вольфрамит, 14-пятидневка, 15-республика, 16-дегустация, 17-дешифровка, 18-подсвечник, 19-глубиномер, 20-трудолюбие, 21-фильмотека, 22-погремушка, 23-ускоритель, 24-демография, 25-центрифуга, 26-манускрипт, 27-эскадрилья, 28-меблировка, 29-этнография, 30-умывальник, 31-Лев Яшин, 32-сподумен.
Пустышки
В таких арифметических ребусах все цифры заменены на точки, звёздочки, кружочки, в общем, на одинаковые символы.

В обычных «пустышках» часто для подсказки открывают некоторые цифры, либо какую-то из цифр (какую точно, не известно) помечают специальным знаком. Получаются «пустышки с подсказками».

C картинками
Последнее время в интернете стали популярны ребусы, в которых задана система уравнений, где неизвестные заменены картинками. Например, вот такая задачка:

Она сводится к решению обычной системы из двух уравнений с двумя неизвестными.{(3x=2y+1),(x+2=y):}
Перенесём все неизвестные налево, известные направо, до множим второе уравнение на 2 и из первого уравнения вычтем второе. Получим 3x-2x + 2y-2y = 1-(-4). Сокращаем и получаем x=5, а значит y=7. Простейшая задачка для ученика 4-5 класса.
Начиналось-то всё просто, но потом картинки стали с подвохом. Например, вот эта. С виду ничего необычного.

Видим авокадо (x), связку бананов (y), апельсины (z).
{(x+x+x=30),(x+y+y=18),(y-2z=2),(z+x+y=?):}
Из первого уравнения x=10, подставляем x во второе, получаем y=4, подставляем y в третье, получаем z=1, значит 1+10+4=15. Всё вроде бы просто. Так будут решать 95% людей. Но 5% заметят, что нижняя связка бананов поменьше, чем верхние. Верхние связки бананов = 4, потому что там по 4 банана. А вот в нижней 3 банана, значит её нужно считать как 3. А теперь внимательно смотрим на апельсины. Сколько их внизу? Один? А не половинка ли? Похоже, что в третьей строке целый апельсин разрезан пополам. И получается совсем другая система.
{(x+x+x=30),(x+4y+4y=18),(4y-z=2),(z/2+x+3y=?):}
И значит, что целый апельсин = 2, а пол-апельсина = 1. И значит, что правильным ответом будет 1+10+3 = 14, а не 15.
Считать апельсины целыми или половинками в общем-то не важно. Всё равно внизу будет единица. Главное, что бананов три, а не четыре. Замечу, что некоторые особо дотошные люди могут утверждать, что в третьем уравнении не две половинки, а половинка и целый, то есть полтора апельсина. Но тогда задача в целых числах не решается, а это некрасиво  Поэтому мы так считать не будем.
Поэтому мы так считать не будем.
Бывают и ещё более замороченные задачки с ещё более глубокими подвохами. Например, вот такая, от Леонида Каганова:

Попробуйте её решить сами без подсказок, а потом почитайте на сайте по ссылке, до чего до решались там 
Чёт и нечет
Чётные цифры (0,2,4,6,8) помечены буквой Ч, а нечётные (1,3,5,7,9) – буквой Н.

С буквами
Это классика математических ребусов, в них цифры заменены буквами. Чаще всего авторы подобных задач стараются так подобрать буквы, чтобы в отдельных местах читались слова. Остальные же места, где слова не получаются, остаются, как в пустышках. Иногда в некоторых местах также оставляют подсказки.

Математические ребусы квадрат
Одна из разновидностей ребусов — магические квадраты. Как их решать? На самом деле совсем не сложно, когда точно понимаешь, что нужно сделать, каковы правила разгадывания и что такого особенного в этих квадратных таблицах.
Чтобы решить магический квадрат нужно заполнить пустые ячейки таким образом, чтобы сумма чисел по любой горизонтали, по любой вертикалям и по диагоналям была одинаковой. В данном случае равнялась сумма чисел должна равняться 9. 
Вариант 1 Расшалившиеся монстрики стерли нечаянно цифры в квадрате. Нужно помочь им восстановить эти цифры, решив пример на сложение. Так как по горизонтали и по вертикали присутствуют не все цифры найдем магическое число, сложив цифры по диагонали. 5 + 3 + 1 = 9 . Значит в пустые ячейки нужно вписать такие цифры, чтобы при сложении в разных направлениях получилось 9. 1 столбец: 9 – 3 – 5 = 1 2 столбец: 9 – 3 – 1 = 5 3 столбец: 9 – 5 – 1 = 3 Сделаем проверку решив примеры таким же образом в линиях. 1 линия: 9 – 3 – 1 = 5 2 линия: 9 – 3 – 5 = 1 3 линия: 9 – 5 – 1 = 3
Расшалившиеся монстрики стерли нечаянно цифры в квадрате. Нужно помочь им восстановить эти цифры, решив пример на сложение. Так как по горизонтали и по вертикали присутствуют не все цифры найдем магическое число, сложив цифры по диагонали. 5 + 3 + 1 = 9 . Значит в пустые ячейки нужно вписать такие цифры, чтобы при сложении в разных направлениях получилось 9. 1 столбец: 9 – 3 – 5 = 1 2 столбец: 9 – 3 – 1 = 5 3 столбец: 9 – 5 – 1 = 3 Сделаем проверку решив примеры таким же образом в линиях. 1 линия: 9 – 3 – 1 = 5 2 линия: 9 – 3 – 5 = 1 3 линия: 9 – 5 – 1 = 3  Вариант 2 Здесь представлено задание посложнее. Требуется расставить цифры в пустые ячейки так, чтобы узнать магическое число, благодаря чему и сам квадрат станет магическим. Подсказка: используйте цифры 5, 8, 9, 12, 13, 15.
Вариант 2 Здесь представлено задание посложнее. Требуется расставить цифры в пустые ячейки так, чтобы узнать магическое число, благодаря чему и сам квадрат станет магическим. Подсказка: используйте цифры 5, 8, 9, 12, 13, 15.  Тут уж вряд ли получится найти решение не вооружившись бумагой и ручкой. Придется хорошо подумать и подключить воображение. ОТВЕТ: магическое число = 32.
Тут уж вряд ли получится найти решение не вооружившись бумагой и ручкой. Придется хорошо подумать и подключить воображение. ОТВЕТ: магическое число = 32.  А у вас получилось?
А у вас получилось?
Вариант 3 А вот немного другая разновидность квадрата- ребуса. Выполнив несложные математические действия, нужно заполнить пустые квадраты цифрами и знаками сложения или вычитания. 
Источники
- https://qulady.ru/matematicheskie-rebusy-dlya-1-2-3-4-5-6-klassov-s-otvetami-kak-samomu-pridumat-matematicheskie-rebusy-dlya-rebenka.html
- https://logiclike.com/math-logic/matematicheskie-rebusy
- https://steshka.ru/rebusy-s-chislami-i-ciframi
- https://alekseevaee.ru/matematicheskij-mir/golovolomki/rebusy/68-rebusy-po-matematike
- https://IQsha.ru/ilove/post/matematicheskie-rebusy-s-otvetami-slozhnye-i-legkie-rebusy-po-matematike
- http://nozdr.ru/games/quest/math/arith
- https://luckclub.ru/primery-matematicheskih-rebusov-1-klass-2-klass-3-klass-4-klass-v-kartinkah-s-otvetami-gde-skachat
МБОУ ДОД Дворец творчества детей и молодежи города Ростова-на-Дону
Донская академия наук юных исследователей им. Ю.А. Жданова
Математика/Дебют
Исследовательская работа
Тема: «Математические ребусы».
Автор работы:
Бенько Елизавета, 5А класс,
МБОУ СОШ № 7 г. Сальск.
Руководитель: Бабина Наталья Алексеевна,
учитель математики
МБОУ СОШ № 7г. Сальск.
г. Сальск
2015 г.
Оглавление
I Введение……………………………………………………………………..3
II Основная часть………………………………………………………………4-16
2.1.История возникновения и развития ребусов…………………………….4-5
2.2. Математические ребусы на замену букв и «звёздочек» цифрами……5-9
2.3. Математические ребусы с различными предметами …..…………….10-14
2.4.Составление ребусов…………………………………………………………..14-16
III Заключение…………………………………………………………………17
Источники……………………………………………………………………… 18
I
Введение
Математические знания мы применяем не только на уроках математики, но и в повседневной жизни. Мне повезло, что математика мне нравится. Однако, трудность для меня составляют задачи, для решения которых надо применить логические рассуждения. Я читала, что любые свои способности человек может развить, в той или иной мере. Как же развить математические способности? В интернете я нашла массу высказываний такого характера:
-«Чтобы развить математические способности, необходимо решать задачи на сообразительность, задачи-шутки, математические ребусы и головоломки». [10]
-«Разгадывание ребусов является отличной гимнастикой для развития интеллекта школьника».[10]
-«Разгадывание ребусов прекрасно стимулирует развитие интеллекта , развивает умение делать логические выводы, учит мыслить». [11]
Я поверила, что решение различных головоломок поможет мне развить математические способности.
Тема работы: «Математические ребусы».
Цель: научиться решать математические ребусы.
Актуальность темы: на уроках математики необходимо решать задачи не только по определённым правилам, но и нестандартные задачи.
Гипотеза: решение ребусов поможет мне развить логическое мышление.
Степень изученности: в курсе математики школы не рассматриваются ребусы.
Задачи:
- Найти различные источники с информацией о ребусах;
- Изучить математические ребусы различных видов;
- Исследовать возможные пути решения ребусов.
Объект изучения: математические ребусы
Предмет изучения: методы и способы решения математических ребусов
Методы исследования: изучение различных источников информации, анализ, обобщение и систематизация материала.
II
Основная часть
2.1 В начале своей работы я решила выяснить: историю возникновения ребусов и что такое математический ребус.
Зародился ребус во Франции в XV веке. Первоначально ребусом называли особого рода ежегодные выступления во время карнавалов, содержащие остроумные обозрения местной жизни, называвшиеся “новостями дня”. В дальнейшем слово “ребус” получило то значение, в котором оно употребляется настоящее время.
Первый печатный сборник ребусов, составленный Этьеном Табуро, был издан во Франции в 1582 году. Затем ребусы распространились в Англии, Германии, Италии.
Английский писатель и математик Чарльз Лютвидж Доджсон, более известный под псевдонимом Льюис Кэрролл, один из самых популярних детских писателей XIX века, автор сказок “Алиса в Стране чудес” и “Алиса в Зазеркалье”, часто использовал ребусы в многочисленной переписке с юными почитателями своего творчества. В своих письмах он часто заменял часть слов картинками либо изображал буквы в зеркальном отображении. Для прочтения таких загадочных писем нужна была смекалка, что очень нравилось детям.
В России первые ребусы появились на страницах журнала “Иллюстрация” в 1845 году. Большой популярностью пользовались ребусы, нарисованные художником И. Волковым в журнале “Нива”.
Первое упоминание о печатных ребусах во времена Советской власти появились в 1937 году: появились буклеты которые носили название “Как читать ребусы” . Во время Великой Отечественной войны, в 1942 году московская полиграфическая фабрика выпускает сборник ребусов А.А. Рязанова “В часы досуга: ребусы” В 1945 году, после окончания войны выходит небольшая брошюра художника-иллюстратора и иллюзиониста Георгия Кельсиевича Бедарева “Ребусы”. [9]
В настоящее время ребус – одна из самых популярных и распространённых игр. В ребусе можно зашифровать пословицы, поговорки, отрывки из стихотворений, отдельные фразы и слова. В математической энциклопедии говорится: « Математическими ребусами называют задания на восстановление записей вычислений».
Условие математического ребуса содержит либо целиком зашифрованную запись (цифры заменены буквами), либо только часть записи (стертые цифры заменены точками или звездочками)». Ребусы такого вида мне знакомы. Они встречались в олимпиадных заданиях. Решив несколько ребусов, я заметила, что их можно разбить на два типа:
2.2. Первый тип ─ это те ребусы, в записи которых встречаются звёздочки. Требуется найти набор цифр, при подстановке которых вместо звездочек выполнится условие, сформулированное в задаче.
Решить такой ребус означает найти все возможные наборы цифр, удовлетворяющие условию задачи.
Примеры:
1. Восстановите поврежденную запись
Решение:
Ответ. 99 + 9 = 108
- Восстановите поврежденную запись
Решение:
Ответ. 99 + 99 = 198.
- Решить ребус
Ответ.354 + 384 = 738.
- Решить ребус на умножение.
- Восстановить цифры в записи следующего деления.
Ответ.1431 : 27 = 53.
Второй тип ─ это те ребусы, в записи которых встречаются буквы. Требуется определить цифры, при подстановке которых в эту запись вместо букв выполняется условие, сформулированное в тексте задачи.
При решении ребусов этого типа следует помнить, что разные буквы заменяются разными цифрами, а одинаковые буквы – одинаковыми цифрами.
Примеры.
- Решить ребус.
Решение
Очевидно, Д≤4. В разряде сотен имеем А + А = А, значит, А = 0 (без перехода) или А = 9 (с переходом). Значение А = 0 не подходит, так как в разряде единиц А + А = Р (получаем А = Р = 0). Значит, А = 9, Р = 8, Е = 7. Тогда 2М + 1 = 10 + Т, Т < 9, значит М = 5 или 6 (так как получается переход), а значения 7 и 8 уже заняты буквами Е и Р. При М = 6 получается решение:
Ответ. 18969 + 18969 = 37938.
- Решить ребус
Решение
Так как КА + КА + КА оканчивается на КА, то КА = 50, а значит, К = 5, А = 0. Так как Ш + Ш + Ш + 1 оканчивается на 0, то Ш = 3. Так как сумма трех чисел, начинающихся на 5 может начинаться лишь с 1, то С = 1. Рассматривая варианты для О, получаем, что О = 6 или О = 7, а значит, Б = 9 или Б = 2. Итак, получаем два варианта решения:
- Решить ребус
Ответ.
С = 4; П = 3; Т = 2; Р = 7; К = 8; О = 9.
- Решить ребус, если известно, что наибольшая цифра в числе СИЛЕН равна 5:
Решение
Так как наибольшая цифра в числе «СИЛЕН» равна 5, а С = 1, то остальные 4 цифры в данном числе будут 2, 3, 4, 5. Так как Н < 6, то И = 2. А значит, Н = 4. Так как Л > Е (в самом деле так как Е + 1 = Л, то Л > Е, ведь Л и Е меньше 5 по условию), то Л = 5, Е = 3. А тогда уже легко находим остальные цифры: Ш = 8, Р = 9. В итоге получается: 9382 + 3152 = 12534
Ответ.9382 + 3152 = 12534
В процессе решения я узнала, что при разгадке математических ребусов надо не только уметь хорошо вычислять, используя знания об арифметических действиях их свойствах, но и проявить смекалку, терпение, выдержку и настойчивость. Есть математические ребусы, имеющие несколько решений. Поэтому нельзя ограничиваться отысканием только одного решения.
Мы с моим преподавателем провели исследование по следующим вопросам:
-сколько времени, в среднем, занимает решение несложного ребуса;
-всегда ли школьники находят все решения.
В исследовании приняли участие 23 ученика 5 «A» класса.
Результаты исследований помещены в таблицу 1.
Таблица 1.
|
№ |
Вид ребуса |
Затрачено времени (в среднем) |
Рассмотрены все случаи решения. (в %) |
|
|
1 |
Ребусы со звёздочками |
20 мин |
20 % |
|
|
2 |
Ребусы с буквами |
15 мин |
40% |
Анализ данных таблицы позволяет сделать выводы:
1. Решение даже самого простого ребуса методом перебора занимает много времени, так как каждая неизвестная может принимать до десяти значений.
2. Каждое решение нужно доводить до конца, чтобы убедиться, что нет других решений, или найти все решения.
Я заметила, что ограничить варианты перебора по количеству переменных позволят следующие утверждения:
- Если в записи используется 10 различных букв, значит, при решении надо использовать все 10 цифр.
- Если используется более 10 букв, то ребус не имеет решения.
- Если в записи числа буква расположена в старшем разряде, то ее значение не может равняться нулю.
- Если в одном из слагаемых, получаемых при умножении, все буквы совпадают с буквами в множимом, то соответствующий разряд множителя содержит 1 единицу.
- Если отсутствует одно из слагаемых, получаемых при умножении, то соответствующий разряд множителя содержит 0 единиц.
2.3. Кроме рассмотренных мною ребусов существуют и другие. В толковом словаре С. И. Ожегова даётся такое толкование слова «ребус» ─ «загадка», в которой искомое слово или фраза изображены комбинацией фигур, букв или знаков».
Такие ребусы я ещё не решала. Оказалось, что для их отгадывания надо знать 12 правил:
- 1-ое правило. Если перед нарисованным предметом или знаком слева стоит одна или две запятые, то в соответствующем слове надо отбросить одну или две первые буквы.
Пример. ,100 , здесь в слове «сто» надо отбросить первую букву «с» и читать как «то».
- 2-ое правило. Если запятые стоят справа после нарисованного предмета или знака, то в соответствующем слове надо отбросить одну или две последние буквы.
Пример. Здесь в слове «дом» надо отбросить последнюю букву «м» и читать «до».
- 3-е правило. Если над нарисованным предметом или рядом с ним написана и зачёркнута буква, то её надо отбросит. Если же после буквы стоит знак равенства и другая буква, тогда первую букву заменяют второй.
Пример. Л в слове «глаз» надо убрать букву «л» и получим «газ».
- 4-е правило. Если два каких-нибудь предмета или буквы нарисованы одна в другой, то их названия читаются с прибавлением предлога «в».
Пример. В-О-ДА ДА .
5-е правило. Если изображение какой – нибудь буквы состоит из другой буквы или буквосочетаний, то этот рисунок читают с прибавлением предлога «из».
- 6-е правило. Если одна фигура или буква нарисована под другой, то читать надо с прибавлением предлога «на», «над» или «под».
Пример. Читать надо так: З-НА-К.
- 7-е правило. Если за какой-нибудь буквой или предметом стоит другая буква или предмет, то читать надо с прибавлением предлога «за».
Пример. Читается так: КА-ЗА-НЬ.
- 8-е правило. Если по какой-нибудь букве написана другая буква или буквосочетание, то читается с прибавлением предлога «по».
Пример. Читаем: ПО-Р-Т.
Пример. Получаем: Л-У-К.
- 10-е правило. Если в ребусе встречаются изображения предметов в перевёрнутом виде или нарисована стрелка, то их наименования надо читать с конца.
Пример . Вместо «ДОМ» читаем «МОД».
- 11-е правило. Цифры рядом с изображениями задают новый порядок букв.
- Пример. Вместо слова «куб» читаем: «бук»
12-е правило. Часто в ребусах слоги «до», «ре», «ми», «соль», «ля», «си»,изображают соответствующими нотами.
2.3. Изучив, правила, я приступила к решению . Из всех ребусов, которые я искала в различных источниках, я выбирала математические . Сначала я училась решать те, в которых применяется только одно из двенадцати правил. Примеры таких задач:
1. Решение: ЧИ-СЛОН. Получим: «Число».
2. . Решение: ЛУНА-Ч. Уберём две буквы в слове «ЛУНА»: ЛУНА-Ч. Ответ: «Луч».
3. . Решение: Буква «З» находится на букве «К», поэтому читаем с предлогом «на»: З-НА-К. Получим: «Знак».
4. О . Решение: О-ДЖИН. Уберём букву «Ж». Читаем: «Один».
5. . Решение: Цифра «7» находится в букве «О». Читаем: В-О-СЕМЬ. Ответ: «Восемь».
6.
Решение: КВА-Д-РОТ. Заменим букву «о» на «а». Ответ: «Квадрат».
2.4. Далее, я приступила к решению более сложных математических ребусов, где надо применить несколько правил.
Решить ребусы:
Решение.
Имеем: СТО-ПЕНЬ.В слове «сто» третью букву «о» заменим на «е». Получим: СТЕ-ПЕНЬ. Ответ: «Степень».
Решение.
Применим четвёртое правило: КОТ-В-Е-КОТ. Применим второе правило: КОТВЕКОТ. Получим: «Ответ».
Решение.
Имеем: ОДИН-А-МЕТР.В слове «один» уберём первую и последнюю буквы и получим ДИ-А-МЕТР. Ответ: «Диаметр».
Решение.
ТРИ-РЕМЕНЬ . Заменим в первом слове первую букву «Т» на «П», получим ПРИ-РЕМЕНЬ. Уберём три последние буквы во втором слове, получим: ПРИ-РЕМ. Стрелка вверху второй картинки показывает, что оставшиеся буквы надо читать в обратном порядке. Ответ: «Пример».
Решение. Имеем: ЛИСТ-Е-ПЕНЬ .Уберём в первом слове две первых буквы, получим СТ-Е-ПЕНЬ. Ответ: «Степень».
Решение.
Так как: по букве «к» написана буква «а»,то имеем: ПО-К-А;
– за слогом «те» находится слог «ль», тогда получим: ЗА-ТЕ-ЛЬ.
Получим: ПО-К-А-ЗА-ТЕ-ЛЬ. Ответ: «Показатель»
Решение.
Имеем: МАК-СЕМЬ-А-КИТ-А. В слове мак букву «к» заменим на «т»,
В слове «семь» уберём первую и последнюю буквы, слово «кит» читаем с конца, так как изображение кита в перевёрнутом виде. Получим: МАТ-ЕМ-А-ТИК-А. Ответ: «Математика».
Решение. Имеем: ПАР-О-ИЗ –В-*ЕДЕ**-КНИГА-Е . В слове «пар» уберём букву «а», в слове «книга» уберём первую букву и две последних. Получим: ПР-О-ИЗ-В-ЕДЕ-НИ-Е. Ответ: «Произведение»
Решение. Имеем: НОС-НО-В-А-КНИГА-Е.В слове «нос» уберём первую букву,В слове «книга» уберём первую букву и две последних. Получим : ОС-НО-В-А-НИ-Е. Ответ: «Основание».
Решение. УС-ЛОБ-ВИЛЫ-Е. В слове «лоб» убираем последнюю букву, а в слове «вилы» – две последние. Получим: УС-ЛО-ВИ-Е. Ответ: «Условие».
Решение. Имеем: П-РАМА-Я. Заменим «а» на «я». Ответ: «Прямая».
Решение. На рисунке: ПЕРО-РЕ-НОС. В слове «перо» убираем две последние буквы. Получим: ПЕ-РЕ-НОС. Ответ: «Перенос».
Решение. Имеем: ДОМ-КА-ЗА- ТЕ-ЕЛЬ . Применим правила. Ответ: «Показатель».
Решение. На рисунке: КОСА-Т-ЕЛЬ-НА-Я. Применим правила. Ответ: «Касательная».
При решении ребусов с предметами я заметила, что:
- Правила лучше запоминаются в процессе решения ребусов.
- Название всего, что изображено на картинках в ребусе, надо читать только в именительном падеже.
- Необходимо учитывать наличие синонимов.
Трудности, которые возникали при решении ребусов:
- Надо правильно назвать изображённый на рисунке предмет.
- Картинка в ребусе может иметь не одно название. Примеры:
-нога, лапа;
-глаз, око;
-флаг, знамя;
– рыба-общее название; сазан, карась, щука – конкретное названия;
-птица ─ общее название: петух, чайка, голубь –конкретные названия.
- Надо понять , как соотносятся между собой фрагменты рисунка.
Пример: рисунок ДА можно прочитать В-О-ДА ( в «о» находится «да») или ДА-В-О («да» находится в «о»). Выбираем подходящее.
Чтобы преодолеть эти трудности, нужны смекалка и логика.
Я составила алгоритм для решения ребусов:
1.Надо назвать по частям изображённые предметы ( возможно это будет несколько синонимов), буквы, цифры.
2.Применить правила к каждому слову.
3. Оставить подходящие слова.
4. Составить по смыслу зашифрованный текст.
2.4. После того, как я решила десятка три ребусов, я попробовала сама составить несколько ребусов.
Решение. Имеем: РАДУГА-УСЫ.В слове радуга заменим букву «у» на «и», уберем две последние буквы, в слове усы уберем последнюю букву. Получим: ради- ус. Ответ: «Радиус».
Решение. Имеем: дом- лук- ь. Слово «дом» читаем с конца, так как изображение дома в перевёрнутом виде. В слове «лук» поменяем порядок букв. Получим: мод- ул- ь. Ответ: «Модуль».
Решение. Имеем: три- уголь- клубника. В слове «три» меняем третью букву на «е» ,в слове клубника уберем четыре первые буквы и одну последнюю. Получим: тре- уголь- ник. Ответ: «Треугольник».
Решение. Имеем: чи- слон- ит- ель. В слове слон уберем две последние буквы. Получим: чи- сл- ит- ель. Ответ: «Числитель» .
Я составила алгоритм составления ребусов:
- Надо задумать слово.
- Подобрать картинки, которые подходят к части слова.
- Лишние буквы удалить с помощью запятых или заменить некоторые буквы.
Составить ребус, оказалось, нетрудно. Главная трудность ─ сгруппировать картинки, чтобы они держались вместе и передвигались вместе с текстом. А, чтобы нарисовать картинки от руки, необходимо затратить много времени.
III
Заключение
Изучив различные источники, я узнала, что такое ребусы, изучила правила их решения, исследовала способы решения.
Ребусы это задачи, представленные в занимательной форме, очень интересны. Их хочется решать, они увлекают своей необычностью, неочевидностью ответа. Появляется желание совершить пусть даже нелёгкий путь поиска решения. Каждое самостоятельно решенное задание – это возможно, небольшая, но всё же победа.
Решая ребусы, я заметила, что это занятие развивает сообразительность, смекалку, а также усидчивость. Формирует внимательность, упорство в достижении цели, способствует творческому поиску чего – то нового, учит терпению, что мне просто необходимо для успешной учёбы.
Опрос показал, что ребусы не так популярны, как, например кроссворды. А ведь даже для взрослых – это хорошая разрядка от трудных ежедневных проблем и замечательный способ проведения семейного досуга.
Полезность этой игры просто трудно переоценить. Я узнала, что условия ребусов могут быть заданы в стихотворной форме. Это очень интересно. Я продолжу изучение ребусов.
Результаты моей работы:
1.Я расширила свой кругозор.
2.Я научилась решать ребусы различных видов.
3.Я научилась составлять ребусы.
5.У меня и у моей семьи появилось новое творческое увлечение, которое поможет мне развить сообразительность, усидчивость, упорство, что так необходимо мне для успешной учёбы.
Источники:
1. Березнев А.В. «Кроссворды, игры, загадки»: Сборник – Ростов-на-Дону, 1998
2. Трошин В.В. « Магия чисел и фигур». Занимательные материалы по математике . М.: Глобус, 2007.
3.Ожёгов С. И. и Шведова Н.Ю. « Толковый словарь Русского языка». М.:ООО «ИТИ Технологии»,2003.
4.Удальцова Н.В. Математика: «Математические шарады и ребусы».Москва.2010.
5. Фарков А. В. «Математические кружки в школе. 5 – 8 классы».
М.: Айрис-пресс, 2008.
6. Шарыгин И. Ф., Шевкин А. В. Математика: Задачи на смекалку: Учеб. пособие для 5 – 6 кл. общеобразоват. учреждений. М.: Просвещение, 2000.
7.http://yandex.ru/images/search?text=%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%9B%D1%8F%D0%B3%D1%83%D1%88%D0%BA%D0%B8%20%D0%BD%D0%B0%D1%80%D0%B8%D1%81%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D0%B5&uinfo=sw-1366-sh-768-ww-1350-wh-596-pd-1-wp-16x9_1366x768 – картинки.
8.http://www.igraza.ru/page-1-1-20.html – картинки.
9.http://rebus1.com/index.php?item=rebus&mode=2- история ребусов.
10.http://allriddles.ru/ru/rebuses/ – чем полезны ребусы.
11. http://elancev.narod.ru/kids/ref_reb/ref_reb.htm – чем полезны ребусы.
Сборники ребусов по математике с ответами. Ребус это головоломка в которой зашифровано по определенным правилам может быть не только отдельное слово, но и пословица, поговорка, цитата, загадка и даже целый небольшой рассказ.
Существует огромное множество видов и примеров различной сложности ребусов. Например в математическом ребусе все слова и фразы, загадки, задачи, стихи могут быть зашифрованы не только в виде картинок, букв, цифр, но и других всевозможных знаков, количество которых не ограничивается.
ВИДЫ РЕБУСОВ
- Литературные это когда в ребусе зашифровываются слова или предложения. Используются различные методы; картинки – ребусы, ребусы с запятыми, с цифрами, картинки перевертыши и т.д.
- Музыкальные это ребусы в которых используются картинки музыкальных нот. В таком ребусе картинка может означать либо само слово, либо нота является частью слова.
- Математические ребусы это ребусы из простых задач по математике на сложение, вычитание, умножение и другие. Все цифры или некоторые заменены картинками или другими символами. Задача заключается в том, чтобы восстановить вид примера математическими цифрами.
СБОРНИК РЕБУСОВ ПО МАТЕМАТИКЕ
Сборники ребусов по математике для 5, 6, 7 классов представлены с ответами и предназначены для развития логики, мышления и расширения словарного запаса. Все математические ребусы с ответами можно свободно и без регистрации скачать в формате pdf.
СБОРНИК РЕБУСОВ ПО МАТЕМАТИКЕ ДЛЯ 5-7 КЛАССОВ
- Сборник № 1
- Сборник № 2
- Сборник № 3
- Сборник № 4
- Сборник № 5
- Сборник № 6
- Сборник № 7
- Сборник № 8
- Сборник № 9
- Сборник № 10
- Сборник № 11
- Сборник № 12
- Сборник № 13
- Сборник № 14
- Сборник № 15
- Сборник № 16
- Сборник № 17
- Сборник № 18
- Сборник № 19
- Сборник № 20
- Сборник № 21
- Сборник № 22
- Сборник № 23
- Сборник № 24
ОТВЕТЫ
- Ответы к сборнику
СБОРНИК РЕБУСОВ ПО МАТЕМАТИКЕ С ОТВЕТАМИ
- Сборник № 1
- Сборник № 2
- Сборник № 3
- Сборник № 4
- Сборник № 5
- Сборник № 6
- Сборник № 7
- Сборник № 8
- Сборник № 9
- Сборник № 10
- Сборник № 11
- Сборник № 12
- Сборник № 13
- Сборник № 14
- Сборник № 15
- Сборник № 16
ПРИМЕРЫ РЕБУСОВ
ОТВЕТЫ
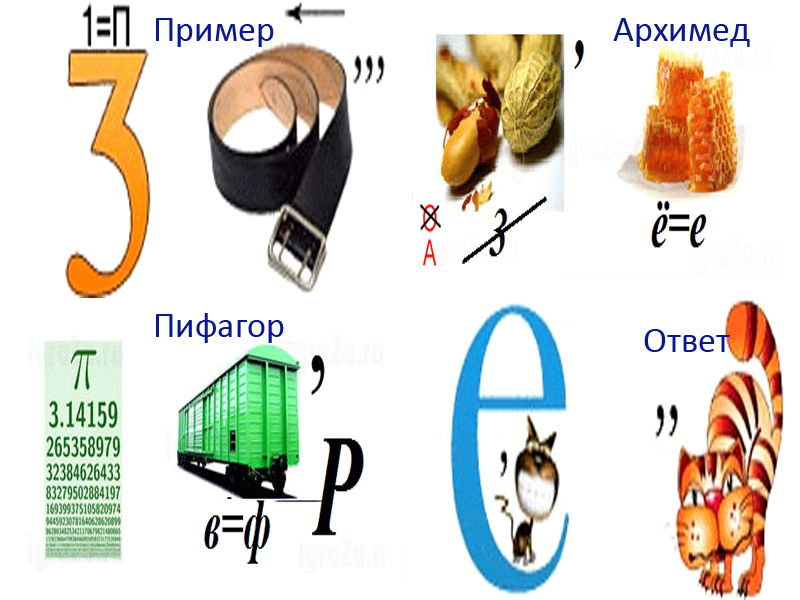
- Показатель
- Наклонная
- Подобие
- Стереометрия
- Теорема Пифагора
- Теорема
- Отрезок
- Задача
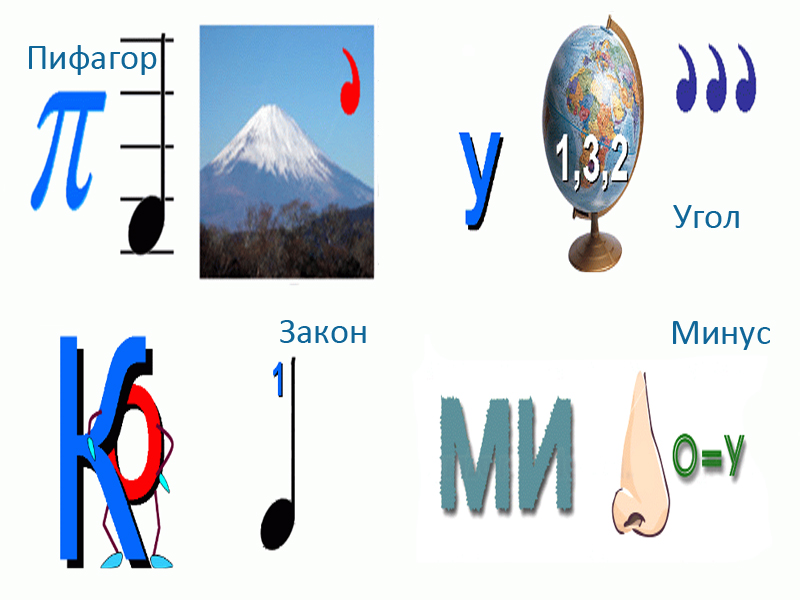
- Пифагор
МАТЕМАТИЧЕСКИЕ РЕБУСЫ



Математические ребусы
Работу выполнила ученица 5 класса МБОУ «Сатинская СОШ»
Синковец Дарья
Руководитель Истомина Нина Владимировна

Что такое ребус?
- Ребус – это головоломка в которой зашифровано слово. Это слово дается в виде рисунков с использованием букв и цифр, а также определенных фигур или предметов. Ребус — одна из самых интересных головоломок.

Правила для разгадывания ребусов
1.Запятая в самом начале слова говорит о том, что нужно убрать первую букву в этом слове, а запятая в конце — убрать последнюю букву в слове. Две за
пятых — убираем две буквы.
2.Зачеркнутые цифры говорят о том, что буквы стоящие на этом месте убираются.
3.Не зачеркнутые цифры показывают, что буквы, стоящие на месте 2 и 3 надо поменять местами.
4.Если рисунок в перевернутом виде, то загаданное с помощью картинки слово читается справа налево.
5.«Стрелка» или знак «равно» говорят о том, что одну букву надо заменить другой.
6.Буквы, слова или картинки могут изображаться внутри других букв, над другими буквами, под и за ними. Тогда добавляются предлоги: В, НА, НАД, ПОД, ЗА.
7.Цифры под картинкой указывают на то, что из данного слова нужно взять буквы, стоящие на местах под номерами 7,2,4,3,8 и составить их в том порядке, в котором расположены цифры.

Ребус №1
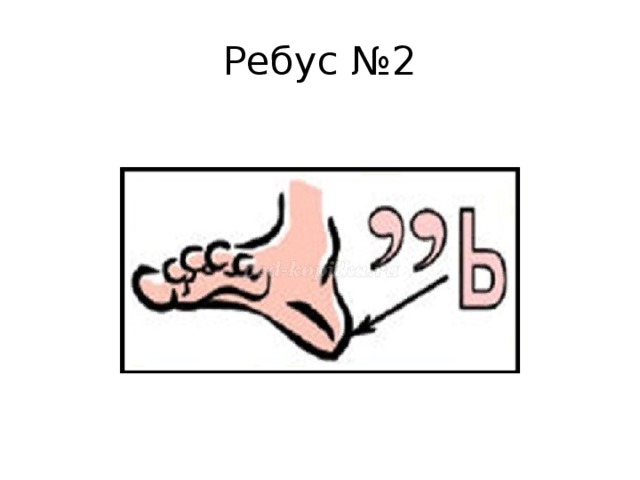
Ребус №2

Ребус №3

Ребус №4

Ребус №5
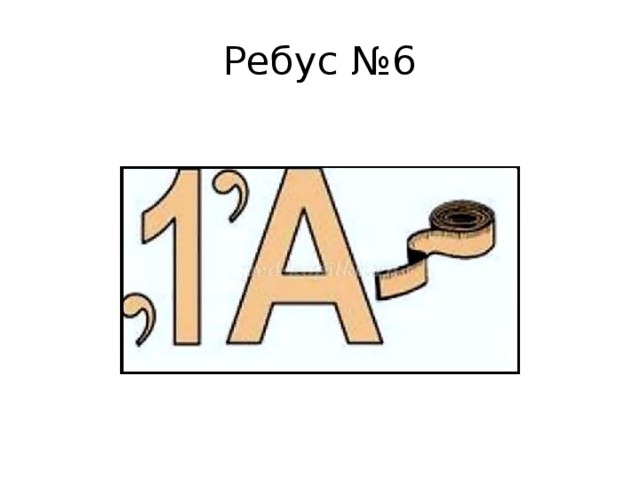
Ребус №6

Ребус№7
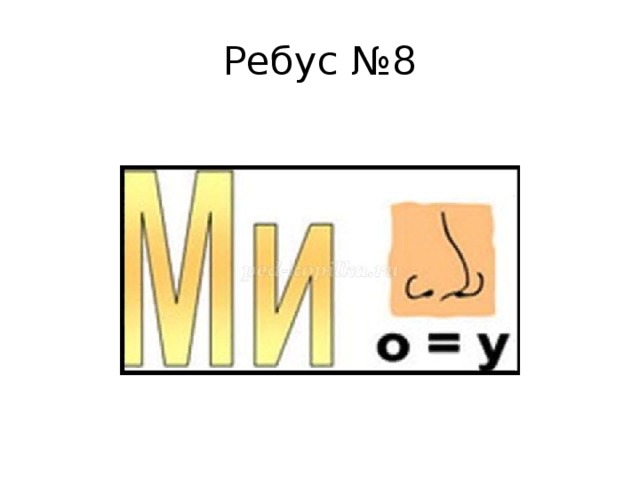
Ребус №8

Ребус №9

Ребус №10

Ответы
- 1.Доказательство
- 2.Пять
- 3.Конус
- 4.Вершина
- 5.Задача
- 6.Диаметр
- 7.Знаменатель
- 8.Минус
- 9.Два
- 10.Сложение