Как составить рекурсию - Сайт, где вы сможете решить свои вопросы

Рекурсия — одно из самых распространенных алгоритмических понятий. Если говорить просто, то рекурсивным алгоритм становится, если вызывает сам себя.

Головоломка Ханойские башни состоит из трёх стержней, пронумеруем их слева направо: 1, 2 и 3. Также в головоломке используется стопка дисков с отверстием посередине. Радиус дисков уменьшается снизу вверх. Изначально диски расположены на левом стержне (стержень 1), самый большой диск находится внизу. Диски в игре перемещаются по одному со стержня на стержень. Диск можно надеть на стержень, только если он пустой или верхний диск на нём большего размера, чем перемещаемый. Цель головоломки — перенести все диски со стержня 1 на стержень 3. Попробуйте нашу интерактивную версию Ханойских башен и узнайте, как переместить все диски с одного стержня на другой.

Ханойские башни: Вывод списка действий, необходимых для решения головоломки «Ханойские башни».

Входные данные: Целое число $n$.
Выходные данные: Последовательность ходов для решения головоломки «Ханойские башни» из $n$ дисков.

Решить головоломку с одним диском легко — просто переместите его на правый стержень. Головоломка на два диска ненамного сложнее. Сначала нужно переместить маленький диск на стержень посередине, а большой — на стержень справа. Затем переместить маленький диск на большой на правом стержне.

Версия на три диска чуть сложнее, но и ее можно решить с помощью следующих семи шагов:

Переместить диск со стержня 1 на стержень 3

– Переместить диск со стержня 1 на стержень 2

– Переместить диск со стержня 3 на стержень 2

– Переместить диск со стержня 1 на стержень 3

– Переместить диск со стержня 2 на стержень 1

– Переместить диск со стержня 2 на стержень 3

– Переместить диск со стержня 1 на стержень 3

Теперь давайте посчитаем, сколько шагов потребуется для решения версии на четыре диска. Нам нужно обязательно переместить самый большой диск, но для этого придётся сперва поместить все остальные диски на пустой стержень. Если у нас не три диска, а четыре, то нужно переложить три верхних диска на пустой стержень (7 действий), а затем переместить самый большой диск (1 действие). Теперь нужно снова переместить три диска с «временного» стержня на самый большой диск (еще 7 действий). Весь процесс будет состоять из $7 + 1 + 7 = 15$ действий.

Обобщим. Чтобы переместить $n$ дисков с левого стержня на правый, сначала необходимо переместить $n – 1$ дисков на стержень посередине. Затем, когда диск под номером $n$, самый большой, оказывается на правом стержне, нужно переместить на него оставшиеся диски со стержня посередине. Чтобы переместить $n-1$ дисков со стержня посередине направо, нужно сначала переместить $n-2$ дисков на стержень слева, затем переместить $(n-1)$-й диск вправо, потом переместить $n-2$ дисков с левого стержня на правый и так далее.

На первый взгляд задача «Ханойские башни» может показаться сложной. Тем не менее данный рекурсивный алгоритм находит нужные перемещения дисков всего за 8 строк!

 HanoiTowers(n,fromPeg,toPeg)
    if n = 1:
        output “Move disk from peg fromPeg to peg toPeg”
        return
    unusedPeg = 6 - fromPeg - toPeg
    HanoiTowers(n−1,fromPeg,unusedPeg)
    output “Move disk from peg fromPeg to peg toPeg”
    HanoiTowers(n−1,unusedPeg,toPeg)

Переменные $fromPeg, toPeg$ и $unusedPeg$ указывают на три разных стержня. Таким образом, HanoiTowers(n, 1, 3) перемещает диски ($n$ шт.) с первого стержня на третий. Переменная $unusedPeg$ указывает, какой из трёх стержней можно использовать для временного хранения первых ($n-1$) дисков. Обратите внимание, что $fromPeg+toPeg+unusedPeg$ всегда равняется $1+2+3 = 6$. Таким образом, значение переменной $unusedPeg$ можно определить как $6 – fromPeg – toPeg$. Представленная таблица показывает результаты $6 – fromPeg – toPeg$ для всех возможных переменных $fromPeg$ и $toPeg$.

fromPeg	toPeg	unusedPeg
1	2	3
1	3	2
2	1	3
2	3	1
3	1	2
3	2	1

Определив $unusedPeg$ как $6 – fromPeg – toPeg$, операторы

HanoiTowers(n−1,fromPeg,unusedPeg)
output “Move disk from peg fromPeg to peg toPeg”
HanoiTowers(n−1,unusedPeg,toPeg)

выполняют более простую задачу: они сначала перемещают $n-1$ дисков на временный стержень, затем перекладывают большой диск, а потом складывают на него оставшиеся $n-1$ дисков. Обратите внимание, что нет необходимости указывать, какой диск игрок должен переложить с $fromPeg$ на $toPeg$: перемещается всегда тот диск, что является верхним на $fromPeg$.

💡 Остановитесь и подумайте:
Сколько нужно действий, чтобы переместить $6$ дисков?

Хотя решение Ханойских башен можно уложить в 9 строк псевдокода, его выполнение займет на удивление много времени. Решение головоломки на пять дисков состоит из 31 действия. А в решении башни из сотни дисков количество действий будет больше, чем атомов на Земле. Такое резкое увеличение числа действий для HanoiTowers неудивительно. Заметим, что каждый раз, когда вызывается HanoiTowers(n, 1, 3), алгоритм дважды вызывает сам себя для перемещения $n-1$ дисков, что запускает четыре вызова для перемещения $n-2$ дисков и так далее.

Это можно проиллюстрировать с помощью рекурсивного дерева, изображенного на рис.. Вызов HanoiTowers(4, 1, 3) приводит к вызовам HanoiTowers(3, 1, 2) и HanoiTowers(3, 2, 3); каждый из них вызывает HanoiTowers(2, 1, 3), HanoiTowers(2, 3, 2) и HanoiTowers(2, 2, 1), HanoiTowers(2, 1, 3) и так далее. Каждый вызов подпрограммы HanoiTowers занимает определенное время. Мы хотим узнать, сколько времени уйдёт на такой алгоритм.

Чтобы вычислить время выполнения HanoiTowers размера $n$, мы введём в рассмотрение функцию $T(n)$ — количество перемещений дисков, которые выполняет HanoiTowers(n). Получается следующее уравнение:

$$
T (n) = 2 cdot T (n – 1) + 1 , .
$$

Начиная с $T (1) = 1$, это рекуррентное соотношение задаёт последовательность:

$$
1, 3, 7, 15, 31, 63,
$$

и так далее. Мы можем вычислить $T (n)$, прибавив 1 с обеих сторон и обнаружив, что

$$
T (n) + 1 = 2 cdot T (n – 1) + 1 + 1 = 2cdot(T (n – 1) + 1) , .
$$

Если мы введём новое обозначение, $U(n) = T (n) + 1$, то $U(n) = 2 cdot U(n – 1)$. Таким образом, нужно решить следующее рекуррентное соотношение:

$$
U(n) = 2 cdot U(n – 1) , .
$$

Начиная с $U(1) = 2$, получаем последовательность

$$
2, 4, 8, 16, 32, 64, dotsc
$$

То есть, $U(n) = 2^n$ и $T(n) = U(n) – 1 =2^n – 1$. Следовательно, HanoiTowers(n) — экспоненциальный алгоритм.

Источник

Можно представить, что рекурсивная функция уже написана. При решении задачи использовать её как уже написанную. После этого убедиться, что существуют граничные условия, при которых рекурсия остановится.

Например, пусть у нас есть следующая задача: нужно найти число возможных способов размена 100 рублей монетами 10 рублей, 5 рублей, 2 рубля и 1 рубль.

То есть нам надо написать функцию f(сумма, набор_монет), которую мы сможем вызвать так: result = f(100, [10, 5, 2, 1]). Первый аргумент – сумма, которую нам надо разменять, а второй – список из уникальных монет, с помощью которых можно представить эту сумму.

Представим, что функция f уже написана. Как теперь мы можем ей воспользоваться? Ключевой момент: придумаем способ разделения возможных вариантов, желательно простой.

Например, заметим, что 100 рублей можно разменять как с использованием десятирублёвой монеты, так и без использования десятирублёвой монеты. Эта идея, можно сказать, и есть решение задачи.

Сумма этих вариантов будет равна искомому числу. Тогда реализацию функции f можно записать как сумму рекурсивных вызовов самой себя с “укороченными” аргументами: f(90, [1, 2, 5, 10]) + f(100, [1, 2, 5]).

f(90, [1, 2, 5, 10]) – мы как бы “забрали” десятирублёвую монету из 100, но не ограничиваем дальнейший выбор монет;

f(100, [1, 2, 5]) – мы ничего не забрали из суммы, но ограничили набор монет.

Оба слагаемых вызываются рекурсивно. При этом видно, что количество вариантов будет уменьшаться с каждым рекурсивным вызовом.

Остаётся добавить граничные условия, чтобы функция не вызывалась бесконечно. Для этого нужно определить, при каких аргументах возвращать 1, а при каких – 0.

Источник

Пошаговые примеры на Python

Рекурсивная функция вызывает себя несколько раз, пока не будет выполнено какое-либо условие остановки.

Это страшно. Сам по себе вызов функции очень опасен, так как он относительно менее интуитивно понятен и может вызвать некоторую ошибку времени выполнения, если мы не будем относиться к нему с особой осторожностью. Раньше меня это очень пугало, но я смог сформулировать трехэтапный подход, который придаст вам уверенности в написании собственных рекурсивных функций без ошибок.

Пример

В качестве примера возьмем факториальную функцию. Я продемонстрирую это на Python, но та же логика применима и к другим языкам.

1. Рекурсивный случай – поток

Во-первых, нам нужно определить рекурсивный случай, то есть как факториальная функция определяется с помощью факториальных функций. Мы точно знаем, что:

n! = n × (n-1) × (n-2) × ... × 3 × 2 × 1

Это можно переписать рекурсивным образом, где факториальная функция применяется как к левой, так и к правой сторонам:

n! = n × (n-1)!

Это можно выразить на Python:

def factorial(n):
    return n * factorial(n-1)

2. Базовый вариант – критерий остановки.

Но в приведенном выше коде есть ошибка. Рассмотрим factorial(2), который вызывает factorial(1), который вызывает factorial(0) и т. Д. Функция продолжает вызывать себя без остановки, и это проблематично. Следовательно, нам нужен базовый случай для нашей рекурсивной функции, когда она перестает вызывать себя.

Факториал 0 и 1 определяется как 0! = 1! = 1. Это наши базовые случаи, и мы можем жестко запрограммировать их в нашу функцию.

def factorial(n):
    if n in [0,1]:
        return 1
    else:
        return n * factorial(n-1)

Рекурсивная функция перестает вызывать себя, когда попадает в factorial(1). Следовательно, вызов factorial(2) возвращает 2 * factorial(1), который возвращает 2 * 1 = 2.

3. Случай непреднамеренного происшествия – ограничение

Самая важная вещь, которую следует учитывать при написании рекурсивной функции, – это убедиться, что функция останавливается для каждого возможного аргумента n. Уверены ли мы, что наша функция не будет работать вечно ни при каких n?

Как насчет factorial(-1)? А что насчет factorial(1.5)?

У нас есть базовые случаи для n = 0 и n = 1, а наш рекурсивный случай вызывает саму функцию с аргументом n-1. Это означает, что функция достигнет базового случая, только если factorial(n) начинается с неотрицательного целого числа n.

Например, factorial(-1) вызывает factorial(-2), который вызывает factorial(-3), и мы никогда не сможем достичь базовых случаев. То же самое для нецелых n.

Давайте предотвратим это. Хотя для этого существует множество различных методов, мы будем использовать простой метод утверждения в Python, который выдает ошибку, если n не является неотрицательным целым числом. Другими словами, мы заставляем аргумент n быть неотрицательным целым числом n >= 0 and int(n) == n.

Другой пример

Другой очень распространенный пример – вычисление числа Фибоначчи. Он определяется следующими рекурсивными и базовыми случаями:

# recursive case
fibo(n) = fibo(n-1) + fibo(n-2)
# base cases
fibo(0) = 0
fibo(1) = 1

Обратите внимание, что оба базовых случая необходимо закодировать в функции, чтобы избежать ошибок времени выполнения, поскольку fibo(n) вызывает как fibo(n-1), так и fibo(n-2).

Наконец, ограничьте n, чтобы избежать непреднамеренного использования рекурсивной функции. Простой.

Предостережения

Использование рекурсий может сделать ваш код компактным и элегантным, поскольку сложное вычисление разбивается на множество простых подзадач. Однако рекурсия может потребовать больших вычислительных ресурсов и памяти.

Например, рекурсивная функция числа Фибоначчи – очень неэффективный способ вычисления числа. Подумайте о fibo(5): он вызывает fibo(3) и fibo(4). Первый вызывает fibo(1) и fibo(2), тогда как последний вызывает fibo(2) и fibo(3). Обратите внимание, что fibo(2) и fibo(3) без необходимости запускаются более одного раза.

Эта проблема становится более серьезной для большего n. Ниже можно найти гораздо более эффективный способ вычисления числа Фибоначчи. Очевидно, что рекурсия более элегантна (хотя иногда и менее читаема) и компактна.

Выводы

Рекурсивный случай – это поток функции.
Базовый случай – это критерий остановки , который останавливает поток.
Непреднамеренные случаи могут вызвать ошибку времени выполнения, и с ними следует бороться, ограничивая область аргументов.
Остерегайтесь потребления памяти вашими рекурсивными функциями.

Спасибо за прочтение! Если вы хотите улучшить свои навыки работы с Python, вам могут быть полезны следующие статьи:

Источник

В этом руководстве мы поговорим о различных аспектах рекурсивных функций и реализуем рекурсивные функции в Python с нуля.

Будучи профессиональным программистом, вы должны отлично разбираться в таких базовых вещах, как переменные, условные операторы, типы данных, спецификаторы доступа, вызовы функций, области видимости и т.д. Эти знания нужны как тем, кто пишет промежуточное ПО, так и веб-разработчикам. Это основы, которые должен знать каждый.

Одной из таких фундаментальных концепций является рекурсия, и ее невероятно важно знать при написании функций определенного типа.

Возможно, вы уже знаете, что «рекурсия — это когда функция вызывает сама себя». Но что происходит под капотом? Как рекурсия влияет на физическую память? Можете ли вы превратить любую другую функцию в рекурсивную? В нашей статье вы найдете ответы на эти фундаментальные вопросы.

В частности, мы рассмотрим следующие темы:

Базовая анатомия рекурсивной функции
Представление памяти рекурсивной функции:
- Дерево
- Стек
Отслеживание рекурсии
Пространственно-временной анализ рекурсивной функции
Реализация простой рекурсивной функции в Python

Анатомия рекурсивной функции

Вероятно, сам термин «рекурсия» вам уже знаком. Сейчас мы рассмотрим эту концепцию еще раз, но более увлекательно, чем в учебнике.

Вернемся к определению рекурсии: «Рекурсия – это функция, которая вызывает сама себя». Давайте рассмотрим пример, подтверждающий это определение:

void A(n){
    if(n>=1){
        A(n-1);
        print(n);
    }
}

Вы можете видеть, что функция A() вызывает сама себя. Это пример рекурсии, где A() — рекурсивная функция.

Давайте теперь изучим некоторые основные совйства рекурсивной функции.

Основные принципы работы рекурсивной функции

Рекурсивная функция должна иметь следующие два свойства:

Рекуррентное отношение
Условие прекращения

Рассмотрим приведенный выше фрагмент кода, чтобы понять эти моменты. Ясно, что функция представляет собой конкретное рекуррентное соотношение:

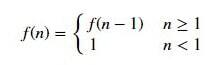
n ≤ 1 — условие завершения, или условие привязки, или базовое условие. Когда оно выполняется, рекурсия останавливается. Указание этого условия является обязательным. В противном случае функция попадет в бесконечный цикл и будет выполняться непрерывно, чего нам не очень хочется.

Обратите внимание, что приведенный выше фрагмент кода не соответствует какому-либо конкретному языку программирования. Основная цель здесь — показать пример рекурсивной функции.

Вы, должно быть, сейчас думаете, зачем вообще писать рекурсивную функцию, если есть лучшие альтернативы? Да, отследить рекурсию иногда бывает сложно, но, освоив эту тему, вы обнаружите, что рекурсия прекрасна с точки зрения читабельности программы и переменных.

Для выполнения рекурсии не нужны дополнительные переменные, однако для остановки требуется правильное условие завершения. Найти его часто бывает непросто. Опять же, здесь вам поможет только практика!

Далее в этом руководстве мы посмотрим, насколько красивой и маленькой может быть программа, если она реализована с помощью рекурсии. Теперь давайте перейдем к представлению памяти рекурсивной функции.

Представление памяти рекурсивной функции

В этом разделе мы изучим, как рекурсивные функции представляются в памяти с помощью деревьев и стеков.

Рассмотрим уже знакомую нам рекурсивную функцию A():

void A(n){
    if(n>=1){
        A(n-1);
        print(n);
    }
}

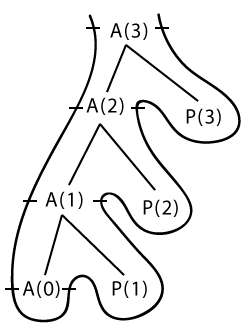
Итак, давайте начнем с представления памяти с помощью деревьев. Это может показаться немного сложным, но на самом деле нужно просто разобраться. Если бы вы записывали каждый вызов функции в виде дерева, как бы это выглядело?

Дерево

Здесь следует отметить пару моментов:

Функция вызывается с параметром A(3) и поэтому здесь выполняются 4 (= 3 + 1) вызова функций. Если обобщить, то при вызове A(n) потребуется всего (n+1) вызовов функции.
Вызовы P() — это выводы, созданные функцией print(n).
Функция A(0) приведет к невыполнению условия if, так как мы получим n < 1, что, в свою очередь, приведет к завершению работы рекурсивной функции.

Мы начали именно с древовидного представления, потому что оно необходимо для представления рекурсивной функции в стеке. Вы увидите это сейчас.

Стек

Стек — структура данных, организованных по принципу LIFO (англ. last in — first out, «последним пришел — первым ушел»).

От редакции Pythonist. О стеке можно почитать в статье «Реализация стека на Python».

Для представления стека вам придется пройти по дереву сверху вниз и слева направо. Следующее изображение прояснит это.

Интерпретация этого странного дерева

Имейте в виду, что стек состоит из двух операций:

push используется для вставки элемента в стек
pop — для извлечения элемента из стека.

Мы начинаем обход дерева в порядке сверху вниз и слева направо:

встречая вызов функции, вы помещаете его в стек
встречая вызов print() (т.е. P()), вы просто печатаете соответствующий элемент

Результатом обхода дерева от A(3) до A(0) будут следующие элементы стека (в перевернутом виде):

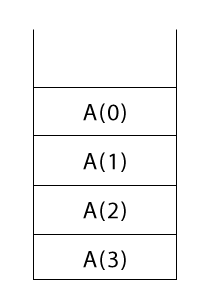
Теперь вы начинаете вторую половину обхода дерева, т. е. слева направо. Встречая вызов функции во второй раз, вы его удаляете (pop). Удивительно, но первым будет удален тот элемент стека, который последним попал в стек (LIFO, помните?).

Также на своем пути вы столкнетесь с тремя вызовами P(): P(1), P(2) и P(3). Вы выведете их на экран в том порядке, в котором они появляются на пути вашего обхода:

1 2 3

Наконец, когда вы закончите процесс обхода, стек будет полностью пуст.

Стек после полного извлечения всех элементов

Вы увидели, как представить простую рекурсивную функцию в памяти, используя дерево и стек. Теперь давайте посмотрим, как отслеживать рекурсию.

Отслеживание рекурсии

В этом разделе мы прежде всего рассмотрим, как методично отслеживать рекурсию. Возьмем в качестве примера следующую рекурсивную функцию:

void A(n){
    if(n>=1){
        A(n-1);
        print(n);
    }
}

Важный момент: при каждом вызове функции в памяти создается запись активации, содержащая локальные переменные этой функции и указатель инструкции. Указатель обозначает следующую задачу, которая должна быть выполнена, когда вызов возвращается к этой функции.

К примеру, функция с именем main() вызвала указанную выше функцию A() как A(3). Давайте пронумеруем строки A() из оператора if для лучшего понимания:

void A(n){
    1. if(n>0)
    2. {
        3. print(n-1);
        4. A(n-1);
    5. }
}

Записи активации будут выглядеть следующим образом:

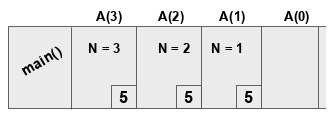
Как упоминалось ранее, функции имеют свои копии локальных переменных и указатели инструкций (в данном случае — номера строк). После того, как A(0) завершит работу, функция произведет выталкивание (pop). Обратите внимание, что здесь используется горизонтальный стек — точно такой же, как те, которые вы видели ранее в уроке. Кроме того, пока записи помещаются в стек, также будет выполняться печать, и будут напечатаны следующие элементы:

2 1 0

Здесь важно отметить указатели инструкций, потому что часто в рекурсивной функции управление переходит к той же функции, но с другим значением переменной. Указатели помогают поддерживать синхронизацию. Вы можете следовать этому же процессу, чтобы отследить рекурсию, используя представление в виде дерева.

Итак, а теперь давайте разберем, как выполнять пространственно-временной анализ рекурсивной функции.

Пространственно-временной анализ рекурсивной функции

Давайте быстро вспомним, что подразумевается под пространственным и временным анализом функции (также известными как пространственная и временная сложность).

Предполагается, что для заданного ввода функция должна производить некоторый вывод. Однако сколько времени для этого потребуется функции? Временная сложность — показатель приблизительного времени (также употребляется термин «время выполнения» функции). Аналогично, пространственная сложность — приблизительные требования к пространству (памяти) для функции (при заданных входных данных). Но зачем вообще нужны эти показатели?

Зная временную и пространственную сложность функции, вы можете легко прикинуть, как она может вести себя при входных данных разного размера. Вам не придется проверять это вручную.

Если у вас есть две функции, выполняющие одну и ту же задачу, какую из них выбрать? Какие метрики вы рассмотрите, чтобы принять решение? Да, вы правильно угадали. Вы сравните эти функции, проанализировав их пространственно-временную сложность, и выберете ту, которая работает лучше и эффективнее.

Давайте теперь возьмем простую рекурсивную функцию и проанализируем ее пространственную и временную сложность.

void A(n){
    if(n>1) // Anchor condition
    {
       return A(n-1);
    }
}

Временная сложность

Прежде всего проведем анализ временной сложности. Предположим, что общее время, затраченное на вышеуказанную функцию A(), равно T(n).

T(n) представляет собой сумму времени, затраченного на сравнение, действительно ли n больше 1, и времени, затраченного на выполнение A(n-1).

T(n) можно выразить так:

Т (n) = 1 + Т (n-1),

где 1 — время, затраченное на сравнение (туда можно поставить любую константу).

Каково будет время (T(n)) для выполнения A(n-1)?

Т(n−1) = 1 + T(n−2)

Аналогично,

T(n−2) = 1 + T(n−3) и так далее.

Если внимательно отнестись к уравнениям, то можно заметить, что все они связаны. Не так ли? Если вы подставите их друг в друга, вы получите

T(n) = 1 + (1 + T(n−2)) = 2 + T(n−2) = 3 + T(n−3) = .... = k + T(n−k) ( после запуска функции k раз)

Теперь вам нужно определить, в какой момент функция остановится. В соответствии с заданным условием мы можем написать:

Предположим, что после выполнения k раз функция перестает выполняться. Если так, то должно быть:

n − k = 1 => k = n − 1

Теперь подставим значение k (= n-1) в нашу формулу T(n) = k + T(n−k):

Т(n) = (n-1) + Т(n-(n-1))

=> Т (n) = (n-1) + T(1)

=> T(n) = n−1 + 1 = n // Для T(1) требуется только сравнение.

По правилу асимптотического анализа T(n) = n можно переписать как T(n) = O(n). Это означает, что временная сложность функции (при наихудшем случае) равна O(n).

Здесь вы можете немного притормозить и внимательно понаблюдать за каждым шагом этого процесса. Настоятельно рекомендуется делать это на бумаге, чтобы понять все до мельчайших деталей.

Пространственная сложность

Анализ пространственной сложности функции прост. Эта функция находится в памяти и не использует никаких дополнительных переменных. Поэтому можно сделать вывод, что пространственная сложность функции O(n).

Теперь давайте соберем все это вместе и реализуем простую рекурсивную функцию на Python.

Сейчас мы напишем рекурсивную функцию для нахождения факториала заданного числа. Затем мы напишем итеративную версию той же функции. Итак, давайте начинать:

# Рекурсивная функция factorial_recursion()
def factorial_recursion(n):  
   if n == 1:  
       return n  
   else:  
       return n*factorial_recursion(n-1)

# Вызов функции
num = 7
print("The factorial of ",num," is ",factorial_recursion(num))

# Output:
# The factorial of  7  is  5040

Помните два ключевых момента для написания рекурсивной функции?

Рекуррентное отношение
Условие прекращения

В этом случае рекуррентное соотношение может быть следующим:

f(n) = n!

f(n) = n ∗ f(n−1) и так далее.

Условие завершения — когда n равно 1.

Просто, верно?

Теперь давайте реализуем итеративную версию той же функции.

def factorial_iterative(num):
    factorial = 1
    if num < 0:
        print("Sorry, factorial does not exist for negative numbers")
    elif num == 0:
        print("The factorial of 0 is 1")
    else:
        for i in range(1,num + 1):
           factorial = factorial*i
        print("The factorial of",num,"is",factorial)
factorial_iterative(7)

# Output:
# The factorial of 7 is 5040

Вы можете четко заметить разницу между двумя версиями. Рекурсивная намного красивее итеративной, не так ли?

Заключение

Вы дошли до конца. Поздравляем! В этом руководстве мы подробно разрбрали рекурсивные функции в Python. Начиная с абсолютных основ и заканчивая анализом пространственной и временной сложностей рекурсивной функции, мы охватили все. Более того, мы увидели, как рекурсия может быть полезна для решения определенных задач. Теперь вы должны быть в состоянии решать задачи, используя рекурсию. Возможно, вам будет интересно решить задачу поиска чисел Фибоначчи в заданном диапазоне.

Кроме того, стоит обратить внимание на решение некоторых распространенных задач, таких как двоичный поиск, сортировка слиянием, Ханойская башня и т.д. при помощи рекурсии. Это, безусловно, сделает вас более подкованным программистом.

Надеемся, данная статья была вам полезна! Успехов в написании кода!

Перевод статьи «Understanding Recursive Functions in Python».

Источник

Пошаговые примеры на Python

Пример

1. Рекурсивный случай – поток

2. Базовый вариант – критерий остановки.

3. Случай непреднамеренного происшествия – ограничение

Другой пример

Предостережения

Выводы

Анатомия рекурсивной функции

Основные принципы работы рекурсивной функции

Представление памяти рекурсивной функции

Дерево

Стек

Интерпретация этого странного дерева

Отслеживание рекурсии

Пространственно-временной анализ рекурсивной функции

Временная сложность

Пространственная сложность

Заключение

Вам также может понравиться

Как найти площадь благоустройства

Как найти работу администратором ресторана

Как исправить ошибку на счетах бухгалтерского учета

Добавить комментарий Отменить ответ