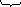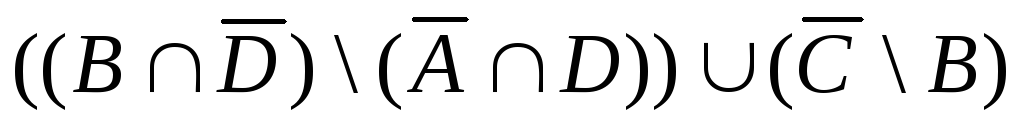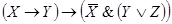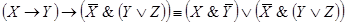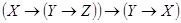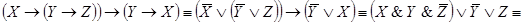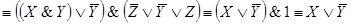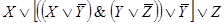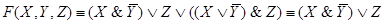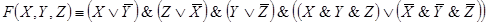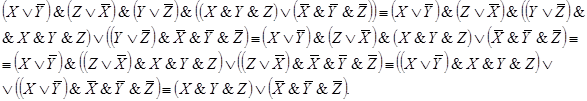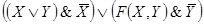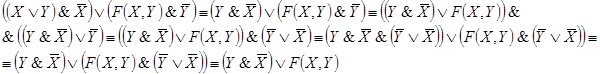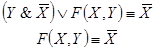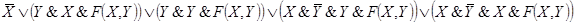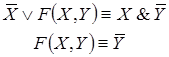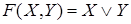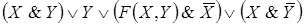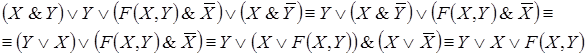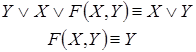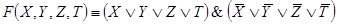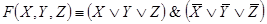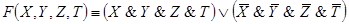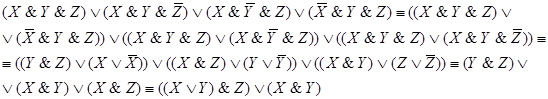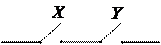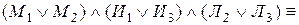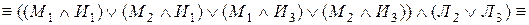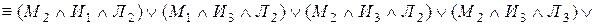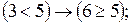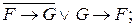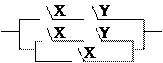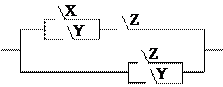Теория
булевых функций широко применяется к
теории электрических сетей, а именно к
контактным схемам.
Как
известно из физики, электромагнитные
реле имеют контакты двух типов:
-
замыкающие
(контакт замыкается при подаче тока
на катушку) и -
размыкающие
(контакт размыкается при подаче тока
на катушку).
Каждому
реле сопоставляется переменная х. При
этом все замыкающие контакты обозначим
х, размыкающие –
Тогда для
любой булевой функции можно построить
релейно-контактную схему по правилам:
Конъюнкции
двух высказываний соответствует
последовательное соединение контактов:
-
хy
(последовательное соединение);
Дизъюнкции
двух высказываний – параллельное
соединение:
-
хy
(параллельное соединение);
Пусть
R
– релейно-контактная схема, содержащая
n
реле. Каждой такой схеме сопоставляется
функция
проводимости
R(х1,
х2,
…хn),
где

х2,
…хn)=
1, если при заданных значениях х1,
х2,
…хn
схема проводит ток;
0,
если при заданных значениях х1,
х2,
…хn
схема не проводит ток;
И
наоборот: Всякой булевой функции f
сопоставляется релейно-контактная
схема R,
для которой R
=f
Из
двух релейно-контактных схем более
простой
является схема, содержащая наименьшее
количество контактов.
Две
схемы считаются эквивалентными,
если они одновременно проводят или не
проводят ток (то есть имеют равносильные
функции проводимости).
Для
упрощения схем необходимо:
-
записать
функцию проводимости данной схемы; -
упростить
функцию, используя формулы основных
равносильностей; -
по
полученной функции восстановить схему.
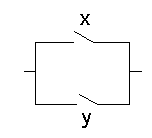
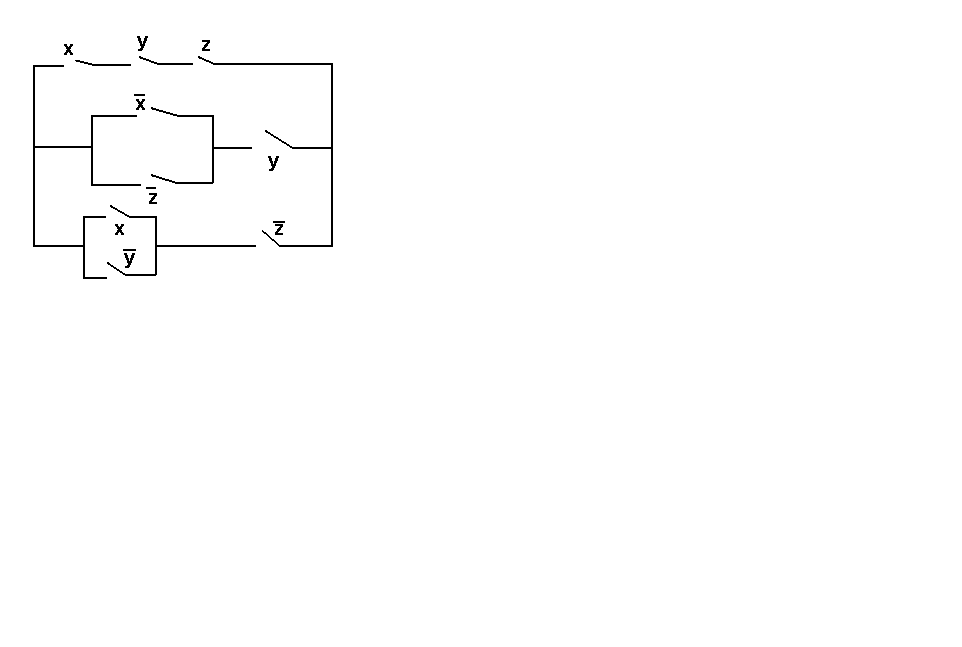
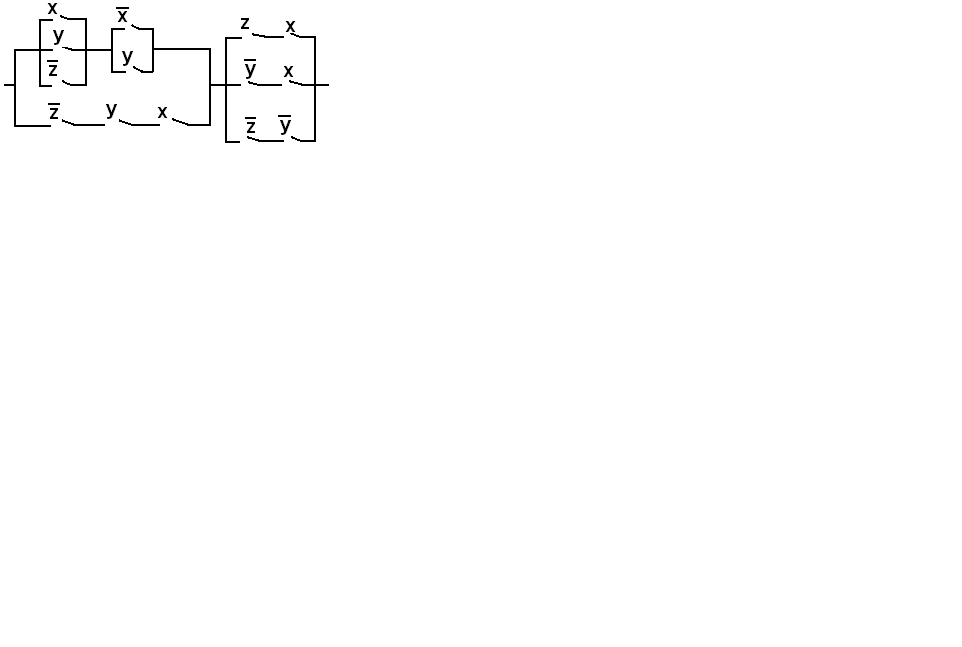
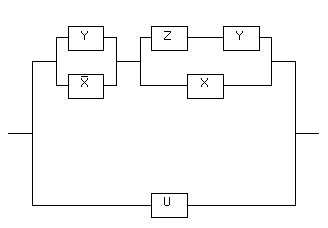
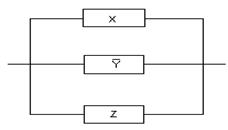
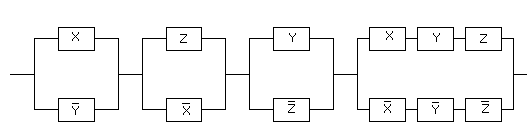
Пример
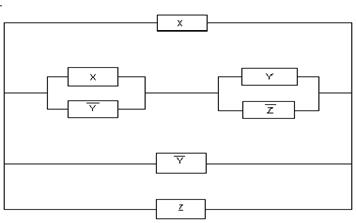
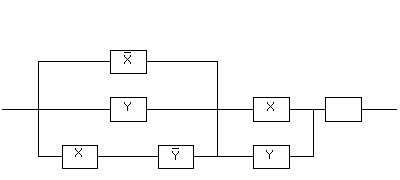
1. Упростить
схему:
Решение:
Составляем
функцию проводимости:
R(x,
y, z) =
используем
законы равносильностей и
упрощаем
формулу:
-
0
выполним
группировку (по закону дистибутивности)
– в первом, втором и третьем слагаемом
вынесем общий множитель – х; в четвертом
и пятом также вынесем общий множитель:
1 1
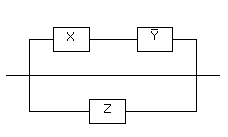
Итак,
после упрощения поллучили: R(x,
y, z)
= xy
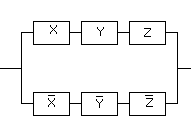
Воостановим
схему по полученной упрощенной функции:
Варианты контрольных работ: Рекомендации по выбору варианта контрольной работы:
-
Вам необходимо
знать свой порядковый номер в списке
Вашей группы. -
По “порядковому
номеру” находят нужный столбец во
второй или третей строке нижеприведенной
таблицы; -
по первой
строке “варианты к/р” определяется
нужный Вам вариант
|
Вариант К/р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер по списку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер по списку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВАРИАНТ
№ 1
-
Даны
множества
А
= {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С
= {3, 4, 5, 8} D
={2, 5, 8}
J
= {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы логики
высказываний
-
Составить
таблицу истинности булевой функции
-
Упростить
булеву функцию
-
Составить
СДНФ функции, заданной таблицей
истинности
|
x |
y |
z |
F(x,y,z) |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
-
Упростить
релейно-контактную
схему.
ВАРИАНТ
№ 2
-
Даны
множества
А
= {a,
b,
c,
i} В
= {a,
d,
f,
g,
i,
o}
С
= {g, t, o, d} D = {f, i, o, g}
J
= {a, b, c, d, f, g, i, o, t}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
3.
Составить таблицу истинности булевой
функции
-
Упростить
булеву функцию
-
Составить
СКНФ функции, заданной таблицей
истинности
|
x |
y |
z |
F(x,y,z) |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 3
-
Даны
множества
А
= {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С
= {3, 4, 5, 8} D
={2, 5, 8}
J
= {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
-
Составить
таблицу истинности булевой функции
-
Упростить
булеву функцию
-
Составить
СДНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
1
1
1
1
1
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 4
-
Даны
множества
А
= {a,
b,
c,
i} В
= {a,
d,
f,
g,
i,
o}
С
= {g, t, o, d} D = {f, i, o, g}
J
= {a, b, c, d, i, f, g, o, t}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
3.
Упростить булеву функцию
-
Упростить
булеву функцию
-
Составить
СКНФ функции, заданной таблицей
истинности
|
x |
y |
z |
F(x,y,z) |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 5
-
Даны
множества
А
= {x,
y,
z,
w,
v,
r} В
= {w,
r,
t,
s}
С
= {t, s, v, x, q} D = {y, z, w}
J
= {x, y, z, v, w, r, s, t, q}
Из
каких элементов состоит множество
2.
Составить таблицу истинности формулы
высказываний
-
Составить
таблицу истинности булевой функции
-
Упростить
булеву функцию
-
Составить
СДНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 6
-
Даны
множества
А
= {3, 5, 6, 7, 10} В = {3, 5, 6, 8}
С
= {4, 5, 6, 8, 11} D
= {4, 9, 10}
J
= {3, 4, 5, 6, 7, 8, 9, 10, 11}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
3.
Упростить булеву функцию
-
Упростить
булеву функцию
-
Составить
СКНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 7
-
Даны
множества
А
= {x,
y,
z,
w,
v,
r} В
= {w,
r,
t,
s}
С
= {t, s, v, x, q} D = {y, z, w}
J
= {x, y, z, v, w, r, s, t, q}
Из
каких элементов состоит множество
2.
Составить таблицу истинности формулы
высказываний
-
Составить
таблицу истинности булевой функции
-
Упростить
булеву функцию
-
Составить
СДНФ функции, заданной таблицей
истинностиa
b
c
F(a,b,c)
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 8
-
Даны
множества
А
= {3, 5, 6, 7, 10} В = {3, 5, 6, 8}
С
= {4, 5, 6, 8, 11} D
= {4, 9, 10}
J
= {3, 4, 5, 6, 7, 8, 9, 10, 11}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
3.
Упростить булеву функцию
-
Упростить
булеву функцию
-
Составить
СКНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
0
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 9
-
Даны
множества
А
= {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С
= {3, 4, 5, 8} D
={2, 5, 8}
J
= {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из
каких элементов состоит множество
2.
Составить таблицу истинности формулы
высказываний
-
Составить
таблицу истинности булевой функции
-
Упростить
булеву функцию
-
Составить
СДНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 10
-
Даны
множества
А
= {a,
b,
c,
i} В
= {a,
d,
f,
g,
i,
o}
С
= {g, t, o, d} D = {f, i, o, g}
J
= {a, b, c, d, i, f, g, o, t}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
3.
Упростить булеву функцию
-
Упростить
булеву функцию
-
Составить
СКНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 11
-
Даны
множества
А
= {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С
= {3, 4, 5, 8} D
={2, 5, 8}
J
= {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из
каких элементов состоит множество
2.
Составить таблицу истинности формулы
высказываний
-
Составить
таблицу истинности булевой функции
-
Упростить
булеву функцию
-
Составить
СДНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 12
-
Даны
множества
А
= {x,
y,
z,
q} В
= {x,
p,
r,
t,
q,
m}
С
= {t,
n,
m,
p} D
= {r,
q,
m,
n}
J
= {x,
y,
z,
p,
q,
r,
t,
m,
n}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
3.
Упростить булеву функцию
-
Упростить
булеву функцию
-
Составить
СКНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 13
-
Даны
множества
А
= {1, 2, 3, 5, 4, 6} В = {5, 6, 8, 7}
С
= {8, 7, 4, 1, 9} D
= {2, 3, 5}
J
= {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из
каких элементов состоит множество
2.
Составить таблицу истинности формулы
высказываний
-
Составить
таблицу истинности булевой функции
-
Упростить
булеву функцию
-
Составить
СДНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
1
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 14
-
Даны
множества
А
= {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С
= {3, 4, 5, 8} D
={2, 5, 8}
J
= {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
3.
Упростить булеву функцию
-
Упростить
булеву функцию
-
Составить
СКНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
0
-
Упростить
релейно-контактную схему.
ВАРИАНТ № 15
-
Даны
множества
А
= {3, 5, 6, 7, 10} В = {3, 5, 6, 8}
С
= {4, 5, 6, 8, 11} D
= {4, 9, 10}
J
= {3, 4, 5, 6, 7, 8, 9, 10, 11}
Из
каких элементов состоит множество
-
Составить
таблицу истинности формулы высказываний
3.
Упростить булеву функцию
-
Упростить
булеву функцию
-
Составить
СКНФ функции, заданной таблицей
истинностиx
y
z
F(x,y,z)
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
0
-
Упростить
релейно-контактную схему.
Применение булевых функций к релейно-контактным схемам
Булевы функции широко применяются при описании работы дискретных управляющих систем (контактных схем, схем из функциональных элементов, логических сетей и т.д.), при исследовании некоторых электрических цепей, так называемых релейно-контактных схем.
Идея применения. Под релейно-контактной схемой понимается Устройство из проводников и двухпозиционных контактов. Оно может быть предназначено, например, для соединения (или разъединения) полюсов источника тока с некоторым потребителем. Контакты релейно-контактной схемы могут быть двух типов: замыкающие и размыкающие. Каждый контакт подключен к некоторому реле (переключателю). К одному реле может быть подключено несколько контактов — как замыкающих, так и размыкающих. Технически реле представляет собой катушку с металлическим сердечником (магнитопроводом), вблизи которого находится соответствующий контакт.
Когда через катушку пропускается электрический ток, металлический сердечник намагничивается и замыкает все находящиеся при нем замыкающие контакты. Одновременно все размыкающие контакты, относящиеся к данному реле, размыкаются. Поскольку замыкающие контакты при отсутствии в реле электрического тока разомкнуты, то они называются также нормально разомкнутыми. Аналогично, размыкающие контакты называются также нормально замкнутыми. При обесточивании обмоток реле (т.е. когда реле отключается) все замыкающие контакты снова размыкаются, а все размыкающие, замыкаются.
Каждому реле ставится в соответствие своя булева переменная или
, или
, которая принимает значение 1, когда реле срабатывает, и принимает значение 0 при отключении реле. На чертеже все замыкающие контакты, подключенные к реле
, обозначаются тем же символом
, а все размыкающие контакты, подключенные к этому реле, обозначаются отрицанием
. Это означает, что при срабатывании реле
все его замыкающие контакты х проводят ток и им сопоставляется значение 1, а все размыкающие контакты
не проводят электрический ток и им сопоставляется значение 0. При отключенном реле
создается противоположная ситуация: все его замыкающие контакты
разомкнуты, т. е. в этот момент им сопоставляется (переменная
принимает) значение 0, а все его размыкающие контакты
замкнуты, т. е. в этот момент им сопоставляется (другими словами, переменная
принимает) значение 1.
Всей релейно-контактной схеме тогда ставится в соответствие булева переменная , зависящая от булевых переменных
, сопоставленным тем реле, которые участвуют в схеме. Если при данном наборе состояний реле
(некоторые из этих реле находятся в рабочем состоянии под током, остальные отключены, т.е. “обесточены”) вся релейно-контактная схема проводит электрический ток, то переменной
ставится в соответствие (другими словами, переменная
принимает) значение 1. Если же при этом наборе состояний реле
схема не проводит электрический ток, то считаем, что переменная у принимает значение 0. Поскольку каждый набор состояний реле
характеризуется набором, составленным из нулей и единиц и имеющим длину
, то данная релейно-контактная схема определяет некоторое правило, по которому каждому такому набору длины
, составленному из нулей и единиц, сопоставляется либо 0, либо 1. Таким образом, каждая релейно-контактная схема, в которой занято
независимых реле (контактов в ней может быть
или больше), определяет некоторую булеву функцию
от
аргументов. Она принимает значение 1 на тех и только тех наборах значений аргументов
, которые соответствуют тем состояниям реле
, при которых данная схема проводит электрический ток. Такая булева функция
называется функцией проводимости данной релейно-контактной схемы.
Таким образом, теория булевых функций предоставляет математические модели реальных физических релейно-контактных схем.
Рассмотрим некоторые релейно-контактные схемы и найдем их функции проводимости. Первая схема состоит из двух последовательно соединенных контактов и
, т. е. контактов, связанных с двумя независимыми реле
и
, каждое из которых срабатывает независимо от другого:
Ясно, что данная схема проводит электрический ток тогда и только тогда, когда оба контакта и
замкнуты, т. е. только тогда, когда оба переменных
и
принимают значение 1. Булева функция от двух аргументов
, удовлетворяющая такому условию, нам хорошо известна. Это конъюнкция
. Таким образом, функцией проводимости релейно-контактной схемы, состоящей из двух последовательно соединенных контактов
и
, является конъюнкция
. Говорят, что последовательное соединение двух контактов реализует конъюнкцию соответствующих этим контактам булевых переменных.
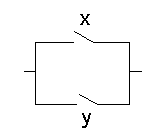
Вторая релейно-контактная схема состоит из двух параллельно соединенных контактов и
Ясно, что эта схема проводит электрический ток в том и только в том случае, когда по меньшей мере один из контактов ( или
) замкнут, т.е. лишь в случае, когда хотя бы одна из булевых переменных (
или
) принимает значение 1. Булева функция от двух аргументов
и
, удовлетворяющая этому условию, также хорошо нам известна. Это, дизъюнкция
. Таким образом, функцией проводимости релейно-контактной схемы, состоящей из двух параллельно соединенных контактов
и
, является дизъюнкция
. Говорят, что параллельное соединение двух контактов реализует дизъюнкцию соответствующих этим контактам булевых переменных.
Итак, с помощью релейно-контактных схем можно реализовывать булевы функции: конъюнкцию, дизъюнкцию и отрицание. Возможна ли аналогичная реализация и других булевых функций? Ответ на поставленный вопрос позволяет дать теорема 10.5. Поскольку всякая булева функция на основании этой теоремы может быть выражена через конъюнкцию, дизъюнкцию и отрицание, причем отрицание стоит лишь непосредственно около переменных и не стоит ни около каких внутренних скобок, а конъюнкция, дизъюнкция и отрицание, как показано только что, реализуются на релейно-контактных схемах, то и всякая булева функция может быть реализована с помощью релейно-контактной схемы, т. е. может быть построена такая схема, для которой данная булева функция служит функцией проводимости.
Реализуем, например, в виде релейно-контактных схем булевы функции — импликацию и эквивалентность. Для этого выразим их через конъюнкцию, дизъюнкцию и отрицание. Такие выражения известны (см. теорему 9.5):
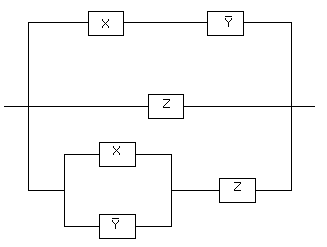
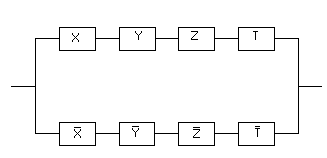
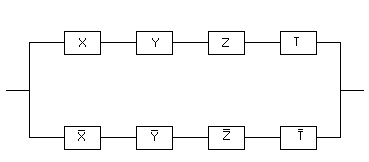
Предлагается самостоятельно нарисовать схему, реализующую функцию . Релейно-контактная схема, реализующая функцию
, будет состоять из двух последовательно соединенных ветвей, первая из которых реализует булеву функцию
, а вторая — булеву функцию
. В свою очередь, первая из ветвей будет состоять из двух параллельных участков, один из которых содержит контакт
, а второй — контакт
. Аналогично, вторая ветвь также будет состоять из двух параллельных участков, один из которых содержит контакт
, а другой — контакт
. Изображаем полученную релейно-контактную схему (чтобы упростить рисунки, не будем изображать сами контакты, а ограничимся символом булевой переменной, соответствующей данному контакту):
Две основные задачи теории релейно-контактных схем
Составление релейно-контактных схем с заданными условиями работы называется задачей синтеза релейно-контактных схем и является первой важной задачей, состоящей в том, что требуется построить схему, которая проводила бы электрический ток лишь при вполне определенных задаваемых условиях.
Естественно было бы выбирать для каждой булевой функции самую простую или одну из самых простых реализующих ее релейно-контактных схем. Поэтому упрощение релейно-контактных схем называется задачей анализа таких схем и является второй важной задачей теории релейно-контактных схем. Две релейно-контактные схемы, составленные из одних и тех же реле, называются равносильными, если одна из них проводит ток тогда и только тогда, когда другая схема проводит ток. Другими словами, две схемы, составленные из одних и тех же реле, равносильны, если они обладают одинаковыми функциями проводимости, зависящими от одних и тех же переменных. Из двух равносильных схем более простой считается та, которая содержит меньшее число контактов. Задача упрощения релейно-контактной схемы состоит в нахождении более простой равносильной ей схемы. Обычно она решается следующим образом. Для данной релейно-контактной схемы записывается ее функция проводимости. Затем эта функция с помощью тождественных преобразований, использующих известные свойства булевых функций, упрощается, т.е. сводится к функции, имеющей меньшее число вхождений переменных, нежели исходная функция. Наконец строится релейно-контактная схема, отвечающая упрощенной булевой функции.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Анализ и синтез релейно-контактных схем
Одно из применений алгебры высказываний – анализ и синтез релейно-контактных схем.
Еще в 1910 году физик П.С. Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-контактных схем. Каждой схеме можно поставить в соответствие некоторую формулу алгебры высказываний, и каждая формула алгебры высказываний реализуется с помощью некоторой схемы.
Рассмотрим 2-х-полюсные переключатели, т.е. такие, которые имеют два состояния: «замкнуто» — 1, «разомкнуто» — 0. На схеме будем изображать:
Определение 7. Переключатель, который сблокирован с X так, что он замкнут, если X разомкнут, и разомкнут, если X замкнут, называется инверсным и обозначается 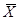
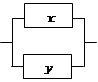
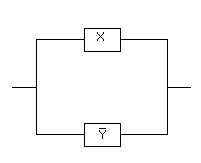
Конъюнкция двух высказываний X и Y будет представлена двухполюсной схемой с последовательным соединением двух переключателей X и Y.
Эта схема пропускает ток тогда и только тогда, когда истины и X, и Y одновременно, то есть истина конъюнкция X&Y.
Дизъюнкция двух высказываний X и Y изобразится двухполюсной схемой с параллельным соединением двух переключателей X и Y.
X 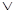
Эта схема пропускает ток в случае, если истинно высказывание X или истинно высказывание Y, то есть истина дизъюнкция X 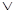
Таким образом, всякую булеву формулу можно трактовать как некоторую последовательно-параллельную схему от 2-х-полюсных переключателей. Все свойства булевых операций переносятся на соответствующие операции над переключателями. Формула, которую можно составить для каждой схемы называется функцией проводимости схемы, а таблица значений – условиями работы схемы.
Определение 8. Две схемы называются равносильными, если имеют одинаковые функции проводимости.
Анализ схемы заключается в следующем: для данной схемы составляется функция проводимости, которая на основании законов булевых функций упрощается и для нее строится новая, более простая схема, которая обладает теми же электрическими свойствами.
Синтез схем заключается в построении схем с заданными электрическими свойствами. На основании заданных электрических свойств строится таблица условий работы схемы и затем функция проводимости, представляющая собой СДНФ, а по ней строится схема.
Задача 1.Составить РКС, обладающая следующей функцией проводимости:
Задача 2.Составить РКС обладающая следующей функцией проводимости:
Задача 3.Составить РКС обладающая следующей функцией проводимости:
Ей соответствует функция проводимости:
F(X,Y,Z)
F(X,Y,Z) 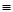
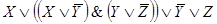
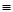
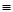
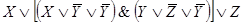
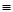
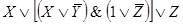
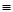
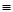
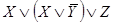
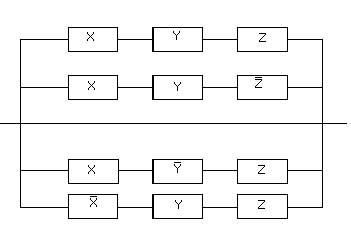
Этой же функции проводимости соответствует более простая схема.
Ей соответствует функция проводимости:
Этой же функции проводимости соответствует более простая схема.
Ей соответствует функция проводимости:
Задача 7.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
Задача 8.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
Задача 9.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
Задача 10.Построить РКС с четырьмя переключателями, которая проводит ток тогда и только тогда, когда замыкаются не все переключатели, а только некоторые из них.
Составим таблицу значений функции проводимости F (X, Y, Z, T) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция F (X, Y, Z, T) обращается в 0, запишем для неё выражение, используя СКНФ, потому что наборов значений аргументов, на которых функция обращается в 0, значительно меньше, чем наборов значений аргументов, на которых функция обращается в 1, и значит, СКНФ будет более простой, чем СДНФ:
Задача 11. Построить схему с тремя переключателями, которая замыкается тогда и только тогда, когда замкнут либо один, либо два переключателя. При построении использовать не более шести контактов.
Составим таблицу значений функции проводимости F (X, Y, Z) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция
F (X, Y, Z, T) обращается в 1, запишем для неё выражение, используя СКНФ, потому что наборов значений аргументов, на которых функция обращается в 0, значительно меньше, чем наборов значений аргументов, на которых функция обращается в 1, и значит, СКНФ будет более простой, чем СДНФ:
Задача 12.Требуется составить схему с четырьмя переключателями X, Y, Z, T. Схема должна проводить ток тогда и только тогда, когда будут замкнуты переключатели X и Y или Z и T.
Составим таблицу значений функции проводимости F (X, Y, Z, T) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция
F (X, Y, Z, T) обращается в 1, запишем для неё выражение, используя СДНФ:
Задача 13.Построить контактную схему для оценки результатов некоторого спортивного соревнования тремя судьями при следующих условиях: судья, засчитывающий результат, нажимает имеющуюся в его распоряжении кнопку, а судья, не засчитывающий результат, кнопки не нажимает. В случае, если кнопки нажали не менее двух судей должна загореться лампочка (положительное решение судей принято простым большинством голосов).
Работа РКС описывается функцией Буля трех переменных F (X, Y, Z), где переменные высказывания X, Y, Z означают:
Таблица истинности функции F (X, Y, Z) имеет вид:
| X Y Z | F(X, Y, Z) |
| 1 1 1 | |
| 1 1 0 | |
| 1 0 1 | |
| 0 1 1 | |
| 1 0 0 | |
| 0 1 0 | |
| 0 0 1 | |
| 0 0 0 |
Этой же функции проводимости соответствует более простая схема.
Источник
Релейно-контактные схемы
Укажем на применение алгебры логики к анализу и синтезу релейно-контактных схем. Среди технических средств автоматизации значительное место занимают устройства релейно-контактного действия. Они находят широкое применение в телефонии, телеуправлении, автоматике и телемеханике, на железнодорожном транспорте, в вычислительной технике. Сейчас при конструировании таких устройств все больше и больше используется алгебра логики. Впервые идея использования алгебры логики для построения автоматических устройств была выдвинута в 1910 году известным физиком П.Эренфестом. Но только в 30-х годах эта идея нашла свое воплощение в работах советского физика В.И. Шестакова, американского математика К.Шеннона и японского инженера А.Накосима.
Контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакт бывает в двух состояниях:
а) контакт разомкнут и тогда ему приписывают 0;

Контакт «не 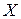
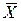
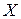
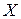
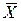
Дизъюнкции 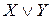
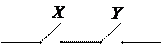
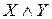
Каждый контакт подключен к некоторому реле. В схеме одинаковыми буквами обозначаются контакты, подключенные к одному и тому же реле. Всей схеме ставится в соответствие булева функция F, которая равна 1, если схема проводит ток, и 0 в противном случае. Эта функция называется функцией проводимости схемы, а ее таблица – условиями работы схемы. Две схемы с одинаковыми функциями проводимости называются равносильными. Средства алгебры высказываний позволяют упрощать схемы, используя отношение равносильности формул алгебры высказываний.
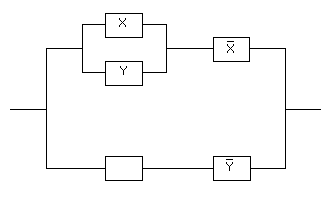
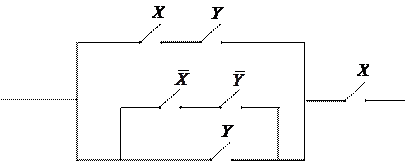
□ По данной схеме запишем формулу, определяющую функцию проводимости, и упростим ее:
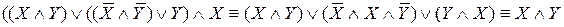
Таким образом, 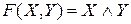
§5. Решение логических задач методами алгебры логики.
Под логической задачей будем понимать задачу, где основным видом деятельности является выявление отношений между объектами задачи, а не нахождение количественных характеристик объектов. Суть применения алгебры логики к решению логических задач состоит в том, что, имея конкретные условия логической задачи, стараются записать их в виде формулы алгебры логики. В дальнейшем путем равносильных преобразований упрощают полученную формулу. Простейший вид формулы, как правило, приводит к ответу на все вопросы задачи.
Покажем на ряде конкретных примеров, как использовать возможности алгебры логики для решения элементарных логических задач.
Пример 1. При составлении расписания уроков на некоторый день учителя просили, чтобы их уроки были:
1. математик – первым или вторым;
2. историк – первым или третьим;
3. литератор – вторым или третьим.
Можно ли удовлетворить просьбы всех учителей?
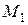
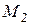
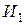
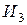
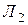
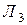
Тогда на языке алгебры эту задачу можно записать в виде формулы , после равносильных преобразований которой можно будет дать ответ на вопрос задачи:
Выяснили, что имеется две возможности:
1. 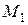
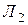
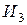
2. 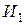
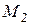
Вопросы для самоконтроля по теме «Логика высказываний»
1. Что понимается под высказыванием? Привести примеры.
2. Являются ли высказываниями следующие предложения:
а) два плюс два равно пяти;
б) функция 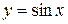
в) существует рациональное число такое, что х > 7.
3. Определить операции отрицания, дизъюнкции, конъюнкции, импликации, эквиваленции и задать их с помощью таблиц истинности.
4. Найти истинностные значения следующих высказываний:
а)
б) 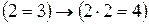
в) 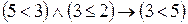
5. Что понимается под формулой алгебры высказываний?
6. Найти значения формул при заданных значениях высказывательных переменных:
а) 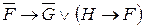
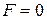
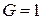
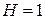
б) 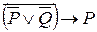
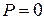
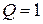
7. Построить таблицу истинности формулы 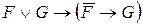
8. Что называется тождественно истинной (ложной) формулой? Проверить, является ли каждая из формул тождественно истинной:
а)
б) 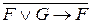
9. Какие формулы называются равносильными? Как доказать равносильность формул? Проверить равносильность
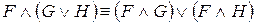
10. Записать первые десять основных равносильностей алгебры высказываний. Доказать законы поглощения и законы де Моргана.
11. Записать законы двойного отрицания; исключения импликации; введения дизъюнкции; введения конъюнкции; замены эквиваленции; контрапозиции; противоположностей; доказательства от противного; транзитивности импликации; транзитивности эквиваленции. Обосновать законы доказательства от противного и закон контрапозиции.
12. Упростить формулу 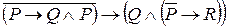
13. Преобразовать формулу 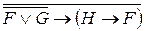
14. Перевести предложение на логический язык и построить его отрицание: «Если вечером я буду не занята, то пойду в кино или на дискотеку».
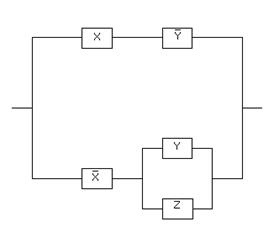
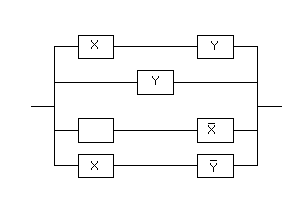
15. Упростить релейно-контактную схему:
16. Ввести понятие функции проводимости для релейно-контактной схемы. Найти функцию проводимости и условия работы для схемы:
17. Один из братьев Витя, Толя, Коля разбил окно. В разговоре участвуют еще двое братьев – Андрей и Дима.
– Это мог сделать только Витя или Толя – сказал Андрей.
– Я окно не разбивал, – возразил Витя, – Коля тоже.
– Вы оба говорите неправду, – заявил Толя.
– Нет, Толя, один из них сказал правду, а другой неправду, – возразил Дима.
–Ты, Дима, неправ, – вмешался Коля.
Их отец, которому, конечно, можно доверять, уверен, что трое братьев сказали правду. Кто разбил окно?
Источник
Библиографическое описание:
Медведева, Я. С. Применение булевых функций к релейно-контактным схемам / Я. С. Медведева. — Текст : непосредственный // Молодой ученый. — 2016. — № 3 (107). — С. 8-11. — URL: https://moluch.ru/archive/107/25480/ (дата обращения: 19.05.2023).
На данный момент наиболее актуальна проблема анализа и синтеза релейно-контактных схем при проектировании различных электронных приборов, в системе водоснабжения. Из этого можно сделать вывод, что методы логического анализа и синтеза релейно-контактных схем находят широкое применение в разных бытовых жизненных ситуациях.
Целью данной статьи является — исследовать применение релейно-контактных схем при решении профессиональных и жизненных ситуаций с помощью обращения к булевым функциям.
Релейно-контактной схемой называется устройство из проводников и двухпозиционных контактов, через которые полюсы источника тока связаны с некоторым потребителем. Контакты могут быть замыкающими и размыкающими. Каждый контакт подключен к некоторому реле (переключателю). Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие контакты разомкнуты; в противном случае — наоборот. Каждому реле ставится в соответствие своя пропозициональная переменная x Она принимает значение 1, если через реле проходит ток, и 0 в противном случае. На чертежах все замыкающие контакты, подключенные к реле x, обозначаются символом x, а размыкающие — символом . Это означает, что при срабатывании реле x все его размыкающие контакты
не проводят ток и им сопоставляется 0. При отключении реле создается противоположная ситуация. Всей схеме также ставится в соответствие булева переменная y, которая равна 1, если схема проводит ток, и 0 в противном случае. Переменная y, соответствующая схеме, очевидно, является булевой функцией от переменных
,
, …,
реле. Эта функция называется функцией проводимости схемы, а ее таблица — условиями работы схемы [1].
В теории релейно-контактных схем важнейшим являются следующие задачи:
задача синтеза релейно-контактных схем — это составление релейно-контактных схем с заданными условиями работы, которые зависят от функций, которые эта схема должна выполнять;
задача анализа релейно-контактных схем — это получение наиболее простой схемы, реализующей данную формулу [2].
Теперь перейдем непосредственно к решению практических задач на применение булевых функций к релейно-контактным схемам.
Задача № 1. Составить схему, позволяющую включать и выключать свет в вашей комнате любым из трех различных выключателей. Выключатели расположены у входа в комнату, над постелью и у письменного стола [3].
Используя условия, которым должна удовлетворять искомая схема, составим сначала таблицу значений функции проводимости F этой схемы. В нее войдут три неизвестных x, y,z, которые будут соответствовать трем выключателям. В последнем столбце таблицы.будем указывать 1, если свет горит и 0, если света нет. Рассмотрим набор переменных (0,0,0) (все выключатели в положении «выключен»), свет в этот момент также не горит — значение функции проводимости F будет равно 0. При наборе переменных (1,1,1) (все выключатели в положении «включен»), свет в этот момент горит — значение функции проводимости F будет равно 1. По условию задачи, при изменении положения любого из выключателей должен загореться свет, то есть на наборах (1,0,0), (0,1,0) и (0,0,1) функция F равна 1. При следующем изменении положения любого из выключателей свет должен выключиться, то есть на наборах (1,1,0), (1,0,1) и (0,1,1) функция F равна 0 (табл.1).
Таблица 1
|
x |
y |
z |
F |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
Зная теперь все наборы значений аргумента, на которых функция F обращается в 1, запишем выражение для нее, используя алгоритм приведения функции к совершенной дизъюнктивной нормальной форме по таблице истинности [2], а уже затем упростим его:
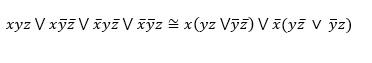
Изображаем релейно-контактную схему, обладающую найденной функцией проводимости (рис.1).Любую схему можно задать формулой алгебры логики, при этом конъюнкции двух высказываний соответствует последовательное соединение двух переключателей, а дизъюнкции двух высказываний — параллельное соединение двух переключателей. При этом ток будет проходить через данные схемы тогда и только тогда, когда истинностное значение соответствующей формулы — «истина» [2].
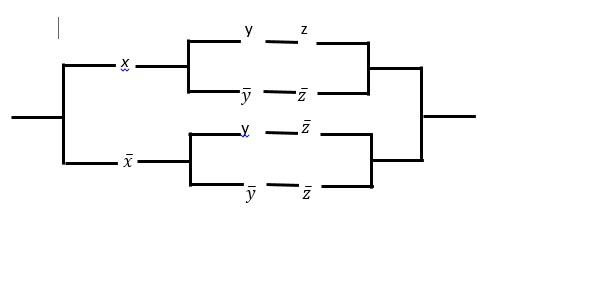
Рис. 1.
Задача № 2.
В спортивном комитете, например заводском, собралось 5 судей. Каждый из них должен голосовать за принятие различных решений. Решение принимается большинством голосов, но только при том дополнительном условии, что за него голосует председатель комитета. Судьи голосуют путем нажатия кнопки, замыкающей переключатель, расположенный под столом, за которым они сидят. Замыкая переключатель, они голосуют «за», размыкая «против». Начертите наиболее простую схему, позволяющую автоматически видеть результаты голосования. В простейшем случае просто с помощью лампочки, — зажглась — решение принято, не зажглась,- нет [3].
Решение.
Используя условия, которым должна удовлетворять искомая схема, составим сначала таблицу значений функции проводимости F этой схемы. В нее войдут пять неизвестных x, y,z,u, t, так как переключатели замыкают пять судей, где x — председатель, его выделяем особо в виду условий задачи. В последнем столбце таблицы указано условие, при котором свет не горит — 0, 1- свет включится (табл. 2).
Таблица 2
|
x |
Y |
z |
u |
t |
F |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
Зная теперь все наборы значений аргумента, на которых функция F обращается в 1, запишем выражение для нее, используя совершенную дизъюнктивную нормальную форму, а уже затем упростим его:
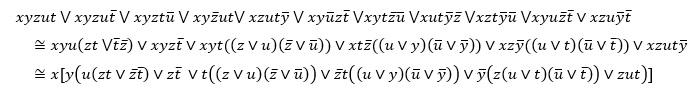
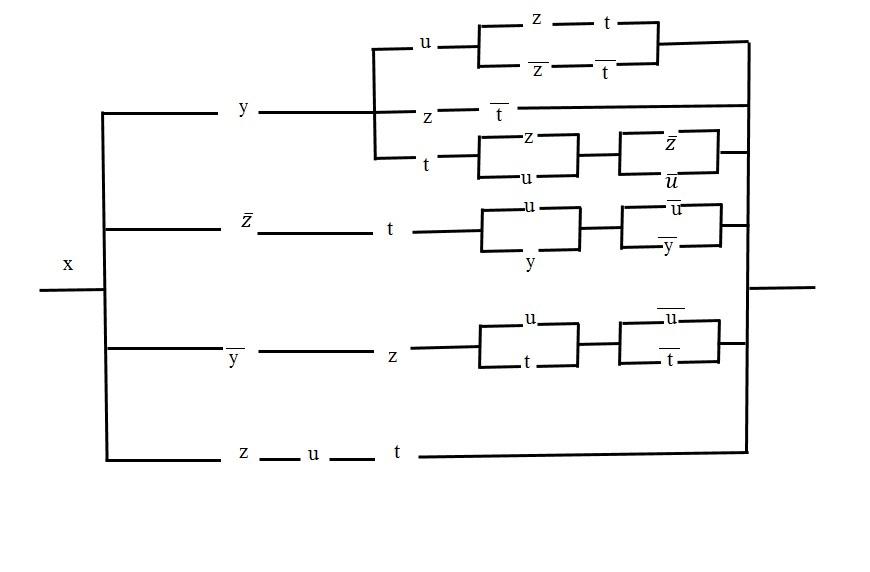
Рис. 2.
Литература:
- Игошин В. И. Задачи и упражнения по математической логике и теории алгоритмов: учеб. пособие для студ. высш. учебн. Заведений/ В. И. Игошин. — 3-е изд., стер. — М.: Издательский центр «Академия», 2007.- 304 с.
- Сангалова М. Е. Курс лекций по математической логике: учеб. пособие / М. Е. Сангалова; ГОУ ВПО, «Арзамас. гос. пед. ин-т им. А. П. Гайдара». Арзамас, 2006. 98 с.
- http://electrik.info/main/fakty/229-buleva-algebra-chast-1-nemnogo-istorii.html
Основные термины (генерируются автоматически): схема, искомая схема, противный случай, свет, функция, значение функции проводимости, последний столбец таблицы, простая схема, релейно-контактная схема, совершенная дизъюнктивная нормальная форма.
Похожие статьи
Анализ существующих алгоритмов перевода функции алгебры…
Рассмотрены существующие алгоритмы перевода функции алгебры логики в вероятностную функцию при
На последнем этапе мы получаем искомую вероятность, т. е
В противном случае удобным оказывается алгоритм наращивания путей, т. к. за счет использования…
Анализ существующих алгоритмов перевода функции алгебры…
Рассмотрены существующие алгоритмы перевода функции алгебры логики в вероятностную функцию при
На последнем этапе мы получаем искомую вероятность, т. е
В противном случае удобным оказывается алгоритм наращивания путей, т. к. за счет использования…
Построение логических схем с использованием Matlab/Simulink…
блок, элемент, свойство блока, логическое умножение, логическое сложение, логическая функция, логическая схема, возможность модификаций, блок Инверсий, XOR.
Построение логических схем с использованием Matlab/Simulink…
блок, элемент, свойство блока, логическое умножение, логическое сложение, логическая функция, логическая схема, возможность модификаций, блок Инверсий, XOR.
Применение электроокулографии для управления указателем…
Работой схемы управляет микроконтроллер. Он используется для настройки работы схемы, для обработки поступающей информации, а также для отсылки ее по протоколу
Таким образом, описанное устройство является портативным, простым в реализации и относительно недорогим.
Применение электроокулографии для управления указателем…
Работой схемы управляет микроконтроллер. Он используется для настройки работы схемы, для обработки поступающей информации, а также для отсылки ее по протоколу
Таким образом, описанное устройство является портативным, простым в реализации и относительно недорогим.
Логические схемы и таблицы в обучении истории
Схемы и таблицы на уроках истории помогают выделить главное, они «запирают» информацию в замкнутое пространство. При составлении схем, таблиц ученик совершает логические операции: анализ, синтез, сравнение…
Логические схемы и таблицы в обучении истории
Схемы и таблицы на уроках истории помогают выделить главное, они «запирают» информацию в замкнутое пространство. При составлении схем, таблиц ученик совершает логические операции: анализ, синтез, сравнение…
Формирование логического мышления учащихся через…
Итак, вопрос использования интерактивных опорных схем на уроках математики имеет большое практическое значение для современной школы.
Введем новую переменную . Тогда первое уравнение системы можно будет переписать в более простом виде: с+ ‑2,5=0. Решим это…
Формирование логического мышления учащихся через…
Итак, вопрос использования интерактивных опорных схем на уроках математики имеет большое практическое значение для современной школы.
Введем новую переменную . Тогда первое уравнение системы можно будет переписать в более простом виде: с+ ‑2,5=0. Решим это…
Расчет переходных процессов при помощи классического…
Рассмотрим электрическую схему. Рис. 1. Схема цепи.
Операторный метод анализа позволяет сводить линейные дифференциальные уравнения к более простым алгебраическим уравнениям, что в ряде случаев упрощает расчеты.
Расчет переходных процессов при помощи классического…
Рассмотрим электрическую схему. Рис. 1. Схема цепи.
Операторный метод анализа позволяет сводить линейные дифференциальные уравнения к более простым алгебраическим уравнениям, что в ряде случаев упрощает расчеты.
Анализ уязвимости переполнения буфера | Статья в журнале…
В качестве адреса выбирается какой-либо элемент таблицы GOT, соответствующий функции, которая будет в дальнейшем вызываться программой.
В самом простейшем случае шеллкод может разместиться в буфере уязвимой программы.
Анализ уязвимости переполнения буфера | Статья в журнале…
В качестве адреса выбирается какой-либо элемент таблицы GOT, соответствующий функции, которая будет в дальнейшем вызываться программой.
В самом простейшем случае шеллкод может разместиться в буфере уязвимой программы.
Формальная логика в инженерной деятельности
С тех пор логика высказываний успешно применяется в теории электрических цепей, в частности при исследовании релейно–контактных схем [6, 12, 14]. Действительно, любой параллельно-контактной схеме можно поставить в соответствие логическую формулу…
Формальная логика в инженерной деятельности
С тех пор логика высказываний успешно применяется в теории электрических цепей, в частности при исследовании релейно–контактных схем [6, 12, 14]. Действительно, любой параллельно-контактной схеме можно поставить в соответствие логическую формулу…
Похожие статьи
Анализ существующих алгоритмов перевода функции алгебры…
Рассмотрены существующие алгоритмы перевода функции алгебры логики в вероятностную функцию при
На последнем этапе мы получаем искомую вероятность, т. е
В противном случае удобным оказывается алгоритм наращивания путей, т. к. за счет использования…
Анализ существующих алгоритмов перевода функции алгебры…
Рассмотрены существующие алгоритмы перевода функции алгебры логики в вероятностную функцию при
На последнем этапе мы получаем искомую вероятность, т. е
В противном случае удобным оказывается алгоритм наращивания путей, т. к. за счет использования…
Построение логических схем с использованием Matlab/Simulink…
блок, элемент, свойство блока, логическое умножение, логическое сложение, логическая функция, логическая схема, возможность модификаций, блок Инверсий, XOR.
Построение логических схем с использованием Matlab/Simulink…
блок, элемент, свойство блока, логическое умножение, логическое сложение, логическая функция, логическая схема, возможность модификаций, блок Инверсий, XOR.
Применение электроокулографии для управления указателем…
Работой схемы управляет микроконтроллер. Он используется для настройки работы схемы, для обработки поступающей информации, а также для отсылки ее по протоколу
Таким образом, описанное устройство является портативным, простым в реализации и относительно недорогим.
Применение электроокулографии для управления указателем…
Работой схемы управляет микроконтроллер. Он используется для настройки работы схемы, для обработки поступающей информации, а также для отсылки ее по протоколу
Таким образом, описанное устройство является портативным, простым в реализации и относительно недорогим.
Логические схемы и таблицы в обучении истории
Схемы и таблицы на уроках истории помогают выделить главное, они «запирают» информацию в замкнутое пространство. При составлении схем, таблиц ученик совершает логические операции: анализ, синтез, сравнение…
Логические схемы и таблицы в обучении истории
Схемы и таблицы на уроках истории помогают выделить главное, они «запирают» информацию в замкнутое пространство. При составлении схем, таблиц ученик совершает логические операции: анализ, синтез, сравнение…
Формирование логического мышления учащихся через…
Итак, вопрос использования интерактивных опорных схем на уроках математики имеет большое практическое значение для современной школы.
Введем новую переменную . Тогда первое уравнение системы можно будет переписать в более простом виде: с+ ‑2,5=0. Решим это…
Формирование логического мышления учащихся через…
Итак, вопрос использования интерактивных опорных схем на уроках математики имеет большое практическое значение для современной школы.
Введем новую переменную . Тогда первое уравнение системы можно будет переписать в более простом виде: с+ ‑2,5=0. Решим это…
Расчет переходных процессов при помощи классического…
Рассмотрим электрическую схему. Рис. 1. Схема цепи.
Операторный метод анализа позволяет сводить линейные дифференциальные уравнения к более простым алгебраическим уравнениям, что в ряде случаев упрощает расчеты.
Расчет переходных процессов при помощи классического…
Рассмотрим электрическую схему. Рис. 1. Схема цепи.
Операторный метод анализа позволяет сводить линейные дифференциальные уравнения к более простым алгебраическим уравнениям, что в ряде случаев упрощает расчеты.
Анализ уязвимости переполнения буфера | Статья в журнале…
В качестве адреса выбирается какой-либо элемент таблицы GOT, соответствующий функции, которая будет в дальнейшем вызываться программой.
В самом простейшем случае шеллкод может разместиться в буфере уязвимой программы.
Анализ уязвимости переполнения буфера | Статья в журнале…
В качестве адреса выбирается какой-либо элемент таблицы GOT, соответствующий функции, которая будет в дальнейшем вызываться программой.
В самом простейшем случае шеллкод может разместиться в буфере уязвимой программы.
Формальная логика в инженерной деятельности
С тех пор логика высказываний успешно применяется в теории электрических цепей, в частности при исследовании релейно–контактных схем [6, 12, 14]. Действительно, любой параллельно-контактной схеме можно поставить в соответствие логическую формулу…
Формальная логика в инженерной деятельности
С тех пор логика высказываний успешно применяется в теории электрических цепей, в частности при исследовании релейно–контактных схем [6, 12, 14]. Действительно, любой параллельно-контактной схеме можно поставить в соответствие логическую формулу…
Карта Карно представляет собой таблицу для задания логических функций в СДНФ. Например, для функции, заданной табл. 5, карта Карно представлена в табл. 6.
Расположение клеток в таблице позволяет легко определить склеивающиеся между собой члены, так как каждой клетке карты Карно соответствует вершина куба. Допускающие склеивание конституенты располагаются в соседних ячейках по строкам и столбцам, или в виде квадратов и им соответствует одна импликанта, ранг которой меньше, чем ранги склеиваемых конституент. Заметим, что соседними считаются не только рядом стоящие ячейки, но и ячейки, находящиеся на противоположных концах любого столбца и любой строки.
Таблица 6
Так, склеивая конституенты, расположенные во второй и третьей строках табл. 6, получаем импликанту – – X2, а конституентам двух последних строк соответствует импликанта Х1 – -. Следовательно, минимальная форма заданной булевой функции имеет вид (см. пример 16)
.
Пример 17. Минимизировать с помощью карты Карно функцию f(X1, Х2, Ч3), заданную табл. 4.
Решение. Построим для минимизирующую карту (табл. 7)
Таблица 7
Объединим соседние клетки, соответствующие единичным значениям функции f, в максимальные интервалы, как показано в табл. 7. Сопоставим каждому максимальному интервалу импликанты Ч1 и . Следовательно, минимальная форма имеет вид:
.
Пример 18. Минимизировать булеву функцию
.
Решение. Используя таблицы истинности, построим для заданной функции f карту Карно (табл. 8).
Объединим соседние клетки, соответствующие единичному значению функции, в максимальные интервалы, как показано в табл. 8. Следовательно, минимальная форма данной функции имеет вид
Таблица 8
.
Если булева функция f зависит от четырех аргументов, то с помощью минимизирующей карты можно находить сокращенную ДНФ.
Пример 19. Пусть функция f(X1, X2, Х3, Х4) задана та6л. 9. Построить сокращенную ДНФ.
Решение. Максимальные интервалы, соединяющие клетки, соответствующие единичным значениям функции f, выбираются так, как показано в табл. 9. Сопоставляя им простые импликанты, получим сокращенную ДЗЦ.
Таблица 9
Построение оптимальных контактно-релейных схем
Проблема проектирования логических схем сводится к отысканию оптимальной эквивалентной схемы, состоящей из возможно меньшего числа элементов. С математической точки зрения эта проблема сводится к задаче минимизации булевой функции, соответствующей заданной схеме. Для построения оптимальной схемы необходимо сделать следующее.
1. По заданной схеме составить соответствующую ей булеву функцию.
2. Привести эту функцию к ДНФ.
3. Минимизировать записанную в ДНФ булеву функцию одним из описанных выше способов
4. Построить релейно-контактную схему, соответствующую минимальной ДНФ.
Приведем примеры.
Пример 20. Построить оптимальную релейно-контактную схему, эквивалентную схеме на рис. l0.
2
Решение.
1. Составим по этой схеме булеву функцию
.
2. Эта функция записана в ДНФ, поэтому предварительных ее преобразований не требуется.
3. Склеиваем первый член с третьим:
.
4. Строим релейно-контактную схему, соответствующую полученной функции:
2
В упрощенной схеме вместо 9 контактов исполь-зу-ют-ся только 5.
Пример 21. Построить оптимальную релейно-контактную схему, эквивалентную схеме на рис. 12.
2
Решение.
1. Заданной схеме соответствует булева функция
.
2. Представим эту функцию в ДНФ
.
3. Склеивая второй член с четвертым, а затем проводя операцию поглощения, получим
.
4. Строим оптимальную релейно-контактную схему (рис. 13).
2
Упражнения
1. Минимизировать с помощью карт Карно следующие булевы функции:
а)
;
б) ;
в)
;

д) ;
е) .
2. Минимизировать булевы функции методом Квайна:
а) ;
б)
;
в)
;
г)
.
3. Построить для булевой функции модель куба и минимизировать её. Функция f задана табл. 10, 11, 12.
Таблица 10
|
X1 |
X2 |
X3 |
f(X1,X2,X3) |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Таблица 11
|
X1 |
X2 |
X3 |
f(X1,X2,X3) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Таблица 12
|
X1 |
X2 |
X3 |
f(X1,X2,X3) |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
4. Построить для булевой функции f(X1,X2,X3), записанной в СДНФ, модель куба и минимизировать функцию f:
a) ;
б) ;
в) .
5. Для заданной модели куба (рис. 14 а, б, в) записать булеву функцию в СДНФ и минимизировать её.
6. Построить оптимальные контактно-релейные схемы для схем, заданных на рис. 15-18.
2
2
2
2