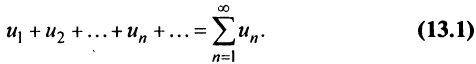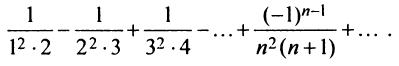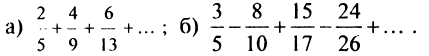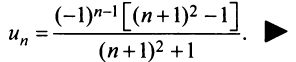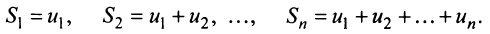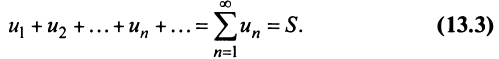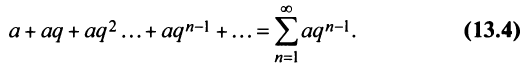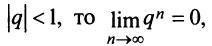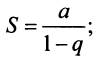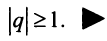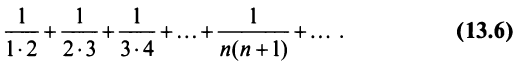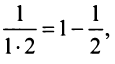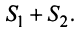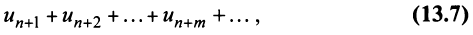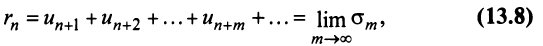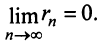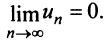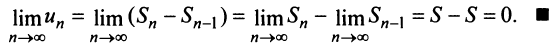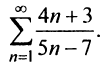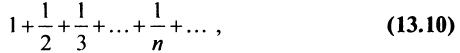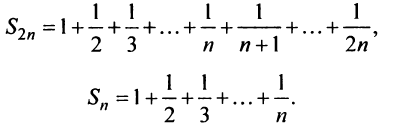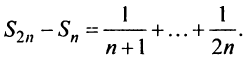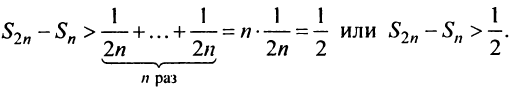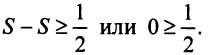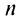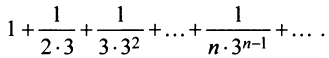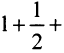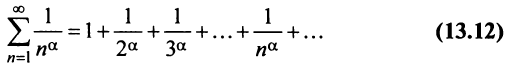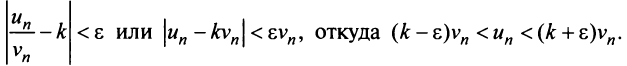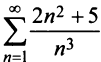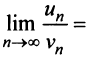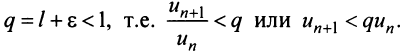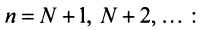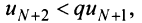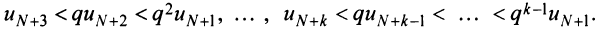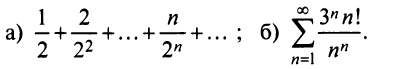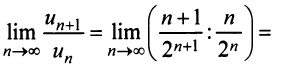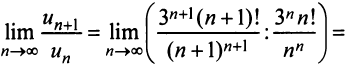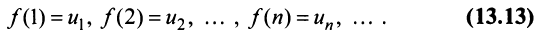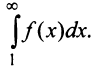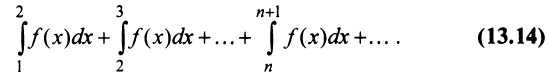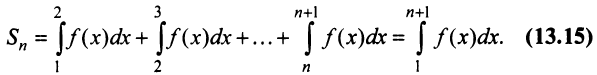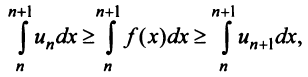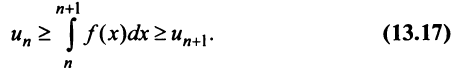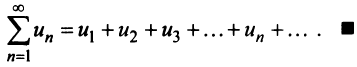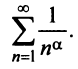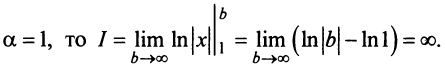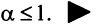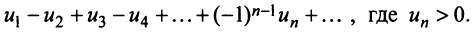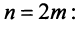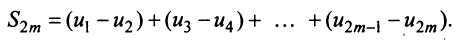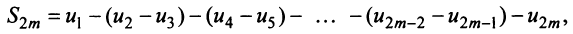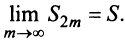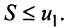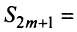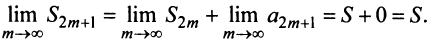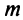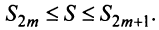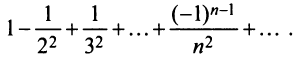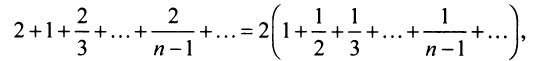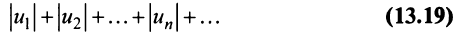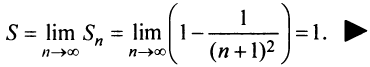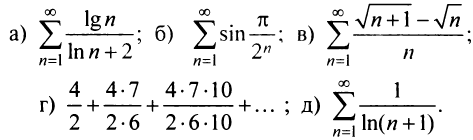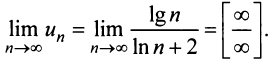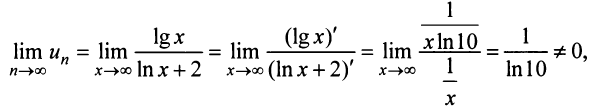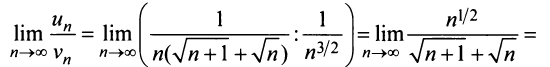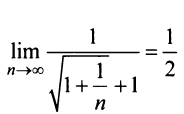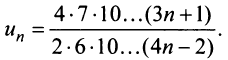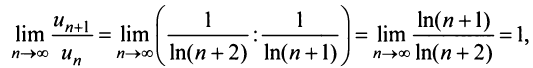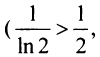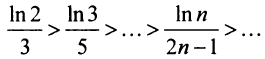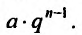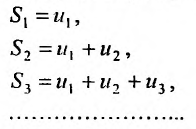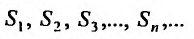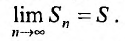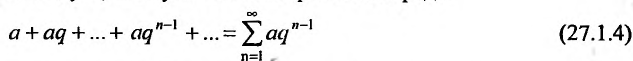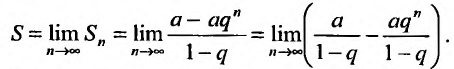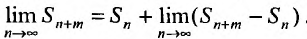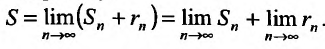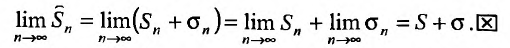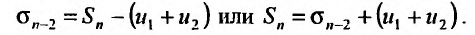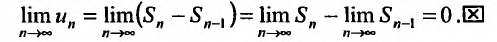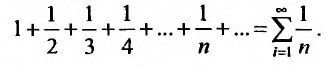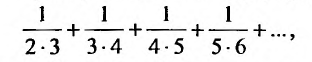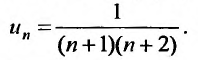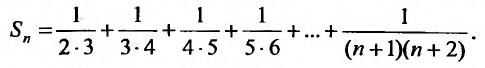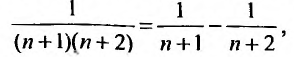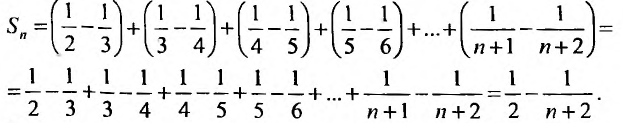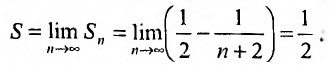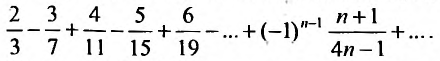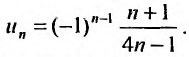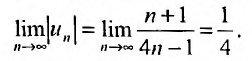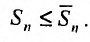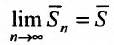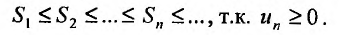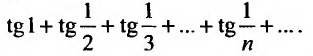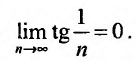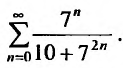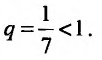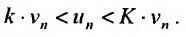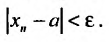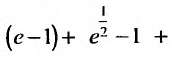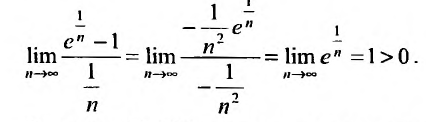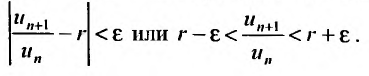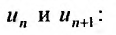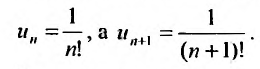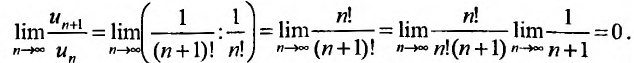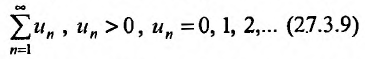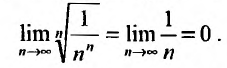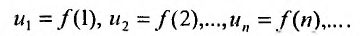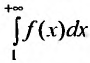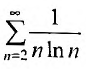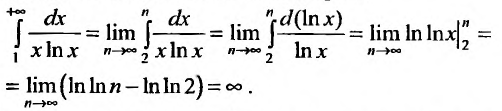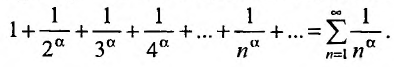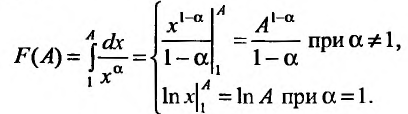Содержание:
Числовые ряды:
При решении ряда математических задач, в том числе и в приложениях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Из теории действительных чисел известно лишь, что означает сумма любого конечного числа чисел. Задача суммирования бесконечного множества слагаемых решается в теории рядов.
Основные понятия. Сходимость ряда
Определение. Числовым рядом называется бесконечная последовательность чисел
Числа 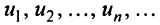
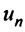
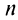
Ряд (13.1) считается заданным, если известен его общий член 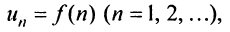
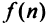
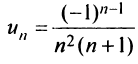
Более сложной является обратная задача: по нескольким первым членам ряда написать общий член. Эта задача имеет бесконечно много решений, но иногда удается найти самое естественное решение.
Пример:
Найти в простейшей форме общий член ряда:
Решение:
Нетрудно убедиться, что для ряда а) общий член 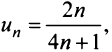
Рассмотрим суммы конечного числа членов ряда:
Сумма п первых членов ряда 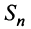
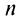
Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.
Число 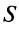
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
Пример:
Исследовать сходимость геометрического ряда, т.е. ряда, составленного из членов геометрической профессии
Решение:
Необходимо установить, при каких значениях знаменателя профессии 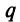
Из школьного курса алгебры известно, что сумма 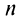
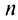
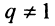
Возможно несколько случаев:
1) если
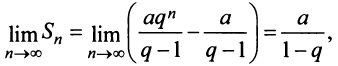
2) если 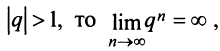
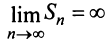
3) если 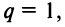
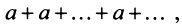
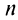
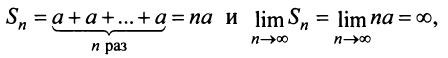
4) если 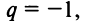
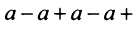
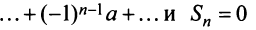
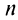
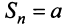
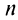
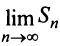
Таким образом, геометрический ряд сходится к сумме 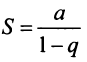
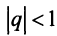
Пример:
Найти сумму ряда
Решение:
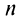
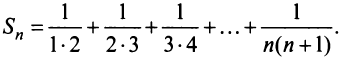
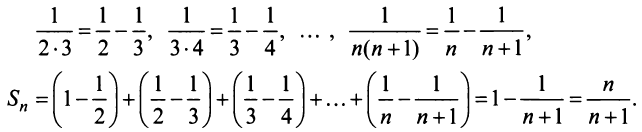
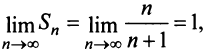
Свойства сходящихся рядов. 1. Если ряд 
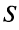
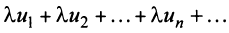
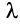
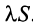
2. Если ряды 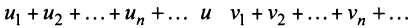
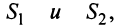
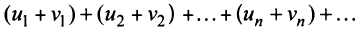
Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.
3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
Пусть в сходящемся ряде (13.1) отброшены 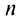
имеющий частичную сумму 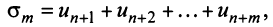
Очевидно, что 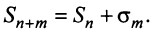
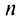
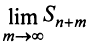
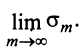
Ряд (13.7), полученный из данного отбрасыванием его первых 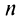
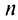
Если сумму 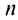
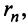
то сумму ряда (13.1) можно представить в виде
В результате мы подошли к свойству 4.
4. Для того чтобы ряд (13.1) сходился, необходимо и достаточно, чтобы при 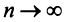
Это свойство вытекает из теоремы о связи бесконечно малых с пределами функций (см. § 6.3).
Установить сходимость (расходимость) ряда путем определения 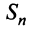
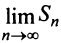
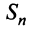
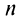
Необходимый признак сходимости. Гармонический ряд
Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена 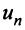

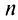
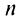
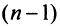
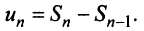
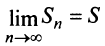
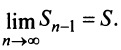
Пример №1
Проверить выполнение необходимого признака для ряда (13.6).
Решение:
Выше было доказано, что ряд (13.6) сходится, и действительно 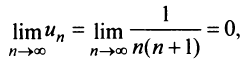
Следствие. Если предел общего члена ряда (13.1) при 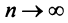
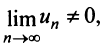
Предположим противное, т.е. ряд (13.1) сходится. Но в этом случае из приведенной выше теоремы следует 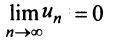
Пример №2
Исследовать сходимость ряда
Решение:
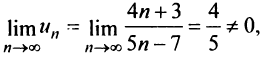
Замечание. Следует подчеркнуть, что рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если 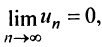
В качестве примера рассмотрим ряд
называемый гармоническим.
Необходимый признак сходимости выполнен: 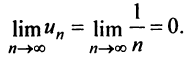

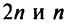
Найдем разность
Заменяя в сумме каждое слагаемое наименьшим, равным 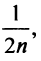
Предположим противное, т.е. что гармонический ряд сходится, тогда 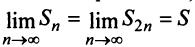
Мы пришли к противоречию, следовательно, наше предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится. ■
В следующих двух параграфах рассмотрим достаточные признаки сходимости.
Ряды с положительными членами
Теорема (признак сравнения). Пусть даны два ряда с положительными членами: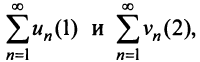
Тогда: а) если сходится ряд 2, то сходится и ряд 1; б) если расходится ряд 1, то расходится и ряд 2.

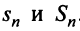
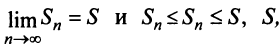
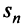
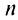
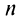
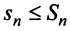
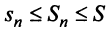
Следовательно, на основании признака существования предела (см. § 6.5) последовательность 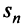
б) Применим метод доказательства от противного. Предположим, что ряд 2 сходится. Тогда согласно первой части теоремы сходится и ряд 1, что противоречит предположению; т.е. ряд 2 расходится. ■
Замечание. Так как сходимость ряда не изменяется при отбрасывании конечного числа членов ряда, то условие (13.11) не обязательно должно выполняться с первых членов рядов и только для членов с одинаковыми номерами 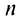
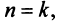
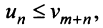
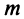
Пример №3
Исследовать сходимость ряда
Решение:
Сравним данный ряд со сходящимся геометрическим рядом 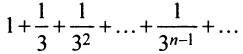
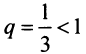
Так как члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда 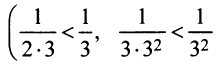
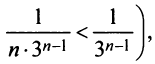
Пример №4
Исследовать сходимость ряда
Решение:
Сравним данный ряд с гармоническим 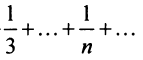
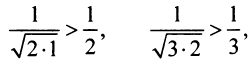
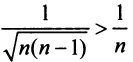
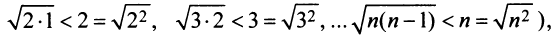
сходится при 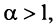
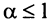
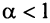
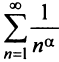
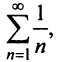
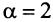
Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (13.11), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т.п.). В ряде случаев более простым оказывается предельный признак сравнения.
Теорема (предельный признак сравнения)
Теорема (предельный признак сравнения). Если 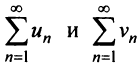
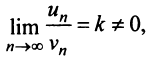

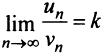
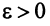
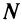
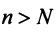
Если ряд 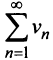
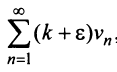
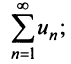
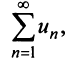
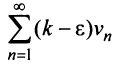
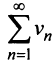
Пример №5
Исследовать сходимость ряда
Решение:
Сравним данный ряд с расходящимся гармоническим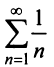
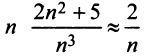
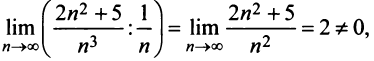
Весьма удобным на практике является признак Даламбера.
Теорема (признак Даламбера)
Теорема (признак Даламбера). Пусть для ряда 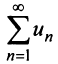
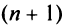
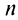
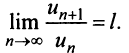
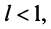
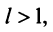
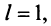
Из определения предела последовательности следует, что для любого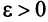
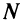
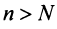
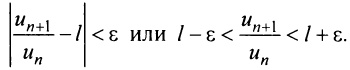
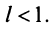
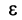
Последнее неравенство будет выполняться для всех 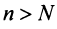
Получили, что члены ряда 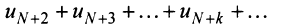
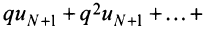
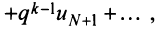
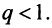
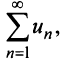
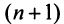
2) Пусть 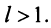
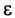
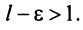
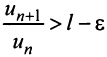
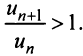
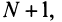
Пример №6
Исследовать сходимость рядов:
Решение:
а) Так как 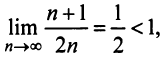
б) Так как
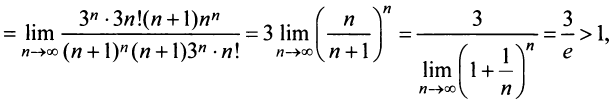
Замечание 1. Если 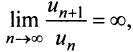
Замечание 2. Если 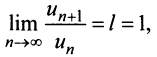
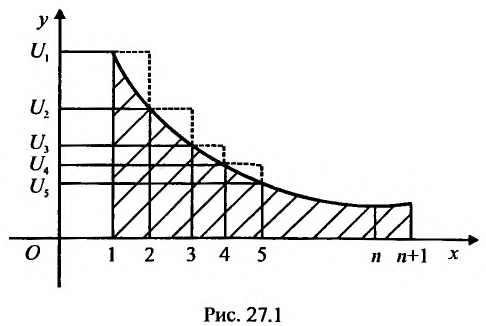
Теорема (интегральный признак сходимости)
Теорема (интегральный признак сходимости). Пусть дан ряд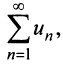

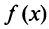
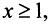
Тогда для сходимости ряда 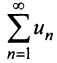
Рассмотрим ряд
Его 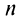
Сходимость ряда (13.14) означает существование предела последовательности его частичных сумм (13.15), т.е. сходимость несобственного интеграла 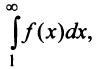
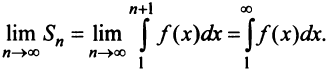
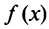
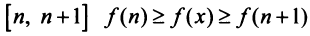
Интегрируя (13.16) на отрезке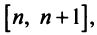
откуда
Если ряд 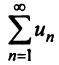
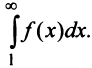
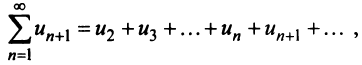
Пример №7
Исследовать сходимость обобщенного гармонического ряда
Решение:
Пусть 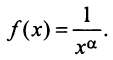
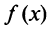
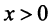
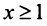
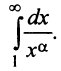
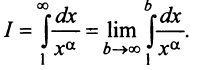
Если 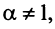
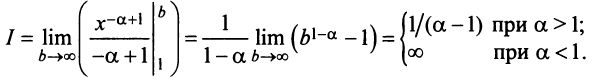
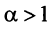
Ряды с членами произвольного знака
Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 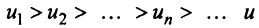
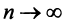
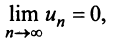
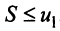
Рассмотрим последовательность частичных сумм четного числа членов при
Эта последовательность возрастающая (так как с ростом 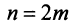
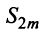
откуда следует, что 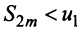
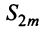
Попутно заметим, что, переходя к пределу в неравенстве 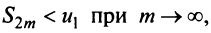
Теперь рассмотрим последовательность частичных сумм нечетного числа членов при 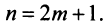
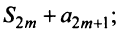
Итак, при любом 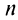
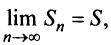
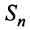
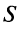
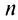
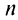
Из рис. 13.1 вытекает еще одна оценка для суммы 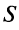
Пример №8
Исследовать сходимость ряда
Решение:
Так как члены знакочередующегося ряда убывают по абсолютной величине 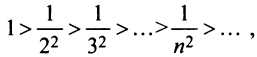
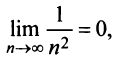
Замечание. В теореме Лейбница существенно не только условие 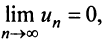
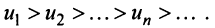
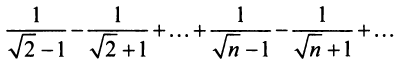
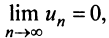
т.е. «удвоенного» гармонического ряда.
Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.
По формуле (13.9) сумму сходящегося ряда можно представить как сумму 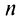
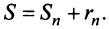
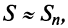
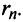
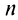
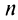
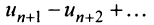
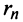
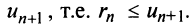
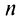
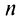
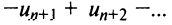
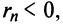
Пример №9
Какое число членов ряда 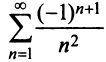
Решение:
По условию 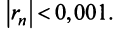
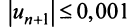
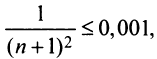
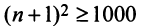
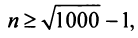
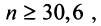
Знакопеременные ряды. Пусть 
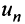
Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного ряда (13.1)
сходится, то сходится и данный ряд.
Обозначим 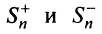
Тогда частичная сумма данного ряда 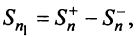
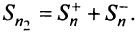
Последовательности 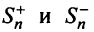
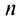
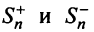
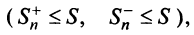
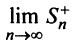
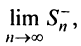
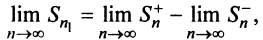
Следует отметить, что обратное утверждение неверно. Ряд (13.19) может расходиться, а ряд (13.1) сходиться. Например, ряд 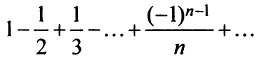
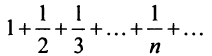
Поэтому введем следующие определения.
Определение 1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.
Определение 2. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Таким образом, рассмотренный выше ряд 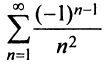
Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся — в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.
Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.
Условно сходящиеся ряды такими свойствами не обладают.
Возьмем, например, ряд 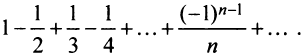
Перепишем ряд в виде:
т.е. от перестановки членов ряда сумма его уменьшилась в 2 раза.
Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
Пример №10
Найти сумму ряда 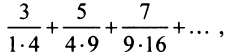
Решение:
Очевидно, что общий член ряда
Представим сумму 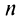
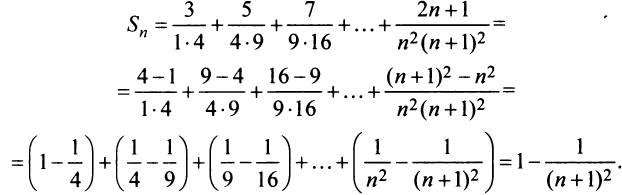
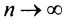
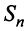
Пример №11
Исследовать сходимость ряда:
Решение:
а) Проверим выполнение необходимого признака сходимости, найдя предел общего члена:
Для вычисления предела отношения двух бесконечно больших функций натурального аргумента правило Лопиталя непосредственно применять нельзя, ибо для таких функций не определено понятие производной. Поэтому применяя теорему о «погружении» дискретного аргумента 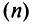
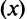
следовательно, ряд расходится.
б) Очевидно, что задан ряд с положительными членами, так как 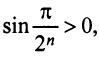
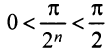
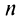
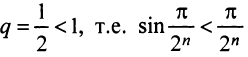
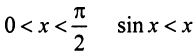
в) Представим общий член ряда в виде
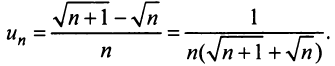
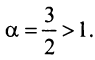
есть конечное число, не равное нулю, то данный ряд, так же как и «эталонный», сходится.
г) Применим признак Даламбера, заметив, что общий член ряда 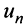
Тогда 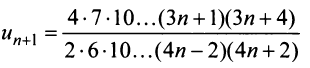
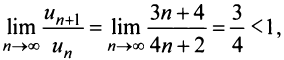
д) Применим признак Даламбера:
т.е. вопрос о сходимости ряда остается открытым. Проверим выполнение необходимого признака (с этого можно было начать исследование): 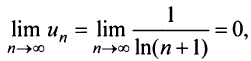
Применим признак сравнения в более простой предельной форме. Сравним данный ряд, например, с гармоническим.
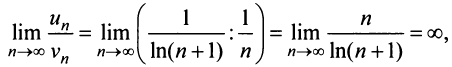
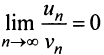
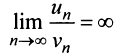
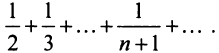
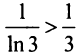
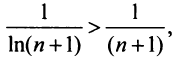
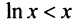
Пример №12
Исследовать сходимость ряда:
Решение:
а) Предел общего члена ряда 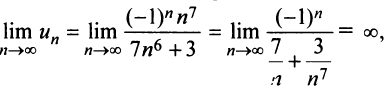
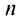
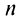
б) Так как члены знакочередующегося ряда, начиная со второго, убывают по абсолютной величине —
и предел общего члена 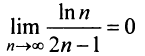
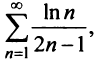
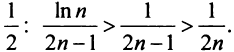
в) Ряд, составленный из абсолютных величин членов данного ряда, сходится, так как его члены меньше членов сходящегося ряда (13.12) при 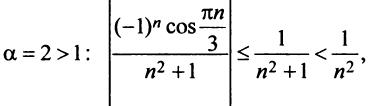
Определение ряда и его сходимость
Пусть
бесконечная последовательность чисел.
Определение 27.1.1. Выражение
называется числовым рядом, а элементы последовательности 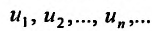
Поскольку выражение (27.1.2) рассматривается как единое целое, то для задания ряда необходимо задать каждый его член 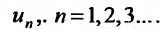
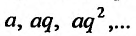
Припишем теперь определенный смысл выражению (27.1.2), т.е. введем определение.
Определение 27.1.2. Сумма n первых членов ряда (27.1.2) 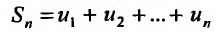
Ясно, что первая, вторая, третья и т.д. частичные суммы ряда
составляют бесконечную последовательность:
Определение 27.1.3. Ряд (27.1.2) называется сходящимся, если последовательность 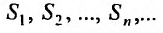
Значение S этого предела называется суммой ряда (27.1.2). Ряд (27.1.2) называется расходящимся, если последовательность его частичных сумм предела не имеет (например, если члены последовательности возрастают по модулю неограниченно).
Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов.
В принципе можно доказывать сходимость или расходимость каждого ряда, а также вычислять сумму сходящегося ряда, опираясь непосредственно на определения сходимости и суммы. Для этого в каждом случае составляется аналитическое выражение для n- ой частичной суммы ряда и находится предел этого выражения при возрастании n.
Пример:
Для ряда 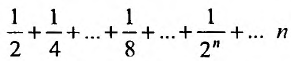
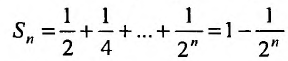
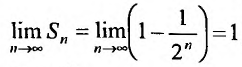
Пример:
Последовательность вида
называется геометрической прогрессией, где а – первый член, а
q – её знаменатель; выражение 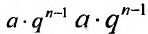
Числовой ряд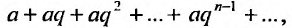
Если в прогрессии (27.1.3) имеется только конечное число членов, то прогрессия называется конечной; в противном случае, если за каждым членом прогрессии следует ещё хотя бы один член, то прогрессия называется бесконечной.
В случае конечной прогрессии 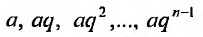
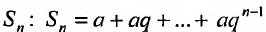
Известно, что при 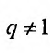
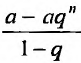
называется предел её частичных сумм 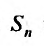
Так как а и q от n не зависят, то последнюю формулу представим в виде:
Если 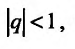
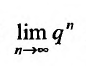
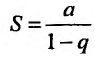
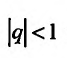
но, сходится и ряд (27.1.4). Если же 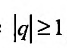
Итак, мы привели примеры, в которых исследование сходимости рядов проводили, применяя определение 27.1.3., т.е. вычисляли частичные суммы и находили предел их последовательностей. Ясно, что в общем случае, составление аналитического выражения для n- ой частичной суммы трудный вопрос. Кроме того, при исследовании рядов нередко значения сумм не представляют интереса, т.к. нужно определить только сходится ряд или нет. Поэтому представляют интерес методы анализа рядов, когда не требуется вычислять суммы рядов. Далее перейдем к изложению таких методов.
Свойства сходящихся рядов
Пусть дан ряд
Определение 27.2.1. Ряд 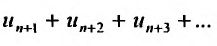
Очевидно, m- я частичная суммаn -го остатка ряда равна разности 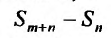
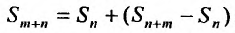
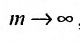
Предел слева есть сумма исходного ряда, а предел справа-сумма 
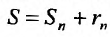
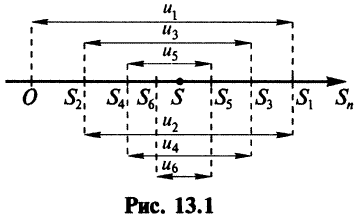
Теорема 27.2.1. Если ряд (27.2.1) сходится, то сумма его n-го остатка с ростом n стремится к нулю.
Доказательство. Выше показано, что 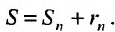
Но для сходящегося ряда 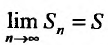
Рассмотрим теперь свойства сходящихся рядов, которые позволяют действовать с ними, как с конечными суммами.
Теорема 27.2.2. Если ряд
имеет сумму S, то ряд
полученный из предыдущего умножением всех членов на одно и тоже число a, имеет сумму aS.
Доказательство. Обозначим последовательность частичных сумм ряда (27.2.2) 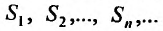
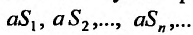
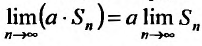
(27.2.2) сходится, то 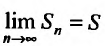
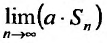
Теорема 27.2.3. Если ряды
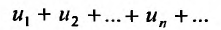
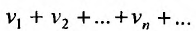
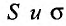
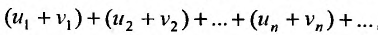
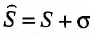
Доказательство. Пусть 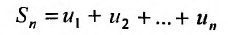
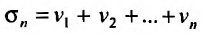
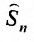
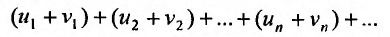
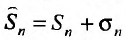
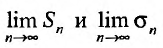
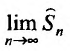
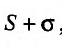
Следствие. Разность двух сходящихся рядов-ряд сходящийся.
Теорема 27.2.4. Свойства сходимости или расходимости ря-,ki не нарушается, если в ряде исключить или приписать к нему любое конечное число членов.
Доказательство. Пусть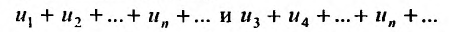
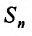
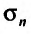
Из этого равенства следует, что, если 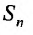
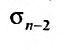
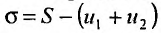
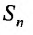
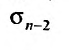
Теорема 27.2.5. (Необходимое условие сходимости ряда). Если ряд 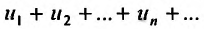
Доказательство. Пусть ряд 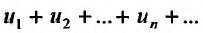
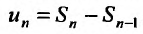
Отметим, что условие (27.2.4) не является достаточным, т.е. общий член может стремиться к нулю, но ряд все же может быть расходящимся. Но если общий член ряда не стремится к нулю, то ряд будет расходящийся.
- Заказать решение задач по высшей математике
Пример №13
Исследуем на сходимость гармонический ряд
Решение:
Вначале находим предел общего члена: 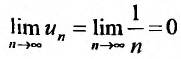
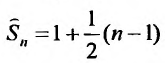
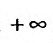
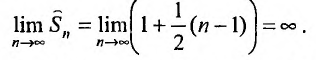
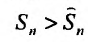
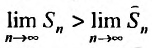
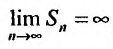
Пример №14
Найти формулу для общего члена ряда
считая, что каждый его последующий член определяется по тому же закону, по которому образованы записанные члены, и найти ею сумму.
Решение:
Каждый член данного ряда представляет собой дробь, числитель которой равен 1, а знаменатель равен произведению двух последовательных натуральных чисел 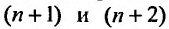
Для вычисления суммы ряда составим n -ую частичную сумму:
Представим выражение для общего члена в виде разности:
тогда
Переходя к пределу, получаем сумму ряда:
Пример №15
Исследовать сходимость ряда
Решение:
Общий член ряда определяется формулой
Вычислим предел модуля общего члена:
Так как предел общего члена не стремится к нулю, то ряд расходится.
Признаки сходимости числовых знакоположительных рядов
Рассмотрим числовые ряды с положительными членами. Существует много приёмов, называемых признаками сходимости, позволяющих установить сходимость или расходимость числовых рядов Так мы познакомились с методом исследования сходимости ряда на основании выяснения имеет ли предел последовательность частичных сумм. Стремление к нулю члена ряда по мерс роста его номера также является признаком сходимости, хотя только необходимым. Ниже мы приведём ряд достаточных признаков сходимости.
Признаки сравнения
Теорема 27.3.1. (I признак сравнения). Пусть
и
два ряда, причём члены первого ряда, начиная с некоторого номера k , не превосходят соответствующих членов второго
Тогда из сходимости ряда (27.3.2) следует сходимость ряда (27.3.1), а из расходимости ряда (27.3.1) следует расходимость ряда (27.3.2).
Доказательство. Так как исключение конечного числа членов ряда не влияет на его сходимость (теорема 27.2.4.), то достаточно доказать теорему для случая когда неравенства (27.3.3) выполняются для k = 1.
Пусть 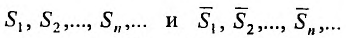
Пусть ряд (27.3.2) сходится. Тогда сходится соответствующая последовательность частичных сумм ряда (27.3.2), т.е.
Поскольку выполняются неравенства (27.3.3), то члены последовательности частичных сумм ряда (27.3.1) удовлетворяют неравенству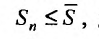
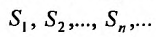
Поэтому, в силу признака Больцано-Всйсрштраса, последовательность частичных сумм ряда (27.3.1) сходится. По определению 27.1.3, сходится и ряд (27.3.1).
Пусть теперь ряд (27.3.1) расходится. Это значит, что его частичные суммы неограниченно возрастают. Но тогда, в силу неравенств (27.3.3), неограниченно возрастают и частичные суммы ряда (27.3.2), что означает, что этот ряд расходится.
Пример №16
Пусть дан ряд
Исследуем его сходимость.
Решение:
Необходимый признак выполняется, т.е.
Для исследования сходимости заданного ряда применим 1 признак
сравнения (теорему 27.3.1). Сравним заданный ряд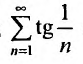
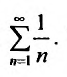
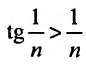
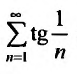
Пример №17
Исследовать сходимость ряда
Решение:
Очевидно, что предел общего члена при возрастании т стремится к нулю.
Сравним данный ряд, общий член которого 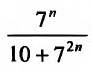
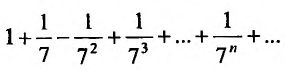
Поскольку 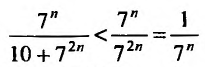
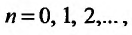
Теорема 27.3.2. (II признак сравнения). Если для рядов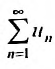
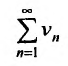
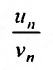
то ряды 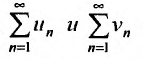
Доказательство. Предельное соотношение (27.3.4), в силу определения 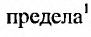
выполняется неравенство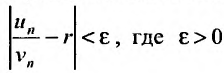
Обозначив 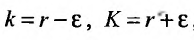
Предположим, что ряд 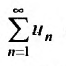
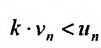
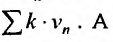
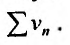
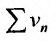
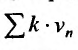
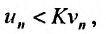
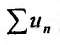
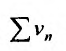
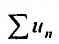
Последовательность 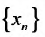
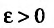
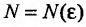
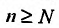
Пример №18
Исследовать сходимость ряда
Решение:
Очевидно, что 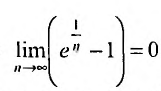
Теорема 27.3.2 выполняется, поэтому из расходимости гармонического ряда 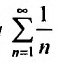
Признаки Д’Аламбсра и Коши
Иногда вместо признаков сравнения оказываются полезными некоторые специальные признаки сходимости ряда. Отметим среди них признаки Д’Аламбсра и Коши, непосредственно получающиеся из признаков сравнения, если в качестве ряда сравнения взять соответствующим образом выбранную геометрическую прогрессию.
Теорема 27.3.3. (признак Д’Аламбера). Если для ряда
с положительными членами существует такой номер 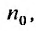
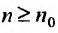
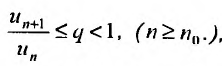
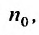
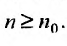
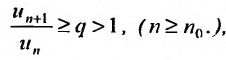
Доказательство. Пусть 0 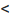
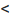
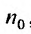
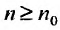
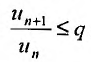
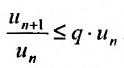
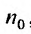
Ряд 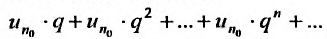
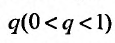
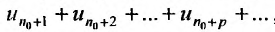
т.к. на сходимость ряда не влияет исключение конечного числа е^ членов.
Если же существует такое 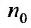
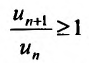
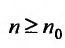
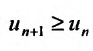
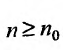
Так как по предположению 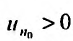
Следствие 1. Пусть существует предел отношения последующего члена ряда (27.3.6) к предыдущему равный r :
Тогда, если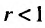
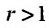
Доказательство. Воспользовавшись определением предела, для фиксированного 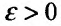
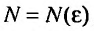
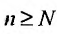
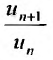
Рассмотрим правую часть двойного неравенства: 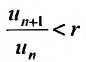
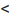
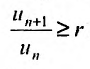
Пример №19
Рассмотрим ряд 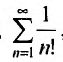
Решение:
Выпишем вначале значения
Затем вычислим предел отношения последующего члена ряда к предыдущему:
Так как этот предел меньше 1, то, в силу следствия 1, данный ряд сходится.
Заметим, что при исследовании сходимости ряда обычно (как правило, но не всегда) применяют следствие 1 из теоремы 27.3.3.
Теорема 27.3.4. (признак Kouiu). Если для ряда
с положительными членами, начиная с некоторого номера 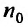
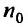
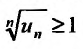
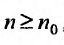
Доказательство. Пусть существует такой номер 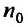
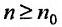
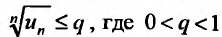
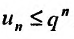
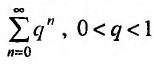
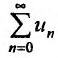
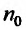
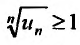
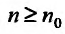
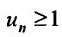
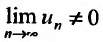
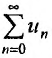
Следствие 2. Пусть существует предел корня n -ой степени из n-го члена ряда (27.3.9):
Тогда, если 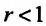
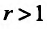
Доказательство. Из определения предела следует, что для фиксированного 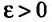
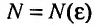
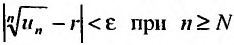
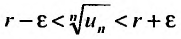
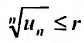
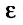
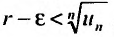
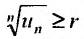
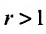
Пример №20
Рассмотрим ряд 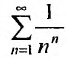
Решение:
Выпишем значение n-го члена ряда 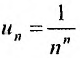
Так как этот предел меньше 1, то, согласно следствию 2, ряд сходится.
Замечание. Если пределы (27.3.8) и (27.3.10) равны 1, то для исследования сходимости ряда (27.3.9) нужно применять другие признаки, с которыми можно ознакомиться в [3].
Интегральный признак сходимости
Рассмотрим признак, достоинство которого состоит в исключительно высокой его чувствительности. Этим признаком проводится исследование сходимости там, где сформулированные признаки Д’Аламбсра и Коши «не работают».
Каждый член числового ряда 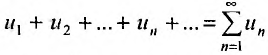
Эта функция определена пока только для целых положительных значений аргумента. Поэтому, доопределив значение функции f для всех нецелых значений аргумента, больших единицы, мы сможем, говорить о функции f(x), принимающей значения для любого 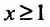
члены которого положительны и не возрастают 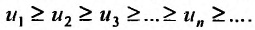
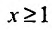
расходится интеграл
Доказательство. Пусть члены ряда (27.3.11) удовлетворяют условиям теоремы. Изобразим их графически, откладывая по оси Ох независимую переменную, а по оси Оу – соответствующие значения 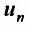
При таком графическом изображении сумма n первых членов ряда 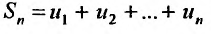
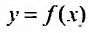
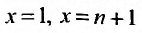
С другой стороны, криволинейная трапеция содержит сумму площадей вписанных прямоугольников, которая равна 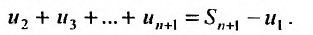
Из (27.3.12) и (27.3.13) следует неравенство:
Предположим, что несобственный интеграл 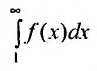
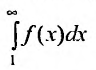
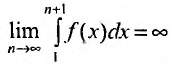
Пример №21
Исследовать сходимость ряда
Решение:
Применим интегральный признак. Рассмотрим функцию 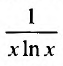
Так как несобственный интеграл расходится, то расходится и ряд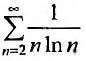
Замечание. Исследовать сходимость данного ряда при помощи следствий 1 и 2 не представляется возможным, так как соответствующие пределы равны 1.
Пример №22
Исследовать сходимость ряда Дирихле
Решение:
Если 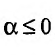
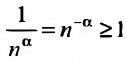
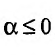
Пусть а > 0, тогда необходимый признак, очевидно, выполняется. Применим интегральный признак Коши. Введем функцию
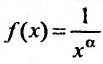
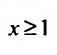
Вычислим определенный интеграл, записанный под знаком предела:
Если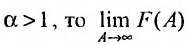
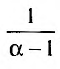
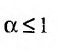
Таким образом, при a>1 несобственный интеграл 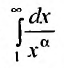
- Знакопеременные ряды
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
Числовой последовательностью называют ряд чисел, полученных по некоторому правилу или формуле.
Например, правило «все положительные четные числа по возрастанию начиная с двойки» задает последовательность: (2; 4; 6; 8; 10…) А правило «первое число равно (3), а каждое следующее число в два раза больше предыдущего» формирует последовательность: (3; 6; 12; 24; 48….)
Ниже разобраны несколько разных способов задания числовых последовательностей.
Числа, образующие последовательность, называются ее членами
(или элементами). И каждое из этих чисел имеет свой порядковый номер.
Например, в последовательности (3; 6; 12; 24; 48…) тройка является первым членом (порядковый номер – один), шестерка – вторым (ее номер по порядку равен двум), двенадцать – третьим и т.д.
В математике последовательность обозначают маленькой латинской буквой, а каждый отдельный ее элемент – той же буквой с числовым индексом равным порядковому номеру этого элемента.
То есть, если последовательность (3; 6; 12; 24; 48…) обозначить как (a_n), то можно записать, что (a_1=3), (a_2=6), (a_3=12), (a_4=24) и так далее.
Иными словами, для последовательности (a_n={ 3;: 6; :12; : 24; : 48; : 96; : 192; : 384…}).
|
порядковый номер элемента |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
… |
|
обозначение элемента |
(a_1) |
(a_2) |
(a_3) |
(a_4) |
(a_5) |
(a_6) |
(a_7) |
(a_8) |
… |
|
значение элемента |
(3) |
(6) |
(12) |
(24) |
(48) |
(96) |
(192) |
(384) |
… |
Отметим, что членами последовательности необязательно должны быть различные числа. Она может состоять из одних и тех же чисел, например, выглядеть вот так: (1; : 1; : 1; : 1…) .
Способы задания числовых последовательностей
Все способы формирования числовых последовательностей можно разделить на три большие группы:
– I способ: словесный. Здесь все просто – в буквальном смысле словами описывается каким образом можно вычислить элементы искомой последовательности.
Пример: Напишите первые пять членов последовательности квадратов натуральных чисел.
Решение: Натуральными называют числа, возникающие естественным образом при счете количества предметов, то есть: (1; : 2; : 3; : 4; : 5) и т.д. Нашу же последовательность формируют квадраты этих чисел, то есть (1^2;: 2^2; : 3^2; : 4^2; : 5^2…) . Таким образом, имеем ответ: (1; : 4; : 9; : 16; : 25…)
Ответ: (1; : 4; : 9; : 16; : 25…)
Отметим, что последовательности в начале статьи заданы именно словесным способом.
– II способ: аналитический (формулой энного члена). Тут значение каждого элемента последовательности вычисляется по некоторой формуле, в которую подставляется порядковый номер этого элемента.
Пример: Последовательность задана формулой: (b_n=frac{n-1}{n^2}). Вычислите первые пять членов этой последовательности.
Решение: Вычислим (b_1). Это первый член последовательности, то есть его порядковый номер (n) равен единице. Тогда его значение равно (b_1=frac{1-1}{1^2} =frac{0}{1}=0).
У второго члена (n=2), то есть его значение равно (b_2=frac{2-1}{2^2} =frac{1}{4}).
Третий ((n=3)): (b_3=frac{3-1}{3^2} =frac{2}{9}).
Четвертый ((n=4)): (b_4=frac{4-1}{4^2} =frac{3}{16}).
Пятый ((n=5)): (b_5=frac{5-1}{5^2} =frac{4}{25}) .
Готово. Можно писать ответ.
Ответ: (b_n= {0; : frac{1}{4}; : frac{2}{9}; : frac{3}{16}; : frac{4}{25}…}).
Обратите внимание, что при таком задании последовательности, значение каждого элемента зависит только от его порядкового номера. И поэтому, если нам нужно вычислить, например, пятнадцатый элемент, мы можем это сделать сразу, не вычисляя предыдущие четырнадцать.
Пример: Последовательность задана формулой: (a_n=8+5n-n^2). Вычислите (a_9).
Решение: Нужно вычислить значение девятого элемента, то есть порядковый номер (n=9). Подставляем в формулу: (a_9=8+5·9-9^2=8+45-81=-28).
Ответ: (a_9=-28).
III способ: рекуррентное соотношение. Звучит страшно, но суть проста – здесь дается начало последовательности (один или несколько первых элементов) и правило, по которому из предыдущего (или нескольких предыдущих) членов последовательности можно вычислить следующий.
Пример: Последовательность задана условиями: (c_1=4), (c_{n+1}=c_n+3). Вычислите первые пять членов этой последовательности.
Решение: Первый член нам известен: (c_1=4).
Второй мы получим, подставив в формулу вместо (n) единицу: (c_{1+1}=c_1+3)
(c_2=c_1+3=4+3=7)
Третий ((n=2)): (c_{2+1}=c_2+3 )
(c_3=c_2+3=7+3=10).
Четвертый ((n=3)): (c_{3+1}=c_3+3)
(c_4=c_3+3=10+3=13).
Пятый ((n=4)): (c_{4+1}=c_4+3)
(c_5=c_4+3=13+3=16).
Нужные пять элементов вычислены. Теперь можно записывать ответ.
Ответ: (c_n={4; : 7; : 10; : 13; : 16…}).
В этом примере мы по сути получали следующий элемент из предыдущего путем прибавления к предыдущему тройки. Логично, ведь формула (c_{n+1}=c_n+3) требовала именно этого. В ней (c_n) – это предыдущий элемент, а (c_{n+1}) – следующий за ним (ведь его номер на единицу больше).
На практике могут встречаться более сложные формулы, в которых следующий элемент вычисляется из двух, трех или даже большего количества предыдущих.
Пример: У последовательности известны первые два элемента (z_1=2;) (z_2=5). Так же известна формула следующего элемента (z_{n+2}=3z_{n+1}-z_n). Вычислите значения третьего, четвертого и пятого членов.
Решение: Слева будем писать текущую последовательность, а справа вести вычисления очередного элемента.
|
Последовательность на данный момент: |
Вычисления: |
||||||||||||
|
Так как формула дана для элемента с номером (n+2), то чтобы найти (z_3) нужно подставлять вместо (n) единицу:
|
||||||||||||
|
Теперь найдем (z_4), подставив вместо (n) двойку: (z_{2+2}=3z_{2+1}-z_2) (z_4=3z_3-z_2=3·13-5=34) |
||||||||||||
|
Наконец вычисляем (z_5), подставляя вместо (n) тройку: (z_{3+2}=3z_{3+1}-z_3) (z_5=3z_4-z_3=3·34-13=89) |
||||||||||||
|
Готово. Можно писать ответ. |
Ответ: (c_3=13); (c_4=34); (c_5=89).
Важное отличие рекуррентного способа задания последовательности от аналитического – при рекуррентном мы не можем посчитать следующий элемент, не зная предыдущих. То есть, если нам нужно вычислить, например, пятнадцатый элемент, придется сначала вычислить все, что идут до него.
Как определить является ли число элементом последовательности?
Во всех предыдущих примерах мы находили значения элементов последовательности – чему равен третий, пятый или девятый член. Иначе говоря, выясняли какое именно число стоит в последовательности на таком-то месте.
Но в практике встречается также обратная задача – значение известно и надо выяснить, есть ли оно среди элементов некоторой последовательности? А если есть, то на каком месте?
Пример (ОГЭ): Какое из чисел ниже есть среди членов последовательности (a_n=n^2-n):
а) (1) б) (3) в) (6) г) (10) ?
Решение: Из условия задачи понятно, что одно из этих чисел точно является элементом последовательности. Поэтому мы можем просто вычислять элементы по очереди, пока не найдем нужный:
(a_1=1^2-1=0) – мимо.
(a_2=2^2-2=2) – тоже не то.
(a_3=3^2-3=6) – есть!
Нужный элемент найден.
Ответ: (6).
Такой метод решения годится только если заранее известно, что элемент точно в последовательности есть. Потому что если его вдруг там нет – это можно проверять вечность, последовательность ведь бесконечна!
Поэтому в такой ситуации пользуются следующим алгоритмом:
-
Подставляют заданное число в формулу (n) -го члена вместо (a_n);
-
Решая полученное уравнение, находят неизвестное (n);
-
Если (n) – натуральное, то данное число – член последовательности.
Пример: Выяснить, является ли число (3) членом последовательности (a_n=)(frac{51+2n}{n+4}) ?
Решение:
|
(a_n=)(frac{51+2n}{n+4}) |
Если число (3) – член последовательности, то значит при некотором значении (n), формула (frac{51+2n}{n+4}) должна дать нам тройку. Найдем это (n) по алгоритму выше. |
|
(3=)(frac{51+2n}{n+4}) |
Решаем это уравнение. Умножаем левую и правую части на знаменатель ((n+4)). |
|
(3cdot (n+4)=51+2n) |
Получилось линейное уравнение. Раскрываем скобки слева. |
|
(3n+12=51+2n) |
Собираем неизвестные слева, числа справа… |
|
(3n-2n=51-12) |
…и приводим подобные слагаемые. |
|
(n=39) |
Готово. Найденное значение – это то число, которое надо подставить вместо (n) в формулу (frac{51+2n}{n+4}), чтоб получилось тройка (можете проверить это сами). Значит (39)-ый член последовательности равен трем. |
Ответ: Да, число (3) является элементом данной последовательности.
Смотри также:
Арифметическая прогрессия
Геометрическая прогрессия
На этой странице вы узнаете
- Как мы привыкаем к последовательностям на протяжение нашей жизни?
- Что такое золотое сечение?
Что значит “действовать последовательно”? Мы делаем что-то по определенным принципам, не нарушаем правила. Все наши действия будут иметь логику, которую мы сможем отследить. В математике также можно составлять числа в строгом порядке. Называться такие ряды будут последовательностями.
Понятие последовательности
Посмотрим на несколько рядов чисел и порассуждаем.
По какому принципу составлен ряд чисел 1, 2, 3, 4, 5 и т.д.? Всё просто: к каждому новому числу прибавляют единицу.
А какой принцип в ряде чисел 2, 4, 6, 8 и т.д.? Здесь к каждому новому числу прибавляют 2.
Что можно сказать про ряд 2, 4, 8, 16, 32 и т.д.? Каждое новое число умножают на 2.
Все приведенные выше ряды чисел будут называться последовательностью. Как описать ее одним термином?
Ненадолго вспомним функции чисел. Разберем функцию f(x)=x+1.
Если x = 0, то f(x) = 1.
Если x = 1, то f(x) = 2.
Если x = 2, то f(x) = 3.
Если x = 3, то f(x) = 4.
Внимательно посмотрим на значения функции: это и будет наша первая последовательность 1, 2, 3, 4, 5. Мы можем сделать вывод, что последовательность можно задать с помощью функции.
На самом деле, любая последовательность и есть функция. Теперь дадим определение.
Последовательность — функция, заданная на множестве натуральных чисел или его части.
То есть подставлять в такую функцию можно только натуральные числа.
Подробнее про функцию, ее значение, область определения и другие свойства можно прочесть в статье «Определение и график функции».
Аргумент будет обозначать порядковый номер числа в последовательности. Первое число в последовательности будет задаваться х = 1, второе число х = 2, n число как х = n.
Числа, которые образуют последовательность, — это члены последовательности. И у каждого члена последовательности есть свой порядковый номер.
Как же обозначаются члены последовательности? Не будем же мы каждый раз писать “двадцатый член последовательности” или что-то подобное?
Для членов последовательности существует свое обозначение: an, где индекс после буквы а обозначает порядковый номер члена последовательности.
Например,
- а1 — первый член последовательности,
- а20 — двадцатый член последовательности,
- а100 — сотый член последовательности и так далее.
Таким образом можно обозначить любой член последовательности.
Вспомним считалочки, которые мы использовали в играх в детстве: “Раз, два, три, четыре, пять, вышел зайчик погулять”. Первая строчка многих подобных считалочек — это последовательность натуральных чисел 1, 2, 3, 4, 5.
Дальше в школе на уроках физкультуры нас распределяют по командам, присваивая каждому свой номер. И это тоже последовательность.
Потом мы поступаем в вуз и попадаем в списки абитуриентов, тоже — в ещё одну последовательность.
Способы задания числовой последовательности
Рассмотрим, каким способами можно задать числовую последовательность.
Первый способ — это указать все члены последовательности. Однако он не всегда удобен, поскольку в последовательности может быть бесконечное количество членов.
Второй способ мы уже использовали — это задать общую формулу. Тогда можно будет найти любой член последовательности. В этом случае нужно будет подставить порядковый номер члена последовательности в формулу.
Допустим, дана последовательность an = 3n + 40, и нам нужно найти третий член последовательности. Тогда нужно подставить n = 3 в формулу:
a3 = 3 * 3 + 40 = 9 + 40 = 49.
Аналогичным способом можно будет найти любой член в данной последовательности.
Рассмотрим ещё пример. Что мы можем сказать про последовательность чисел 2, 4, 12, 32, 88 и так далее? Определенный закон здесь вывести достаточно сложно. Всё потому, что следующий член последовательности зависит от предыдущего.
Обратим внимание на третий член последовательности: 12 = 2 * 6 = 2(2 + 4). А если посмотреть на четвертый член последовательности? 32 = 2 * 16 = 2(4 + 12).
И так с каждым членом последовательности: он равен удвоенной сумме двух предыдущих членов.
Это еще один способ задания последовательности, когда используется рекуррентная формула. Ее особенность в том, что каждый член последовательности выражен с помощью предыдущих членов последовательности.
Одним из примеров такой последовательности будут числа Фибоначчи. Это последовательность, в которой первые два члена равны 1, а все следующие являются суммой двух предшествующих им.
Числа Фибоначчи выглядят так: 1, 1, 2, 3, 5, 8, 13, 21 и так далее.
Как задать их с помощью рекуррентной формулы? Допустим, мы хотим найти член an в этой последовательности. Мы знаем, что для этого нужно сложить два предыдущих члена, то есть an-1 и an-2. Вот мы и получили формулу.
an = an-1 + an-2.
Золотое сечение — это пропорциональное деление отрезка на неравные части. При этом весь отрезок относится к большей части, как меньшая часть этого отрезка относится в большей его части.
Золотое сечение можно представить в виде “завитка”, который вписан в прямоугольник. Прямоугольник будет делиться на квадраты, стороны которых равны числам Фибоначчи.
Принципы золотого сечения позволяет построить гармоничную композицию, а значит, применяются в архитектуре и искусстве. Более того, их можно встретить в природе. Форма ракушек, завитки ростков, семена подсолнуха, шишки, даже ураган (если посмотреть на него сверху) имеют форму золотого сечения или приближенную к нему.

Виды числовых последовательностей
Возьмем обычную последовательность натуральных чисел 1, 2, 3, 4, 5, …, an. Мы можем сказать, что каждый следующий член последовательности больше, чем предыдущий. Такие последовательности называются возрастающими.
Если перевернуть ее и получить последовательность 5, 4, 3, 2, 1, …, an — последовательность будет называться убывающей. Для такой последовательности обязательно, чтобы каждый следующий член был меньше, чем предыдущий.
Что, если мы просто будем менять знак числа? Например, −1, 1, −1, 1 и так далее? Тогда последовательность будет ни убывающей и ни возрастающей.
Такую последовательность можно задать с помощью формулы an = (-1)n.
Разумеется, не все последовательности бывают бесконечными. Ранее мы рассматривали только бесконечные последовательности: в них можно было подставить любое значение n.
Возьмем последовательность простых однозначных чисел: 2, 3, 5, 7. Больше однозначных чисел нет — продолжить последовательность мы не можем.
Последовательность, в которой ограничено количество членов, будет называться конечной последовательностью. Если же в последовательности не ограничено количество членов, и их можно задавать до бесконечности, то такая последовательность будет называться бесконечной последовательностью.
Фактчек
- Последовательность — функция, заданная на множестве натуральных чисел или его части.
- Каждый член последовательности имеет свой номер, который отображается в индексе. Например, a1 — первый член последовательности, а a25 — двадцать пятый.
- Последовательность можно задать несколькими способами. Во-первых, выписать все члены последовательности. Во-вторых, задать общую формулу. В-третьих, задать рекуррентную формулу.
- Рекуррентная формула — это формула, в которой каждый следующий член последовательности зависит от предыдущих. Ярким примером такой последовательности являются числа Фибоначчи, где каждое число является суммой двух предыдущих.
- Последовательности бывают возрастающими и убывающими. В возрастающих последовательностях каждый следующий член больше предыдущего, а в убывающей каждый следующий член последовательности меньше предыдущего. В бесконечных последовательностях не ограничено количество членов. А в конечных последовательностях количество членов ограничено.
Проверь себя
Задание 1.
Выберите конечную числовую последовательность.
- Числа Фибоначчи.
- Четные положительные числа.
- Нечетные трехзначные числа.
- Нечетные отрицательные числа.
Задание 2.
Выберите убывающую последовательность.
- 10, 9, 8, 7, 6, 5, …, an
- Числа Фибоначчи
- 1, 2, 3, 4, 5, …, an
- 1, 3, 5, 7, 9, …, an
Задание 3.
Выберите возрастающую последовательность.
- 100, 90, 80, …, an
- (frac{1}{2}), (frac{1}{3}), (frac{1}{4}), …, an
- Числа Фибоначчи
- −1, −2, -3, …, an
Задание 4.
Какая последовательность является числами Фибоначчи?
- 1, 2, 3, 4, 5, …
- 1, 1, 2, 3, 5, 8, …
- 1, 4, 9, 16, 25, …
- 1, (frac{1}{2}), (frac{1}{3}), (frac{1}{4}), …
Ответы: 1. — 3 2. — 1 3. — 3 4. — 2
Данная статья представляет собой структурированную и подробную информацию, которая может пригодиться во время разбора упражнений и задач. Мы рассмотрим тему числовых рядов.
Данная статья начинается с основных определений и понятий. Далее мы стандартные варианты и изучим основные формулы. Для того, чтобы закрепить материал, в статье приведены основные примеры и задачи.
Базовые тезисы
Для начала представим систему: a1, a2…, an,… , где ak∈R, k=1,2….
Для примера, возьмем такие числа, как: 6,3,-32,34,38,-316,… .
Числовой ряд – это сумма членов ∑akk=1∞=a1+a2+…+an+… .
Чтобы лучше понять определение, рассмотрим данный случай, в котором q = -0.5: 8-4+2-1+12-14+…=∑k=1∞(-16)·-12k .
ak является общим или k–ым членом ряда.
Он выглядит примерно таким образом -16·-12k .
Частичная сумма ряда выглядит примерно таким образом Sn=a1+a2+…+an , в которой n –любое число. Sn является n-ой суммой ряда.
Например, ∑k=1∞(-16)·-12k есть S4=8-4+2-1=5 .
S1,S2,…,Sn,… образуют бесконечную последовательность числового ряда.
Для ряда n –ая сумму находится по формуле Sn=a1·(1-qn)1-q=8·1–12n1–12=163·1–12n . Используем следующую последовательность частичных сумм: 8,4,6,5,…,163·1–12n,… .
Ряд ∑k=1∞ak является сходящимся тогда, когда последовательность обладает конечным пределом S=lim Snn→+∞ . Если предела нет или последовательность бесконечна, то ряд ∑k=1∞ak называется расходящимся.
Суммой сходящегося ряда ∑k=1∞ak является предел последовательности ∑k=1∞ak=lim Snn→+∞=S .
В данном примере lim Snn→+∞=lim 163т→+∞·1-12n=163·lim n→+∞1–12n=163 , ряд ∑k=1∞(-16)·-12k сходится. Сумма равна 163: ∑k=1∞(-16)·-12k=163 .
В качестве примера расходящегося ряда можно привести сумму геометрической прогрессии со знаменателем большем, чем единица: 1+2+4+8+…+2n-1+…=∑k=1∞2k-1.
n-ая частичная сумма определяется выражением Sn=a1·(1-qn)1-q=1·(1-2n)1-2=2n-1, а предел частичных сумм бесконечен: limn→+∞Sn=limn→+∞(2n-1)=+∞.
Еще одим примером расходящегося числового ряда является сумма вида∑k=1∞5=5+5+…. В этом случае n-ая частичная сумма может быть вычислена как Sn=5n. Предел частичных сумм бесконечен limn→+∞Sn=limn→+∞5n=+∞.
Сумма подобного вида как ∑k=1∞=1+12+13+…+1n+… – это гармонический числовой ряд.
Сумма ∑k=1∞1ks=1+12s+13s+…+1ns+… , где s –действительное число, является обобщенно гармоническим числовым рядом.
Определения, рассмотренные выше, помогут вам для решения большинства примеров и задач.
Для того, чтобы дополнить определения, необходимо доказать определенные уравнения.
- ∑k=1∞1k – расходящийся.
Действуем методом от обратного. Если он сходится, то предел конечен. Можно записать уравнение как limn→+∞Sn=S и limn→+∞S2n=S . После определенных действий мы получаем равенство limn→+∞(S2n-Sn)=0 .
Напротив,
S2n-Sn=1+12+13+…+1n+1n+1+1n+2+…+12n–1+12+13+…+1n=1n+1+1n+2+…+12n
Справедливы следующие неравенства 1n+1>12n, 1n+1>12n,…, 12n-1>12n . Получаем, что S2n-Sn=1n+1+1n+2+…+12n>12n+12n+…+12n=n2n=12 . Выражение S2n-Sn>12 указывает на то, что limn→+∞(S2n-Sn)=0 не достигается. Ряд расходящийся.
- b1+b1q+b1q2+…+b1qn+…=∑k=1∞b1qk-1
Необходимо подтвердить, что сумма последовательности чисел сходится при q<1 , и расходится при q≥1 .
Согласно приведенным выше определениям, сумма n членов определяется согласно формуле Sn=b1·(qn-1)q-1 .
Если q<1 верно
limn→+∞Sn=limn→+∞b1·qn-1q-1=b1·limn→+∞qnq-1-limn→+∞1q-1==b1·0-1q-1=b1q-1
Мы доказали, что числовой ряд сходится.
При q = 1 b1+b1+b1+…∑k=1∞b1 . Суммы можно отыскать с использованием формулы Sn=b1·n , предел бесконечен limn→+∞Sn=limn→+∞b1·n=∞. В представленном варианте ряд расходится.
Если q = -1, то ряд выглядит как b1-b1+b1-…=∑k=1∞b1(-1)k+1 . Частичные суммы выглядят как Sn=b1 для нечетных n, и Sn=0 для четных n. Рассмотрев данный случай, мы удостоверимся, что предела нет и ряд является расходящимся.
При q>1 справедливо limn→+∞Sn=limn→+∞b1·(qn-1)q-1=b1·limn→+∞qnq-1-limn→+∞1q-1==b1·∞-1q-1=∞
Мы доказали, что числовой ряд расходится.
- Ряд ∑k=1∞1ks сходится, если s > 1 и расходится, если s≤ 1 .
Для s = 1 получаем ∑k=1∞1k , ряд расходится.
При s < 1 получаем 1ks≥1k для k, натурального числа. Так как ряд является расходящимся ∑k=1∞1k , то предела нет. Следуя этому, последовательность ∑k=1∞1ks неограниченна. Делаем вывод, что выбранный ряд расходится при s < 1.
Необходимо предоставить доказательства, что ряд ∑k=1∞1ks сходится при s > 1.
Представим S2n-1-Sn-1 :
S2n-1-Sn-1=1+12s+13s+…+1(n-1)s+1ns+1(n+1)s+…+1(2n-1)s–1+12s+13s+…+1(n-1)s=1ns+1(n+1)s+…+1(2n-1)s
Допустим, что 1(n+1)s<1ns, 1(n+2)s<1ns, …, 1(2n-1)s<1ns , тогда S2n-1-Sn-1=1ns+1(n+1)s+…+1(2n-1)s<<1ns+1ns+…+1ns=nns=1ns-1
Представим уравнение для чисел, которые являются натуральными и четными n=2: S2n-1-Sn-1=S3-S1=12s+13s<12s-1n=4: S2n-1-Sn-1=S7-S3=14s+15s+16s+17s<14s-1=12s-12n=8: S2n-1-Sn-1=S15-S7=18s+19s+…+115s<18s-1=12s-13…
Получаем:
∑k=1∞1ks=1+12s+13s+14s+…+17s+18s+…+115s+…==1+S3-S1+S7-S3+S15+S7+…<<1+12s-1+12s-12+12s-13+…
Выражение 1+12s-1+12s-12+12s-13+… – это сумма геометрической прогрессии q=12s-1 . Согласно исходным данным при s>1, то0<q<1 . Получаем, ∑k=1∞<1+12s-1+12s-12+12s-13+…=11-q=11-12s-1 . Последовательность ряда при s > 1 увеличивается и ограничивается сверху 11-12s-1 . Представим, что есть предел и ряд является сходящимся ∑k=1∞1ks .
Ряд ∑k=1∞ak знакоположителен в том случае, если его члены >0 ak>0, k=1,2,… .
Ряд ∑k=1∞bk знакочередующийся, если знаки чисел отличаются. Данный пример представлен как∑k=1∞bk=∑k=1∞(-1)k·ak или ∑k=1∞bk=∑k=1∞(-1)k+1·ak , где ak>0, k=1,2, … .
Ряд ∑k=1∞bk знакопеременный, так как в нем множество чисел, отрицательных и положительных.
Второй вариант ряд – это частный случай третьего варианта.
Приведем примеры для каждого случая соответственно:
6+3+32+34+38+316+…6-3+32-34+38-316+…6+3-32+34+38-316+…
Для третьего варианта также можно определить абсолютную и условную сходимость.
Знакочередующийся ряд ∑k=1∞bk абсолютно сходится в том случае, когда ∑k=1∞bk также считается сходящимся.
Подробно разберем несколько характерных вариантов
Если ряды 6-3+32-34+38-316+… и 6+3-32+34+38-316+… определяются как сходящиеся, то верно считать, что 6+3+32+34+38+316+…
Знакопеременный ряд ∑k=1∞bk считается условно сходящимся в том случае, если ∑k=1∞bk – расходящийся, а ряд ∑k=1∞bk считается сходящимся.
Подробно разберем вариант ∑k=1∞(-1)k+1k=1-12+13-14+… . Ряд ∑k=1∞(-1)k+1k=∑k=1∞1k , который состоит из абсолютных величин, определяется как расходящийся. Этот вариант считается сходящимся, так как это легко определить. Из данного примера мы узнаем, что ряд ∑k=1∞(-1)k+1k=1-12+13-14+… будет считаться условно сходящимся.
Особенности сходящихся рядов
Проанализируем свойства для определенных случаев
- Если ∑k=1∞ak будет сходится, то и ряд ∑k=m+1∞ak также признается сходящимся. Можно отметить, что ряд без m членов также считается сходящимся. В случае, если мы добавляем к ∑k=m+1∞ak несколько чисел, то получившийся результат также будет сходящимся.
- Если ∑k=1∞ak сходится и сумма = S, то сходится и ряд ∑k=1∞A·ak , ∑k=1∞A·ak=A·S , где A –постоянная.
- Если ∑k=1∞ak и ∑k=1∞bk являются сходящимися , суммы A и B тоже, то и ряды ∑k=1∞ak+bk и ∑k=1∞ak-bk также сходятся . Суммы будут равняться A + B и A – B соответственно.
Определить, что ряд сходится ∑k=1∞23k·k3 .
Изменим выражение ∑k=1∞23k·k3=∑k=1∞23·1k43 . Ряд ∑k=1∞1k43 считается сходящимся, так как ряд ∑k=1∞1ks сходится при s > 1. В соответствии со вторым свойством, ∑k=1∞23·1k43 .
Определить, сходится ли ряд ∑n=1∞3+nn52 .
Преобразуем изначальный вариант ∑n=1∞3+nn52=∑n=1∞3n52+nn2=∑n=1∞3n52+∑n=1∞1n2 .
Получаем сумму ∑n=1∞3n52 и ∑n=1∞1n2 . Каждый ряд признается сходящимся согласно свойству. Так, как ряды сходятся, то исходный вариант тоже.
Вычислить, сходится ли ряд 1-6+12-2+14-23+18-29+… и вычислить сумму.
Разложим исходный вариант:
1-6+12-2+14-23+18-29+…==1+12+14+18+…-2·3+1+13+19+…==∑k=1∞12k-1-2·∑k=1∞13k-2
Каждый ряд сходится, так как является одним из членов числовой последовательности. Согласно третьему свойству, мы можем вычислить, что исходный вариант также является сходящимся. Вычисляем сумму: Первый член ряда ∑k=1∞12k-1 =1 , а знаменатель =0.5, за этим следует, ∑k=1∞12k-1=11-0.5=2 . Первый член ∑k=1∞13k-2=3, а знаменатель убывающей числовой последовательности=13. Получаем:∑k=1∞13k-2=31-13=92 .
Используем выражения, полученные выше, для того, чтобы определить сумму 1-6+12-2+14-23+18-29+…=∑k=1∞12k-1-2·∑k=1∞13k-2=2-2·92=-7
Необходимое условие для определения, является ли ряд сходящимся
Если ряд ∑k=1∞ak является сходящимся, то предел его k-ого члена =0: limk→+∞ak=0 .
Если мы проверим любой вариант, то нужно не забывать о непременном условии. Если оно не выполняется, то ряд расходится. Если limk→+∞ak≠0 , то ряд расходящийся.
Следует уточнить, что условие важно, но не достаточно. Если равенство limk→+∞ak=0 выполняется , то это не гарантирует, что ∑k=1∞ak является сходящимся.
Приведем пример. Для гармонического ряда ∑k=1∞1k условие выполняется limk→+∞1k=0 , но ряд все равно расходится.
Определить сходимость ∑n=1∞n21+n .
Проверим исходное выражение на выполнение условияlimn→+∞n21+n=limn→+∞n2n21n2+1n=limn→+∞11n2+1n=1+0+0=+∞≠0
Предел n-ого члена не равен 0. Мы доказали, что данный ряд расходится.
Как определить сходимость знакоположительного ряда.
Если постоянно пользоваться указанными признаками, придется постоянно вычислять пределы. Данный раздел поможет избежать сложностей во время решения примеров и задач. Для того, чтобы определить сходимость знакоположительного ряда, существует определенное условие.
Для сходимости знакоположительного ∑k=1∞ak, ak>0 ∀k=1,2,3,… нужно определять ограниченную последовательность сумм.
Как сравнивать ряды
Существует несколько признаков сравнения рядов. Мы сравниваем ряд, сходимость которого предлагается определить, с тем рядом, сходимость которого известна.
Первый признак
∑k=1∞ak и∑k=1∞bk – знакоположительные ряды. Неравенство ak≤bk справедливо для k = 1, 2, 3, … Из этого следует, что из ряда ∑k=1∞bk мы можем получить∑k=1∞ak . Так как ∑k=1∞ak расходится, то ряд∑k=1∞bk можно определить как расходящийся.
Данное правило постоянно используется для решения уравнений и является серьезным аргументом, которое поможет определить сходимость. Сложности могут состоять в том, что подобрать подходящий пример для сравнения можно найти далеко не в каждом случае. Довольно часто ряд выбирается по принципу, согласно которому показатель k-ого члена будет равняться результату вычитания показателей степеней числителя и знаменателя k-ого члена ряда. Допустим, что ak=k2+34k2+5 , разность будет равна 2 – 3 = -1. В данном случае можно определить, что для сравнения необходим ряд с k-ым членом bk=k-1=1k , который является гармоническим.
Для того, чтобы закрепить полученный материал, детально рассмотрим пару типичных вариантов.
Определить, каким является ряд ∑k=1∞1k-12 .
Так как предел =0 limk→+∞1k-12=0 , мы выполнили необходимое условие. Неравенство будет справедливым1k<1k-12 для k, которые являются натуральными. Из предыдущих пунктов мы узнали, что гармонический ряд ∑k=1∞1k – расходящийся. Согласно первому признаку, можно доказать, что исходный вариант является расходящимся.
Определить, является ряд сходящимся или расходящимся∑k=1∞1k3+3k-1 .
В данном примере выполняется необходимое условие, так как limk→+∞1k3+3k-1=0 . Представляем в виде неравенства 1k3+3k-1<1k3 для любого значения k. Ряд ∑k=1∞1k3 является сходящимся, так как гармонический ряд ∑k=1∞1ks сходится при s > 1. Согласно первому признаку, мы можем сделать вывод, что числовой ряд является сходящимся.
Определить, является каким является ряд ∑k=3∞1kln(ln k) .limk→+∞1kln(ln k)=1+∞+∞=0 .
В данном варианте можно отметить выполнение нужного условия. Определим ряд для сравнения. Например, ∑k=1∞1ks . Чтобы определить, чему равна степень, расммотрим последовательность {ln(ln k)}, k=3,4,5…. Члены последовательности ln (ln 3), ln (ln 4), ln (ln 5), … увеличивается до бесконечности. Проанализировав уравнение, можно отметить, что, взяв в качестве значения N = 1619, то члены последовательности >2. Для данной последовательности будет справедливо неравенство 1kln(ln k)<1k2 . Ряд ∑k=N∞1k2 сходится согласно первому признаку, так как ряд ∑k=1∞1k2 тоже сходящийся. Отметим, что согласно первому признаку ряд ∑k=N∞1kln(ln k) сходящийся. Можно сделать вывод, что ряд ∑k=3∞1kln(ln k) также сходящийся.
Второй признак
Допустим, что ∑k=1∞ak и ∑k=1∞bk – знакоположительные числовые ряды.
Если limk→+∞akbk≠∞ , то ряд ∑k=1∞bk сходится, и ∑k=1∞ak сходится также.
Если limk→+∞akbk≠0 , то так как ряд ∑k=1∞bk расходится, то ∑k=1∞ak также расходится.
Если limk→+∞akbk≠∞ и limk→+∞akbk≠0 , то сходимость или расходимость ряда означает сходимость или расходимость другого.
Рассмотрим ∑k=1∞1k3+3k-1 с помощью второго признака. Для сравнения ∑k=1∞bk возьмем сходящийся ряд∑k=1∞1k3 . Определим предел: limk→+∞akbk=limk→+∞1k3+3k-11k3=limk→+∞k3k3+3k-1=1
Согласно второму признаку можно определить, что сходящийся ряд∑k=1∞1k3 означается, что первоначальный вариант также сходится.
Определить, каким является ряд ∑n=1∞k2+34k3+5 .
Проанализируем необходимое условие limk→∞k2+34k3+5=0 , которое в данном варианте выполняется. Согласно второму признаку, возьмем ряд ∑k=1∞1k. Ищем предел: limk→+∞k2+34k3+51k=limk→+∞k3+3k4k3+5=14
Согласно приведенным выше тезисам, расходящийся ряд влечет собой расходимость исходного ряда.
Третий признак
Рассмотрим третий признак сравнения.
Допустим, что ∑k=1∞ak и _∑k=1∞bk – знакоположительные числовые ряды. Если условие выполняется для некого номера ak+1ak≤bk+1bk , то сходимость данного ряда∑k=1∞bk означает, что ряд ∑k=1∞ak также является сходящимся. Расходящийся ряд ∑k=1∞ak влечет за собой расходимость ∑k=1∞bk .
Признак Даламбера
Представим, что ∑k=1∞ak – знакоположительный числовой ряд. Если limk→+∞ak+1ak<1, то ряд является сходящимся, если limk→+∞ak+1ak>1 , то расходящимся.
Замечание 1
Признак Даламбера справедлив в том случае, если предел бесконечен.
Если limk→+∞ak+1ak=-∞ , то ряд является сходящимся, если limk→∞ak+1ak=+∞ , то расходящимся.
Если limk→+∞ak+1ak=1 , то признак Даламбера не поможет и потребуется провести еще несколько исследований.
Определить, является ряд сходящимся или расходящимся ∑k=1∞2k+12k по признаку Даламбера.
Необходимо проверить, выполняется ли необходимое условие сходимости. Вычислим предел, воспользовавшись правилом Лопиталя: limk→+∞2k+12k=∞∞=limk→+∞2k+1’2k’=limk→+∞22k·ln 2=2+∞·ln 2=0
Мы можем увидеть, что условие выполняется. Воспользуемся признаком Даламбера: limk→+∞=limk→+∞2(k+1)+12k+12k+12k=12limk→+∞2k+32k+1=12<1
Ряд является сходящимся.
Определить, является ряд расходящимся ∑k=1∞kkk! .
Воспользуемся признаком Даламбера для того, чтобы определить рассходимость ряда: limk→+∞ak+1ak=limk→+∞(k+1)k+1(k+1)!kkk!=limk→+∞(k+1)k+1·k!kk·(k+1)!=limk→+∞(k+1)k+1kk·(k+1)==limk→+∞(k+1)kkk=limk→+∞k+1kk=limk→+∞1+1kk=e>1
Следовательно, ряд является расходящимся.
Радикальный признак Коши
Допустим, что ∑k=1∞ak – это знакоположительный ряд. Еслиlimk→+∞akk<1 , то ряд является сходящимся, если limk→+∞akk>1 , то расходящимся.
Замечание 2
Данный признак будет считаться справедливым только в том случае, если предел бесконечен. Другими словами, если limk→+∞akk=-∞, то ряд сходится, если limk→+∞akk=+∞ , то ряд расходится.
Еслиlimk→+∞akk=1 , то данный признак не дает никакой информации – требуется проведение дополнительного анализа.
Данный признак может быть использован в примерах, которые легко определить. Случай будет характерным тогда, когда член числового ряда – это показательно степенное выражение.
Для того, чтобы закрепить полученную информацию, рассмотрим несколько характерных примеров.
Определить, является ли знакоположительный ряд ∑k=1∞1(2k+1)k на сходящимся.
Нужное условие считается выполненным, так как limk→+∞1(2k+1)k=1+∞+∞=0 .
Согласно признаку, рассмотренному выше, получаем limk→+∞akk=limk→+∞1(2k+1)kk=limk→+∞12k+1=0<1 . Данный ряд является сходимым.
Сходится ли числовой ряд ∑k=1∞13k·1+1kk2 .
Используем признак, описанный в предыдущем пункте limk→+∞13k·1+1kk2k=13·limk→+∞1+1kk=e3<1 , следовательно, числовой ряд сходится.
Интегральный признак Коши
Допустим, что ∑k=1∞ak является знакоположительным рядом. Необходимо обозначить функцию непрерывного аргумента y = f(x), которая совпадаетan= f(n) . Если y = f(x) больше нуля, не прерывается и убывает на [a; +∞) , где a≥1
, то в случае, если несобственный интеграл ∫a+∞f(x)dx является сходящимся, то рассматриваемый ряд также сходится. Если же он расходится, то в рассматриваемом примере ряд тоже расходится.
При проверке убывания функции можно использовать материал, рассмотренный на предыдущих уроках.
Рассмотреть пример ∑k=2∞1k·ln k на сходимость.
Условие сходимости ряда считается выполненным, так как limk→+∞1k·ln k=1+∞=0 . Рассмотрим y=1x·ln x . Она больше нуля, не прерывается и убывает на [2; +∞) . Первые два пункта доподлинно известны, а вот на третьем следует остановиться подробнее. Находим производную: y’=1x·ln x’=x·ln x’x·ln x2=ln x+x·1xx·ln x2=-ln x+1x·ln x2 . Она меньше нуля на [2; +∞) . Это доказывает тезис о том, что функция является убывающей.
Собственно, функция y=1x·ln x соответствует признакам принципа, который мы рассматривали выше. Воспользуемся им: ∫2+∞dxx·ln x=limA→+∞∫2Ad(ln x)ln x=limA→+∞ln(ln x)2A==limA→+∞(ln(ln A)-ln(ln 2))=ln(ln(+∞))-ln(ln 2)=+∞
Согласно полученным результатам, исходный пример расходится, так как несобственный интеграл является расходящимся.
Докажите сходимость ряда ∑k=1∞1(10k-9)(ln(5k+8))3 .
Так как limk→+∞1(10k-9)(ln(5k+8))3=1+∞=0 , то условие считается выполненным.
Начиная с k=4, верное выражение 1(10k-9)(ln(5k+8))3<1(5k+8)(ln(5k+8))3 .
Если ряд∑k=4∞1(5k+8)(ln(5k+8))3 будет считаться сходящимся, то, согласно одному из принципов сравнения, ряд ∑k=4∞1(10k-9)(ln(5k+8))3 также будет считаться сходящимся. Таким образом, мы сможет определить, что исходное выражение также является сходящимся.
Перейдем к доказательству ∑k=4∞1(5k+8)(ln(5k+8))3 .
Так как функция y=15x+8(ln(5x+8))3 больше нуля, не прерывается и убывает на [4; +∞) . Используем признак, описанный в предыдущем пункте:
∫4+∞dx(5x+8)(ln(5x+8))3=limA→+∞∫4Adx(5x+8)(ln(5x+8))3==15·limA→+∞∫4Ad(ln(5x+8)(ln(5x+8))3=-110·limA→+∞1(ln(5x+8))2|4A==-110·limA→+∞1(ln(5·A+8))2-1(ln(5·4+8))2==-110·1+∞-1(ln 28)2=110·ln 282
В полученном сходящемся ряде, ∫4+∞dx(5x+8)(ln(5x+8))3 , можно определить, что ∑k=4∞1(5k+8)(ln(5k+8))3 также сходится.
Признак Раабе
Допустим, что ∑k=1∞ak – знакоположительный числовой ряд.
Если limk→+∞k·akak+1<1 , то ряд расходится, еслиlimk→+∞k·akak+1-1>1 , то сходится.
Данный способ определения можно использовать в том случае, если описанные выше техники не дают видимых результатов.
Исследование на абсолютную сходимость
Для исследования берем ∑k=1∞bk . Используем знакоположительный ∑k=1∞bk . Мы можем использовать любой из подходящих признаков, которые мы описывали выше. Если ряд ∑k=1∞bk сходится, то исходный ряд является абсолютно сходящимся.
Исследовать ряд ∑k=1∞(-1)k3k3+2k-1 на сходимость ∑k=1∞(-1)k3k3+2k-1=∑k=1∞13k3+2k-1 .
Условие выполняется limk→+∞13k3+2k-1=1+∞=0 . Используем ∑k=1∞1k32 и воспользуемся вторым признаком: limk→+∞13k3+2k-11k32=13 .
Ряд ∑k=1∞(-1)k3k3+2k-1 сходится. Исходный ряд также абсолютно сходящийся.
Расходимость знакопеременных рядов
Если ряд ∑k=1∞bk – расходящийся, то соответствующий знакопеременный ряд ∑k=1∞bk либо расходящийся, либо условно сходящийся.
Лишь признак Даламбера и радикальный признак Коши помогут сделать выводы о ∑k=1∞bk по расходимости из модулей ∑k=1∞bk . Ряд ∑k=1∞bk также расходится, если не выполняется необходимое условие сходимости, то есть, если limk→∞+bk≠0 .
Проверить расходимость 17,272,-673,2474,12075-72076, … .
Модуль k-ого члена представлен как bk=k!7k .
Исследуем ряд ∑k=1∞bk=∑k=1∞k!7k на сходимость по признаку Даламбера: limk→+∞bk+1bk=limk→+∞(k+1)!7k+1k!7k=17·limk→+∞(k+1)=+∞ .
∑k=1∞bk=∑k=1∞k!7k расходится так же, как и исходный вариант.
Является ли ∑k=1∞(-1)k·k2+1ln(k+1) сходящимся.
Рассмотрим на необходимое условие limk→+∞bk=limk→+∞k2+1ln(k+1)=∞∞=limk→+∞=k2+1′(ln(k+1))’==limk→+∞2k1k+1=limk→+∞2k(k+1)=+∞ . Условие не выполнено, поэтому ∑k=1∞(-1)k·k2+1ln(k+1) ряд расходящийся. Предел был вычислен по правилу Лопиталя.
Признаки для условной сходимости
Признак Лейбница
Если величины членов знакочередующегося ряда убывают b1>b2>b3>…>… и предел модуля =0 при k→+∞ , то ряд ∑k=1∞bk сходится.
Рассмотреть ∑k=1∞(-1)k2k+15k(k+1) на сходимость.
Ряд представлен как ∑k=1∞(-1)k2k+15k(k+1)=∑k=1∞2k+15k(k+1) . Нужное условие выполняется limk→+∞=2k+15k(k+1)=0 . Рассмотрим ∑k=1∞1k по второму признаку сравнения limk→+∞2k+15k(k+1)1k=limk→+∞2k+15(k+1)=25
Получаем, что ∑k=1∞(-1)k2k+15k(k+1)=∑k=1∞2k+15k(k+1) расходится. Ряд ∑k=1∞(-1)k2k+15k(k+1) сходится по признаку Лейбница: последовательность2·1+15·1·11+1=310, 2·2+15·2·(2+1)=530, 2·3+15·3·3+1, … убывает и limk→+∞=2k+15k(k+1)=0 .
Ряд условно сходится.
Признак Абеля-Дирихле
∑k=1+∞uk·vk сходится в том случае, если {uk} не возрастает, а последовательность ∑k=1+∞vk ограничена.
Исследуйте 1-32+23+14-35+13+17-38+29+… на сходимость.
Представим
1-32+23+14-35+13+17-38+29+…=1·1+12·(-3)+13·2+14·1+15·(-3)+16·=∑k=1∞uk·vk
где {uk}=1, 12, 13, … – невозрастающая, а последовательность {vk}=1, -3 , 2, 1, -3, 2, … ограничена {Sk}=1, -2, 0, 1, -2, 0, … . Ряд сходится.
Сразу отметим, что единой универсальной методики для решения задач на числовые ряды нет. Закономерности, по которым числа следуют друг за другом, могут быть самыми разными, и научиться быстро решать такого рода задачи можно только путём практики – прорешав большое количество других задач на ряды.
Рассмотрим самые простые случаи.
Надо продолжить ряд
1) 2 4 6 8 …
В этом случае всё просто – каждое следующее число на 2 больше предыдущего (т.е. это ряд чётных чисел, или арифметическая прогрессия с шагом 2), поэтому следующее число будет 10
2) 4 8 16 32 …
Тут каждое следующее число в 2 раза больше предыдущего (геометрическая прогрессия), поэтому следующим будет число 64
3) 6 11 17 24 …
Этот случай уже чуть сложнее. В этом числовом ряду разница между соседними числами на 1 больше, чем разница между предыдущими
11 – 6 = 5
17 – 11 = 6
24 -17 = 7
Как видим, шаг (разница) между соседними числами каждый раз увеличивается на 1.
Соответственно, после 24 будет число, которое на 8 больше, то есть 32
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Пример 1
Ряд: 18 10 6 4 …
Взглянув на этот ряд, можно достаточно быстро понять, что разница между соседними числами с каждым шагом сокращается в 2 раза
18 – 10 = 8
10 – 6 = 4 (8:4 = 2)
6 – 4 = 2 (4:2 = 2)
Следовательно, следующий шаг – это 2:2 = 1, то есть число будет 4-1 = 3
Пример 2
Ряд: 7 15 31 63
Этот ряд противоположен предыдущему. Тут разница между соседними числами с каждым шагом увеличивается в 2 раза
15 – 7 = 8
31 – 15 = 16 (16:8 = 2)
63 – 31 = 32 (32:16 = 2)
Следующий шаг будет 32∙2 = 64, соответственно, следующее число будет 63 + 64 = 127
Ответ: 127
Пример 3
Ряд: 2 4 8 10 20 22 44 46 92 94
Взглянем на этот ряд подробнее.
4 – 2 = 2
8:4 = 2
10 – 8 =2
20:10 = 2
То есть одно число на 2 больше предыдущего, а следующее – в 2 раза больше предыдущего.
Далее опять – на 2 больше, и потом в два раза больше.
Следующие числа в этом ряду:
22 – 20 = 2
44:22 = 2
46 – 44 = 2
92:46 = 2
94 – 92 = 2
Соответственно, следующее число будет в 2 раза больше, чем 94. Т.е. это будет 94∙2 = 188
Ответ: 188
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 4
Ряд: 1 2 3 5 7 11 13 17 19
В этом ряду бесполезно искать закономерности, насколько соседние числа отличаются друг от друга. Все числа в этом ряду – простые, то есть без остатка делятся только на 1 и на само себя. Соответственно, следующим в ряду будет следующее после 19 простое число, то есть 23.
После того, как вы поняли, что это ряд простых чисел, то вы поняли, почему иные закономерности в этом ряду искать бесполезно – ведь математики до сих пор не нашли закона, по которому распределяются простые числа, и как можно по формуле (а не путём перебора) найти следующее простое число, зная предыдущие.
Ответ: 23
Дата публикации
02.05.2020