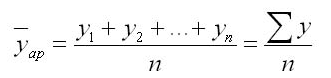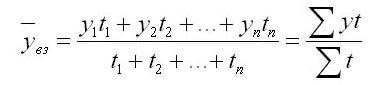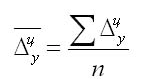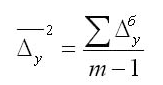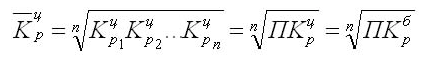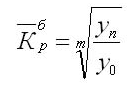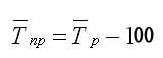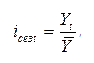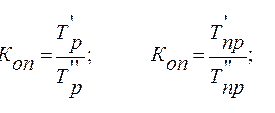Содержание курса лекций «Статистика»
Статистическое изучение динамики социально-экономических явлений
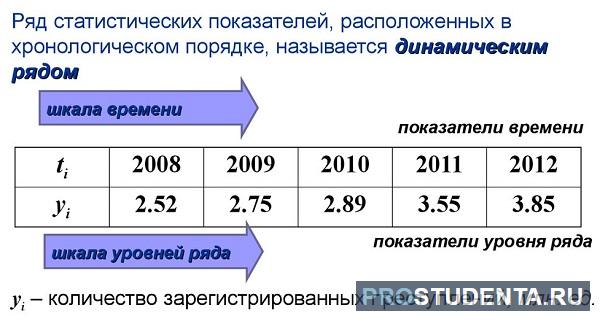
Процессы и явления социально-экономической жизни общества, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении. Для того, чтобы выявить тенденции и закономерности социально-экономического развития явлений, статистика строит особые ряды статистических показателей, которые называются рядами динамики (иногда их называют временными рядами), то есть ‑ это ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В англоязычной литературе для временных рядов используется термин «time series». Ряды динамики получаются в результате сводки и обработки материалов периодического статистического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности. Значения показателя, составляющие ряд динамики, называются уровнями ряда.
Каждый ряд динамики характеризуется двумя параметрами: значениями времени и соответствующими им значениями уровней ряда. Уровни ряда обычно обозначаются «yt»: y1, y2 и т.д. В качестве показателя времени в рядах динамики могут указываться отдельные периоды (сутки, месяцы, кварталы, годы и т.д.) времени или определенные моменты (даты). Время в рядах динамики обозначается через «t».
Ряд динамики состоит из двух элементов:
1) уровня ряда (значения изучаемого показателя);
2) моментов (периодов) времени, когда фиксируется этот показатель.
Основные способы обработки рядов динамики:
1) укрупнение интервалов и расчет для них средних показателей;
2) сглаживание уровней способом скользящей средней;
3) выравнивание по аналитическим формулам.
Суть последнего способа заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени.
Ряды динамики, как правило, представляют в виде таблицы или графически.
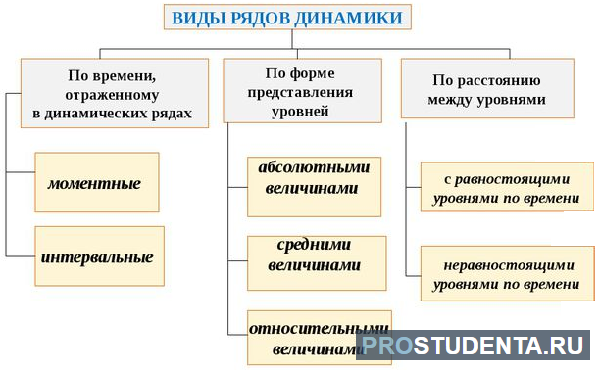
Ряды динамики могут быть классифицированы по следующим признакам:
В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом ряды динамики абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин ‑ как производные.
Ряды динамики абсолютных величин наиболее полно характеризуют развитие процесса или явления, например, грузооборота транспорта, инвестиций в основной капитал, добычи топлива, уставного капитала коммерческих банков и т.д.
Ряды относительных величин могут характеризовать во времени темпы роста (или снижения) определенного показателя; изменение удельного веса того или иного показателя в совокупности или изменение показателей интенсивности отдельных явлений, например, удельного веса приватизированных предприятий в той или иной отрасли; производства продукции на душу населения; структуры инвестиций в основной капитал по отраслям экономики, индекса потребительских цен и т.д.
Ряды динамики средних величин служат для характеристики изменения уровня явления, отнесенного к единице совокупности, например: данные о среднегодовой численности занятых в экономике; о средней урожайности отдельных сельскохозяйственных культур, о средней заработной плате в отдельных отраслях и т.д.
В зависимости от характера временного параметра ряды динамики делятся на моментные и интервальные.
Уровни моментных рядов динамики характеризуют явление по состоянию на определенный момент времени.
Пример. Моментный ряд динамики, характеризующий численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г., представлен в таблице 13.1.
Таблица 13.1 ‑ Численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г
| Дата | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 |
| Численность персонала, чел. | 780 | 810 | 880 | 930 | 940 | 970 |
Следует помнить, что моментные ряды абсолютных величин нельзя суммировать. Бессмысленно, например, складывать численность персонала по состоянию на 1 января, 1 февраля и т.д. Полученная сумма ничего не выражает, так как в ней многократно повторяются одни и те же единицы совокупности.
Ряд, в котором уровни характеризуют результат, накопленный или вновь произведенный за определенный интервал времени, называется интервальным.
Пример. Интервальный ряд динамики, представлен в таблице 13.2.
Таблица 13.2. ‑ Характеристика динамики объема розничного товарооборота
| Дата | 2004 | 2005 | 2006 | 2007 | 2008 |
| Товарооборот, млн. руб. | 28,3 | 31,9 | 38,3 | 42,3 | 45,2 |
Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда вполне реальный показатель, например, общий объем розничного товарооборота за 2004-2008 г.г.
В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями и не равноотстоящими уровнями во времени.
Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называются равноотстоящими, пример (табл. 13.1 и табл. 13.2).
Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются не равноотстоящими, пример(табл. 13.3).
Пример. Рядом динамики с не равноотстоящими уровнями во времени может служить объем экспорта продукции предприятия, представленный в таблице 13.3.
Таблица 13.3. – Динамика объема экспорта продукции предприятия
| Годы | 1993 | 1996 | 1998 | 2000 | 2004 |
| Объем экспорта, млн. долл. | 1110 | 1220 | 1320 | 1450 | 1640 |
По числу показателей можно выделить изолированные (одномерные) и комплексные (многомерные) ряды динамики.
Если ведется анализ во времени одного показателя ряда, то ряд динамики изолированный (например, данные о производстве газа по годам). В многомерном ряду представлена динамика нескольких показателей, характеризующих одно явление.
Сопоставимость уровней и смыкание рядов динамики
Важнейшим условием правильного построения рядов динамики является сопоставимость всех входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.
Рассмотрим основные причины несопоставимости уровней ряда динамики.
Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения и единиц счета.
Пример. Нельзя сравнивать и анализировать цифры о производстве тканей, если за одни годы оно дано в погонных метрах, а за другие ‑ в квадратных метрах.
На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей.
Например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие ‑ с убранной, то такие уровни будут несопоставимы.
В процессе развития во времени, прежде всего, происходят количественные измерения явлений, а затем на определенных ступенях совершаются качественные скачки, приводящие к изменению закономерностей явления. Поэтому научный подход к изучению рядов динамики заключается в том, чтобы ряды, охватывающие большие периоды времени, разделять на такие, которые бы объединяли лишь однокачественные периоды развития совокупности, характеризующейся одной закономерностью развития.
Важно также, чтобы в ряду динамики интервалы или моменты, по которым определены уровни, имели одинаковый экономический смысл.
Например, при изучении роста поголовья скота бессмысленно сравнивать цифры поголовья по состоянию на 1 октября с данными 1 января, так как первая цифра включает не только скот, оставшийся на зимовку, но и предназначенный к убою, а вторая цифра включает только скот, оставленный на зимовку. Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.
Несопоставимость уровней ряда может возникнуть вследствие изменений территориальных границ областей, районов и так далее.
Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых являются несопоставимыми. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).
Пример. Предположим, что в N-ом регионе имеются данные об общем объеме оборота розничной торговли за 2013-2015 гг. в фактически действующих ценах, и за 2015-2018 гг. ‑ в сопоставимых ценах (табл. 13.4.).
Таблица 13.4 ‑ Динамика общего объема оборота розничной торговли (млрд. руб.) цифры условные
|
Годы |
2013 | 2014 | 2015 | 2016 | 2017 |
2018 |
|
Оборот розничной торговли, млрд. руб. (в фактически действующих ценах) |
19,7 | 20 | 21,2 | |||
| Оборот розничной торговли, млрд. руб. (в сопоставимых ценах) | 22,8 | 24,6 | 25,2 |
26,1 |
||
| Сомкнутый ряд абсолютных величин (в сопоставимых ценах; млрд. руб.) |
21,3 |
21,5 | 22,8 | 24,6 | 25,2 |
26,1 |
| Сопоставимый ряд относительных величин (в % к 2005 г.) |
92,9 |
94,3 | 100 | 107,9 | 110,5 |
114,5 |
Решение. Чтобы проанализировать динамику общего объема розничной торговли за 2013-2018 гг., необходимо сомкнуть (объединить) приведенные выше два ряда в один. А чтобы уровни нового ряда были сопоставимы, необходимо пересчитать данные 2003-2005 гг. в сопоставимые цены. Для этого на основе данных об объеме розничной торговли за 2005 г. в фактических и сопоставимых ценах находим соотношение между ними: 22,8:21,2 = 1,08. Умножая на полученный коэффициент данные за 2003-2005 гг., приводим их, таким образом, к сопоставимому виду с последующими уровнями. Сомкнутый (сопоставимый) ряд динамики показан в предпоследней строке таблицы 13.4.
Другой способ смыкания рядов заключается в том, что уровни года, в котором произошли изменения (в нашем примере ‑ уровни 2005 г.), как до изменений, так и после изменений (для нашего примера ‑ в фактических и сопоставимых ценах, т.е. 21,2 и 22,8) принимаются за 100%, а остальные пересчитываются в процентах по отношению к этим уровням соответственно (в нашем примере в фактических ценах ‑ по отношению к 21,2, в сопоставимых ценах ‑ к 22,8). В результате получаем сомкнутый ряд динамики, который показан в последней строке таблицы 13.4.
Та же проблема приведения к сопоставимому виду возникает и при параллельном анализе развития во времени экономических показателей отдельных стран, административных и территориальных районов. Это, во-первых, вопрос о сопоставимости цен сравниваемых стран, во-вторых, вопрос о сопоставимости методики расчета сравниваемых показателей. В таких случаях ряды динамики приводятся к одному основанию, то есть к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.
Аналитические показатели ряда динамики
На практике для количественной оценки динамики явлений широко применяется ряд основных аналитических показателей. К таким показателям относятся, абсолютный прирост при этом принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение – базисным.
Абсолютный прирост (∆y ) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста.
∆y – абсолютный прирост – это разность между уровнями ряда динамики. Может быть цепным или базисным:
(13.1) – абсолютный прирост цепной
(13.2)- абсолютный прирост базисный
Показатель интенсивности изменения уровня ряда ‑ в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста.
Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы).
Тр– темп роста – относительный показатель, получающийся в результате сопоставления двух уровней одного ряда динамики. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем:
(13.3) – темп роста цепной
либо как базисные, когда все уровни сопоставляются с одним и тем же уровнем, выбранным за базу сравнения (при умножении на 100 – в процентном выражении):
(13.4) – темп роста базисный
Между цепными и базисными темпами роста существует взаимосвязь: произведение всех цепных темпов роста равно последнему базисному.
Т пр – темп прироста – относительный показатель, показывающий, насколько один уровень ряда динамики больше или меньше другого, принимаемого за базу сравнения:
(13.5)
При делении абсолютного прироста (цепного) на темп прироста (цепной) получим показатель, называемый значением одного процента прироста – А:
(13.6)- значение одного процента прироста
Пример. Произведем расчет и анализ динамики заключения браков в Омской области за 2000–2003 гг., используя формулы вышеизложенных показателей и данные табл. 13.5. За базу сравнения примем уровень 2000 года.
Таблица 13.5 – Показатели изменения уровней ряда динамики
|
Показатели |
Год | |||
| 2000 | 2001 | 2002 |
2003 |
|
|
Заключение браков, единиц |
13277 | 15130 | 15880 |
16458 |
Абсолютные приросты, ∆y
Далее в табл. 13.6 приведем всю совокупность показателей ряда динамики, позволяющую посмотреть взаимосвязи между ними.
Таблица 13.6 – Показатели изменения уровней ряда динамики
| Показатели | Год | |||
| 2000 | 2001 | 2002 | 2003 | |
| 1. Заключение браков, единиц | 13277 | 15130 | 15880 | 16458 |
| 2. Темпы роста базисные: | − | 1,14 | 1,196 | 1,24 |
| 2.1. коэффициенты | ||||
| 2.2. проценты | − | 114 | 119,6 | 124 |
| 3. Темпы роста цепные: | − | 1,14 | 1,05 | 1,036 |
| 3.1. коэффициенты | ||||
| 3.2. проценты | − | 114 | 105 | 103,6 |
| 4. Абсолютные приросты, ед. | − | 1853 | 2603 | 3181 |
| 4.1. базисные (2000 г.) | ||||
| 4.2. цепные (по годам) | − | 1853 | 750 | 578 |
| 5. Темпы прироста базисные | − | 0,14 | 0,196 | 0,24 |
| 5.1. коэффициенты | ||||
| 5.2. проценты | − | 14 | 19,6 | 24 |
| 6. Темпы прироста цепные | − | 0,14 | 0,05 | 0,036 |
| 6.1. коэффициенты | ||||
| 6.2. проценты | − | 14 | 5 | 3,6 |
| 7. Абсолютное значение 1 % пр. | − | 132,36 | 150 | 160,6 |
При изучении ряда динамики важно проследить за направлением и размером изменений уровня ряда во времени. С этой целью для динамических рядов рассчитываются следующие показатели.
Среднегодовой темп роста, ориентированный на достижение конечного уровня (yn) в исследуемом периоде, можно рассчитать как среднюю геометрическую из годовых темпов роста по следующим формулам:
(13.7)
Если же ориентация берется на достижение суммарного значения (объема) исследуемого показателя за определенный период, то для расчета среднего коэффициента (темпа) роста используется так называемая средняя параболическая вида
(13.8)
где значение k определяется по специальной таблице для расчета средних коэффициентов роста (снижения) по средней параболической.
Пример. Таблица 13.7 – Данные о вводе в действие жилой площади в городе N
| Год | 2002 | 2003-2008 |
| Введено млн. кв. м общей площади, уi | 62,5 | 394,7 |
Определим среднегодовой темп роста ввода в действие жилой площади за 2003‑2008 гг. (т.е. за 6 лет), ориентированный на достижение общей суммы введенного жилья за указанный период (т.е. 394, 7 млн. кв.м).
Решение. Используем формулу (13.8) средней параболической:
далее по таблице для расчета средних коэффициентов роста (снижения) по средней параболической в графе n=6 находим значение, наиболее близкое к полученному отношению (6,315). Это число 6,323, которому соответствует =1,015. Это искомый среднегодовой коэффициент роста ввода жилья за 6 лет. Отсюда, среднегодовой темп роста ввода в действие жилой площади за указанный период составлял 101,5%, а среднегодовой темп прироста был равен 101,5% ‑ 100% =1,5%.
Пример. Таблица 13.8 – Данные о прибыли на предприятии за 2000‑2005 гг.
| Год | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Валовая прибыль, млн руб. | 566 | 521 | 447 | 428 | 391 | 367 |
Рассчитаем среднегодовой темп роста(снижения) за 2000‑2005 гг., ориентированный:
- достижение фактического уровня в 2005 г. по формуле (13.7)
или 91,7%, т.е. ежегодно объем прибыли уменьшался в среднем на 8,3%;
- если при расчете ориентироваться на общий объем, за 5 лет, то применим для расчета формулу (13.8):
Пример. Имеются данные о численности мужской части населения Омской области за 5 лет на начало года (табл. 10.11):
далее по таблице =0,91, т.е. среднегодовое снижение прибыли при общем объеме за 5 лет составило 9%.
На практике, т.к конечный уровень ряда может быть случайным(нехарактерным), чаще применяется расчет по формуле (13.8), где учитывается сумма уровней за n лет.
Прогнозирование на основе рядов динамики
Суть нижеприведенного способа (выравнивание по аналитическим формулам) заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени, т.е.
Таблица 13.9 – Численность мужской части населения в 1999–2003 гг. (на 1.01.),
| Год | 1999 | 2000 | 2001 | 2002 | 2003 |
| Численность
тыс. чел. |
1028,8 | 1020,1 | 1010,7 | 999,6 | 989,8 |
Найдем линию тренда и, используя полученное уравнение, сделаем прогноз на будущее (определим численность мужской части населения в Омской области в 2006 году).
Предположим, что численность населения изменяется во времени по прямой:
(13.9)
Для нахождения параметров а0 и а1 решим систему нормальных уравнений, отвечающих требованию способа наименьших квадратов
(13.10)
Далее в табл. 10.12 рассчитаны необходимые для решения системы уравнения суммы: ∑, ∑t, ∑t2, ∑yt. Годы последовательно обозначим как 1, 2, 3, 4, 5 (n=5).
Таблица 13.10 – Расчетные данные для определения параметров уравнения тренда
| Год | Число мужчин, тыс. чел. yi | Условное обозначение времени, t | t2 | y·t | Уравнение тренда |
| 1999 | 1028,8 | 1 | 1 | 1028,8 | 1029,5 |
| 2000 | 1020,1 | 2 | 4 | 2040,2 | 1019,65 |
| 2001 | 1010,7 | 3 | 9 | 3032,1 | 1009,8 |
| 2002 | 999,6 | 4 | 16 | 3998,4 | 999,95 |
| 2003 | 989,8 | 5 | 25 | 4949 | 990,1 |
| ∑ | 5049 | 15 | 55 | 15048,5 | 5049 |
Из системы уравнений получим a1 = −9,85; а0 = 1039,35;
Отсюда искомое уравнение тренда
Для 2006 года t = 8; следовательно, То есть по прогнозу численность мужской части населения в Омской области в 2006 году составит 960,55 тыс. чел.
Для решения данной задачи можно использовать и второй способ, упрощенный. Если время t обозначить так, чтобы ∑t = 0, т.е. счет вести от середины ряда, то система упростится и примет вид
(13.11)
В этом случае каждое уравнение решается самостоятельно:
(13.12)
(13.13)
Необходимые для расчета параметров уравнения суммы приведем в табл. 10.13.
Таблица 13.11 – Расчетные данные для определения параметров уравнения тренда
| Год | Число мужчин, тыс. чел. yi | Условное обозначение времени, t | t2 | yt | Уравнение тренда |
| 1999 | 1028,8 | -2 | 4 | -2058 | 1029,5 |
| 2000 | 1020,1 | -1 | 1 | -1020 | 1019,65 |
| 2001 | 1010,7 | 0 | 0 | 0 | 1009,8 |
| 2002 | 999,6 | 1 | 1 | 999,6 | 999,95 |
| 2003 | 989,8 | 2 | 4 | 1979,6 | 990,1 |
| Итого | 5049 | 0 | 10 | -98,5 | 5049 |
Тогда и
Уравнение тренда в этом случае будет имеет вид
Для 2006 г. t = 5; следовательно,
Эта величина условная, рассчитанная при предположении, что линейная закономерность изменения численности мужской части населения, принятая для 1999–2003 гг., сохранится на последующий период до 2006 г.
Контрольные задания.
По данным статистических ежегодных изданий: «Российский статистический ежегодник», «Россия в цифрах» и т.п. выберите несколько показателей, постройте и проанализируйте ряды динамики, найдите линию тренда и, используя полученное уравнение, сделайте прогноз на 3 года вперед.
АНОНС…полный текст будет опубликован позднее… в соответствии с графиком занятий
Содержание курса лекций «Статистика»
Чтобы получить выраженные в числах изменения социальной и экономической среды, в статистике применяются разные методы. Среди них выделяется упорядочивание данных с использованием временной последовательности. Ряд динамики – это статистические значения в хронологическом порядке.
Ряд динамики может состоять из:
- значений, связанных с определенным моментом, – датой, днем, и др.;
- данных, связанных с периодом времени. Уровень ряда динамики это и есть полученный показатель.
Виды рядов динамики
Объединение радов происходит по:
- Времени. Это моментные и интервальные ряды.
- Форме представления. К ним относятся абсолютные, относительные и средние величины.
- Интервалам времени. Подразделяются на равномерные и неравномерные ряды.
- Числу смысловых статистических величин. Это изолированные и комплексные ряды.
Чтобы без ошибок построить динамические ряды, необходимо сопоставлять уровни рядов разных периодов. Для этого у них должны быть однородные величины. Также ряды предполагают охват явления с одинаковой полнотой.
Не допускать погрешностей в анализе динамики помогает смыкание рядов динамики. Суть понятия в проведении подготовительной работы до основных расчетов. Во время подготовки ряды объединяются в один. Уровни этих рядов рассчитаны по разным методологиям. Смыкание также включает преобразования, при которых абсолютные уровни рядов приводятся к общему основанию. Это действие помогает избежать несопоставимости уровней.
Анализ показателей в рядах динамики
Ряд динамики характеризует изменения данных внутри этого ряда. Статистические данные необходимо сравнивать также между рядами. По формулам можно определить основные показатели.
Разность уровней ряда динамики называется абсолютным приростом. Показатель демонстрирует, на сколько изменился каждый последующий уровень.
∆УЦ=Уi-Уi-1,
где Уi – уровень У1-УЦ,
Уi-1 – уровень предыдущего периода.
Отношение уровней ряда динамики называется темпом (коэффициентом) роста. По нему видно, во сколько раз изменились последовательные значения.
τp=УiУi-1,
где У1 – начальный уровень ряда.
Темп прироста. Показывает процентное отличие между последовательными уровнями.
Тпр=Тр-1
Если сравнивать между собой числа без всякой системы, не получится грамотно проанализировать ситуацию и выстроить новую стратегию. Например, продвижение продукта на основе маркетинговой стратегии. Использование формул поможет высчитать, какую прибыль принесло компании конкретное решение за анализируемый период.
Анализ показателей за длительный промежуток
Если есть задача оценить изменения, которые касаются длинного временного отрезка, эффективно применить средние показатели. В статистике для их определения используются следующие понятия.
Средний уровень ряда динамики. Применим для интервальных равноотстоящих рядов
→y=∑yn,
где n – число уровней ряда.
Если ряды неравноотстоящие, средний уровень интервального ряда динамики определяется как
→y=∑yt∑t,
где t – длина интервалов времени между уровнями.
Использование перечисленных методов позволяет применять полученные значения в экономике. Определять эффективность финансовых вложений, прогнозировать результаты. В управление предприятиями и бухгалтерию также можно внедрить данные методы для планирования и распределения бюджета.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
16. Показатели динамического ряда, их вычисление и практическое применение.
Динамический
ряд
― ряд однородных сопоставимых величин,
показывающих изменение изучаемого
явления во времени. Это статистическая
форма отображения развития явлений во
времени. Числа, составляющие динамический
ряд, принято называть уровнями ряда.
Уровни
ряда могут быть представлены абсолютными
числами, относительными и средними
величинами.
Различают
следующие виды динамических рядов.
Простой
― ряд,
составленный из абсолютных величин,
характеризующих
динамику одного
явления.
Простые
ряды являются исходными для построения
производных рядов.
Производный
― ряд, состоящий из средних или
относительных величин.
Интервальный
ряд состоит
из последовательного ряда чисел,
характеризующих изменение явления на
определенный период (по времени).
Моментный ряд
состоит из величин, определяющих размеры
явления не за какой-либо отрезок времени,
а на определенную дату — момент.
Для более глубокого
понимания сути развития общественных
явлений исчисляют такие показатели
динамического ряда, как абсолютный
прирост, темп прироста, темп роста,
абсолютное значение 1% прироста.
Абсолютным
приростом
называют разницу между каждым последующим
уровнем и уровнем предыдущим. Абсолютный
прирост может быть положительным и
отрицательным.
Темпом роста
называется отношение каждого последующего
уровня к предыдущему, выраженному в
процентах.
Темпом прироста
называется отношение абсолютного
прироста к предыдущему
уровню, принятому за 100%.
Так
как каждому относительному показателю
соответствуют определенные абсолютные
величины, то при изучении темпов прироста
нужно обязательно учитывать, какая
абсолютная величина соответствует
каждому проценту прироста, каково его
содержание. Для этого исчисляется такой
показатель, как абсолютное
значение одногопроцентаприроста.
Он определяется как частное от деления
абсолютного прироста за определенный
период на темп прироста в процентах за
этот же период.
Для иллюстрации
расчетов рассмотренных статистических
показателей приведем ряд динамики.
Приведем пример.
Необходимо дать анализ динамики
рождаемости в определенном районе
(таблица 5).
Т а б л и ц а 5 —
Динамика
рождаемости в регионе за 1996–2005гг.
|
Год |
Рождаемость, % |
Абсолютный |
Темп прироста, |
Темп роста, % |
Абсолютное |
|
1996 |
9,4 |
— |
— |
— |
— |
|
1997 |
8,9 |
– 0,5 |
– 5,3 |
94,7 |
0,09 |
|
1998 |
9,2 |
0,3 |
3,4 |
103,4 |
0,09 |
|
1999 |
9,3 |
0,1 |
1,1 |
101,1 |
0,09 |
|
2000 |
9,4 |
0,1 |
1,1 |
101,1 |
0,09 |
|
2001 |
9,2 |
– 0,2 |
– 2,1 |
97,9 |
0,10 |
|
2002 |
8,9 |
– 0,3 |
– 3,3 |
96,7 |
0,09 |
|
2003 |
9,0 |
0,1 |
1,1 |
101,1 |
0,09 |
|
2004 |
9,1 |
0,1 |
1,1 |
101,1 |
0,09 |
|
2005 |
9,2 |
0,1 |
1,1 |
101,1 |
0,09 |
Порядок
вычисления следующий:
1. Определяем
абсолютный прирост: 8,9 – 9,4 = – 0,5; 9,2 –
8,9 = 0,3 и т.д.
Вычисляем темп
прироста: – 0,5×100/9,4 = – 5,3 и т.д.
3. Находим темп
роста: 8,9×100/9,4 = 94,7 и т.д.
4. Получаем абсолютное
значение 1% прироста: – 0,5/ – 5,3 = 0,09
Динамический ряд
не всегда состоит из уровней, последовательно
изменяющихся в сторону снижения или
увеличения. Нередко уровни динамического
ряда резко колеблются, и это не позволяет
выявить основную тенденцию, свойственную
изучаемому явлению за определённый
период времени. В таких случаях проводится
выравнивание динамического ряда.
Существует несколько способов выравнивания
динамического ряда: укрупнения интервала,
сглаживание путем вычисления скользящей
средней, аналитическое выравнивание
по прямой и др.
Рассмотрим
выравнивание по прямой линии, которое
осуществляется следующим образом:
Уt
(теоретические уровни) = аo+а1t,
где t
— условное обозначение времени, аo
и а1
— параметры искомой прямой, которые
находятся из решения системы уравнений:
na0
+ a1Σt
= Σy;
a0Σt
+ a1Σt2
= Σyt;
где y
— фактические уровни; n
— число рядов динамики. Система уравнений
упрощается, если t
подобрать так, чтобы их сумма равнялась
0, т.е. начало отсчета времени перенести
в середину рассматриваемого периода.
Тогда:
a0
= Σy/n;
a1
= Σyt/
Σt2.
Подставляя
полученные значения a0
и a1
в формулу,
вычисляют все значения теоретического
уровня.
Рассмотрим следующий
пример (таблица 6):
Т а б л и ц а 6:
Выравнивание
рождаемости за 2003–2008 г г.
|
Год |
Рождаемость, (у) |
Условное
обозначение |
у×t |
t×t |
Теоретический |
Трехлетние |
|
2003 |
9,4 |
– 5 |
– 47 |
25 |
11 |
– |
|
2004 |
8,9 |
– 3 |
– 26,7 |
9 |
10,1 |
9,2 |
|
2005 |
9,2 |
– 1 |
– 9,2 |
1 |
9,3 |
8,8 |
|
2006 |
8,3 |
1 |
8,3 |
1 |
8,5 |
8,9 |
|
2007 |
9,4 |
3 |
18,8 |
9 |
7,7 |
8,7 |
|
2008 |
8.4 |
5 |
25,2 |
25 |
6,9 |
– |
n = 6 Σy
= 53,6 Σyt = –
30,6 Σ
tt=70.
Если ряд четный,
отсчет ведется с 1 (середина ряда), затем
последовательно нечетные числа 3, 5, 7 и
т.д. в обе стороны (вверх с – ; вниз с +);
если ряд нечетный, отсчет условного
обозначения времени ведется с 0 (середина
ряда), затем — 1, 2, 3 и т.д. в обе стороны.
Порядок
вычисления следующий:
Уt
(теоретические уровни) = аo+а1t;
a0
=
Σy/n; a1
=
Σyt/ Σt2;
a0
= 8,9 a1
= – 0,4;
8,9 + (– 0,4) × (– 5) =
11;
8,9 + (– 0,4) × (– 3) =
10,1; и т.д.
Порядок
вычисления скользящей средней:
Для 2004 года (9,4 +
8,9 + 9,2) / 3 = 9,2.
Для 2005 года (8,9 +
9,2 + 8,3) / 3 = 8,8 и т.д.
Укрупнение интервала
производят путём суммирования данных
за ряд смежных периодов (таблица 7).
Т а б л и ц а 7
|
Года |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
|
Рождаемость |
9,4 |
8,9 |
9,2 |
8,3 |
9,4 |
8,4 |
За 2003–2005 рождаемость
составляет 9,4+8,9+9,2=27,5.
За 2006–2008 рождаемость
составляет 8,3+9,4+8,4=26,1.
17.
Связи
между явлениями (функциональная,
корреляционная). Виды корреляционной
связи по силе и направлению. Метод
корреляции рядов (Пирсона), этапы
вычисления коэффициента корреляции,
оценка достоверности
Все явления в
природе и обществе находятся во взаимной
связи. По характеру зависимости явлений
различают:
функциональную
(полную);
корреляционную
(неполную) связи.
Функциональная
связь означает
строгую зависимость явлений, когда
любому значению одного из них всегда
соответствует определенное одно и тоже
значение другого.
При корреляционной
же связи
одной и той же величине одного признака
соответствуют разные величины другого.
Например: между ростом и весом имеется
корреляционная связь, между заболеваемостью
злокачественными новообразованиямии
возрастом и т.д.
По направлению
различают прямые и обратные корреляционные
связи. При прямой ― увеличение одного
из признаков ведет к увеличению другого;
при обратном же ― с увеличением одного
признака второй уменьшается.
По силе связь может
быть сильной, средней и слабой. На основе
статистического анализа можно установить
наличие связи, ее направление и измерить
ее силу.
Одним из способов
измерения связи между явлениями является
вычисление коэффициента корреляции,
который обозначается rху.
Наиболее
точным является метод квадратов
(Пирсона), при котором коэффициент
корреляции определяется по формуле:

где
rху
― коэффициент корреляции между
статистическим рядом X
и Y.
dх
― отклонение каждого из чисел
статистического ряда X
от своей средней арифметической.
dу
― отклонение каждого из чисел
статистического ряда Y
от своей средней арифметической.
В зависимости от
силы связи и ее направления коэффициент
корреляции может находиться в пределах
от 0 до 1 (-1). Коэффициент корреляции,
равный 0, говорит о полном отсутствии
связи. Чем ближе уровень коэффициента
корреляции к 1 или (-1), тем соответственно
больше, теснее измеряемая им прямая или
обратная связь. При коэффициенте
корреляции равном 1 или (-1) связь полная,
функциональная.
Схема оценки
силы корреляционной связи по коэффициенту
корреляции
|
Сила связи |
Величина |
|
|
прямой связи (+) |
обратной связи |
|
|
Связь отсутствует |
0 |
0 |
|
Связь малая |
от 0 до +0,29 |
от 0 до –0,29 |
|
Связь средняя |
от +0,3 до +0,69 |
от –0,3 до –0,69 |
|
Связь большая |
от +0,7 до +0,99 |
от –0,7 до –0,99 |
|
Связь полная (функциональная) |
+1,0 |
–1,0 |
Для вычисления
коэффициента корреляции по методу
квадратов составляется
таблица из 7 колонок. Разберем процесс
вычисления на примере:
ОПРЕДЕЛИТЬ СИЛУ
И ХАРАКТЕР СВЯЗИ МЕЖДУ
СОДЕРЖАНИЕМ ЙОДА
В ВОДЕ И ПОРАЖЕННОСТЬЮ ЗОБОМ:
|
Содержание |
Пора- жен- ность зобом в % (Vy) |
dx |
dy |
dx |
dx2 |
dy2 |
|
201 |
0,2 |
63 |
–3,6 |
–226,8 |
3969 |
0,04 |
|
178 |
0,6 |
40 |
–3,2 |
–128,0 |
1600 |
0,36 |
|
155 |
1,1 |
17 |
–2,7 |
–45,9 |
289 |
1,21 |
|
154 |
0,8 |
16 |
–3,0 |
–48,0 |
256 |
0,64 |
|
126 |
2,5 |
–12 |
–1,3 |
–15,6 |
144 |
6,25 |
|
81 |
4,4 |
–57 |
0,6 |
–34,2 |
3249 |
19,36 |
|
71 |
16,9 |
–67 |
13,1 |
–877,7 |
4489 |
285,61 |
|
Σ |
Σ |
Σ |
1. Определяем
среднее содержание йода в воде (в мг/л).
мг/л
2.Определяем среднюю
пораженность зобом в %.
3. Определяем
отклонение каждого Vx
от Мx,
т.е. dx.
201–138=63; 178–138=40 и
т.д.
4. Аналогично
определяем отклонение каждого Vу
от Mу,
т.е. dу.
0,2–3,8=-3,6; 0,6–38=-3,2
и т.д.
5. Определяем
произведения отклонений. Полученное
произведение суммируем и получаем.
6.
dх
возводим в квадрат и результаты суммируем,
получаем.
7.
Аналогично возводим в квадрат dу,
результаты суммируем, получим
8.
Наконец, все полученные суммы подставляем
в формулу:
Для решения вопроса
о достоверности коэффициента корреляции
определяют его среднюю ошибку по формуле:
(Если
число наблюдений менее 30, тогда в
знаменателе n–1).
В нашем примере
Величина коэффициента
корреляции считается достоверной, если
не менее чем в 3 раза превышает свою
среднюю ошибку.
В нашем примере
Таким образом,
коэффициент корреляции не достоверен,
что вызывает необходимость увеличения
числа наблюдений.
Коэффициент
корреляции можно определить несколько
менее точным, но намного более легким
способом ― методом рангов (Спирмена).
Оценка достоверности:
1. оценка достоверности
интенсивного показателя:
m
= √P
x q / n( корень со всего)
где
p – показатель, выраженный в %, ‰, %оо и
т.д.
q
= (100 – р), при p выраженном в %;
или
(1000 – р), при p выраженном в ‰
или
(10000 – р), при p выраженном в %оо и т.д.
t=1,
достоверность 68,3%
t=2,
95,5%
t=3,
99,7%
2. Оценка достоверности
разности 2 интенсивных показателей

м1 и м2 ошибки репрезентативности.
3. оценка достоверности
среднеарифметической

σ – среднеквадратическое
отклонение
n
– число наблюдений
T=M/m,
если t
больше 2 , ср. арифметическая достоверна.
4.оценка
достоверности разности 2 ср. арифметических
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статистика занимается не только обработкой накопленных данных, но и нахождением тенденций в различных парных показателях, которые связаны друг с другом, что успешно решается применением инструмента «ряды динамики в статистике».
Оглавление:
- Понятие о рядах динамики
- Пример ряда динамики и его характеристика
- Виды рядов динамики
- Правила построения рядов динамики
- Средние характеристики ряда динамики
- Показатели анализа рядов динамики
- Анализ сезонных колебаний
- Приведение рядов динамики к одинаковому основанию
- Аналитическое выравнивание ряда динамики
- Примеры решения задач на тему «Ряды динамики в статистике»
Классическим примером является изменение каких-либо показателей за определенный промежуток времени, что в конце концов сводится не к изучению попарной зависимости (показатель – время), а к изучению изменений показателей в динамике.
Понятие о рядах динамики
Строгое понятие для ряда динамики обозначено в статистике так.
Динамические ряды (иными словами ряд динамики или временной ряд) – это распределенные в увеличивающемся порядке дискретных значений выбранного статистического параметра за последовательные временные промежутки.
Если рассмотреть динамический ряд, будет очевидно, что он наполнен данными в формате y1t1, y2t2, y3t3…yntn. Применительно к временному ряду, значением у будет называться «уровень ряда», при этом первый член ряда (у1) называется базисным (начальным) уровнем, а уn – конечным уровнем. Через обозначение t будет обозначаться временной показатель, который соответствует каждому из уровней ряда.
При построении графической зависимости временного ряда, функция будет иметь вид t(y), где по оси y (ординат) будут отложены значения уровней ряда (параметр у), а по оси х (ось абсцисс) будут отложены временные значения параметра t.
Пример ряда динамики и его характеристика
В качестве примера, рассмотрим следующий ряд.
Таблицу можно озаглавить так: «Годовой выпуск препарата «Ибупрофен» в 2013-2018гг. в млн. уп.»
| Год | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| Годовой объем выпуска, млн. уп. | 88,1 | 91,3 | 96,5 | 99,3 | 101,8 | 100,7 |
В данном ряду можно обнаружить присутствие следующих показателей:
- имеется показатель t, которому соответствует строка «Год», содержащая информацию о периоде, за который выпускался препарат «Ибупрофен»;
- имеется показатель у, который показывает годовой объем производства препарата «Ибупрофен»;
- показатели t и у соотнесены.
На основании изложенного, можно сделать вывод, что перед нами находится временной ряд.
Виды рядов динамики
В зависимости от характеризующего критерия, существует несколько разновидностей динамических рядов.
По временной характеристике различают моментальные и интервальные:
- Для интервальных рядов характерна результативность. Иными словами такой ряд может состоять из суммарной характеристики, которая произошла на данный момент времени t (например, сколько продукции произведено на момент времени, сколько человеко-дней зарегистрировано за определенный период).
- Для моментальных рядов характерно мгновенное значение изучаемой характеристики. К таковым относится, например, объем запаса на требуемое время, затраты времени на временной интервал и др.
При характеристике по показателю t выделяют неполные и полные ряды. Неполными считаются такие, в которых не соблюдается одинаковый промежуток между соседними значениями времени. Для полных, такой интервал соблюден.
Кроме этого, существует классификация по количеству показателей. Существуют изолированные – во времени анализируется всего один показатель и многомерные, когда во времени анализ ведется для целого ряда параметров, которые связаны между собой одним процессом.
Правила построения рядов динамики
Когда производится построение временных рядов, то для них должны соблюдаться общие требования:
- Составитель должен придерживаться принципа периодизации развития, когда разбивка на временные этапы должна быть как можно более однородной и подчиняться единому принципу развития. При этом могут использоваться методы параллельной периодизации, многомерного статистического анализа, а также исторический метод.
- Данные, которые объединяются в многомерный временной ряд, должны обеспечивать возможность сопоставления между собой. Иными словами, должен быть определенный общий признак, например, территориальность, единицы измерения и др.
- Временные интервалы должны быть гармонично подобраны в соответствии с вариативностью наблюдаемой характеристики. Это значит, что для величины, которая слишком часто меняет свое значение, интервал должен быть чаще, а для стабильной величины его следует сделать шире.
- Следует соблюдать систематизацию по временной характеристике – не допускать пропуска временных точек, а если таковые возникли, то интерполировать значения внутри пропущенного интервала.
Средние характеристики ряда динамики
Главный показатель, характеризующий среднее значение абсолютных показателей (y1, y2…yn) – это средний уровень ряда. Если основные интервалы не изменялись, то следует пользоваться выражением для расчета (где t – количество уровней):
Чуть сложнее будет выглядеть методика расчета, если были временные пропуски или они неравны. Вычисления выполняются через арифметическую взвешенную:
Здесь y1, y2…yn – это абсолютные уровни ряда, а t1, t2…tn – протяженности временных интервалов.
Для описания удобно пользоваться параметром среднего абсолютного прироста, представляющим собой среднее от прироста за равные временные промежутки. Когда использованы гармоничные интервалы, формула выглядит так:
Для приведенного выражения обозначение n – это число приростов за выбранный период.
Также есть методика расчетов с использованием базисного абсолютного прироста при равенстве интервалов для смыкания рядов:
Значение m – это количество уровней в выбранном периоде.
Показательная характеристика – средний темп роста, он отображает как происходило изменение уровней рядя (коррелируя с единицами времени). Вычисления для цепных показателей выведены через расчет средней геометрической:
В данном выражении n – количество цепных коэффициентов, Кц – сами цепные коэффициенты.
Когда даны все значения уровней, то выражение значительно упрощается:
Иногда требуется охарактеризовать срединный темп прироста, рассчитывающийся по уравнению на основании уже известных средних темпов роста (Тр):
Показатели анализа рядов динамики
Всего имеются 5 характеристик, предназначающихся для выполнения анализа:
- абсолютный прирост – это параметр, получающийся при нахождении разности определенного уровня и базисного (или тем, который следует до него). Возможен ответ со знаком «-». Выражения для расчета выглядят так:
- коэффициент роста – значение, которое характеризует, в какое количество раз увеличился (или снизился) конкретно взятый для анализа уровень по сравнению с базисным или любым другим (например, идущим перед выбранным). Формула сводится к делению значения анализируемого уровня на значение базисного (отношение уровней):
- темп роста – характеризует процентное соотношение анализируемого показателя в сопоставлении с базисным. Вычисления выполняются перемножением значения коэффициента роста на сто процентов;
- темп прироста – процентный порог возрастания или снижения значения уровня в сопоставлении с базисным. При обсчете необходимо из 100 вычесть показатель темпа роста;
- абсолютное значение 1% прироста будет получено при делении абсолютного прироста на темп прироста. Эти характеристики не относятся к обязательным элементам.
Анализ сезонных колебаний
Если взять для анализа временной ряд, в котором собраны объемы продаж противовирусных препаратов за 5 лет, то будет очевидно, что ежегодно происходят колебания (снижение или увеличение) продаж, которые повторяются. Такие колебания будут именоваться сезонными.
Чтобы устранить нежелательное влияние таких колебаний, проводится аналитическое изучение, выполняющееся либо с помощью гармонического исследования, либо с учетом индекса сезонности.
Индекс сезонности – это фактическая характеристика того, в какое количество раз анализируемый уровень увеличен или уменьшен относительно срединного:
Тут Yt – это уровень, предполагаемый к анализу, а Ȳ – это средний уровень всего ряда.
Более сложный анализ предполагает выделение гармонических колебаний. Для этого производится выравнивание по ряду Фурье (так называемые «гармоники»), и высчитывают, какие гармоники наиболее сопоставимы с анализируемым рядом. Общий вид ряда Фурье для двух гармоник выражается формулой:
Индекс сезонности
Для того чтобы не вычислять относительную разницу в процентах между каждым месяцем во временном ряду, можно вычислить один параметр – индекс сезонности.
Индекс сезонности рассчитывается на основании следующих показателей:
- среднего по анализируемому показателю в указанный временной промежуток за три и более года (yi);
- среднего значения анализируемого показателя внутри одного временного периода (года) – y.
По результатам сопоставления получается значение, которое так или иначе соотносится с уровнем в 100%. Если присутствует значимое отклонение в меньшую сторону, то это является свидетельством присутствия сезонного колебания.
Приведение рядов динамики к одинаковому основанию
Во время работы с несколькими явлениями, описывающими один процесс, может вызывать интерес сопоставление рядов динамики. С целью корректного сопоставления потребуется приведение к одному основанию. Сопутствующей операцией является вычисление коэффициента опережения или отставания.
К каждому ряду находится базисный уровень и вычисляются темпы роста и прироста рядов. Для каждого ряда должен быть выбран аналогичный временной интервал.
Сравнение проводится на основании отношения базисного темпа роста (опционально – прироста) в аналогичном временной интервале. Выражения для расчета достаточно просты:
Аналитическое выравнивание ряда динамики
При определении каких-либо закономерностей во временных рядах и возможности прогнозирования отдельных тенденций, применяется методика аналитического выравнивания. С этой целью производится приближение к определенной алгебраической зависимости, наиболее точно описывающей ряд.
Методика укрупнения интервалов представляет собой преобразование, когда временные промежутки делаются более длительными, что позволяет более точно оценить общий вектор тенденции и понять, какое направление будет иметь зависимость.
Методика скользящей средней основана на особенности временных рядов погашать случайные отклонения от среднего уровня. Каждому звену с использованием простого среднеарифметичнского значения нужно рассчитывать уровень, в котором рандомные колебания сведены к минимуму.
Методика аналитического выравнивания – под конкретный ряд подбирается зависимость, которая более полно отражает алгебраическую зависимость.
Примеры решения задач на тему «Ряды динамики в статистике»
Классическим упражнением является определение вида и показателей для ряда динамики.
Задача. Для указанного временного ряда высчитать: его вид, цепной и базисный прирост, темп роста/прироста, средний темп прироста.
| Отчетный год | Суммарный объем производства, млрд. руб. |
| 2014 | 18 |
| 2015 | 16 |
| 2016 | 17 |
| 2017 | 16 |
| 2018 | 12 |
Согласно определению, этот ряд динамики относится к интервальному, поскольку в условии приведен четкий промежуток времени. Произведем расчет показателей.
Абсолютные показатели
Абсолютные приросты (по цепному способу):
16 – 18 = – 2 млрд. руб.
17 – 16 = 1 млрд. руб.
16 – 17 = – 1 млрд. руб.
12 – 16 = – 4 млрд. руб.
Абсолютные приросты (по базисному методу):
16 – 18 = -2 млрд. руб.
17 – 18 = – 1 млрд. руб.
16 – 18 = -2 млрд. руб.
12 – 18 = – 6 млрд. руб.
Относительные показатели
Цепные темпы роста:
16/18 х 100 = 88,8%;
17/16 х 100 = 106%;
16/17 х 100 = 94,1%;
12/16 х 100 = 75%.
Базисные темпы роста:
16/18 х 100 = 88,8%;
17/18 х 100 = 94,4%;
16/18 х 100 = 88,8%;
12/18 х 100 = 66,6%.
Цепные темпы прироста:
-2/18 х 100 = -11,1%;
1/16 х 100 = 6,25%;
-1/17 х 100 = -5,88%;
4/16 х 100 = 25%.
Базисные темпы прироста:
-2/18 х 100 = -11,1%
1/18 х 100 = 5,55%
-2/18 х 100 = -11,1%
-6/18 х 100 = -33,3%
Средний уровень временного ряда:
(18 + 16 + 17 + 16 + 12) / 5 = 15,8.
Среднегодовой абсолютный прирост:
(12 — 18) / (5 — 1) = -1,5 млрд. руб.
Среднегодовой темп прироста:
90.36 – 100 = -9.64%.
Таким образом временные ряды занимают важное место среди статистических объектов.
Основное их преимущество заключается в широком практическом применении, которое позволяет использовать ряды динамики для наблюдений за физическими величинами и экономическими показателями. Важно знать о нюансах, которые помогут правильно проанализировать такие ряды.