Пусть
требуется изучить статистическую
совокупность относительно некоторого
количественного признака X.
Числовые значения признака будем
обозначать через хi.
Из
генеральной совокупности извлекается
выборка объёма п.
-
Количественный
признак Х
– дискретная
случайная величина.
Наблюдаемые
значения хi
называют вариантами,
а последовательность вариантов,
записанных в возрастающем
порядке, –
вариационным
рядом.
Пусть
x1
наблюдалось n1
раз,
x2
наблюдалось n2
раз,
xk
наблюдалось nk
раз,
причем
![]()
.
Числа ni
называют
частотами,
а их отношение к объёму выборки, т.е.
![]()
,
–
относительными
частотами (или
частостями), причем
![]()
.
Значение
вариант и соответствующие им частоты
или относительные
частоты можно записать в виде таблиц 1
и 2.
Таблица
1
|
Варианта |
x1 |
x2 |
… |
xk |
|
Частота |
n1 |
n2 |
… |
nk |
Таблицу
1 называют дискретным
статистическим
рядом распределения (ДСР) частот, или
таблицей частот.
Таблица
2
|
Варианта |
x1 |
x2 |
… |
xk |
|
Относительная |
w1 |
w2 |
… |
wk |
Таблица
2
ДСР
относительных частот, или
таблица относительных частот.
Определение.
Модой
называется наиболее часто встречающийся
вариант, т.е. вариант с наибольшей
частотой. Обозначается xмод.
Определение.
Медианой
называется
такое значение признака, которое делит
всю статистическую совокупность,
представленную в виде вариационного
ряда, на две равных по числу части.
Обозначается
![]()
.
Если
n
нечетно, т.е. n
= 2m
+ 1,
то
=
xm+1.
Если
n
четно, т.е. n
= 2m,
то
![]()
.
Пример
3.
По результатам наблюдений: 1, 7, 7, 2, 3, 2,
5, 5, 4, 6, 3, 4, 3, 5, 6, 6, 5, 5, 4, 4 построить ДСР
относительных частот. Найти моду и
медиану.
Решение.
Объем выборки n
= 20. Составим ранжированный ряд элементов
выборки: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6,
7, 7. Выделим варианты и подсчитаем их
частоты (в скобках): 1 (1), 2 (2), 3 (3),
4 (4),
5 (5), 6 (3), 7 (2). Строим таблицу:
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
wi |
1/20 |
2/20 |
3/20 |
4/20 |
5/20 |
3/20 |
2/20 |
Наиболее
часто встречающийся вариант xi
=
5. Следовательно, xмод
=
5. Так
как объем выборки n
– четное число, то
![]()
Если
на плоскости нанести точки
![]()
и соединить их отрезками прямых, то
получим полигон
частот.
Если
на плоскости нанести точки
![]()
,
то получим полигон
относительных частот.
Пример 4.
Построить полигон частот и полигон
относительных частот по данному
распределению выборки:
|
xi |
4 |
7 |
8 |
12 |
17 |
|
ni |
2 |
4 |
5 |
6 |
3 |
|
wi |
2/20 |
4/20 |
5/20 |
6/20 |
3/20 |
Решение.
На рисунке 2 показан полигон частот и
на рисунке 3 – полигон относительных
частот.


Рис.
2 Рис.
3
Замечание.
Чем круче полигон, тем равномернее
процесс.
-
Пусть
количественный признак X
– непрерывная
случайная величина,
принимающая значения из интервала
(а,b).
Весь диапазон наблюдаемых данных делят
на частичные
интервалы
[хi;
xi+1),
которые берут обычно одинаковыми по
длине:

=
xi+1
–
xi
(i
= 0, 1, …, k).
Для определения величины интерваламожно использовать формулу
Стерджеса:
![]()
где
(xmax
–
xmin)
разность между наибольшим и наименьшим
значениями признака, k
= 1 + log2
n
число интервалов (log2
n
3,322
lg
n).
Если окажется, что h
дробное число, то за длину частичного
интервала следует брать либо ближайшее
целое число, либо ближайшую простую
дробь. За начало первого интервала
рекомендуется брать величину xнач
=
xmin
–
![]()
.
В каждом
из частичных интервалов подсчитывают
число наблюдаемых значений, т.е. частоту
ni.
По частотам находят относительные
частоты
![]()
.
Полученные интервалы и соответствующие
им частоты (или относительные частоты)
записывают в виде таблицы 3. При этом
правая граница последнего интервала
тоже включается.
Таблица
3
|
Частичный |
[x0, |
[x1, |
… |
[xk-1, |
|
Относительная |
w1 |
w2 |
… |
wk |
Таблица
3 называется интервальным
статистическим рядом распределения
(ИСР) относительных частот,
который задаёт распределение
выборки. Аналогично
составляется ИСР
частот.
Пример
5.
Измерили рост (с точностью до см) 30
наудачу отобранных студентов. Результаты
измерений таковы:
178,
160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175, 170, 166, 159,
173,
182, 167, 171, 169, 179, 165, 156, 179, 158, 171, 175, 173, 164, 172.
Построить
интервальный статистический ряд
относительных частот.
Решение.
Для
удобства проранжируем полученные
данные:
153,
154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167,
169,
170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186.
Отметим,
что Х
рост студента
непрерывная случайная величина. Как
видим, xmin
=
153, хmax
=
186; по формуле Стерджеса, при n
= 30, находим длину частичного интервала
![]()
Примем
![]()
= 6. Тогда хнач
= 153 –
![]()
=150.
Исходные данные разбиваем на шесть (k
=
1 + log230
= 5,907
6) интервалов:
[150,
156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186].
Подсчитав
число студентов ni,
попавших в каждый из полученных
промежутков, получим ИСР:
|
[xi,xi+1) |
[150, |
[156, |
[162, |
[168, |
[174,180) |
[180,186] |
|
ni |
4 |
5 |
6 |
7 |
5 |
3 |
|
wi |
4/30 |
5/30 |
6/30 |
7/30 |
5/30 |
3/30 |
Первая
и третья строчка таблицы образует ИСР
относительных частот.
Замечание.
При
решении учебных задач на построение
ИСР можно пользоваться следующими
правилами.
-
Назначаются нижняя
граница а
и верхняя граница b
для вариант так, чтобы отрезок [a;
b]
вместил всю выборку; часто полагают
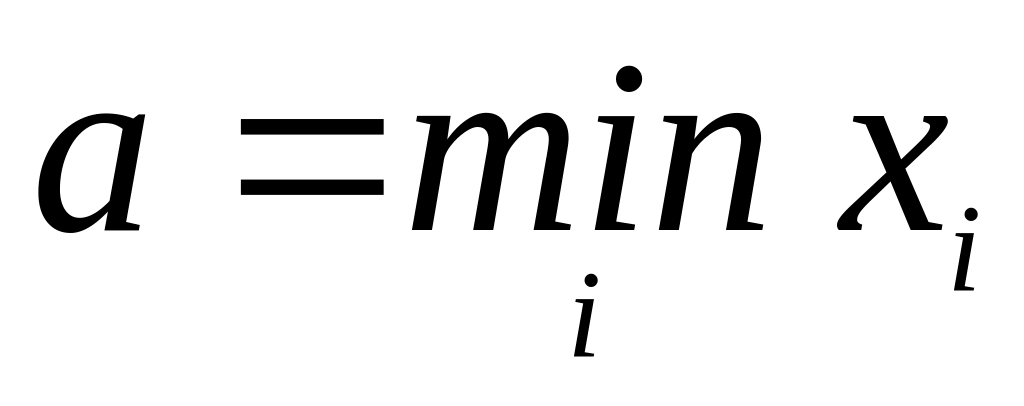
,

,
но иногда a
и b
назначают из соображений удобства, но
не слишком далеко от

и

. -
Находится число
k
равных по длине частичных интервалов
варьирования, которое зависит от объема
выборки и обычно 6
k
20;
рассчитывается длина интервалов
группирования

.
Интервальный
статистический ряд распределения,
представленный графически, называется
гистограммой.
Гистограмма
относительных частот
строится следующим образом: по оси
абсцисс откладываются
интервалы (хi;
хi+1)
и на каждом из них строится прямоугольник
высотой
![]()
где
![]()
;
![]()
.
Площадь
i–го
прямоугольника
![]()
.
Площадь
всей гистограммы
![]()
.
З
амечание:
гистограмма на рисунке 4 – гистограмма
относительных частот.
x3
Рис.
4
Можно
построить гистограмму
частот,
высоты прямоугольников которых равны
![]()
.
Пример 6.
Построить гистограмму частот по данному
ИСР частот:
|
[xi; |
[100; |
[120; |
[140; |
[160; |
[180; |
|
ni |
20 |
50 |
80 |
40 |
10 |
Решение.
По ИСР частот находим длину частичных
интервалов
![]()
= 20 и высоты прямоугольников hi
=
![]()
.
Результаты занесем в таблицу:
|
[xi; |
[100; |
[120; |
[140; |
[160; |
[180; |
|
ni |
20 |
50 |
80 |
40 |
10 |
|
hi |
1 |
2,5 |
4 |
2 |
0,5 |
Искомая
гистограмма частот изображена на рис.
5.

hi
xi
xi
Рис.
5
В
теории вероятностей гистограмме
относительных частот соответствует
график плотности распределения
вероятностей. Распределение выборки,
задаваемое интервальным статистическим
рядом (табл. 3) или таблицей относительных
частот (табл. 2), называется эмпирическим
распределением случайной величины.
По
теореме Бернулли относительная частота
wi,
появление события в п
независимых
испытаниях
сходится
по вероятности к вероятности рi
этого события
![]()
.
Значит во второй строке таблицы 3 и
таблицы 2 стоят
приближённые значения вероятностей рi
следующих событий
![]()
и
![]()
,
поэтому
распределение выборки называют
эмпирическим распределением случайной
величины X.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:

Построим кумуляту и эмпирическую функцию распределения: 

Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) – результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | – |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту

Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
- Главная
- Полезные советы
- Построить интервальный статистический ряд и гистограмму распределения.
Построить интервальный статистический ряд и гистограмму распределения.
Для имеющейся совокупности опытных данных (выборки) требуется:
1) Построить интервальный статистический ряд и гистограмму распределения;
2) Вычислить выборочную среднюю, выборочную дисперсию, выборочное среднеквадратичное отклонение, коэффициент вариации;
3) Выбрать теоретический закон распределения.
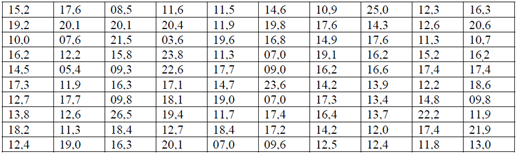
Решение:
Для построения интервального ряда, определим по формуле Старджесса число интервалов: ![]()
Тогда величина интервала равна ![]() − разность между наибольшим и наименьшим значениями признака.
− разность между наибольшим и наименьшим значениями признака.
Отсюда имеем: ![]()
По этим данным составим интервальный статистический ряд:
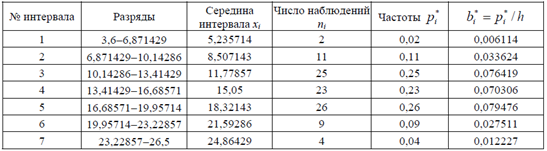
Выборочное среднее определим по формуле среднего арифметического взвешенного:
![]()
Выборочная дисперсия равна:
![]()
Выборочное среднеквадратичное отклонение равно квадратному корню из дисперсии: ![]()
Коэффициент вариации равен: ![]()
Полученному статистическому ряду соответствует нормальное распределение. В качестве теоретического закона распределения используем нормальное распределение с математическим ожиданием 15,148 и дисперсией 19,79.
Если испытываете трудности в написании курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена – от 99 рублей.
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Статистическое распределение выборки
Содержание:
- Примеры использования формул и таблиц для решения практических задач
- Статистический интервальный ряд распределения
Предположим случай, когда из генеральной совокупности извлекается некоторая выборка, при этом каждому значению соответствует некоторый параметр, означающий количество раз, когда появлялось данное значение. Здесь $x_1$ было зафиксировано $n_1$ раз, $x_2$ было обнаружено $n_2$$x_k$ выявлено $n_k$. При этом
$sum_{i=1}^{k}n_i=n$
Где n — объём рассматриваемой выборки.
Определение 1
Используется следующая терминология: $x_k$ носят наименование вариантов, а последовательность таких вариантов, зафиксированный по возрастанию именуется вариационным рядом. Количество наблюдений каждого из вариантов носят название частот. При этом частное частот и выборки называют относительными частотами.
Определение 2
Статистическое распределение —это название всего набора вариантов и частот, которые с ними соотносятся. Чаще всего задаётся с помощью специальной таблицы, где представлены частоты, а также интервалы им соответствующие.
| $x_1$ | $x_2$ | … | $x_k$ |
| $n_1$ | $n_2$ | … | $n_k$ |
| $frac{n_1}{n}$ | $frac{n_2}{n}$ | $frac{n_k}{n}$ |
Здесь в первой строке представлены варианты, во второй частоты, в третьеq взяты относительные частоты.
Для определения размера интервала используется следующее выражение:
$d=frac{x_{max}- x_{min}}{1+3,332cdot lg n}$
Здесь $x_{max}$, $x_{min}$ наибольшее и наименьшее значения ряда вариантов, а n характеризуем объём выборки.
Примеры использования формул и таблиц для решения практических задач
Пример 1
В ходе проведения измерений в однородных группах, были определены следующие значения выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74. Необходимо использовать данные значения, что определить ряд распределения частот и ряд распределения относительных частот.
Решение.
1) Составим статистический ряд распределения частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| ni | 2 | 4 | 8 | 2 | 4 |
2) Рассчитаем суммарный размер выборки: n=2+4+8+2+4=20. Определим относительные частоты, для этого используем формулы: ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Теперь зафиксируем в таблице распределение относительных частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| wi | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
Контрольная сумма должна равняться единице: 0,1+0,2+0,4+0,1+0,2=1.
Полигон частот
Название «полигоном частот» применяют для обозначения ломаной линии, каждый отрезок, которой соединяют точки $(х_1,n_1),(х_2,n_2),…,(х_k,n_k)$. Для построения на графике полигона частот по оси абсцисс отмечают варианты $х_2$, при этом на оси ординат отсчитывают– соответствующие частоты $n_i$. Когда полученные точки $(х_i,n_i)$ соединяются с помощью отрезков, то автоматически получают полигон частот.
Статистический интервальный ряд распределения.
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются, если число различающихся вариант в полученной выборке не слишком большое. Также применение возможно, когда дискретность имеет важное значение для экспериментатора. В тех случаях, когда важный для задачи признак генеральной совокупности Х распределяется непрерывным образом, либо его дискретность нет возможности учесть, то варианты предпочтительнее всего группировать, чтобы получить интервалы.
Статистическое распределение допустимо задавать в том числе в качестве последовательности интервалов и частот, соответствующих этим интервалам. При это за частоту какого-либо интервала принимается сумма всех частот, вошедших в данный интервал.
Особенно следует отметить ,что $h_i-h_{i-1}=h$ при всех i, т.е. группировка проводится с равным шагом h. Также в вопросе группировки можно ориентироваться на ряд полученных опытным путём рекомендацийу, касающихся таких параметров, как а, k и $h_i$:
1. $Rраз_{мах}=X_{max}-X_{min}$
2. $h=R/k$; k-число групп
3.$ kgeq 1+3.321lgn$ (формула Стерджеса)
4. $a=x_{min}, b=x_{max}$
5.$ h=a+h_i, i=0,1…k$
Определённую в ходе решения задачи группировку удобнее всего скомпоновать и перевести в вид специальной таблицы, которая также может именоваться — «статистический интервальный ряд распределения»:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Частоты | n1 | n2 | … | nk-1 | nk |
Таблицу подобного вида можно сделать, поменяв частоты $n_i$ на относительные частоты:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Отн. частоты | w1 | w2 | … | wk-1 | wk |

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример 2
На склад пришла крупная партия деталей. Из них методом случайного отбора взято 50 экземпляров. Рассматривая изделия по одному, особенно интересующему признаку — размеру, определённому с точностью до 1 см, получим следующий вариационный ряд: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Требуется произвести расчёт и определить статистический интервальный ряд распределения.
Решение
Найдём параметры выборки используя сведения из условия задачи.
$k geq1+3,321cdot lg50=1+3.32lg(5cdot10)=1+3.32(lg5+lg10)=6.6$
Получили a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.
| Интервалы группировки | 22-26 | 26-30 | 30-34 | 34-38 | 38-42 | 42-46 | 46-50 |
| Частоты | 1 | 4 | 10 | 18 | 9 | 5 | 3 |
| Отн. частоты | 0.02 | 0.08 | 0.2 | 0.36 | 0.18 | 0.1 | 0.06 |
Десятичные логарифмы от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| lnn≈ | 0 | 0.3 | 0.48 | 0.6 | 0.7 | 0.78 | 0.85 | 0.9 | 0.95 | 1 |
Не получается написать работу самому?
Доверь это кандидату наук!
