Как составить ряд штурма - Сайт, где вы сможете решить свои вопросы

Ряд Штурма (система Штурма) для вещественного многочлена — последовательность многочленов, позволяющая эффективно определять количество корней многочлена на промежутке и приближённо вычислять их с помощью теоремы Штурма^[⇨].

Ряд и теорема названы именем французского математика Жака Штурма, определившего ряд и его свойства, а также разработавшего конструктивный способ построения такого ряда в 1829 году.

Определение[править | править код]

Рассмотрим многочлен f(x) с вещественными коэффициентами. Конечная упорядоченная последовательность отличных от нуля многочленов с вещественными коэффициентами:

$f_{0}(x),f_{1}(x),...,f_{s}(x)quad$

называется рядом Штурма для многочлена f(x) , если выполнены следующие условия:

Значением ряда Штурма в точке называется количество смен знака в последовательности $f_{0}(c),f_{1}(c),...,f_{s}(c)$ после исключения нулей.

Иногда ряд Штурма также определяют как построенный определённым образом^[⇨] ряд Штурма.

Теорема Штурма[править | править код]

Пусть f(x) — ненулевой многочлен с вещественными коэффициентами, $f_{0}(x),f_{1}(x),...,f_{s}(x)$ — некоторый ряд Штурма для него, [a,b] — промежуток вещественной прямой, причём . Тогда число различных корней многочлена f(x) на промежутке [a,b] равно , где W(c) — значение ряда Штурма в точке .

Построение[править | править код]

Ряд Штурма существует для любого ненулевого вещественного многочлена.

Пусть многочлен f(x) , отличающийся от константы, не имеет кратных корней. Тогда ряд Штурма для него можно построить, например, следующим образом:

Для произвольного многочлена (возможно с кратными корнями), отличающегося от константы, можно положить:

$f_{0}(x)={frac {f(x)}{(f(x),f'(x))}}$

и далее следовать приведенному выше способу. Здесь — наибольший общий делитель многочленов f(x) и f'(x) .

Если многочлен f(x) есть ненулевая константа, то его ряд Штурма состоит из единственного многочлена $f_{0}(x)=f(x)$ .

Применение[править | править код]

Ряд Штурма используется для определения количества вещественных корней многочлена на промежутке (см. теорему Штурма). Отсюда вытекает возможность его использования для приближённого вычисления вещественных корней методом двоичного поиска.

Пример[править | править код]

Построим указанным выше способом ряд Штурма для многочлена $f(x)=(x-1)(x-3)=x^{2}-4x+3$

Многочлен $f_{i}(x)$	Знак многочлена в точке

$f_{0}(x)=x^{2}-4x+3$
$f_{1}(x)=2x-4$
$f_{2}(x)=1$
Значение ряда в точке

Таким образом, по теореме Штурма^[⇨] число корней многочлена f(x) равно:

См. также[править | править код]

Теорема Декарта
Обобщенная теорема Штурма

Литература[править | править код]

Кострикин А. И. Введение в алгебру, ч. 1 «Основы алгебры», изд. 2 исправленное, — Физматлит, Москва, 2004.
Шафаревич И. Р. О решении уравнений высших степеней (метод Штурма). — М.: Гостехиздат, 1954.
Штурма теорема — статья из Математической энциклопедии. Проскуряков И. В.

Источник

Пусть дан многочлен n
степени с действительными коэффициентами
(1)

По основной теореме алгебры многочлен
имеет ровно n корней если
многочлен имеет комплексные корни то
они встречаются парами как комплексные
сопряжённые. Комплексных корней всегда
четное число, по этому число действительных
корней с учетом кратности либо равно
степени многочлена либо на четное число
меньше, в частности любой многочлен не
четной степени имеет худобы 1 действительный
корень.

Представляет интерес определения
точного числа действительных корней
многочлена а также промежутков их
принадлежности. Можно показать, что все
действительные корни многочлена
принадлежат интервалу

Ответить на вопрос сколько многочлен
имеет действительных корней в заданном
интервале позволяет теорема штурма, в
которой используются функции штурма.

Для построения ряда штурма выполняют
следующую процедуру: находят производную
многочлена как функции f(x)
это будет некоторый многочлен с
действительными коэффициентами. Для
многочленов f(x)
и f`(x)
выполняют алгоритм похожий на алгоритм
Евклида:

Если данный многочлен не имеет кратных
корней то в этом случае
то последний остаток является многочленом
нулевой степени то есть числом.
Последовательность многочленов:
называется ряд функций штурма. В
дальнейшем нас будут интерисовать знаки
тех значений которые принимают функции
ряда штурма по этому функции образующее
последовательность (2) можно находить
с точностью до постоянного положительного
множителя.

Т(Штурма): Если a,b

и не являются корнями многочлена
f(x)не
имеющего кратных корней то число
действительных корней этого многочлена
принадлежащих интервалу (a,b),

где s(x)
количество перемен знаков в ряде
функций штурма соответственно в точках
a,b.

§29 Отыскание рациональных корней многочлена

Т1: Если рациональное число
является корнем многочлена f(x)
то свободный член делится на p
а старший коэффициент делится на q.

Доказательство:

по
условию. Обе части этого выражения
умножим на

/…СБ4/

2 часть доказательства

Левая часть делится на q
.

Если старший член равен 1 (нормированный)
то все рациональные корни этого многочлена
являются целыми числами причем делителями
свободного член

,,

,
cследовательно корень
целый.

Т2: Если рациональное число

где p,q
взаимно простые является

корнем многочлена f(x)
то для любого целого числа k:

применима теорему о делении

Доказательство:

Если предположить, что (

Получаем, что наша дробь сократима, что
противоречит нашему условию. Мы пришли
к тому, что
делится не может следовательно

■

Следствие: Если многочлен с целыми
коэффициентами нормированный то его
рациональными корнями могут быть только
такие целые числа для которых при любом

Доказательство:

По Т2

30 Т(Критерий не приводимости Эйзенштейна):

Если в многочлене с целыми коэффициентами
f(x) коэффициенты
все до старшего делятся на некоторое
простое число p и старший
коэффициент не делится на p
причем ,
то такой многочлен не приводим над
полем рациональных чисел Q.

Доказательство:

Пусть эти требования выполняются но
многочлен является приводимым то есть
представляется в виде произведения:

пусть

Подставим выражения для
в равенство(2).

Выполним почвенное умножение в правой
части равенства, приведем подобные
слагаемые и воспользуемся определением
равных многочленов то есть мы приравняем
соответствующие коэффициенты:

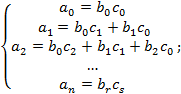
По условию теоремы
Учитывая, что ,
то ,
тогда либо
или либо .
По условию
.
Продолжая так и далее получим, что
от куда следует, что ,
что противоречит условию, что и доказывает
нашу теорему. Заметим, что рассматривая
второй случай также пришли к противоречию.
В этом случае было бы получено, что

что значит и
что противоречит теореме.

■

Замечание: Из теоремы следует
существование многочленов сколь угодно
большой степени с целыми коэффициентами
не приводимыми над полем Q.
Например
является не приводимым над Q.

Пример 1:

Доказать не приводимость многочленов
пользуясь критерием Эйзенштейна:

На полем Q не приводим.

Алгебраические числа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание

1 Определение
- 1.1 Связанные определения
2 Теорема Штурма
3 Построение
4 Применение
- 4.1 Пример
5 Литература
6 См. также

Определение

Рассмотрим многочлен f(x) с вещественными коэффициентами. Конечная упорядоченная последовательность отличных от нуля многочленов с вещественными коэффициентами

называется рядом Штурма для многочлена f(x) , если выполнены следующие условия:

Иногда ряд Штурма также определяют как построенный определённым образом ряд Штурма.

Связанные определения

Теорема Штурма

Пусть f(x) — ненулевой многочлен с вещественными коэффициентами, — некоторый ряд Штурма для него, [a, b] — промежуток вещественной прямой, причём . Тогда число различных корней многочлена f(x) на промежутке [a,b] равно , где W(c) — значение ряда Штурма в точке .

Построение

Ряд Штурма существует для любого ненулевого вещественного многочлена.
Пусть многочлен f(x) , отличающийся от константы, не имеет кратных корней. Тогда ряд Штурма для него можно построить, например, следующим образом:

Для произвольного многочлена, отличающегося от константы, можно положить

$f_0(x) = frac{f(x)}{(f(x),f^'(x))}$

и далее следовать приведенному выше способу. Здесь — наибольший общий делитель многочленов f(x) и f^'(x) . Если многочлен f(x) есть ненулевая константа, то его ряд Штурма состоит из единственного многочлена .

Применение

Пример

Построим указанным выше способом ряд Штурма для многочлена

Многочлен	Знак многочлена в точке




Значение ряда в точке

Таким образом, по теореме Штурма число корней многочлена f(x) равно:

Литература

Кострикин А. И. Введение в алгебру, ч. 1 «Основы алгебры», изд. 2 исправленное, — Физматлит, Москва, 2004.
Шафаревич И. Р. О решении уравнений высших степеней (метод Штурма). — М.: Гостехиздат, 1954.

См. также

Теорема Декарта

Источник

Определение

Рассмотрим многочлен [math]displaystyle{ f(x) }[/math] с вещественными коэффициентами. Конечная упорядоченная последовательность отличных от нуля многочленов с вещественными коэффициентами:

[math]displaystyle{ f_0(x), f_1(x), …, f_s(x) quad }[/math]

называется рядом Штурма для многочлена [math]displaystyle{ f(x) }[/math], если выполнены следующие условия:

множества корней [math]displaystyle{ f_0 }[/math] и [math]displaystyle{ f }[/math] совпадают;
[math]displaystyle{ f_s(x) quad }[/math] не имеет вещественных корней;
если [math]displaystyle{ f_k(c) = 0 quad }[/math] и [math]displaystyle{ 1leqslant kleqslant s – 1 }[/math], то [math]displaystyle{ f_{k-1}(c)f_{k+1}(c) lt 0 }[/math];
если [math]displaystyle{ f(c) = 0 quad }[/math], то произведение [math]displaystyle{ f_0(c)f_1(c) quad }[/math] меняет знак с минуса на плюс, когда [math]displaystyle{ x }[/math], возрастая, проходит через точку [math]displaystyle{ c }[/math], то есть когда существует такое [math]displaystyle{ delta gt 0 }[/math], что [math]displaystyle{ f_0(x)f_1(x) lt 0 quad }[/math] для [math]displaystyle{ xin (c-delta, c) }[/math] и [math]displaystyle{ f_0(x)f_1(x) gt 0 quad }[/math] для [math]displaystyle{ xin (c, c+delta) }[/math].

Значением ряда Штурма в точке [math]displaystyle{ c }[/math] называется количество смен знака в последовательности [math]displaystyle{ f_0(c), f_1(c), …, f_s(c) }[/math] после исключения нулей.

Иногда ряд Штурма также определяют как построенный определённым образом^[⇨] ряд Штурма.

Теорема Штурма

Пусть [math]displaystyle{ f(x) }[/math] — ненулевой многочлен с вещественными коэффициентами, [math]displaystyle{ f_0(x), f_1(x), …, f_s(x) }[/math] — некоторый ряд Штурма для него, [math]displaystyle{ [a, b] }[/math] — промежуток вещественной прямой, причём [math]displaystyle{ f(a)f(b)neq 0 }[/math]. Тогда число различных корней многочлена [math]displaystyle{ f(x) }[/math] на промежутке [math]displaystyle{ [a,b] }[/math] равно [math]displaystyle{ W(a)-W(b) }[/math], где [math]displaystyle{ W(c) }[/math] — значение ряда Штурма в точке [math]displaystyle{ c }[/math].

Построение

Ряд Штурма существует для любого ненулевого вещественного многочлена.

Пусть многочлен [math]displaystyle{ f(x) }[/math], отличающийся от константы, не имеет кратных корней. Тогда ряд Штурма для него можно построить, например, следующим образом:

[math]displaystyle{ f_0(x)=f(x) }[/math];
[math]displaystyle{ f_1(x)=f_0′(x) }[/math];
Если [math]displaystyle{ f_k(x) }[/math] ([math]displaystyle{ kgt 0 }[/math]) имеет корни, то [math]displaystyle{ f_{k+1}(x) = – f_{k-1}(x) bmod f_k(x) }[/math], где [math]displaystyle{ f(x)bmod g(x) }[/math] — остаток от деления многочлена [math]displaystyle{ f(x) }[/math] на многочлен [math]displaystyle{ g(x) }[/math] в кольце многочленов [math]displaystyle{ R [x] }[/math], иначе [math]displaystyle{ s = k }[/math] и построение заканчивается.

Для произвольного многочлена (возможно с кратными корнями), отличающегося от константы, можно положить:

[math]displaystyle{ f_0(x) = frac{f(x)}{(f(x),f'(x))} }[/math],

и далее следовать приведенному выше способу. Здесь [math]displaystyle{ (f(x),f'(x)) }[/math] — наибольший общий делитель многочленов [math]displaystyle{ f(x) }[/math] и [math]displaystyle{ f'(x) }[/math].

Если многочлен [math]displaystyle{ f(x) }[/math] есть ненулевая константа, то его ряд Штурма состоит из единственного многочлена [math]displaystyle{ f_0(x)=f(x) }[/math].

Применение

Пример

Построим указанным выше способом ряд Штурма для многочлена [math]displaystyle{ f(x)=(x-1)(x-3)=x^2-4x+3 }[/math]

Многочлен [math]displaystyle{ f_i(x) }[/math]	Знак многочлена в точке
[math]displaystyle{ -infty }[/math]	[math]displaystyle{ 0 }[/math]	[math]displaystyle{ 1 }[/math]	[math]displaystyle{ 2 }[/math]	[math]displaystyle{ 3 }[/math]	[math]displaystyle{ 4 }[/math]	[math]displaystyle{ +infty }[/math]
[math]displaystyle{ f_0(x)=x^2-4x+3 }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ 0 quad }[/math]	[math]displaystyle{ – quad }[/math]	[math]displaystyle{ 0 quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]
[math]displaystyle{ f_1(x)=2x-4 }[/math]	[math]displaystyle{ – quad }[/math]	[math]displaystyle{ – quad }[/math]	[math]displaystyle{ – quad }[/math]	[math]displaystyle{ 0 quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]
[math]displaystyle{ f_2(x)=1 }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]	[math]displaystyle{ + quad }[/math]
Значение ряда в точке	[math]displaystyle{ 2 quad }[/math]	[math]displaystyle{ 2 quad }[/math]	[math]displaystyle{ 1 quad }[/math]	[math]displaystyle{ 1 quad }[/math]	[math]displaystyle{ 0 quad }[/math]	[math]displaystyle{ 0 quad }[/math]	[math]displaystyle{ 0 quad }[/math]

Таким образом, по теореме Штурма^[⇨] число корней многочлена [math]displaystyle{ f(x) }[/math] равно:

[math]displaystyle{ 2-0=2 }[/math] на промежутке [math]displaystyle{ (-infty, +infty) }[/math]
[math]displaystyle{ 2-0=2 }[/math] на промежутке [math]displaystyle{ (0, 4) }[/math]
[math]displaystyle{ 2-1=1 }[/math] на промежутке [math]displaystyle{ (0, 2) }[/math]

См. также

Теорема Декарта
Обобщенная теорема Штурма

Литература

Кострикин А. И. Введение в алгебру, ч. 1 «Основы алгебры», изд. 2 исправленное, — Физматлит, Москва, 2004.
Шафаревич И. Р. О решении уравнений высших степеней (метод Штурма). — М.: Гостехиздат, 1954.
Штурма теорема — статья из Математической энциклопедии. Проскуряков И. В.

Источник

Приветствую Вас, уважаемые Читатели! Проблема решения уравнений преследовала всех нас со средней школы: сначала мы постигали простейшие линейные и квадратные уравнения, иногда заглядывая в биквадратные и кубические, а иногда и в уравнения высших степеней. Для уравнений степени выше второй уже приходилось применять нестандартные методы, а их решение часто зависело от воли случая.

Источник: https://present5.com/presentation/49364104_140392470/image-3.jpg

Такие же трудности одолевали и математиков до начала 19 века, ведь им никак не удавалось найти универсальный способ решения уравнений степени выше или равной пятой. Все надежды на это разбил гениальный французский математик Эварист Галуа, доказав с помощью своей прорывной теории, что общего решения в радикалах такие уравнения не имеют.

Источник: https://dic.academic.ru/pictures/wiki/files/87/WWirt.jpg

Впрочем, в практической деятельности иногда нет необходимости находить точное значение переменных, ведь достаточно решения с некоторой точностью. Оказалось, что такой универсальный алгоритм в математике существует. Он получил своё имя в честь Жака Шарля Штурма. С его помощью можно определить количество корней ЛЮБОГО алгебраического уравнения на наперед заданных промежутках, что, фактически, ведет к их нахождению с той точностью, с которой заданы такие интервалы. Рассмотрим этот алгоритм подробнее. Поехали!

Крутейший алгоритм Штурма, который позволяет находить корни любых уравнений

Давайте, не решая уравнение, определим, сколько корней оно имеет на отрезке [0;10]. Для этого нам необходимо найти первую производную от исходной функции, а потом вычислить и взять с обратным знаком остаток от их деления:

Теперь у нас три функции: исходная, её производная, а также остаток от их деления. Следующим шагом мы уже делим производную на найденный остаток. Еще раз деление столбиком показывать не буду, а просто покажу результат:

На этом деление заканчивается (пришли к многочлену с нулевой степенью), а мы выходим на финишную прямую. Нам необходимо вычислить знаки четырех функций на концах отрезка:

После расчетов мы должны вычислить количество перемен знаков и вычесть одно из другого. Результат окажется равным количеству действительных корней уравнения на заданном промежутке! Для проверки построим график:

Проверим, как работает алгоритм, например, от -4 до 0:

Получилось! Жаль, что про этот алгоритм не рассказывали в школе, мне кажется, он мог бы упростить решение целого ряда “заковыристых” задач. Но и без этого алгоритм крутейший, достойный всяческого внимания.

Источник

Определение[править | править код]

Теорема Штурма[править | править код]

Построение[править | править код]

Применение[править | править код]

Пример[править | править код]

См. также[править | править код]

Литература[править | править код]

§29 Отыскание рациональных корней многочлена

30 Т(Критерий не приводимости Эйзенштейна):

Содержание

Определение

Связанные определения

Теорема Штурма

Построение

Применение

Пример

Литература

См. также

Определение

Теорема Штурма

Построение

Применение

Пример

См. также

Литература

Вам также может понравиться

Как найти abc по графику

Как найти кубический метр по размерам

Как найти жанровые особенности

Добавить комментарий Отменить ответ