Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена.
Ряд Тейлора был известен задолго до публикаций Брука Тейлора[1] — его использовали ещё в XIV веке в Индии[2], а также в XVII веке Грегори и Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами.
В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Обобщением понятия ряда Тейлора в функциональном анализе является ряд Фантапье.
Определение[править | править код]
1. Многочленом Тейлора функции 



,
используемая в приближённых вычислениях, как обобщение следствия теоремы Лагранжа о среднем значении дифференцируемой функции:
- при
верно
.
При записи суммы использованы обозначение 


2. Рядом Тейлора в точке 



с общим членом
, зависящим от параметра
.
Другими словами, рядом Тейлора функции 


.[3]
Как указано ниже в примерах, наличия бесконечной дифференцируемости функции 


3. Рядом Тейлора в точке 


удовлетворяющей в некоторой окрестности 

называется степенной ряд
.
В отличие от вещественного случая, из условий следует, что найдётся такое значение радиуса 


4. В случае 
называется рядом Маклорена.
Аналитическая функция[править | править код]
1. Функция 








то есть 


Функция называется аналитической на промежутке (на множестве), если она является аналитической в каждой точке этого промежутка (множества).
2. Степенной ряд 


Если в 



Таким образом, для аналитической в точке 




Следствие. Функция 




3. Вопрос: будет ли для произвольной бесконечно дифференцируемой в точке 






Ответ: нет.
Существуют бесконечно дифференцируемые функции вещественной переменной, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности

Примеры. Функции вещественной переменной 

являются бесконечно дифференцируемыми в точке 
Следовательно, ряды Тейлора всех этих функций с параметром 
Однако, для любого 


в которых функции отличны от 
Таким образом, эти функции не являются в точке 
Доказательство
Доказательство проведём для функции 
Функция 
для всех 
Для 

Функция 



дополненная пределами слева
и справа 

Найдём производную функции 

По определению:

Поскольку для 

то
докажем, что для произвольного 

Применение правила Лопиталя непосредственно к частям
не приводит к результату.
Выполним замену переменной: 

Пусть 
Применяя правило Лопиталя 




.
Таким образом,
.
Найдём (для 
производных функции 
И так далее. Во всех случаях, очевидно,
получается произведение
на сумму целых отрицательных степеней

Конечная сумма
бесконечно малых является бесконечно малой.
Таким образом,

Вычисляя последовательно по определению (как выше) производные 

обнаруживаем, что все производные в
точке 
Область сходимости ряда Тейлора[править | править код]
Ряд Тейлора, являясь степенным рядом, имеет в качестве области сходимости круг (с центром в точке 
и интервал (с центром в точке 
1. Например, функция 





2. Радиус сходимости ряда Тейлора можно определить, например, по формуле Даламбера:
.
3. Рассмотрим для примера экспоненциальную функцию 



4. От параметра — точки разложения 
Например, разложим в общем случае (для произвольного 


Можно доказать с помощью формулы суммы геометрической прогрессии, что данный ряд, как функция аргумента 


Действительно,
.
Область сходимости ряда может быть задана неравенством 





Формула Тейлора[править | править код]
Предположим, что функция 









Достаточно легко доказать, что такой многочлен имеет вид 








Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Различные формы остаточного члена[править | править код]
В форме Лагранжа:
В форме Коши:
В интегральной форме:
Ослабим предположения:
- В асимптотической форме (форме Пеано, локальной форме):
Критерий аналитичности функции[править | править код]
Основной источник: [5]
Предположим, что некоторую функцию 



Во-первых, необходимым условием аналитичности функции является сходимость ряда Тейлора в некоторой непрерывной области. Действительно, если ряд Тейлора сходится всего в одной точке, то это точка 

Во-вторых, по формуле Тейлора в ряд Тейлора с остаточным членом может быть разложена любая (а не только аналитическая) функция, бесконечно дифференцируемая в окрестности, содержащей точку 





Очевидно, что функция 






В качестве примера рассмотрим экспоненциальную функцию 



Остаточный член разложения этой функции в форме Лагранжа имеет вид 



Здесь используется, что на фиксированном промежутке экспонента ограничена некоторым числом 
Причем, как видно, предел остаточного члена равен нулю для любых 

Ряды Маклорена некоторых функций[править | править код]
- Гиперболические функции[6][10]:
- Обратные гиперболические функции[6][11]:
Формула Тейлора для функции двух переменных[править | править код]
Пусть функция 


Введём дифференциальный оператор
.
Тогда разложение (формула Тейлора) функции 



где 
Следует иметь в виду, что операторы 
в 



Аналогичным образом формула строится для функций любого числа переменных, меняется только число слагаемых в операторе 
В случае функции одной переменной 
Формула Тейлора многих переменных[править | править код]
Для получения формулы Тейлора функции 



Тогда разложение (формула Тейлора) функции по степеням 

где 

Для функции 


В другой форме ряд Тейлора можно записать таким образом:

Пример разложения в ряд Маклорена функции трёх переменных[править | править код]
Найдём выражение для разложения в ряд Тейлора функции трёх переменных 




Разложение в ряд Тейлора запишется в виде
Учитывая, что
получим
Например, при 
Примечания[править | править код]
- ↑ Taylor, Brook, Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (London, 1715), pages 21-23 (Proposition VII, Theorem 3, Corollary 2). Translated into English in D. J. Struik, A Source Book in Mathematics 1200—1800 (Cambridge, Massachusetts: Harvard University Press, 1969), pages 329—332.
- ↑ Gupta R. C. The Madhava-Gregory series, Math. Education 7 (1973), B67-B70.
- ↑ Запорожец Г. И. «Руководство к решению задач по математическому анализу» — С. 371
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления. — Мифрил, 1996. — С. Том 1, глава 4, параграф 6.
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления для втузов. — тринадцатое. — МОСКВА “НАУКА”, 1985. — С. Том 2, глава 16, параграф 16.
- ↑ 1 2 3 4 5 6 Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — 4-е изд. — М.: Наука, 1963.
- ↑ Цукер Р. Тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 37—43. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 44—47. — 832 с. — 50 000 экз.
- ↑ При значении x, близком к 1, эта расчётная формула сходится медленно, т.е. даёт большую погрешность при приближении функции суммой первых нескольких членов ряда. Поэтому можно воспользоваться формулой
где
- ↑ Цукер Р. Гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 48—49. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 50—53. — 832 с. — 50 000 экз.
Литература[править | править код]
- Ильин В. А., Садовничий В. А., Сендов Б. Х. Математический анализ, ч. 1, изд. 3, ред. А. Н. Тихонов. М.: Проспект, 2004.
- Камынин Л. И. Математический анализ. Т. 1, 2. — 2001.
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр, Интерактивный компьютерный учебник.
- Маркушевич А. И. Теория аналитических функций. В 2 т. — Изд. 2-е. — М.: Наука, 1967. — Т. 1: Начала теории. — 486 с.
- Нарасимхан Р. Анализ на действительных и комплексных многообразиях. — пер. с англ. Е. М. Чирки. — М.: Мир, 1971. — 232 с.
- Петрова С. С., Романовска Д. А. К истории открытия ряда Тэйлора. // Историко-математические исследования. — М.: Наука, 1980. — № 25. — С. 10—24.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 1. — 432 с.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 2. — 560 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. В 3 т. — Изд. 8-е. — М.: ФИЗМАТЛИТ, 2003. — Т. I. — 680 с. — ISBN ISBN 5-9221-0156-0.
Степенные ряды в форме рядов Тейлора и Маклорена
Степенные ряды и, в частности, ряды Тейлора являются одним из видов функциональных рядов.
Степенной ряд в общем виде записывается как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots – постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости, когда для частичных сумм Sn(x)S_n(x) существует предел, сумма ряда S(x)S(x):
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n,limn→∞Sn(x)=S(x)S_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n, quad limlimits_{n to infty } S_n (x) = S (x)
Возьмем функцию действительной переменной f(x)f(x), которая является бесконечно дифференцируемой в точке x0x_0. Такую функцию можно разложить в степенной ряд следующего вида:
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{”}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд по степеням двучлена (x−x0)(x-x_0) называют рядом Тейлора.
В случае x0=0x_0=0 полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{”}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Ряд Тейлора можно записать в другом виде. Полагая:
x−x0=t,f(x)=f(x0+t)=g(t)x-x_0=t, quad f(x)=f(x_0+t)=g(t)
ряд Тейлора
f(x)=f(x0+t)=f(0)+f′(x0)1!t+f′′(x0)2!t2+…+f(n)(x0)n!tn+…=∑k=0∞f(k)(x0)k!tkf(x)=f(x_0+t)=f(0)+dfrac{f{‘}(x_ 0)}{1!} t +dfrac{f{”}(x_0)}{2!}t^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}t^k
сводится к ряду Маклорена:
g(t)=g(0)+g′(0)1!t+…+g(n)(0)n!tn+…=∑k=0∞g(k)(0)k!tkg(t)=g(0)+dfrac{g{‘}( 0)}{1!}t +ldots+dfrac{g^{(n)}(0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{g^{(k)}(0)}{k!}t^k
Как и в случае произвольного степенного ряда, ряды Тейлора и Маклорена имеют интервал сходимости.
Пример
Разложим в ряд Тейлора функцию:
f(x)=1xf(x)=dfrac{1}{x}
в окрестности точки x0=1x_0=1.
С помощью замены:
x−x0=x−1=tx-x_0=x-1=t
функция сводится к виду:
f(x)=f(t+1)=11+tf(x)=f(t+1)=dfrac {1}{1+t}
Полученное выражение при ∣t∣<1|t|<1 является суммой бесконечно убывающей геометрической прогрессии знаменателем (−t)(-t), и ряд записывается в виде:
11+t=1−t+t2−t3+…+(−1)ntn+…=∑k=0∞(−1)ktkdfrac {1}{1+t}=1-t+t^2-t^3+ldots+(-1)^{n}t^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}t^{k}
Возвращаясь к переменной xx, получаем разложение по степеням двучлена (x−1)(x-1):
1x=1−(x−1)+(x−1)2−(x−1)3+…+(−1)n(x−1)n+…=∑k=0∞(−1)k(x−1)k,∣x−1∣<1dfrac {1}{x}=1-(x-1)+ (x-1)^2-(x-1)^3+ldots+(-1)^{n}(x-1)^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}(x-1)^{k}, quad |x-1|<1
Формула Тейлора
Следствием разложения функции в степенной ряд является соответствующая формула Тейлора. Если функция f(x)f(x) имеет в точке x0x_0 производные до nn –го порядка включительно, то функцию f(x)f(x) можно представить с помощью формулы Тейлора:
f(x)=f(x0)+f′(x0)1!(x−x0)+…+f(n)(x0)n!(x−x0)n+Rn(x)f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +R_n (x)
или
f(x)=∑k=0nf(k)(x0)k!(x−x0)k+Rn(x)f(x)= sumlimits_{k=0}^{n} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k +R_n (x),
где функция Rn(x)R_n (x) называется остаточным членом.
Формы остаточного члена
Существует несколько форм для остаточного члена. В частности, если f(x)f(x) дифференцируема (n+1)(n+1) раз в окрестности x0x_0, то Rn(x)R_n (x) может быть представлена в форме Лагранжа:
Rn(x)=f(n+1)(ξ)(n+1)!xn+1,x<ξ<x0R_n (x)=dfrac {f^{(n+1)}(xi)}{(n+1)!} x^{n+1}, quad x<xi<x_0 или x<ξ<x0x<xi<x_0.
Если функция f(x)f(x) дифференцируема (n−1)(n-1) раз в окрестности x0=0x_0=0, то Rn(x)R_n(x) может быть представлена в форме Пеано:
Rn(x)=o((x−x0)n)R_n(x)=o((x-x_0)^n).
Учитывая, что ряд Тейлора можно свести к ряду Маклорена, запишем формулу Тейлора для основных элементарных функций в окрестности x0=0x_0=0 и укажем соответствующие интервалы сходимости.
Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+o(xn),∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+o(x^n),quad |x|<infty
Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+o(x2n),∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ o(x^{2n}),quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+o(x2n+1),∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ o(x^{2n+1}),quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+o(x2n+2),∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ o(x^{2n+2}),quad |x|le{1}
Логарифмическая функция:
ln(1+x)=x1!−x22!+x33!−…+(−1)n+1xnn!+o(xn),x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ o(x^n),quad xin (-1;1]
Степенная функция:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+o(xn)(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ o(x^n)
Пример 1
Разложим, используя формулу Тейлора, функцию
f(x)=(x+1)ln(x2+2x+2)f(x)=(x+1)ln (x^2+2x+2)
в окрестности точки x0=−1x_0=-1 с точностью до o((x+1)7)o((x+1)^7).
Выполнив замену переменной
x−x0=x+1=tx-x_0=x+1=t
получаем:
g(t)=tln(1+t2)g(t)=tln(1+t^2)
Используя разложение логарифмической функции, получаем:
g(t)=t(t21!−(t2)22!+(t2)33!+o((t2)3))=t3−t52+t76+o(t7)g(t)=t left( dfrac{t^2}{1!}-dfrac{(t^2)^2}{2!}+dfrac{(t^2)^3}{3!}+o((t^2)^3) right)=t^3-dfrac{t^5}{2}+dfrac{t^7}{6}+o(t^7)
Выполняем далее обратную замену переменной:
f(x)=(x+1)3−(x+1)52+(x+1)76+o((x+1)7)f(x)= (x+1)^3-dfrac{(x+1)^5}{2}+dfrac{(x+1)^7}{6}+o((x+1)^7)
Пример 2
Разложим, используя формулу Тейлора, функцию
f(x)=(x2−4x)cos(2x−4)f(x)=(x^2-4x)cos{(2x-4)}
в окрестности точки x0=2x_0=2 с точностью до o((x−5)5)o((x-5)^5).
Выполнив замену переменной:
x−x0=x−2=t,x=t+2x-x_0=x-2=t, quad x=t+2
получаем:
g(t)=(t2−4)cos2tg(t)=(t^2-4)cos{2t}
Используя разложение тригонометрической функции, получаем:
g(t)=(t2−4)(1−(2t)22!−(2t)44!+o(t5))=(t2−4)(1−2t2+2t43+o(t5))g(t) =(t^2-4) left( 1-dfrac{(2t)^2}{2!}-dfrac{(2t)^4}{4!}+o(t^5) right) =(t^2-4) left( 1-2t^2+dfrac{2t^4}{3}+o(t^5) right)
Раскрываем скобки, ограничиваясь слагаемыми со степенью t не выше пяти:
g(t)=(t2−2t4)−(4−8t2+8t43+o(t5))=−4+9t2−143t4+o(t5)g(t) =(t^2-2t^4)- left( 4-8t^2+dfrac{8t^4}{3}+o(t^5) right) =-4+9t^2-dfrac{14}{3} t^4+o(t^5)
Выполняя обратную замену переменной, получаем:
f(x)=−4+9(x−2)2−143(x−2)4+o((x−2)5)f(x)=-4+9(x-2)^2-dfrac{14}{3}(x-2)^4+o((x-2)^5)
Применение формулы Тейлора при x, стремящемся к бесконечности
При необходимости представить функцию с помощью формулы Тейлора при x→∞x to infty с точностью до o(1xn)oleft( dfrac {1} {x^n}right), последовательно:
- выполняем замену переменной t=1xt=dfrac{1}{x};
- полученную функцию g(t)g(t) представляем с помощью формулы Тейлора с необходимой точностью;
- с помощью обратной замены переменных находим искомое выражение для f(x)f(x).
Пример
Разложим, используя формулу Тейлора, функцию
f(x)=2x−x2−1f(x)=2x-sqrt{x^2-1}
с точностью до o(1×3)oleft( dfrac {1} {x^3}right) при x→+∞x to +infty.
Выполнив замену переменной
t=1x,x=1tt=dfrac{1}{x}, quad x=dfrac{1}{t}
получаем:
g(t)=2t−1t2−1=2−(1−t2)1/2tg(t)=dfrac {2}{t}-sqrt {dfrac{1}{t^2}-1}=dfrac{2-(1-t^2)^{1/2}}{t}
Учитывая требуемую точность o(t3)o(t^3), используем разложение степенной функции в ряд Тейлора с точностью до o(t4)o(t^4):
g(t)=2−(1−t22−t48)+o(t4)t=1t+t2−t38+o(t3)g(t)=dfrac {2-left( 1-dfrac{t^2}{2}-dfrac{t^4}{8}right)+o(t^4)}{t}=dfrac{1}{t}+dfrac{t}{2}-dfrac{t^3}{8}+o(t^3)
Выполняя обратную замену переменной, находим:
f(x)=x+12x−18×3+o(1×3),x→+∞f(x)=x+dfrac{1}{2x}- dfrac {1}{8x^3}+ oleft( dfrac {1} {x^3}right), quad x to +infty
Применение формула Тейлора при вычислении пределов
С помощью разложения функции с использованием формулы Тейлора при вычислении пределов можно избавиться от неопределённостями различного вида. Проиллюстрируем использование формулы Тейлора на примере вычисления предела функции с неопределенностью вида (00)left( dfrac {0} {0}right).
Пример 1
Вычислим, используя формулу Тейлора, предел:
limx→1ex−ecos(x−1)sin(x−1)limlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}
Заменим ex{e^{x}} и тригонометрические функции их разложениями в степенные ряды в окрестности x0=1x_0=1, находим:
limx→1ex−ecos(x−1)sin(x−1)=limx→1(e+e(x−1)+e(x−1)22!+e(x−1)33!+…)−e(1−(x−1)22!+…)(x−1)−(x−1)33!+…=elimx→1(x−1)+(x−1)2+(x−1)36+…(x−1)−(x−1)36+…=elimx→11+(x−1)+(x−1)26+…1−(x−1)26+…=elimlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}=limlimits_{x to 1} dfrac {left(e+e(x-1)+dfrac{e(x-1)^2}{2!}+dfrac{e(x-1)^3}{3!} +ldots right)-eleft( 1-dfrac{(x-1)^2}{2!}+ ldots right)} {(x-1)-dfrac{(x-1)^3}{3!}+ ldots}= elimlimits_{x to 1 } dfrac {(x-1)+(x-1)^2+ dfrac{(x-1)^3}{6}+ldots} {(x-1)- dfrac{(x-1)^3}{6}+ldots} =e limlimits_{x to 1 } dfrac {1+(x-1) +dfrac{(x-1)^2}{6}+ldots} {1- dfrac{(x-1)^2}{6}+ldots} =e
Тест по теме «Формула и ряд Тейлора»
-
Понятие ряда Тейлора.
Начать изучение
-
Остаточный член формулы Тейлора.
Начать изучение
-
Разложение элементарных функций в ряд Тейлора.
Начать изучение
-
Разложение показательной и гиперболической функций в ряд Тейлора.
Начать изучение
-
Разложение тригонометрических функций в ряд Тейлора.
Начать изучение
-
Разложение логарифмической функции в ряд Тейлора.
Начать изучение
-
Разложение степенной функции в ряд Тейлора.
Начать изучение
-
Элементарные функции комплексного переменного.
Начать изучение
Понятие ряда Тейлора.
Определение.
Если функция (f(x)) определена в некоторой окрестности точки (x_{0}) и имеет в точке (x_{0}) производные всех порядков, то степенной ряд
$$
f(x_{0}) + sum_{n=1}^{infty}frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}label{ref1}
$$
называется рядом Тейлора функции (f) в точке (x_{0}).
Пусть функция (f) регулярна в точке (x_{0}), то есть представляется в некоторой окрестности точки (x_{0}) сходящимся к этой функции степенным рядом
$$
f(x) = sum_{n = 0}^{infty}a_{n}(x-x_{0})^{n},quad |x-x_{0}| < rho, rho > 0.label{ref2}
$$
Тогда по теореме, доказанной здесь, функция (f) бесконечно дифференцируема в окрестности точки (x_{0}), причем коэффициенты ряда eqref{ref2} выражаются формулами
$$
a_{0} = f(x_{0}),quad a_{n} = frac{f^{(n)}(x_{0})}{n!},quad n in mathbb{N}.label{ref3}
$$
Таким образом, степенной ряд для функции (f(x)), регулярной в данной точке (a), совпадает с рядом Тейлора функции (f) в точке (a).
Если известно, что функция (f(x)) бесконечно дифференцируема в точке (a) (и даже в некоторой окрестности этой точки), то нельзя утверждать, что составленный для этой функции ряд Тейлора eqref{ref1} сходится при (x neq x_{0}) к функции (f(x)).
Рассмотрим функцию (f(x) = e^{-1/x^{2}}), (x neq 0), (f(0) = 0). Эта функция определена на (R),
$$
f'(x) = frac{2}{x^{3}}e^{-1/x^{2}}, f″(x) = left(frac{4}{x^{6}}-frac{6}{x^{4}}right)e^{-1/x^{2}}quadmbox{при} x neq 0,nonumber
$$
откуда с помощью индукции легко показать, что
$$
f^{(n)}(x) = e^{-1/x^{2}} Q_{3n} left(frac{1}{x}right) mbox{при} x neq 0,nonumber
$$
где (Q_{3n}(t)) — многочлен степени (3n) от (t). Воспользуемся тем, что (displaystylelim_{x rightarrow 0}frac{1}{|x|^{k}}e^{-1/x^{2}}=0) для любого (k in mathbb{N}) (решение можно посмотреть здесь), и докажем, что
$$
f^{(k)}(0) = 0 mbox{для любого} k in mathbb{N}.label{ref4}
$$
Утверждение eqref{ref4} верно при (k = 1), так как (f'(0) = displaystylelim_{x rightarrow 0}frac{e^{-1/x^{2}}}{x} = 0), откуда, предположив, что формула eqref{ref4} справедлива при (k = n), находим
$$
f^{(n + 1)}(0) = lim_{x rightarrow 0}frac{f^{(n)}(x)-f^{(n)}(0)}{x} = lim_{x rightarrow 0} frac{1}{x} Q_{3n} left(frac{1}{x}right) e^{-1/x^{2}} = 0.nonumber
$$
Таким образом, по индукции доказано равенство eqref{ref4}, и поэтому все коэффициенты ряда Тейлора eqref{ref1} в точке (x_{0} = 0) для рассматриваемой функции равны нулю.
Так как (e^{-1/x^{2}} neq 0) при (x neq 0), то сумма ряда Тейлора для функции (f) не совпадает с (f(x)) при (x neq 0). Иначе говоря, эту функцию нельзя представить рядом Тейлора, сходящимся к ней в окрестности точки (x_{0} = 0).
Причина этого явления становится понятной, если функцию (f) рассматривать в комплексной плоскости. В самом деле, функция (f(z) = e^{-1/z^{2}}) не является непрерывной в точке (z = 0), так как (f(x) = e^{-1/x^{2}} rightarrow 0) при (x rightarrow 0), a (f(iy) = e^{1/y^{2}} rightarrow +infty) при (y rightarrow 0).
Остаточный член формулы Тейлора.
Пусть функция (f(x)) бесконечно дифференцируема в точке (x_{0}). Тогда ей можно поставить в соответствие ряд eqref{ref1}. Обозначим
$$
S_{n}(x) = sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k},label{ref5}
$$
$$
r_{n}(x) = f(x)-S_{n}(x)label{ref6}
$$
и назовем (r_{n}(x)) остаточным членом формулы Тейлора для функции (f) в точке (x_{0}). Если существует
$$
lim_{x rightarrow 0} r_{n}(x) = 0,label{ref7}
$$
то согласно определению сходимости ряда ряд eqref{ref1} сходится к функции (f(x)) в точке (x), то есть
$$
f(x) = sum_{n = 0}^{infty}frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}.label{ref8}
$$
Теорема 1.
Если функции (f(x)), (f'(x)), …, (f^{(n + 1)}(x)) непрерывны на интервале (Delta = (x_{0}-delta, x_{0} + delta)), где (delta > 0), то для любого (x in Delta) остаточный член формулы Тейлора для функции (f) в точке (x_{0}) можно представить:
- в интегральной форме
$$
r_{n}(x) = frac{1}{n!} intlimits_{x_{0}}^{x} (x-t)^{n}f^{(n + 1)}(t) dt;label{ref9}
$$ - в форме Лагранжа
$$
r_{n}(x) = frac{f^{(n + 1)}(xi)}{(n + 1)!}(x-x_{0})^{n + 1},label{ref10}
$$
где (xi) принадлежит интервалу с концами (x_{0}) и (x).
Доказательство.
(circ) Формула eqref{ref10} доказана в здесь. Докажем формулу eqref{ref9} методом индукции. В силу равенств eqref{ref5} и eqref{ref6} нужно показать, что
$$
f(x)-f(x_{0}) = sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k} + frac{1}{n!} intlimits_{x_{0}}^{x} (x-t)^{n}f^{(n + 1)}(t) dt.label{ref11}
$$
Воспользуемся равенством (displaystyleintlimits_{x_{0}}^{x} f'(t) dt = f(x)-f(x_{0})) и преобразуем его левую часть с помощью формулы интегрирования по частям:
$$
intlimits_{x_{0}}^{x} f'(t) dt =-left.intlimits_{x_{0}}^{x} f'(t)d(x-t) = [-f'(x)(x-t)]right|_{t = x_{0}}^{t = x} + intlimits_{x_{0}}^{x} (x-t)f″(t) dt =\= f'(x_{0})(x-x_{0}) + intlimits_{x_{0}}^{x} (x-t)f″(t) dt.nonumber
$$
Таким образом,
$$
f(x)-f(x_{0}) = f'(x_{0})(x-x_{0}) + intlimits_{x_{0}}^{x} (x-t)f″(t) dt,nonumber
$$
то есть формула eqref{ref11} верна при (n = 1). Предположим, что формула eqref{ref11} является верной для номера (n-1), то есть
$$
f(x)-f(x_{0}) = sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k} + frac{1}{(n-1)!} intlimits_{x_{0}}^{x} (x-t)^{n-1}f^{(n)}(t) dt.label{ref12}
$$
Преобразуем интеграл в правой части формулы eqref{ref12}, применив формулу интегрирования по частям:
$$
frac{1}{(n-1)!} intlimits_{x_{0}}^{x} (x-t)^{n-1}f^{(n)}(t) dt = -frac{1}{n!} intlimits_{x_{0}}^{x} f^{n}(t)dt((x-t)^{n}) =\= left.left(-frac{1}{n!}f^{n}(t)(x-t)^{n}right)right|_{t = x_{0}}^{t = x} + frac{1}{n!} intlimits_{x_{0}}^{x}(x-t)^{n}f^{(n + 1)}(t) dt =\= frac{1}{n!}f^{(n)}(x_{0})(x-x_{0})^{n} + frac{1}{n!} intlimits_{x_{0}}^{x}(x-t)^{n}f^{(n + 1)}(t) dt.nonumber
$$
Отсюда следует, что равенство eqref{ref12} можно записать в виде eqref{ref11}. Формула eqref{ref9} доказана. (bullet)
Теорема 2.
Если функция (f) и все ее производные ограничены в совокупности на интервале (Delta = (x_{0}-delta, x_{0} + delta)), то есть
$$
exists M > 0: forall x in Delta rightarrow |f^{(n)}(x)| leq M, n = 0,1,2,ldots,label{ref13}
$$
то функция (f) представляется сходящимся к ней в каждой точке интервала (Delta) рядом Тейлора eqref{ref8}.
Доказательство.
(circ) Пусть (x in (x_{0}-delta, x_{0} + delta)). Тогда, используя формулу eqref{ref10} и условие eqref{ref13}, получаем
$$
|r_{n}(x)| leq M frac{|x-x_{0}|^{n + 1}}{(n + 1)!}.label{ref14}
$$
Так как (displaystylelim_{x rightarrow 0} frac{a^{n}}{n!} = 0) для любого (a > 0) (пример разобран здесь), то из eqref{ref14} следует, что выполняется условие eqref{ref7}, то есть в точке (x) справедливо равенство eqref{ref8}. (bullet)
Замечание 1.
Теорема 2 остается в силе, если условие eqref{ref13} заменить следующим условием:
$$
exists M > 0 exists C > 0: forall x in Delta rightarrow |f^{(n)}(x)| leq MC^{n}, n = 0, 1, 2, ldotsnonumber
$$
Разложение элементарных функций в ряд Тейлора.
Найдем разложение основных элементарных функций в ряд Тейлора в окрестности точки (x_{0} = 0), то есть в ряд вида
$$
f(x) = sum_{n = 0}^{infty}frac{f^{(n)}(0)}{n!}x^{n},label{ref15}
$$
который называют рядом Маклорена. Заметим, что коэффициенты (displaystylefrac{f^{(n)}(0)}{n!}) разложения eqref{ref15} для основных элементарных функций (показательной, гиперболических, тригонометрических и других) были найдены в разделе про формулу Тейлора.
Разложение показательной и гиперболической функций в ряд Тейлора.
Пусть (f(x) = e^{x}). Тогда для любого (x in (-rho, rho)), где (rho > 0), выполняются неравенства
$$
0 < f(x) < e^{rho},quad 0 < f^{(n)}(x) < e^{rho}, n in mathbb{N}.nonumber
$$
По теореме 2 ряд eqref{ref15} для функции (f(x) = e^{x}) сходится к этой функции на интервале ((-rho, rho)) при любом (rho > 0), то есть радиус сходимости этого ряда (R = +infty). Так как для функции (f(x) = e^{x}) выполняются равенства (f(0) = 1), (f^{(n)}(0) = 1) для любого (n), то по формуле eqref{ref15} получаем разложение в ряд Маклорена показательной функции
$$
e^{x} = sum_{n = 0}^{infty}frac{x^{n}}{n!},label{ref16}
$$
Используя разложение eqref{ref16} и формулы
$$
operatorname{ch} x = frac{e^{x} + e^{-x}}{2},quad operatorname{sh} x = frac{e^{x}-e^{-x}}{2},nonumber
$$
находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса:
$$
operatorname{ch} x = sum_{n = 0}^{infty}frac{x^{2n}}{2n!},label{ref17}
$$
$$
operatorname{sh} x = sum_{n = 0}^{infty}frac{x^{2n + 1}}{(2n + 1)!},label{ref18}
$$
Радиус сходимости каждого из рядов eqref{ref17}, eqref{ref18} (R = +infty).
Разложение тригонометрических функций в ряд Тейлора.
Пусть (f(x) = sin x). Тогда (|f(x)| leq 1) и (|f^{(n)}(x)| leq 1) для всех (n in mathbb{N}) и для всех (x in R). По теореме 2 ряд eqref{ref15}для функции (f(x) = sin x) сходится для любого (x in (-infty, +infty)), то есть радиус сходимости этого ряда (R = +infty).
Если (f(x) = sin x), то (f(0) = 0), (f^{(2n)}(0) = 0), (f'(0) = 1), (f^{(2n + 1)}(0) = (-1)^{n}) для любого (n), и по формулеeqref{ref15}получаем разложение синуса в ряд Маклорена:
$$
sin x = sum_{substack{n = 0}}^{infty} frac{(-1)^{n}}{(2n + 1)!}x^{2n + 1}.label{ref19}
$$
Пусть (f(x) = cos x). Тогда (|f(x)| leq 1), (|f^{(n)}(x)| leq 1) для всех (n) и для всех (x in R), (f(0) = 1), (f'(0) = 0), (f^{(2n)}(0) = (-1)^{n}) и, (f^{(2n + 1)}(0) = 0) для всех (n). По формуле eqref{ref15} получаем
$$
cos x = sum_{n = 0}^{infty} frac{(-1)^{n}}{2n!}x^{2n}.label{ref20}
$$
Радиус сходимости каждого из рядов eqref{ref19} и eqref{ref20} (R = +infty).
Разложение логарифмической функции в ряд Тейлора.
Пусть (f(x) = ln(1 + x)). Тогда
$$
f^{(n)}(x) = frac{(-1)^{n-1}(n-1)!}{(1 + x)^{n}},label{ref21}
$$
откуда находим
$$
frac{f^{(n)}(0)}{n!} = frac{(-1)^{n-1}}{n}.label{ref22}
$$
(circ) Оценим остаточный член (r_{n}(x)), пользуясь формулой eqref{ref9} при (x_{0} = 0). Преобразуем эту формулу, полагая (t = tau x). Тогда (dt = x dtau), (1-x =x(1-tau)) и формула eqref{ref9} примет вид
$$
r_{n}(x) = frac{x^{n + 1}}{n!} intlimits_0^1 (1-tau) f^{(n + 1)}(tau x) dtau.label{ref23}
$$
Если (f(x) = ln(x + 1)), то по формуле eqref{ref23}, используя равенство eqref{ref21}, получаем
$$
r_{n}(x) = (-1)^{n}x^{n + 1} intlimits_0^1 frac{(1-tau)^{n}}{(1 + tau x)^{n + 1}} d tau.label{ref24}
$$
Пусть (|x| < 1). Тогда справедливы неравенства
$$
|1 + tau x| geq 1-tau|x| geq 1-tau,label{ref25}
$$
$$
|1 + tau x| geq 1-|x|,label{ref26}
$$
так как (0 leq tau leq 1). Отсюда следует, что при любом (n in mathbb{N}) выполняется неравенство
$$
|1 + tau x|^{n + 1} geq (1-tau)^{n}(1-|x|).label{ref27}
$$
Используя неравенство eqref{ref27}, из формулы eqref{ref24} получаем следующую оценку остаточного члена:
$$
|r_{n}(x)| leq |x|^{n + 1} intlimits_0^1 frac{dtau}{1-|x|} = frac{|x|^{n + 1}}{1-|x|},nonumber
$$
откуда следует, что (r_{n}(x) rightarrow 0) при (n rightarrow infty), если (|x| < 1).
Пусть (x = 1). Тогда (1 + tau x = 1 + tau), ((1 + tau)^{n + 1} geq 1), (1-tau geq 0), так как (0 leq tau leq 1). Поэтому из формулы eqref{ref24} следует, что (|r_{n}(1)| leq displaystyleintlimits_0^1 (1-tau)^{n}dtau = frac{1}{n + 1}), откуда получаем: (r_{n}(1) rightarrow 0) при (n rightarrow infty).
Итак, если (x in (-1, 1]), то остаточный член (r_{n}(x)) для функции (f(x) = ln (1 + x)) стремится к нулю при (n rightarrow infty), то есть ряд Маклорена сходится к (f(x)). (bullet)
Из формулeqref{ref15}и eqref{ref22} получаем разложение функции (ln (1 + x)) в ряд Маклорена
$$
ln (1 + x) = sum_{n=1}^{infty} frac{(-1)^{n-1}}{n} x^{n},label{ref28}
$$
радиус сходимости которого (R = 1).
Формула eqref{ref28} справедлива при (x = 1), и поэтому
$$
ln 2 = sum_{n=1}^{infty} frac{(-1)^{n-1}}{n} = 1-frac{1}{2} + frac{1}{3}-frac{1}{4} + ldots + frac{(-1)^{n-1}}{n} + ldotsnonumber
$$
Заменяя в формуле eqref{ref28} (x) на (-x), получаем
$$
ln (1-x) =-sum_{n=1}^{infty} frac{x^{n}}{n}.label{ref29}
$$
Разложение степенной функции в ряд Тейлора.
Пусть (f(x) = (1 + x)^{alpha}). Если (alpha = 0), то (f(x) = 1), а если (alpha = n), где (n in mathbb{N}), то (f(x)) — многочлен степени (n), который можно записать по формуле бинома Ньютона в виде конечной суммы:
$$
f(x) = sum_{k=0}^{n} C_{n}^{k}x^{k}.nonumber
$$
Покажем, что если (alpha notin mathbb{N}) и (a neq 0), то функция (f(x) = (1 + x)^{alpha}) представляется при каждом (x in (-1, 1)) сходящимся к ней рядом Маклорена
$$
(1 + x)^{alpha} = sum_{n = 0}^{infty} C_{alpha}^{n}x^{n},label{ref30}
$$
где
$$
C_{alpha}^{0} = 1,quad C_{alpha}^{n} = frac{alpha(alpha-1)ldots(alpha-(n-1))}{n!}.label{ref31}
$$
(circ) Так как
$$
f^{(n + 1)}(x) = alpha(alpha-1)ldots(alpha-n)(1 + x)^{alpha-(n-1)},label{ref32}
$$
то по формуле eqref{ref23} получаем
$$
r_{n}(x) = A_{n}x^{n + 1} intlimits_0^1 left(frac{1-tau}{1 + tau x}right)^{n} (1 + tau x)^{alpha-1} dtau,label{ref33}
$$
где
$$
A_{n} = frac{alpha(alpha-1)ldots(alpha-n)}{n!}.
$$
Выберем число (m in mathbb{N}) таким, чтобы выполнялось условие (|a| leq m). Тогда при всех (n geq m) справедливы неравенства
$$
|A_{n}| leq frac{m(m + 1)ldots(m + n)}{n!} leq frac{(m + n)!}{n!} = (n + 1)ldots(n + m) leq (2n)^{m}.label{ref34}
$$
Используя неравенства eqref{ref25} и eqref{ref26}, а также неравенство (|1 + tau x| leq 1 + |x|), получаем
$$
0 leq frac{1-tau}{1 + xtau} leq 1,label{ref35}
$$
$$
|1 + tau x|^{alpha-1}leq beta(x)=left{begin{array}{lc}(1 + |x|)^{alpha-1},&mbox{если} alpha geq 1, \(1-|x|)^{alpha-1},&mbox{если} alpha < 1,end{array} right.label{ref36}
$$
Из формулы eqref{ref33} и оценок eqref{ref34}-eqref{ref36} следует неравенство
$$
|r_{n}(x)| leq beta(x) 2^{m}n^{m}|x|^{n + 1},label{ref37}
$$
которое справедливо при всех (n geq m) и для каждого (x in (-1, 1)).
Так как (displaystylelim_{t rightarrow +infty} frac{t^{m}}{a^{t}}) при (a > 1), то (displaystylelim_{n rightarrow infty} frac{n^{m}}{(1/|x|)^{n + 1}} = 0). Поэтому из соотношения eqref{ref37} следует, что (r_{n}(x) rightarrow 0) при (n rightarrow infty) для каждого (x in (-1, 1)), то есть справедливо равенство eqref{ref30}, причем радиус сходимости ряда eqref{ref30} в случае, когда (alpha neq 0) и (alpha notin mathbb{N}), равен 1. (bullet)
Отметим важные частные случаи формулы eqref{ref30}:
$$
frac{1}{1 + x} = sum_{n = 0}^{infty} (-1)^{n}x^{n},label{ref38}
$$
$$
frac{1}{1-x} = sum_{n = 0}^{infty} x^{n}.label{ref39}
$$
В заключение заметим, что при разложении функций в ряд Тейлора обычно используют формулы eqref{ref16}—eqref{ref20}, eqref{ref28}-eqref{ref30} и применяют такие приемы, как: представление данной функции в виде линейной комбинации функций, ряды Тейлора для которых известны; замена переменного; почленное дифференцирование и интегрирование ряда.
Пример 1.
Разложить в ряд Маклорена функцию (f(x)) и найти радиус сходимости (R) ряда, если:
- (displaystyle f(x) = frac{1}{1 + x^{2}});
- (displaystyle f(x) = frac{1}{sqrt{1 + x^{2}}});
- (displaystyle f(x) = frac{2x-1}{x^{2}-x-6}).
Решение.
- (triangle) Используя формулу eqref{ref38}, получаем ряд
$$
frac{1}{1 + x^{2}} = sum_{n = 0}^{infty} (-1)^{n}x^{2n},label{ref40}
$$
радиус сходимости которого (R = 1). - Из равенства eqref{ref30} следует, что (displaystylefrac{1}{sqrt{1 + x^{2}}} = sum_{n = 0}^{infty} C_{-1/2}^{n}x^{2n}), где
$$
C_{-1/2}^{n} = frac{displaystyleleft(-frac{1}{2}right)left(-frac{1}{2}-1right)ldotsleft(-frac{1}{2}-(n-1)right)}{n!} = frac{(-1)^{n}1cdot3ldots(2n-1)}{2^{n}n!} = frac{(-1)^{n}(2n-1)!!}{2^{n}n!}.nonumber
$$
Следовательно,
$$
frac{1}{sqrt{1 + x^{2}}} = 1 + sum_{n=1}^{infty} frac{(-1)^{n}(2n-1)!!}{2^{n}n!}x^{2n}, R = 1.label{ref41}
$$ - Так как (f(x) = displaystylefrac{1}{x + 2} + frac{1}{x-3} = frac{1}{displaystyle2left(1 + frac{x}{2}right)}-frac{1}{displaystyle3left(1-frac{x}{3}right)}), то, применяя формулы eqref{ref38} и eqref{ref39}, получаем ряд
$$
frac{2x-1}{x^{2}-x-6} = sum_{n = 0}^{infty} left(frac{(-1)^{n}}{2^{n + 1}}-frac{1}{3^{n + 1}}right)x^{n}, R = 2. blacktrianglenonumber
$$
Пример 2.
Разложить в ряд Маклорена функции
$$
operatorname{arctg} x,nonumber
$$
$$
operatorname{arcsin} x,nonumber
$$
$$
ln(x + sqrt{1 + x^{2}}),nonumber
$$
и найти радиусы сходимости (R) рядов.
Решение.
- (triangle) Почленно интегрируя ряд eqref{ref40}, получаем
$$
operatorname{arctg} x = intlimits_0^x frac{dt}{1 + t^{2}} = sum_{n = 0}^{infty} (-1)^{n} frac{x^{2n + 1}}{2n + 1},quad R = 1.nonumber
$$ - Заменяя в формуле eqref{ref41} (x^{2}) на (-x^{2}), получаем
$$
frac{1}{sqrt{1-x^{2}}} = 1 + sum_{n=1}^{infty} frac{(2n-1)!!}{2^{n}n!}x^{2n},quad R = 1.nonumber
$$
откуда следует, что
$$
operatorname{arcsin} x = intlimits_0^x frac{dt}{1-t^{2}} = x + sum_{n=1}^{infty} frac{(2n-1)!!}{2^{n}n!(2n + 1)}x^{2n + 1}, R = 1.nonumber
$$ - Почленно интегрируя ряд eqref{ref41}, получаем
$$
ln(x + sqrt{1 + x^{2}}) = intlimits_0^x frac{dt}{1 + t^{2}} = x + sum_{n=1}^{infty} frac{(-1)^{n}(2n-1)!!}{2^{n}n!(2n + 1)}x^{2n + 1}, R = 1. blacktrianglenonumber
$$
Пример 3.
Разложить в ряд Тейлора в точке (x_{0} = 2) функцию (f(x) = ln(4 + 3x-x^{2})).
Решение.
(triangle) Так как (4 + 3x-x^{2} = -(x-4)(x + 1)), то, полагая (t = x-2), получаем
$$
f(x) = ln(4-x)(x + 1) = g(t) = ln(2-t)(3 + t) = ln 6 + lnleft(1-frac{t}{2}right) + lnleft(1 + frac{t}{3}right).nonumber
$$
Используя формулы eqref{ref28} и eqref{ref29}, отсюда находим
$$
g(t) = ln 6-sum_{n=1}^{infty} frac{t^{n}}{n2^{n}} + sum_{n=1}^{infty} frac{(-1)^{n-1}t^{n}}{n3^{n}},quad |t| < 2.nonumber
$$
Следовательно,
$$
ln(4 + 3x-x^{2}) = ln 6 + sum_{n=1}^{infty} left(frac{(-1)^{n-1}}{3n}-frac{1}{2^{n}}right)frac{(x-2)^{n}}{n}, R = 2. blacktrianglenonumber
$$
Элементарные функции комплексного переменного.
Показательная, гиперболические и тригонометрические функции комплексного переменного (z) определятся соответственно формулами
$$
e^{z} = sum_{n = 0}^{infty} frac{z^{n}}{n!},label{ref42}
$$
$$
operatorname{ch} z = sum_{n = 0}^{infty} frac{z^{2n}}{(2n)!},label{ref43}
$$
$$
operatorname{sh} z = sum_{n = 0}^{infty} frac{z^{2n + 1}}{(2n + 1)!},label{ref44}
$$
$$
cos z = sum_{n = 0}^{infty} frac{(-1)^{n}z^{2n}}{(2n)!},label{ref45}
$$
$$
sin z = sum_{n = 0}^{infty} frac{(-1)^{n}z^{2n + 1}}{(2n + 1)!}.label{ref46}
$$
Радиус сходимости (R) каждого из рядов eqref{ref42}-eqref{ref46} равен (+infty). Заменяя в равенстве eqref{ref42} (z) на (iz) и (-iz), получаем
$$
e^{iz} = sum_{n = 0}^{infty} frac{i^{n}z^{n}}{n!},qquad e^{-iz} = sum_{n = 0}^{infty} frac{(-1)^{n}i^{n}z^{n}}{n!}.label{ref47}
$$
Используя равенства eqref{ref47} и формулы eqref{ref45}, eqref{ref46}, находим
$$
frac{e^{iz} + e^{-iz}}{2} = cos z, frac{e^{iz}-e^{-iz}}{2i} = sin z,label{ref48}
$$
откуда следует, что
$$
e^{iz} = cos z + i sin z.label{ref49}
$$
Полагая в формуле eqref{ref42} (z = z_{1}) и (z = z_{2}). и перемножая соответствующие ряды, можно показать, что
$$
e^{z_{1}}e^{z_{2}} = e^{z_{1} + z_{2}}.label{ref50}
$$
Пусть (z = x + iy), где (x in R), (y in R). Тогда из равенства eqref{ref50} и формулы eqref{ref49} находим
$$
e^{z} = e^{x + iy} = e^{x}(cos y + i sin y).label{ref51}
$$
Из формулы eqref{ref51} следует, что
$$
e^{z + 2pi i} = e^{z},nonumber
$$
то есть (e^{z}) — периодическая функция с периодом (2pi i). Поэтому для каждого комплексного (z neq 0) уравнение
$$
e^{w} = zlabel{ref52}
$$
имеет бесконечное множество решений вида (w + i2pi n), где (w) — одно из решений уравнения eqref{ref52}, (n in Z).
Если (w = u + iv), то (z = e^{w} = e^{u}(cos v + i sin v)), откуда получаем
$$
|z| = e^{u},quad u = ln |z|,quad v = arg z.nonumber
$$
Пусть (varphi) — какое-нибудь значение аргумента числа (z). Тогда
$$
v = varphi + 2pi n, n in Z.nonumber
$$
Таким образом, все решения уравнения eqref{ref52}, если их обозначить символом (operatorname{Ln} z), задаются формулой
$$
operatorname{Ln} z = ln |z| + i(varphi + 2pi n),label{ref53}
$$
где (varphi) — одно из значений аргумента числа (z) ((z neq 0)), (n in Z).
По заданному значению (z) значение (w) из уравнения eqref{ref52} определяется, согласно формуле eqref{ref53}, неоднозначно (говорят, что логарифмическая функция (operatorname{Ln} z) является многозначной).
Пример 4.
Разложить в степенной ряд в окрестности точки (z = 0) функцию (f(z) = e^{z}sin z).
Решение.
(triangle) Используя формулы eqref{ref48} и eqref{ref50}, получаем
$$
f(z) = e^{z}left(frac{e^{iz}-e^{-iz}}{2i}right) = frac{1}{2i}(e^{z(1 + i)}-e^{z(1-i)}).nonumber
$$
Так как (1 + i = sqrt{2}e^{ipi/4}), (1-i = sqrt{2}e^{-ipi/4}), то по формуле eqref{ref42} находим
$$
f(z) = sum_{n = 0}^{infty} frac{2^{n/2}}{n!} left(frac{e^{ipi n/4}-e^{-ipi n/4}}{2i}right)z^{n},nonumber
$$
откуда в силу второго из равенств eqref{ref48} следует, что
$$
e^{z}sin z = sum_{n = 0}^{infty} frac{2^{n/2}}{n!} sin frac{pi n}{4}z^{n}.nonumber
$$
Радиус сходимости ряда (R = +infty). (blacktriangle)
Разложение функций в степенные ряды. Ряд Тейлора
Общая постановка задачи разложения функции в ряд в комплексной области формулируется так же, как и в действительной области. А именно, для заданной функции , определенной в области
и удовлетворяющий в ней него которым дополнительным условиям, требуется найти ряд вида
который бы сходился в области
и его сумма в этой области совпадала с
.
Постановка задачи разложения функции в степенной ряд
Для функции , аналитической в области
, найти ряд
, сходящийся к
в круге
, принадлежащем области
, то есть
(3.15)
Равенство (3.15) означает, что является суммой ряда в круге
.
Для решения задачи нужно, очевидно, найти коэффициенты ряда по заданной функции ; найти круг сходимости ряда и установить сходимость ряда именно к
. Последнее, напомним, означает, что для точек круга выполняется неравенство
для любого
и
.
Все поставленные вопросы решаются с помощью следующей теоремы.
Теорема Тейлора о разложении функции в степенной ряд
Теорема 3.4. Функция, аналитическая в области , в окрестности каждой точки
этой области представляется в виде степенного ряда (3.15), радиус сходимости
которого не меньше, чем расстояние от точки
до границы области
. Коэффициенты ряда вычисляются по формуле
(3.16)
где — произвольный контур, принадлежащий области
и охватывающий точку
, в частности,
— окружность
или по формуле
(3.17)
На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.
Алгоритм разложения аналитической функции в степенной ряд
1. Найти производные от данной функции: .
2. Вычислить значения производных в точке ; записать коэффициенты по формуле (3.17). Составить ряд по степеням
с этими коэффициентами, который соответствует данной функции
3. Найти область сходимости полученного ряда и записать разложение (3.15).
Если функция не имеет конечных особых точек, то ряд сходится к ней во всей плоскости, .
Утверждение 3.3
1. Функция, аналитическая в точке , раскладывается в окрестности этой точки в степенной ряд.
2. На границе круга сходимости ряда есть хотя бы одна особая точка функции, т.е. радиус сходимости круга равен расстоянию от центра разложения до ближайшей особой точки функции.
3. Степенной ряд в круге сходимости является рядом Тейлора для своей суммы, т.е. коэффициенты ряда вычисляются по формулам (3.16), (3.17).
Примеры разложения функций по степеням z
Пример 3.13. Записать разложения по степеням функций
.
Решение
Задачу решаем по вышеприведенному алгоритму.
1. Найдем производные:
В поставленной задаче . По формуле (3.17) имеем
3. Нетрудно убедиться, что все составленные ряды сходятся во всей комплексной плоскости, . В результате получаем формулы, которые ранее были приняты за определения соответствующих функций:
В результате получены так называемые основные разложения.
Пример 3.14. Записать разложения по степеням функций: а)
; б)
.
Решение
Задачу можно решать, пользуясь алгоритмом, а можно использовать формулы (3.13) для суммы членов геометрической профессии. Заданные функции являются аналитическими во всей комплексной плоскости за исключением одной точки . Для каждого случая получаем:
заметим, что здесь
для
.
Пример 3.15. Записать разложения по степеням функций: а)
; б)
.
Решение
Разложения записываются для однозначных ветвей многозначного выражения. Выбор ветви определяется заданием функции в точке .
a) Функция определена во всей комплексной плоскости за исключением , т.е. в двусвязной области
. Чтобы получить односвязную область из
, проведем разрез, соединяющий точки
и
. Из условия
следует, что точка
должна быть внутренней точкой области. Поэтому выбираем разрез, не проходящий через
. например по лучу
. В полученной односвязной области, где
, функция
является однозначной аналитической функцией. Далее решаем задачу по алгоритму.
1. Находим производные (формулу устанавливаем по индукции):
2. По формуле (3.17):
3. Находим радиус сходимости ряда: , где
. В результате получаем
б) Функция определена всюду в
за исключением
, т.е. в двусвязной области. В односвязной области, полученной из
путем разреза по лучу
, функция является однозначной , аналитической. Задачу можно решать, как и выше, т.е. по алгоритму, а можно использовать полученный выше результат, введя обозначение
. Для
, удовлетворяющих неравенству
имеем разложение
. Заменяя
на
, получаем результат
Разложения основных функция в степенной ряд
Разложения, полученные в результате решения примеров 3.13-3.15, носят название основных (табличных) разложений. Выпишем их:
Основные разложения позволяют при решении примеров на разложение функции в ряд Тейлора не пользоваться сформулированным выше алгоритмом, сложность которого связана с техникой дифференцирования и составления формулы общего члена.
Утверждение 3.4. При разложении функции в ряд Тейлора используются основные (табличные) разложения и действия над рядами. Радиус сходимости ряда может быть получен по виду раскладываемой функции без использования формулы общего члена ряда и формул для нахождения радиуса. Радиус сходимости ряда, полученного при разложении данной функции в окрестности точки , равен расстоянию от центра разложения — точки
до ближайшей особой точки функции. Если функция является аналитической всюду, то
.
Пример 3.16. Разложить по степеням функции комплексного переменного:
Решение
а) Обозначим через
и, используя табличное разложение для функции
, получим ответ:
, то есть
.
б) Запишем функцию в виде произведения и, используя разложение для
, получим ответ:
, то есть
.
в) Чтобы воспользоваться одним из основных разложений, применим тригонометрическую формулу — формулу “понижения”. Получим:
Заметим, что свободный член разложения в этой записи встречается дважды, поэтому нужно привести подобные члены. Для этого в записи рада отделим слагаемое при — свободный член:
В результате имеем .
Из этого разложения можно найти значение производной любого порядка функции в точке
, так как эти значения связаны формулой (3.17) с коэффициентами разложения:
. Поэтому, учитывая, что в разложении присутствуют только четные степени, заключаем, что все производные нечетных порядков от
в точке
равны нулю, а производная, например, десятого порядка не равна нулю. Найдем ее, используя равенство
, где
— коэффициент в разложении
при
, т.е. в записанном выше разложении нужно взять
. Получим
г) Функция определена всюду, кроме . В односвязной области, например в плоскости с разрезом по лучу
, где
, возможно выделение однозначных ветвей многозначного выражения
(рис. 3.1). Выбираем ту ветвь, для которой
, то есть из
получаем
. Разложим аналитическую функцию
по степеням
в круге
; радиус круга
— расстояние от центра разложения
до граничной точки
.
Чтобы воспользоваться основным разложением, преобразуем функцию следующим образом:
Тогда, обозначая через
и используя основное разложение для
, получаем
при условии
, т.е. в круге
.
Пример 3.17. Разложить в окрестности точки ветвь функции
, для которой
.
Решение
Функция определена всюду в
, кроме точек
, т.е. в трехсвязной области — плоскости с выколотыми точками
и
. Чтобы получить односвязную область, проведем разрезы по лучам, выходящим из этих точек. Например, луч из точки
выберем параллельным мнимой оси,
, а луч из точки
— по действительной оси:
. В полученной односвязной области (рис. 3.2) каждая ветвь является аналитической функцией и раскладывается в ряд в круге
(
— расстояние от
до границы). Здесь ветвь задается условием:
, то есть из
при
.
Далее, чтобы использовать основное разложение, преобразуем функцию:
Для числа в силу выбора ветви берем
, а функции
и
раскладываем в ряды, как в предыдущем примере:
В области , принадлежащей выбранной односвязной области, сходятся оба ряда. Используя свойство сложения рядов, получаем окончательный результат:
При разложении функции в ряд в окрестности точки , т.е. по степеням
, удобно использовать замену
и полученную после замены функцию раскладывать по степеням
.
Пример 3.18. Разложить по степеням функции: a)
; б)
в)
.
Решение
а) Обозначим через
, и, используя тригонометрическую формулу для функции
, получим:
. Здесь
и
— постоянные величины, а для функций
и
используем основные разложения. В результате получим
то есть ряд вида , где коэффициент
определяется следующим образом:
для
и
для
.
б) Можно, как и выше, использовать вспомогательную переменную, а можно сделать то же самое, применив простое преобразование: . Здесь
— постоянная величина, функция
раскладывается в ряд как функция
по степеням
. Получаем ответ:
, или
.
в) Обозначая через
, получаем функцию
. Разложение этой функции по степеням
найдено в примере 3.16:
Возвращаясь к исходной переменной, получаем разложение исходной функции в круге (рис. 3.3):
Пример 3.19. Разложить по степеням функции:
.
Решение
Данные функции являются простейшими рациональными (элементарными) дробями. Для их разложения используется формула суммы членов бесконечно убывающей геометрической прогрессии . В первом случае формула используется непосредственно, при
, во втором — после преобразования
получаем
. Разложение заданных функций имеет вид
(3.18)
(3.19)
Соотношения (3.18),(3.19) обобщают формулу , которая получается из них при
.
При разложении дроби замечаем, что она является производной от
, то есть
, поэтому ее разложение можно получить, используя дифференцирование ряда:
Ответ удобнее записать в виде .
Очевидно, повторяя процедуру дифференцирования, можно получить разложение элементарных дробей вида при любом натуральном
.
Алгоритм разложения рациональных дробей в ряд Тейлора
Рассмотрим примеры на разложение в ряд Тейлора рациональных дробей
где и
— многочлены. Первые этапы решения задачи аналогичны этапам интегрирования этих дробей. Приведем полный алгоритм.
1. Если дробь неправильная , следует выделить целую часть дроби многочлен.
2. Правильную рациональную дробь разложить на элементарные дроби:
а) записать дробь в виде суммы элементарных дробей вида с неопределенными коэффициентами
, где
— корень знаменателя,
— его кратность;
б) найти неопределенные коэффициенты.
3. Разложить элементарные дроби в степенные ряды. Основными приемами при этом являются применение формул (3.13),(3.18),(3.19) и правила дифференцирования ряда (см. пример 3.19)).
При разложении по степеням можно предварительно ввести вспомогательную переменную
.
Пример 3.20. Разложить по степеням функции: а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь неправильная, поэтому выделяем целую часть: .
2. Полученная правильная дробь является элементарной дробью.
3. Записываем разложение элементарной дроби и получаем:
Для разложения дроби можно было использовать формулу (3.19) при
.
Для нахождения окончательного ответа нужно сделать преобразование приведения подобных членов, так как в полученном выражении свободный член встречается дважды. Имеем
, то есть
.
б) Воспользуемся алгоритмом.
1. Дробь неправильная, выделяем целую часть. Можно, как и выше, применить преобразование дроби:
Можно для выделения целой части применить метод деления “углом”, или, обозначая i + 2 = t, произвести почленное деление на одночлен
2,3. Записываем разложение заданной функции, используя формулу (3.19) для правильной дроби:
Окончательный ответ: .
Получен ряд вида , где
. Нетрудно проверить равенство:
.
Пример 3.21. Функцию разложить в ряд Тейлора в окрестности точки
, если а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем ее на элементарные дроби. Для этого представим дробь в виде
где и
— неопределенные коэффициенты, которые находим из тождества
Полагая последовательно и
, получаем
.
Записываем дробь в виде суммы дробей: .
3. Раскладываем по степеням г каждую элементарную дробь:
В общей области сходимости — круге — записываем сумму рядов разложение исходной дроби:
б) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Разложение дроби на элементарные получено в предыдущем пункте:
3. Раскладываем по степеням каждую элементарную дробь:
Записываем разложение исходной дроби в круге
При разложении по степеням, можно было сделать замену
в исходной дроби.
Радиусы сходимости в обоих случаях можно определить заранее, до записи» разложения — по виду функции. Ее особыми точками являются точки и
. В первом случае ближайшей к точке
является точка
, расстояние между точками равно единице и, следовательно,
; во втором — обе особые точки удалены от
на расстояние, равное двум, и
.
Пример 3.22. Разложить по степеням функции (рациональные дроби): а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем правильную дробь на элементарные дроби, предварительно разложив знаменатель на множители:
, где
и
.
Представим дробь в виде . Находим коэффициенты
и
из тождества
, т.е. из системы
Дробь представлена в виде суммы: .
3. Раскладываем элементарные дроби по степеням
Записываем ответ:
б) Воспользуемся алгоритмом.
1,2. Раскладываем дробь на элементарные:
, где
— неопределенные коэффициенты.
Находим коэффициенты из тождества .
Приравнивая коэффициенты при одинаковых степенях , имеем
3. Раскладываем элементарные дроби по степеням
Для исходной дроби получаем разложение:
или, складывая ряды: .
Окончательный ответ: .
Пример 3.23. Разложить по степеням функции: а)
; б)
.
Решение
Обе дроби правильные; раскладывать на более простые нет необходимости. Используя основные разложения, получаем ответы:
а) ;
б) или
.
Пример 3.24. Используя разложение функции по степеням
, найти значение производной седьмого порядка в точке
.
Решение
Пример 3.25. Записать разложение функций a) и б)
по степеням
до члена, содержащего
.
Решение
а) Применим метод подстановки ряда в ряд, используя основные разложения для функций и
. Имеем
, или, подставляя:
где . Записывать большее число слагаемых нет необходимости, так как уже у следующего (первого отброшенного) младшая степень равна
.
Возведение в степень рядов, как и перемножение рядов, производится по правилам действий с многочленами, в частности применяется формула бинома Ньютона:
Так как младшая степень выражения
равна трем, следовательно,
— шести, то для записи результата следует взять из первых двух скобок по два слагаемых, а из остальных по одному, т.е.
Приводя подобные члены, получим окончательный ответ:
или .
Разложение, очевидно, можно получить, вычисляя коэффициенты разложения по формуле (3.17), что более громоздко.
б) Разложение можно получить, используя формулу (3.17) для коэффициентов либо произведя деление ряда
на ряд
методом деления “утлом” или методом неопределенных коэффициентов.
Применим последний прием. Разложение по степеням
ищем в виде
По определению деления имеем тождество
Перемножаем ряды справа и приравниваем коэффициенты полученного ряда известным коэффициентам при соответствующих степенях ряда, записанного слева. Получаем систему уравнений
из которой находим коэффициенты .
Ответ получаем в виде . Это разложение справедливо в круге
, так как
— ближайшая к
особая точка функции тангенса
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

As the degree of the Taylor polynomial rises, it approaches the correct function. This image shows sin x and its Taylor approximations by polynomials of degree 1, 3, 5, 7, 9, 11, and 13 at x = 0.
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function’s derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century.
The partial sum formed by the first n + 1 terms of a Taylor series is a polynomial of degree n that is called the nth Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as n increases. Taylor’s theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of the infinite sequence of the Taylor polynomials. A function may differ from the sum of its Taylor series, even if its Taylor series is convergent. A function is analytic at a point x if it is equal to the sum of its Taylor series in some open interval (or open disk in the complex plane) containing x. This implies that the function is analytic at every point of the interval (or disk).
Definition[edit]
The Taylor series of a real or complex-valued function f (x) that is infinitely differentiable at a real or complex number a is the power series
where n! denotes the factorial of n. In the more compact sigma notation, this can be written as
where f(n)(a) denotes the nth derivative of f evaluated at the point a. (The derivative of order zero of f is defined to be f itself and (x − a)0 and 0! are both defined to be 1.)
With a = 0, the Maclaurin series takes the form:[1]
or in the compact sigma notation:
Examples[edit]
The Taylor series of any polynomial is the polynomial itself.
The Maclaurin series of 1/1 − x is the geometric series
So, by substituting x for 1 − x, the Taylor series of 1/x at a = 1 is
By integrating the above Maclaurin series, we find the Maclaurin series of ln(1 − x), where ln denotes the natural logarithm:
The corresponding Taylor series of ln x at a = 1 is
and more generally, the corresponding Taylor series of ln x at an arbitrary nonzero point a is:
The Maclaurin series of the exponential function ex is
The above expansion holds because the derivative of ex with respect to x is also ex, and e0 equals 1. This leaves the terms (x − 0)n in the numerator and n! in the denominator of each term in the infinite sum.
History[edit]
The ancient Greek philosopher Zeno of Elea considered the problem of summing an infinite series to achieve a finite result, but rejected it as an impossibility;[2] the result was Zeno’s paradox. Later, Aristotle proposed a philosophical resolution of the paradox, but the mathematical content was apparently unresolved until taken up by Archimedes, as it had been prior to Aristotle by the Presocratic Atomist Democritus. It was through Archimedes’s method of exhaustion that an infinite number of progressive subdivisions could be performed to achieve a finite result.[3] Liu Hui independently employed a similar method a few centuries later.[4]
In the 14th century, the earliest examples of specific Taylor series (but not the general method) were given by Madhava of Sangamagrama.[5][6] Though no record of his work survives, writings of his followers in the Kerala school of astronomy and mathematics suggest that he found the Taylor series for the trigonometric functions of sine, cosine, and arctangent (see Madhava series). During the following two centuries his followers developed further series expansions and rational approximations.
In late 1670, James Gregory was shown in a letter from John Collins several Maclaurin series (











In 1691–1692, Isaac Newton wrote down an explicit statement of the Taylor and Maclaurin series in an unpublished version of his work De Quadratura Curvarum. However, this work was never completed and the relevant sections were omitted from the portions published in 1704 under the title Tractatus de Quadratura Curvarum.
It was not until 1715 that a general method for constructing these series for all functions for which they exist was finally published by Brook Taylor,[8] after whom the series are now named.
The Maclaurin series was named after Colin Maclaurin, a professor in Edinburgh, who published the special case of the Taylor result in the mid-18th century.
Analytic functions[edit]
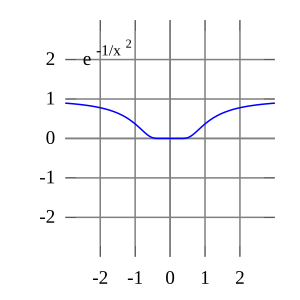
The function e(−1/x2) is not analytic at x = 0: the Taylor series is identically 0, although the function is not.
If f (x) is given by a convergent power series in an open disk centred at b in the complex plane (or an interval in the real line), it is said to be analytic in this region. Thus for x in this region, f is given by a convergent power series
Differentiating by x the above formula n times, then setting x = b gives:
and so the power series expansion agrees with the Taylor series. Thus a function is analytic in an open disk centered at b if and only if its Taylor series converges to the value of the function at each point of the disk.
If f (x) is equal to the sum of its Taylor series for all x in the complex plane, it is called entire. The polynomials, exponential function ex, and the trigonometric functions sine and cosine, are examples of entire functions. Examples of functions that are not entire include the square root, the logarithm, the trigonometric function tangent, and its inverse, arctan. For these functions the Taylor series do not converge if x is far from b. That is, the Taylor series diverges at x if the distance between x and b is larger than the radius of convergence. The Taylor series can be used to calculate the value of an entire function at every point, if the value of the function, and of all of its derivatives, are known at a single point.
Uses of the Taylor series for analytic functions include:
- The partial sums (the Taylor polynomials) of the series can be used as approximations of the function. These approximations are good if sufficiently many terms are included.
- Differentiation and integration of power series can be performed term by term and is hence particularly easy.
- An analytic function is uniquely extended to a holomorphic function on an open disk in the complex plane. This makes the machinery of complex analysis available.
- The (truncated) series can be used to compute function values numerically, (often by recasting the polynomial into the Chebyshev form and evaluating it with the Clenshaw algorithm).
- Algebraic operations can be done readily on the power series representation; for instance, Euler’s formula follows from Taylor series expansions for trigonometric and exponential functions. This result is of fundamental importance in such fields as harmonic analysis.
- Approximations using the first few terms of a Taylor series can make otherwise unsolvable problems possible for a restricted domain; this approach is often used in physics.
Approximation error and convergence[edit]

The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full period centered at the origin.

The Taylor polynomials for ln(1 + x) only provide accurate approximations in the range −1 < x ≤ 1. For x > 1, Taylor polynomials of higher degree provide worse approximations.

The Taylor approximations for ln(1 + x) (black). For x > 1, the approximations diverge.
Pictured is an accurate approximation of sin x around the point x = 0. The pink curve is a polynomial of degree seven:
The error in this approximation is no more than |x|9 / 9!. For a full cycle centered at the origin (−π < x < π) the error is less than 0.08215. In particular, for −1 < x < 1, the error is less than 0.000003.
In contrast, also shown is a picture of the natural logarithm function ln(1 + x) and some of its Taylor polynomials around a = 0. These approximations converge to the function only in the region −1 < x ≤ 1; outside of this region the higher-degree Taylor polynomials are worse approximations for the function.
The error incurred in approximating a function by its nth-degree Taylor polynomial is called the remainder or residual and is denoted by the function Rn(x). Taylor’s theorem can be used to obtain a bound on the size of the remainder.
In general, Taylor series need not be convergent at all. And in fact the set of functions with a convergent Taylor series is a meager set in the Fréchet space of smooth functions. And even if the Taylor series of a function f does converge, its limit need not in general be equal to the value of the function f (x). For example, the function
is infinitely differentiable at x = 0, and has all derivatives zero there. Consequently, the Taylor series of f (x) about x = 0 is identically zero. However, f (x) is not the zero function, so does not equal its Taylor series around the origin. Thus, f (x) is an example of a non-analytic smooth function.
In real analysis, this example shows that there are infinitely differentiable functions f (x) whose Taylor series are not equal to f (x) even if they converge. By contrast, the holomorphic functions studied in complex analysis always possess a convergent Taylor series, and even the Taylor series of meromorphic functions, which might have singularities, never converge to a value different from the function itself. The complex function e−1/z2, however, does not approach 0 when z approaches 0 along the imaginary axis, so it is not continuous in the complex plane and its Taylor series is undefined at 0.
More generally, every sequence of real or complex numbers can appear as coefficients in the Taylor series of an infinitely differentiable function defined on the real line, a consequence of Borel’s lemma. As a result, the radius of convergence of a Taylor series can be zero. There are even infinitely differentiable functions defined on the real line whose Taylor series have a radius of convergence 0 everywhere.[9]
A function cannot be written as a Taylor series centred at a singularity; in these cases, one can often still achieve a series expansion if one allows also negative powers of the variable x; see Laurent series. For example, f (x) = e−1/x2 can be written as a Laurent series.
Generalization[edit]
There is, however, a generalization[10][11] of the Taylor series that does converge to the value of the function itself for any bounded continuous function on (0,∞), using the calculus of finite differences. Specifically, one has the following theorem, due to Einar Hille, that for any t > 0,
Here Δn
h is the nth finite difference operator with step size h. The series is precisely the Taylor series, except that divided differences appear in place of differentiation: the series is formally similar to the Newton series. When the function f is analytic at a, the terms in the series converge to the terms of the Taylor series, and in this sense generalizes the usual Taylor series.
In general, for any infinite sequence ai, the following power series identity holds:
So in particular,
The series on the right is the expectation value of f (a + X), where X is a Poisson-distributed random variable that takes the value jh with probability e−t/h·(t/h)j/j!. Hence,
The law of large numbers implies that the identity holds.[12]
List of Maclaurin series of some common functions[edit]
Several important Maclaurin series expansions follow.[13] All these expansions are valid for complex arguments x.
Exponential function[edit]

The exponential function ex (in blue), and the sum of the first n + 1 terms of its Taylor series at 0 (in red).
The exponential function 
.
It converges for all x.
The exponential generating function of the Bell numbers is the exponential function of the predecessor of the exponential function:
Natural logarithm[edit]
The natural logarithm (with base e) has Maclaurin series
They converge for 
Geometric series[edit]
The geometric series and its derivatives have Maclaurin series
All are convergent for 
Binomial series[edit]
The binomial series is the power series
whose coefficients are the generalized binomial coefficients
(If n = 0, this product is an empty product and has value 1.) It converges for 
When α = −1, this is essentially the infinite geometric series mentioned in the previous section. The special cases α = 1/2 and α = −1/2 give the square root function and its inverse:
When only the linear term is retained, this simplifies to the binomial approximation.
Trigonometric functions[edit]
The usual trigonometric functions and their inverses have the following Maclaurin series:
All angles are expressed in radians. The numbers Bk appearing in the expansions of tan x are the Bernoulli numbers. The Ek in the expansion of sec x are Euler numbers.
Hyperbolic functions[edit]
The hyperbolic functions have Maclaurin series closely related to the series for the corresponding trigonometric functions:
The numbers Bk appearing in the series for tanh x are the Bernoulli numbers.
Polylogarithmic functions[edit]
The polylogarithms have these defining identities:
The Legendre chi functions are defined as follows:
And the formulas presented below are called inverse tangent integrals:
In statistical thermodynamics these formulas are of great importance.
Elliptic functions[edit]
The complete elliptic integrals of first kind K and of second kind E can be defined as follows:
The Jacobi theta functions describe the world of the elliptic modular functions and they have these Taylor series:
The regular partition number sequence P(n) has this generating function:
The strict partition number sequence Q(n) has that generating function:
Calculation of Taylor series[edit]
Several methods exist for the calculation of Taylor series of a large number of functions. One can attempt to use the definition of the Taylor series, though this often requires generalizing the form of the coefficients according to a readily apparent pattern. Alternatively, one can use manipulations such as substitution, multiplication or division, addition or subtraction of standard Taylor series to construct the Taylor series of a function, by virtue of Taylor series being power series. In some cases, one can also derive the Taylor series by repeatedly applying integration by parts. Particularly convenient is the use of computer algebra systems to calculate Taylor series.
First example[edit]
In order to compute the 7th degree Maclaurin polynomial for the function
,
one may first rewrite the function as
.
The Taylor series for the natural logarithm is (using the big O notation)
and for the cosine function
.
The latter series expansion has a zero constant term, which enables us to substitute the second series into the first one and to easily omit terms of higher order than the 7th degree by using the big O notation:
Since the cosine is an even function, the coefficients for all the odd powers x, x3, x5, x7, … have to be zero.
Second example[edit]
Suppose we want the Taylor series at 0 of the function
We have for the exponential function
and, as in the first example,
Assume the power series is
Then multiplication with the denominator and substitution of the series of the cosine yields
Collecting the terms up to fourth order yields
The values of 

Third example[edit]
Here we employ a method called “indirect expansion” to expand the given function. This method uses the known Taylor expansion of the exponential function. In order to expand (1 + x)ex as a Taylor series in x, we use the known Taylor series of function ex:
Thus,
Taylor series as definitions[edit]
Classically, algebraic functions are defined by an algebraic equation, and transcendental functions (including those discussed above) are defined by some property that holds for them, such as a differential equation. For example, the exponential function is the function which is equal to its own derivative everywhere, and assumes the value 1 at the origin. However, one may equally well define an analytic function by its Taylor series.
Taylor series are used to define functions and “operators” in diverse areas of mathematics. In particular, this is true in areas where the classical definitions of functions break down. For example, using Taylor series, one may extend analytic functions to sets of matrices and operators, such as the matrix exponential or matrix logarithm.
In other areas, such as formal analysis, it is more convenient to work directly with the power series themselves. Thus one may define a solution of a differential equation as a power series which, one hopes to prove, is the Taylor series of the desired solution.
Taylor series in several variables[edit]
The Taylor series may also be generalized to functions of more than one variable with[14][15]
For example, for a function 
where the subscripts denote the respective partial derivatives.
Second-order Taylor series in several variables[edit]
A second-order Taylor series expansion of a scalar-valued function of more than one variable can be written compactly as
where D f (a) is the gradient of f evaluated at x = a and D2 f (a) is the Hessian matrix. Applying the multi-index notation the Taylor series for several variables becomes
which is to be understood as a still more abbreviated multi-index version of the first equation of this paragraph, with a full analogy to the single variable case.
Example[edit]

Second-order Taylor series approximation (in orange) of a function f (x,y) = ex ln(1 + y) around the origin.
In order to compute a second-order Taylor series expansion around point (a, b) = (0, 0) of the function
one first computes all the necessary partial derivatives:
Evaluating these derivatives at the origin gives the Taylor coefficients
Substituting these values in to the general formula
produces
Since ln(1 + y) is analytic in |y| < 1, we have
Comparison with Fourier series[edit]
The trigonometric Fourier series enables one to express a periodic function (or a function defined on a closed interval [a,b]) as an infinite sum of trigonometric functions (sines and cosines). In this sense, the Fourier series is analogous to Taylor series, since the latter allows one to express a function as an infinite sum of powers. Nevertheless, the two series differ from each other in several relevant issues:
- The finite truncations of the Taylor series of f (x) about the point x = a are all exactly equal to f at a. In contrast, the Fourier series is computed by integrating over an entire interval, so there is generally no such point where all the finite truncations of the series are exact.
- The computation of Taylor series requires the knowledge of the function on an arbitrary small neighbourhood of a point, whereas the computation of the Fourier series requires knowing the function on its whole domain interval. In a certain sense one could say that the Taylor series is “local” and the Fourier series is “global”.
- The Taylor series is defined for a function which has infinitely many derivatives at a single point, whereas the Fourier series is defined for any integrable function. In particular, the function could be nowhere differentiable. (For example, f (x) could be a Weierstrass function.)
- The convergence of both series has very different properties. Even if the Taylor series has positive convergence radius, the resulting series may not coincide with the function; but if the function is analytic then the series converges pointwise to the function, and uniformly on every compact subset of the convergence interval. Concerning the Fourier series, if the function is square-integrable then the series converges in quadratic mean, but additional requirements are needed to ensure the pointwise or uniform convergence (for instance, if the function is periodic and of class C1 then the convergence is uniform).
- Finally, in practice one wants to approximate the function with a finite number of terms, say with a Taylor polynomial or a partial sum of the trigonometric series, respectively. In the case of the Taylor series the error is very small in a neighbourhood of the point where it is computed, while it may be very large at a distant point. In the case of the Fourier series the error is distributed along the domain of the function.
See also[edit]
- Asymptotic expansion
- Generating function
- Laurent series
- Madhava series
- Newton’s divided difference interpolation
- Padé approximant
- Puiseux series
- Shift operator
Notes[edit]
- ^ Thomas & Finney 1996, §8.9
- ^ Lindberg, David (2007). The Beginnings of Western Science (2nd ed.). University of Chicago Press. p. 33. ISBN 978-0-226-48205-7.
- ^ Kline, M. (1990). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. pp. 35–37. ISBN 0-19-506135-7.
- ^ Boyer, C.; Merzbach, U. (1991). A History of Mathematics (Second revised ed.). John Wiley and Sons. pp. 202–203. ISBN 0-471-09763-2.
- ^ “Neither Newton nor Leibniz – The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala” (PDF). MAT 314. Canisius College. Archived (PDF) from the original on 2015-02-23. Retrieved 2006-07-09.
- ^ S. G. Dani (2012). “Ancient Indian Mathematics – A Conspectus”. Resonance. 17 (3): 236–246. doi:10.1007/s12045-012-0022-y. S2CID 120553186.
- ^ Turnbull, Herbert Westren, ed. (1939). James Gregory; Tercentenary Memorial Volume. G. Bell & Sons. pp. 168–174.Roy, Ranjan (1990). “The Discovery of the Series Formula for π by Leibniz, Gregory and Nilakantha” (PDF). Mathematics Magazine. 63 (5): 291–306. doi:10.1080/0025570X.1990.11977541.Malet, Antoni (1993). “James Gregorie on Tangents and the “Taylor” Rule for Series Expansions”. Archive for History of Exact Sciences. 46 (2): 97–137. doi:10.1007/BF00375656. JSTOR 41133959.
- ^ Taylor, Brook (1715). Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (in Latin). London. p. 21–23 (Prop. VII, Thm. 3, Cor. 2). Translated into English in Struik, D. J. (1969). A Source Book in Mathematics 1200–1800. Harvard University Press. pp. 329–332. ISBN 978-0-674-82355-6. Re-translated into English by Ian Bruce (2007) as Methodus Incrementorum Directa & Inversa, 17centurymaths.com.Feigenbaum, L. (1985). “Brook Taylor and the method of increments”. Archive for History of Exact Sciences. 34 (1–2): 1–140. doi:10.1007/bf00329903.
- ^ Rudin, Walter (1980), Real and Complex Analysis, New Delhi: McGraw-Hill, p. 418, Exercise 13, ISBN 0-07-099557-5
- ^ Feller, William (2003) [1971]. An introduction to probability theory and its applications. Vol. 2 (3rd ed.). Wiley. pp. 230–2. ISBN 9789971512989. OCLC 818811840.
- ^ Hille, Einar; Phillips, Ralph S. (1957), Functional analysis and semi-groups, AMS Colloquium Publications, vol. 31, American Mathematical Society, pp. 300–327.
- ^ Feller 2003, p. 231
- ^ Most of these can be found in (Abramowitz & Stegun 1970).
- ^ Hörmander, Lars (2002) [1990]. “1. Test Functions §1.1. A review of Differential Calculus”. The analysis of partial differential operators. Vol. 1 (2nd ed.). Springer. Eqq. 1.1.7 and 1.1.7′. doi:10.1007/978-3-642-61497-2_2. ISBN 978-3-642-61497-2.
- ^ Kolk, Johan A.C.; Duistermaat, J.J. (2010). “Taylor Expansion in Several Variables”. Distributions: Theory and applications. Birkhauser. pp. 59–63. doi:10.1007/978-0-8176-4675-2_6. ISBN 978-0-8176-4672-1.
References[edit]
- Abramowitz, Milton; Stegun, Irene A. (1970), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, Ninth printing
- Thomas, George B. Jr.; Finney, Ross L. (1996), Calculus and Analytic Geometry (9th ed.), Addison Wesley, ISBN 0-201-53174-7
- Greenberg, Michael (1998), Advanced Engineering Mathematics (2nd ed.), Prentice Hall, ISBN 0-13-321431-1
- Roy, Ranjan (2021) [1st ed. 2011]. Series and Products in the Development of Mathematics. Vol. 1 (2nd ed.). Cambridge University Press.
External links[edit]
- “Taylor series”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. “Taylor Series”. MathWorld.






![{displaystyle R_{n}(x)={(x-a)^{n+1} over (n+1)!}f^{(n+1)}[a+theta (x-a)]qquad p=n+1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9581ea19ed64de9723d6f3725f0470e9a0f23c)
![{displaystyle R_{n}(x)={(x-a)^{n+1}(1-theta )^{n} over n!}f^{(n+1)}[a+theta (x-a)]qquad p=1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/616cdc3cb043af06990a174a073b35ea0e3fbee1)

![{displaystyle R_{n}(x)=o[(x-a)^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7eca3be3644e41dedb8f25e26357ddb9a08386d)


![R_n(x,y)=dfrac {mathrm{T}^{(n+1)} f(xi,zeta)} {(n+1)!}, xi in [x_0,x], zeta in [y_0,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/144e134c30b8d4c579305c2bbaf6591647deb6c9)
























![{displaystyle f(x)={begin{cases}e^{-1/x^{2}}&{text{if }}xneq 0\[3mu]0&{text{if }}x=0end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae050e61cde6a0fdeda1f237f75846465579462d)










![{displaystyle {begin{aligned}sin x&=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-cdots &&{text{for all }}x\[6pt]cos x&=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}-cdots &&{text{for all }}x\[6pt]tan x&=sum _{n=1}^{infty }{frac {B_{2n}(-4)^{n}left(1-4^{n}right)}{(2n)!}}x^{2n-1}&&=x+{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}+cdots &&{text{for }}|x|<{frac {pi }{2}}\[6pt]sec x&=sum _{n=0}^{infty }{frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{frac {x^{2}}{2}}+{frac {5x^{4}}{24}}+cdots &&{text{for }}|x|<{frac {pi }{2}}\[6pt]arcsin x&=sum _{n=0}^{infty }{frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{frac {x^{3}}{6}}+{frac {3x^{5}}{40}}+cdots &&{text{for }}|x|leq 1\[6pt]arccos x&={frac {pi }{2}}-arcsin x\&={frac {pi }{2}}-sum _{n=0}^{infty }{frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={frac {pi }{2}}-x-{frac {x^{3}}{6}}-{frac {3x^{5}}{40}}-cdots &&{text{for }}|x|leq 1\[6pt]arctan x&=sum _{n=0}^{infty }{frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{frac {x^{3}}{3}}+{frac {x^{5}}{5}}-cdots &&{text{for }}|x|leq 1, xneq pm iend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/158a0ae14d1c9e0d1dc21c268f7e2169b9066dc7)
![{displaystyle {begin{aligned}sinh x&=sum _{n=0}^{infty }{frac {x^{2n+1}}{(2n+1)!}}&&=x+{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}+cdots &&{text{for all }}x\[6pt]cosh x&=sum _{n=0}^{infty }{frac {x^{2n}}{(2n)!}}&&=1+{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}+cdots &&{text{for all }}x\[6pt]tanh x&=sum _{n=1}^{infty }{frac {B_{2n}4^{n}left(4^{n}-1right)}{(2n)!}}x^{2n-1}&&=x-{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}-{frac {17x^{7}}{315}}+cdots &&{text{for }}|x|<{frac {pi }{2}}\[6pt]operatorname {arsinh} x&=sum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{frac {x^{3}}{6}}+{frac {3x^{5}}{40}}-cdots &&{text{for }}|x|leq 1\[6pt]operatorname {artanh} x&=sum _{n=0}^{infty }{frac {x^{2n+1}}{2n+1}}&&=x+{frac {x^{3}}{3}}+{frac {x^{5}}{5}}+cdots &&{text{for }}|x|leq 1, xneq pm 1end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cda808c97562eca785bd172eb7739711b338730a)






![{displaystyle {frac {2}{pi }}K(x)=sum _{n=0}^{infty }{frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}x^{2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc8e464983f3fdf2071ed149ed55bba842544a2d)
![{displaystyle {frac {2}{pi }}E(x)=sum _{n=0}^{infty }{frac {[(2n)!]^{2}}{(1-2n)16^{n}(n!)^{4}}}x^{2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85daf53e01f72f0f0c820811910a77974657052e)


![{displaystyle vartheta _{00}(x)^{-1/6}vartheta _{01}(x)^{-2/3}{biggl [}{frac {vartheta _{00}(x)^{4}-vartheta _{01}(x)^{4}}{16,x}}{biggr ]}^{-1/24}=sum _{n=0}^{infty }P(n)x^{n}=prod _{k=1}^{infty }{frac {1}{1-x^{k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c898219336ceb853f972d83f60a14049d671523)
![{displaystyle vartheta _{00}(x)^{1/6}vartheta _{01}(x)^{-1/3}{biggl [}{frac {vartheta _{00}(x)^{4}-vartheta _{01}(x)^{4}}{16,x}}{biggr ]}^{1/24}=sum _{n=0}^{infty }Q(n)x^{n}=prod _{k=1}^{infty }{frac {1}{1-x^{2k-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa5dd403c225903926ad0c45788a5f1a0a5fb67c)
















![{displaystyle {begin{aligned}f_{x}&=e^{x}ln(1+y)\[6pt]f_{y}&={frac {e^{x}}{1+y}}\[6pt]f_{xx}&=e^{x}ln(1+y)\[6pt]f_{yy}&=-{frac {e^{x}}{(1+y)^{2}}}\[6pt]f_{xy}&=f_{yx}={frac {e^{x}}{1+y}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80a9f65e179df2db5256dc15097892be2ded7c6d)




